引用本文
单泽彪, 石要武, 高兴泉. 基于Simulink实现的数模混合控制系统仿真新方法. 2014, 44(2): 548-553[SHAN Ze-biao, SHI Yao-wu, GAO Xing-quan. Simulation method of digital-analog hybrid control system based on Simulink. 吉林大学学报(工学版), 2014, 44(2): 548-553]  
Permissions
Copyright©2014, 吉林大学学报编辑部
版权所有.吉林大学学报编辑部
基于Simulink实现的数模混合控制系统仿真新方法
单泽彪1, 石要武1, 高兴泉2
1.吉林大学 通信工程学院,长春 130022
2.吉林化工学院 信息与控制工程学院,吉林省 吉林市 132022

单泽彪(1986),男,博士研究生.研究方向:阵列信号处理,先进控制与系统仿真.

基金:国家自然科学基金项目(51075175); 吉林省科技发展计划项目(20090148);
摘要

提出了一种采用Simulink实现数模混合控制系统的仿真方法。控制系统中实际的被控对象用连续Simulink模块构建的非线性连续系统来描述,同时采用Simulink模块与M函数相结合的形式,用信号上升沿触发子系统模拟闭环控制系统中的数字处理单元,即数字滤波与控制器部分,从而可真实地模拟周期性采集数据并处理数据的过程,最终实现数模混合控制系统的仿真。以连续搅拌反应釜基于卡尔曼滤波的状态反馈控制问题为实例,阐述了该仿真方法的具体实现过程。闭环仿真结果验证了该方法的有效性。

关键词: 自动控制技术; 数模混合控制; 卡尔曼滤波; 触发子系统; 仿真实现
中图分类号:TP273 文献标志码:A 文章编号:1671-5497(2014)2-548-6
Simulation method of digital-analog hybrid control system based on Simulink
SHAN Ze-biao1, SHI Yao-wu1, GAO Xing-quan2
1.CollegeofCommunicationEngineering,JilinUniversity ,Changchun 130022,China
2.CollegeofInformationandControlEngineering,JilinInstituteofChemicalTechnology,Jilin 132022,China
Fund:
Abstract

A simulation method based on Kalman filter for nonlinear continuous systems fulfilled by trigger subsystem block is proposed. In this method the form of Simulink blocks is combined with M-functions to simulate the process of periodic sampling and processing by micro-computers, accordingly the functions of D/A and A/D and the online filter processing are achieved perfectly. The implementation process of the proposed method is introduced. Simulation of the Continuous Stirred Tank Reactor (CSTR) system is carried out to demonstrate the implementation of the proposed method in detail. Results show the efficiency of the proposed method.

Keyword: automatic control technology; digital-analog hybrid control; Kalman filter; trigger subsystem; simulation implementation
0 引 言

带有数字信号处理环节的控制系统是一个能处理模拟和数字信号的混合系统,这样的系统进行模拟仿真对进行实际系统预设计来说是非常有意义的[ 1]。MATLAB/Simulink是目前应用最广的系统建模、分析与仿真等问题的理想工具[ 2]。对于混合系统仿真,一般常有两种实现思路,一种是完全由Simulink模块搭建的离散控制系统[ 3, 4],即先将连续被控对象数学模型离散化,用Simulink离散模块进行单纯的离散系统仿真,这样不可避免地会造成失真,越加偏离生产实际情况;第二种方法完全由程序编写连续系统仿真[ 5, 6],这样又不如由Simulink搭建模块仿真直观形象。虽然利用S函数亦可实现对连续系统的数字滤波,但是S函数的编写比较复杂,在滤波的工程实现、现场调试及通用型方面都存在着局限性。

本文提出一种基于Simulink实现的混合系统的仿真方法,即用触发子系统模块来模拟数字处理器,用周期性的方波来触发该系统,从而实现差分求解等数字信号处理的过程。本文以卡尔曼滤波为例,介绍了一种基于Simulink对连续系统实时数字滤波仿真实现的方法,即把Simulink模块与M函数通过触发子系统模块相结合。其中主程序由Simulink模块搭建,滤波器由M函数编写,通过触发子系统模块来模拟计算机离散采样、周期计算的过程,同时利用外部全局变量来存储历史数据,以达到实时计算并估计状态的目的;触发子系统模块具有的零阶保持器的特性[ 7],又使滤波输出转换为连续信号,可以直接予以示波观测或送至控制器进行控制。整个过程实现了D/A及A/D转换的功能,从而逼真地反映出实际生产中采集数据及处理数据的过程。对于众多基于实际控制模型如汽车、机器人及双容系统等生产过程被控对象的算法仿真问题[ 5, 8, 9],均可采用本文方法进行仿真验证。文中最后给出了该方法对连续搅拌反应釜(CSTR)进行卡尔曼滤波的仿真应用。

1 数模混合控制系统

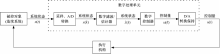
考虑一个连续系统的状态反馈控制问题。当利用状态反馈控制器确定执行机构动作时,需要用传感器测量状态变量以便实现反馈。但在很多情况下,只有部分状态可以直接测量得到,其他状态不易测得或测量的成本很高,这时就需要采用状态估计器(如卡尔曼滤波器)针对系统的某些状态量来估计出不易测量的状态,并利用所有得到的状态根据状态反馈控制律获取执行机构的控制动作大小,从而形成一个闭环的状态反馈控制。其中要求所有的数据滤波和处理过程在数字处理系统(例如单片机、计算机或DSP)中实现,那么该系统涉及的信号既包括实际被控对象输出的模拟信号,也包括数据的数字处理过程,因此它是一个典型的数模混合控制系统,其结构示意图如图1所示:

图1 典型数模混合控制系统方框图Fig.1 Digital-analog hybrid control system

该控制系统工作过程如下:将连续系统测量得到的模拟信号x(t)输入至采样器,每隔一定时间(采样周期)对x(t)进行采样,再经A/D转换器转换成数字量x(k),数字滤波器根据测量输出估计出系统的状态 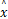(k),数字控制器根据状态反馈控制律利用估计出来的状态量求出控制量u(k)来决定执行机构动作的大小,后经D/A转换器及保持器转换为模拟量u(t),最后送至执行机构,并对实际的被控对象进行控制。下面以连续搅拌反应釜的状态反馈控制为例,介绍一种基于Simulink的数模混合控制系统仿真实现方法。

2 数模混合控制系统的实现
2.1 连续搅拌反应釜

考虑一个工业生产中广泛应用的连续搅拌反应釜(CSTR)的控制问题,其运动特性可以用以下非线性方程来描述[ 10]

:

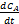(1)
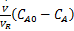
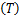
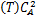
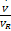
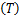
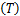
= -k1 C A-k3

=- C B+k1 C A-k2 C B(2)

(3)
= (T0-T)+ (T K-T)-

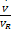
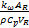
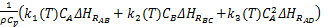
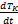(4)
=

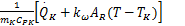
式中:C A和C B分别为组分A与组分B的浓度;T和T K分别为反应温度和冷却温度。ki(i=1,2,3)为反应速度;Δ 为k1的反应热;Δ 为k2的反应热;Δ 为k3的反应热;ρ为液体密度;Cp为质量定压热容;kω为冷却套的传热系数; AR为冷却套的面积; VR为反应器的体积; mK为冷却液质量; CPK为冷却液的热容。

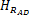
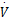
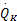
该系统的控制问题是通过实时调整系统的两个操作变量(物料进给率 /V R和冷却套中的散热量 )使组分B的浓度达到预定要求的值,这里反应器的进料温度T0和组分A的初始浓度C A0可以作为系统的外部干扰。该系统是个连续的系统,所以可以用连续Simulink模块根据运动方程进行搭建。

现在考虑构建一个状态反馈控制系统。该状态反馈需要知道系统的4个状态,即进料浓度、进料温度、物料进给率和冷却套散热率,从现在的工艺条件或经济方面考虑,在此采用卡尔曼滤波的方法通过实时测量反应温度和冷却温度来在线估计浓度值并经控制器后得到状态值。

2.2 卡尔曼滤波器在Simulink中的仿真实现

卡尔曼滤波方法是在Wiener平稳随机过程的滤波理论基础上建立的一种递推式滤波方法[ 11],可借助于前一时刻的滤波结果,递推出下一时刻的状态估计量,因而大大提高了下一时刻的滤波精度。卡尔曼滤波的数据处理过程实际上是离散的状态空间方程叠代求解的过程,需要借助混合控制系统中的数字处理单元来实现。在本文提出的仿真中,卡尔曼滤波器的运算过程以及数字控制器的处理过程通过周期性地调用M函数文件完成,而触发调用动作的模块由Simulink中带有脉冲信号发生器的触发子系统模块来实现。在编写M函数文件时利用外部全局变量来实现对历史数据的存储,并且运用evalin和assignin两个函数对历史数据进行读取与存储。

具体实现过程如下:

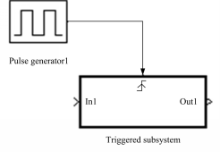
(1)选用端口与子系统(Ports & subsystems)模块库中的触发子系统(Triggered subsystem)模块模拟数字处理单元,如图2所示:

图2 添加脉冲信号发生器模块的触发子系统Fig.2 Triggered subsystem with pulse signal generator

它是一个执行外部输入触发的子系统模块,其中的触发端口决定着该模块是否执行。

(2)触发端口的触发信号选用信号源(Sources)模块库中的脉冲信号发生器(Pulse generator)模块输出的信号。在该外接输入下,可模拟采样量化的特性,实现A/D转换的功能,其中矩形脉冲的周期近似为数字处理单元的采样周期,其大小往往根据具体的问题进行经验性设定[ 12]。

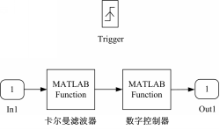
(3)在触发子系统输入输出端之间添加用户自定义函数(User-defined functions)模块库中的MATLAB函数(MATLAB Fun)模块,如图3所示:

图3 触发子系统模块的内部结构Fig.3 Internal structure of triggered subsystem

在MATLAB函数模块中可以填写欲调用的函数名称或M函数文件名称,本文中该处由两个串联的函数组成,一个是卡尔曼滤波M函数,另一个是数字控制器M函数。

卡尔曼滤波过程即是周期性采集系统输入信号、并进行叠代求解的过程。因此在MATLAB实现时需要先进行某些变量的初始化。这里,编制M文件初始化状态估计的初值 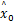,协方差矩阵 P0。假设连续系统离散化后得到如下模型:

x k+1= Ax k+ Gw k, y k= Hx k+ v k式中: x k∈R n为状态向量; y k∈R m为量测向量; v k∈R m为量测噪声; w k∈R p为系统噪声向量。

假设系统噪声和量测噪声是互不相关的零均值高斯白噪声,方差矩阵分别为 Q和 R。初始化后,数字控制器利用卡尔曼滤波器的状态估计值计算出控制量 u k,并将其保持至下一采样周期,送给执行机构。

2 .3 卡尔曼滤波器和状态反馈控制器求解

连续搅拌反应釜( CSTR)系统是个典型的强非线性系统[ 13]。根据文献[10],获得组分 A最大产出率的系统稳定工作点为

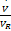
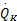
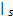
[ CA, CB, T, TK, , , CA0, T0] =

[2 .14 mol/L,1 .09 mol/L,114 .2 ℃,112 .9 ℃,

14 .19 h -1, -1113 .5 kJ/h,5 .1 mol/L,104 .9 ℃]

设计状态反馈控制器首先需将 CSTR非线性系统进行线性化处理。将非线性系统(1)在工作点线性化,并重新定义无量纲状态

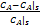
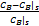
x1 = , x2 = ,

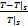
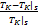
x3 = , x4 =

无量纲控制输入

u1 = , u2 = ,

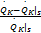
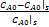
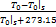
w1 = , w2 =

可得系统在工作点的线性化模型:

( t) = A x( t) + B1u(t)+ B2w(t)

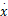
用LQR方法或极点配置法可以求出反馈控制器增益 K,则执行机构控制动作可由控制规律 u( t) = K x( t)求得。

为了采用离散卡尔曼滤波方法,需要得到其离散线性状态空间方程。将非线性系统(1)在稳态工作点线性化并取采样时间为15 s,得到如下离散模型: x( k+1) = A x( k) + B u( k) + G w( k)

y( k) = C x( k) +v( k)式中:

A =

,

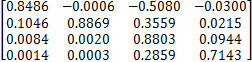
B = ,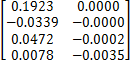

G = , C =

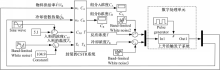
最后,用 MATLAB模块搭建 CSTR带有卡尔曼滤波器的状态反馈控制系统,如图4所示:

图4 带有卡尔曼滤波器的CSTR仿真模块Fig.4 CSTR Simulink module with Kalman filter

其中, CSTR系统由 Simulink模块搭建,卡尔曼滤波器(数字处理单元)由带有有脉冲信号发生器的触发子系统模块来模拟实现。

2.4 仿真结果

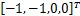
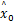
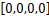
假设实际CSTR系统的初始状态为 x0= ,随着卡尔曼滤波器的工作,该值会逐渐收敛。其他时刻的值可以通过求解非线性微分方程(1)获得。取预先估计的初始状态 = ,控制量为稳态工作点,而实际进料温度和进料浓度是在一定范围内随机变化的[ 14],视为干扰。取如下卡尔曼滤波器参数:

Q = , R = ,

P0= 仿真结果如图5、图6及图7所示:

图5 组分B浓度估计值与实际值的比较Fig.5 Comparison of B concentration

图6 控制量物料进给率Fig.6 Feed rate of material

图7 控制量冷却套散热率Fig.7 Radiation rate of cooling jacket

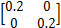
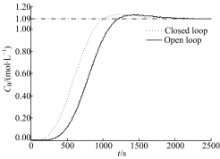
将图5中状态反馈前后的响应曲线对比可知,经过状态反馈后系统响应的调节时间变短,响应速度加快,能迅速达到稳定状态,且无明显的超调,达到了预期的控制效果。

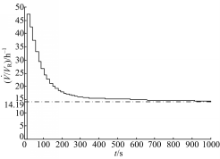
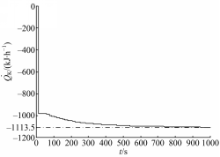
从图6、图7中观测控制量(物料进给率、冷却套散热率)可以看出,曲线呈明显的阶梯状,得知其在完成数字处理后又转化为模拟信号,即实现 D/A转换的功能,从而真实地模拟了周期性采集数据并处理数据的过程,最终实现了数模混合控制系统的仿真。

3 结束语

介绍了一种在Simulink中实现数字滤波控制的方法,就是利用带有信号发生器的触发子系统模块对连续信号进行分析、综合、滤波和估计等模拟数字处理的过程。以连续搅拌反应釜基于卡尔曼滤波的状态反馈控制问题为实例,在对Simulink中触发子系统模块的应用中,可以很好地周期调用由程序编写的卡尔曼滤波器和控制器对用模块搭建的连续系统实施在线滤波估计与控制,实现了数字处理。对这样构成的系统可以运用于一切数字滤波器对连续系统的滤波中,还可以扩展到数字控制器对连续系统的控制中,通用性较强。对CSTR系统进行仿真实现的操作过程及结果表明了该方法是简便、有效和可行的。

The authors have declared that no competing interests exist.

参考文献
[1] Chai T Y, Yue H, Zhai L F. Intelligent decoupling control system of complex industrial process and application[C]∥Preprints of the 16th IFAC World Congress, Prague, Czech, 2005. [本文引用:1]
[2] Podhaisky H, Weiner R, Schmitt B A. Two-step W-methods for stiff ODE systems[J]. Vietnam J Math (S0866-7179), 2002, 30: 591-603. [本文引用:1]
[3] 向博, 高丙团, 张晓华, 等. 非连续系统的Simulink仿真方法研究[J]. 系统仿真学报, 2006, 18(7): 1750-1754.
Xiang Bo, Gao Bing-tuan, Zhang Xiao-hua, et al. Simulink simulation research of uncontinuous system[J]. Journal of System Simulation, 2006, 18(7): 1750-1754. [本文引用:1] [CJCR: 0.914]
[4] 宋永东, 张春明. 基于MATLAB的数字滤波器设计及仿真应用[J]. 延边大学学报: 自然科学版, 2007, 26(2): 34-36.
Song Yong-dong, Zhang Chun-ming. Digital signal filter and simulation application[J]. Journal of Yanan University(Natural Science Edition), 2007, 26(2): 34-36. [本文引用:1] [CJCR: 0.2632]
[5] 孟亚男, 高兴泉, 高玉坤, 等. 反馈线性化方法在双容系统中的仿真应用[J]. 计算机仿真, 2010, 27(4): 367-370.
Meng Ya-nan, Gao Xing-quan, Gao Yu-kun, et al. Simulation applications of input-output feedback linearization to two-tank system control[J]. Computer Simulation, 2010, 27(4): 367-370. [本文引用:2] [CJCR: 0.5628]
[6] 王春民, 栾卉, 杨红应. 倒立摆控制的设计与仿真[J]. 吉林大学学报: 信息科学版, 2009, 27(3): 242-247.
Wang Chun-min, Luan Hui, Yang Hong-ying. Design and simulation of inverted pendulum control[J]. Journal of Jilin University (Information Science Edition), 2009, 27(3): 242-247. [本文引用:1] [CJCR: 0.6484]
[7] 李国勇, 谢克明, 杨丽娟. 计算机仿真技术与CAD——基于MATLAB的控制系统[M]. 北京: 电子工业出版社, 2008. [本文引用:1]
[8] 葛连正, 赵立军, 李瑞峰, 等. 移动机器人非线性前置追踪算法[J]. 吉林大学学报: 工学版, 2010, 40(3): 806-810.
Ge Lian-zheng, Zhao Li-jun, Li Rui-feng, et al. Nonlinear head pursuit tracking algorithm for mobile robots[J]. Journal of Jilin University (Engineering and Technology Edition), 2010, 40(3): 806-810. [本文引用:1] [CJCR: 0.701]
[9] 常胜, 徐洪国, 刘洪飞. 回路成形半挂汽车列车鲁棒控制器设计[J]. 吉林大学学报: 工学版, 2011, 41(6): 1571-1576.
Chang Sheng, Xu Hong-guo, Liu Hong-fei. Loop shaping robust controller design for tractor-semitrailer[J]. Journal of Jilin University (Engineering and Technology Edition), 2011, 41(6): 1571-1576. [本文引用:1] [CJCR: 0.701]
[10] Chen H, Kremling K, Allgower F. Nonlinear predictive control of a benchmark CSTR[C]∥Proceedings of 3rd European Control Conference, Rome, 1995. [本文引用:1]
[11] Welch G, Bishop G. An Introduction to the Kalman Filter[M]. Chapel Hill: University of North Carolina Press, 2006. [本文引用:1]
[12] 周欣然, 陈德池, 刘建成. 采样周期对计算机控制系统的影响及其经验选择[J]. 长沙铁道学院学报, 2002, 20(3): 100-104.
Zhou Xin-ran, Chen De-chi, Liu Jian-cheng. Sample period's affection to the computer control system and its empirical choice[J]. Journal of Changsha Railway University, 2002, 20(3): 100-104. [本文引用:1] [CJCR: 0.3447]
[13] Guo P. Nonlinear predictive functional control based on Hopfield network and its application in CSTR[C]∥International Conference on Machine Learning and Cybernetic, Kunming, China, 2006. [本文引用:1]
[14] 陈虹, 邹卫平, 孙鹏远. 连续搅拌反应釜浓度的滚动时域估计[J]. 系统仿真学报, 2001, 13(增刊): 37-40.
Chen Hong, Zou Wei-ping, Sun Peng-yuan. Moving horizon estimation of concentrations in a continuous stirred tank reactor[J]. Journal of System Simulation, 2001, 13(Sup. ): 37-40. [本文引用:1] [CJCR: 0.914]