黄艳国(1973),男,副教授,博士研究生.研究方向:智能交通运输系统.E-mail:jxhuangyg@126.com
首先定义了新息的概念,通过在线监测新息的变化,将新息的均值和方差作为模糊控制器的输入,利用模糊逻辑对系统状态噪声和测量噪声的权重进行实时调整,建立了基于模糊逻辑的自适应卡尔曼滤波方法。克服了传统滤波器不能对环境变化进行实时跟踪的缺点,适应了交通状态的动态变化。通过用两种方法对广州市快速路段实测数据进行的对比分析发现,该方法与标准卡尔曼滤波相比具有良好的跟踪能力,在自由流状态和稳定流状态下,预测值与实测变化趋势一致,误差较小,拥挤状态相对误差基本维持在10%以下。
First, the new information was defined and its change was online monitored. The mean and variance of new information were input into the fuzzy controller. Then, the fuzzy logic was used to adjust the importance weights of system noise and observation noise. The new method overcomes the shortcomings of traditional filter, which can not real-time track the change of environment. It adapts to the dynamic change of traffic state to realize the optimization estimation. The method was tested on urban expressway in Guangzhou using real-time detection data. The results show that the proposed method has better tracking ability than traditional Kalman filter. There was a slight difference between the prediction result and that of actual observation in free traffic flow state and stable flow, and the relative error was under 10% in congested traffic state.
行程时间是体现道路交通状态的综合性指标,直接反映了道路的整体通畅程度和运输效率。对路径行程时间进行实时动态估计,可以为出行者提供行程时间信息,出行者可进行出行模式、出行时间、出行路径的选择,从而避开拥挤路段,提高出行效率。在行程时间估计与预测方法方面,一些学者分别对高速公路和城市道路进行了相关研究[ 1, 2, 3]。一种方法是根据交通流理论建立精确的数学模型,通过交通仿真对模型进行分析和验证[ 4, 5]。另外一种方法是基于传统的数学和物理模型的数理统计分析方法[ 6, 7, 8],或是采用现代的人工智能优化算法[ 9]。后者与前者的主要区别在于是否能建立系统的实际模型,其方法主要有时间序列法、参数回归法、指数平滑法等。基于机器学习方法的预测模型精度高,文献[ 10, 11]采用支持向量机对行程时间进行预测,此外还有神经网络模型等。这些方法具有较好的学习能力,但需要大量的历史数据,且存在过学习或欠学习以及局部极小值等问题。卡尔曼滤波具有模型参数少且能在线估计的特点,被应用到交通系统预测中,并取得了一定的效果[ 12, 13]。但应用标准卡尔曼滤波时必须已知系统噪声和量测噪声的统计特性,并且噪声必须为零均值白噪声[ 14]。实际应用中由于交通系统的随机性和检测器的误差,噪声随着时间发生变化。若这些先验信息不足或不准确,则会造成估计精度降低,导致滤波器发散。
针对常规卡尔曼滤波器自适应能力差的缺陷,本文在分析噪声对卡尔曼滤波器稳定性影响的基础上提出了一种基于模糊逻辑的自适应卡尔曼滤波算法,利用模糊逻辑自适应控制器来在线调整卡尔曼滤波器参数,防止滤波器发散,提高了滤波器的性能。
城市快速路是满足长距离、快速、安全行驶的需求,控制入口和出口,连续通行的汽车专用道路。与普通的城市主干道相比,快速路与城市各级道路采用立体交叉,并且无信号灯控制,车速较高,通常可达到60~100 km/h,具有车流连续、流量大的特点。与高速公路相对封闭的车流特性相比,相邻进出口匝道间的距离小于高速公路相邻进出口的距离,导致快速路与相交道路之间的交通流转换比较频繁,交织区间距较近,使得快速路进出口交通流比较复杂。因此,在对快速路行程时间进行预测时,不仅要考虑该路段上下游当前的交通流量、交通流密度,还必须考虑入口和出口匝道等因素的影响。
城市快速路包括大量的入口、出口及路段,一条路径的快速路行程时间由大量的基本路段的行程时间组成,而不同路段由于与不同等级的道路交叉,使得出入口的交通流对快速路的影响不同。为此,本文将一条快速路划分为不同的基本路段,并重点分析一条基本路段的行程时间。
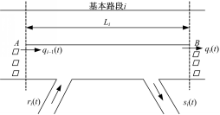
定义1(基本路段) 一条典型的快速路的基本路段包含一个入口和一个出口,路段长度大于1.2 km,如图1所示。
在每条道路、入口及出口都安装了地感线圈,用于检测流量和地点车速。在时段(t-1,t)内通过该路段的交通流量可以按照式(1)计算:
q(t)=α[qi-1 (t)+ri (t)] +(1-α)[qi(t)+si(t)] (1)
式中:qi-1(t)、qi(t)分别为上游路段和下游路段在(t-1,t)时段的交通流量;ri(t)、si(t)分别为入口匝道和出口匝道在时段(t-1,t)内的流量;α为平滑系数,本文中α取0.5。
假定该路段内的交通流量是均匀分布的,qi(t)、ui(t)分别是路段i上的交通流量和区间平均速度,可以得到路段行程时间估计为:
Ti(t)= 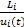
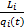
式中:Li为路段i的长度;ki(t)为路段i的密度。
路段行程时间与路段的交通密度k(t)密切相关,根据交通流守恒定律,密度可以表示成如下时间序列:
ki(t)=ki(t-1)+ 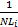
式中:N为主线的车道数。
在实际应用中,快速路的上游(A点)和下游(B点)的地感线圈比较容易采集交通量和地点速度等交通参数,但路段i的区间平均速度ui(t)无法测量。从式(3)中可以看出:当前路段的密度与上一时刻的路段密度、当前路段的交通量相关。若知道上一时刻的交通状态,则可对当前的交通状态进行估计,从而通过式(2)估算出路段的行程时间。
交通系统是复杂的随机系统,当前的交通状态不仅与当前的交通需求有关,而且与上一时刻的状态有关,通过以上对快速路基本路段的交通特性分析,可以采用卡尔曼滤波对路段i下一时段的交通状态和行程时间进行在线实时估计。
图1中,A点的时间平均速度 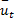
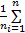
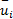
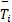
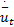
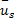
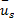 = = 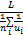 | (4) |
时间平均速度 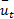
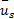
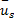 = = 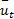 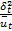 | (5) |
式中: 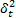
因为区间平均速度 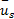
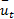

k(t)= Φ( t) k( t-1)+ u( t)+ w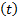 | (6) |
T( t)= H( t) k( t)+ v( t) (7)
式中: Φ( t)为系统的状态转移矩阵; H( t)为量测矩阵; u( t)为输入控制量: u( t)={ q i-1( t)+ r i( k)-[ q i( t)+ s i( t)]}/( NL i); w( t)、 v( t)分别是系统的状态噪声和测量噪声。
因为不同环境和不同时段交通需求存在较大的随机性,同时线圈检测也存在测量误差,因此存在系统状态噪声和测量噪声。假设系统状态噪声和测量噪声是相互独立的高斯白噪声,卡尔曼滤波算法的递推计算公式为:
k( t|t-1)= Φ( t|t-1) k( t-1 |t-1) (8)
P( t|t-1)= Φ( t|t-1) P( t-1 |t-1) ΦT( t|t-1) + Q(9)
式中: Q为系统噪声协方差。
滤波系数为:
K( t) =P( t|t-1) HT( t)[H(t)P(t|t-1)HT(t)+R]-1 (10)
式中: R为测量噪声协方差。
状态更新方程为:
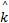
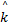
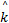
P( t|t)=[1 -K( t) H( t)] P( t|t-1) (12)
行程时间预测值为: 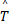
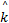
传统的卡尔曼滤波器获得理想滤波效果的条件是事先知道系统状态噪声和测量噪声的统计特性,并假设系统状态噪声和测量噪声是零均值白噪声序列[ 15]。实际应用中,由于交通系统随机性较大,检测器存在误差,使得系统状态噪声和测量噪声随着时间发生变化,先验的噪声特性很难准确得到,不完全符合高斯白噪声的统计特性,从而影响预测的精度。测量噪声协方差 R代表了测量数据的可信度,随着系统状态的不断变化,预先给定的 R值可信度将降低,应根据实际情况而变化。为此,必须考虑噪声对滤波器稳定性能的影响,需要实时调节卡尔曼滤波器的噪声强度,从而达到自适应的目的。在此引入新息(残差)的概念。
t时刻的新息(残差)定义为 t时刻的实际测量值 T( t)和测量方程的估计值 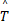
r( t) =T( t) - H( t) k( t|t-1) (13)
新息方差的理论值为:
S( t)= H( t) P( t|t-1) HT( t) + R= H( t)[ Φ( t|t-1) P( t-1 |t-1) Φ( t|t-1) + Q] HT( t) + R(14)
新息包含了新的测量序列 T( t)所提供的信息,是滤波器进行自适应调整最相关的信息源。通过监测新息(残差)均值和方差的变化,对系统状态噪声和测量噪声进行实时调节,从而抑制时变噪声对滤波稳定性造成的影响[ 16]。
选择时间窗为 M的新息序列进行统计平滑,每一时刻新息的均值和实测方差的估值可表示为:
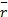
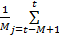
 ( t)= ( t)= 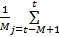 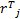 | (16) |
理想状态下新息是均值为0、方差为 S( t)的高斯白噪声序列。利用新息序列的这一特性,通过对新息的均值和方差进行实时监测,可以判别滤波器是否工作在最优状态下。在系统运行过程中,如果新息不是零均值白噪声,则说明滤波器不是处于最优估计的状态。新息是 t时刻滤波器对观测量的预测值 T( t|t-1)与检测器获得的真实观测值 T( k)间的差异,反应了系统相对先验噪声统计模型的变化,是对滤波器进行在线调节和修正的直接信息源。将噪声模型改写为:
Q( t) =a( t) Q(17)
R( t) =b( t) R(18)
式中: a( t)和 b( t)为在线调整权值。
则式(9)可改写为:
P( t|t-1)= Φ( t) P( t-1 |t-1) ΦT( t) +a( t) Q(19)
滤波器的增益为:
K( t) =P( t|t-1) HT( t)·[ H( t) P( t|t-1) HT( t) +b( t) R] -1(20)
相应地,新息的方差为:
S( t)= H( t)[ Φ( t) P( t|t-1) ΦT( t) +a( t) Q] × HT( t) +b( t) R(21)
通过对新息的均值和方差的变化在线监测滤波器的稳定性,当交通环境和状态发生较大变化时,通过调整 a( t)和 b( t)取值改变系统状态噪声和测量噪声的权重,不断调整滤波器增益,对观测信息的可信程度和利用程度做出调整,进而改善滤波性能,提高预测精度。
通过实时检测新息均值和方差,采用模糊控制的方法对参数 a( t)和 b( t)进行自适应调整,其调整策略就是将残差的实际均值和方差与其理论均值和方差相比较,利用模糊逻辑从两者一致程度的大小来实时修正权值系数,以克服系统状态噪声和测量噪声统计特性不确定的影响,实现预测算法性能的在线改进。设新息关于均值和方差的置信度为:
m1( t)= 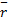
m2( t)=tr 
式中:tr为求迹运算。
在理想状况下, m1( t)为0, m2( t)为1,此时滤波器状态比较稳定,处于最优估计状态。当实际观测噪声增大时,新息的方差 
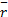
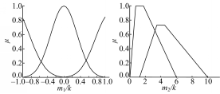
将新息的均值和方差的置信度进行模糊化,并作为模糊输入变量,将权值系数a(t)和b(t)作为模糊输出变量。当m1(t)在0附近,m2(t)在1附近时,滤波器稳定性高;当m1(t)偏离0,m2(t)偏离1时,滤波器稳定性降低。m1(t)和m2(t)的隶属度函数如图2所示。在卡尔曼滤波算法中,利用模糊控制器对参数a(k)和b(t)进行实时调整,利用模糊控制规则确定输出变量a(t)和b(t)的模糊值,采用重心法进行解模糊并获得实际数值。
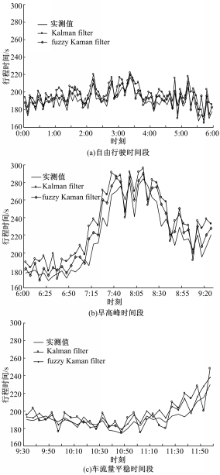
以广州市的广园快速路为实例对快速路行程时间估计方法进行有效性验证。广园快速路是广州市的一条高标准的城市快速路,全长47 km,双向六车道,路口采用全立交的形式。设计车速为地面60 km/h,高架桥80 km/h,每两个收费站之间的直线距离为2~3.5 km不等,在出入口位置都设有检测器,检测交通流量、占有率、车速等交通参数。本文选取了该快速路其中一段作为研究对象,长约2.92 km,包括一个入口匝道和一个出口匝道。匝道和路段各车道安装有环形检测线圈,用来获得流量和速度等交通数据,以5 min为一个间隔,将一天24 h分成288份。为了便于分析行程时间与流量、密度的关系,取3个典型的时段:0∶00~6∶00、6∶00~9∶30以及9∶30~11∶30,分别对应流量较少的自由流状态、早高峰拥挤状态和流量较平稳的稳定状态。本文取2011年9月13日从收费管理站获得的00∶00~12∶00的数据进行预测及结果分析。将原始数据经过预处理后,通过Matlab平台进行编程,仿真实现自适应滤波算法。分别采用标准卡尔曼滤波方法和基于模糊逻辑的卡尔曼滤波方法进行对比分析,预测结果如图3所示。
在时段0∶00~6∶00内,路段车辆数量较少,处于自由行使状态,因此行车速度较高,该路段的行程时间短。由于交通量的波动较少,系统状态噪声和测量噪声的变化不大,从图3(a)中可以看出:传统卡尔曼滤波和自适应滤波对行程时间的预测值与实际观测值基本一致,结果表明采用卡尔曼滤波对行程时间进行预估是可行的。随着时间的推移,交通量不断增加并逐渐进入早高峰期。从图3(b)可以看出:行程时间不断增加,原因是各入口匝道的交通需求增加,同时间距较近的入口和出口对车流产生较大的影响。随着车流的增大,路段出现拥堵现象,车辆之间的相互影响增大,速度下降。两种预测方法预测值与实际值具有相同的变化趋势,但相比标准Kalman滤波方法,本文所提出的预测方法其预测值与实际值更为接近。因入口和出口的交通流波动性较大,系统状态噪声和测量噪声增大,而模糊卡尔曼滤波可根据新息的变化自适应调整噪声强度对滤波器的影响,因此预测值与实际值更为接近。从图3(b)可以看出:交通状态变化较大时,预测值与真实值存在一定的滞后,原因在于入口和出口处交织段对车流的影响,出现了有部分车辆拥挤的现象。在9∶00~11∶30时段内,车辆逐渐减少,交通处于稳定运行状态,从图3(c)可以看出:行程时间逐渐减少,处于一个稳定值,这与实际情况相一致。但相对自由流情况,由于路段上车流较大,受干扰而波动的状况较明显,基于模糊控制的预测方法具有对滤波参数进行调节的功能,故其变化趋势和预测值更接近实际测量值。
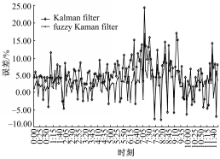
为了对不同时间段行程时间预测结果进一步对比分析其精度和可靠性,对各路段行程时间相对误差进行比较,如图4所示。从图4中可以看出:相比标准的Kalman滤波方法,模糊Kalman滤波方法获得的预测结果的误差指标均较小,具有较好的稳定性,其波动性明显小于传统的Kalman滤波方法。在自由流状态和稳定状态的误差比拥挤状态下小,原因在于随着交通流的增加,交通流的随机性和不确定性增加,系统状态噪声和测量噪声也会增加。当交通干扰较大时,例如交通事故发生的情况下,基于标准的Kalman滤波对行程时间的预测都具有很大的波动性,而基于模糊的自适应卡尔曼滤波的预测精度比前者提高的主要原因:是自适应卡尔曼滤波算法能根据交通的随机性和不确定性动态调整系统的状态噪声和测量噪声。在交通状态突变的情况下,预测结果会产生一定的滞后效应和较大的误差,但并不影响模型整体上的可靠性。除去有限的几个差异较大的周期相对误差接近15%之外,其他周期的相对误差在10%以下,其预测结果满足实际需求。
从城市快速路的交通特性入手,分析了路段行程时间的估计方法。用交通密度作为状态变量,行程时间作为观测量,采用卡尔曼滤波对行程时间进行预测。交通系统的复杂性和随机性使得系统状态噪声和测量噪声先验信息不确定,影响到卡尔曼滤波的精度和稳定性。对此,采用基于模糊逻辑的自适应卡尔曼滤波的方法,根据监测新息的均值和方差的变化对系统状态噪声和测量噪声进行实时调整,从而在线修正滤波器的增益,克服了传统卡尔曼滤波自适应差的缺陷。实例分析结果表明:该方法比传统卡尔曼滤波方法的精度高,在自由流状态和交通流稳定状态下有较好的预测精度。在交通拥挤状态和交通量突变的情况下,预测值存在一定的滞后和误差波动,但不影响整体的可靠性,说明该方法能较好地跟踪系统的状态变化,有较好的适应性,可以对道路行程时间进行实时动态预测。
| [1] |
|
| [2] |
|
| [3] |
|
| [4] |
|
| [5] |
|
| [6] |
|
| [7] |
|
| [8] |
|
| [9] |
|
| [10] |
|
| [11] |
|
| [12] |
|
| [13] |
|
| [14] |
|
| [15] |
|
| [16] |
|