石屹然(1984),男,博士研究生.研究方向:控制理论与控制工程.E-mail:35105767@qq.com
针对火花塞点火(SI)发动机空燃比(AFR)控制系统提出了一种变采样间隔的Modified Volterra模型,并以此为基础,提出了一种基于RBFNN和Modified Volterra模型的SI发动机AFR的联合NMPC 控制方法。该方法既具有RBFNN模型计算量小、预测精度高的特点,又具有可直接计算NMPC最优控制序列的优势,明显地提高了SI发动机AFR的控制精度,大大地减少了常规迭代寻优算法的计算时间。在dSPACE实时仿真试验平台上对平均值发动机模型进行仿真试验,结果表明:本文所提出的NMPC控制方法对SI发动机AFR的控制效果明显优于单独基于Modified Volterra和RBFNN模型的NMPC控制方法。
A variable sampling period Modified Volterra model is proposed for the Air-Fuel Ratio (AFR) control system in Spark Ignition (SI) engine. On this basis, a joint Nonlinear Model Predictive Control (NMPC) method is developed based on the Radial Basis Function Neural Network (RBFNN) model combining with the modified Volterra model. The advantages of this method are small amount of calculation and high prediction accuracy; also the optimal control sequence can be directly calculated. Thus it significantly improves the AFR control performance of SI engine, and greatly reduces the computing time compared with the conventional iterative optimization algorithm. Real-time simulations based on the mean value engine model are conducted on the dSPASCE simulation platform. Results show that the control performance of the proposed method is significantly better than the RBFNN model or the Modified Volterra model based NMPC method.
汽车发动机空燃比(Air fuel ratio,AFR)的控制精度已经成为目前的研究热点[ 1, 2]。该问题的关键问题是如何解决火花塞点火(Spark ignition,SI)发动机高度非线性的问题。Map图加PI反馈补偿的发动机AFR控制方法由于具有结构简单、鲁棒性强、稳态无差等一系列优点,在SI发动机的AFR控制上得到了广泛应用,但该方法存在发动机动态特性变化的问题[ 1, 2, 3]。近年来,非线性模型预测控制(Nonlinear model predict control,NMPC)理论在发动机AFR控制领域的应用受到了广泛的关注[ 4, 5, 6, 7]。其中,Manzie等提出了一种基于自适应RBF神经网络(Radial basis function neural network,RBFNN)模型的发动机AFR的NMPC方法。在该方法中,自适应RBFNN模型被用来对发动机AFR系统输出进行预测,并利用一种带有效集的线性预测控制方法实现了发动机AFR控制[ 2]。在此基础上,Wang等基于RBFNN模型利用Reduced Hessian方法对控制序列进行寻优,并取得了较好的发动机AFR控制效果[ 6]。随后,Wang等利用MLP神经网络对发动机AFR系统进行了辨识,并提出了一种基于MLP模型的发动机AFR控制的NMPC方法[ 7]。然而,由于RBFNN模型一般采用迭代搜索的方法进行控制寻优。反复的迭代计算使得该方法的计算量较大。如果在最优值附近过早地终止迭代搜索,可以减少计算量,但又导致精度下降[ 8]。
基于Volterra模型的NMPC控制方法可以根据Volterra模型的结构,利用最小二乘的方法直接计算NMPC的最优控制序列,从而避免了采用迭代搜索算法所带来的计算量较大的问题[ 8]。根据这一理论,Maner等提出了一种基于二阶Volterra模型的NMPC方法,并将该方法应用于聚合反应釜控制中,取得了良好的控制效果[ 9]。Gruber等针对温室控制问题,对传统Volterra模型进行了改进,并提出了相应的NMPC控制算法[ 10]。Boland等将Volterra模型应用于发动机爆震检测中,取得了较高的辨识精度[ 11]。然而,基于Volterra模型的NMPC方法在模型阶次和模型预测精度方面却存在着矛盾:即较高的模型阶次将使得Volterra模型陷入“维数灾难”,计算量陡增,而较低的模型阶次却由于Volterra模型高次项的缺失,导致模型预测精度下降。
针对上述问题,本文首先提出了一种变采样间隔的Modified Volterra模型以减少Volterra模型建模的计算量。其次,将RBFNN模型和Modified Volterra模型有机地结合在一起,兼取二者之长,利用RBF神经网络模型对系统的输出序列进行预测,然后基于Modified Volterra模型设计了一种具有全局最优解且闭环稳定的SI发动机AFR的NMPC控制算法。利用平均值发动机模型(Mean value engine model,MVEM)[ 12],在Dspace实时试验平台上,对本文方法进行了仿真试验。结果表明:本文所提方法对SI发动机AFR控制效果明显优于单独基于Modified Volterra模型或RBF神经网络模型的NMPC控制方法。
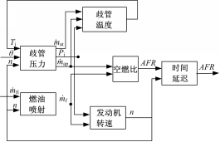
如图1所示,MVEM模型被分成3个子模型以描述发动机进气管的压力、温度、转速以及喷油量的动态过程。该模型的两个系统输入分别为进气阀角度θ和喷油质量流速 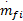
进气管进气动态过程表示如下[ 1]:
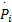
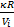

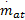
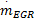
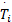
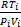
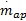
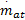

式中:P i为进气管压力;κ为空气的比热容;R为气体常数,这里取2.87×10-7;V i为进气管体积;T i为进气管温度;T a为环境温度; 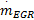
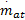
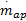
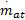
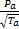
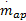
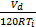
式中:m at0,m at1,θ0,P c为一个定值;η i为容积率;
β1(θ)=1- cosθ-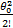 | (5) |
P r=P i/P a (6)
β2(P r)=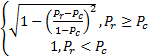 | (7) |
(η i·p i)为归一化的压缩气体压强,可通过式(8)计算得到[ 1]:
η i·p i=s i(n)P i+y i(n) (8)
式中:s i(n)和y i(n)为发动机转速的函数,并且y i<
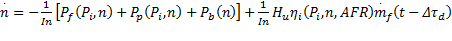 | (9) |
式中:I为归一化处理后的发动机转动惯量;摩擦功率P f、抽运功率P p与进气管压力P i和转速n密切相关,负载功率P b是转速n的函数;Δτ d为喷油的延时时间;容积率η i为进气管压力P i、转速n以及空燃比AFR的函数。
RBF神经网络模型是一个经典的前馈式神经网络模型,由输入层、隐层和输出层组成。
隐层由很多的隐层节点组成。每个隐层节点的非线性激励函数为高斯函数:
φj(t)= exp 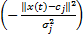
式中: nh为隐层节点的个数;‖ x( t) - c j‖为输入向量 x与第 j个中心点 c的欧几里得距离; σ j用来描述每一个隐层节点的宽度, σ j >0。
RBF神经网络的输出层为隐层节点的一个线性组合。在 t时刻, RBF神经网络模型的第 i个输出为:
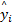
式中: w >0为输出层的权向量; q为输出的个数。
为了训练RBF神经网络模型,本文采用递推K均值算法[ 6]和最小P算法[ 6]来确定中心点cj和隐层节点的宽度σj,并利用递推最小二乘(Recursive least squares,RLS)[ 12]对输出层的权向量 w进行训练,使得RBF神经网络模型适应于发动机动态特性的变化。在SI发动机的控制过程当中,递推最小二乘将对模型参数进行在线更新。
发动机AFR系统是一个多变量的高度非线性系统。其中油门与喷油量是发动机的输入变量;进气管压力,进气管温度,发动机转速及AFR输出为发动机输出变量。为了提供更为精确的预测,对各种不同输入输出变量情况下的RBFNN均方根误差进行对比试验,本文所采用的RBFNN模型输入变量为: 



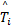
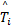
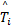
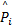
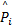
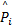

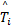
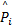
为了激励发动机AFR系统的全部非线性动态特性,本文对各种类型的输入序列如:随机幅值序列(RAS)、M序列,高斯白噪声序列等进行了充分试验并进行辨识误差的均方差比较,最终选定RAS序列作为模型的训练数据。利用RAS序列基于MEVM模型产生20 000组输入输出数据,前10 000组数据用来对模型进行训练,后10 000组数据用来对模型进行验证。其相关参数的设定为:
p=3,λ=0.999,
p(0)=1×108× 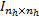
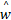
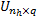
式中: λ为 RLS算法中的遗忘因子; p为 RLS算法中的中间变量; I为单位矩阵; U为一个随机矩阵。
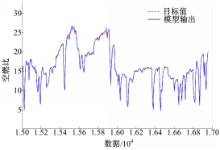
其模型辨识结果如图2所示。
图2中,对比数据为15 000~17 000,采用平均绝对误差(Menn absult error,MAE)对辨识效果进行评价。从图中可以看出,本文所得到的SI发动机AFR辨识模型的精度还是比较高的。
本文采用Volterra模型的目的在于改善SI发动机AFR控制算法的性能。Volterra模型实际上是一个系统的输入输出脉冲响应模型。它只与系统输入及被控输出有关,而影响系统输出的各个中间变量已全部包含在模型的内部参数中。许多文献表明,二阶Volterra模型就可以以较高的精度辨识相当一类的非线性系统[ 10, 11, 12]。为了减少Voletrra模型的复杂程度,本文采用输入为油门开度和喷油量,输出为AFR的二阶Volterra模型。其k时刻的Volterra模型的表达式为[ 10]:
y( k) = h0 + 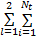
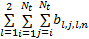
式中: u( k)为输入变量; y( k)为输出变量; h0为直流分量; Nt为截止阶次; a l, j和 b l, j, l, n分别为模型的线性和非线性部分的参数。
值得注意的是 SI发动机的喷油量的过渡过程时间与油门开度的过渡过程时间存在着显著的差异。经试验测定,当喷油量输入保持在0 .0015 kg/s,油门开度为从20 °到60 °的阶跃输入, AFR的过渡过程时间为0 .8 s。当油门开度保持在40 °,喷油量为从0 .0005 kg/s到0 .003 kg/s的阶跃输入, AFR的过渡过程时间为8 s。因此,当采样周期T s =0 .02 s时, Volterra模型的截止阶次应选为N t =8 /0 .02 =400。这将导致 Volterra模型的计算量剧增。因此,本文对各个输入变量采用变间隔采样的方法,对传统 Volterra模型进行改进,提出 Modified Volterra模型。其表达式为:
y( k) = h0 + 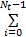
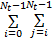
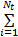
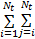
式中: au为与喷油量输入相关的模型线性部分参数; bu为与喷油量输入相关的模型非线性部分参数; av为与油门开度相关的模型线性部分参数; bv为与油门开度相关的模型非线性部分参数; u( k)为喷油量; v( k)为油门开度; tu为由喷油量变化导致的 AFR过渡过程时间; tv为由油门变化导致的 AFR过渡过程时间,取 Tu = 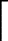
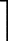
在第 k个采样时刻,对于喷油量 u的数据为 u( k-1), u( k-11),…, u[ k-( Nt -1) ×Tu -1];在第 k+1个采样时刻, u的数据为 u( k), u( k-10),…, u[ k-( Nt -1) ×Tu],以此类推,所有 u的数据都将被利用。这说明,本文所提出的基于变间隔采样的 Modified Volterra模型在有效降低模型截止阶次和计算量的同时,没有丢失任何系统动态特性信息。
本文所采用的 SI发动机 AFR非线性模型预测控制系统结构图如图3所示。
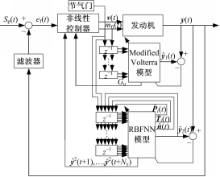 | 图3 基于RBFNN模型与Modified Volterra模型联合NMPC控制结构Fig.3 Control strategy of NMPC based on RBFNN model combined with Modified Volterra model |
图3中,S p为设定值(本文设S p=14.7);e f为系统输出误差; y( t)为系统真实输出; 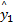
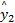
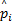
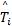
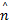
在每个控制周期中, RBFNN模型为非线性控制器提供 AFR的预测输出值 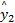
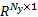
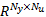
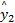
对于未来 Ny步的模型预测输出, RBFNN模型和 Modified Volterra模型可写为[ 10]:
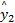
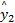
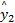
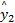
式中:
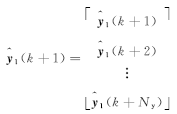 | (23) |
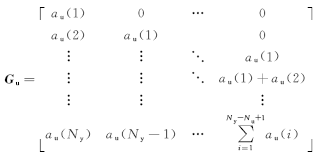 | (24) |
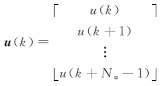 | (25) |
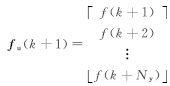 | (26) |
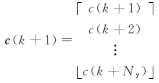 | (27) |
Gu∈ 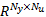
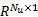
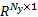
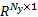
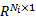
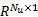
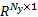
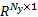
SI发动机真实 AFR输出序列 y( k+1)可写为:
y( k+1) = 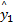
y( k+1) = 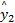
式中: e1( k+1)∈ 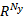
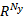
由式(28)可见, SI发动机的真实 AFR输出 y( k+1)由两部分组成:一部分是与 NMPC控制量 u( k)有关的线性部分 Gu u( k),而其剩余的另一部分可写为:
d( k+1) = fu( k+1) + c( k+1) + e1( k+1) (30)
则 d( k+1)∈ 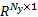
由式(29)和式(30),可得:
d( k+1) = 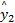
式中: e2( k+1)∈ 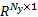
由于 e2( k) = y( k) - y2( k)为可测得的 k时刻 RBFNN模型预测误差,因而可利用 e2( k)对序列 e2( k+1)在一定程度上进行补偿:
e2( k+1) = e2( k) U =[ y( k) - 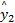
式中: U∈ 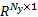
令 NMPC的目标函数为:
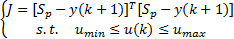 | (33) |
由式(29)和式(31)可得:
y( k+1) = Gu u( k) + d( k+1) (34)
则目标函数式(33)可写为:
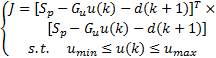 | (35) |
令 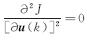
u *( k) =( 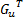
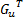
因为 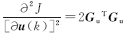
NMPC的控制效果主要依赖于模型预测的精度和优化算法的性能。在式(35)所示的目标函数中,由 Gu u( k) + d( k+1) = 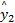
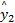
在 k时刻,喷油量的最优控制序列 u *( k)的计算方法如下:
(1)设 i=1。
(2)将 k-1时刻所计算的最优控制序列 u *( k-1)设为初始序列。
(3)利用 RBFNN模型和 Modified Volterra模型所提供的参数矩阵 Gu计算 d i( k+1):
d i( k+1) =- Gu u i( k) + 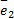
4)计算 u *( k):
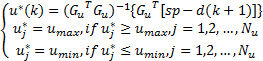 | (38) |
(5)设δ为可接受的偏差,若 u *( k)满足‖ u i( k) - u i-1( k+1)‖≤ δ,则跳出优化算法,并将最优控制序列 u *( k)的第一个控制变量作为真实喷油量输出给 SI发动机;如不满足,则跳出条件,转至(2),令 i=i+1,并利用当前计算控制序列 u i( k)和式(37)重新计算 d i( k+1)。
利用 dSPACE组件建立了 SI发动机 AFR NMPC控制实时仿真平台。利用 dSPACE提供的 RTI软件将 MEVM Simulink模型下载至 DS1005 PPC主板中以模拟被控对象,将 NMPC算法下载至 dSPACE MicroAutoBox( DS1401)以模拟真实汽车中的 ECU控制器。 DS1005 PPC主板与 dSPACE MicroAutoBox之间利用 RS232进行通讯。在观测电脑中,利用 ControlDesk软件对试验结果进行显示和记录。
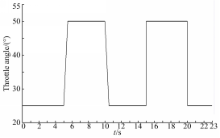
为了对各种算法进行测试,油门输入 θ如图4所示。图4中,油门在t =5 s处,经过0 .5 s从25 °变化至50 °;在t =10 s处经过0 .5 s由50 °变化至25 °;在t =15 s处由25 °阶跃变化至50 °;在t =20 s处由50 °阶跃变化至25 °。
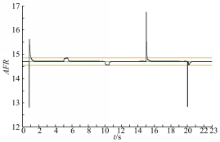
试验1 在本文所提算法中,取预测步数N y为20,控制步数N u为10。其控制输出曲线如图5所示。
在 t=5 s和 t=10 s处,当油门开度缓慢变化时,AFR控制曲线产生了小幅度的波动,但是始终保持在14.7±1%的范围内。在 t=15 s处,当油门开度突然增加时,AFR控制曲线超调至16.75,在0.14 s后调节至14.7±1%范围内,并在0.5 s后稳定在设定值14.7。在 t=20 s处,当油门突然减小时,AFR控制曲线向下超调至12.83,在0.04 s后调节至14.7±1%范围内,并在0.5 s后稳定在设定值14.7。
试验2 为了验证本文算法的性能,采用单独基于Modified Volterra模型的SI发动机AFR NMPC控制算法与本文算法进行对比。前一种算法仅是将本文算法中的RBFNN模型中的AFR预测输出序列替换为Modified Volterra模型预测序列,其余不变。由式(23)和式(29),单独基于Modified Volterra模型的NMPC控制算法的最优控制序列为:
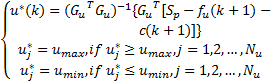 | (39) |
式中:Ny、 Nu与试验1取值相同。
在与试验1完全相同的试验条件下所得到的控制输出曲线如图6所示。与试验1的结果相比较,该方法的 AFR控制精度明显低于本文所提的 NMPC控制方法。在发动机启动阶段(t =0 s至t =2 s),该算法产生了较大幅值的震荡;在t =15 s和t =20 s处, 当油门开度发生快速变化时,也产生了较高的超调,这是由于Modified Volterra模型AFR输出序列的预测精度相对较低所导致的。
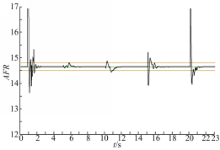 | 图6 基于Modified Volterra模型的NMPC控制算法的AFR控制效果,MAE=0.0873Fig.6 Simulation result of the NMPC algorithm based Modified Volterra model,MAE=0.0873 |
试验3 将文献[6]中所提控制方法与本文方法的控制性能进行对比试验。在与试验1完全相同的试验条件下,采用文献[6]中的Reduced Hessian SQP(Sequential quadratic programming)方法所得到的AFR控制输出曲线如图7所示。
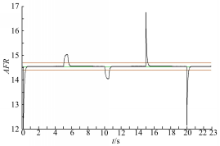 | 图7 基于RBFNN模型的NMPC控制算法的AFR控制效果,MAE=0.0542Fig.7 Simulation result of the NMPC algorithm based RBFNN model,MAE=0.0542 |
文献[ 6]的AFR控制方法与基于Modified Volterra模型的NMPC控制方法相比,由于其AFR输出序列的预测精度较高,使得控制输出曲线相对较为平滑且控制响应速度相对较快,但是当油门变化时AFR均产生了较大的超调。与本文所提算法相比,其控制精度明显降低、调整时间增长,这是由于SQP算法在最优控制序列附近过早收敛所导致的。
针对SI发动机AFR控制系统提出了一种变采样间隔的Modified Volterra模型。并以此为基础提出了一种基于RBFNN模型和Modified Volterra模型的SI发动机AFR的联合NMPC控制方法。Modified Volterra模型的优点是以相对较低的模型截止阶次就可以达到较高的模型辨识精度,从而有效地解决了一类具有不同输入阶跃响应速度的非线性系统的Volterra模型建模计算量大的问题;而同时利用RBFNN模型和Modified Volterra模型的联合NMPC控制方法则既具有RBFNN模型计算量小、模型预测精度高的特点,又可利用Modified Volterra模型直接计算最优且闭环渐进稳定的NMPC控制序列,从而既提高了SI发动机AFR的控制精度又有效地避免了迭代优化方法所导致的大量计算负担。在dSPACE实时仿真试验平台上对发动机基准模型(MEVM模型)进行的AFR实时控制仿真试验结果表明:本文所提NMPC控制方法对SI发动机AFR的控制效果明显优于单独基于Modified Volterra模型或RBFNN模型的NMPC控制效果。
| [1] |
|
| [2] |
|
| [3] |
|
| [4] |
|
| [5] |
|
| [6] |
|
| [7] |
|
| [8] |
|
| [9] |
|
| [10] |
|
| [11] |
|
| [12] |
|
| [13] |
|



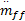

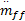
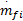
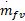 =(1-X f)
=(1-X f) 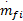
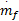 =
= 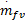
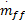
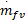
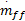

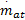
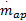 /
/