压机的调平和跟踪控制

引用本文

吴爱国, 杨硕, 张涵, 李长滨. 压机的调平和跟踪控制. 2014, 44(4): 1051-1056
[WU Ai-guo, YANG Shuo, ZHANG Han, LI Chang-bin. Leveling and tracking control of multi-cylinder forging hydraulic press. Journal of Jilin University Engineering and Technology Edition, 2014, 44(4): 1051-1056] 复制到剪切板

Permissions

压机的调平和跟踪控制

吴爱国, 杨硕, 张涵, 李长滨

天津大学电气与自动化工程学院, 天津 300072

作者简介：吴爱国（1954-）,男,教授,博士生导师.研究方向:非线性系统的控制算法及应用. E-mail:agwu@tju.edu.cn

基金:国家科技重大专项项目（2009ZX04004-031）;

摘要

针对多缸锻造液压机系统,在考虑不确定大负载和多缸耦合的情况下建立了非线性系统数学模型。采用广义逆的控制分配方法解决液压缸过驱动问题,进而提出一种二级非线性控制器设计方案。该控制器内环级采用李雅普诺夫直接法控制4个单输入单输出的液压缸压力系统,实现对期望压力的精确快速跟踪;外环级则针对带不确定大负载的多输入多输出系统,采用自适应控制策略并结合控制分配理论获得各缸期望压力。仿真和实验结果表明,该控制策略优于采用滑模变结构方法的单控制器策略,实现了低速运行下的高精度调平和跟踪控制。

关键词: 自动控制技术; 液压缸过驱动; 控制分配; 锻造液压机模型; 自适应控制

中图分类号:TP273 文献标志码:A 文章编号:1671-5497(2014)04-1051-06

Leveling and tracking control of multi-cylinder forging hydraulic press

WU Ai-guo, YANG Shuo, ZHANG Han, LI Chang-bin

School of Electrical Engineering and Automation, Tianjin University,Tianjin 300072, China

Abstract

A nonlinear mathematic model for multi-cylinder forging hydraulic press system is established, in which the uncertainty of large load and the coupling of multi-cylinder is taken into consideration. The over actuation of the hydraulic cylinder is solved using control allocation method based on generalized inverse. Then a two-level nonlinear controller is proposed to solve the above problems. Employing Lyapunov Direct Method, the inner-loop controller controls the four SISO hydraulic cylinder pressure system to achieve accurate and fast tracking for the desired pressure. To control the uncertain large load MIMO system, the out-loop controller is designed using adaptive control strategy, with reference to the control allocation theory, to obtain the desired pressure of each cylinder. Simulation and experiment demonstrate that the strategy proposed is better than the sliding mode variable structure control strategy with single controller, and high-accuracy of the leveling and tracking control under slow running can be achieved.

Keyword: automatic control technology; hydraulic cylinder overactuated; control allocation; hydraulic forging press model; adaptive control

Show Figures

存在强耦合的多缸锻造液压机系统同时会受到大负载扰动、液压系统及元件等非线性因素的影响,当液压缸数超过滑块运动自由度3时,会出现过驱动问题。传统的线性控制技术^{[ 1, 2]}无法在如此恶劣的条件下获得满意的调平和跟踪控制精度。针对有未知负载的液压伺服系统,文献[3-4]使用的反步自适应递推法存在“计算膨胀”的问题。文献[5]针对多缸锻造液压机系统,采用分散滑模控制方法,重点解决了系统耦合问题,但是所建立的数学模型中存在非独立变量,并且滑模控制^{[ 6]}设计过程复杂,并伴随有抖振现象^{[ 7, 8]}。文献[9]研究了多缸同步提升系统,尝试使用二级控制器的设计思路。

在文献[9]研究的基础上,作者对四缸锻造液压机进行具体的建模和控制研究。首先,选取滑块3个方向的运动自由度和液压缸的压力作为独立变量,建立系统的数学模型,并且引进控制分配理论^{[ 10, 11, 12]}来分析液压缸过驱动问题,使各液压缸得到最优压力分配。其次,在控制分配的基础上,设计二级控制器。该控制器的内环级采用李雅普诺夫直接法控制4个单输入单输出的液压缸压力系统,实现对期望压力的精确快速跟踪;外环级则针对带不确定大负载的多输入多输出系统,通过采用基于李雅普诺夫理论的自适应控制策略并结合控制分配理论获得各缸的期望压力。最后,通过仿真和实际运行,并与滑模变结构方法进行对比,验证了本文控制策略的可行性和有效性。

1 多缸液压机系统建模与分析

1.1 系统建模

四缸锻造液压机的下压过程如图1所示。首先,定量泵提供油压,经过比例伺服阀的开口大小控制活塞缸上腔压力,然后推动滑块下压,同时使滑块的运行满足竖直方向的位移跟踪和水平方向的调平精度指标。

	Figure Option View Download New Window
	图1 四缸锻造液压机系统Fig.1 Four-cylinder forging hydraulic press

实际工程中液压缸下腔压力恰好抵消活塞顶杆与滑块的总重量,在滑块的三个自由度方向上,根据牛顿第二定律和刚体定轴转动定律可得滑块的动态模型:

式中: F₁、 F₂、 F₃、 F₄为液压缸的驱动力; F_L为负载力; φ_x为滑块绕 X轴的转角; φ_y为滑块绕 Y轴的转角,两个转角均以转向轴 Z轴正方向为正; M为滑块质量; x_c为滑块质心的位移量; l_x、 l_y分别为驱动力到 X轴和 Y轴的距离; r_x、 r_y分别为负载力到 X轴和 Y轴的距离,其取值可正可负,它的符号取决于负载力的位置; J_x、 J_y分别为滑块绕 X轴和 Y轴的转动惯量。

对液压缸的活塞进行受力分析,4个活塞杆的质量相等,液压缸黏性阻尼系数近似为零,其负载力平衡方程和流量方程分别为:

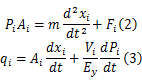
式中: i=1,2,3,4; P_i为第 i个液压缸上腔油压; A_i为第 i个液压缸活塞面积; m为活塞杆质量; x_i为第 i个液压缸活塞缸与滑块接触点的位置; q_i为油的流量; V_i为油腔容积; E_y为等效容积弹性模数。

比例伺服阀的流量方程为:

式中: C_d为比例伺服阀阀口流量系数; P_s为伺服阀的供油压力; u_i为比例伺服阀阀口面积; ρ为油液密度。

综合式(1)~(4)可以得到锻造液压机系统的模型为:

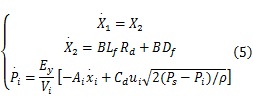
式中:

L_f=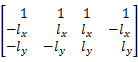

X₁=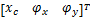

X₂=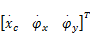

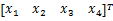
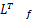
X= = X₁

H=diag( M, J_x, J_y)

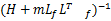
D_f=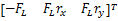

R_d=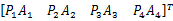

由模型(5)可知,该液压系统是一个复杂的非线性系统,具有耦合、模型不确定性和液压缸过驱动问题,从而难以直接求得满足指标的控制器,并且锻造液压机的不确定负载力最大可达8×10⁶ N,大负载进一步增加了控制的难度,所以必须使用新型、高效的控制算法来满足低速运行下的滑块调平精度和跟踪性能要求。

1.2 液压缸过驱动问题分析

液压缸的数量超过负载运动的自由度,即液压缸数量大于3时,便会产生液压缸过驱动问题。过驱动问题是锻造液压机系统能否进行分级控制的最关键问题,该问题与冗余性问题相似,在航空、航海、汽车等领域遇到的冗余性问题,称之为控制分配问题,文献[10-12]提出了一些行之有效的分配算法,这些控制分配算法为合理解决液压缸冗余问题开辟了新思路。

液压缸过驱动问题的表现形式为:

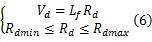
式中: V_d= 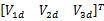为等价的最少数量的驱动力的期望值; V₁ _d为滑块竖直方向上的期望驱动力; V₂ _d、 V₃ _d分别为滑块绕 X轴、 Y轴旋转的期望力矩; R_d为液压缸提供的压力; R_d_min和 R_d_max分别为液压缸压力的最小值和最大值。

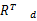
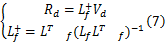
为了节省能量,希望各液压缸出力最小,即得到 R_d的最小二范数解,增加约束条件min( R_d),结合式(6)采用广义逆法可得到:

R_d除以液压缸的活塞面积可以得到期望的油液压力 P₁ _d、 P₂ _d、 P₃ _d、 P₄ _d。本文以四缸液压机为例进行分析,但从分析过程可知,无论液压缸的具体数目是多少,都可以采用控制分配解决系统的过驱动问题,使每一个液压缸的油液压力得到合理的分配。

2 控制策略分析

2.1 控制器结构分析

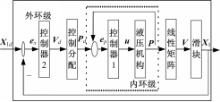
控制分配解决了液压缸的过驱动问题,从而使多缸锻造液压机系统得以分解为二级控制系统,其系统框图如图2所示。

	Figure Option View Download New Window
	图2 多缸锻造液压机二级控制系统Fig.2 Two-level control strategy of multi-cylinder forging hydraulic press

按照多级控制系统先内环后外环的一般原则,由内环开始,逐步向外扩展。本文则应先设计内环级控制器,然后设计外环级控制器。

2.2 内环级控制器设计

液压机构的动态特性为:

= (8)

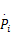
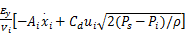
由式(8)可知,液压机构呈现明显的非线性特性,采用李雅普诺夫直接法设计控制率,使得一级控制系统具有优良的跟踪性能。

期望压力为 P_id,误差为 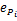=P_id-P_i,开环误差系统为:

设李雅普诺夫函数为:

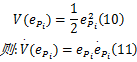
设计由前馈控制和反馈控制组成控制率:

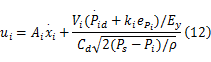
式中: k_i>0,将控制率(12)和开环误差系统(9)代入式(11)可得:

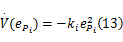
由式(13)可知跟踪系统在李雅普诺夫意义下是稳定的,其动态性能可由反馈系数 k_i进行调节。由式(9)和式(12)可知压力误差以指数形式快速收敛到零。

2.3 外环级控制器设计

内环级压力跟踪控制系统响应快,对外环基本无影响。则外环级动态模型为:

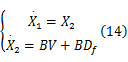
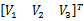
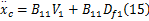
式中: V= 是控制量。因为 B是三维的对角阵,所以该模型无耦合,是3个相互独立的单变量系统,首先设计质心位移量的控制,其动态描述为:

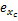
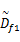
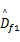
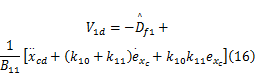
式中: D_f₁为未知负载力,故该对象存在不确定性,为了获得可靠的系统性能,采用基于李雅普诺夫直接法的自适应控制。位移的期望值为 x_cd,跟踪误差为 =x_cd-x_c,未知负载力的估计值为 ,估计误差为 =D_f₁ - , V₁的期望值设计为:

式中: k₁₀和 k₁₁为正常数。

将式(16)代入式(15),可得到按指数形式收敛的闭环误差动态为:

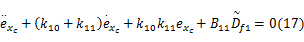
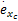
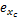
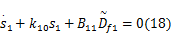
若定义组合跟踪误差 s₁ = +k₁₁ ,则式(17)等价为:

该自适应控制系统的稳定性和未知参数的估计可以用李雅普诺夫理论分析,取李雅普诺夫函数为:

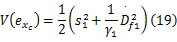
其中正常数 γ₁为自适应增益,易知其导数为:

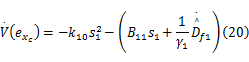
则参数估计值为

由Barbalata引理,易知 s₁收敛到零,由组合跟踪误差的定义可知 s₁收敛到零蕴含着位置误差和速度误差都收敛到零。

同理可得 φ_x、 φ_y跟踪 φ_xd、 φ_yd的控制,则外环级控制器和参数估计为:

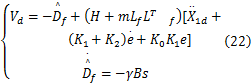
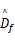
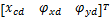
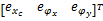
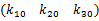
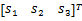
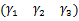
式中:负载的估计值 = ; x_c、 φ_x、 φ_y的期望值为 X₁ _d= ; x_c、 φ_x、 φ_y误差为期望值减去实际值,记为 e= ;反馈矩阵 K₁=diag 和 K₀=diag 中的元素均为正常数,组合跟踪误差为 s= ,自适应增益向量为 γ=diag 。

式(7)(12)(22)便构成了锻造液压机系统的二级控制器。

3 系统仿真和实验验证

系统的控制性能要求如下,滑块中心点的期望位移 x_cd为:

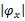
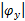
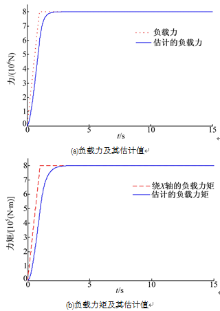
滑块应尽可能保持在调平状态,即 φ_xd=0, φ_yd=0。调平精度指标为0.1 mm/m,即 ≤10^-4rad, ≤10^-4 rad。各个液压缸输出力的取值范围是:0≤ P_i≤3.15×10⁷ Pa,0≤ R_id≤10⁷N,伺服阀的开口面积取值范围为0≤ u_i≤10^-4m²。系统的负载力作用在 Y轴负方向0.1 m处,从零开始线性增加,1 s时增加到最大值8×10⁶ N,并稳定在最大值。本文的负载力与文献[5]中的最大负载力10⁵ N和文献[13]中的最大负载力350 N相比,应归为大吨位负载,其控制难度大幅度增加。

	Figure Option View Download New Window
	图3 负载力和负载力矩的估计Fig.3 Load estimation and load torque estimation

仿真时选择合适的自适应增益,获得负载力和负载力矩的自适应估计值,如图3所示。对于锻造液压机的不确定负载,上述估计算法估计效果良好,当反抗力恒定之后,估计值基本无偏差。

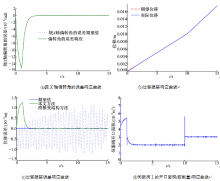
系统的调平效果如图4(a)所示,其最大偏差小于1.6×10^-5 rad,是实际控制指标的六分之一,调节时间为3 s,实现了滑块的高精度、快速调平。系统的给定位移和跟踪性能如图4(b)所示,位移跟踪误差如图4(c)所示,虚线为滑模变结构控制方法的控制效果,其精度基本在1×10^-4m以内,精度可以满足控制指标要求,但是抖振现象特别明显,不利于系统的稳定。实线为本文方法,过渡时间短,并且运行到2.5 s时跟踪误差为零,实现完全稳定跟踪,在10 s时,给定速度由0.001 m/s变化为0.0015 m/s,两种方法都有较强的鲁棒性。综上可知系统在低速、变速情况下,本文方法优于滑模变结构控制方法。图4(d)为系统的控制量,即伺服阀开口面积,图中为伺服阀1的响应曲线。

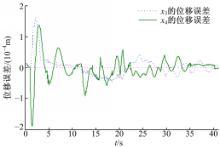
	Figure Option View Download New Window
	图4 有未知负载力时系统的响应Fig.4 System response under uncertainty load

实际的锻造液压机系统参数如表1所示,并且锻造液压机上的位移尺的测量误差为0.001 mm。根据滑块尺寸和调平精度要求,控制指标等价为滑块四角的位移跟踪误差的绝对值小于0.175 mm。图5为锻造液压机实际运行时滑块两个角的位移误差曲线,滑块下行速度为0.001 m/s,1 s前为空载运行,之后为压制运行,接触负载之后位移误差增加,经过约0.3 s的调节,位移误差的绝对值就小于0.175 mm,随后的压制过程中误差基本稳定在0.090 mm以内。说明系统具有快速调节能力,鲁棒性好,调平和跟踪误差小,满足了工程指标。因此,本文的控制策略是有效的。

表1 多缸液压机相关参数的取值 Table 1 Parameters of multi-cylinder hydraulic press

	Figure Option View Download New Window
	图5 实际位移误差响应Fig.5 Response of actual displacement error

4 结束语

本文建立了多缸锻造液压机的数学模型,应用广义逆的控制分配理论解决了过驱动问题。此外,该系统二级控制器分别采用李雅普诺夫直接法和自适应控制方法设计,与采用滑模变结构方法的单控制器相比,结构清晰,计算简明。并且能保证系统不存在抖振现象,提高了控制精度,增强了稳定性。通过仿真对比实验和实际运行,验证了该二级控制器的优势和实用性,能够保证多缸锻造液压机系统快速、精确、稳定的运行。

The authors have declared that no competing interests exist.

参考文献

View Option

[1]	Cho S J, Lee J C, Jeon Y H, et al. The development of a position conversion controller for hydraulic press systems[C]∥IEEE International Conference on Robotics and Biomimetics, Guilin, China, 2009: 2019-2022. [本文引用:1]
[2]	Chen M, Huang M H, Zhou Y C, et al. Synchronism control system of heavy hydraulic press[C]∥IEEE International Conference on Measuring Technology and Mechatronics Automation, Zhangjiajie, China, 2009: 17-19. [本文引用:1]
[3]	Claude Kaddissi, Jean-Pierre Kenne, Maarouf Saad. Indirect adaptive control of an electrohydraulic servo system based on nonlinear backstepping[J]. IEEE Transactions on Mechatronics, 2011, 16(6): 1171-1177. [本文引用:1] [JCR: 3.135]
[4]	UrsI U, Ursu F, Popescu F. Backstepping design for controlling electrohydraulic servos[J]. Journal of the Franklin Institute, 2006, 343: 94-110. [本文引用:1] [JCR: 2.418]
[5]	贾超, 吴爱国, 郑爱红. 一类多缸液压机的分散滑模控制[J]. 仪器仪表学报, 2012, 33(7): 1513-1520. Jia Chao, Wu Ai-guo, Zheng Ai-hong. Decentralised sliding mode control for a class of multi-cylinder hydraulic press[J]. Chinese Journal of Scientific Instrument, 2012, 33(7): 1513-1520. [本文引用:1] [CJCR: 0.785]
[6]	Guan Cheng, Pan Shuang-xia. Adaptive sliding mode control of electro-hydraulic system with nonlinear unknown parameters[J]. Control Engineering Practice, 2008, 16(11): 1275-1284. [本文引用:1] [JCR: 1.669]
[7]	Huerta H, Loukianov A G, Canedo J M. Decentralized sliding mode block control of multimachine power systems[J]. International Journal of Electrical Power & Energy Systems, 2010, 32(1): 1-11. [本文引用:1]
[8]	Utkin V, Lee H. Chattering problem in sliding mode control system[C]∥Proceedings of the 2006 International Workshop on Variable Structure Systems, Alghero, Sardinia, 2006: 346-350. [本文引用:1]
[9]	Hong S, Chiug T C. Motion synchronization for dual-cylinder electrohydraulic lift systems[J]. IEEE/ASME Transactions on Mechatronics, 2002, 7(2): 171-181. [本文引用:1] [JCR: 3.135]
[10]	Alwi H, Edwards C H. Fault tolerant control using sliding modes with on-line control allocation[J]. Automatica, 2008, 44(7): 1859-1866. [本文引用:1] [JCR: 2.919]
[11]	Johansen T A, Fuglset T P, Tondel P, et al. Optimal constrained control allocation in marine surface vessels with rudders[J]. Control Engineering Practice, 2008, 16(4): 457-464. [本文引用:1] [JCR: 1.669]
[12]	Wang Jun-min, Longoria Raul G. Coordinated and reconfigurable vehicle dynamics control[J]. IEEE Transactions on Control Systems Technology, 2009, 17(3): 723-732. [本文引用:1] [JCR: 2.0]
[13]	贾超, 吴爱国. 基于李雅普诺夫直接法的电液伺服系统控制[J]. 吉林大学学报: 工学版, 2012, 42(3): 696-701. Jia Chao, Wu Ai-guo. Control method for electro-hydraulic servo system based on Lyapunov direct method[J]. Journal of Jilin University(Engineering and Technology Edition), 2012, 42(3): 696-701. [本文引用:1] [CJCR: 0.701]

2009

0.0

... 传统的线性控制技术^[1,2]无法在如此恶劣的条件下获得满意的调平和跟踪控制精度 ...

2009

0.0

... 传统的线性控制技术^[1,2]无法在如此恶劣的条件下获得满意的调平和跟踪控制精度 ...

2011

3.135

0.0

2006

2.418

0.0

. 2006, 343:null-null

Backstepping design for controlling electrohydraulic servos

2012

0.0

0.785

2008

1.669

0.0

. 2008, 16(11):1275-1284 DOI:10.1016/j.conengprac.2008.02.002

Adaptive sliding mode control of electro-hydraulic system with nonlinear unknown parameters

Abstract In this paper, an adaptive sliding control method is presented for an electro-hydraulic system with nonlinear unknown parameters, which enter the system equations in a nonlinear way. Previous adaptive control methods of hydraulic system always assume that the original control volumes are certain and known, which can guarantee that all system unknown parameters occur linearly. But in practical hydraulic systems, the original control volumes are unknown or change; as a result some unknown parameters appear nonlinearly. The proposed control method in this paper is to present a nonlinear adaptive controller with adaptation laws to compensate for the nonlinear uncertain parameters caused by the varieties of the original control volumes. The main feature of the scheme is that by combining sliding mode control method, a novel-type Lyapunov function is developed to construct an asymptotically stable adaptive controller and adaptation laws, which can compensate for the system uncertain nonlinearities, linear uncertain parameters, and especially for the nonlinear uncertain parameters caused by the various of the original control volumes. The experimental results show that the nonlinear control algorithm, together with the adaptation scheme, gives a good performance for the specified tracking task in the presence of nonlinear unknown parameters.

... 文献[5]针对多缸锻造液压机系统,采用分散滑模控制方法,重点解决了系统耦合问题,但是所建立的数学模型中存在非独立变量,并且滑模控制^[6]设计过程复杂,并伴随有抖振现象^[7,8] ...

2010

0.0

. 2010, 32(1):1-11 DOI:10.1016/j.ijepes.2009.06.016

Decentralized sliding mode block control of multimachine power systems

Abstract A decentralized sliding mode stabilizing excitation controller for multimachine Electric Power Systems (EPS) is designed. The block control approach is used in order to derive a nonlinear sliding manifold, on which the inherent plant model nonlinearities are compensated and the mechanical dynamics are linearized. A local Sliding Mode Speed Stabilizer (SMSS) and Sliding Mode Voltage Regulator (SMVR) control is designed to achieve attractiveness of the derived manifold, regulate the terminal voltage and stabilize the speed of each generation unit in spite of high level external disturbances. The simulation of the Western System Coordinating Council (WSCC) system exhibits the comparison between the traditional Automatic Voltage Regulator/Power System Stabilizer (AVR/PSS) and proposed SMSS/SMVR control schemes.

2006

0.0

2002

3.135

0.0

2008

2.919

0.0

. 2008, 44(7):1859-1866 DOI:10.1016/j.automatica.2007.10.034

Fault tolerant control using sliding modes with on-line control allocation

Abstract This paper proposes an on-line sliding mode control allocation scheme for fault tolerant control. The effectiveness level of the actuators is used by the control allocation scheme to redistribute the control signals to the remaining actuators when a fault or failure occurs. The paper provides an analysis of the sliding mode control allocation scheme and determines the nonlinear gain required to maintain sliding. The on-line sliding mode control allocation scheme shows that faults and even certain total actuator failures can be handled directly without reconfiguring the controller. The simulation results show good performance when tested on different fault and failure scenarios.

... 首先,选取滑块3个方向的运动自由度和液压缸的压力作为独立变量,建立系统的数学模型,并且引进控制分配理论^[10,11,12]来分析液压缸过驱动问题,使各液压缸得到最优压力分配 ...

2008

1.669

0.0

. 2008, 16(4):null-null

Optimal constrained control allocation in marine surface vessels with rudders

2009

2.0

0.0

2012

0.0

0.701

. 2012, 42(3):696-701

Control method for electro-hydraulic servo system based on Lyapunov direct method

1. Department of Engineering &Automation, Tianjin University, Tianjin 300072, China; 2. School of Electrical Engineering, Tianjin University of Technology, Tianjin 300384, China

A position tracking control scheme was proposed for a common class of electro-hydraulic servo system based on the Lyapunov direct method. A simple Lyapunov function was constructed for the system and specific methods were given to decide the related parameters and to get the control law. The system stability was ensured symptotically and the scheme could be applied to all electro-hydranlic servo systems with this kind of mathematical model. Taking a super low-speed hydraulic press system as an example, the proposed control scheme was applied successfully. The simulation result proved the validity of the proposed control scheme.

针对一类常见的电液伺服系统模型,提出了一种基于李雅普诺夫(Lyapunov)直接法的位置跟踪控制方法。为此类系统构造了一种形式简单的Lyapunov函数,并给出了确定其相关参数及求取控制律的具体方法,从而确保了整个系统的渐近稳定,适用于所有数学模型具有此类形式的电液伺服系统。以超低速锻造液压系统为例,应用该方法成功构造出了Lyapunov函数,并得到了使系统渐近稳定的控制律。仿真结果证实了本文方法的有效性。