卡尔曼滤波器是线性高斯环境下的最优滤波器。然而,卡尔曼滤波器对系统模型不确定性异常敏感。为了拓宽卡尔曼滤波器的应用范围或寻找其他替代方法,鲁棒滤波理论一直受到广泛关注^{[ 1, 2, 3, 4, 5, 6, 7, 8]}。传统的鲁棒滤波器设计方法包括H_∞滤波、H₂/H_∞滤波、保性能估计和协方差受限估计等。相比于传统的鲁棒滤波器,最小二乘鲁棒滤波器设计不需要计算滤波器存在条件,并且适合在线实时计算,因而在近些年得到众多研究人员的关注^{[ 1, 8]}。在最小二乘鲁棒滤波器发展的初期,滤波器设计仍需知道过程噪声的统计特性,最近Cong等^{[ 8]}提出了一种基于迭代策略的最小二乘鲁棒滤波器设计方法,在此种方法中,过程噪声被当成一个模有界的变量。

测量数据丢失广泛存在于实际应用之中^{[ 9, 10, 11, 12]},比如应用光电经纬仪跟踪目标,当目标飞入云层等障碍物时,光学系统观测不到目标,因而无法返回脱靶量,在这种情况下测量数据出现了丢失现象。测量数据丢失是滤波器性能变坏甚至不稳定的重要因素。而此类数据丢失现象的迭代鲁棒滤波器设计问题却没有被充分研究。因此,作者在文献[1,8]的基础上,针对系统中存在的输入不确定性、模型参数不确定性和测量数据传输中存在的丢失现象,给出了基于迭代策略和博弈论的迭代鲁棒滤波器设计方法。最后,仿真验证了本文方法的有效性。

考虑下面含有输入不确定性、模型参数不确定性和测量数据丢失现象的动态系统:

式中: x_k∈ℝ ⁿ是要估计的系统状态; y_k∈ℝ ^m是测量输出; A_k、 B_k、 H_k是具有适当维数的矩阵; v_k∈ℝ ^m是均值为零、协方差为 R_k>0的高斯白噪声; u_k和 ΔH_k是模有界的不确定项,不失一般性假设‖ u_k‖≤1, ΔH_k具有如下结构:

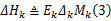
式中: E_k、 M_k是具有合适维数的已知时变矩阵,‖ Δ_k‖≤1是一个时变不确定项; λ_k∈ℝ是一个与系统初始状态以及其他信号均不相关的随机二进制切换序列,具有如下统计特性:

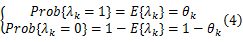
式中: θ_k∈[0 1]是已知标量。

测量模型(2)最早在文献[12]中用来描述测量丢失现象,随后在文献[4]和[11]等中得到了广泛应用。由式(2)可知,当 λ_k=1时,滤波器接收到的信号是传感器测量信号;当 λ_k=0时,滤波器接收到的信号是测量噪声 v_k,测量信号在传输的过程中丢失。

注释1:本文所考虑的系统为线性离散系统,对于非线性系统,可在其工作点附近进行线性化处理,将其近似地转化成式(1)(2)所示的线性离散系统进行研究。一个常用的线性化方法是在系统工作点附近进行泰勒展开。

常见的递推滤波器设计可分为两步,即预测更新和测量更新。在预测更新阶段,通过系统动态方程和 k时刻的最优估计值,可以得到 k+1时刻的最优预测值。在测量更新阶段,利用最新得到的测量信息,可以对状态预测值做进一步的修订,使新得到的状态估计值更加精确。针对含有测量信息丢失、输入不确定性和模型参数不确定性的动态系统,利用最小最大博弈论,本文同样是沿用这两个设计步骤。

预测更新阶段:

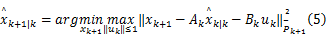
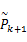
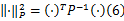
式中: 是一个后面将给出定义的权重矩阵,式(5)中的模值方程有如下定义:

记 x_k的估计误差为 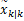=x_k- ,并且假设估计误差协方差满足如下限制:

式中: P_k|k>0。

测量更新阶段:

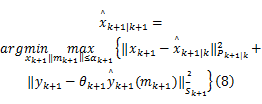
式中: ( m_k+1)􀰛 H_k+1 +E_k+1 m_k+1; 是一个后面将给出定义的权重矩阵; m_k+1具有如下的结构形式:

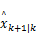
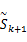
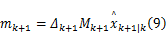
最小二乘鲁棒滤波器设计依赖于以下受限最大化问题:

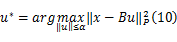
式中: P是一个对称正定矩阵; α是一个已知标量。

引理1^{[ 8]}:当 x≠0时,式(10)有如下形式的解:

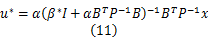
式中: β^*∈ M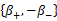􀰛 并满足:

目标方程(10)的最大值为:

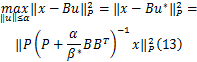
在上面的式子中, β₊和 β_-分别满足:

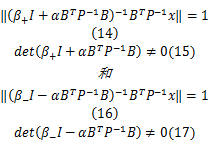
引理2^{[ 8]}:当 x=0时, u^*是 B^T P^-1 B的一个特征向量。

根据引理1和引理2,预测更新有如下表达式:

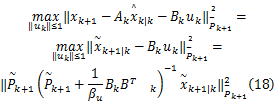
式中: 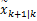=x_k+1 -A_k 。

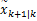
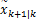
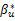
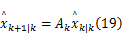
获得预测更新方程的一个难点在于 β_u是 的函数,而此时 未知。为了解决这个问题,本文首先假设 β_u= 是一个已知的常数,进而可以求得预测更新方程的一个近似解,然后通过一个算法逼近预测更新方程的精确值。关于逼近算法的内容将在第3节中详细讨论。对式(18)两端求关于 x_k+1的导数,并令这个导数为零,可以得到如下的预测更新方程:

进而可得状态的预测误差为:

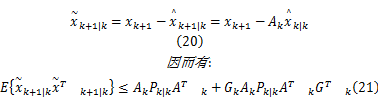
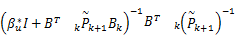
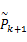
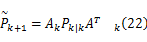
式中: G_k= ,其中的 有如下表达式:

进而,预测更新协方差的上界有如下表达式:

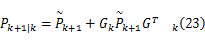
在测量更新阶段,根据引理1和引理2,有:

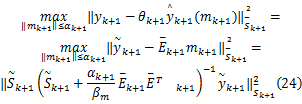
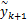
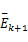
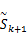
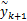
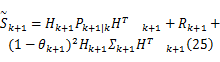
式中: =y_k+1 -θ_k+1 H_k+1 ; =θ_k+1 E_k+1; 是 的协方差,并且具有如下表达式:

式中: Σ_k+1 =A_kΕ 。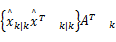

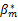
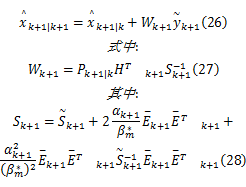
推导测量更新方程时,将会遇到与推导预测更新方程一样的困难,同样也是先假设 β_m为一个已知的常数。令 β_m= ,将式(24)代入到式(8),对式(8)两端求关于 x_k+1的导数,并令这个导数为零,可以得到如下的测量更新方程:

因此,估计误差协方差有如下上界:

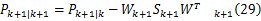
由式(27)可知, W_k+1的计算用到了 S_k+1的逆矩阵,因此需要进一步讨论矩阵 S_k+1的可逆性。由式(28)可得:

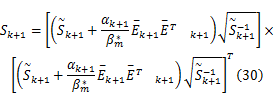
据引理1和式(24)可知,式(30)小括号里面的矩阵是可逆矩阵。另一方面,由式(7)(22)(23)(25)以及矩阵 Σ_k+1和 R_k+1的定义可知,矩阵 存在且可逆。因此, S_k+1是可逆矩阵。

本节利用博弈论获得了一个递推最小二乘鲁棒滤波器。然而,新获得的滤波器的精度并不太高,因为预测更新方程和测量更新方程的推导都假设 β_u和 β_m为已知的常数。因此,必须采取措施来弥补这方面的不足。

本节将利用迭代策略解决上一节鲁棒滤波器设计中存在的问题,具体的迭代算法如下所示:

第一步:假设 和 P_k|k是已知的,根据先前的分析,状态预测方程为 =A_k 。测量预测误差为 =y_k+1 -θ_k+1 H_k+1 。假设 是 的初始值,对于 i≥0,重复下面的第二步到第六步。

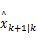
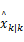
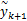
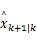
第二步:计算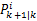

式中: = 。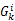

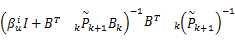
第三步:根据第一步、第二步和引理1计算 :

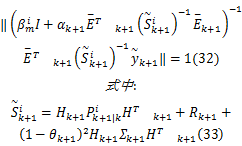
第四步:将 应用到测量更新方程, 和 可计算如下:

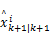
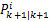
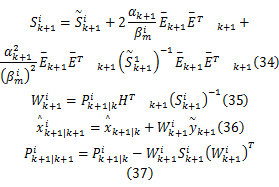
第五步:如果‖ - ‖≤ ξ_m, ξ_m是一个给定的常值,迭代结束, 是 k+1时刻期望的值;否则进入第六步。

第六步:计算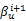

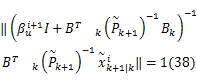
式中: = - 。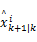

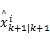
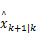
如果‖ - ‖≤ ζ_u,迭代结束,否则,返回到第二步继续进行迭代,其中 ζ_u是一个给定的常数。

作为一个例证,将新得到的迭代鲁棒滤波器应用到下面含输入不确定性、模型参数不确定性和测量数据丢失现象的目标追踪系统。

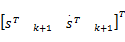
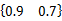
式中: Γ是采样周期; x_k+1 = 由运动目标在时刻 kΓ的位置和速度组成; y_k是进行滤波计算的测量数据; v_k是一个零均值单位方差的高斯白噪声序列; γ_k∈ℝ是一个随机二进制切换序列,其取1的概率为Prob =θ= 。

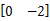
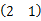
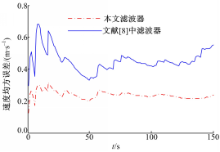
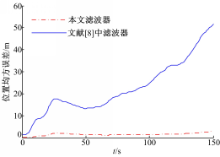
仿真系统的初始值假设为 x₀ = ; P_{0 |0} =diag ; α_k=0 .02; Γ=0 .1 s。将本文得到的迭代鲁棒滤波器和文献[8]中的迭代鲁棒滤波器在仿真中进行了比较,从图1~图4的仿真结果可以看到,本文得到的迭代鲁棒滤波器具有更高的精度。这是因为本文对测量丢失现象和不确定性进行了补偿,而文献[8]仅仅对不确定性进行了补偿。

图1

Fig.1

	Figure Option ViewDownloadNew Window
	图1 位置均方误差( θ=0.9°)Fig.1 Mean square error for position( θ=0.9°)

图2

Fig.2

	Figure Option ViewDownloadNew Window
	图2 速度均方误差( θ=0.9°)Fig.2 Mean square error for velocity( θ=0.9°)

图3

Fig.3

	Figure Option ViewDownloadNew Window
	图3 位置均方误差( θ=0.7°)Fig.3 Mean square error for position( θ=0.7°)

图4

Fig.4

	Figure Option ViewDownloadNew Window
	图4 速度均方误差( θ=0.7°)Fig.4 Mean square error for velocity( θ=0.7°)

研究了含测量数据丢失现象的不确定系统的迭代鲁棒滤波器设计问题。本文方法的基本思想是:引入了一个随机二进制序列来描述测量数据的丢失现象,不确定性被描述成模有界的变量,通过最小最大博弈论和迭代策略最终获得所期望的迭代鲁棒滤波器。与文献[8]相比,本文得到的滤波器具有更宽的适用性和更高的精度,仿真结果也证明了该方法的有效性。