作者简介:康冰(1978-)男,博士研究生.研究方向:计算机视觉及模式识别.E-mail:kangbing@jlu.edu.cn
针对搜索机器人路径规划问题,提出了一种改进的蚁群算法。算法构建一个栅格环境模型,并设置禁忌策略将部分栅格归为禁忌栅格以避免路径死锁;采用折返蚂蚁,且正向与反向蚂蚁分别采用不同搜索策略,来提高算法的收敛速度;构造路径综合评定目标函数,提高搜索最优路径的能力。实验表明:即使在复杂的环境中,本文算法也能快速地规划出最优路径。
An improved ant colony algorithm for path planning of searching robot is proposed. In this algorithm, a grid environment model is established and a taboo strategy is adopted to avoid path deadlock. Meanwhile, the retracing ants, which adopt different searching strategies between the forward and backward directions, are used to increase the convergent speed of the algorithm. Moreover, an objective function of path evaluation is constructed to improve the ability of path searching. Extensive experiments demonstrate that the proposed algorithm can plan the optimal path even in a complicated environment.
移动机器人是集多种技术于一体的复杂控制系统,路径规划是其核心技术之一[ 1]。目前,对于救援搜索机器人的研究主要集中于个体上,且多为需要人工操作的半自主系统,对自主智能式机器人和群体机器人的研究较少,而使用群体机器人可以扩大搜索范围,提高工作效率,并且多个机器人协同作业,可以提高信息的可靠性和准确性[ 2]。
蚁群算法最初应用于解决TSP问题,是一种利用正反馈的群智能算法,具有并行性、强鲁棒性、全局最优等优点,在很多实际问题的路径规划中得到应用。如文献[3]将蚁群算法应用于无人机的航路优化中,使无人机能够高效地避过障碍与雷达,文献[4]将蚁群算法应用于矿难救援的局部路径规划中,取得良好的效果。本文将蚁群算法应用于智能搜索机器人的路径规划中,在算法上为搜索机器人的群体智能化提供了一种可行的方案。
本文探讨的搜索机器人路径规划问题为:在一幅存在静态障碍物且终点未知的栅格图中,机器人按照某一性能指标或某些指标自主地寻找一条从起点到受困人员的最优路径,且机器人与障碍物无碰撞。
蚁群算法在广泛应用于路径规划时,也存在着收敛速度慢,易陷入局部最优等缺点。相关研究大多停留在理论层面,缺少对实际问题的考虑。本文联系实际应用对蚁群算法的收敛速度慢、易陷入局部最优解、算法停滞等做出改进,使算法在最短时间内寻找到最优路径。
栅格法简单有效,对障碍物的适应能力强,可大大减小建模的复杂性,便于计算机存储和处理,并可防止丢失部分可行路径,已被广泛用于环境建模方法。故采用序号法和二维直角坐标相结合的方式建立栅格模型(见图1)。如图2所示,其中黑色栅格抽象为障碍栅格,白色栅格抽象为自由栅格。block[ x][ y]表示节点 i处( xi, yi)的信息,设起始节点为 s,终止节点为 g。在栅格图中,栅格序号值 c与位置坐标( x, y)的对应关系为:
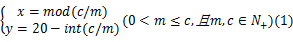
式中:mod为取余运算;int为取整运算; m为每一行的栅格数。
受灾现场的目标点未知,机器人找到目标点后,以起始点与目标的连线为对角线建立栅格图,确定搜索范围。
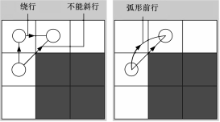
单个机器人的搜索范围有限,只能识别自身周围的8个栅格,而栅格的大小略大于搜索机器人的体积。机器人不能等效为质点,因障碍物的阻挡,因此不能斜行前进,只能有4个行走方向。机器人可以选择弧形前行的方式,缩短绕行距离,扩大行走范围。
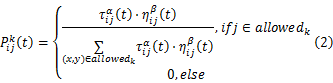
式中: 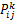
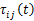
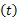
随后提出如下蚁群系统对上述蚁群算法做出改进:
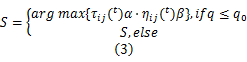
式中: S为改进后的蚁群系统状态转移规则; q是在[0,1]区间均匀分布的随机数; q0的大小决定了利用先验知识与探索新路径之间的相对重要性,其中 ηij( t)为:
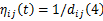
式中: dij为节点 i到 j的距离。
当蚁群完成一次循环后,需进行路径信息素的更新:
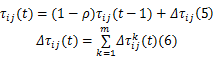
式中: ρ∈ 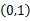
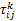

式中: Q为新增信息素强度因子; Lk为第 k只蚂蚁搜索到的路径长度。
在基本蚁群算法中,蚂蚁很容易陷入如U型障碍物发生死锁,导致算法停滞,文献[7]提出了蚂蚁回退策略,增强了算法的鲁棒性。但当U型障碍物很多时,蚂蚁需要反复回退、反复判断是否在U型路径中,增加了计算量。本文采用设置禁忌栅格的方式进行优化,当蚂蚁进入U型路径时,将入口节点压栈处理,并不再采用转移概率公式运动到下一点,而是按惯性直接前行,这样可简化路径选择的运算量。若存在出口,该蚂蚁通过后则继续前行;若无出口,则蚂蚁回退到入口,并将该U型栅格标定为禁忌栅格,提醒其他蚂蚁不再行走。
在传统的蚁群算法中信息素挥发因子 ρ为常量,可能导致算法陷入局部最优解,文献[8]给出一种自适应改进方法:
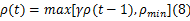
式中: ρmin为 ρ的最小值; γ为预设的衰减常数,一般取为0.95。
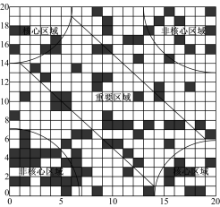
式(8)是基于时间的函数,本文在此基础上,进一步提出基于空间的改进策略。由于最短路径多集中出现于在起始点与终点的连线附近区域,因此将对角线附近区域定义为重要区域;而起点与终点附近区域尤为重要,定义为核心区域,需加大搜索力度;而与核心区域相对的两个对角区域,出现最短路径的概率最小,定义为非核心区域,如图3所示。第一只蚂蚁搜索到目标点后,建立搜索范围,将整个区域划分为核心区域、非核心区域和重要区域,并通过调节 ρ值实现:
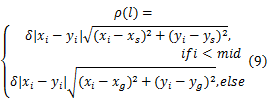
式中:( xi, yi)为节点 i的坐标;( xs, ys)为起点坐标;( xg, yg)为终点坐标;mid为中间分割线; δ为某一常数;使 ρ( l)与 ρ( t)处于同一量级。
因此,信息素更新的公式改为:
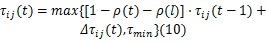
引入 ρ( l)后,在非核心区域内 ρ( l)值较大,可加速信息素的挥发,减小蚂蚁进入该区域搜索的概率;在重要区域内,信息素含量较高,而在核心区域内 ρ( l)值最小,信息素含量最高,蚂蚁更倾向于在该区域内搜索,这样既防止蚂蚁陷入局部最优,又减少了搜索的盲目性,加快了收敛速度。
在实际应用中,机器人搜索到达目标点后,应返回到起始点。为更大限度地发挥蚂蚁个体的搜索能力,文献[9]提出一种带折返的迭代方式,但这种方式会造成正向信息素对反向信息素的干扰,本文提出新的改进策略,蚂蚁个体由起点到达终点,则进行信息素更新;随即返回起点,再次更新信息素完成单个蚂蚁一次迭代。这样可以减少蚂蚁迭代时的等待,加大了蚂蚁的重复利用率,提高了搜索效率。
在正向前行和反向折返过程中,分别采用不同的转移策略。
(1)正向搜索策略
对式(2)的启发信息 ηij 
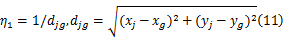
式中: djg为 j点到目标点 g的距离。
采用当前节点到目标点的距离作为启发信息,可大大加强蚂蚁搜索的目的性,加快算法的收敛速度。为防止搜索空间过小,需加大正向信息素因子 αf( αf >1),增大信息素对下一节点选择的比重。
若 djg≤ dig,定义节点 j为近距节点;若 djg>dig,定义节点 j为远距节点。
蚂蚁转移一般采用的是轮盘赌选择法,按距离因素搜索时,按上述表述,远距节点无需搜索,仅需计算几个近距节点,因此allowed k可更改为所有近距节点,采用这种策略可进一步减小计算量,加快算法的收敛速度。
(2)反向折返搜索策略
为减小正向搜索产生的信息素对折返过程造成的影响,增强搜索的随机性,需减小反向信息素因子 αb( αb <1),减小信息素对下一节点选择的比重,式(2)中的 ηij 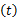
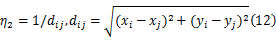
采用 η2作为启发信息可增强蚂蚁搜索的随机性,适当扩大搜索空间。
采用折返搜索策略可实现正向蚂蚁与折返蚂蚁之间的优势互补,弥补各自搜索时的不足,提高了蚂蚁的利用率和搜索效率,兼顾了算法的收敛速度和多样性。
由于在实际应用中,机器人寻找的为最优路径而非最短路径,因此引入计算量和转折量作为新的评定指标,构造综合评定目标函数。机器人在应用中常采用嵌入式系统,在选择节点时可能会因计算量大而导致机器人短暂停滞,因此应尽量减少大量的计算,引入计算量评定目标函数:
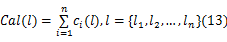
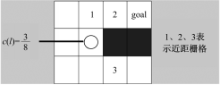
图4为节点计算量示意图。
当节点 i的可行节点 j为障碍栅格或远距节点时,节点 j无需带入转移概率公式计算,当节点 j为近距节点时才需要计算,因此每个节点计算量不同:

机器人在急速转弯时,会造成一定的能量损耗,因此应尽量避免机器人的大量转弯,使机器人按原定方向前行,即保持一定的“惯性”,增强路径的平滑性,引入转折量评定目标函数:
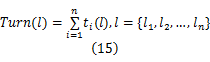
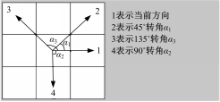
不同的转角对前行的影响也不同,因此加入转角的惩罚措施:因为蚂蚁是在栅格图中移动,转角只能为45°、90°、135°,3种转角采用不同的权重系数,加大对大转角的惩罚力度。图5为转角惩罚示意图。
ti( l) =λ1 t45 °+λ2 t90 °+λ3 t135 °(16)
式中: λ1、 λ2、 λ3为权重系数,暂定 λ2 =2 λ1, λ3 =3 λ1; t45 °=π/4, t90 °=π/2, t135 °=(3 π) /4。
因此综合评定函数为:
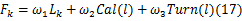
式中: ω1、 ω2、 ω3代表不同的权值大小。
信息素更新策略变为 Δ 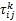
Step1 改进蚁群算法初始化。循环次数 Nc=0,时间 t=0,出动蚂蚁波数 Ncmax,将 m只蚂蚁放在栅格图中Start位置。按式(9)确定 ρ( l),分配起始空间各区域信息素浓度 τij( t)。
Step2 发动 m只蚂蚁根据正向搜索策略进行最佳路径搜索。当有蚂蚁找到目标点时,填充禁忌表,运用式(13)(15)确定并记录下计算量 Cal( l)、转折量 Turn( l),及此路线的综合评定函数 Fk,对未找到终点的蚂蚁,使其死亡,不进行信息素的更新。对找到终点的蚂蚁,按式(7)得出信息素增量,根据式(8)确定当前信息素衰减因子,根据式(10)更新整个障碍空间内信息素。
Step3 更新信息素后,蚂蚁立即调转方向,根据反向搜索策略搜索起始点。在找到起始点后,再次按照所走路线计算并记录 Cal( l)、 Turn( l)、 Fk值,确定信息素增量,信息素衰减因子,并更新整个障碍空间内的信息素。
Step4 当出动的所有蚂蚁都已返回起点后,填充禁忌表,完成一次循环,找出此次循环最短路径,循环次数 Nc=Nc+1。
Step5 若循环次数 Nc
为验证算法的性能,本文首先使用Matlab编写仿真程序。硬件环境如下:CPU为Core i3,2.13 GHz,2 G内存。
仿真中各参数设定如下:蚂蚁的个数为50只,信息素初始浓度 Δτij( t) =8,正向信息素因子 αf =1 .2,反向信息素因子 αb =0 .8,新增信息素强度因子 Q=1,衰减常数 γ=0.95,最小信息素挥发因子 ρmin =0 .1,权重系数 λ1 =1,权值 ω1: ω2: ω3 =5 ∶2 ∶1, q0 =0 .35。实验在20×20的栅格图中进行。
由表1的数据可以看出,虽然本文算法与基本蚁群算法、文献[7]算法找到的最短路径相同,但由于综合评价函数的引入,使得计算量、转折量都优于其他算法,因此,得到的最优路径效果更好。
| 表1 本文算法与其他蚁群算法仿真比较 Table 1 Simulation comparison between proposed and other ant colony optimization algorithms |
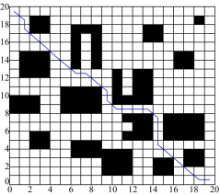
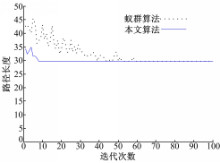
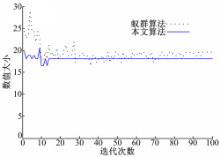
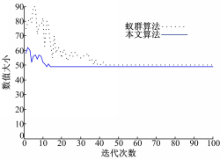
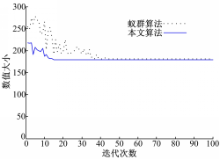
本文算法寻找到的最优路径如图6所示。最短路径、转折量、计算量及综合评价的收敛速度如图7~图10所示。
从仿真对比结果中可以看出:与基本蚁群算法相比,本文算法的收敛速度明显加快,全局寻优能力有很大的提高。从各个评价量的收敛曲线对比中可以看出,本文算法寻得的最优路径的计算量和转折量都有一定程度的减少。
在随机生成的30×30的栅格中运行规划出最优路径如图11所示。大量仿真实验证明,本文算法针对复杂地图具有较强的适应能力,即使在复杂的障碍环境中,该算法仍可以规划出最优路径。
本文根据搜索机器人的实际情况,对蚁群算法做出一定的改进,考虑到机器人的体积采用弧形前行的方式躲避障碍;设置禁忌栅格,防止搜索时路径死锁,且加快了搜索速度;采用折返蚂蚁的搜索方式,且正向蚂蚁与反向蚂蚁搜索策略不同,实现优势互补,加快了算法的收敛速度;在信息素的更新方式上,采用基于时间和空间的信息素更新策略,避过非核心区,使算法更加快速地收敛。构造新的路径综合评定函数,考虑到除距离外,计算量、转折量对最优路径的影响,使算法寻优规划更加合理。
| [1] |
|
| [2] |
|
| [3] |
|
| [4] |
|
| [5] |
|
| [6] |
|
| [7] |
|
| [8] |
|
| [9] |
|