汽车TCS液压控制单元特性测试与控制应用

引用本文

赵健, 张进, 朱冰, 吴坚. 汽车TCS液压控制单元特性测试与控制应用. 吉林大学学报: 工学版, 2014, 44(5): 1240-1246[ZHAO Jian, ZHANG Jin, ZHU Bing, WU Jian. Test and application of hydraulic control unit in automotive traction control system. Journal of Jilin University (Engineering and Technology Edition), 2014, 44(5): 1240-1246] 复制到剪切板

Permissions

汽车TCS液压控制单元特性测试与控制应用

赵健¹, 张进¹, 朱冰^1,², 吴坚¹

1.吉林大学汽车仿真与控制国家重点实验室, 长春 130022

2.吉林大学工程仿生教育部重点实验室, 长春 130022

通信作者:朱冰（1982-）,男,副教授,博士.研究方向:汽车地面系统分析与控制,工程仿生学. E-mail:zhubing@jlu.edu.cn

作者简介:赵健（1978-）,男,副教授,博士.研究方向:汽车地面系统分析与控制.E-mail:zhaojian@jlu.edu.cn

基金:国家自然科学基金项目（51105169, 51175215, 51205156）; 中国博士后科学基金项目（2011M500053, 2012T50292）

摘要

为实现汽车牵引力控制系统(TCS)中的主动液压制动控制精细调节,搭建了基于dSPACE的液压控制单元(HCU)性能测试系统,对HCU电磁阀特征参数进行了试验辨识,确定了采用脉宽调制控制(PWM)进行制动压力控制时目标压力梯度和目标占空比的映射关系。将测试分析结果应用于基于滑模控制的TCS算法,确定了基于目标压力梯度的PWM车轮制动控制逻辑,并在Matlab/Simulink和AMESim联合仿真环境下进行了仿真验证。结果表明:所设计的主动制动控制算法能以较高精度有效调节车轮滑转率,从而改善车辆行驶性能。

关键词: 车辆工程; 牵引力控制; 制动压力调节; 试验辨识; 脉宽调制; 滑模控制

中图分类号:U463.5 文献标志码:A 文章编号:1671-5497(2014)05-1240-07

Test and application of hydraulic control unit in automotive traction control system

ZHAO Jian¹, ZHANG Jin¹, ZHU Bing^1,², WU Jian¹

1.State Key Laboratory of Automotive Simulation and Control, Jilin University, Changchun 130022, China

2.Key Laboratory of Bionic Engineering of Ministry of Education, Jilin University, Changchun 130022, China

Abstract

In order to modify the hydraulic brake pressure accurately for Traction Control System (TCS), a Hydraulic Control Unit (HCU) test system based on dSPACE was developed. Using this system, the characteristic parameters of HCU valves were identified, and the relationship between the desired pressure gradient and target duty cycle in Pulse Width Modulation (PWM) brake control was obtained. In addition, the experiment and analysis results were used in the sliding-mode-based traction control algorithm and the wheel brake control logic based on target pressure gradient was proposed. The algorithm was verified using Matlab/Smulink and AMESim co-simulation. The results show that the proposed active brake control algorithm can provide high accurate regulation of wheel slip ratio, thus, the vehicle driving performance can be improved effectively.

Keyword: vehicle engineering; traction control system; brake pressure regulation; test identification; pulse width modulation; sliding mode control

Show Figures

0 引言

作为液压制动控制的执行机构,液压控制单元(Hydraulic control unit,HCU)的性能对基于主动制动控制的汽车动力学控制系统,如制动防抱死系统(Anti-lock braking system,ABS)、牵引力控制系统(Traction control system,TCS)和电子稳定控制系统(Electronic stability control,ESC)等具有重要影响。HCU的响应特性和品质以及它与制动系统和控制逻辑匹配的好坏都会影响最终控制效果^{[ 1]}。

由于HCU同时包含离散和连续特性,且其液压元件具有很强的非线性,因此,建立精确物理模型具有很大难度,近年来,国内外学者对HCU都进行了广泛的研究。系统中液压制动管路设置、不同工况下制动压力的估计误差以及HCU阀口特性等都将显著影响控制精度^{[ 2]},这些均是制约汽车主动制动控制系统发展的关键问题。文献[3]表明,若能根据HCU特性对车轮制动进行优化的非线性控制,则可以有效提高车轮滑动率控制精度。因此,一些研究开始关注在制动控制中考虑HCU特性以改善控制效果^{[ 4, 5]}。

汽车TCS系统可通过向驱动轮施加主动制动力矩,使驱动轮滑转率保持在最佳值附近,从而显著提高车辆在恶劣路面下的驱动能力。在研究HCU响应特性并建立简单精确的HCU模型的基础上设计TCS算法,可以进一步提高控制效果,滑模变结构控制由于具有响应快速、鲁棒性好、实现简单等优点,非常适用于TCS算法开发^{[ 6]}。

本文首先基于Matlab和dSPACE实时开发与测试环境搭建液压测试系统,对典型TCS系统HCU进行参数辨识和PWM控制试验研究,并将测试分析结果应用于TCS控制,设计基于主动制动控制的TCS滑模控制算法,根据期望的压力梯度计算得到目标占空比,对制动压力进行PWM控制,最后在MATLAB/Simulink和AMESim联合仿真控制下对控制算法进行了验证。

1 HCU测试系统

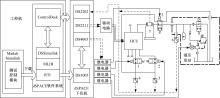
测试系统如图1所示。系统由工控机、dSPACE下位机、驱动系统和液压系统组成,其中:

(1)液压系统由液压泵站(其中8为动力源),二位二通常开阀1、2,二位四通阀3,流量传感器7和压力传感器4、5、6组成。HCU在系统中的安装位置如图1所示,所采用的HCU为X型管路布置,只进行一个回路的测试(一个接主缸的接口,一个接前轮缸的接口和一个接对侧后轮缸的接口),另一路的3个接口堵死。增压响应测试时,制动液经泵站流经阀3、流量传感器7流入HCU,再分两路流出,分别经过阀1、2流回阀3,最终回到油箱。减压响应测试时,将阀3通电,制动液经HCU两个接轮缸的接口流入,由接主缸的接口流出。

(2)试验者通过工控机实现对试验的控制,程序的编制在Matlab/Simulink环境下实现,并经dSPACE提供的RTI接口下载到dSPACE下位机中,试验者可以通过ControlDesk实现试验参数的实时修改、试验数据的显示与处理。dSPACE下位机中包括处理器板DS1005、多功能接口板DS2202、DS2211和I/O接口板DS4003,所有的板卡都安装在PX20扩展箱中。试验过程中,由上位机将试验控制程序下载至DS1005,通过接口板卡实现传感器信号的采集和驱动信号的发生。

(3)驱动系统由两部分组成,一部分用于驱动HCU电磁阀和泵电机,另一部分用于驱动测试系统电磁阀和动力源。

HCU电机和阀的驱动由独立的功率驱动电路来实现。HCU泵电机的特点是瞬间启动电流大,响应速度快,稳定状态下要求的驱动电流达到11 A,因此选用了英飞凌(Infineon)公司生产的BTS442智能高端电源开关芯片,它的负载电流可达21 A,可以满足电机的工作要求。HCU电磁阀为两位两通高速开关阀,要求的动作频率高,可达到100 Hz以上,阀线圈电阻很小,所需电流在1~3 A,因此,采用Infineon TLE5226智能四通道低端开关芯片作为驱动芯片,其工作电压为4.8~32 V,负载两端最大压差为60V,提供了独立四通道的电磁阀驱动能力。另外,还附加设计了短路保护、过载保护、过压保护以及过温保护等功能。该驱动电路模块接收DS2211发出的信号并加以放大,实现HCU的功率驱动。

液压测试系统的电机和电磁阀工作在稳态,没有响应速度的要求,因此,用继电器实现控制,继电器的控制可由DS4003实现。

(4)压力传感器信号和流量传感器信号由DS2202采集。其中,3个压力传感器分别用于测量HCU一个回路的入口(1个)和出口(2个)的压力状态。

	Figure Option View Download New Window
	图1 HCU测试系统方案Fig.1 Test system of hydraulic control unit

2 HCU液压响应特性测试

2.1 阀特性辨识

HCU电磁阀可以被简化成一个阀口,其压力-流量特性可由下式表示^{[ 7]}:

$\begin{matrix} Q = C_{d} A \sqrt[]{\frac{2}{ρ} (p_{i} - p_{o})} (1) \end{matrix}$

式中: $\begin{matrix} Q \end{matrix}$ 为流过阀的流量; C_d为阀口流量系数; $\begin{matrix} A \end{matrix}$ 为阀口流通面积; $\begin{matrix} ρ \end{matrix}$ 为流体密度; p_i为阀入口压力; p_o为阀出口压力。

对于确定的电磁阀,阀完全打开时,阀口流量系数 C_d、阀口流通面积 $\begin{matrix} A 和制动液的密度 ρ \end{matrix}$ 都可以认为是定值,因此,电磁阀的流量特性可以简化为:

$\begin{matrix} Q = C \cdot Δ p^{0.5} (2) \end{matrix}$

式中: $\begin{matrix} C \end{matrix}$ 为阀口系数。

$\begin{matrix} C = C_{d} A {(ρ / 2)}^{0.5} (3) \end{matrix}$

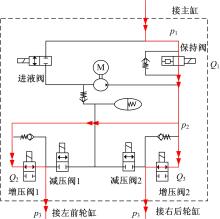
采用X型布置的HCU一个独立回路的液压系统如图2所示。

	Figure Option View Download New Window
	图2 HCU液压系统图Fig.2 Hydraulic circuit of HCU

以增压响应特性试验研究为例,HCU每个独立管路的增压试验中共有两个车轮通道,每个车轮增压回路中串联有1个增压阀和1个保持阀,其中保持阀为两个通路共用,因此增压特性测试与参数辨识共涉及3个电磁阀,阀口流量方程为:

$\begin{matrix} Q_{i} = C_{i} \cdot Δ p^{0.5} (4) \end{matrix}$

式中: i=1,2,3分别表示保持阀、左前增压阀和右后增压阀。

如图2所示,流过3个阀的流量分别为 $\begin{matrix} Q_{1} 、 Q_{2} 、 Q_{3}, 保持阀入口压力记为 p_{1}, 保持阀出口压力即增压阀入口压力记为 p_{2}, 增压阀出口压力记为 p_{3}, 其中, p_{1} 和 p_{3} \end{matrix}$ 分别为HCU入口和出口的压力,可以通过试验测得,而 $\begin{matrix} p_{2} \end{matrix}$ 是HCU内部的压力,不能直接测得。

将泵站视为一个理想恒压源,控制其输入压力稳定在1,2,…,12 MPa,并测定流过HCU的流量以及HCU进出口压力。

(1)两轮同时增压

将HCU所有电磁阀保持不通电状态,由泵站进行增压操作,制动液经HCU保持阀和同一回路上的两个增压阀流过HCU回到泵站油箱。测量HCU入口的制动压力 $\begin{matrix} p_{1}^{(1)} \end{matrix}$ 、出口的制动压力 $\begin{matrix} p_{3}^{(1)} \end{matrix}$ (两路出口连接在一起)和流过HCU的制动液流量 $\begin{matrix} Q_{1}^{(1)} \end{matrix}$ 。

(2)前轮增压

将图1中的二位二通阀1通电,制动液经HCU保持阀和测试回路中的前轮增压阀流过HCU,测量HCU入口制动压力 $\begin{matrix} p_{1}^{(2)} \end{matrix}$ 、通向前轮出口的制动压力 $\begin{matrix} p_{3}^{(2)} \end{matrix}$ 和流过的制动液流量 $\begin{matrix} Q_{1}^{(2)} \end{matrix}$ 。

(3)后轮增压

将图1中的二位二通阀2通电,制动液经HCU保持阀和测试回路中的后轮增压阀流过HCU,测量HCU入口制动压力 $\begin{matrix} p_{1}^{(3)} \end{matrix}$ 、通向后轮出口的制动压力 $\begin{matrix} p_{3}^{(3)} \end{matrix}$ 和流过的制动液流量 $\begin{matrix} Q_{1}^{(3)} \end{matrix}$ 。

两轮通道同时开启时,通过HCU的流量为:

$\begin{matrix} Q_{1}^{(1)} = Q_{2}^{(1)} + Q_{3}^{(1)} (5) \end{matrix}$

只有前轮通道开启时,通过HCU的流量为:

$\begin{matrix} Q_{1}^{(2)} = Q_{2}^{(2)} (6) \end{matrix}$

只有后轮通道开启时,通过HCU的流量为:

$\begin{matrix} Q_{1}^{(3)} = Q_{3}^{(3)} (7) \end{matrix}$

可以得到以下方程组:

$\begin{matrix} \{\begin{matrix} Q_{1}^{(1)} = C_{1} {(p_{1}^{(1)} - p_{2}^{(1)})}^{0.5} \\ Q_{1}^{(1)} = C_{2} {(p_{2}^{(1)} - p_{3}^{(1)})}^{0.5} + \\ C_{3} {(p_{2}^{(1)} - p_{3}^{(1)})}^{0.5} \\ Q_{1}^{(2)} = C_{1} {(p_{1}^{(2)} - p_{2}^{(2)})}^{0.5} \\ Q_{1}^{(2)} = C_{2} {(p_{2}^{(2)} - p_{3}^{(2)})}^{0.5} \\ Q_{1}^{(3)} = C_{1} {(p_{1}^{(3)} - p_{2}^{(3)})}^{0.5} \\ Q_{1}^{(3)} = C_{3} {(p_{2}^{(3)} - p_{3}^{(3)})}^{0.5} \end{matrix} (8) \end{matrix}$

式中: $\begin{matrix} C_{1} 、 C_{2} 、 C_{3} 以及 p_{2}^{(1)} 、 p_{2}^{(2)} 、 p_{2}^{(3)} \end{matrix}$ 六个变量未知,其他参量均通过试验测得,未知数与方程数目相同,可求解。由于每个试验均进行了12个压力点的测试,因此可以求得12组解。

求解过程中,发现根据试验数据无法得到合理的 $\begin{matrix} C_{1} 实数解, 求得的 p_{2} \end{matrix}$ 如图3所示,由图可见3种试验条件下的压力曲线几乎完全重合,且保持阀出口压力几乎都等于HCU的入口压力,这说明对整个HCU系统而言,保持阀起不到阀口节流作用,可以将其简化为一段管路,阀口节流作用完全由增压阀实现。

	Figure Option View Download New Window
	图3 TCS隔离阀出口压力Fig.3 Curves of pressure at TCS isolation valve outlet

根据12组测试结果可以直接由HCU的进出口压力及式(4)对增压阀进行回归并对结果进行平均,得到阀口系数为:

$\begin{matrix} C_{2} = 0.3948, C_{3} = 0.1853 (9) \end{matrix}$

拟合曲线和测试结果如图4所示。拟合曲线与试验数据的残差平方和SSE、决定系数Rsquare和标准差RMSE如表1所示。可以看出,拟合结果具有很高的精度,以上简化合理。

	Figure Option View Download New Window
	图4 HCU增压试验拟合曲线Fig.4 Fitted curves of HCU pressurizing test

表1 拟合结果统计特性 Table 1 Statistic characteristics of fitting data

2.2 PWM增压控制测试

HCU中所采用的轮缸压力控制阀均为高速开关阀,应用合适的PWM控制方法可以实现精确的轮缸压力控制^{[ 4]}。采用PWM控制HCU电磁阀时,轮缸压力与流量关系可以表示为:

$\begin{matrix} \begin{matrix} Q = \frac{A}{A_{\max}} C_{d} A_{\max} \sqrt[]{\frac{2}{ρ} Δp} = \\ k_{A} (D) \cdot C \cdot Δ p^{0.5} (10) \end{matrix} \end{matrix}$

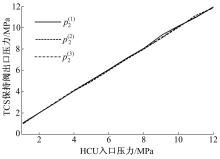
式中: A_max为占空比为100%时的阀口流通面积; $\begin{matrix} D \end{matrix}$ 为占空比; $\begin{matrix} k_{A} 为无因次有效阀口开度; k_{A} (D) 为不同占空比 D 下阀口有效通流面积 A 与 A_{\max} 的比值, 是与 D 相关的函数, 利用试验测得的阀口两端压差和平均流量以及上文计算得到的增压阀阀口系数, 即可求解 k_{A} (D) 。 \end{matrix}$

图5为根据实测值计算得到的 $\begin{matrix} k_{A} (D) \end{matrix}$ 与按直线方程进行拟合得到的结果。由于增压阀是常开阀, D=100%对应阀口全关。

	Figure Option View Download New Window
	图5 有效阀口开度与占空比的关系Fig.5 Relationship between effective valve opening area and duty ratio

轮缸压力可以采用式(1)估算,反之,也可通过控制所需增压梯度和当前轮缸压力计算目标占空比。

$\begin{matrix} \overset{\cdot}{p} = k_{A} (D) \frac{β_{V}}{V} C \sqrt[]{p_{in} - p_{w}} (11) \end{matrix}$

式中: β_V为制动液体积弹性模量; $\begin{matrix} V \end{matrix}$ 为轮缸中制动液量; p_in为轮缸进液阀入口压力; p_w为当前轮缸压力。

3 TCS压力控制应用

采用滑模控制设计TCS控制算法。驱动工况下,轮胎的纵向滑转率定义为:

$\begin{matrix} s = \frac{ωr - v}{ωr} (12) \end{matrix}$

式中: $\begin{matrix} ω 为车轮旋转角速度; r 为轮胎有效半径; v \end{matrix}$ 为纵向车速。

实际滑转率与理想滑转率的差值 $\begin{matrix} e \end{matrix}$ 及其导数作为状态变量:

$\begin{matrix} \{\begin{matrix} e = s - s_{0} \\ \overset{\cdot}{e} = \overset{\cdot}{s} \end{matrix} (13) \end{matrix}$

式中: $\begin{matrix} s_{0} \end{matrix}$ 为轮胎最佳滑转率。

切换函数为:

$\begin{matrix} δ = ce + \overset{\cdot}{e} = \overset{\cdot}{s} + c [s - s_{0}] (14) \end{matrix}$

式中: $\begin{matrix} c \end{matrix}$ 为滑模面系数。

考虑到控制的快速性要求,采用指数趋近率对轮胎的滑移率进行滑模变结构控制,取:

$\begin{matrix} \overset{\cdot}{δ} = c \overset{\cdot}{e} + \overset{\cdot \cdot}{e} = - ε \cdot sign (δ) - kδ (15) \end{matrix}$

式中: $\begin{matrix} ε 为等速趋近速率; k \end{matrix}$ 为指数趋近阶次,二者均为正实数,则有:

$\begin{matrix} δ \overset{\cdot}{δ} = - ε |δ| - k δ^{2} < 0 (16) \end{matrix}$

满足滑模变结构控制的全局达到条件,则滑动模态存在,控制方法可行。

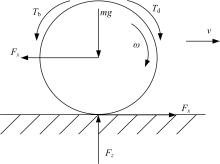
求式(12)的一阶和二阶导数,将 $\begin{matrix} \overset{\cdot}{s} \end{matrix}$ 和 $\begin{matrix} \overset{\cdot \cdot}{s} \end{matrix}$ 代入式(15),并略去高阶项,可得:

$\begin{matrix} \begin{matrix} \overset{\cdot \cdot}{ω} = - c \overset{\cdot}{ω} + \\ \frac{ωr}{v} [c \frac{\overset{\cdot}{v}}{r} + 2 \overset{\cdot}{s} \overset{\cdot}{ω} - ωε \cdot sign (δ) - ω k δ] (17) \end{matrix} \end{matrix}$

忽略滚动阻力,驱动轮在驱动工况下的受力如图6所示,动力学平衡方程为:

$\begin{matrix} I_{w} \overset{\cdot}{ω} = T_{d} - (T_{b} + F_{x} r) (18) \end{matrix}$

式中: T_d为作用在驱动轮上的驱动力矩; T_b为作用在驱动轮上的制动力矩; $\begin{matrix} F_{x} \end{matrix}$ 为地面对车轮的纵向作用力; I_w为车轮转动惯量。

	Figure Option View Download New Window
	图6 单轮驱动模型Fig.6 Single wheel driving model

对式(18)两边求导,得:

$\begin{matrix} {\overset{\cdot}{T}}_{b} = {\overset{\cdot}{T}}_{d} - ({\overset{\cdot}{F}}_{x} r + I_{w} \overset{\cdot \cdot}{ω}) (19) \end{matrix}$

将式(17)代入式(19)即可得到所需的驱动轮制动力矩变化率 $\begin{matrix} {\overset{\cdot}{T}}_{b}, \end{matrix}$ 进而求得制动压力梯度:

$\begin{matrix} {\overset{\cdot}{p}}_{b} = K_{b} {\overset{\cdot}{T}}_{b} (20) \end{matrix}$

式中: K_b为制动轮缸压力与制动器制动力矩的换算系数,由轮缸活塞面积、制动器效能因数和制动器有效半径决定。

考虑到电磁阀工作死区,并为了减小轮缸压力的波动,设定压力梯度门限为 $\begin{matrix} {\overset{\cdot}{p}}_{b 0}, 当 {\overset{\cdot}{p}}_{b} \end{matrix}$ 小于门限时,采取保压操作,即:

$\begin{matrix} {\overset{\cdot}{p}}_{b} = \{\begin{matrix} 0, - {\overset{\cdot}{p}}_{b 0} < {\overset{\cdot}{p}}_{b} < {\overset{\cdot}{p}}_{b 0} \\ {\overset{\cdot}{p}}_{b}, 其他 \end{matrix} (21) \end{matrix}$

最后,依据式(11)将目标压力梯度转换为占空比。将占空比发送给HCU中相应电磁阀即可产生期望制动压力,实现对TCS系统的闭环控制。

4 仿真结果分析

为验证上述算法,在Matlab/Simulink和AMESim环境下建立基于单轮车辆模型的联合仿真平台,如图7所示。单轮车辆模型和滑模变结构控制器在Simulink环境下搭建,制动系统模型在AMESim环境下搭建,二者的数据交互通过AMESim提供的应用程序API和Simulink S函数来实现。其中,单轮车辆模型采用文献[8]中的方法建立,发动机模型采用查表法实现,变速器给定档位和传动比,车轮模型参见图6,轮胎模型也采用查表实现。

	Figure Option View Download New Window
	图7 单轮车辆模型的Matlab/Simulink与AMESim联合仿真平台Fig.7 Co-simulation system of Matlab/Simulink and AMESim for single wheel model

仿真在附着系数为0.2的路面上进行,初始车速为0.5 m/s,变速器保持3档不变,油门开度100%。仿真结果如图8、图9所示。

	Figure Option View Download New Window
	图8 车辆速度曲线Fig.8 Curves for vehicle speed

	Figure Option View Download New Window
	图9 主动制动控制压力曲线与发动机力矩曲线Fig.9 Curves for active brake pressure and engine torque

图8(a)为无牵引力控制的轮速与车速曲线。由图可见,没有牵引力控制的情况下,驱动轮迅速发生打滑,远远超出目标轮速,导致车辆牵引性能变差,8 s后车速为10.4 m/s。

图8(b)为有牵引力控制的轮速与车速曲线。图9为主动制动控制压力曲线和发动机力矩曲线。由图可见,采用本文的控制算法,虽然发动机力矩由于外特性曲线精度问题有一些不连续,但制动压力仍能很好跟随发动机力矩的变化趋势,对驱动轮上的驱动力矩施加控制。使驱动轮的打滑得到有效控制,在经过控制最初阶段的微小波动之后,驱动轮转速保持在目标轮速附近,8 s后车速达到13.2 m/s,较无牵引力控制的情况提高了26%。

5 结束语

本文进行了制动系统HCU特性测试,并将试验研究结果应用于TCS控制。试验结果表明:增压时HCU各通道可以简化为一个阀口,而阀口节流作用是由轮缸增压阀决定的;在阀口参数辨识的基础上,可以建立控制所需增压梯度和当前轮缸压力与目标占空比的关系,并用于控制系统设计。仿真结果表明:在基于滑模控制的TCS算法中考虑制动系统响应特性进行PWM控制,可以有效控制驱动轮在低附着路面上的打滑,进而提高车辆的牵引性能。

The authors have declared that no competing interests exist.

参考文献

View Option

[1]	Kevin O'Dea. Anti-lock braking performance and hydraulic brake pressure estimation[C]∥2005 SAE World Congress, Detroit, Michigan, USA , 2005. [本文引用:1]
[2]	Ahn C, Kim B, Lee M. Modeling and control of an anti-lock brake and steering system for cooperative control on split-mu surfaces[J]. International Journal of Automotive Technology, 2012, 13(4): 571-581. [本文引用:1] [JCR: 0.69]
[3]	Mehdi Mirzaei, Hossein Mirzaeinejad. Optimal design of a non-linear controller for anti-lock braking system[J]. Transportation Research Part C: Emerging Technologies, 2012, 24: 19-35. [本文引用:1] [JCR: 2.006]
[4]	朱冰, 赵健, 李静, 等. 面向底盘集成控制的液压制动压力估算方法[J]. 吉林大学学报: 工学版, 2009, 39(增刊): 22-26. Zhu Bing, Zhao Jian, Li Jing, et al. Hydraulic brake pressure estimation for integrated chassis control[J]. Journal of Jilin University (Engineering and Technology Edition), 2009, 39(Sup. ): 22-26. [本文引用:2] [CJCR: 0.701]
[5]	孟爱红, 王治中, 宋健, 等. 汽车ESP液压控制单元关键部件建模与系统仿真[J]. 农业机械学报, 2013, 44(2): 1-5. Meng Ai-hong, Wang Zhi-zhong, Song Jian, et al. Critical component modeling and system simulation of hydraulic control unit of automotive electronic stability program[J]. Transactions of the Chinese Society for Agricultural Machinery, 2013, 42(2): 1-5. [本文引用:1]
[6]	Kang Ming-xin, Li Liang, Li Hong-zhi, et al. Coordinated vehicle traction control based on engine torque and brake pressure under complicated road conditions[J]. Vehicle System Dynamics: International Journal of Vehicle Mechanics and Mobility, 2012, 50(9): 1473-1494. [本文引用:1]
[7]	黎启柏. 液压元件手册[M]. 北京: 冶金工业出版社, 2000. [本文引用:1]
[8]	喻凡. 车辆动力学及其控制[M]. 北京: 机械工业出版社, 2010. [本文引用:1]

2005

0.0

... HCU的响应特性和品质以及它与制动系统和控制逻辑匹配的好坏都会影响最终控制效果^[1] ...

2012

0.69

0.0

. 2012, 13(4):571-581 DOI:10.1007/s12239-012-0055-y

Modeling and control of an anti-lock brake and steering system for cooperative control on split-mu surfaces

1. Department of Mechanical Engineering, The University of Michigan, Ann Arbor, MI, 48109, USA 2. Korea Electric Power Corporation, Munji-ro 65, Yuseong-gu, Daejeon, 305-380, Korea 3. Hyundai Motor Company, 772-1 Jangdeog-dong, Hwaseong-si, Gyeonggi, 445-706, Korea

Abstract The brake and steering systems in vehicles are the most effective actuators that directly affect the vehicle dynamics. In general, the brake system affects the longitudinal dynamics and the steering system affects the lateral dynamics; however, their effects are coupled when the vehicle is braking on a non-homogenous surface, such as a split-mu road. The yaw moment compensation of the steering control on a split-mu road is one of the basic functions of integrated or coordinated chassis control systems and has been demonstrated by several chassis suppliers. However, the disturbance yaw moment is generally compensated for using the yaw rate feedback or using wheel brake pressure measurement. Access to the wheel brake pressure through physical sensors is not cost effective; therefore, we modeled the hydraulic brake system to avoid using physical sensors and to estimate the brake pressure. The steering angle controller was designed to mitigate the non-symmetric braking force effect and to stabilize the yaw rate dynamics of the vehicle. An H-infinity design synthesis was used to take the system model and the estimation errors into account, and the designed controller was evaluated using vehicle tests.

... 系统中液压制动管路设置、不同工况下制动压力的估计误差以及HCU阀口特性等都将显著影响控制精度^[2],这些均是制约汽车主动制动控制系统发展的关键问题 ...

2012

2.006

0.0

. 2012, 24:null-null

Optimal design of a non-linear controller for anti-lock braking system

2009

0.0

0.701

... 因此,一些研究开始关注在制动控制中考虑HCU特性以改善控制效果^[4,5] ...

... 2 PWM增压控制测试HCU中所采用的轮缸压力控制阀均为高速开关阀,应用合适的PWM控制方法可以实现精确的轮缸压力控制^[4] ...

2013

0.0

... 因此,一些研究开始关注在制动控制中考虑HCU特性以改善控制效果^[4,5] ...

2012

0.0

... 在研究HCU响应特性并建立简单精确的HCU模型的基础上设计TCS算法,可以进一步提高控制效果,滑模变结构控制由于具有响应快速、鲁棒性好、实现简单等优点,非常适用于TCS算法开发^[6] ...

2000

0.0

... 1 阀特性辨识HCU电磁阀可以被简化成一个阀口,其压力-流量特性可由下式表示^[7]: ...

2010

0.0