动态约束下可重构模块机器人分散强化学习最优控制

引用本文

董博, 刘克平, 李元春. 动态约束下可重构模块机器人分散强化学习最优控制. 吉林大学学报:工学版, 2014, 44(5): 1375-1384[DONG Bo, LIU Ke-ping, LI Yuan-chun. Decentralized reinforcement learning optimal control for time varying constrained reconfigurable modular robot. Journal of Jilin University (Engineering and Technology Edition), 2014, 44(5): 1375-1384] 复制到剪切板

Permissions

动态约束下可重构模块机器人分散强化学习最优控制

董博¹, 刘克平², 李元春²

1.吉林大学控制科学与工程系, 长春 130022

2.长春工业大学控制工程系, 长春 130012

通信作者:李元春（1962-）,男,教授,博士生导师.研究方向:智能机械与机器人控制.E-mail:liyc@mail.ccut.edu.cn

作者简介:董博（1986-）,男,博士研究生.研究方向:智能机械与机器人控制.E-mail:bodong09@mails.jlu.edu.cn

基金:国家自然科学基金项目（61374051,60974010）; 吉林省科技发展计划项目（20110705）

摘要

基于ction-critic-identifier(ACI)与RBF神经网络,提出了一种外界动态约束下的可重构模块机器人分散强化学习最优控制方法,解决了存在强耦合不确定性的模块机器人系统的连续时间非线性最优控制问题。文中将机器人动力学模型描述为一个交联子系统的集合,基于连续时间MDPs性能指标,结合ACI与RBF神经网络,对子系统最优值函数,最优控制策略及总体不确定项进行辨识,使系统满足HJB方程下的最优条件,从而使可重构模块机器人子系统渐进跟踪期望轨迹,跟踪误差收敛且有界。采用Lyapunov理论对系统稳定性进行证明,数值仿真验证了所提出的分散控制策略的有效性。

关键词: 自动控制技术; 可重构模块机器人; 强化学习; 非线性最优控制; 分散控制

中图分类号:TP273 文献标志码:A 文章编号:1671-5497(2014)05-1375-10

Decentralized reinforcement learning optimal control for time varying constrained reconfigurable modular robot

DONG Bo¹, LIU Ke-ping², LI Yuan-chun²

1.Department of Control Science and Engineering,Jilin University,Changchun 130022,China

2.Department of Control Engineering,Changchun University of Technology,Changchun 130012,China

Abstract

Based on Action-Critic-Identifier (ACI) and Radial Basis Function (RBF) neural network, a novel decentralized reinforcement learning optimal control method for time varying constrained reconfigurable modular robot is presented. The continuous time nonlinear optimal control problem of strongly coupled uncertainty robotic system is solved. The dynamics of the robot is described as a synthesis of interconnected subsystems. As a precondition to the continuous-time MDPs performance indicators, the optimal value function, optimal control policy and global uncertainty of the subsystems are estimated combing with ACI and RBF network. The optimal conditions of HJB equation with regard to the subsystem are satisfied, so that the reconfigurable modular robot system can track the desired trajectory in a short time and the estimation error can converge to zero in finite time. The stability of the system is confirmed by Lyapunov theory. Simulations are performed to illustrate the effectiveness of the proposed decentralized control scheme.

Keyword: automatic control technology; reconfigurable modular robot; reinforcement learning; nonlinear optimal control; decentralized control

Show Figures

0 引言

可重构模块机器人是一类具有标准接口与模块可以根据不同的任务需求对自身构形进行重新组合与配置的机器人。根据模块设计的概念及子系统分散控制理论,可重构模块机器人可以在不同的外界环境与约束下根据不同的任务需要来改变自身构形,且不需要重新设计控制器。此外,可重构模块机器人的模块关节还包括了通讯、驱动、控制、传动等单元,使重构后的机器人对新的工作环境具有更好的适应性。

许多学者对可重构模块机器人的动力学与控制方法进行了研究。文献[1]提出了一种基于VGSTA-ESO的可重构模块机器人分散自抗扰控制方法,文中设计了一种高精度VGSTA-ESO,用来对子系统模型非线性项与子系统交联项进行辨识,从而实现关节轨迹跟踪控制。基于计算力矩法,文献[2]提出了一种基于速度观测模型的可重构机械臂模糊RBF神经网络补偿控制方法,通过Lyapunov函数对神经网络权值、隶属度函数中心与宽度进行更新,并证明补偿控制算法一致有界。文献[3]提出了一种可重构模块机器人分散自适应模糊滑模控制方法,采用模糊逻辑系统估计子系统未知动力学模型,并通过带有自适应结构的滑模控制器补偿交联项及模糊估计误差。文献[4]提出了一种基于观测器的可重构模块机器人自适应模糊控制器,采用自适应模糊系统对子系统未知动力学模型进行辨识,并通过状态估计的方式来重构子系统交联项。

近年来,可重构模块机器人系统的最优控制问题成为机器人控制领域研究的热点与难点之一,而强化学习算法自诞生之日起就被认为是解决此类问题最有效的方法。强化学习是一种从环境到行为映射的学习方法,其目的是将环境中的报酬与评价信号最大化。与监督学习相比,强化学习不需要预知各种状态下的导师信号,而是在与环境的交互过程中学习,由于其具有在非线性模型不确定性条件下的自适应优化能力,因而在解决复杂模型的优化策略与最优控制等问题方面有着独特的优势^{[ 5, 6, 7, 8]}。

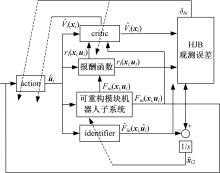
本文基于马尔可夫决策过程(Markov decision processes,MDPs)连续时间性能指标,将ACI与RBF神经网络相结合,在外界动态约束下提出一种可重构模块机器人分散强化学习最优控制策略,解决了存在强耦合不确定性的模块机器人的连续时间非线性最优控制问题。采用ACI对系统Hamilton jacobi bellman(HJB)方程进行辨识,其中critic网络可以辨识系统最优值函数,action网络用来辨识系统最优控制策略,最后通过identifier网络对系统模型非线性项与子系统交联项进行辨识,并利用RBF神经网络对ACI网络权值进行更新,使系统满足HJB方程下的最优条件,以此来满足机器人子系统对期望轨迹的跟踪要求。

1 问题描述

可重构模块机器人末端所受外部动态约束为:

$\begin{matrix} Φ (q, t) = 0 (1) \end{matrix}$

式中: $\begin{matrix} q \in R^{n} \end{matrix}$ 为可重构模块机器人的关节变量;函数 $\begin{matrix} Φ : R^{n} \to R^{m}, m \end{matrix}$ 为外部限制条件维数。

在动态约束下, $\begin{matrix} n \end{matrix}$ 自由度的可重构模块机器人动力学方程可以描述为:

$\begin{matrix} \begin{matrix} M (q) \overset{\cdot \cdot}{q} + C (q, \overset{\cdot}{q}) \overset{\cdot}{q} + G (q) + F (q, \overset{\cdot}{q}) = \\ u + J_{Φ}^{T} (q, t) f (2) \end{matrix} \end{matrix}$

式中: $\begin{matrix} M (q) \in R^{n \times n} \end{matrix}$ 为惯性矩阵; $\begin{matrix} C (q, \overset{\cdot}{q}) \overset{\cdot}{q} \in R^{n} \end{matrix}$ 为哥氏力和离心力项; $\begin{matrix} G (q) \in R^{n} \end{matrix}$ 为重力项; $\begin{matrix} F (q, \overset{\cdot}{q}) \in R^{n} \end{matrix}$ 为摩擦项; $\begin{matrix} u \in R^{n} \end{matrix}$ 为关节力矩向量; $J_{Φ}^{T} (q, t) f$ 为模块机器人末端接触力, $\begin{matrix} J_{Φ} (q, t) \end{matrix}$ 为雅克比矩阵, $\begin{matrix} f \end{matrix}$ 为与之对应的拉格朗日乘子。

在对自由空间运行的模块机器人引入 $\begin{matrix} m 个约束后, 由于约束 (1) 的限制, 系统失去了 m 个自由度, 因此, 机器人的自由度由 n 变为 n - m, 即仅需 n - m \end{matrix}$ 个独立关节变量即可完全描述系统的受限运动。

定义关节变量表示形式如下:

$\begin{matrix} q = [\begin{matrix} q_{1} \\ q_{2} \end{matrix}], q_{1} \in R^{n - m}, q_{2} \in R^{m} (3) \end{matrix}$

将式(3)代入式(1)可得:

$\begin{matrix} Φ (q_{1}, Ω (q, t), t) = 0 \end{matrix}$

其中, $\begin{matrix} q_{2} = Ω (q_{1}, t), \end{matrix}$ 式(3)可用独立变量 $\begin{matrix} q_{1} \end{matrix}$ 完全描述:

$\begin{matrix} q = [\begin{matrix} q_{1} \\ Ω (q_{1}, t) \end{matrix}] (4) \end{matrix}$

对式(4)求导可得:

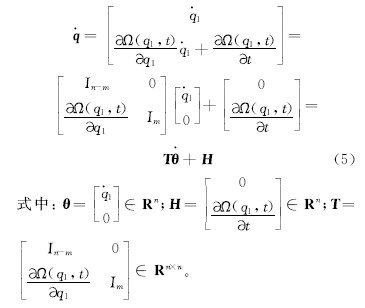
对 $\begin{matrix} q \end{matrix}$ 求二阶导数可得:

$\begin{matrix} \overset{\cdot \cdot}{q} = T \overset{\cdot \cdot}{θ} + \overset{\cdot}{T} \overset{\cdot}{θ} + \overset{\cdot}{H} (6) \end{matrix}$

将式(5)(6)代入式(2)可得:

$\begin{matrix} \begin{matrix} M (q) (T \overset{\cdot \cdot}{θ} + \overset{\cdot}{T} \overset{\cdot}{θ} + \overset{\cdot}{H}) + C (q, \overset{\cdot}{q}) (T \overset{\cdot}{θ} + \overset{\cdot}{H}) + \\ G (q) + F (q, \overset{\cdot}{q}) = u + J_{Φ}^{T} (q, t) f (7) \end{matrix} \end{matrix}$

定义 $\begin{matrix} E = [\begin{matrix} I_{(n - m) \times (n - m)} \\ 0_{m \times (n - m)} \end{matrix}] \in R^{n \times (n - m)}, \end{matrix}$ 由此可得: $\begin{matrix} θ = [\begin{matrix} q_{1} \\ 0 \end{matrix}] = E q_{1} 。 \end{matrix}$ 因此,式(2)可以分解为如下形式:

$\begin{matrix} \begin{matrix} \overset{n}{\sum_{j = 1}} M_{ij} (q) [(TE {\overset{\cdot \cdot}{q}}_{1})_{j} + (\overset{\cdot}{T} E {\overset{\cdot}{q}}_{1})_{j} + {\overset{\cdot}{H}}_{j}] + \\ {\bar{G}}_{i} (q) - f_{i} + \overset{n}{\sum_{j = 1}} C_{ij} (q, \overset{\cdot}{q}) [(TE {\overset{\cdot}{q}}_{1})_{j} + H_{j}] + \\ F_{i} (q_{i}, {\overset{\cdot}{q}}_{i}) = u_{i} (8) \end{matrix} \end{matrix}$

式中: $\begin{matrix} (TE {\overset{\cdot \cdot}{q}}_{1})_{j} 、 (\overset{\cdot}{T} E {\overset{\cdot}{q}}_{1})_{j} 、 (TE {\overset{\cdot}{q}}_{1})_{j} 、 H_{j} \end{matrix}$ 分别为 $\begin{matrix} (TE {\overset{\cdot \cdot}{q}}_{1}) 、 (\overset{\cdot}{T} E {\overset{\cdot}{q}}_{1}) 、 (TE {\overset{\cdot}{q}}_{1}) 、 H 的第 j \end{matrix}$ 个分量; $\begin{matrix} {\bar{G}}_{i} (q) 、 F_{i} (q_{i}, {\overset{\cdot}{q}}_{i}) \end{matrix}$ 分别为向量 $\begin{matrix} G (q) 、 F (q, \overset{\cdot}{q}) 的第 i \end{matrix}$ 个分量; $\begin{matrix} f_{i} 为第 i \end{matrix}$ 个关节所受的外界约束力; $\begin{matrix} M_{ij} (q) \end{matrix}$ 和 $\begin{matrix} C_{ij} (q, \overset{\cdot}{q}) \end{matrix}$ 分别为矩阵 $\begin{matrix} M (q) \end{matrix}$ 和 $\begin{matrix} C (q, \overset{\cdot}{q}) 的第 ij \end{matrix}$ 个分量。

子系统动力学模型可以改写为:

$\begin{matrix} \begin{matrix} M_{i} (q_{i}) {\overset{\cdot \cdot}{q}}_{i} + C_{i} (q_{i}, {\overset{\cdot}{q}}_{i}) {\overset{\cdot}{q}}_{i} + G_{i} (q_{i}) + \\ F_{i} (q_{i}, {\overset{\cdot}{q}}_{i}) + Z_{i} (q, \overset{\cdot}{q}, \overset{\cdot \cdot}{q}) - f_{i} = u_{i} (9) \\ 式中 : \\ Z_{i} (q, \overset{\cdot}{q}, \overset{\cdot \cdot}{q}) = \overset{n}{\sum_{j = 1, j \neq i}} M_{ij} (q) [{(TE {\overset{\cdot \cdot}{q}}_{1})}_{j} + \\ {(\overset{\cdot}{T} E {\overset{\cdot}{q}}_{1})}_{j} + {\overset{\cdot}{H}}_{j}] + \\ M_{ii} (q) [{(TE {\overset{\cdot \cdot}{q}}_{1})}_{i} + {(\overset{\cdot}{T} E {\overset{\cdot}{q}}_{1})}_{i} + {\overset{\cdot}{H}}_{i}] - \\ M_{i} (q_{i}) {\overset{\cdot \cdot}{q}}_{i} + \overset{n}{\sum_{j = 1, j \neq i}} C_{ij} (q, \overset{\cdot}{q}) [{(TE {\overset{\cdot}{q}}_{1})}_{j} + H_{j}] + \\ C_{ii} (q, \overset{\cdot}{q}) [{(TE {\overset{\cdot}{q}}_{1})}_{j} + H_{j}] - \\ C_{i} (q_{i}, {\overset{\cdot}{q}}_{i}) {\overset{\cdot}{q}}_{i} + [{\bar{G}}_{i} (q) - G_{i} (q_{i})] (10) \end{matrix} \end{matrix}$

令 $\begin{matrix} x_{i} = [x_{i 1}, x_{i 2}]^{T} = [q_{i}, {\overset{\cdot}{q}}_{i}]^{T}, i = 1, \dots, n, \end{matrix}$ 式(9)所示的外界动态约束下的可重构模块机器人子系统动力学模型可以转换成如下状态空间的形式:

$\begin{matrix} S_{i} : \{\begin{matrix} {\overset{\cdot}{x}}_{i 1} = x_{i 2} \\ {\overset{\cdot}{x}}_{i 2} = - f (x_{i}, u_{i}) - h_{i} (q, \overset{\cdot}{q}, \overset{\cdot \cdot}{q}) \\ y_{i} = x_{i 1} \end{matrix} (11) \end{matrix}$

式中: $\begin{matrix} x_{i} \end{matrix}$ 为子系统状态向量; $\begin{matrix} y_{i} \end{matrix}$ 为子系统输出向量; $\begin{matrix} f (x_{i}, u_{i}) \end{matrix}$ 为子系统模型非线性项; $\begin{matrix} h_{i} (q, \overset{\cdot}{q}, \overset{\cdot \cdot}{q}) \end{matrix}$ 为子系统交联项。

$\begin{matrix} f (x_{i}, u_{i}) \end{matrix}$ 与 $\begin{matrix} h_{i} (q, \overset{\cdot}{q}, \overset{\cdot \cdot}{q}) \end{matrix}$ 可以表示为:

$\begin{matrix} \{\begin{matrix} f (x_{i}, u_{i}) = M_{i}^{- 1} (q_{i}) [C_{i} (q_{i}, {\overset{\cdot}{q}}_{i}) {\overset{\cdot}{q}}_{i} + G_{i} (q_{i}) + \\ F_{i} (q_{i}, {\overset{\cdot}{q}}_{i}) - f_{i} - u_{i} \\ h_{i} (q, \overset{\cdot}{q}, \overset{\cdot \cdot}{q}) = M_{i}^{- 1} (q_{i}) Z_{i} (q, \overset{\cdot}{q}, \overset{\cdot \cdot}{q}) \end{matrix} (12) \end{matrix}$

本文基于MDPs连续时间性能指标,针对外界动态约束下的可重构模块机器人子系统动力学方程建立HJB方程,结合ACI与RBF神经网络分别对HJB方程中的最优值函数、最优控制策略及子系统非线性项进行辨识,并设计权值更新率对网络权值进行更新,从而得出满足HJB方程的相应最优解,以此来满足动态约束下可重构模块机器人子系统关节轨迹跟踪要求。

2 基于ACI的分散强化学习最优控制

假设1 期望轨迹 $\begin{matrix} y_{id}, {\overset{\cdot}{y}}_{id}, {\overset{\cdot \cdot}{y}}_{id}, \end{matrix}$ 输入增益矩阵 $\begin{matrix} b_{i} (x_{i}) \end{matrix}$ 有界且已知。则式(11)可以变形为如下的状态方程:

$\begin{matrix} S_{i} : \{\begin{matrix} {\overset{\cdot}{x}}_{i 1} = x_{i 2} \\ {\overset{\cdot}{x}}_{i 2} = - [F (x_{i}, u_{i}) + h_{i} (q, \overset{\cdot}{q}, \overset{\cdot \cdot}{q})] + b_{i} (x_{i}) u_{i} \\ y_{i} = x_{i 1} \end{matrix} (13) \end{matrix}$

式中: $\begin{matrix} F (x_{i}, u_{i}) = f (x_{i}, u_{i}) + b_{i} (x_{i}) u_{i} 。 \end{matrix}$

假设2 子系统交联项 $\begin{matrix} h_{i} (q, \overset{\cdot}{q}, \overset{\cdot \cdot}{q}) \end{matrix}$ 有界,且满足:

$\begin{matrix} |h_{i} (q, \overset{\cdot}{q}, \overset{\cdot \cdot}{q})| \leq δ_{i 0} + \overset{n}{\sum_{j = 1}} δ_{ij} (|s_{ij}|) (14) \end{matrix}$

式中: $\begin{matrix} δ_{i 0} > 0 \end{matrix}$ 为未知常数; $\begin{matrix} δ_{ij} (|s_{ij}|) \geq 0 \end{matrix}$ 为未知光滑Lipschitz函数。

定义一类马尔可夫决策过程为一个五元组: $\begin{matrix} < \begin{matrix} X & A & R & P & J \end{matrix} >; x_{i}, x_{j} \in X; a \in A \end{matrix}$ 。其中, $\begin{matrix} X \end{matrix}$ 为环境状态集; $\begin{matrix} A \end{matrix}$ 为状态有限连续行为集; $\begin{matrix} R_{ij}^{a} = E {r_{t + Δt} | x_{t} = x_{i}, a_{t} = a, x_{t + Δt} = x_{j}} \end{matrix}$ 为报酬函数,即状态 $\begin{matrix} x_{i} \end{matrix}$ 时agent采用行为 $\begin{matrix} a \end{matrix}$ 转移到状态 $\begin{matrix} x_{j} \end{matrix}$ 时的瞬时报酬; $\begin{matrix} P_{ij}^{a} = \Pr {x_{t + Δt} = x_{j} | x_{t} = x_{i}, a_{t} = a} \end{matrix}$ 为状态转移函数,即状态 $\begin{matrix} x_{i} \end{matrix}$ 时agent采用行为 $\begin{matrix} a \end{matrix}$ 转移到状态 $\begin{matrix} x_{j} \end{matrix}$ 时的转移概率; $\begin{matrix} J \end{matrix}$ 为策略优化的性能指标,记为: $\begin{matrix} J (x (t)) = \int_{t}^{\infty} r (x (τ), u (x)) dτ, \end{matrix}$ 其中 $\begin{matrix} t < τ < \infty, u \in U \end{matrix}$ 为控制策略。对于式(13)中连续时间带有非线性函数的系统状态,其最优值函数可以定义为:

$\begin{matrix} \begin{matrix} V_{i}^{*} (x_{i} (t)) = \min_{u_{i}} \int_{t}^{\infty} r_{i} (x_{i} (τ), u_{i} (x_{i})) dτ \\ (15) \end{matrix} \end{matrix}$

式中: $\begin{matrix} r_{i} (x_{i}, u_{i}) \end{matrix}$ 为当前状态下的报酬函数^{[ 6]}。

$\begin{matrix} r_{i} (x_{i}, u_{i}) = x_{i}^{T} Q x_{i} + u_{i}^{T} R u_{i} = Q_{r} (x_{i}) + u_{i}^{T} R u_{i} (16) \end{matrix}$

式中: $\begin{matrix} Q_{r} (x_{i}) \end{matrix}$ 连续可导且正定; $\begin{matrix} R \end{matrix}$ 为正定对称矩阵。

若采用式(15)中的最优值函数 $\begin{matrix} V_{i}^{*} (x_{i}) \end{matrix}$ (以下均按此表示最优值函数),则可以给出关于子系统(13)、最优值函数 $\begin{matrix} V_{i}^{*} (x_{i}) 、 \end{matrix}$ 控制策略 $\begin{matrix} u_{i} \end{matrix}$ 的Hamiltonian-jacobi-bellman(HJB)方程^{[ 9]}:

$\begin{matrix} \begin{matrix} HJ B_{i} (x_{i}, u_{i}, \nabla V_{i}^{*}) = \min_{u_{i}} [r_{i} (x_{i}, u_{i}) + \\ \nabla V_{i}^{*} (- F (x_{i}, u_{i}) - h_{i} (q, \overset{\cdot}{q}, \overset{\cdot \cdot}{q}) + b_{i} (x_{i}) u_{i})] = \\ \min_{u_{i}} [r_{i} (x_{i}, u_{i}) + \nabla V_{i}^{*} F_{ui} (x_{i}, u_{i})] (17) \end{matrix} \end{matrix}$

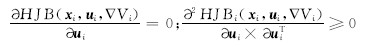
引理1^{[ 10]} 对于给定式(13)的可重构模块机器人子系统,若要保证式(17)中的HJB方程的极值相对于 $\begin{matrix} u_{i} \in U \end{matrix}$ 具有平稳点,其最优值函数及最优控制策略必须要满足如下条件:

若上述条件满足,则可以得出下列结论:

(1)采用有界控制策略 $\begin{matrix} u_{i} \end{matrix}$ 可以保证HJB方程达到局部最小值,且满足控制输入端所施加的约束。

(2)系统Hessian矩阵正定,所采用的控制策略 $\begin{matrix} u_{i} (\cdot) : [t_{0}, t_{f}), u_{i} \in U \end{matrix}$ 可使式(17)全局最小。

(3)如果最优控制策略存在,那么它是唯一的。

若报酬函数光滑,且采用最优控制策略 $\begin{matrix} u_{i}^{*}, \end{matrix}$ 则式(17)的HJB方程满足如下等式:

$\begin{matrix} \begin{matrix} HJ B_{i}^{*} (x_{i}, u_{i}^{*}, \nabla V_{i}^{*}) = \min_{u_{i}^{*}} [r_{i} (x_{i}, u_{i}^{*}) + \\ \nabla V_{i}^{*} F_{ui} (x_{i}, u_{i}^{*})] = 0 (18) \end{matrix} \end{matrix}$

其中,最优控制策略可以表示为:

由式(18)(19)可知,若最优值函数 $\begin{matrix} V_{i}^{*} (x_{i}) \end{matrix}$ 已知且连续可导, $\begin{matrix} V_{i}^{*} (0) = 0, \end{matrix}$ 最优控制策略 $\begin{matrix} u_{i}^{*} (x_{i}) 、 \end{matrix}$ 系统不确定项 $\begin{matrix} F_{ui} (x_{i}, u_{i}) \end{matrix}$ 已知,则式(18)所示的HJB方程成立且可解。然而,实际情况当中, $\begin{matrix} V_{i}^{*} (x_{i}) \end{matrix}$ 并非处处可导,且最优控制策略 $\begin{matrix} u_{i}^{*} (x_{i}) \end{matrix}$ 与系统不确定项 $\begin{matrix} F_{ui} (x_{i}, u_{i}) \end{matrix}$ 未知,因此,采用一般方法求解HJB方程显然是不可行的。为了解决上述问题,本文采用ACI方法,结合RBF神经网络来对HJB方程中的最优值函数,最优控制策略及系统不确定项进行辨识,ACI的结构框图如图1所示。其中,采用action网络来辨识系统最优控制策略 $\begin{matrix} u_{i}^{*} (x_{i}) \end{matrix}$ ,记为 $\begin{matrix} {\hat{u}}_{i} (x_{i}); \end{matrix}$ 采用critic网络辨识最优值函数 $\begin{matrix} V_{i}^{*} (x_{i}) \end{matrix}$ 记为 $\begin{matrix} {\hat{V}}_{i} (x_{i}) \end{matrix}$ ;

	Figure Option View Download New Window
	图1 action-critic-identifier结构框图Fig.1 Architecture of action-critic-identifier

采用鲁棒神经网络identifier辨识系统不确定部分 $\begin{matrix} F_{ui} (x_{i}, u_{i}) \end{matrix}$ ,记为 $\begin{matrix} {\hat{F}}_{\hat{u} i} (x_{i}, {\hat{u}}_{i}), \end{matrix}$ 辨识后的HJB方程可表示为:

$\begin{matrix} \begin{matrix} H \hat{J} B_{i}^{*} (x_{i}, {\hat{u}}_{i}, \nabla {\hat{V}}_{i}) = \\ \min_{u_{i}} [r_{i} (x_{i}, {\hat{u}}_{i}) + \nabla {\hat{V}}_{i} {\hat{F}}_{\hat{u} i} (x_{i}, {\hat{u}}_{i})] (20) \end{matrix} \end{matrix}$

HJB方程的辨识误差为:

$\begin{matrix} \begin{matrix} δ_{hi} = H \hat{J} B_{i}^{*} (x_{i}, {\hat{u}}_{i}, \nabla {\hat{V}}_{i}) - \\ HJ B_{i}^{*} (x_{i}, u_{i}^{*}, \nabla V_{i}^{*}) (21) \end{matrix} \end{matrix}$

对于一类经典RBF神经网络^{[ 11]}可以表示为:

$\begin{matrix} N (x) = W^{*T} S (x) + ε (x) (22) \end{matrix}$

式中: $\begin{matrix} W^{*} \end{matrix}$ 为理想神经网络权值; $\begin{matrix} ε (x) \end{matrix}$ 为逼近误差,在节点数量足够、节点中心及中心宽度构建合理的情况下,RBF神经网络可以逼近任意的连续函数。

最优值函数与最优控制策略可以分别表示为:

$\begin{matrix} \begin{matrix} V_{i}^{*} (x_{i}) = W_{i}^{T} S_{i} (x_{i}) + ε_{ic} (x_{i}) (23) \\ u_{i}^{*} (x_{i}) = - \frac{1}{2} R^{- 1} b_{i}^{T} (x_{i}) [{\overset{\cdot}{S}}_{i} (x_{i})^{T} W_{i} + {\overset{\cdot}{ε}}_{ia} (x_{i})] (24) \end{matrix} \end{matrix}$

式中: $\begin{matrix} S_{i} (x_{i}) \end{matrix}$ 为光滑神经网络基函数; $\begin{matrix} W_{i} \in R^{n} \end{matrix}$ 为未知理想神经网络权值。

采用critic网络和action网络分别对 $\begin{matrix} V_{i}^{*} (x_{i}) \end{matrix}$ 与 $\begin{matrix} u_{i}^{*} (x_{i}) \end{matrix}$ 进行估计:

$\begin{matrix} \begin{matrix} {\hat{V}}_{i} (x_{i}) = W_{i c}^{T} S_{i} (x_{i}) (25) \\ {\hat{u}}_{i} (x_{i}) = - \frac{1}{2} R^{- 1} b_{i}^{T} (x_{i}) {\overset{\cdot}{S}}_{i} (x_{i})^{T} {\hat{W}}_{ia} (26) \end{matrix} \end{matrix}$

式中: $\begin{matrix} {\hat{W}}_{ic} (t) \end{matrix}$ 和 $\begin{matrix} {\hat{W}}_{ia} (t) \end{matrix}$ 分别为critic网络和action网络的权值,权值估计误差为:

$\begin{matrix} \begin{matrix} {\tilde{W}}_{ic} (t) = W_{i} - {\hat{W}}_{ic} (t) (27) \\ {\tilde{W}}_{ia} (t) = W_{i} - {\hat{W}}_{ia} (t) (28) \end{matrix} \end{matrix}$

critic网络权值可按如下LS更新率进行更新:

$\begin{matrix} {\overset{\cdot}{\hat{W}}}_{ic} = - η_{c} Γ \frac{ω}{1 + υ ω^{T} Γω} δ_{hi} (29) \end{matrix}$

式中: $\begin{matrix} η_{c} 、 υ \end{matrix}$ 为正常数增益; $\begin{matrix} ω \in R^{n} \end{matrix}$ 为critic网络的回归向量; $\begin{matrix} Γ \in R^{n \times n} \end{matrix}$ 为对称估计增益矩阵。

action网络的权值可采用如下的梯度更新率进行更新^{[ 8]}:

式中:proj(·)为投影算子; $\begin{matrix} η_{a 1} 、 η_{a 2} \end{matrix}$ 为正增益。

在对 $\begin{matrix} {\hat{V}}_{i} (x_{i}) \end{matrix}$ 与 $\begin{matrix} {\hat{u}}_{i} (x_{i}) \end{matrix}$ 进行估计后,结合RBF神经网络,带有控制策略的子系统非线性不确定项 $\begin{matrix} F_{ui} (x_{i}, u_{i}) \end{matrix}$ 可以表示为:

$\begin{matrix} \begin{matrix} F_{\hat{u} i} (x_{i}, {\hat{u}}_{i}) = {\overset{\cdot}{x}}_{i 2} = \\ W_{i F}^{T} κ (Λ_{iF}^{T} x_{i 2}) + ε_{iF} (x_{i 2}) + b_{i} (x_{i}) {\hat{u}}_{i} (31) \end{matrix} \end{matrix}$

式中: $\begin{matrix} {\hat{u}}_{i} \end{matrix}$ 为 $\begin{matrix} u_{i} \end{matrix}$ 的估计值; $\begin{matrix} κ (\cdot) \end{matrix}$ 为神经网络基函数; $\begin{matrix} W_{iF} 、 Λ_{iF} \end{matrix}$ 为未知理想神经网络权值。

为了解决非线性项对子系统的影响,设计一类鲁棒神经网络identifier对 $\begin{matrix} F_{\hat{u} i} (x_{i}, {\hat{u}}_{i}) \end{matrix}$ 进行辨识,可以表示为:

$\begin{matrix} {\hat{F}}_{\hat{u} i} ({\hat{x}}_{i}, {\hat{u}}_{i}) = {\overset{\cdot}{\hat{x}}}_{i 2} = {\hat{W}}^{T}_{iF} {\hat{κ}}_{iF} + b_{i} (x_{i}) {\hat{u}}_{i} + μ (32) \end{matrix}$

式中: $\begin{matrix} {\hat{κ}}_{iF} \end{matrix}$ 为identifier网络基函数的估计值; $\begin{matrix} μ \in R^{n} \end{matrix}$ 为误差反馈项,记为^{[ 12]}:

$\begin{matrix} \begin{matrix} μ = k x_{i 2} (t) - k x_{i 2} (0) + ϑ (33) \\ \overset{\cdot}{ϑ} = (kα + γ) {\tilde{x}}_{i 2} + β_{1} sat ({\tilde{x}}_{i 2}) (34) \end{matrix} \end{matrix}$

式中: $\begin{matrix} k, α, γ, β_{1} \end{matrix}$ 为正常数控制增益; $\begin{matrix} sat (\cdot) \end{matrix}$ 为饱和函数。

identifier网络的状态估计误差为:

$\begin{matrix} \begin{matrix} {\tilde{F}}_{ui} (x_{i}, u_{i}) = {\overset{\cdot}{\tilde{x}}}_{i 2} = \\ W_{iF}^{T} κ_{iF} - {\hat{W}}^{T}_{iF} {\hat{κ}}_{iF} + ε_{iF} (x_{i 2}) - μ (35) \end{matrix} \end{matrix}$

$\begin{matrix} {\hat{W}}_{iF} 、 {\hat{Λ}}_{iF} \end{matrix}$ 可以按照下式进行更新:

$\begin{matrix} \begin{matrix} {\overset{\cdot}{\hat{W}}}_{iF} = proj (Γ_{iWF} {\overset{\cdot}{\hat{κ}}}_{iF} {\hat{Λ}}^{T}_{iF} {\overset{\cdot}{\hat{x}}}_{i 2} {\tilde{x}}^{T}_{i 2}) (36) \\ {\overset{\cdot}{\hat{Λ}}}_{iF} = proj (Γ_{iΛF} {\overset{\cdot}{\hat{x}}}_{i 2} {\tilde{x}}^{T}_{i 2} {\hat{W}}^{T}_{iF} {\overset{\cdot}{\hat{κ}}}_{iF}) (37) \end{matrix} \end{matrix}$

式中: $\begin{matrix} Γ_{iWF} 、 Γ_{iΛF} \end{matrix}$ 为增益矩阵。

定义滤波辨识误差:

$\begin{matrix} e_{ir} = {\overset{\cdot}{\tilde{x}}}_{i 2} + α {\tilde{x}}_{i 2} (38) \end{matrix}$

对式(38)求导可得:

$\begin{matrix} \begin{matrix} {\overset{\cdot}{e}}_{ir} = {\overset{\cdot \cdot}{x}}_{i 2} - {\overset{\cdot \cdot}{\hat{x}}}_{i 2} + α {\overset{\cdot}{\tilde{x}}}_{i 2} = \\ W_{iF}^{T} {\overset{\cdot}{κ}}_{iF} Λ_{iF}^{T} {\overset{\cdot}{x}}_{i 2} - W_{iF}^{T} {\hat{κ}}_{iF} - {\hat{W}}^{T}_{iF} {\overset{\cdot}{\hat{κ}}}_{iF} {\hat{Λ}}^{T}_{iF} {\hat{x}}_{i 2} + {\overset{\cdot}{ε}}_{iF} (x_{i 2}) - \\ {\hat{W}}^{T}_{iF} {\overset{\cdot}{\hat{κ}}}_{iF} {\hat{Λ}}^{T}_{iF} {\overset{\cdot}{\hat{x}}}_{i 2} - γ {\tilde{x}}_{i 2} - β_{1} sa t ({\tilde{x}}_{i 2}) - k e_{ir} + α {\overset{\cdot}{\tilde{x}}}_{i 2} (39) \end{matrix} \end{matrix}$

对式(39)中的 $\begin{matrix} {\hat{W}}^{T}_{iF} {\overset{\cdot}{\hat{κ}}}_{iF} {\hat{Λ}}^{T}_{iF} {\overset{\cdot}{\hat{x}}}_{i 2} \end{matrix}$ 项进行分解可得:

$\begin{matrix} \begin{matrix} {\hat{W}}^{T}_{iF} {\overset{\cdot}{\hat{κ}}}_{iF} {\hat{Λ}}^{T}_{iF} {\overset{\cdot}{\hat{x}}}_{i 2} = \\ \frac{1}{2} {\overset{\cdot}{\hat{κ}}}_{iF} {\overset{\cdot}{\hat{x}}}_{i 2} [(Λ_{iF}^{T} - {\tilde{Λ}}^{T}_{iF}) (W_{iF}^{T} - {\tilde{W}}^{T}_{iF}) + \\ (W_{iF}^{T} - {\tilde{W}}^{T}_{iF}) ({\tilde{Λ}}^{T}_{iF} - Λ_{iF}^{T})] = \\ \frac{1}{2} {\overset{\cdot}{\hat{κ}}}_{iF} {\overset{\cdot}{\hat{x}}}_{i 2} [{\tilde{W}}^{T}_{iF} (Λ_{iF}^{T} - {\tilde{Λ}}^{T}_{iF}) + (W_{iF}^{T} - {\tilde{W}}^{T}_{iF}) {\tilde{Λ}}^{T}_{iF}] - \\ \frac{1}{2} {\overset{\cdot}{\hat{κ}}}_{iF} {\overset{\cdot}{\hat{x}}}_{i 2} [W_{iF}^{T} (Λ_{iF}^{T} - {\tilde{Λ}}^{T}_{iF}) + (W_{iF}^{T} - {\tilde{W}}^{T}_{iF}) Λ_{iF}^{T}] = \\ \frac{1}{2} W_{iF}^{T} {\overset{\cdot}{\hat{κ}}}_{iF} {\hat{Λ}}^{T}_{iF} {\overset{\cdot}{\tilde{x}}}_{i 2} + \frac{1}{2} {\hat{W}}^{T}_{iF} {\overset{\cdot}{\hat{κ}}}_{iF} Λ_{iF}^{T} {\overset{\cdot}{\tilde{x}}}_{i 2} - \\ \frac{1}{2} W_{iF}^{T} {\overset{\cdot}{\hat{κ}}}_{iF} {\hat{Λ}}^{T}_{iF} {\overset{\cdot}{x}}_{i 2} - \frac{1}{2} {\hat{W}}^{T}_{iF} {\overset{\cdot}{\hat{κ}}}_{iF} Λ_{iF}^{T} {\overset{\cdot}{x}}_{i 2} + \\ \frac{1}{2} {\tilde{W}}^{T}_{iF} {\overset{\cdot}{\hat{κ}}}_{iF} {\hat{Λ}}^{T}_{iF} {\overset{\cdot}{\hat{x}}}_{i 2} + \frac{1}{2} {\hat{W}}^{T}_{iF} {\overset{\cdot}{\hat{κ}}}_{iF} {\tilde{Λ}}^{T}_{iF} {\overset{\cdot}{\hat{x}}}_{i 2} (40) \end{matrix} \end{matrix}$

由此,式(39)可以化简为:

$\begin{matrix} {\overset{\cdot}{e}}_{ir} = P_{F 1} + P_{F 2} + P_{F 3} - k e_{ir} - γ {\tilde{x}}_{i 2} - β_{1} sat ({\tilde{x}}_{i 2}) (41) \end{matrix}$

其中, $\begin{matrix} {\tilde{W}}^{T}_{iF} = W_{iF}^{T} - {\hat{W}}_{iF}^{T}; {\tilde{Λ}}^{T}_{iF} = Λ_{iF}^{T} - {\hat{Λ}}^{T}_{iF} 。 \end{matrix}$

$\begin{matrix} \begin{matrix} P_{F 1} = \frac{1}{2} W_{iF}^{T} {\overset{\cdot}{\hat{κ}}}_{iF} {\hat{Λ}}^{T}_{iF} {\overset{\cdot}{\tilde{x}}}_{i 2} + \\ \frac{1}{2} {\hat{W}}^{T}_{iF} {\overset{\cdot}{\hat{κ}}}_{iF} Λ_{iF}^{T} {\overset{\cdot}{\tilde{x}}}_{i 2} - {\hat{W}}^{T}_{iF} {\overset{\cdot}{\hat{κ}}}_{i F} {\hat{Λ}}^{T}_{iF} {\hat{x}}_{i 2} + \\ α {\overset{\cdot}{\tilde{x}}}_{i 2} - {\hat{W}}^{T}_{iF} {\hat{κ}}_{iF} (42) \\ P_{F 2} = - \frac{1}{2} W_{iF}^{T} {\overset{\cdot}{\hat{κ}}}_{iF} {\hat{Λ}}^{T}_{iF} {\overset{\cdot}{x}}_{i 2} - \frac{1}{2} {\hat{W}}^{T}_{iF} {\overset{\cdot}{\hat{κ}}}_{iF} Λ_{iF}^{T} {\overset{\cdot}{x}}_{i 2} + \\ W_{iF}^{T} {\overset{\cdot}{κ}}_{iF} Λ_{iF}^{T} {\overset{\cdot}{x}}_{i 2} + {\overset{\cdot}{ε}}_{iF} (x_{i 2}) (43) \\ P_{F 3} = \frac{1}{2} {\tilde{W}}^{T}_{iF} {\overset{\cdot}{\hat{κ}}}_{iF} {\hat{Λ}}^{T}_{iF} {\overset{\cdot}{\hat{x}}}_{i 2} + \frac{1}{2} {\hat{W}}^{T}_{iF} {\overset{\cdot}{\hat{κ}}}_{iF} {\tilde{Λ}}^{T}_{iF} {\overset{\cdot}{\hat{x}}}_{i 2} (44) \end{matrix} \end{matrix}$

由假设1及式(36)(37)(38)可知, $\begin{matrix} P_{F 1} 、 P_{F 2} 、 P_{F 3} \end{matrix}$ 存在上界,表示为:

$\begin{matrix} \{\begin{matrix} ‖ P_{F 1} ‖\leq λ_{1} (‖ E_{i} ({\tilde{x}}^{T}_{i 2}, e^{T}_{ir}) ‖) ‖ E_{i} ({\tilde{x}}^{T}_{i 2}, e^{T}_{ir}) ‖ \\ ‖ P_{F 2} ‖\leq ζ_{1} \\ ‖ P_{F 3} ‖\leq ζ_{2} \end{matrix} (45) \end{matrix}$

由式(42)(43)(44)可知:

$\begin{matrix} \begin{matrix} ‖ {\overset{\cdot}{P}}_{F 2} + {\overset{\cdot}{P}}_{F 3} ‖\leq ζ_{3} + ζ_{4} λ_{2} (‖ E_{i} ({\tilde{x}}^{T}_{i 2}, e^{T}_{ir}) ‖) \\ ‖ E_{i} ({\tilde{x}}^{T}_{i 2}, e^{T}_{ir}) ‖, E_{i} ({\tilde{x}}^{T}_{i 2}, e^{T}_{ir}) = {[\begin{matrix} {\tilde{x}}^{T}_{i 2} & e^{T}_{ir} \end{matrix}]}^{T} \in R^{2 \times n}, λ_{1} (\cdot) 、 λ_{2} (\cdot) \end{matrix} \end{matrix}$ 为全局可逆的增函数, $\begin{matrix} ζ_{i} (i = 1,2, 3,4) \end{matrix}$ 为可计算的正常数。

定理对于外界动态约束下的可重构模块机器人子系统动力学模型(9)及状态方程(13),若采用式(25)(26)(32)所示的critic网络、action网络及identifier网络分别对子系统的最优值函数 $\begin{matrix} V_{i}^{*} (x_{i}) 、 \end{matrix}$ 最优控制策略 $\begin{matrix} u_{i}^{*} (x_{i}) \end{matrix}$ 及系统不确定项 $\begin{matrix} F_{ui} (x_{i}, u_{i}) \end{matrix}$ 进行辨识,且采用式(29)(30)(36)(37)所示的更新率对网络权值进行更新,即可得到满足式(20)的HJB方程相应的最优解,使得外界动态约束下的可重构模块机器人子系统闭环稳定,且辨识误差收敛有界,各关节变量渐进跟踪期望轨迹,跟踪误差有界收敛。

证明定义Lyapunov函数:

$\begin{matrix} \begin{matrix} U_{1} (d) \leq V_{iL} (x_{i 2}, e_{ir}) \leq U_{2} (d) \\ \{\begin{matrix} U_{1} (d) = \frac{1}{2} \min (1, γ) ‖ d ‖^{2} \\ U_{2} (d) = \max (1, γ) ‖ d ‖^{2} \end{matrix} (49) \end{matrix} \end{matrix}$

对式(46)求导:

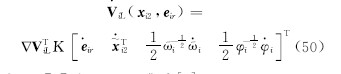
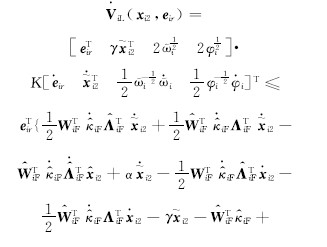
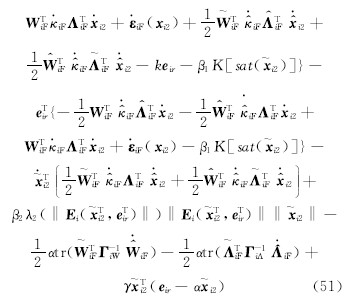
式中: $\begin{matrix} K [\cdot] \end{matrix}$ 为Filipov集合^{[ 13]}。

$\begin{matrix} {\overset{\cdot}{V}}_{iL} (x_{i 2}, e_{ir}) \end{matrix}$ 可进一步变形为:

将式(42)(43)(44)代入(51),可得:

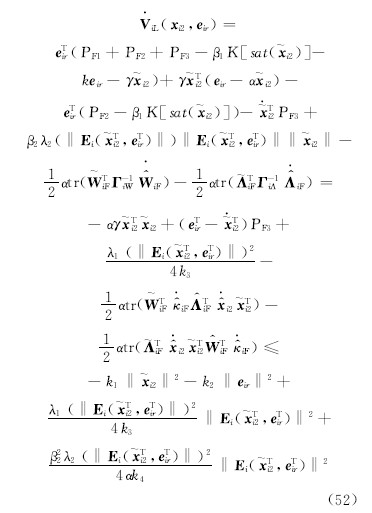
由此可知,对任意正常数c,则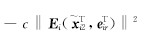为一个一致连续且上界存在的负定函数。其中,上界表示为:

$\begin{matrix} D = \{d (t) | U_{2} (d) < λ^{- 1} (2 \sqrt[]{k_{\min} ξ})\} (54) \end{matrix}$

因此,根据Lyapunov稳定性理论可知,系统是稳定的。

3 仿真实例

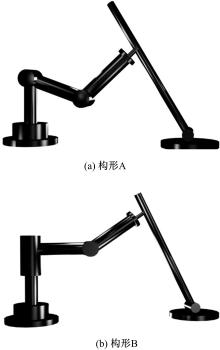
为了验证所提出的基于ACI的分散强化学习最优控制方法的有效性并考查误差的收敛情况,本文采用两组不同的二自由度受外界动态约束的可重构模块机器人构形来进行仿真。其中,构形实例如图2所示。

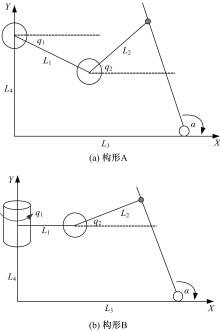
	Figure Option View Download New Window
	图2 动态约束下可重构模块机器人仿真图Fig.2 Configuration A and B for varying constrained robot

为了便于对上述构形实例进行分析,将上述构形转化为如图3所示的解析图。其中,外界动态约束可以定义为一类绕确定自由度旋转的长柱,构形A与构形B的约束方程如下:

$\begin{matrix} \begin{matrix} Φ_{A} (q, t) = L_{1} \cos q_{1} + L_{2} \cos q_{2} - \\ [L_{3} + L_{4} cotα (t)] \\ Φ_{B} (q, t) = L_{1} + L_{2} \cos q_{2} - [L_{3} + L_{4} cotα (t)] \end{matrix} \end{matrix}$

	Figure Option View Download New Window
	图3 解析图Fig.3 The analytic chart

式中: $\begin{matrix} α (t) 表示外界约束与 x 轴的夹角, α (t) = 0.75 π + 0.2 \sin \frac{t}{2} \end{matrix}$ 。

构形A与构形B的关节角初值定义为 $\begin{matrix} q_{1} (0) = 2, q_{2} (0) = 2, \end{matrix}$ 关节初速度为零,构形A与构形B的动力学模型表示为:

$\begin{matrix} \begin{matrix} M_{A} (q) = \\ [\begin{matrix} 0.36 \cos (q_{2}) + 0.6066 & 0.18 \cos (q_{2}) + 0.1233 \\ 0.18 \cos (q_{2}) + 0.1233 & 0.1233 \end{matrix}] \\ M_{B} (q) = \\ [\begin{matrix} 0.17 - 0.1166 co s^{2} (q_{2}) & - 0.06 \cos (q_{2}) \\ - 0.06 \cos (q_{2}) & 0.1233 \end{matrix}] \end{matrix} \end{matrix}$

$\begin{matrix} \begin{matrix} C_{A} (q, \overset{\cdot}{q}) = \\ [\begin{matrix} - 0.36 \sin (q_{2}) {\overset{\cdot}{q}}_{2} & - 0.18 \sin (q_{2}) {\overset{\cdot}{q}}_{2} \\ 0.18 \sin (q_{2}) ({\overset{\cdot}{q}}_{1} - {\overset{\cdot}{q}}_{2}) & 0.18 \sin (q_{2}) {\overset{\cdot}{q}}_{1} \end{matrix}] \\ C_{B} (q, \overset{\cdot}{q}) = \\ [\begin{matrix} 0.1166 \sin (2 q_{2}) {\overset{\cdot}{q}}_{2} & 0.06 \sin (q_{2}) {\overset{\cdot}{q}}_{2} \\ 0.06 \sin (q_{2}) {\overset{\cdot}{q}}_{2} & 0 \end{matrix}] \end{matrix} \end{matrix}$

$\begin{matrix} \begin{matrix} G_{A} (q) = [\begin{matrix} - 5.88 \sin (q_{1} + q_{2}) - 17.64 \sin (q_{1}) \\ - 5.88 \sin (q_{1} + q_{2}) \end{matrix}] \\ G_{B} (q) = [\begin{matrix} 0 \\ - 5.88 \cos (q_{2}) \end{matrix}] \end{matrix} \end{matrix}$

$\begin{matrix} \begin{matrix} F_{A} (q, \overset{\cdot}{q}) = [\begin{matrix} {\overset{\cdot}{q}}_{1} + 10 \sin (3 q_{1}) + 2 sgn ({\overset{\cdot}{q}}_{1}) \\ 1.2 {\overset{\cdot}{q}}_{2} + 5 \sin (2 q_{2}) + sgn ({\overset{\cdot}{q}}_{2}) \end{matrix}] \\ F_{B} (q, \overset{\cdot}{q}) = [\begin{matrix} 0 \\ 1.5 {\overset{\cdot}{q}}_{2} + \sin (q_{2}) + 1.2 sgn ({\overset{\cdot}{q}}_{2}) \end{matrix}] \end{matrix} \end{matrix}$

构形A的期望轨迹如下:

$\begin{matrix} \begin{matrix} y_{1 d} = 0.5 \cos (t) + 0.2 \sin (3 t) \\ y_{2 d} = Ω (y_{1 d}, t) = \\ \arcsin [\frac{L_{1} \sin (α (t) - y_{1 d}) - L_{3} \sin (α (t))}{L_{2}}] + α (t) \end{matrix} \end{matrix}$

构形B的期望轨迹如下:

$\begin{matrix} \begin{matrix} y_{1 d} = 0 \\ y_{2 d} = Ω (y_{1 d}, t) = \\ \arcsin [\frac{L_{1} \sin (α (t)) - L_{3} \sin (α (t))}{L_{2}}] + α (t) \end{matrix} \end{matrix}$

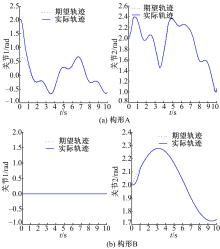
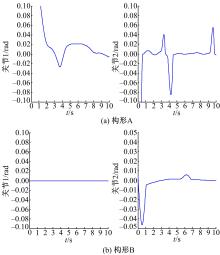
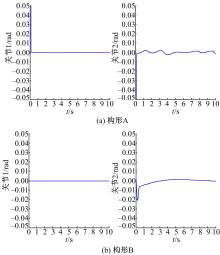
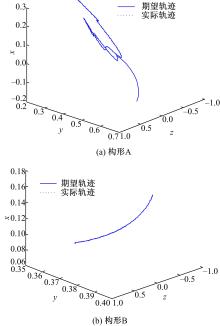
其中,构形B由于外界动态约束的限制,关节1变量为零。ACI中所定义的参数如下: $\begin{matrix} k = 800, α = 300, υ = 0.005, η_{a 1} = 10, η_{a 2} = 50, η_{c} = 20, β_{1} = 0.2, β_{2} = 2, γ = 0.5 。 \end{matrix}$

为了证实所采用的方法可以应用在不同的构形当中,并验证基于ACI的分散强化学习最优控制方法对子系统期望轨迹的跟踪性能,文中分别采用标准RBF神经网络控制方法与基于ACI的分散强化学习最优控制方法进行对比仿真。图4、图5为采用RBF神经网络补偿系统模型非线性项与子系统交联时的关节跟踪曲线及误差曲线。图6、图7为采用ACI对系统HJB方程中最优值函数、最优控制策略及模型非线性项进行辨识时关节的跟踪曲线及误差曲线。图8为采用ACI的末端轨迹跟踪曲线。通过仿真图可以看出:采用标准RBF神经网络对期望轨迹进行跟踪时,关节子系统跟踪速度较慢,且跟踪误差较大;而采用基于ACI与强化学习的分散最优控制策略后,关节子系统可以在0.2 s内跟踪期望轨迹,且跟踪误差小于±0.05。由此可知,基于ACI与强化学习的分散最优控制策略可以应用于不同构形的受外界动态约束的可重构模块机器人,且在不同构形中均可使子系统关节变量在极短的时间内跟踪期望轨迹,误差收敛且波动范围极小。

	Figure Option View Download New Window
	图4 采用RBF神经网络的轨迹跟踪曲线Fig.4 Trajectory tracking curve with RBF

	Figure Option View Download New Window
	图5 采用RBF神经网络的跟踪误差曲线Fig.5 Tracking error curve with RBF

	Figure Option View Download New Window
	图6 采用ACI强化学习的轨迹跟踪曲线Fig.6 Trajectory tracking curve with ACI

	Figure Option View Download New Window
	图7 采用ACI强化学习的跟踪误差曲线Fig.7 Tracking error curve with ACI

	Figure Option View Download New Window
	图8 采用ACI强化学习的末端轨迹Fig.8 Tip trajectory curve with ACI

4 结束语

结合ACI和RBF神经网络,提出了一种外界动态约束下的可重构模块机器人分散强化学习最优控制方法,解决了存在强耦合不确定性的可重构模块机器人系统的连续时间非线性最优控制问题。首先,建立了存在外界动态约束下的可重构模块机器人动力学模型,并将其划分为交联子系统的集合。其次,以马尔可夫决策过程性能指标为基础,针对子系统状态方程定义最优值函数与最优控制策略的观念表达式,将模型非线性项与子系统交联项划分为一类总体不确定项,并设计子系统HJB方程。之后,采用ACI对HJB方程中相应的最优函数进行辨识,其中action网络用来辨识子系统最优控制策略,critic网络对子系统最优值函数进行辨识,再通过identifier网络对子系统总体非线性不确定项进行估计,从而使子系统满足HJB方程下的最优化条件,使可重构模块机器人子系统渐进跟踪期望轨迹,且跟踪误差有界收敛。通过Lyapunov理论,对所提出的分散强化学习最优控制策略进行稳定性证明。最后,通过对两组不同构形的可重构模块机器人进行数值仿真,进一步验证了所提出的分散控制策略的有效性。

The authors have declared that no competing interests exist.

参考文献

View Option

[1]	Li Yuan-chun, Dong Bo. Decentralized ADRC control for reconfigurable manipulators based on VGSTA-ESO of sliding mode[J]. Information-an International Interdisciplinary Journal, 2012, 15(6): 2453-2465. [本文引用:1] [JCR: 0.358]
[2]	李英, 朱明超, 李元春. 基于速度观测模型的可重构机械臂补偿控制[J]. 控制理论与应用, 2008, 25(5): 891-897. Li Ying, Zhu Ming-chao, Li Yuan-chun. Velocity observer based compensator for motion control of a reconfigurable manipulator[J]. Control Theory & Applications, 2008, 25(5): 891-897. [本文引用:1] [JCR: 1.717]
[3]	朱明超, 李元春. 可重构机械臂分散自适应模糊滑模控制[J]. 吉林大学学报: 工学版, 2009, 39(1): 170-176. Zhu Ming-chao, Li Yuan-chun. Decentralized adaptive sliding mode control for reconfigurable manipulators using fuzzy logic[J]. Journal of Jilin University(Engineering and Technology Edition), 2009, 39(1): 170-176. [本文引用:1] [CJCR: 0.701]
[4]	朱明超, 李英, 李元春. 基于观测器的可重构机械臂分散自适应模糊控制[J]. 控制与决策, 2009, 24(3): 429-434. Zhu Ming-chao, Li Ying, Li Yuan-chun. Observer-based decentralized adaptive fuzzy control for reconfigurable manipulator[J]. Control and Decision, 2009, 24(3): 429-434. [本文引用:1] [CJCR: 0.907]
[5]	Xu Yan-kai, Cao Xi-ren. Lebesgue-sampling-based optimal control problems with time aggregation[J]. IEEE Transactions on Automatic Control, 2011, 56(5): 1097-1109. [本文引用:1] [JCR: 2.718]
[6]	Lewis F L, Vrabie D. Reinforcement learning and adaptive dynamic programming for feedback control[J]. IEEE Circuits and Systems Magzine, 2009, 9(3): 32-50. [本文引用:2]
[7]	Xu Xin, He Han-gen, Hu De-wen. Efficient reinforcement learning using recursive least-squares methods[J]. Journal of Artificial Intelligence Research, 2002, 16: 259-292. [本文引用:1] [JCR: 1.056]
[8]	Lewis F L, Liu De-rong. Reinforcement Learning and Approximate Dynamic Programming for Feedback Control[M]. New York: Wiley-IEEE Press, 2012. [本文引用:2]
[9]	Lewis F L, Syrmos V L. Optimal Control[M]. New York: John Wiley & Sons, Inc, 1995. [本文引用:1] [JCR: 1.062]
[10]	Sassano M, Astolfi A. Dynamic approximate solutions of the HJ inequality and of the HJB equation for input-affine nonlinear systems[J]. IEEE Transactions on Automatic Control, 2012, 57(10): 2490-2503. [本文引用:1] [JCR: 2.718]
[11]	吴玉香, 王聪. 基于确定学习的机器人任务空间自适应神经网络控制[J]. 自动化学报, 2013, 39(6): 806-815. Wu Yu-xiang, Wang Cong. Deterministic learning based adaptive network control of robot in task space[J]. Acta Automatica Sinica, 2013, 39(6): 806-815. [本文引用:1] [CJCR: 0.572]
[12]	Patre P M, MacKunis W, Kaiser K, et al. Asymptotic tracking for uncertain dynamic systems via a multilayer neural network feedforward and RISE feedback control structure[J]. IEEE Transactions on Automatic Control, 2008, 53(9): 2180-2185. [本文引用:1] [JCR: 2.718]
[13]	Paden B, Sastry S. Calculus for computing Filippov's differential inclusion with application to the variable structure control of robot manipulators[J]. IEEE Transactions on Circuits Systems, 1987, 3(1): 73-82. [本文引用:1]

2012

0.358

0.0

2008

1.717

0.0

. 2008, 25(5):891-897

Velocity observer based compensator for motion control of a reconfigurable manipulator

针对可重构机械臂动力学中存在的模型参数摄动和外界扰动,本文阐述了一种基于速度观测模型的模糊RBF神经网络补偿控制算法.利用Lyapunov函数给出了网络的权值、隶属度函数中心和宽度倒数的在线更新律,并证明了所提出的观测模型及其补偿控制算法的最终一致有界性.最后以RRP(revolute-revolute-prismatic)构形的可重构机械臂为例,通过仿真研究了算法对轨迹跟踪问题的有效性,同时与基于速度观测模型的RBF神经网络补偿控制进行了仿真对比及分析,给出了神经网络和模糊神经网络在可重构机械臂轨迹控制应用中各自的优缺点.

2009

0.0

0.701

. 2009, 39(1):170-176

Decentralized adaptive sliding mode control for reconfigurable manipulators using fuzzy logic

College of Communication Engineering,Jilin University,Changchun 130022,China

For reconfigurable manipulators, it is very difficult to design effective controllers due to diverse configurations. To satisfy the concept of modular software design, a decentralized adaptive fuzzy sliding mode control scheme for the reconfigurable manipulators was proposed. The dynamics of the manipulators was represented as a set of interconnected subsystems. Then fuzzy logic system was used to approximate the unknown dynamics of the subsystem, and a sliding mode controller with an adaptive scheme was designed to avoid both interconnection term and fuzzy approximation error. These subsystem controllers constitute a modular control network to achieve atable and reliable motion of a reconfigurable manipulator. Simulation results show the validity of the proposed decentralized control scheme.

为了适应软件模块化的设计观念，提出一种可重构机械臂的分散自适应模糊滑模控制方案,把可重构机械臂的动力学描述为一个交联子系统的集合。使用模糊逻辑系统逼近子系统动力学模型，然后设计自适应滑模控制器抵消交联项和模糊逼近误差对轨迹跟踪性能的影响。这些子系统控制器组成一个模块化的控制网络，协调工作实现可重构机械臂稳定可靠的运动。最后，仿真结果证明了提出的分散控制方案的有效性。

2009

0.0

0.907

. 2009, 24(3):429-434

Observer-based decentralized adaptive fuzzy control for reconfigurable manipulator

提出一种基于观测器的可重构机械臂分散自适应模糊控制方案.将可重构机械臂的动力学描述为一个交联子系统的集合,子系统控制器由自适应模糊系统和鲁棒控制项组成.基于状态观测器观测值构建的自适应模糊系统用于逼近子系统动力学模型和交联项,鲁棒控制项用于抵消模糊逼近误差对轨迹跟踪的影响.数值仿真证明了所提出的分散控制方案的有效性.

2011

2.718

0.0

... 与监督学习相比,强化学习不需要预知各种状态下的导师信号,而是在与环境的交互过程中学习,由于其具有在非线性模型不确定性条件下的自适应优化能力,因而在解决复杂模型的优化策略与最优控制等问题方面有着独特的优势^[5,6,7,8] ...

2009

0.0

... 式中: ri(xi,ui)为当前状态下的报酬函数^[6] ...

2002

1.056

0.0

2012

0.0

... action网络的权值可采用如下的梯度更新率进行更新^[8]: ...

1995

1.062

0.0

... 若采用式(15)中的最优值函数 Vi*(xi)(以下均按此表示最优值函数),则可以给出关于子系统(13)、最优值函数 Vi*(xi)、控制策略 ui的Hamiltonian-jacobi-bellman(HJB)方程^[9]: ...

2012

2.718

0.0

... 引理1^[10] 对于给定式(13)的可重构模块机器人子系统,若要保证式(17)中的HJB方程的极值相对于 ui∈U具有平稳点,其最优值函数及最优控制策略必须要满足如下条件: ...

2013

0.0

0.572

. 2013, 39(6):806-815 DOI:10.3724/SP.J.1004.2013.00806

Deterministic learning based adaptive network control of robot in task space

College of Automation Science and Engineering, South China University of Technology, Guangzhou 510640

Deterministic learning can achieve locally-accurate approximation of the unknown closed-loop system dynamics while attempting to control a class of nonlinear systems producing recurrent trajectories. Based on deterministic learning, an adaptive neural control algorithm is proposed for unknown robots in task space using radial basis function (RBF) networks. The designed adaptive neural controller can not only guarantee all signals in the closed-loop system uniformly ultimately bounded, but also achieve convergence of partial network weights to their optimal values. It can also learn the unknown closed-loop system dynamics in a stable control process along recurrent tracking orbits. The learned knowledge stored as constant network weights can be reused in a same or similar control task to improve the control performance and to save time and energy. Simulation results demonstrate the effectiveness of the proposed approach.

针对产生回归轨迹的连续非线性动态系统, 确定学习可实现未知闭环系统动态的局部准确逼近. 基于确定学习理论, 本文使用径向基函数(Radial basis function, RBF)神经网络为机器人任务空间跟踪控制设计了一种新的自适应神经网络控制算法, 不仅实现了闭环系统所有信号的最终一致有界, 而且在稳定的控制过程中, 沿着回归跟踪轨迹实现了部分神经网络权值收敛到最优值以及未知闭环系统动态的局部准确逼近. 学过的知识以时不变且空间分布的方式表达、以常值神经网络权值的方式存储, 可以用来改进系统的控制性能, 也可以应用到后续相同或相似的控制任务中, 节约时间和能量. 最后, 用仿真说明了所设计控制算法的正确性和有效性.

... 对于一类经典RBF神经网络^[11]可以表示为: ...

2008

2.718

0.0

... μ∈Rn为误差反馈项,记为^[12]: ...

1987

0.0

... 式中: K·为Filipov集合^[13] ...