基于改进操作模式PID的砷盐除钴过程氧化还原电位控制

引用本文

伍铁斌, 阳春华, 李勇刚, 朱红求, 桂卫华, 王雅琳. 基于改进操作模式PID的砷盐除钴过程氧化还原电位控制. 吉林大学学报: 工学版, 2014, 44(5): 1385-1391[WU Tie-bin, YANG Chun-hua, LI Yong-gang, ZHU Hong-qiu, GUI Wei-hua, WANG Ya-lin. Improved operational pattern-PID based control of ORP in cobalt removal process using arsenic salt. Journal of Jilin University (Engineering and Technology Edition), 2014, 44(5): 1385-1391] 复制到剪切板

Permissions

基于改进操作模式PID的砷盐除钴过程氧化还原电位控制

伍铁斌^1,², 阳春华¹, 李勇刚¹, 朱红求¹, 桂卫华¹, 王雅琳¹

1.中南大学信息科学与工程学院, 长沙 410083

2.湖南人文科技学院机电工程系, 湖南娄底 417000

通信作者:阳春华（1965-）,女,教授,博士生导师.研究方向:复杂系统建模、优化与控制. E-mail:ychh@mail.csu.edu.cn

作者简介:伍铁斌（1981-）,男,博士研究生.研究方向:复杂系统建模、优化与控制.E-mail:wutiebin81@163.com

基金:国家杰出青年科学基金项目 (61025015); 国家“十二五”科技支撑计划项目 (2012BAF03B05); 国家自然科学基金项目(61174133, 61273159); 湖南省科技厅计划项目（2014GK3033,2012CK4018）; 湖南省教育厅优秀青年项目（14B097）

摘要

针对砷盐除钴过程的时变性、非线性和时滞导致氧化还原电位(ORP)稳定控制困难的问题,提出了一种基于改进操作模式的参数自整定的PID控制方法。为提高操作模式匹配的可靠性和快速性,提出一种考虑参数重要性的改进的模糊C-均值聚类算法对操作模式进行聚类;然后采用二步匹配法匹配出相似的操作模式。由于砷盐净化除钴工段系统参数会随时间发生变化,在操作模式重用时对不同时间的操作模式的解(PID参数)赋予不同的模糊加权值,增强了重用结果的可靠性。工业运行结果表明:本文提出的方法能有效降低ORP波动程度,应对复杂的工况变化。

关键词: 自动控制技术; 砷盐除钴; 氧化还原电位; 操作模式

中图分类号:TP273 文献标志码:A 文章编号:1671-5497(2014)05-1385-07

Improved operational pattern-PID based control of ORP in cobalt removal process using arsenic salt

WU Tie-bin^1,², YANG Chun-hua¹, LI Yong-gang¹, ZHU Hong-qiu¹, GUI Wei-hua¹, WANG Ya-lin¹

1.School of Information Science &Engineering, Central South University, Changsha 410083, China

2.Department of Electrical and Mechanical Engineering, Hu'nan Institute of Humanities Science and Technology, Loudi 417000, China

Abstract

To solve the problem of stability control of Oxidation-Reduction Potential (ORP), which is caused by time variation, nonlinearity and time-delay in the process of cobalt removal using arsenic salt, an improved operational pattern based PID parameter tuning method is put forward. In order to improve the reliability and speed of operational pattern matching, first, an improved fuzzy C-mean clustering algorithm for operational pattern clustering is presented. Then, a two-step search method is used to match the similar operational patterns. Finally, since the system parameters of the cobalt removal process vary with time, to improve the reliability of the reused operational pattern solutions, which are PID parameters, different weighting values are assigned to the operational solutions in different times when the operational pattern is reused. A real industrial cobalt removal process control results show that the proposed method can effectively reduce the fluctuation of ORP degree and deal with complicated changing conditions.

Keyword: automatic control technology; cobalt removal process using arsenic salt; oxidation-reduction potential; operational pattern

Show Figures

0 引言

钴离子是硫酸锌溶液净化中最难去除和危害最大的杂质之一^{[ 1]}。为保证溶液钴离子浓度达标,经常过量添加锌粉,造成锌粉的极大浪费^{[ 2, 3]}。奥托昆普研究认为砷盐净化除钴过程是典型的氧化还原过程,在一定范围内氧化还原电位(Oxidation-reduction potential,ORP)越负(相同条件下,锌粉添加得越多,ORP越负,溶液还原性越强^{[ 4]}),置换除钴反应速率越快^{[ 5]}。相同条件下,溶液中的铜、钴等杂质离子和砷盐浓度越高,则ORP越正。由于受企业生产目标、前后工段和设备因素的影响,造成反应器入口的流量经常大幅度波动,流量越大,单位时间内进入反应器的杂质离子越多,且国内矿源复杂,溶液中的杂质离子经常频繁、大幅度地变化,即影响ORP的因素频繁、大幅度波动,具有非线性特点,而且添加锌粉的效果需经过一段时间才体现在ORP上,具有时滞性。除钴过程工况的复杂变化,造成ORP的稳定控制非常困难。PID控制算法由于参数意义明确、容易实现等优点被广泛应用于工业过程控制中。但对于非线性较强的系统,采用参数固定的PID控制算法难以达到很好的控制效果,目前出现了大量的PID参数智能整定策略^{[ 6, 7, 8, 9, 10]},取得了较好的效果。但对于长流程、非线性和时滞性强的工业过程,一般PID参数整定策略根据输入、输出频繁调整PID参数,很难满足应用要求^{[ 11]}。在工业生产过程中,经常根据以往实践经验实现新问题的定量求解^{[ 12, 13, 14]}。本文提出了基于改进操作模式的PID参数优化方法,控制锌粉的添加,工业现场运行结果表明,该算法非常有效,实现了ORP的稳定控制。

1 氧化还原电位简介

ORP能反映水溶液的氧化能力或还原能力,即溶液放出或获得电子的能力,ORP越负,则溶液的还原能力越强,反之,则氧化性越强。溶液一般是含有多种氧化还原偶的氧化还原系统,所以ORP测量电极反应的是一个混合电位^{[ 4]}。是各氧化还原偶电极电位的加权平均值,而每个氧化还原偶的权重取决于其与(ORP)电极的电子交换电流 $\begin{matrix} I_{0} 。 \end{matrix}$

对于由 $\begin{matrix} m \end{matrix}$ 个氧化还原偶组成的体系,其氧化还原电位 E_h为^{[ 4]}:

$\begin{matrix} \begin{matrix} E_{h} = \overset{m}{\sum_{j = 1}} \frac{|I_{0 j}|}{\sum |I_{0 j}|} [E_{h j}^{0} + \frac{RT}{n_{j} F} \ln \frac{(O x_{j}) (H^{+})^{α}}{(Re d_{j})}] (1) \\ I_{0} = nFA K_{0} C_{ox}^{α} C_{Red}^{1 - α} (2) \end{matrix} \end{matrix}$

式中: $\begin{matrix} E_{h j}^{0} \end{matrix}$ 为标准电极电位; $\begin{matrix} R \end{matrix}$ 为气体常数(8.315 Jmol^-1K^-1); $\begin{matrix} F \end{matrix}$ 为Faraday常数(96496 C mol^-1), $\begin{matrix} T \end{matrix}$ 为绝对温度(K); $\begin{matrix} n \end{matrix}$ 为氧化还原偶半反应中的电子转移数; $\begin{matrix} (O x_{j}) \end{matrix}$ 和 $\begin{matrix} (Re d_{j}) \end{matrix}$ 分别表示氧化还原偶中氧化型物质和还原型物质的活度(或有效浓度); $\begin{matrix} A 为用于测量的 (惰性) 电极的表面极; K_{0} \end{matrix}$ 为氧化还原化学反应速率和该反应与用于测量的(惰性)电极的电子交换速率的混合速率常数; $\begin{matrix} α 为电子传递系数; C \end{matrix}$ 为有效浓度。

在砷盐净化除钴中,溶液中有多种氧化还原偶并存,主要有Zn²⁺/Zn、Cu²⁺/Cu、H⁺/H₂、Co²⁺/Co、Ni²⁺/Ni、Cd²⁺/Cd、HAsO₂/As等,都影响了氧化还原电位。

2 砷盐净化除钴工艺分析

某锌冶炼企业砷盐净化除钴过程优化控制简图如图1所示。砷盐除钴是在温度、pH值、铜离子浓度和砷盐浓度等合理的情况下,向各反应器中连续加入锌粉,使各反应器的ORP值保持在合适的范围内,从而使硫酸锌溶液中的钴离子以合金的形式沉淀下来。

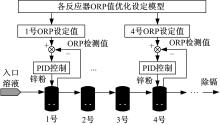	Figure Option View Download New Window
	图1 砷盐净化除钴优化控制简图Fig.1 Schematic diagram of Optimal-control of cobalt removal process with Arsenic salt

砷盐净化除钴入口溶液中主要有除铜工序后溶液(简称“除铜后液”,150~350 m³/h)、砷盐溶液(0.05~0.2 m³/h)。砷盐起稳定剂和活化剂的作用,高浓度的砷盐溶液是根据除铜后液中铜(100~500 mg/L)、钴(15~50 mg/L)和镍离子(5~20 mg/L)的摩尔量按某一算法添加。

在砷盐净化除钴过程中,锌粉是唯一添加的还原剂,通过连续添加锌粉,使溶液的ORP保持在合适的范围,即保持溶液的还原能力在某一合适范围,保证钴离子等杂质离子在一定时间内降至符合电解的要求。由于1号反应器入口溶液流量、杂质离子浓度、砷盐等波动极大,即单位时间内进入除钴反应器的杂质离子和砷盐波动非常大,因此,需要频繁、大幅度调整锌粉添加量,以保证ORP在合适的范围。

砷盐净化除钴系统具有时变性、强非线性、时滞性和多影响因素的特点,经常出现PID参数设定不合理引起ORP的大幅度波动(正负误差需控制在5 mV以内,误差绝对值平均在2 mV以内);而对于这种数学模型难以建立的系统,使得一些基于数学模型的智能优化方法难以满足要求。针对ORP控制的复杂特点,本文提出了基于改进操作模式的PID参数优化方法,用于控制锌粉的添加,使ORP实际值较好地跟随优化设定值。

3 基于操作模式的PID参数整定

操作模式优化就是从工业运行数据中挖掘出入口工况参数、控制参数及控制指标之间的关系,并根据入口工况参数寻找合适的控制参数,使得控制指标达到最优。

砷盐净化除钴积累了大量的工业运行数据,挖掘出PID控制效果较好的情况,将工况参数和对应的PID参数组成一个操作模式,操作模式的集合即构成一个优良操作模式库。本文根据入口的工况参数,从优良操作模式库中寻找与之匹配的操作模式,通过操作模式重用得到较优的PID参数。

3.1 改进的PID算法

砷盐净化除钴过程通过添加锌粉控制反应器中溶液的ORP,控制算法采用增量式PID算法。由于溶液中锌粉单质越多(Zn²⁺/Zn的标准电极电位为-0.762 V),ORP越负,即锌粉与ORP呈负相关关系,所以对基本增量式PID算法做如下修改(添加了“-”):

$\begin{matrix} \begin{matrix} Δu (k) = - [k_{p} (e (k) - e (k - 1)) + k_{i} e (k) + \\ k_{d} (e (k) - 2 e (k - 1) + e (k - 2))] (3) \\ u (k) = u (k - 1) + Δu (k) (4) \end{matrix} \end{matrix}$

式中: $\begin{matrix} e (k) \end{matrix}$ 和 $\begin{matrix} e (k - 1) \end{matrix}$ 分别为第 $\begin{matrix} k \end{matrix}$ 和 $\begin{matrix} k - 1 \end{matrix}$ 时刻的ORP检测值与ORP设定值之间的差; $\begin{matrix} k_{p} 、 k_{i} \end{matrix}$ 和 $\begin{matrix} k_{d} \end{matrix}$ 分别为PID控制器的比例、积分和微分系数( $\begin{matrix} k_{p} 、 k_{i} \end{matrix}$ 和 $\begin{matrix} k_{d} \end{matrix}$ 均大于等于0); $\begin{matrix} u (k) \end{matrix}$ 为第 $\begin{matrix} k \end{matrix}$ 时刻的锌粉添加量。

3.2 基于改进操作模式的PID参数调整框架

基于改进操作模式的PID参数整定模型如图2所示。首先将除钴反应器入口的重要工况参数进行标准化,然后采用改进的模糊C-均值聚类方法聚类,将匹配出的结果进行模糊重用,再采用专家规则对一些结果不理想的PID参数进行修正并输出结果,储存与原操作模式库中的操作模式相似度低的新操作模式或者相似度高而解显著不同但控制效果好的新操作模式,并定期对一些相似度极高的操作模式进行精简。

	Figure Option View Download New Window
	图2 基于改进操作模式的PID参数调整框架Fig.2 Improved operational pattern based PID parameter optimization

3.3 操作模式表述

对第一个除钴反应器ORP影响较大(也是对锌粉消耗影响较大)的入口工况参数有除铜后液流量( $\begin{matrix} f_{1} \end{matrix}$ ),除铜溶液中的铜离子浓度( $\begin{matrix} f_{2} \end{matrix}$ )、钴离子浓度( $\begin{matrix} f_{3} \end{matrix}$ )、镍离子浓度( $\begin{matrix} f_{4} \end{matrix}$ )、砷盐溶液流量( $\begin{matrix} f_{5} \end{matrix}$ )、砷盐溶液中砷盐浓度( $\begin{matrix} f_{6} \end{matrix}$ ),先将入口工况参数 $\begin{matrix} f_{q} (q = 1,2, \dots, 6) \end{matrix}$ 进行标准化,消除量纲不同的影响。6个入口工况参数即为操作模式的描述特征,对应的PID参数为操作模式解。操作模式的表述如下:

$\begin{matrix} X_{k} = \{F_{k}, J_{k}\} (5) \end{matrix}$

式中: $\begin{matrix} X_{k} \end{matrix}$ 为第 $\begin{matrix} k \end{matrix}$ 个操作模式, $\begin{matrix} k = 1, \dots, N, N \end{matrix}$ 为操作模式的数量; $\begin{matrix} F_{k} = (f_{1, k}, f_{2, k}, \dots, f_{6, k}) \end{matrix}$ 为操作模式的描述特征; $\begin{matrix} J_{k} = (j_{1, k}, j_{2, k}, j_{3, k}) \end{matrix}$ 为操作模式 $\begin{matrix} X_{k} \end{matrix}$ 的解特征, $\begin{matrix} j_{1, k}, j_{2, k} \end{matrix}$ 和 $\begin{matrix} j_{3, k} \end{matrix}$ 分别代表PID控制器中的 $\begin{matrix} k_{p} 、 k_{i} \end{matrix}$ 和 $\begin{matrix} k_{d} \end{matrix}$ 三个参数。

在操作模式求解过程中,操作模式匹配的质量关系到整个操作模式优化的成败,操作模式库中需要存储大量的操作模式来满足应用的需求,随着操作模式库中操作模式的增加,会出现操作模式检索效率下降的沼泽现象,本文提出一种改进的模糊C-均值聚类算法对源操作模式进行聚类,在聚类过程中,充分考虑各工况参数的重要程度,可极大地提高操作模式匹配的准确度和速度。

3.4 改进的模糊C-均值聚类

由Bezdek^{[ 15]}提出的模糊C-均值聚类算法,以最小类内平方误差和为聚类准则。

设 $\begin{matrix} X = {X_{1}, X_{2}, \dots, X_{N}} \subset R^{q}, R^{q} 为每个操作模式包含 q \end{matrix}$ 个属性(分量), $\begin{matrix} μ_{ji} 为第 j 个操作模式对第 i \end{matrix}$ 类的隶属度, μ_ji∈[0,1]( $\begin{matrix} \overset{c}{\sum_{i = 1}} \end{matrix}$ μ_ji=1),μ_ji的具体计算方法见文献[15], $\begin{matrix} 1 \leq j \leq N, 1 \leq i \leq c; v_{i} 为第 i 类的聚类中心, 求 X \end{matrix}$ 的模糊 C-均值聚类就是求式(6)目标函数最小。

$\begin{matrix} J (U, V) = \overset{N}{\sum_{j = 1}} \overset{c}{\sum_{i = 1}} u_{ji}^{m} d_{ji}^{2} (6) \end{matrix}$

式中: $\begin{matrix} d_{ji} = ‖ x_{j} - v_{i} ‖ 为第 j 个操作模式到第 i 类的欧氏距离, 距离越小表示两个操作模式越相似; 加权指数 m > 1 是控制聚类结果的模糊程度常数, 本文中 m 取 2, c \end{matrix}$ 取6(即分为6大类)。

传统的模糊 C-均值聚类算法采用欧氏距离计算操作模式到类中心的距离,将操作模式数据中每一个工况参数视为同等重要,对数据有等划分的趋势,而工业生产中操作模式的各工况参数的重要程度并不一样,如果每个工况参数赋予相同的权重,会严重影响聚类的合理性。

将欧氏距离修改为:

$\begin{matrix} d r_{ji} = \overset{q}{\sum_{l = 1}} λ_{l} (x_{j, l} - v_{i, l})^{2} (7) \end{matrix}$

式中: $\begin{matrix} λ_{l} (l = 1,2, \dots, q) \end{matrix}$ 为操作模式中各工况参数的权重,满足 $\begin{matrix} \overset{q}{\sum_{l = 1}} \end{matrix}$ λ_l=1,0≤λ_l≤1。本文考虑除铜后液流量、铜、钴和镍离子的浓度,砷盐溶液流量,砷盐溶液中砷盐浓度对锌粉消耗影响的大小(对锌粉消耗影响越大,对 ORP影响也越大),根据专家经验设置 $\begin{matrix} λ_{1}, λ_{2}, \dots, λ_{6} \end{matrix}$ 分别为0 .23,0 .22,0 .14,0 .1,0 .16,0 .15。

由于 $\begin{matrix} q \end{matrix}$ 维向量空间两条空间向量,即使两点距离一定,它们的夹角余弦值也可以随意变化,所以仅采用欧氏距离计算两个向量之间的相似程度存在局限性。故有的采用 CAD( Cosine angle distance)计算两个操作模式间的相似度, CAD形式如下:

$\begin{matrix} \cos θ_{ji} = \frac{\overset{q}{\sum_{l = 1}} x_{j, l} \times v_{i, l}}{\sqrt[]{\overset{q}{\sum_{l = 1}} x_{j, l}^{2}} \sqrt[]{\overset{q}{\sum_{l = 1}} v_{i, l}^{2}}} (8) \end{matrix}$

显然,余弦值越大,表示两个操作模式越相似。但采用 CAD方法计算两个操作模式的相似度为1时(夹角为0 °),两个操作模式的模并不一定相同,即两个操作模式并不完全相似。

为克服相似度测量不准确的问题,本文提出了一种新的相似度计算方法,该方法融合了改进欧氏距离和 CAD方法的优点,包含距离相似度和余弦相似度两部分:

$\begin{matrix} \begin{matrix} D S_{ji} = \frac{\overset{q}{\sum_{l = 1}} λ_{l} (x_{j, l} - v_{i, l})^{2}}{D_{Max}} (9) \\ C S_{ji} = 1 - \frac{\overset{q}{\sum_{l = 1}} x_{j, l} \times v_{i, l}}{\sqrt[]{\overset{q}{\sum_{l = 1}} x_{j, l}^{2}} \sqrt[]{\overset{q}{\sum_{l = 1}} v_{i, l}^{2}}} (10) \\ dne w_{ji} = α_{1} D S_{ji} + α_{2} C S_{ji} (11) \\ D R_{r, s} = \overset{q}{\sum_{l = 1}} λ_{l} (x_{r, l} - x_{s, l})^{2} (12) \\ r, s = 1, \dots, N; r \neq s \\ 式中 : \\ D_{Max} = \max (D R_{r, s}, r, s = 1, \dots, N, r \neq s) (13) \end{matrix} \end{matrix}$

$\begin{matrix} dne w_{ji} 为第 j 个操作模式与第 i \end{matrix}$ 类的混合距离,其值越小表示越相似; $\begin{matrix} D_{Max} \end{matrix}$ 为操作模式库中任一两个操作模式之间的加权欧氏距离的最大值; $\begin{matrix} α_{1} 、 α_{2} 为权重系数 (α_{1} + α_{2} = 1), \end{matrix}$ 根据实际情况确定其权重大小,本文都取0 .5。

模糊 C-均值聚类目标函数修改为:

$\begin{matrix} J (U, V) = \overset{N}{\sum_{j = 1}} \overset{c}{\sum_{i = 1}} u_{ji}^{2} dne w_{ji}^{2} (14) \end{matrix}$

3 .5 操作模式匹配

操作模式匹配是根据新问题的描述从操作模式库中匹配出最佳操作模式作为新问题求解依据,是操作模式优化中极为重要的环节。

本文操作模式匹配分为两步,首先根据式(15)计算待求操作模式与各聚类中心的相似度 $\begin{matrix} Sim \end{matrix}$ ,找到相似度最大的类,然后计算待求操作模式与相似度最大的类中所有操作模式的相似度,将相似度大于某一个阈值的操作模式全部搜索出来,如果符合要求的操作模式的数量大于或等于 $\begin{matrix} K (本文 K 取 5), 那么与待求操作模式之间相似度最高的 K 个操作模式被作为匹配结果输出; 如果满足要求的操作模式的数量小于 K, 那么将阈值减去一个正数 (取 0.05), 直到检索到 K \end{matrix}$ 个相似的操作模式为止。

$\begin{matrix} Sim = 1 - dne w_{ji} (15) \end{matrix}$

操作模式库中与待求的操作模式的描述特征相似度达到阈值的将全部被搜索出来。

3 .6 操作模式模糊重用

由于砷盐净化除钴具有温度高、强腐蚀性和强酸性的特点,系统参数将随时间缓慢变化,离当前时间越久远,该操作模式的借鉴作用越小^{[ 16]}。因此,需要对检索出的不同时期的操作模式赋予不同的模糊加权隶属度 $\begin{matrix} β_{t} 。 \end{matrix}$ 设共有 $\begin{matrix} K \end{matrix}$ 个操作模式,第1个操作模式离待求操作模式最近,离待求操作模式时间间隔(本文时间间隔以月为单位)为 $\begin{matrix} T_{1} (定义 T_{1} = 0), \dots, 第 K \end{matrix}$ 个操作模式离待求操作模式时间最久远,间隔时间为 $\begin{matrix} T_{K}, \end{matrix}$ 那么第 $\begin{matrix} t \end{matrix}$ 个操作模式的非线性模糊加权隶属度 $\begin{matrix} β_{t} \end{matrix}$ 定义为:

$\begin{matrix} β_{t} = f (t) = (1 - ε) \sqrt[]{\frac{T_{K} - T_{t}}{T_{K}}} + ε (16) \end{matrix}$

式中: $\begin{matrix} ε \in [0,1] 为常数 (本文 ε 取 0.3), ε \end{matrix}$ 越小,则时间越远的操作模式的模糊加权值 $\begin{matrix} β_{t} \end{matrix}$ 就越小; $\begin{matrix} ε = β_{K} \leq \dots \leq β_{1} = 1 。 \end{matrix}$

设在操作模式库中匹配到的 $\begin{matrix} K 个操作模式对应的解特征 J_{t} = (j_{t, 1}, j_{t, 2}, j_{t, 3}) = (k p_{t}, k i_{t}, k d_{t}) (t = 1,2, \dots, K); \end{matrix}$ 当前操作模式的解为 $\begin{matrix} J_{PID} = (j_{1}, j_{2}, j_{3}) = (kp, ki, kd), \end{matrix}$ 其计算公式为:

$\begin{matrix} \begin{matrix} j_{p} = (\overset{K}{\sum_{t = 1}} β_{t} \times j_{t, p}) (\overset{K}{\sum_{t = 1}} β_{t},) p = 1,2, 3 \\ (17) \end{matrix} \end{matrix}$

3.7 操作模式的存储与精简

操作模式库会随着时间的推移不断增加,为了将操作模式库控制在一定规模内,并且保证操作模式具有典型性,基本包含工业现场可能出现的工况,必须对操作模式库进行维护。

在3 .5节中进行操作模式匹配时,如果匹配出的操作模式与待求操作模式的最大相似度大于等于0.95,当待求操作模式的解与相似度最大的操作模式的解存在明显不同,并且根据专家经验判断待求操作模式的控制效果较好时(砷盐除钴过程的恶劣环境,会导致系统参数随时间缓慢变化,随着时间推移,相同工况的最优解会发生变化),则存储该操作模式,否则不存储该操作模式。如果匹配出的操作模式与待求操作模式的最大相似度小于0.95,并且待求操作模式的控制效果较好时,则存储该操作模式。

为控制操作模式库的规模,每15天进行一次操作模式库的精简,对每一类(模糊 C-均值聚类后)中操作模式相似度大于等于0.98的操作模式,删除离当前时间最远的操作模式。

通过对新操作模式的选择性存储和对时间久远的操作模式进行精减,在控制操作模式库规模的同时,也保证了操作模式库的典型性和实用性。

4 工业实验结果

对国内某锌冶炼厂砷盐净化除钴工序的1号反应器进行了约2个月的实验。采用 PC机( CPU: Intel酷睿 i5 -3210 M)从 PLC(西门子 S400)实时获取工业运行的 ORP、除铜后溶液流量等实时检测数据,并手工输入杂质离子浓度数据,利用 PC机强大的计算能力,采用本文方法实现 PID参数的优化,然后将优化后的参数下达到 PLC。

图3( a)为采用基于人工经验 PID参数设定(方法 a)的 ORP控制曲线;图3( b)为采用基于基本操作模式^{[ 14]}的 PID参数设定(方法 b)的 ORP控制曲线;图3( c)为采用本文提出的基于改进操作模式的 PID参数整定方法(方法 c)运行2个月后的 ORP控制曲线(由于除钴反应器中溶液并非绝对均匀,所以 ORP实际曲线存在下降的过程中有上升的现象,上升过程中有下降的现象)。

	Figure Option View Download New Window
	图3 ORP控制实际曲线Fig.3 Control curve of ORP

由于工业现场连续运行,砷盐除钴工况不停变化, ORP的优化设定值会根据工况的变化而调整,故3个实际运行曲线的 ORP设定值是不一样的。所以只能从控制效果上进行比较,工业现场主要从 ORP的实际检测值偏离 ORP设定值的程度进行评价。

采用人工经验设定的 PID参数控制锌粉添加时, ORP实际值偏离 ORP设定值的绝对值最大为9 .5 mV(从一个状态转移到另外一个过程的过渡过程除外),误差绝对值的平均值高达3 .51 mV;采用基本操作模式优化 PID参数时, ORP实际控制效果明显好于采用人工经验的控制效果;采用本文方法时, ORP实际值偏离 ORP设定值的绝对值最大仅为4 .6 mV(过渡过程除外),误差绝对值的平均值仅为1 .65 mV, ORP实际值能较好地跟踪 ORP设定值,大幅度降低了 ORP波动的范围,明显优于前两种 PID参数调整的效果,完全满足工业应用的要求(要求最大误差在 ±5 .0 mV以内,平均绝对误差小于2 mV)。

5 结束语

添加锌粉除钴过程是典型的氧化还原过程,通过 ORP的优化设定达到锌粉的优化添加,针对 ORP控制的时变性、强非线性、时滞等复杂特点,提出了基于改进的操作模式的 PID参数调整算法。工业运行结果表明:该方法能有效应对砷盐除钴过程入口工况参数的变化,取得很好的控制效果,为类似的冶金过程的 PID控制的参数整定提供了新的思路。

The authors have declared that no competing interests exist.

参考文献

View Option

[1]	Bϕckman O, ϕstvold T. Products formed during cobalt cementation on zinc in zinc sulfate electrolytes[J]. Hydrometallurgy, 2000, 54(2/3): 65-78 [本文引用:1] [JCR: 2.169]
[2]	Stole-Hansen K, Wregget D A, Gowanlock D, et al. Model based analysis and control of a cementation process[J]. Computers and Chemical Engineering, 1997, 21(Sup. ): 1099-1103 [本文引用:1] [JCR: 2.091]
[3]	Wang Ling-yun, Gui Wei-hua, Kok L T, et al. Optimal control problems arising in the zinc sulphate electrolyte purification process[J]. Journal of Global Optimization, 2009, 5(4): 705-718 [本文引用:1] [JCR: 1.307]
[4]	Bohn Hinrich L. Redox potentials[J]. Soil Science, 1970, 112(1): 39-43 [本文引用:3] [JCR: 1.051]
[5]	Fugleberg S, Jarvinen A, Yllo E. Recent development in solution purification at Outokumpu Zinc Plant, Kokkola[C]∥, Proceedings International Symposium-World Zinc '1993, HobartMelbourne, 1993: 241-247 [本文引用:1]
[6]	刘金琨. 先进PID控制MATLAB仿真[M]. 3版. 北京: 电子工业出版社, 2011. [本文引用:1]
[7]	Mohammad Shamsuzzoha. A new approach for PID controller tuning from closed-loop setpoint experiment[J]. Chemical Engineering Transactions, 2011, 24: 445-450 [本文引用:1]
[8]	王介生, 高宪文. 基于改进混合蛙跳算法的电渣重熔过程多变量PID控制器设计[J]. 控制与决策, 2011, 26(11): 1731-1734 Wang Jie-sheng, Gao Xian-wen. Design of multi-variable PID controller of electroslag remelting process based on improved shuffled frog leaping algorithm[J]. Control and Decision, 2011, 26(11): 1731-1734 [本文引用:1] [CJCR: 0.907]
[9]	杨智, 陈志堂, 范正平, 等. 基于改进粒子群优化算法的PID控制器整定[J]. 控制理论与应用, 2010, 27(10): 1345-1352 Yang Zhi, Chen Zhi-tang, Fan Zheng-ping, et al. A tuning of PID controller based on improved particle swarm optimization[J]. Control Theory and Applications, 2010, 27(10): 1345-1352 [本文引用:1] [CJCR: 0.555]
[10]	潘天红, 李士勇. 基于即时学习的非线性系统自适应PID控制[J]. 控制理论与应用, 2009, 26(10): 1180-1184 Pan Tian-hong, Li Shi-yong. Adaptive PID control for nonlinear systems based on lazy learning[J]. Control Theory and Applications, 2009, 26(10): 1180-1184 [本文引用:1] [CJCR: 0.555]
[11]	晏静文, 侯忠生. 学习增强型PID控制系统的收敛性分析[J]. 控制理论与应用, 2010, 27(6): 761-766 Yan Jing-wen, Hou Zhong-sheng. Convergence analysis of learning-enhanced PID control system[J]. Control Theory and Applications, 2010, 27(6): 761-766 [本文引用:1] [CJCR: 0.555]
[12]	耿增显, 柴天佑. 基于案例推理的浮选过程智能优化设定[J]东北大学学报: 自然科学版, 2008, 29(6): 761-764 Geng Zeng-xian, Chai Tian-you. Intelligently optimal index setting for flotation process by CBR[J]. Journal of Northeastern University (Natural Science), 2008, 29(6): 761-764 [本文引用:1] [CJCR: 0.593]
[13]	袁平, 王福利, 毛志忠. 基于案例推理的电弧炉终点预报[J]东北大学学报: 自然科学版, 2011, 32(12): 1673-1676 Yuan Ping, Wang Fu-li, Mao Zhi-zhong. CBR based endpoint prediction of EAF[J]. Journal of Northeastern University(Natural Science), 2011, 32(12): 1673-1676 [本文引用:1] [CJCR: 0.593]
[14]	桂卫华, 阳春华, 李勇刚, 等. 基于数据驱动的铜闪速熔炼过程操作模式优化及应用[J]自动化学报, 2009, 35(5): 718-723 Gui Wei-hua, Yang Chun-hua, Li Yong-gang, et al. Data-driven operational-pattern optimization for copper flash smelting process[J]. Acta Automatica Sinica, 2009, 35(5): 718-723 [本文引用:2] [CJCR: 0.572]
[15]	Bezdek J C. Pattern Recognition with Fuzzy Objective Function Algorithms[M]. New York: Plenum Press, 1981. [本文引用:1]
[16]	Lin Chun-fu, Wang De-sheng. Fuzzy support vector machines[J]. IEEE Transactions on Neural Networks, 2002, 13(2): 465-467 [本文引用:1] [JCR: 2.952]

2000

2.169

0.0

. 2000, 54(2<italic/>/3):null-null

Products formed during cobalt cementation on zinc in zinc sulfate electrolytes

... 0 引言钴离子是硫酸锌溶液净化中最难去除和危害最大的杂质之一^[1] ...

1997

2.091

0.0

. 1997, 21(Sup.):null-null

Model based analysis and control of a cementation process

... 为保证溶液钴离子浓度达标,经常过量添加锌粉,造成锌粉的极大浪费^[2,3] ...

2009

1.307

0.0

... 为保证溶液钴离子浓度达标,经常过量添加锌粉,造成锌粉的极大浪费^[2,3] ...

1970

1.051

0.0

... 奥托昆普研究认为砷盐净化除钴过程是典型的氧化还原过程,在一定范围内氧化还原电位(Oxidation-reduction potential,ORP)越负(相同条件下,锌粉添加得越多,ORP越负,溶液还原性越强^[4]),置换除钴反应速率越快^[5] ...

... 溶液一般是含有多种氧化还原偶的氧化还原系统,所以ORP测量电极反应的是一个混合电位^[4] ...

... 对于由 m个氧化还原偶组成的体系,其氧化还原电位E_h为^[4]: ...

1993

0.0

2011

0.0

... 但对于非线性较强的系统,采用参数固定的PID控制算法难以达到很好的控制效果,目前出现了大量的PID参数智能整定策略^[6,7,8,9,10],取得了较好的效果 ...

2011

0.0

2011

0.0

0.907

. 2011, 26(11):1731-1734

Design of multi-variable PID controller of electroslag remelting process based on improved shuffled frog leaping algorithm

Based on the technique features and mathematical model of electroslag remelting(ESR) process, a multivariable self-tuning PID controller tuned optimally by an improved shuffled frog leaping algorithm(ISFLA) is proposed to control the two-input-two-output(TITO) ESR process. A new frog leaping rule is proposed to enhance the SFLA’s local search capabilities, which adjusts the frog local search space and the step of each flog’s jump dynamically and randomly by emulating frog’s perception and action uncertainties in order to prevent premature convergence and improve the search efficiency of SFLA. The simulation results and industrial application tests show the feasibility and effectiveness of the proposed control method.

根据电渣重熔过程的工艺特点和数学模型, 提出了基于改进混合蛙跳算法(ISFLA) 的多变量参数自整定 PID 控制策略. 提出一种新的蛙跳规则, 用以增强SFLA 的局部搜索能力. 该规则主要通过模拟青蛙的感知和运动的不确定性来动态随机地调整青蛙的局部搜索空间和步长, 以防止SFLA 算法过早收敛, 提高算法的搜索效率. 仿真结果和工业应用实验均表明了所提出控制方法的可行性和有效性.

2010

0.0

0.555

2009

0.0

0.555

. 2009, 26(10):1180-1184

Adaptive PID control for nonlinear systems based on lazy learning

当使用先进策略整定PID控制器参数时,往往要依赖于系统所辨识的模型,而模型的精度与优化算法的计算效率直接影响到系统的控制效果.本文利用即时学习算法的本质自适应特点(建模数据在时间与空间上相邻性),来提高辨识模型的精度,并基于广义最小方差的性能指标,用等价多项式的方法,推导出PID形式的控制律,从而避免其他优化算法带来的计算量,提高了控制精度与计算效率.仿真结果验证了该方法的有效性. Abstract： When applying advanced strategies to determine the parameters of a PID controller, a model need to be identified for the controlled system. The predicted precision and the computation efficiency of the identifying algorithm directly affect the control performance of the system. To improve the precision, lazy learning algorithm, which has a essentially adaptive characteristics(i.e.,in which the data used for modeling are not only neighbors in time domain, but also neighbors in space domain), is used to identify the model of system. By employing the generalized minimum variance as the performance function and using the polynomial method, the control-law is derived for the PID controller, in which its parameters are tuned online in the process of the lazy learning identification. Simulation results show good performances of this algorithm.

2010

0.0

0.555

. 2010, 27(6):761-766

Convergence analysis of learning-enhanced PID control system

针对具有可重复性的一般离散时间非线性系统,在已存在的PID控制系统的基础上,利用重复性的特点,给出了一种学习增强型PID控制方法,严格证明了收敛性,并通过快速路交通系统的仿真验证了该方法的有效性和优越性.该种方法的主要特点是,不需要对已有的PID控制装置和系统做任何改动,只需在PID控制器的外环加上迭代学习控制器即可,是一种模块化的设计.该方法实现了P1D与迭代学习控制的优势互补.

... 但对于长流程、非线性和时滞性强的工业过程,一般PID参数整定策略根据输入、输出频繁调整PID参数,很难满足应用要求^[11] ...

2008

0.0

0.593

... 在工业生产过程中,经常根据以往实践经验实现新问题的定量求解^[12,13,14] ...

2011

0.0

0.593

... 在工业生产过程中,经常根据以往实践经验实现新问题的定量求解^[12,13,14] ...

2009

0.0

0.572

... 在工业生产过程中,经常根据以往实践经验实现新问题的定量求解^[12,13,14] ...

... 图3(b)为采用基于基本操作模式^[14]的PID参数设定(方法b)的ORP控制曲线 ...

1981

0.0

... 4 改进的模糊C-均值聚类由Bezdek^[15]提出的模糊C-均值聚类算法,以最小类内平方误差和为聚类准则 ...

2002

2.952

0.0

... 6 操作模式模糊重用由于砷盐净化除钴具有温度高、强腐蚀性和强酸性的特点,系统参数将随时间缓慢变化,离当前时间越久远,该操作模式的借鉴作用越小^[16] ...