车内噪声直接影响着汽车的乘坐舒适性,并成为人们衡量汽车品质的一个关键指标^{[ 1]}。车内噪声可分为:固体传播噪声和空气传播噪声两类。一般地,低频车内噪声(20~200 Hz)主要由固体传播,而高频噪声则以空气传播为主。由于低频噪声的频率范围很低,可以通过基于波动声学的有限元或边界元方法进行分析研究^{[ 2]}。

声固耦合模型已经广泛应用于车内低频噪声预测的研究。Kavarana等^{[ 3]}提出了一种能够削减声腔模态的相对重要性的方法,该方法使在汽车设计阶段需要避开的声腔模态阶数减少。Surkutwar等^{[ 4]}通过对车内噪声传递路径进行分析,应用模态贡献度分析及面板贡献度分析确定了对响应峰值有较大影响的结构位置,通过添加加强梁的方法降低了某客车的车内噪声。Sung等^{[ 5]}通过模态贡献度分析和面板贡献度分析方法对某轿车的车内噪声进行了分析,并提出了通过修改车身局部结构进而改善车内噪声的措施。在控制车身结构噪声方面,对结构本身的修改一般很难从全局范围改善结构的声辐射性能,由于黏弹性阻尼材料具有高阻尼的特性,而且能在相当宽的频带内起到抑制振动和噪声的作用,所以在汽车上得到大量应用。Wu等^{[ 6]}通过涂贴阻尼层的方法降低了商用车驾驶室的车内噪声,但阻尼层的布置位置、厚度等都将影响其降低噪声的性能。韩志明^{[ 7]}通过对阻尼层的拓扑优化,在不影响降噪性能的同时将阻尼层的涂贴位置减少了一半。臧献国等^{[ 8]}通过遗传算法对阻尼层的厚度进行了优化,提高了阻尼材料的利用率。

本文以某轿车为研究对象,建立了该车的声固耦合有限元模型,从而预测了该车的车内低频噪声。分析了车身结构各壁板对驾驶员耳旁声压级的灵敏度。通过对车内噪声影响较大的结构件上添加阻尼层实现了对车内噪声的控制,并通过试验设计实现了阻尼层的优化,达到了在涂贴较少的阻尼层的同时降低车内噪声的目的。

由于轿车车身主要由钣金件组成,通常采用四节点和三节点的壳单元进行划分,车身中各处焊点采用CWELD焊接单元模拟。

将轿车CAD模型适当简化后,以15 mm的单元尺寸对轿车白车身结构进行单元划分,划分完毕的模型含单元共226 253个,其中三角形单元12 876个,满足计算精度的要求。正确设置轿车白车身中各结构的属性,得到轿车白车身的有限元模型。

对白车身进行模态分析,并与试验模态分析的结果进行对比,验证模型的有效性。 表1列出了计算模态和试验模态的结果。

表1

Table 1

表1(Table 1)

表1 白车身计算模态和试验模态的对比 Table 1 Comparison results between the analysis and experiment modal of BIW 阶数 计算频率/Hz 试验频率/Hz 振型描述 误差/% 1 29.57 30.23 一阶扭转 2.19 2 33.22 32.51 一阶弯曲 2.18 3 34.59 34.68 斜塌模态 0.26

表1 白车身计算模态和试验模态的对比 Table 1 Comparison results between the analysis and experiment modal of BIW

通过 表1可以看出:计算模态与试验模态的各阶振型基本一致,各阶频率误差最大不超过5%,计算结果与试验结果基本吻合,说明所建立的白车身有限元模型是有效的,能用于进一步的分析。在白车身基础上,添加车门,车窗及行李厢盖等部件,完成整车有限元模型的建立。

利用封闭车身结构有限元模型,建立考虑座椅结构的车内声腔有限元模型。声学单元的理想尺寸是大约每个波长划分为6个单元,实际通常采用的声学单元为100~200 mm^{[ 9]}。本文声腔采用100 mm的单元进行划分。

将声腔有限元模型与整车有限元模型耦合,完成的声固耦合模型如 图1所示。

图1

Fig.1

	Figure Option ViewDownloadNew Window
	图1 轿车声固耦合模型(隐去车窗)Fig.1 Structural-acoustic coupling model of the vehicle(hiding the doors)

利用建立的声固耦合有限元模型(见 图1),采用MSC/Nastran中的模态法进行频率响应分析。由于20 Hz是人耳能感受到的最低频率,而低频噪声主要是由集中在200 Hz以下的车身结构振动引起的,因此将频率响应分析的频率计算区间设置为20~200 Hz。而在采用模态法计算频率响应时,为了保证计算精度,模态计算的终止频率应该大于频率响应计算频率的1.5倍以上,一般取频响计算频率的1.5~2倍。综合考虑计算精度及计算时间,将频率响应分析的模态计算频率设置为0~300 Hz。

汽车在匀速行驶时,车身主要受到动力总成悬置激励和路面不平度通过悬架传递到车身的激励。主要包括:动力总成前、后、左、右4个悬置点对车身的激励,前悬架左右减振器塔座对车身的激励,后悬架左右减振器、弹簧与车身连接点对车身的激励。通过试验测量被试轿车以50 km/h匀速行驶时的动力总成悬置激励和路面不平度通过悬架对车身的激励。将试验测得的各点对车身的激励施加在模型中的相应位置并进行频率响应分析。完成频率响应分析后得到驾驶员耳旁声压级的频率为20~200 Hz。

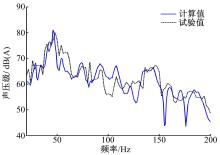
图2将频率响应的计算结果与试验结果进行了对比。从图中可以看出:计算声压级幅值普遍高于试验值,这是由于在声固耦合模型中未考虑车内吸声材料的吸声特性造成的。但二者的轮廓基本相同,各峰值出现的频率也基本一致,说明该模型能用于对车内低频噪声的预测。

图2

Fig.2

	Figure Option ViewDownloadNew Window
	图2 驾驶员耳旁声压级的计算值与试验值的对比Fig.2 Confrontation of experimental value and simu-lation value SPL around the driver’s ear

灵敏度分析是指轿车声学质量随设计参数的变化梯度。灵敏度计算方法主要有:直接求导法和伴随结构法两种^{[ 10]}。直接求导法推导简单,无论是一阶还是高阶灵敏度都可以很方便地应用,因而较为常用,本文采用的就是直接求导法。结构灵敏度分析包括静态灵敏度分析和动态灵敏度分析。在静态灵敏度分析中,关注的结构性能指标为位移和应力值等;而动态灵敏度分析有特征灵敏度分析(即特征值灵敏度分析)、特征向量灵敏度分析、传递函数灵敏度分析和动力响应灵敏度分析等^{[ 11]}。本文分析方法就属于动态灵敏度分析。

将封闭声腔模型的车身结构的厚度作为设计变量,包括轿车前挡风玻璃、后挡风玻璃、车顶、防火墙、地板前部、地板中部、地板后部、行李厢隔板、左右前后车门及车窗共十六组板件。

选取驾驶员耳旁声压级为目标函数,对噪声频率分别为47、108、161 Hz情况下的驾驶员耳旁噪声进行灵敏度分析,分析结果整理后如 表2所示。

表2

Table 2

表2(Table 2)

表2 各壁板的灵敏度 Table 2 Sensitivity of the panels around the cavity 结构位置 噪声频率/Hz 47 108 161 前挡风玻璃 0.021 0.00095 -0.0113 后挡风玻璃 -0.0234 -0.00027 -0.00297 车顶 -0.0402 -0.0163 0.0181 防火墙 -0.0242 -0.0047 -0.0572 车底中部地板 0.0076 0.0122 0.00036 车底前部地板 0.0056 0.00488 -0.0127 车底后部地板 -0.0808 -0.0263 0.00722 行李厢隔板 0.0084 0.0143 0.0295 左前门 0.0018 0.0267 0.00025 左后门 0.0223 0.0626 0.091 右前门 -0.0044 -0.00073 0.024 右后门 -0.0232 -0.00759 0.00117 右后门玻璃 -0.00015 -0.001 0.00005 左前门玻璃 0.00079 0.00213 -0.00415 左后门玻璃 -0.00058 -0.0015 0.00085 右前门玻璃 0.00054 -0.002 -0.0028

表2 各壁板的灵敏度 Table 2 Sensitivity of the panels around the cavity

由于同一结构在不同的频率下对响应点的影响因子不同,所以应选择在各峰值频率下对响应都有影响的结构进行改进。根据灵敏度分析的结果,发现防火墙和车底后部地板在3个峰值频率下对驾驶员耳旁声压级影响较大。分析相应频率下两处结构的模态,寻找结构中振幅较大的位置,在发生振动的金属壁板上涂贴阻尼层,能有效地减小金属板件弯曲振动的强度并缩短振动时间,抑制其振动,从而达到减振降噪的目的^{[ 12]}。

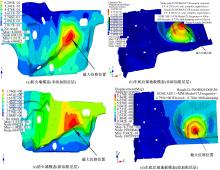
以频率为47 Hz时的防火墙和车底后部地板为例,此时,防火墙的模态(最大位移和最小位移分别为1.935 mm和1.085 mm)和行李箱地板模态(最大位移和最小位移分别为30.52 mm和0.002 mm)分别如 图3(a)和(b)所示。

图3

Fig.3

	Figure Option ViewDownloadNew Window
	图3 壁板模态Fig.3 Modal shapes of panels

图4

Fig.4

	Figure Option ViewDownloadNew Window
	图4 壁板结构Fig.4 FE models of panels

对应原车中两处结构在相应位置未涂贴阻尼材料。因此在原车防火墙及行李箱地板振动位移最大的位置涂贴阻尼层,涂贴位置如 图4所示。涂贴阻尼层后相应频率下防火墙与车后部地板的模态如 图3(c)(最大位移和最小位移分别为0.88 mm和0.102 mm)和 图3(d)(最大位移和最小位移分别为8.28 mm和0.99 mm)所示。对比添加阻尼层前后的结构模态,振动的幅值均有所下降。

对添加阻尼层的模型进行频率响应分析,得到驾驶员耳旁声压级的响应。 图5对添加阻尼层前后的驾驶员耳旁声压级进行了对比,添加阻尼层后驾驶员耳旁声压级总体得到降低,但降低的幅值有限,频率为47 Hz时,峰值仅降低了0.42 dB(A),因此需要对阻尼层的布置进行进一步优化。

图5

Fig.5

	Figure Option ViewDownloadNew Window
	图5 添加阻尼层前后的驾驶员耳旁声压级对比Fig.5 Comparison of the SPL around the driver’s ear before and after damping layer layout modification

车身阻尼层多采用沥青材料的自由阻尼层,其密度和厚度对车内噪声有较大影响^{[ 13]}。

根据灵敏度分析结果,防火墙与行李箱地板对声压级有较大影响,所以分别选取防火墙和行李箱地板阻尼层的密度及厚度为试验优化设计的四个因素,试验因素A、B、C、D分别为行李箱地板阻尼层的厚度、密度及防火墙阻尼层的厚度、密度。每个因素选取3个水平。应用L₉(3⁴)正交表安排试验,设置9次试验方案,计算后得到试验结果。利用极差分析法对试验结果进行计算,试验方案、结果及结果分析如 表3所示。

本次优化中有两个目标,属于多目标优化。多目标优化方法有:综合评分法和综合平衡法。综合评分法通过对各目标的评分将多目标转化为单目标。综合平衡法将各目标的最优条件综合平衡,找出使每个目标都尽可能好的条件^{[ 14]}。

表3

Table 3

表3(Table 3)

表3 试验方案及试验结果计算表 Table 3 Test plan and results 试验方案 行李箱地板阻尼层 防火墙阻尼层 峰值 /dB(A) 质量 /kg A厚度 /mm B密度 /(kg·m-3) C厚度 /mm D密度 /(kg·m-3) 1 1 1500 1 1500 80.371 1.354 2 1 2500 2 2500 80.352 2.32 3 1 3500 3 3500 80.420 3.338 4 2 1500 2 3500 80.400 2.81 5 2 2500 3 1500 80.478 4.501 6 2 3500 1 2500 80.580 6.203 7 3 1500 3 2500 80.456 4.139 8 3 2500 1 3500 80.604 6.668 9 3 3500 2 1500 80.752 9.286 峰值 /dB(A) y1 y2 y3 R 80.381 80.482 80.604 0.233 80.409 80.478 80.584 0.175 80.518 80.501 80.451 0.067 80.534 80.562 80.501 0.061 - - - - - - - - 质量 /kg y1 y2 y3 R 2.337 4.505 6.698 4.360 2.767 4.496 6.276 3.508 4.742 4.805 5.708 0.967 4.742 4.805 3.993 0.749 - - - - - - - -

表3 试验方案及试验结果计算表 Table 3 Test plan and results

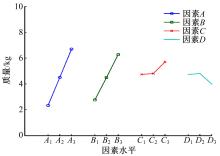
运用综合平衡法针对两个目标进行综合优化,绘出各因素水平的趋势图(见 图6和 图7),找出最优方案。从 表3可以看出,4个因素对两个目标的由主到次的关系为:峰值: A-B-C-D;质量: A-B-C-D。

图6

Fig.6

	Figure Option ViewDownloadNew Window
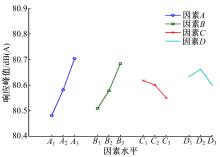	图6 响应峰值-因素水平趋势图Fig.6 Relationship between the levels of factor and SPL peak value around the driver’s ear

图7

Fig.7

	Figure Option ViewDownloadNew Window
	图7 质量因素水平趋势图Fig.7 Relationship between the levels of factor and mass of damping layout

综合考虑两个目标,要求两个目标最小。从趋势图及因素主次可以看出,随着因素 A、 B三个水平的增大,两个目标都增大,因素 D选取 D₂时两个目标同时取得最大值,取 D₃时两个目标同时取得最小值。因此,因素 A选择 A₁,因素 B选择 B₁因素 D选择 D₃。因素 C对两个目标有不同的影响, C₁到 C₃峰值响应减小,而质量增加。从峰值最小考虑, C₃最好,从质量角度考虑, C₁最好。针对两个指标的因素水平趋势图中 C₁与 C₂相当接近, C₂与 C₃差别较大,如果选择 C₃将导致质量大幅增加。因此选择 C₂是合理的。阻尼层的优化方案为 A₁ B₁ C₂ D₃。即车底后部地板采用密度为1500 kg/m³,厚度为1 mm的阻尼层,防火墙采用密度为3500 kg/m³,厚度为2 mm的阻尼层。

图8

Fig.8

	Figure Option ViewDownloadNew Window
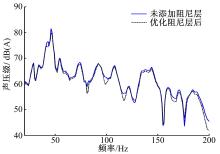	图8 采用优化阻尼层后与未采用阻尼层的响应对比Fig.8 Comparison of the SPL around driver’s ear with optimized and unoptimized damping layout

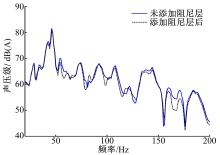
优化前后声压级曲线对比如 图8所示。优化阻尼层后,相对于未添加阻尼层的响应峰值降低了1.13 dB(A),总声压级从61.28 dB(A)降至60.66 dB(A),涂贴的阻尼层质量从3.338 kg降为1.403 kg,降低了1.935 kg。可见采用优化阻尼层后各个频率处的响应均有所改善。

(1)采用本文建立的轿车声固耦合模型所预测的车内低频噪声与试验结果具有较好的一致性,说明该模型有较高的准确性。

(2)通过灵敏度分析,得到了车身各结构对驾驶员耳旁噪声声压级的灵敏度。

(3)针对两个不同的优化目标,各因素的主次和最优组合不完全相同,分析了各因素水平对两个目标的影响。

(4)采用综合平衡法对两个目标进行了综合优化,找到了阻尼层布置的最优方案。

(5)得到了一个合理的阻尼层优化方案,使车内低频噪声峰值降低了1.13 dB(A);总声压级降低了0.62 dB(A);阻尼层的总质量降低了1.935 kg。