高峰时段公交客流分配的Logit模型改进

引用本文

张晓亮, 赵淑芝, 刘华胜, 高祥涛. 高峰时段公交客流分配的Logit模型改进. 44(6): 1616-1621
ZHANG Xiao-liang, ZHAO Shu-zhi, LIU Hua-sheng, GAO Xiang-tao. Improvement of public transportation assignment Logit model during peak period. Journal of Jilin University Engineering and Technology Edition, 44(6): 1616-1621 复制到剪切板

Permissions

高峰时段公交客流分配的Logit模型改进

张晓亮¹, 赵淑芝¹, 刘华胜¹, 高祥涛²

1.吉林大学交通学院,长春 130022

2.吉林省工程咨询科技公司,长春 130061

通信作者:赵淑芝(1958-),女,教授,博士生导师.研究方向:交通运输系统规划.E-mail:zhaosz@jlu.edu.cn

作者简介:张晓亮(1987-),男,博士研究生.研究方向:交通运输系统规划.E-mail:zxl10@mails.jlu.edu.cn

基金:国家自然科学基金项目(51378237);

摘要

首先定义了站点滞留系数,并对其进行计算,根据站点间有、无直达线路及站点拥挤情况将站点分为3类。从时间函数、换乘惩罚函数、发车间隔三个方面对Logit模型进行了改进。然后通过实例分析了模型中参数α和T_f对分配结果的影响,并对参数α和T_f进行了标定。最后对分配结果进行误差分析,验证了模型的有效性。

关键词: 交通运输系统工程; 公交客流分配; Logit模型; 高峰时段

中图分类号:U491.1 文献标志码:A 文章编号:1671-5497(2014)06-1616-06

Improvement of public transportation assignment Logit model during peak period

ZHANG Xiao-liang¹, ZHAO Shu-zhi¹, LIU Hua-sheng¹, GAO Xiang-tao²

1.College of Transportation, Jilin University, Changchun 130022, China

2.Jilin Engineering Consulting Technology, Changchun 130061, China

Abstract

An improved public transportation assignment Logit model during peak period is proposed. First, the station arrest coefficient is defined and calculated. According to the transit stations with and without nonstop line and the crowding level, the stations are classified into three categories. The Logit model is improved from the aspects of the time function, sanction function and departure interval. Then, using a practical case, the influences of the parametersα andT_f in the model on the transit assignment are analyzed, andα and Tf are calibrated. Finally, error analysis of the transit assignment results is carried out, which validates the model.

Keyword: engineering of communications and transportation system; public transportation assignment; Logit model; peak period

Show Figures

公交客流分配是公交线网规划的核心问题^{[ 1]},国内外学者对此进行了大量研究^{[ 2]}。现有分配模型大体分为两类:①随机用户平衡模型^{[ 3, 4]},从公交乘客的角度,考虑乘车费用、时间费用、换乘费用等,使每个人的出行成本最小。②网络均衡配流模型^{[ 5, 6]},从公交网络的角度,考虑网络结构及乘客的分布,使网络中资源被均衡利用。这些模型对全天的客流分配结果均较为理想,但是对高峰时段的客流分配结果不尽如人意。高峰时段作为交通矛盾突出的时段,有着乘客必须在时间窗限制内完成出行的特殊性。在不拥挤的站点,乘客仍然可以坚持选择运行时间短、费用低、少换乘的线路,然而在拥挤的站点,部分乘客则不得不放弃上述原则中的一个或若干个。此时既不满足乘客的出行费用最低,也不满足网络全局最优。而且高峰时段公交OD以及同一公交线路的上下行客流量存在着较大的不对称性。以上原因导致现有模型客流分配的结果误差较大。

针对上述问题,本文分析了高峰时段公交客流的特点,将公交站点分为拥挤站点和不拥挤站点,并从换乘惩罚、共线路径选择等角度对Logit模型进行改进,然后分别对不同类别的站点进行了客流分配。

1 站点拥挤程度的判定

1.1 模型假设

(1)高峰时段公交站点间的OD矩阵 Z已经获得。

(2)公交线网较为完善,任意两交通区之间的公交出行无需借助其他交通工具即可完成。

(3)不考虑交通拥堵以及特殊天气等情况,行车间隔等于发车间隔。

此外,在本节中不考虑乘客的换乘次数,乘客总是能通过零次或若干次换乘到达目的地。

1.2 相关变量的定义

设研究区域共有 n个交通小区; s条公交线路; m个公交站点;交通小区 i有 w_i个公交站点, m= $\begin{matrix} \overset{n}{\sum_{i = 1}} \end{matrix}$ w_i。将公交站点按照交通小区的顺序重新排序,公交站点用 g_i表示,出发地的公交站点用 e_i表示,目的地的公交站点用 f_j表示。从 e_i到 f_j的高峰小时客流量为 a_ij, G={ a_ij};从 e_i到 f_j的高峰小时路段客流量为 u_ij,高峰小时路段客流量矩阵为 H, H={ u_ij};设 s条公交线路高峰小时可承载路段客流量矩阵为 K_d,从站点 e_i到站点 f_j的可承载路段客流量为 $\begin{matrix} {v^{d}}_{ij} \end{matrix}$ , K_d ={ $\begin{matrix} {v^{d}}_{ij} \end{matrix}$ }。公交线路 l_c的高峰小时发车间隔为 h_c;单车额定载客量为 q_c;单车座位数为 r_c;站立面积为 s_c。座位数和站立空间之比在一般情况下是在车辆内部初始设计时,出于获得舒适站立目的而设置的指标^{[ 7]}。参照乘客舒适度指标(见表1),人数密度取参考值2.5 per/m²,则 s_c=0 .4( q_c-r_c)。公交站点 e_i和 f_j间,可使用座位数为 $\begin{matrix} r_{ij}^{k} \end{matrix}$ ,可使用站立面积为 $\begin{matrix} s_{ij}^{k} \end{matrix}$ ,人均占地面积为 $\begin{matrix} v_{ij}^{c} \end{matrix}$ 。定义 $\begin{matrix} v_{ij}^{x} \end{matrix}$ 为 t_i至 t_j方向的站点 t_i的站点滞留系数, $\begin{matrix} v_{ij}^{c} \end{matrix}$ 代表站点 t_i( t_i至 t_j方向)的拥挤程度,对应的矩阵 R={ $\begin{matrix} r_{ij}^{k} \end{matrix}$ }, S= $\begin{matrix} \{s_{ij}^{k}\} \end{matrix}$ , K_s ={ $\begin{matrix} v_{ij}^{c} \end{matrix}$ }, K_x={ $\begin{matrix} v_{ij}^{x} \end{matrix}$ }。显然矩阵 Z、 H、 K_d、 R、 S、 K_s、 K_x均为 m阶方阵。

1.3 站点滞留系数矩阵的计算

(1)将矩阵 H、 K_d、 R、 S初始化,使 u_ij= $\begin{matrix} {v^{d}}_{ij} \end{matrix}$ = $\begin{matrix} r_{ij}^{k} \end{matrix}$ = $\begin{matrix} s_{ij}^{k} \end{matrix}$ =0。

(2)生成路段客流量矩阵 H。

若从 e_i到 f_j的最佳路径不途经其他公交站点,则令: u_ij=u_ij+a_ij。

若从 e_i到 f_j的最佳路径途经站点 g_r,则: u_ij=u_ij+a_ij, u_ir=u_ir+a_ij, u_rj=u_rj+a_ij。

(3)生成高峰小时公交线路可承载路段客流量矩阵 K_d。

若公交线路 l_c经过站点 e_i且经过站点 e_j,则令: $\begin{matrix} {v^{d}}_{ij} \end{matrix}$ = $\begin{matrix} {v^{d}}_{ij} \end{matrix}$ + $\begin{matrix} \frac{60}{h_{c}} \end{matrix}$ q_c, $\begin{matrix} {v^{d}}_{ji} \end{matrix}$ = $\begin{matrix} {v^{d}}_{ij} \end{matrix}$ , $\begin{matrix} r_{ij}^{k} \end{matrix}$ = $\begin{matrix} r_{ij}^{k} \end{matrix}$ + $\begin{matrix} \frac{60}{h_{c}} \end{matrix}$ r_c, $\begin{matrix} r_{ij}^{k} \end{matrix}$ = $\begin{matrix} r_{ji}^{k} \end{matrix}$ , $\begin{matrix} s_{ij}^{k} \end{matrix}$ = $\begin{matrix} s_{ij}^{k} \end{matrix}$ + $\begin{matrix} \frac{24}{h_{c}} \end{matrix}$ ( q_c-r_c), $\begin{matrix} s_{ij}^{k} \end{matrix}$ = $\begin{matrix} s_{ji}^{k} \end{matrix}$ 。

(4)生成路段人均占地面积矩阵 K_s。

$\begin{matrix} v_{ij}^{c} = \{\begin{matrix} s_{ij}^{k} \cdot (u_{ij} - r_{ij}^{k})^{- 1}, 若 u_{ij} - r_{ij}^{k} > 0 \\ 1, 否则 \end{matrix} \end{matrix}$

(5)生成站点滞留系数矩阵 K_x。

以单位站立地面面积表示公交乘客舒适度如表1所示^{[ 7]}。根据各路段车内人均占地面积,将乘客的站立状态分为5种,用向量 λ_i=( λ₁, λ₂, λ₃, λ₄, λ₅)表示。

表1 公交乘客舒适度(以单位站立地面面积表示) Table 1 Comfort of passenger(by every person’s area)

若 $\begin{matrix} v_{ij}^{c} \end{matrix}$ ≥0 .67,则令 $\begin{matrix} v_{ij}^{x} \end{matrix}$ =λ₁;若0 .67 > $\begin{matrix} v_{ij}^{c} \end{matrix}$ ≥0 .29,则令 $\begin{matrix} v_{ij}^{x} \end{matrix}$ =λ₂;若0 .29 > $\begin{matrix} v_{ij}^{c} \end{matrix}$ ≥0 .22,则令 $\begin{matrix} v_{ij}^{x} \end{matrix}$ =λ₃;若0 .22 > $\begin{matrix} v_{ij}^{c} \end{matrix}$ ≥0 .18,则令 $\begin{matrix} v_{ij}^{x} \end{matrix}$ =λ₄;若0 .18 > $\begin{matrix} v_{ij}^{c} \end{matrix}$ ,则令 $\begin{matrix} v_{ij}^{x} \end{matrix}$ =λ₅。

$\begin{matrix} v_{ij}^{x} \end{matrix}$ =λ₅或 $\begin{matrix} v_{ij}^{x} \end{matrix}$ =λ₄的站点有两种情况:①途经站点 t_i发往站点 t_j方向的公交车到达站点 t_i时,车内已经十分拥挤,站点 t_i候车的乘客很难进入公交车中;②站点 t_i候车至站点 t_j方向的乘客较多,后上车的乘客很难进入公交车中。这些站点经常会出现由于车内太拥挤候车乘客不得不等下一辆公交车或改为其他交通方式出行的情况。

2 邻接矩阵

图的定义:一个图 G是指一个有序的三元组( V( G), E( G), ψ_G),其中 V( G)是非空的顶点集,内部的元素称为图 G的顶点, E( G)是与 V( G)不相交的边集,内部的元素称为图 G的边, ψ_G是关联函数,它使 G的每条边对应于 G的无序顶点对。

邻接矩阵的定义:设图 G=( V, E)的顶点集 V( G) ={ v₁, v₂, v₃,…, v_p},用 a_ij表示 G中顶点 v_i与 v_j之间的边数,则 n阶方阵 M( G) = $\begin{matrix} (a_{ij})_{n \times n} \end{matrix}$ 称为 G的邻接矩阵。

定理^{[ 8]} 设 M( G)是 G的邻接矩阵,则 G中连接 v_i到 v_j长度为 l的途径数目等于 M^l( G) = $\begin{matrix} (a_{ij}^{(l)})_{p \times p} \end{matrix}$ 中位于第 i行、第 j列处的元素 $\begin{matrix} a_{ij}^{(l)} \end{matrix}$ 。

以公交站点为顶点,若两公交站点之间存在一条直达公交,则连接一条边,构建网络图 G,建立邻接矩阵 X( G) = $\begin{matrix} (x_{ij})_{m \times m} \end{matrix}$ 。 X^k( G) = $\begin{matrix} (x_{ij}^{(k)})_{m \times m} \end{matrix}$ , $\begin{matrix} x_{ij}^{(k)} \end{matrix}$ 表示图 G中从 e_i到 f_j的长度为 k的链的数量,即从 e_i到 f_j经过 k-1次换乘的公交路径的数量。

3 Logit模型的改进

3.1 Logit模型存在的问题

Logit模型是效用理论在交通工程领域应用的突出体现。现有的Logit模型中,根据旅行时间、票价、换乘方便性、乘客舒适性等因素建立广义费用函数,再由路径间广义费用的绝对差或相对差计算路径的选择概率。本文对Logit模型深入研究分析发现,运用现有的Logit模型对高峰时段进行客流分配时存在以下3点不足:

(1)未考虑将要换乘车辆的到达时间及车内拥挤情况等不确定因素对乘客选择路径的影响。

(2)模型中以换乘时间或换乘距离记入广义费用函数中的方式计算换乘惩罚值,导致计算结果对短距离换乘的惩罚值偏大,对长距离换乘的惩罚值偏小。

(3)模型中没有考虑各路径第一辆公交车到达的先后顺序对乘客选择路径的影响,尤其是选择共线路径时的影响。

针对以上3个问题,本文对Logit模型进行如下改进:

(1)在时间函数中引入变量,以表示不确定因素的影响。

(2)根据换乘距离建立换乘惩罚函数,以表示换乘距离对各路径选择的影响。

(3)分析发车间隔对乘客选择各路径的影响,再结合Logit模型及换乘惩罚函数计算各路径的客流分配率。

3.2 时间函数 T_ij( l_c)的改进

乘坐直达公交线路 l_c从 e_i到 f_j的时间函数为:

$\begin{matrix} T_{ij} (l_{c}) = T_{ij}^{x} (l_{c}) + Vo t^{- 1} \cdot P_{ij} (l_{c}) (1) \end{matrix}$

式中: $\begin{matrix} T_{ij}^{x} \end{matrix}$ ( l_c)为公交线路 l_c从 e_i到 f_j的行驶时间,min; P_ij( l_c)为公交线路 l_c从 e_i到 f_j的票价,元; Vot^{[ 9]}为以公共交通方式出行的时间价值,元/min。

对于有换乘的路径,由于将要换乘车辆的到达时间及车内拥挤情况均为不确定因素,所以定义 T_f为换乘惩罚时间,以表示不确定因素的影响。

乘坐第 k个换乘方案经过 m-1次换乘从 e_i到 f_j的时间函数用 T_ij( $\begin{matrix} l_{m}^{k} \end{matrix}$ )表示:

$\begin{matrix} \begin{matrix} T_{ij} (l_{m}^{k}) = \overset{m}{\sum_{c = 1}} T_{ij}^{x} (l_{c}^{k}) + \overset{m}{\sum_{c = 1}} Vo t^{- 1} \cdot P_{ij} (l_{c}^{k}) + \\ 0.5 \overset{m}{\sum_{c = 1}} h (l_{c}^{k}) + (m - 1) T_{f} (2) \end{matrix} \end{matrix}$

式中: h( $\begin{matrix} l_{c}^{k} \end{matrix}$ )为公交线路 $\begin{matrix} l_{c}^{k} \end{matrix}$ 的行车间隔; m为乘坐公交线路的数量,一次换乘时, m=2,两次换乘时, m=3(假设公交乘客最多可接受两次换乘)。

3.3 换乘惩罚函数的改进

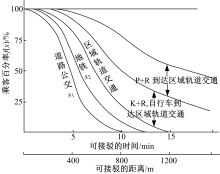
从规划目的来看,可以认为距离公交站点5 min路程(约400 m)的潜在公交乘客都会使用该系统。而在5~10 min路程(400~800 m)间的潜在乘客数逐渐下降直至几乎为零。不同接驳方式的可接受接驳距离范围如图1所示。其中曲线 s₁、 s₂近似满足以下关系式^{[ 7]}:

$\begin{matrix} \begin{matrix} f_{s 1} (x) = 0.5 \cos (0.00125 π \cdot x) + 0.5 \\ f_{s 2} (x) = 0.5 \cos (0.001 π \cdot x) + 0.5 \end{matrix} \end{matrix}$

定义 d( $\begin{matrix} l_{c}^{k} \end{matrix}$ )为第 k个换乘方案中从线路 $\begin{matrix} l_{c (i - 1)}^{k} \end{matrix}$ 到线路 $\begin{matrix} l_{ci}^{k} \end{matrix}$ 的换乘距离,km。定义状态函数 θ( l_c),如果换乘站点为常规公交站点,则 θ( $\begin{matrix} l_{c}^{k} \end{matrix}$ ) =1;如果换乘站点为轨道公交站点,则 θ( $\begin{matrix} l_{c}^{k} \end{matrix}$ ) =0 .8。

将 λ_ij( $\begin{matrix} l_{c}^{k} \end{matrix}$ )定义为从线路 $\begin{matrix} l_{(c - 1)}^{k} \end{matrix}$ 换乘线路 $\begin{matrix} l_{c}^{k} \end{matrix}$ 的换乘惩罚函数:

$\begin{matrix} λ_{ij}^{} (l_{c}^{k}) = \{\begin{matrix} 1, d (l_{c}^{k}) \cdot θ (l_{c}^{k}) \leq 0.4 \\ \cos (1.25 π \cdot d (l_{c}^{k}) \cdot θ (l_{c}^{k})) + 1, 其他 \end{matrix} (3) \end{matrix}$

	Figure Option View Download New Window
	图1 不同接驳方式的可接受接驳距离范围Fig.1 Acceptable shuttle distance by distinct shuttle mode

3.4 客流分配率计算方法的改进

根据站点的拥挤程度将站点分为两类, $\begin{matrix} v_{ij}^{x} \end{matrix}$ =λ₁、 λ₂、 λ₃的站点定义为不拥挤站点, $\begin{matrix} v_{ij}^{x} \end{matrix}$ =λ₄、 λ₅的站点定义为拥挤站点。再结合站点间有无直达线路,将站点分为3类:①有直达线路的不拥挤站点;②无直达线路的不拥挤站点;③拥挤站点。根据站点的类别,对任意两站点之间的有限路径进行搜索,其中常规公交换乘站点以800 m为搜索半径,轨道交通公交换乘站点以1000 m为搜索半径,形成有效路径集。假设 <e_i→ f_j>间共有 d_ij个可行路径,包括 d_ij_,1条直达线路和 d_ij_,2个换乘方案,其中 d_ij_,1 =x_ij。

3.4.1 只考虑发车间隔对乘客选择线路的影响,不考虑线路行程时间和票价等因素的影响

$\begin{matrix} λ_{ij (h)}^{(k)} \end{matrix}$ 表示从 e_i到 f_j第 k个路径的客流分配率,向量 $\begin{matrix} λ_{ij (h)}^{k} \end{matrix}$ = $\begin{matrix} (\begin{matrix} λ_{ij (h)}^{(1)} & λ_{ij (h)}^{(2)} & \dots & λ_{ij (h)}^{(k)} \end{matrix}) \end{matrix}$ 。

$\begin{matrix} λ_{ij (h)}^{(k)} = {h_{(k) c 1}}^{- 1} \cdot {(\overset{d}{\sum_{k = 1}} {h_{(k) c 1}}^{- 1})}^{- 1} (4) \end{matrix}$

式中: h₍ _k₎ _c₁为第 k个路径的第一个公交线路的发车间隔。

3.4.2 只考虑线路行程时间和票价等因素对乘客选择线路的影响,不考虑发车间隔的影响

$\begin{matrix} λ_{ij (t)}^{(k)} \end{matrix}$ 表示从 e_i到 f_j第 k个路径的客流分配率,向量 $\begin{matrix} λ_{ij (t)}^{k} \end{matrix}$ = $\begin{matrix} (\begin{matrix} λ_{ij (t)}^{(1)} & λ_{ij (t)}^{(2)} & \dots & λ_{ij (t)}^{(k)} \end{matrix}) \end{matrix}$ 。由Logit模型计算各有效路径的客流分配率为:

$\begin{matrix} \begin{matrix} λ_{ij (t)}^{(k)} = \exp (- T_{ij} (l_{(m)}^{k}) \cdot α^{- 1}) \cdot \\ {(\overset{d}{\sum_{k = 1}} \exp (- T_{ij} (l_{(m)}^{k}) \cdot α^{- 1}))}^{- 1} (5) \end{matrix} \end{matrix}$

式中: α为灵敏度系数, α≥1。

当 α=1时, α对模型无调节作用;当 α增大时,将减缓 T_ij( $\begin{matrix} l_{(m)}^{k} \end{matrix}$ )对 $\begin{matrix} λ_{ij (t)}^{(k)} \end{matrix}$ 的影响;当 α→ +∞时, $\begin{matrix} \lim_{α \to + \infty} \end{matrix} \begin{matrix} λ_{ij (t)}^{(k)} \end{matrix}$ = $\begin{matrix} \frac{1}{d} \end{matrix}$ ,即 T_ij( $\begin{matrix} l_{(m)}^{k} \end{matrix}$ )对 $\begin{matrix} λ_{ij (t)}^{(k)} \end{matrix}$ 也无影响。

3.4.3 综合考虑换乘距离、发车间隔、行程时间和票价对乘客选择线路的影响

$\begin{matrix} λ_{ij}^{(k)} \end{matrix}$ 表示从 e_i到 f_j第 k个路径的客流分配率,向量 $\begin{matrix} λ_{ij}^{k} \end{matrix}$ = $\begin{matrix} (\begin{matrix} λ_{ij}^{(1)} & λ_{ij}^{(2)} & \dots & λ_{ij}^{(d)} \end{matrix}) \end{matrix}$ 。

(1)有直达线路的不拥挤站点

当 x_ij≠0时,说明从 e_i到 f_j存在直达公交线路,这样站点的乘客几乎不会考虑换乘出行。第 k个路径的客流分配率的计算式为:

$\begin{matrix} λ_{ij}^{(k)} = λ_{ij (h)}^{(k)} \cdot λ_{ij (t)}^{(k)} \cdot {(\overset{d_{ij, 1}}{\sum_{k = 1}} (λ_{ij (h)}^{(k)} \cdot λ_{ij (t)}^{(k)}))}^{- 1} (6) \end{matrix}$

(2)无直达线路的不拥挤站点

当 x_ij=0而 $\begin{matrix} x_{ij}^{1} \end{matrix}$ ≠0,说明从 e_i到 f_j不存在直达公交线路,而存在 $\begin{matrix} x_{ij}^{1} \end{matrix}$ 个一次零换乘的路径。若 x_ij+ $\begin{matrix} x_{ij}^{1} \end{matrix}$ =0而 $\begin{matrix} x_{ij}^{2} \end{matrix}$ ≠0,说明从 e_i到 f_j不存在直达和一次零换乘的路径,而存在 $\begin{matrix} x_{ij}^{2} \end{matrix}$ 个两次零换乘的路径。若 x_ij+ $\begin{matrix} x_{ij}^{1} \end{matrix}$ + $\begin{matrix} x_{ij}^{2} \end{matrix}$ =0,说明不存在两次以内零换乘的路径。第 k个路径的客流分配率的计算式为:

$\begin{matrix} \begin{matrix} λ_{ij}^{(k)} = λ_{ij (h)}^{(k)} \cdot λ_{ij (t)}^{(k)} \cdot \overset{m}{\prod_{c = 2}} λ_{ij} (l_{c}^{k}) \cdot \\ {(\overset{d_{ij, 2}}{\sum_{k = 1}} (λ_{ij (h)}^{(k)} \cdot λ_{ij (t)}^{(k)} \cdot \overset{m}{\prod_{c = 2}} λ_{ij} (l_{c}^{k})))}^{- 1} (7) \end{matrix} \end{matrix}$

(3)拥挤站点

对于拥挤的站点,乘客不单局限于选择直达线路,一次换乘和两次换乘的线路也会被选择。第 k个路径的客流分配率的计算公式为:

当 x_ij≠0时

$\begin{matrix} \begin{matrix} λ_{ij}^{(k)} = λ_{ij (h)}^{(k)} \cdot λ_{ij (t)}^{(k)} \cdot (\overset{d_{ij, 1}}{\sum_{k = 1}} (λ_{ij (h)}^{(k)} \cdot λ_{ij (t)}^{(k)}) + \\ {\overset{d_{ij}}{\sum_{k = d_{ij, 1} + 1}} (λ_{ij (h)}^{(k)} \cdot λ_{ij (t)}^{(k)} \cdot \overset{m}{\prod_{c = 2}} λ_{ij} (l_{c}^{k})))}^{- 1} \end{matrix} \end{matrix}$

当 x_ij=0时

$\begin{matrix} \begin{matrix} λ_{ij}^{(k)} = λ_{ij (h)}^{(k)} \cdot λ_{ij (t)}^{(k)} \cdot \overset{m}{\prod_{c = 2}} λ_{ij} (l_{c}^{k}) \cdot (\overset{d_{ij, 1}}{\sum_{k = 1}} (λ_{ij (h)}^{(k)} \cdot λ_{ij (t)}^{(k)}) + \\ {\overset{d_{ij}}{\sum_{k = d_{ij, 1} + 1}} (λ_{ij (h)}^{(k)} \cdot λ_{ij (t)}^{(k)} \cdot \overset{m}{\prod_{c = 2}} λ_{ij} (l_{c}^{k})))}^{- 1} (8) \end{matrix} \end{matrix}$

3.5 误差分析

高峰时段同一公交线路的上下行客流量存在着较大的不对称性,为了验证模型分配结果的有效性,分别计算线路 l_c上行方向高峰小时分配误差 ω $\begin{matrix} (l_{c}) \end{matrix}$ 和下行方向高峰小时分配误差 ω $\begin{matrix} (l_{c, f}) \end{matrix}$ ,以及整体分配的平均误差 $\begin{matrix} \bar{ω} \end{matrix}$ 和最大误差 ω_max:

$\begin{matrix} \begin{matrix} ω (l_{c}) = |q (l_{c}) - Q (l_{c})| \cdot Q {(l_{c})}^{- 1} (9) \\ ω (l_{c, f}) = |q (l_{c, f}) - Q (l_{c, f})| \cdot Q {(l_{c, f})}^{- 1} (10) \\ \bar{ω} = \sum |q (l_{c}) - Q (l_{c})| \cdot {(\sum Q (l_{c}))}^{- 1} (11) \\ ω_{\max} = \max (ω (l_{c}), ω (l_{c, f})) (12) \end{matrix} \end{matrix}$

式中: q $\begin{matrix} (l_{c}) \end{matrix}$ 为线路 l_c上行方向高峰小时模型分配客流量; Q $\begin{matrix} (l_{c}) \end{matrix}$ 为线路 l_c上行方向高峰小时调查客流量; q $\begin{matrix} (l_{c, f}) \end{matrix}$ 为线路 l_c下行方向高峰小时模型分配客流量; Q $\begin{matrix} (l_{c, f}) \end{matrix}$ 为线路 l_c下行方向高峰小时调查客流量; $\begin{matrix} \bar{ω} \end{matrix}$ 为所有线路分配的平均误差; ω_max为所有线路分配的最大误差。

4 实例分析

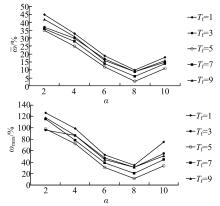
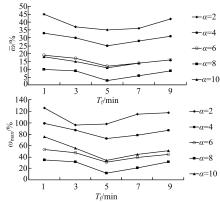
以长春市经济技术开发区(简称经开区)公共交通规划案例为例,将该区域划分为105个交通小区,途经的公交线路共有73条,其中:轨道交通线路2条,常规公交主线10条,公交支线33条,公交分支线28条,共有站点297个。抽取了10条线路进行随车调查,其中包括:轨道交通线路1条,常规公交主线4条,公交支线3条,公交分支线2条。根据文献[9]可知,长春公共交通方式出行的时间价值 Vot=0.12 元/min。对灵敏度系数 α分别为2、4、6、8、10时和换乘惩罚时间 T_f分别为1、3、5、7、9 min时进行全正交实验。对研究区域进行客流分配,将分配结果与调查结果进行误差对比分析,计算 $\begin{matrix} \bar{ω} \end{matrix}$ 和 ω_max。 α与 $\begin{matrix} \bar{ω} \end{matrix}$ 、 ω_max的关系曲线如图2所示; T_f与 $\begin{matrix} \bar{ω} \end{matrix}$ 、 ω_max的关系曲线如图3所示。

	Figure Option View Download New Window
	图2 α与 $\begin{matrix} \bar{ω} \end{matrix}$ 、 ω_max的关系图Fig.2 Connection of α with $\begin{matrix} \bar{ω} \end{matrix}$ and ω_max

	Figure Option View Download New Window
	图3 T_f与 $\begin{matrix} \bar{ω} \end{matrix}$ 、 ω_max的关系图Fig.3 Connection of T_f with $\begin{matrix} \bar{ω} \end{matrix}$ and ω_max

再运用MNL(Multinomial Logit)模型对经开区的高峰时段进行客流分配,采用基于高斯-牛顿法的非线性最小二乘数据拟合法对费用函数进行标定。计算分配结果的误差,Logit模型改进前后误差对比如表2所示。

表2 Logit模型改进前、后误差对比表(%) Table 2 Error contrast of Logit model improvement or not

通过误差分析得知:对于改进Logit模型,当 α=8、 T_f=5 min时,分配结果的 $\begin{matrix} \bar{ω} \end{matrix}$ 和 ω_max均为最小值,此时 $\begin{matrix} \bar{ω} \end{matrix}$ =3.7%、 ω_max=11.8%。其中最大分配误差为公交分支线的下行方向,这主要是由于公交分支线的客流较少,波动较大引起的。与原模型相比,改进后的模型高峰时段客流分配的 $\begin{matrix} \bar{ω} \end{matrix}$ 和 ω_max分别降低了10个百分点和14个百分点;不计公交分支线的分配误差,改进后的模型,高峰时段客流分配的 $\begin{matrix} \bar{ω} \end{matrix}$ 和 ω_max分别降低了8个百分点和11个百分点。实例分析结果表明,该方法误差较小且具有较高的实用性。

5 结束语

对站点的拥挤程度进行了分析,对站点滞留系数进行了定义。根据站点间有、无直达线路及站点拥挤情况将站点分为有直达线路的不拥挤站点、无直达线路的不拥挤站点、拥挤站点3类。从时间函数、换乘惩罚函数、发车间隔三个方面对Logit模型进行了改进。首先,引入换乘惩罚时间 T_f,以表示不确定因素对乘客选择路径的影响,重新定义时间函数。其次,根据换乘距离建立换乘惩罚函数,以表示换乘距离对各路径选择的影响。然后,分析发车间隔对乘客选择各路径的影响,再结合Logit模型及换乘惩罚函数计算各路径的客流分配率。最后通过实例,分析了参数 α和 T_f对分配结果的影响,对参数 $\begin{matrix} \bar{ω} \end{matrix}$ 和 ω_max进行了标定。结果表明:该模型具有较高的理论和实用价值,提高了高峰时段公交客流分配的准确度,丰富了城市公交规划的理论体系。

The authors have declared that no competing interests exist.

参考文献

View Option

[1]	Kato H, Kaneko Y, Inoue M. Comparative analysis of transit assignment: evidence from urban railway system in the Tokyo metropolitan area[J]. Transportation Science, 2010, 37(5): 775-799. [本文引用:1] [JCR: 1.814]
[2]	Szeto W Y, Solayappan M, Jiang Yu. Reliability-based transit assignment for congested stochastic transit networks[J]. Computer-Aided Civil and Infrastructure Engineering, 2011, 26(4): 311-326. [本文引用:1] [JCR: 4.46]
[3]	宋亚萍, 王瑞军, 李会玲, 等. 基于综合运输网络的客流分配优化模型与算法[J]. 中国铁道科学, 2011, 32(5): 127-131. Song Ya-ping, Wang Rui-jun, Li Hui-ling, et al. Optimization model and algorithm of passenger flow assignment based on comprehensive transportation network[J]. China Railway Science, 2011, 32(5): 127-131. [本文引用:1] [CJCR: 0.699]
[4]	Nuzzolo A, Crisalli U, Rosati L. A schedule-based assignment model with explicit capacity constraints for congested transit networks[J]. Transportation Research Part C-Emerging Technologies, 2012, 20(1): 16-33. [本文引用:1] [JCR: 2.006]
[5]	Trozzi V, Kaparias I, Bell M G H, et al. A dynamic route choice model for public transport networks with boarding queues[J]. Transportation Planning and Technology, 2013, 36(1): 44-61. [本文引用:1] [JCR: 0.427]
[6]	Codina E. A variational inequality reformulation of a congested transit assignment model by Cominetti, Correa, Cepeda, and Florian[J]. Transportation Science, 2013, 47(2): 231-246. [本文引用:1] [JCR: 1.814]
[7]	Vuchic V R. 城市公共交通运营、规划与经济[M]. 宋瑞, 何世伟译. 北京: 中国铁道出版社, 2012. [本文引用:3]
[8]	李明哲, 金俊, 石瑞银. 图论及其算法[M]. 北京: 机械工业出版社, 2010. [本文引用:1]
[9]	赵淑芝, 赵贝. 多因素影响下的城市居民出行行为时间价值[J]. 吉林大学学报: 工学版, 2011, 41(1): 47-50. Zhao Shu-zhi, Zhao Bei . Value of travel time of urban resident under multifactor influence[J]. Journal of Jilin University (Engineering and Technology Edition), 2011, 41(1): 47-50. [本文引用:1] [CJCR: 0.701]

2010

1.814

0.0

. 2010, 37(5):775-799 DOI:10.1007/s11116-010-9295-8

Comparative analysis of transit assignment: evidence from urban railway system in the Tokyo metropolitan area

1.Department of Civil Engineering, The University of Tokyo, 7-3-1 Hongo, Bunkyo-ku, Tokyo 113-8656, Japan 2.Department of Civil Engineering, College of Science and Technology, Nihon University, 1-8-14 Kanda-Surugadai, Chiyoda-ku, Tokyo 101-8308, Japan 3.Transportation Planning Department, Creative Research and Planning Co., Ltd., 1-5-4 Higashiyama, Meguro-ku, Tokyo 153-0043, Japan

This paper empirically compares the performance of six traffic assignment methods using the same empirical dataset of route choice. Multinomial logit (MNL), structured multinomial probit (SMNP), user equilibrium (UE), logit-based stochastic user equilibrium (SUE), probit-based SUE, and all-or-nothing (AON) assignment methods are applied to the comparative analysis. The investigated methods include those with three types of error components in their cost functions and two types of flow dependencies. Four methods of generating the route choice set are also compared for use as stochastic traffic assignment methods. The revealed preference data of urban rail route choice in the Tokyo Metropolitan Area are used for the case analysis. The empirical case analysis shows that probit-based SUE provides the best accuracy but requires the longest computation time. It also shows that the heuristics used to generate the choice set influence the method’s accuracy, while the incorporation of route commonality and in-vehicle congestion significantly improves its accuracy. Finally, the implications for practical rail planning are discussed on the basis of the analysis results.

... 公交客流分配是公交线网规划的核心问题^[1],国内外学者对此进行了大量研究^[2] ...

2011

4.46

0.0

. 2011, 26(4):311-326

Reliability-Based Transit Assignment for Congested Stochastic Transit Networks

W. Y. Szeto 1,* ,Muthu Solayappan 2 andYu Jiang 3

1 Department of Civil Engineering, The University of Hong Kong, Hong Kong, China 2 Department of Industrial and Systems Engineering, The National University of Singapore, Singapore 3 Department of Civil Engineering, The University of Hong Kong * To whom correspondence should be addressed. E-mail: <a href="mailto:ceszeto@hku.hk" title="Link to email address" shape="rect">ceszeto@hku.hk</a>.

Abstract: This article proposes a nonlinear complementarity problem (NCP) formulation for the risk-aversive stochastic transit assignment problem in which in-vehicle travel time, waiting time, capacity, and the effect of congestion are considered as stochastic variables simultaneously and both their means and variances are incorporated into the formulation. A new congestion model is developed and captured in the proposed NCP formulation to account for different effects of on-board passengers and passengers waiting at stops. A reliability-based user equilibrium condition is also defined based on the proposed generalized concept of travel time budget referred to as effective travel cost, and is captured in the formulation. A column generation based algorithm is proposed to solve the NCP formulation. A survey was conducted to validate that the degree of risk aversion of transit passengers affects their route choices. Numerical studies were performed to demonstrate the problem and the effectiveness of the proposed algorithm. The results obtained show that underestimating the congestion effect and ignoring the risk aversion behavior can overestimate the patronage of transit service, which have profound implications on the profit of the operators involved and the development of transit network design models.

... 公交客流分配是公交线网规划的核心问题^[1],国内外学者对此进行了大量研究^[2] ...

2011

0.0

0.699

2012

2.006

0.0

. 2012, 20(1):null-null

A schedule-based assignment model with explicit capacity constraints for congested transit networks

2013

0.427

0.0

2013

1.814

0.0

2012

0.0

... 座位数和站立空间之比在一般情况下是在车辆内部初始设计时,出于获得舒适站立目的而设置的指标^[7] ...

... 以单位站立地面面积表示公交乘客舒适度如表1所示^[7] ...

... 其中曲线s₁、s₂近似满足以下关系式^[7]: ...

2010

0.0

... 定理^[8] 设M(G)是G的邻接矩阵,则G中连接v_i到v_j长度为l的途径数目等于M^l(G)=(aij(l))p×p中位于第i行、第j列处的元素 aij(l) ...

2011

0.0

0.701

... Vot^[9]为以公共交通方式出行的时间价值,元/min ...