作者简介:高嵩(1987-),男,博士研究生.研究方向:铝型材三维拉弯成形工艺与控制.E-mail:gao_song@mail.dlut.edu.cn
将多点成形技术思想引入到型材拉弯工艺中,形成三维拉弯柔性成形技术。为了精确地实现型材三维成形,对型材三维拉弯过程中多点模具的自由度进行了分析,设计了可实现4自由度的单元体结构。给出了单元体调形参数的具体计算方法,并提出一种串并结合的单元体调形控制方法。建立了单元体水平和垂直两个方向调形的数学模型。以高铁动车头骨架结构件为例,进行了三维拉弯试验。结果表明:三维拉弯柔性成形装备达到了实际应用的要求。自动化调形技术较人工调形技术生产效率提高60%以上,并降低了劳动强度。
A flexible 3D stretch-bending process was developed based on the idea of multi-point forming technique. To realize precise 3D shape of the profile, the freedom of single multi-point die in the process of 3D stretch-bending was analyzed first, and the structure of fundamental unit with 4-DOF was designed. Then, the calculation method of unit adjusting parameters was presented, and a combination of serial and parallel adjustment control method was proposed. In addition, the mathematical model of the unit was set up. With the structural component of high-speed trains as an example, 3D stretch-bending test was carried out. The experimental results show that the flexible 3D stretch-bending equipment meets the practical requirements. Compared with manual adjustment, automatic unit adjustment can improve the production efficiency by 60%, as well as reduce labor intensity.
作为空间框架的型材结构件已在高铁、动车、飞机和汽车工业中获得广泛应用[ 1]。这些零件的传统成形方法通常使用整体模具拉弯成形[ 2],整体模具拉弯成形是一种刚性成形方法,主要用于实现单一品种的二维拉弯零件的大批量生产,且难以控制回弹量[ 3]。面对当前大批量生产与适应市场动态变化的小批量生产并存的现状,随着现代工业的不断发展,汽车、动车、以及飞机的外形设计趋于复杂化,作为骨架的空间结构件也朝着复杂三维曲面方向发展[ 4]。面对如此趋势,传统整体模具成形方法显得无能为力,而目前能够实现型材三维弯曲的方法有激光弯曲和拉弯两种[ 5],其中激光弯曲加工时间过长,无法应用于实际生产。此外,还有一种近年来出现的扭矩叠加成形技术,通过曲辊施加的扭矩实现三维弯曲,但该方法对弯曲辊的控制精度要求较高[ 6]。
目前,多点成形技术已经广泛地应用于板材冲压成形装备中[ 7]。三维拉弯柔性成形技术是基于多点成形技术的原理,将型材拉弯的整体模具在空间中离散化,成为既可以在水平方向,也可以在垂直方向自由移动的多点模具MPD(Multi-point dies),可实现型材的三维拉弯成形。这种结构不仅克服了传统模具只能二维拉弯的缺点,还具有模具形面的重构性,节省了大量的模具制造成本,缩短了制造周期,并可通过调整模具消除回弹的影响。
在三维拉弯柔性成形系统中,单元体(多点模具的载体)的位置决定了型材零件最终成形质量的优劣。如何根据成形件目标形状,精确地计算单元体的调形位置,并且快速、准确地将单元体调整至目标位置,是三维拉弯柔性成形系统中要解决的关键问题。如果单元体群的位置精度差,必然导致成形效果不好,甚至导致成形失败。本文主要研究了单元体位置参数的计算方法,设计并实现了全自动化的单元体调形控制系统,并以高铁、动车头骨架结构件为例,进行了三维拉弯柔性成形试验,为三维拉弯成形技术在高铁动车、汽车以及飞机制造业中的应用提供了技术指导。
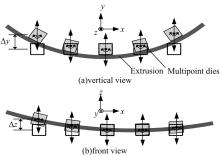
为了实现型材的三维弯曲,多点模具在空间中要随型材位置而变化。如 图1(a)所示,型材在水平方向上弯曲,多点模具在 y轴上应具有不同的位移 Δy,且随着水平方向弯曲角度的增大,模具与底座工作台的角度也增大,多点模具绕 z轴旋转。因此,水平方向上,模具有沿 y轴移动和绕 z轴旋转两个自由度。同样,在垂直方向上,如 图1(b)所示,模具应具有沿 z轴移动和绕 y轴旋转两个自由度。所以,若要实现型材的三维拉弯,则模具应具有4个自由度,分别为沿 y、 z轴移动和旋转,其中 Δy, Δz为受控的单元体调形位置参数,两个旋转自由度为随动机构。
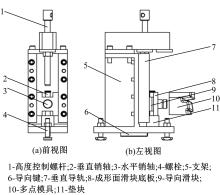
根据1.1节的分析,4自由度柔性单元体结构设计如 图2所示,主要由支架、多点模具、导向滑块、垂直导轨、限位元件等部件组成。
由 图2可知,多点模具的4个自由度分别实现如下:①单元体支架通过底板两端的螺栓固定在主机工作台T型槽上,并且在支架底板设有滚珠丝杠结构的导向键。因此,单元体通过支架可沿模具底座T型槽前后移动,实现多点模具沿 y轴的自由移动。②多点模具通过水平销轴与成形面滑块底板连接,实现了多点模具绕 y轴的旋转。③成形面滑块底板通过垂直销轴与导向滑块连接,实现了多点模具绕 z轴的旋转。④导向滑块可以在垂直导轨上自由移动,通过垫块和高度调整螺杆控制其移动区间,实现沿 z轴的移动[ 8]。
柔性单元体的结构具有以下性质:①模面重构性。通过调整单元体位置和角度,即可实现模面的调整和修正,克服了传统整体模具复杂的模面修正过程,缩短了模具开发周期。②位置受控、旋转随动性质。多点模具的水平位置和垂直位置根据成形件形状确定,是可控变量,而两个旋转角度是随着弯曲的进行而变化,具有随动性质。③模具可换性,型材截面形状和种类的改变仅需更换单元体上的多点模具,不需要更换模具底座和支架及控制单元的运动导向机构部件,降低了模具的制造费用。
单元体调形技术是指按照成形零件的目标形状,考虑成形过程中回弹等因素的影响,通过调整单元体水平和垂直方向位置,实现加工后成形零件与目标形状相吻合的关键技术。由于成形过程中,多点模具在水平和垂直方向发生旋转的影响,单元体三维造型与目标形状不同。因此,单元体调形技术需要计算出与目标形状相对应的单元体水平和垂直位置参数,并实现自动调形过程。
空间曲线可以分为两大类:一类是能直接用解析式表示的规则曲线,如:圆、抛物线、椭圆、双曲线等。当采用规则曲线进行造型时,一般只需给出曲线的解析表达式,并指定成形区域,即包含了曲线的所有参数信息。在拉弯成形零件的设计中,有相当一部分零件的形状可以使用规则曲线直接或拼接而成。另一类是非规则的空间自由曲线,可以使用非均匀有理B样条(NURBS)进行三维曲线造型。
各单元体水平和垂直位置参数直接决定了成形零件最终的几何形状,如果单元体位置计算不当,可能会造成褶皱或破裂等成形缺陷。空间中单元体具有4个自由度,其中多点模具的姿态不受控制,为随动装置,而高度控制螺杆和导向键可以对单元体的 z轴和 y轴的位置进行调节。因此,单元体位置参数的计算可归结为求解各单元体中心空间坐标的问题。
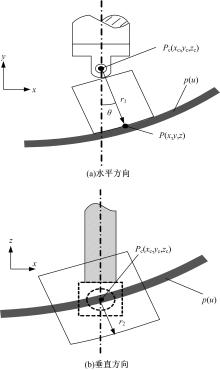
单元体上多点模具与型材水平方向和垂直方向接触的示意图如 图3所示,为了便于计算和表达,图中将型材抽象为一条特征曲线。
假设型材空间特征曲线采用矢函数 p( u)表示,且多点模具的水平旋转轴线与垂直旋转轴线的交点为单元体中心 Pc( xc, yc, zc)。其中单元体坐标 xc为固定已知, yc和 zc为要求解的坐标参数。由于多点模具在成形过程中要随着型材的弯曲发生一定角度的偏转。因此,如 图3(a)所示,对于水平方向上,若要求解 yc的值,就要计算切点 P( x, y, z)的坐标。沿曲线 p( u)上每一点的主法矢 β( u)沿正向或负向移动一个固定距离 d,可以得到该曲线的等距线:
式中: β( u) =α( u) ×γ( u), α( u), γ( u)分别为单位切矢向量和副法矢向量,计算公式如下:
式中:
因此,将多点模具与型材特征曲线切点沿主法矢方向移动一个固定距离——多点模具水平旋转半径 r1,则切点位置与单元体中心位置重合,可得方程:
对于垂直方向上,如 图3(b)所示,尽管也发生了旋转,但型材特征曲线仍然经过中心点,所以 zc可以通过 p( u)的解析式代入或插值求解。
通过求解方程(3),可以得出与 xc相对应 yc的值,将 xc带入 p( u)可以得出 zc。依次计算各单元的位置参数 Pc( xc, yc, zc),就可以生成单元体位置参数的数据文件,进而指导控制系统进行单元体调形。
在板材多点成形装备中,多点模具的调形方法一般有串行调形方式和并行调形方式两种[ 9]。然而相对于板材多点成形装备,三维拉弯柔性成形装备中单元体具有如下特点:①单元数量较少;②每个单元体均需要对 y轴和 z轴分别调形;③多点模具在成形过程中发生旋转。针对单元体群的调形特点,提出以下4种调形方案:①人工调形。通过人工对每个单元体进行调整。该方法调形精度差、效率低,且劳动强度大;②串行水平和垂直调形。采用调形机械手固定在可精确控制位移的直线导轨上,一次调形分别对水平和垂直两个方向进行调整。该种方法调形时间较长、对控制系统设计要求高,若单独调整某个单元体则不易控制,且机械手成本较高;③并行水平和垂直调形。在每个单元体的水平和垂直方向上分别独立地安装一套调形电机装置进行调形。该种方法调形时间最短、控制系统易于实现,但每个单元体需要两套独立调形装置,成本较高;④串行水平调形和并行垂直调形。水平方向上,将调形电机安装在直线导轨上,通过电磁离合器分别对各单元体水平 y轴位移进行调整。垂直方向上,每个单元体均安装一套调形装置,控制垂直螺杆的进给。该方法调形时间适中、易于控制,且成本合理。
通过以上对比分析,第4种调形方法较其他方法具有明显优势。因此,采用此方法实现单元体的调形。 图4为该调形方法的示意图。
每个单元体上有两套调形滚珠丝杠副,分别由串行水平调形电机和垂直调形电机控制。对于水平方向上,调形电机要驱动单元体位移,由于单元体由工作台支撑,所以单元体质量折算到丝杠轴上的等效惯量为0。而单元体移动的过程中与工作台发生摩擦,存在摩擦力矩。设单元体质量为 mL,滚珠丝杠副导程为 L0,摩擦因数为 μ。调形电机选用可精确控制旋转角度的步进电机,设步进电机的转角与力矩分别为: θi( t)、 Ti, Be为阻尼系数,则力矩平衡方程为:
式中: Tf为摩擦力矩,其计算公式为:
式中: η为进给丝杠的正效率。
因此,将单元体各参数代入公式(5),调形步进电机转矩应大于0.5 N·m。根据丝杠的运动传递关系,单元体水平位移为:
设 ω( t)为步进速率(步/s), θ0为步进角,则可以得出单元体水平位移与步进速率及时间的关系:
相对于水平方向,垂直方向上没有负载,只需要控制丝杠的高度。垂直调形电机采用成本相对较低的直流电机,电机每转360°,码盘编码器产生 N0个脉冲,通过计数反馈的脉冲个数 Nz,可以计算出电机的转速和单元体高度的调整量 zn,公式如下:
式中: T为脉冲周期; λ为电机减速比; ε为滚珠丝杠旋转运动转换成直线运动的传动系数。
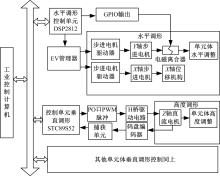
调形控制系统如 图5所示,上位机工控计算机通过RS485总线与下位机各控制单元通信。水平调形控制单元主要完成与上位机通信来获取调形数据以及 X、 Y轴步进电机控制和电磁离合器的通断控制。选用具有较强运算和电机控制能力的工控DSP2812芯片作为水平调形控制单元的CPU。垂直调形控制单元主要控制单元体垂直调形的直流电机,并接收码盘编码器反馈的脉冲信号,实现闭环控制。其控制参数较水平调形相对简单,因此选用具有捕获功能的STC89S52作为垂直调形单元的CPU。
图6为以高铁动车头骨架结构件为目标形状,调整好的柔性单元体群。成形件通过液压机械臂,在单元体构成的包络曲线上拉弯成形,其中,零件的成形质量主要由包络曲线的调形精度决定。
我国自主研发的高铁动车车头所具有的流线造型,是通过三维弯曲的铝型材成形件作为空间骨架实现的。因此,本文以高铁动车头骨架结构件为例,进行了三维柔性拉弯试验。高铁动车头骨架结构件长度为5.42 m;水平方向弯曲半径为18.24 m,弯曲角度为17.04°;垂直方向弯曲半径为13.87 m,弯曲角度为22.40°。铝型材截面几何尺寸如 图7所示。
拉弯试验分别用目标形状以及考虑拉弯后测量的回弹误差对单元体进行调形。试验测得的回弹数据如 表1所示。第1次拉弯用目标零件的几何曲率对单元体进行调形,拉弯后测得的回弹误差较大。因此,第2次拉弯试验将上次试验的回弹误差考虑进来,增大弯曲角度,减小弯曲半径,重新对单元体进行调形,试验结果表明,第2次拉弯的回弹减小了50%以上。再次调形后的第3次试验结果表明,拉弯后成形件的误差小于3%,能够满足高铁动车头骨架结构件的生产要求。
| 表1 回弹数据 Table 1 Springback data |
图8为对经过三维拉弯成形合格的高铁动车头骨架结构件进行检测的效果图,从图中可以看出:铝型材毛料经过拉弯后,分别在水平和垂直两个方向形成了弯曲。回弹误差控制在允许范围内,证明了三维拉弯柔性成形技术的实用性。
表2给出了全自动调形时间与人工调形时间的对比。可以看出,调形时间随着使用单元体数量的增加而延长,通过引入全自动化的调形技术,单个零件的调形时间明显缩短,生产效率提高了60%以上。
| 表2 调形时间比较 Table 2 Comparison of adjustment time |
(1)将多点成形技术应用于型材的三维拉弯成形中,实现了一机多用,降低了生产成本。
(2)调形系统是三维拉弯柔性成形装备的重要组成部分,通过引入全自动化的调形系统,不仅提高了生产效率,同时也提高了单元体群的调形精度,节省了人工成本。
(3)运用三维拉弯柔性成形装备进行高铁动车结构件的试验研究,表明该设备已达到实用阶段。
(4)目前,我国对于空间结构件的三维拉弯成形技术乏善可陈,而需求却日益增长。随着现代工业的飞速发展,必将有越来越多的三维成形零件应用于汽车、动车、飞机制造工业中。因此,型材的三维拉弯柔性成形技术拥有广阔的发展空间。
| [1] |
|
| [2] |
|
| [3] |
|
| [4] |
|
| [5] |
|
| [6] |
|
| [7] |
|
| [8] |
|
| [9] |
|