作者简介:刘坤(1981-),男,副教授,博士.研究方向:下肢智能康复训练设备.E-mail:kunliu@jlu.edu.cn
提出了一种基于非侵入式虚拟传感检测方式分析下肢关节运动学的方法。利用可穿戴式传感系统的检测信号,采用双物理传感器差分算法与双虚拟传感器差分算法相结合的方式,计算下肢关节处虚拟植入的传感器运动状态,在膝关节解剖学坐标系内,实现对膝关节的运动学分析。为了初步验证本方法的正确性与可用性,采用三轴加速度计和地磁力计等开发了一套可穿戴式传感系统,并通过五位受验者进行了实验验证。实验结果表明:本文方法可实现应用穿戴式传感系统进行非侵入式下肢关节运动学检测与分析,进一步改进和提高其测量精度后,可应用于步态分析。
In this paper, a novel approach for analysis of the kinematics of lower limb joint based on non-intrusive virtual sensors is presented. With the signals obtained from a wearable sensor system, the method, which combines a physical-sensor-difference-based algorithm and virtual-sensor-difference-based algorithm, is used to calculate the rotational angles of the virtual sensors supposed to be fixed on the knee joint. Then the data is used to analyze the knee joint kinematics in anatomical coordinate system. To test the approach, a wearable sensor system composed of accelerometers and magnetometers is developed and evaluated on the lower limbs of five subjects. The results show that, without intrusive sensors, the proposed approach is suitable for detecting and analyzing the parameters of the kinematics of lower limb joint with wearable sensor system. After the measuring accuracy is improved, the approach can be applied for gait analysis.
在下肢康复医学领域, 动态评估与诊断下肢残障、帕金森或膝关节置换病人康复阶段的下肢运动姿态与关节运动学参数, 对临床医生制定诊疗方案具有重要的参考价值[1, 2]。在康复理疗阶段, 能非侵入式地检测下肢关节运动学与生物力学数据, 对理疗师更好地监测与评估患者下肢康复状况具有十分重要的意义[3]。在实验室环境下, 典型的下肢运动学与动力学检测设备是高速光学摄像机与力平台相结合的分析系统[4]。但是, 该系统占地空间大, 造价昂贵, 不适合患者在生活中进行穿戴式地动态评估下肢运动状况。随着现代传感器技术的发展, 目前已有很多应用传感器检测与分析下肢运动学与动力学参数的方法[5, 6, 7], 例如膝关节运动角度的计算、大腿和小腿的运动姿态评估等[8, 9, 10]。
在定量诊断因疾病或伤残所致的下肢关节运动状况, 以及定量评估康复理疗方法对膝关节恢复的有效性时, 三维关节运动学参数和三维下肢肢段运动姿态则显得尤为重要。在文献[11, 12]中, 给出了一种应用可穿戴式传感系统测量三维膝关节角的方法, 通过对在大腿与小腿上所测陀螺仪信号进行积分, 获得膝关节屈展角与侧偏角。但是这种方法由于误差的累积积分, 使得所求膝关节角并不准确, 而且文中也未给出适当的校准方法。文献[13]给出了一种结合加速度计和磁力计测量三维关节姿态的方法, 但是该方法仅限于静态评估, 而未推广到动态下人体下肢关节运动状态的分析。文献[14]给出了一种采用三轴加速度计和陀螺仪进行步态分析的方法, 其中所提到的优化算法涉及大量对重力加速度信号的分析与运算, 不适合开发可穿戴式传感系统使用。文献[4, 15]中给出了一种在人体径向面内评估下肢运动学参数的无累积积分误差的方法, 在膝关节和踝关节内假想植入虚拟传感器, 从而应用穿戴于下肢的传感器所测信号, 获得关节运动学参数, 但是此方法只给出了径向面内一个自由度的关节运动状态。文献[16]中给出了只采用加速度计一种传感器来检测下肢关节运动状态的方法, 但该方法不使用积分信号, 避免了累积误差, 但是文中只讨论了径向面内的二维运动状态, 没有在三维运动状态中做深入研究。
在本课题组之前的研究中[7], 已经给出了一种基于双加速度计差分算法检测下肢肢段定位的方法, 并进行了初步实验验证。在该方法中, 仅用一种传感器, 基于两组信号的差值运算(而非积分运算), 便可进行大腿肢段三维运动姿态分析, 从而避免了累积积分误差, 但实验是在对下肢模型进行了诸多理想简化后进行的初步的定性验证, 还需要进一步扩展实验条件的限制, 以使该方法适用于更加复杂的下肢运动条件。
本文将提出一种基于加速度计和地磁力计的可穿戴式传感器构造方法, 用非侵入式虚拟传感器检测评估下肢关节三维运动学参数。基于本文方法, 计算膝关节在解剖学坐标系内的屈展角、内收外展角和旋内旋外角。初步开发了由三轴加速度计、磁力计组成的可穿戴式传感系统, 并且给出了其穿戴测试实验。本文方法不涉及对加速度和角加速度信号的积分运算, 这样就避免了积分误差对计算结果的干扰。另外, 在关节解剖学坐标系内所计算的各方向关节角具有独立性, 从而避免了采用欧拉角计算时受计算顺序影响的弊端。
为分析下肢关节三维运动学参数, 本文基于球套关节模型, 建立基于双物理传感器和双虚拟传感器差分算法的三维关节运动学分析方法, 分析其3个轴向上的屈展角、内收外展角和旋内旋外角。
首先, 给出基于双物理传感器差分算法, 用于计算分析某旋转刚体的旋转角。采用加速度计在下肢肢段某位置进行实际测量时, 其所测信号为该位置的合加速度信号, 其中的运动加速度分量(包括平移与旋转加速度)、重力加速度分量以及误差信号等并不能单独分离出来。此外, 当传感器固定在下肢上的时候, 由于足底触地冲击和肌肉活动, 所测信号也会受皮肤运动干扰而带有测量误差。然而, 当考虑两片相同的传感器安置于同一肢段的不同位置时, 如果能保证两片传感器的相同轴能同方向(同轴同向)放置, 此时, 除了旋转加速度之外, 重力加速度、平移加速度、皮肤运动和其他干扰的影响对于两片传感器的作用应该是一样的。
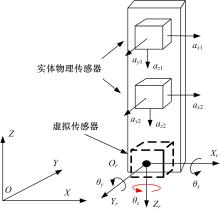 | 图1 基于双物理传感器差分方法计算关节运动角度示意图Fig.1 Calculation for acceleration of rotation joint by double physical-sensors diference based method |
为了充分利用两片传感器所测的旋转加速度信号之间的差值, 提出双物理传感器差分算法。如图1所示, 将两片实体加速度计同轴同向地集成于一块电路板内的已知位置Pij上, 当不考虑误差与干扰时, 所测加速度aij如下所示:
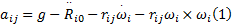
式中:aij为在Pij点处所测的合加速度, i表示肢段标号, j表示点的位置(j=0表示肢段原点); g为重力加速度; Rij为点Pij在绝对坐标系(O-XYZ)内的位置矢量, 则有如下分加速度的矢量表达式:
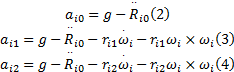
在电路板上固定加速度计的两个位置, 如果相对于板子牵连坐标系(Or-XrYrZr)的原点Or, 其旋转半径分别为r1和r2, 则从式(2)~(4)可以推导出板子牵连运动旋转中心点的加速度矢量为:
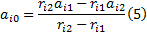
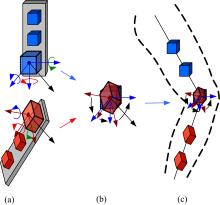 | 图2 基于双虚拟传感器差分算法示意图Fig.2 Illustration of joint rotations based on the double virtual-sensor difference based algorithm |
其次, 在分析膝关节角时, 提出一种双虚拟传感器差分算法, 通过比较虚拟嵌入膝关节内部的两片非真实存在的传感器所测信号之间的差异, 基于膝关节三个轴向上的屈展角、内收外展角和旋内旋外角, 计算三维膝关节角度。
如图2(a)所示, 下肢肢段中大腿和小腿简化成两块刚体模型, 在每块刚体上, 基于图1中的双物理传感器差分算法, 分别集成两片同轴同向安置的加速度计, 按照前面介绍的双物理传感器差分算法, 分别计算出每块刚体各自牵连运动旋转点处的加速度信号。然后, 在每块刚体旋转点处虚拟放置一片和该刚体上物理传感器同轴同向且参数一致的虚拟传感器, 则认为:通过各刚体上双物理传感器差分算法计算出的旋转点处的加速度, 即为该旋转点处虚拟加速度计所测加速度。
再次, 如图2(b)所示, 把两块刚体牵连运动的旋转点置于同一位置, 那么穿戴有传感器系统的下肢模型简化为图2(c)所示。最后, 因为牵连刚体在铰接处绝对运动是唯一的, 据此可以知道, 分别通过牵连点上下两端刚体所计算出的牵连加速度应该是具有相同的绝对加速度, 因此, 两片虚拟传感器也应该具有相同的绝对加速度, 而所测到的两组虚拟加速度之间的不同, 正说明了戴有两组物理传感器的上下两段刚体姿态之间的差异, 即可以用来计算大腿和小腿之间的姿态差, 也就可以计算出膝关节角的变化状态。如果用R表示两片虚拟传感器所测数据At、As之间的旋转矩阵的话, 则有如下关系式:
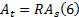
从图2可以看出, 两片虚拟传感器之间的姿态差, 也正是大腿与小腿之间的姿态差, 即膝关节运动角度。如果用θ x表示下肢运动径向面内膝关节的的曲展角, 用θ y表示下肢运动正向面内膝关节的侧倾角, θ z表示膝关节在水平方向的偏转角, 则有如下关系式:
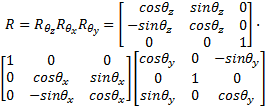
为了计算以上三个轴向上的膝关节角度, 应用同样原理, 在图2内安置加速度计的位置上同样安装地磁力计, 再在膝关节内部同一肢段实体上嵌入与地磁力计同轴同向的虚拟地磁力计, 则该虚拟地磁力计与同一肢段上实体地磁力计应该具有相同信号值, 分别表示为Mt、Ms, 同理, 在膝关节处应用上述的双虚拟传感器差分算法, 则可得到下列表达式:
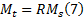
至此, 基于单肢段上每组两片物理传感器的双物理传感器差分算法计算牵连点处虚拟传感器所测信号, 和基于已计算出的关节内两组虚拟传感器所测信号的双虚拟传感器差分算法, 从式(5)(6)(7)可以计算出下肢关节3个轴向的关节运动角。但是上式中的关节运动角实际上是一组欧拉角, 计算时各角之间是非独立的, 因此引进膝关节解剖学坐标系, 在解剖学坐标系内分析膝关节运动角。如文献[17]所述, 引入膝关节解剖学坐标系内的屈展角、内收外展角和旋内旋外角。
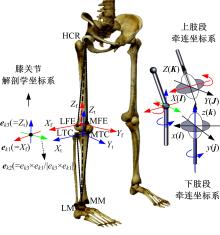 | 图3 膝关节解剖学坐标系定义图Fig.3 Anatomical coordinate system defined in knee joint for knee joint kinematics analysis |
图3给出了本文要用到的解剖学坐标系的示意图, 表1、表2给出了各标定点的解释和大腿与小腿固连的牵连坐标系以及膝关节解剖学坐标系的说明。设矢量(AXt, AYt, AZt)是在胫骨腓骨坐标系(Ot-XtYtZt)内各轴向所测加速度信号或磁力计信号, 矢量(BXf, BYf, BZf)是在股骨坐标系(Of-XfYfZf)内各轴向所测加速度信号或磁力计信号, 那么, 这两组信号与图2中膝关节内两片虚拟传感器所测的信号是一致的。所以, 由式(6)的展开形式即可得到这两组矢量之间的关系如式(8)所示, 其中R的含义同上, 是由欧拉角表示的上下肢段之间的旋转矩阵。
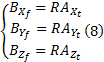
| 表1 下肢骨上的解剖学标定点 Table 1 Anatomical landmarks on lower limb bones |
| 表2 下肢段各坐标系和膝关节解剖学坐标系及其说明 Table 2 Lower limb segments fixed coordinate system and anatomical knee joint coordinate system |
至此, 可以计算膝关节解剖学坐标系内的屈伸角θ f/e、内收外展角θ a/a和旋内旋外角θ i/e如下:

为了验证上述方法, 本文给出基于可穿戴式传感系统的硬件搭建和实验研究。本传感设备由一片微控制器、两片三轴加速度计和两片地磁力计组成。微控制器用来实时读取和存储传感器数据并与主机进行通信和数据传输, 采样频率为100 Hz。
可穿戴式传感系统硬件搭建如图4所示, 在大腿上A、B位置分别同轴同向地安装两片三轴加速度传感器作为一组, 并集成在同一块电路板上, 用于检测相应位置的加速度, 并基于双物理传感器差分算法计算出膝盖处的加速度值, 作为第一片嵌入膝盖内的加速度计的测量值; 同理, 在小腿C、D处也安放两片同轴同向集成于同块电路板上的加速度计组合, 计算出膝盖处另一片虚拟加速度计的测量值, 用于双虚拟传感器差分算法计算膝关节运动角度。在B、C位置分别与该位置加速度计同轴同向集成两片地磁力计, 用于检测地磁信号并作为嵌入膝盖的虚拟地磁力计测量值, 采用双虚拟传感器差分算法计算膝关节运动角度。图4中, O-ZYZ为绝对坐标系, Ot-ZtYtZt为大腿肢段牵连坐标系, Os-ZsYsZs为小腿肢段牵连坐标系, r1和r2分别为膝盖到B点和C点的距离。
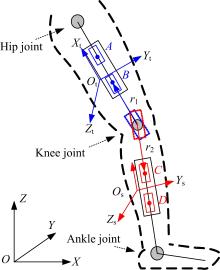 | 图4 可穿戴式传感系统的硬件搭建示意图Fig.4 Illustration for installation of sensors on lower limb to calculate knee joint angles |
图5给出了实际的实验设备图, 为了减少由于下肢运动时肌肉抖动给测量信号带来的干扰误差, 所有传感器被集成在电路板上之后, 又被固定在由钢制滑轨所组成的外骨骼上。为增加设备的通用性, 每段滑轨可以根据被测者大腿或者小腿肢段的长度, 在穿戴安装之前适当调节。在外骨骼的膝关节处, 两条滑轨由允许三自由度转动的球套连轴所连接。在初装前, 根据被测者肢段长度调整好滑轨后, 由自粘式绷带固定于被测者下肢。
 | 图5 实验设备图Fig.5 Experiment equipment using developed wearable sensor system in working space of optical motion system |
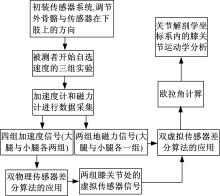
本实验中, 被测者由健康无病史的4名男性和1名女性组成, 要求每名被测者进行3次步行实验, 行进速度根据自己行走习惯分为低速、中速、高速。最终, 从每位被测者的3次实验中得到所需传感信号:4组加速度信号和两组地磁力信号。同时, 本实验采用三维光学运动捕捉成像分析系统, 作为实验的参考与对比系统, 通过捕捉被测者下肢上所安置的全反射点, 得到下肢关节运动学参数。图6给出了本文的实验流程。本实验是作者与日本高知工科大学合作并在其实验室完成, 并得到高知工科大学智能机械系科学伦理委员会审批与授权。
实验所测信号由MCU存储后, 离线传到主机进行分析处理。图7给出了一组基于双物理传感器差分算法计算出的膝关节处的虚拟三轴加速度计所测值。图8给出了一组磁力计所测值。经主机分析运算, 图9给出了基于本文方法得出的膝关节运动角计算值(红色)与高速摄像系统捕获的膝关节运动角参考值(黑色)的对比分析曲线图。表3给出了膝关节角计算值与参考值的数据分析结果。其中RMSE为均方根误差, R是相关系数, emax是最大误差。
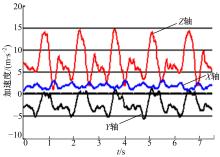 | 图7 膝关节处虚拟加速度计一组所测值Fig.7 One group of accelerations in knee joint regarded as measured by virtual accelerometers |
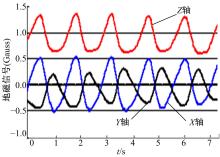 | 图8 膝关节处虚拟磁力计所测一组信号值Fig.8 One group of magnetic field data in knee joint regarded as measured by virtual magnetometers |
通过图9和表3可以看出, 根据可穿戴式传感系统所测信号计算出的膝关节运动角与参考值很接近, 具有较小的均方根误差值和较大的相关系数。由此可见, 本文计算方法是有效的, 并基于此开发可穿戴式传感系统, 采用虚拟传感器进行非嵌入式的膝关节运动角检测来进行下肢运动学分析的思路是可行的。在本文实验中, 同时作用在同一肢段的每组两片加速度计上的重力加速度、平移运动加速度和干扰误差信号是相同的, 误差信号通过双物理传感器差分算法成功得到了消除, 并且计算出了膝关节内部的虚拟加速度值。通过不同肢段上的加速度计可以计算出膝关节内部不同姿态的虚拟加速度计的测量值, 进而通过双虚拟传感器差分算法, 计算出关节运动角。但是, 当可穿戴式传感系统固定于下肢皮肤表面时, 由于肌肉运动, 或者当脚触地时冲击载荷的突增, 必然会产生部分测量误差, 因此导致了由传感器得到的结果和由摄像系统得到的参考数据之间的误差。为了最大限度地减少测量误差的干扰, 本文加入了外骨骼滑轨的设计, 把每组传感器集成在电路板上之后, 固定在外骨骼上, 以最大程度地降低由于肌肉运动所带来的传感器测量误差。另外, 由于传感器到膝关节的距离都是在设备初装的时候测定的, 随着人体行走运动后, 下肢肌肉运动的变化, 这些距离值必然会有微小的实时变化, 这也会造成计算误差。还有一点, 本文实际得到的是膝关节表面牵连旋转点的虚拟加速度和运动角度, 而非真正的膝关节内部加速度, 但是这并不影响膝关节运动角度的计算, 可以作为膝关节内部运动角度应用。
 | 图9 某被测者膝关节解剖学坐标系内的屈伸角θ f/e、内收外展角θ a/a和旋内旋外角θ i/e的计算结果(a) θ f/eFig.9 Rotation angles of knee joint in anatomical coordinate system |
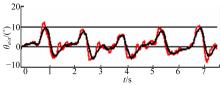 | 图9 某被测者膝关节解剖学坐标系内的屈伸角θ f/e、内收外展角θ a/a和旋内旋外角θ i/e的计算结果(b) θ a/aFig.9 Rotation angles of knee joint in anatomical coordinate system |
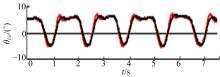 | 图9 某被测者膝关节解剖学坐标系内的屈伸角θ f/e、内收外展角θ a/a和旋内旋外角θ i/e的计算结果(c) θ i/eFig.9 Rotation angles of knee joint in anatomical coordinate system |
| 表3 数据分析结果 Table 3 Analysis result |
在文献[11, 12]中已经说明, 应用陀螺仪信号进行积分的方法获得关节运动角度, 由于信号积分累积误差的存在, 并不适合长时间的检测计算。本文所提出的差分算法完全避免了积分运算的存在, 双物理传感器差分算法, 充分利用了安置在相似运动状态和干扰状态下的两片传感器测量信号之间的差分值, 消除了相同干扰信号误差的影响, 利用了不同位置所测相对转动加速度的差值, 在最大程度上降低了测量误差和计算误差。并且首次提出了应用加速度计和地磁力计在关节解剖学坐标系内, 采用非侵入式虚拟传感器检测与分析关节运动学参数的方法, 避免了对膝关节进行医学解剖。
在文献[13, 14]中, 对人体下肢运动学与动力学的研究, 是从人体运动径向面的平面研究扩展到三维研究的。而对关节三维运动学研究, 通常采用的方法是把关节的3个自由度作为3个铰链序列组合研究的。该方法最大的缺点就是计算结果受非独立的3个铰链轴向计算顺序的影响。本文方法是在膝关节解剖学坐标系内研究三维关节运动, 3个轴向上的屈伸角、内收外展角和旋内旋外角是相互独立的。从实验结果可以看出, 基于本文所阐述的方法, 应用初步开发的可穿戴式传感系统, 可以达到定性地检测与评估膝关节3个轴向运动角的目的, 并且取得比较满意的定量评估结果。
本文实现了双物理传感器差分算法与双虚拟传感器差分算法的结合, 通过在关节解剖学坐标系内分析相互独立的3个轴向的关节角, 实现了非侵入式地分析三维关节运动学的目的, 可为下肢康复运动检测设备的开发提供新的参考和借鉴, 并为开发新型可穿戴式步态分析设备打下基础。
The authors have declared that no competing interests exist.
| [1] |
|
| [2] |
|
| [3] |
|
| [4] |
|
| [5] |
|
| [6] |
|
| [7] |
|
| [8] |
|
| [9] |
|
| [10] |
|
| [11] |
|
| [12] |
|
| [13] |
|
| [14] |
|
| [15] |
|
| [16] |
|
| [17] |
|