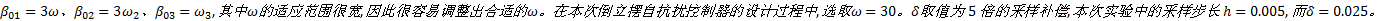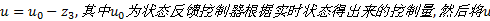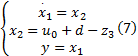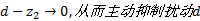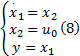作者简介:李贤涛(1986-), 男,博士研究生.研究方向:视轴稳定及自抗扰控制技术.E-mail:lixiantao_86@126.com
针对扩张状态观测器对二阶及二阶以上系统的扰动观测值存在相位滞后的问题,提出了一种基于扰动频率自适应的自抗扰控制的新方法,并在直线型倒立摆装置中进行了实验验证。实验结果表明:本文方法解决了扩张状态观测器对二阶及二阶以上系统的扰动观测值存在相位滞后的问题;在2 Hz以内随机扰动的作用下,对比传统状态反馈控制器,它将扰动隔离度至少提高了7.85 dB,同时,自抗扰控制器具有很强的鲁棒性,允许被控对象参数在15%的范围内浮动。
In order to further improve the isolation degree of disturbance of traditional controller, a new active disturbance-rejection controller based on frequency adaptation of disturbance is proposed. It is verified in the linear inverted pendulum system. The results show that the controller can avoid phase lag when extended state observer observes the disturbance with the high-order form. It can also at least reduce the disturbance error by 7.85 dB compared with the state feedback controller when the perturbation frequency is between 0 Hz and 2 Hz. The proposed controller has strong robustness, allowing the range of system parameters to change within 15%.
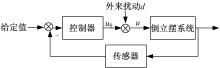
在实际工程中, 不管是天然系统, 还是人造系统, 它本身以及它所在的操作环境都具有一定的不确定性, 我们称之为扰动。由于扰动的影响, 导致系统不能很好地按照期望的方式(按给定的目标轨迹或设定值)进行工作。如:广泛应用于航天、航空光学侦查领域的光电稳定平台, 其扰动主要来源于传动环节及电机自身的摩擦力。外界的速度扰动通过平台及负载之间的摩擦力对光学镜头姿态产生影响, 使视轴的空间指向发生颤振, 最终引起图像模糊[1]。由此可见, 在达到控制目标的过程中, 如何消除各种不确定外扰作用的影响, 是设计控制器时必须考虑的问题。
目前, 在该类系统研究领域常见的设计思想仍为被动抗扰的思想, 即采用传统PID控制器、滞后超前控制器、平方滞后超前控制器或其他经典控制理论, 通过提高开环系统的型别以及低频段的增益来抑制载体扰动对系统的影响。然而由于受到传动链机械谐振环节的影响, 系统的开环剪切频率受到严格的限制, 而且在传统设计模式下系统的低频段增益难以做到更高, 所以系统的扰动隔离度水平难以进一步提高[2], 现代控制理论如最优控制理论、自适应控制理论等可以有效提高光电跟踪系统的性能, 但设计难度大, 计算复杂, 控制系统成本高, 不易在实际工程中得到推广和应用。
相比之下, 自抗扰控制技术[3, 4]是一种不依赖于系统模型的新型控制技术, 它能够主动从被控对象的输入输出信号中把扰动的信息提炼出来, 以这个信息为依据, 估计系统在运动过程中受到的各种扰动[5], 然后将该扰动观测值补偿至系统控制量中, 构成复合校正系统对扰动进行抑制。而且, 此方法不需要对被控对象进行精确建模和对扰动项的物理测量, 它具有响应速度快、精度高、扰动抑制能力强及算法简单等优点。然而, 实验中发现扩张状态观测器(ESO)仅对一阶系统的扰动可以实现实时观测, 对二阶及二阶以上系统扰动的观测均存在明显的相位滞后, 且这种滞后随着扰动频率的增大而不断加大, 呈一一对应的关系, 这严重影响了自抗扰控制策略对扰动的抑制效果。
针对这一问题, 本文提出一种基于扰动频率自适应的自抗扰控制新方法。首先对频率区域进行划分, 然后设计扩张状态观测器分别对各个频率范围中心频率的扰动进行观测, 并根据各个频率点处扰动观测值不同的相位滞后量, 设计相应的相位超前环节。再与频率辨识环节相结合一同构成基于扰动频率自适应的扩张状态观测器, 实现对系统扰动最大限度地实时观测, 最后根据这个扰动观测值生成前馈控制量, 在此基础上结合现代控制理论中的状态反馈控制方法实现倒立摆系统的扰动频率自适应自抗扰控制。
控制结果表明:在扰动频率自适应环节的作用下, 状态扩张观测器能够最大限度地实现对扰动的实时观测, 利用该信息对扰动的影响进行前馈补偿, 在传统控制器的基础上进一步抑制了扰动, 提高了扰动隔离度。从而验证了该方法的有效性和优越性。
倒立摆系统是由水平移动的小车及其支撑的单级倒立摆杆组成[6]。本文实验所使用的倒立摆实验装置是深圳固高科技的GLIP系列, 其实物装置如图1所示。
其数学模型为:
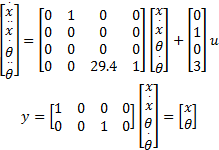
式中: 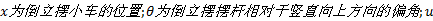
倒立摆在实际运动过程中, 控制器根据摆杆相对于竖直向上方向的偏角和小车相对于零点位置的偏移量计算出施加于小车的加速度控制量 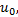
在实际运动过程中, 由于倒立摆滑轨上的摩擦力以及导线拉力对小车运动的影响, 作用在小车上的加速度控制量为 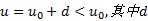
由于控制小车运动的控制量 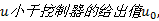
根据系统稳定性及扰动隔离度要求, 设计基于极点配置的状态反馈控制器[7], 即:系统具有较短的调节时间(约2 s)和合适的阻尼(阻尼比为ζ =0.5)。按照这个要求, 并留有一定的裕量, 选取期望的闭环极点为:s=μ i(i=1, 2, 3, 4)。μ 1=μ 2=-10, μ 3=-2+j2 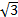
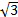
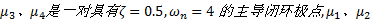
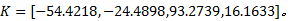
在此状态反馈控制器的作用下, 倒立摆可以自动摆起, 摆杆偏角和小车位置的偏移量均可稳定地维持在1个单位的编码器测量精度之内。由此可见, 状态反馈控制器的稳定性和快速性均满足设计要求, 且控制结果良好。然而在引入扰动 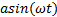
为了提高状态反馈控制器对扰动的抑制能力, 需在保证系统稳定性的同时进一步提高系统的快速性, 即:在保证系统阻尼比的情况下, 使最终配置的闭环极点尽量远离虚轴。然而由于机械谐振环节和系统噪声的影响, 系统的开环剪切频率受到严格的限制, 其闭环极点不能任意配置, 因此其扰动抑制能力难以得到本质上的提高。
实验中发现, 扩张状态观测器(ESO)仅可以对一阶系统的扰动实现实时观测, 对二阶及二阶以上系统扰动的观测值存在着明显的相位滞后(具体实验结果如4.1节所示), 且滞后量与扰动的频率密切相关, 即随着频率的增大而不断加大。因此在采用扰动观测值进行扰动前馈补偿之前, 需要对扰动观测值进行相位超前处理。又因为对于不同的相位滞后(即针对不同频率的扰动), 需要设计不同的相位超前环节进行校正。
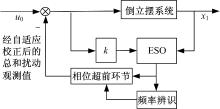
综合上述两方面因素, 本文提出了一种基于扰动频率自适应的自抗扰控制器。首先以0.1n Hz(n为整数)为中心频率对频率区域进行划分, 然后设计三阶扩张状态观测器(ESO)分别对0.1n Hz频率的扰动进行观测, 并根据各个频率点处扰动观测值不同的相位滞后量, 设计相应的相位超前环节。再与频率辨识环节相结合一同构成基于扰动频率自适应的状态扩张观测器, 实现对系统扰动最大限度地实时观测, 最后根据这个扰动观测值生成前馈控制量, 在此基础上结合现代控制理论中的状态反馈控制方法实现倒立摆系统的扰动频率自适应自抗扰控制。其作用原理如图3所示。
倒立摆系统的扰动来源主要为滑轨上摩擦力以及导线拉力对小车运动的影响。可见扰动直接作用的对象为小车, 因此对小车进行单独研究, 倒立摆中小车的数学模型为:

其受扰动影响后的数学模型为:

根据前文所属的自抗扰控制器原理, 设计状态扩张观测器:
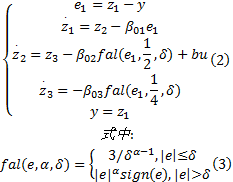
对扰动 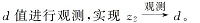
由于扰动观测值存在着较大的相位滞后, 这严重影响了自抗扰控制器对扰动的抑制效果, 因此需要引入相位超前环节, 其具体形式如式(4)所示:
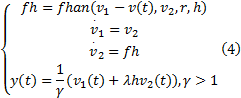
式中:参数 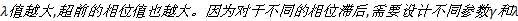
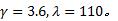
对于正弦信号 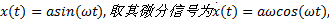
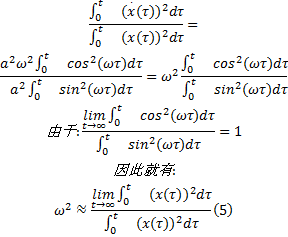
式中: 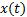

式中: 
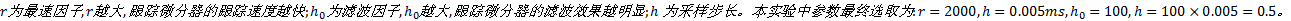
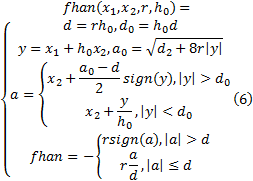
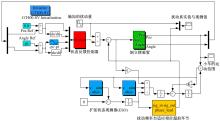
在图1所示的直线型倒立摆装置中, 利用主控计算机人为加入加速度扰动, 图4为主控计算机控制倒立摆的结构框图。本文施加的扰动作用量 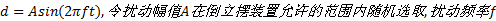
在施加扰动作用量 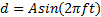
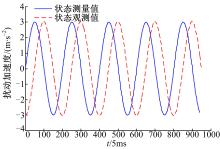
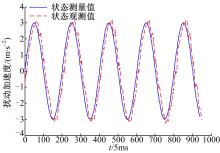
图5为系统引入扰动 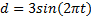
由图5可看出, 扰动的观测值相对于真实值幅值相等, 相位上却存在着0.245 s(大约四分之一个周期)的滞后。由此可见, 直接采用该扰动观测值进行补偿势必会导致扰动抑制效果并不理想, 因此需要对扰动观测值进行超前处理。
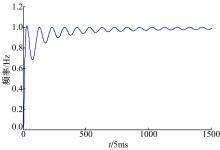
为了对扰动观测值进行相位超前校正, 首先将扰动观测值引入频率辨识环节, 对其扰动频率进行估计。辨识结果如图6所示。由图6可见, 扰动频率的辨识结果在1.2 s之内便可以收敛于0.95~1.05 Hz。
采用该频率范围的相位超前环节参数对扰动观测值进行相位校正。校正结果如图7所示。与图5对比可以明显发现:校正后, 扰动观测值的相位滞后已明显减小, 基本上与扰动的实际值相吻合, 符合扰动前馈的要求。
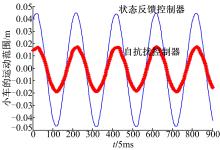
按照式(7)的原理, 将校正后的扰动观测值 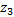
半实物仿真结果表明:单独采用状态反馈控制器, 为了维持倒立摆摆杆不倒, 小车的运动范围为-0.0472~0.0448 m。而采用扰动频率自适应自抗扰控制器, 小车的运动范围为-0.0189~0.0172 m, 为引入自抗扰控制器之前小车运动范围的39.24%, 即扰动 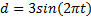
以同样的方法, 令扰动频率在2.0 Hz以内随机变化, 表1为在10个随机扰动频率的作用下, 倒立摆系统分别采用状态反馈控制器和扰动频率自适应自抗扰控制器时小车在滑轨上的运动范围, 以及对比于状态反馈控制器, 采用扰动频率自适应自抗扰控制器扰动隔离度的提高程度。
| 表1 对比于状态反馈控制器扰动隔离度的提高程度 Table 1 Improvement of disturbance isolation degree by using ADRC compared with state feedback controller |
由表1可以明显发现, 在随机选取的各个频率处, 只要该频率的扰动持续1.2 s, 扰动频率自适应扩张状态观测器均能够对扰动 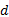
在抗扰控制器参数不变的情况下, 人为改变控制对象的参数k, 使模型参数值上下浮动15%, 即k值由原来的1变化为在0.85~1.15之间任意变动, 然后重新进行4.1节的实验, 对扰动隔离度的提高程度进行测试。表2为k=0.85和k=1.15时的实验结果。
| 表2 当k=0.85和k=1.15时自抗扰控制器扰动隔离度的提高程度 Table 2 Improvement of disturbance isolation degree when k=0.85 and k=1.15 |
对比表1可以明显看出, 当系统参数发生变化时, 自抗扰控制器的扰动抑制能力虽有微小的变化, 但依然保持着明显优于状态反馈控制器的性能。因此, 最终可以得出:基于扰动频率自适应的自抗扰控制器具有较强的鲁棒性。
针对自抗扰控制技术中, 扩张状态观测器对二阶及二阶以上系统的扰动观测存在较大相位滞后的问题, 本文提出了一种基于扰动频率自适应的自抗扰控制新方法并进行了实验验证。实验结果表明:基于扰动频率自适应的自抗扰控制方案成功地解决了自抗扰控制技术中扩张状态观测器对二阶及二阶以上系统的扰动观测存在较大相位滞后的问题, 对比于经典控制方法, 进一步提高了平台对扰动的抑制能力。这为进一步提高扰动隔离度提供了新方法, 对于该算法在实际工程中的应用具有较高的参考价值和实用价值。
The authors have declared that no competing interests exist.
| [1] |
|
| [2] |
|
| [3] |
|
| [4] |
|
| [5] |
|
| [6] |
|
| [7] |
|
| [8] |
|
| [9] |
|
| [10] |
|
| [11] |
|