引用本文
刘瑜, 何友, 王海鹏, 董凯. 基于平方根容积卡尔曼滤波的目标状态与传感器偏差扩维联合估计算法. 45(1): 314-321
LIU Yu, HE You, WANG Hai-peng, DONG Kai. Augmented target tracking algorithm based on SRCKF for joint estimation of state and sensor systematic error. Journal of Jilin University Engineering and Technology Edition, 45(1): 314-321  
Permissions
Copyright©2015, 吉林大学学报编辑部
版权所有.吉林大学学报编辑部
基于平方根容积卡尔曼滤波的目标状态与传感器偏差扩维联合估计算法
刘瑜, 何友, 王海鹏, 董凯
海军航空工程学院 信息融合技术研究所,山东 烟台 264001

作者简介:刘瑜(1986-),男,博士研究生.研究方向:多传感器信息融合.E-mail:liuyu77360132@126.com

基金:国家自然科学基金重点项目(61032001); 山东省自然科学基金项目(ZR2012FQ004)
摘要

针对传感器存在系统偏差条件下的三维目标跟踪问题,基于高斯求积规则与三阶球面-径向容积规则,设计了基于平方根容积卡尔曼滤波的目标状态与传感器系统偏差扩维联合估计算法(Augmented state squared-root cubature Kalman filter, ASSRCKF)。仿真分析表明,ASSRCKF不仅避免了扩维扩展卡尔曼滤波算法因模型线性化误差易导致滤波发散的问题,且克服了扩维不敏卡尔曼滤波算法在高维系统中数值不稳定的缺点,算法实时性好,能更加有效地解决带有系统误差的非线性状态估计问题。

关键词: 通信技术; 雷达组网; 传感器系统偏差; 联合状态估计; 容积卡尔曼滤波
中图分类号:TN957 文献标志码:A 文章编号:1671-5497(2015)01-0314-08
Augmented target tracking algorithm based on SRCKF for joint estimation of state and sensor systematic error
LIU Yu, HE You, WANG Hai-peng, DONG Kai
Research Institute of Information Fusion, Naval Aeronautical and Astronautical University, Yantai 264001,China
Abstract

Considering three dimensional target tracking systems with unknown systematic error, in order to obtain the joint estimation of target state and sensor systematic error, an augmented target tracking algorithm based on Square-root Cubature Kalman Filter (SRCKF) is proposed. The performance of proposed estimation method is analyzed with a numerical example taking account the root mean square error and average computational cost. Simulation results show that the effectiveness of the proposed algorithm is higher than that of the algorithm based on extended Kalman filter in the aspects of estimation accuracy and filtering stability.

Keyword: communication; radar networking; sensor systematic error; joint state estimation; cubature Kalman filter
引言

多传感器信息融合系统通过组网方式利用多部传感器对同一目标的观测信息进行有效融合处理, 可以避免单基地雷达的一些缺点与局限性, 获取全面、可靠的敌我军事态势信息, 理论上能够获得更为精确的目标状态估计, 从而为进一步的环境态势推理提供更为准确可靠的依据, 目前已经在空中交通管制、国土防空、空间监视与卫星遥感等领域中得到了广泛应用[1, 2]。但是, 人们在使用多传感器组网系统时往往发现其融合效果并不如预期那么理想, 原因之一即是传感器量测不仅含有随机误差, 且具有系统偏差[3, 4]。如果这种偏差没有得到妥善处理, 将直接导致目标航迹跟踪质量的下降, 甚至可能出现虚假目标。因此, 考虑到传感器量测与数据互联、航迹建立、航迹关联、航迹滤波及跟踪、航迹管理等后续目标跟踪问题具有紧密联系, 为了提高分布式多传感器网络的数据融合质量, 必须消除或降低传感器量测中的系统偏差对融合的影响。

现有的系统偏差估计算法可分为三类[5]:①离线估计法, 主要代表算法有Burke[6]提出的实时质量控制(RTQC)误差配准算法、Dana[7]提出的广义最小二乘(GLS)误差配准算法、Zhou Yi-feng等[8]提出的精确极大似然(EML)误差配准算法等; ②在线估计法, 主要有Zhou Lin等[9]提出的SA-PSO法、Lin等[10]提出的EX法以及宋强等[11]提出的基于傅立叶变换的航迹对准关联算法; ③目标状态与系统偏差联合估计法, 即将系统误差做为状态向量中的扩维部分, 进行系统误差和目标状态的联合滤波, 主要有Nabaa等[12]提出的基于EKF的扩维方法ASEKF、宋强等[13]提出的基于ASUKF(Augmented state unscented Kalman filter)的实时误差配准算法及Li等[14]提出的基于EM-KF的联合估计算法。

以上算法中, ASUKF利用不敏卡尔曼滤波(Unscented Kalman filter, UKF)实现了目标状态和系统误差的联合实时估计, 取得了比ASEKF更为优良的估计性能。其中, UKF[15]选择2n+1(n为状态维数)个具有权值的Sigma点来近似状态变量的均值, Sigma点经非线性函数传播后捕获的均值和方差能够达到非线性函数真实值的三阶精度, 因此其精度高于EKF, 同时克服了EKF易于发散以及只适用于弱非线性的缺点。但是, UKF需要合理调节系统参数才能达到理想滤波效果, 且在高维系统中UKF容易出现数值不稳定现象, 其应用遇到了困难[16]。

近年来, Arasaratnam同样从分布近似的角度推导出一种3阶球面-径向(Spherical-radial)容积规则, 提出了容积卡尔曼滤波(Cubature Kalman filter, CKF)[17]。CKF通过2n个等权值容积点来传播系统状态的均值和方差, 能获得较高的滤波精度。CKF具备UKF的优点, 且无需像UKF一样调节各参数因子, 其容积点及其权值仅由状态维数唯一确定, 可以预先计算和存储, 算法设计与实现更为简单, 且在高维状态滤波中的优势更为明显, 因而受到了广大学者的高度重视。

基于以上分析, 本文针对带有固定传感器偏差的非线性状态估计问题, 研究并提出一种基于平方根CKF的目标状态与传感器偏差扩维联合估计算法(Augmented state squared-root cubature Kalman filter, ASSRCKF)。ASSRCKF将目标的运动模型和传感器偏差配准模型有机地结合起来, 形成扩维的状态空间模型, 即将传感器偏差作为目标状态向量中的分量, 然后基于平方根CKF滤波, 实现状态与偏差联合实时估计。

1 带有系统偏差的非线性状态估计

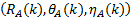
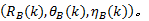
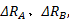
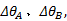
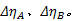
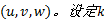
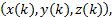
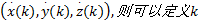
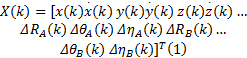
以两部同步雷达A、B构成的雷达网为例, 其量测值分别为 和 假设A、B的距离系统误差分别为 方位角系统误差为 俯仰角系统误差为 雷达A、B在公共坐标系中的坐标分别为(0, 0, 0)、 时刻目标的位置为 速度为 时刻系统的状态向量为

以匀速运动的目标为例, 其运动状态方程可以描述为:

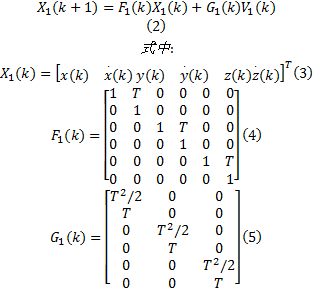
一般情况下, 认为传感器偏差为恒定量或长时间内缓慢变化量, 故其状态方程可以描述为:

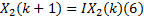
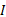
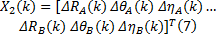
式中: 为单位矩阵, 且

因此, 结合式(2)和式(7), 整个离散系统的动态方程可以表示为:

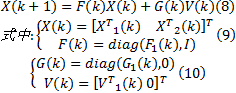
系统的量测方程可以定义为:

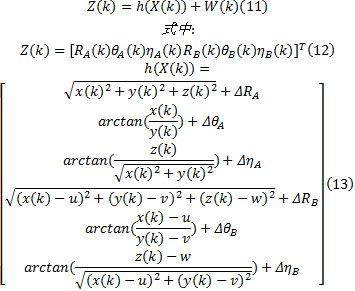
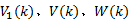
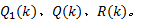
式(9)~(13)中: 为白色高斯随机噪声, 其方差阵分别为

2 平方根容积卡尔曼滤波原理
2.1 基于求容积规则的数值积分近似法

考虑如下具有“ 非线性函数 高斯概率密度” 形式的 维积分[17, 18]:

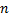
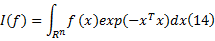
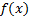
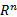
式中: 为任意函数; 为积分区域。

贝叶斯理论求解非线性高斯域滤波的关键问题就在于计算求解式(14)所示的积分。

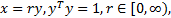
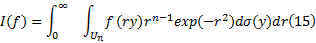
令 则式(14)可表示为:

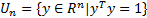
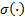
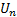
式中: 为半径为1的超球面; 为球面度量单位或 的面积微元。

将式(15)化简得:

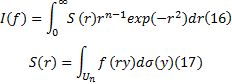
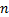
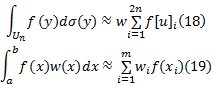
这样, 维积分式(14)变换为如式(16)和(17)所示的球面-径向积分形式, 可采用球面积分原理及径向原理求解, 如式(18)和(19)所示, 从而形成CKF滤波算法。

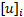
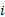
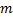
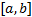
式(18)显示了球面积分原理下一种三阶球面积分结构, 其中, 表示生成算子的第 个元素。式(19)展示了球面径向原理, 即 点高斯积分可以等价为(2m-1)个多项式求和形式, 其中, 为一个在积分区间 上非负的权重函数。

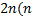
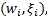
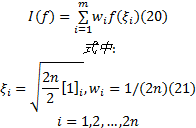
更为具体地, CKF利用球面径向准则选取 为状态维度)个具有相应权值的点集 用于逼近非线性状态的后验均值和协方差, 如下所示:

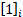
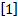
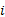
式中: 表示集合 的第 列。

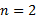
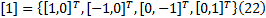
若 , 则有

按照以上方法计算出容积点集之后, 就可以执行CKF中的时间更新和量测更新步骤。

2.2 平方根容积卡尔曼滤波

原理上, CKF滤波过程与UKF类似, 但其理论推导更加严谨[17, 18]。CKF采用了一种全新的点集近似分布方法, 即根据Cubature准则, 利用2 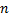个同等权值的Cubature点经非线性系统方程转换后产生新的点, 进而结合权值计算状态的预测, 无需对非线性模型线性化。

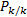
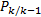
CKF同样具备UKF的优良特性, 可以较好地处理非线性系统的估计问题, 由于其使用更少的采样点, 进一步降低了计算代价, 且在三维以上非线性系统中的优势更为明显, 具有数值精度更高、滤波稳定性更高和可采用平方根策略的优良特性[19]。然而, 在CKF的滤波递推过程中, 每一步都要计算状态估计协方差矩阵 以及一步预测协方差矩阵 的平方根, 具有计算量较大且数值不稳定的缺点。而平方根CKF(Squared-root CKF, SRCKF)在CKF的基础上以Cholesky分解的形式直接传播和更新状态协方差矩阵的平方根, 降低了计算负担, 从而获得更高的计算效率, 同时能保证协方差矩阵的非负定性, 避免了滤波器的发散, 提高了滤波的收敛速度和数值稳定性[18]。SRCKF的时间更新及量测更新递推步骤可参考文献[17]。

3 本文算法

首先将目标的运动模型和传感器偏差配准模型组合在一起, 形成扩维的状态空间模型, 即将传感器偏差作为状态向量中的分量, 然后利用平方根容积卡尔曼滤波技术实现目标状态和传感器偏差的联合估计。因此, 基于SRCKF的目标状态和传感器偏差的扩维联合估计可以称为ASSRCKF。

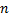
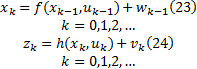
考虑如下 维非线性离散状态空间模型:

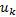
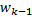
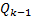
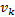
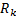
式中: 为已知的控制输入; 过程噪声 为零均值、方差为 的高斯白噪声; 量测噪声 为零均值、方差为 的高斯白噪声。

(1)初始化

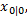
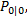
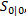
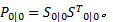
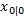
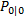
设置状态初值 协方差矩阵初值 协方差矩阵平方根因子的初始值 其中 状态初值 及协方差矩阵初值 的初始化采用文献[20]中所述的方法二。

(2)时间更新( )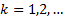

①计算当前状态的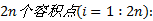

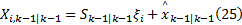
②计算容积点经过非线性状态转移函数的预测值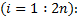

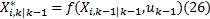
③结合权值与容积点预测值, 估计预测状态(SRCKF采用相等权值):

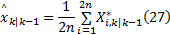
④估计预测误差协方差矩阵的平方根因子:

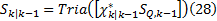
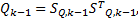
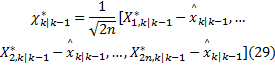
式中: 且

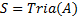
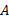
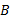
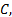
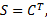
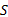
需要说明的是, 算法 意为:先对矩阵 进行QR分解, 得到一个正规正交矩阵 与一个上三角矩阵 令 得到的 为上三角矩阵。

(3)量测更新

①计算更新状态容积点(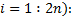

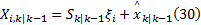
②计算预测量测容积点( ):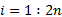

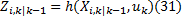
③估计预测量测:

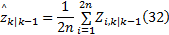
④估计新息协方差矩阵:

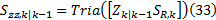
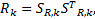
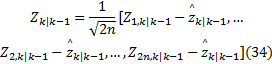
式中: 且

⑤估计互协方差矩阵:

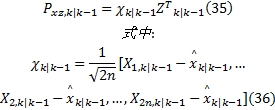
⑥估计SRCKF滤波增益:

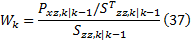
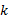
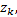
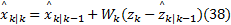
⑦基于 时刻新的量测 更新系统状态:

⑧更新误差协方差矩阵的平方根因子:

4 仿真及分析
4.1 仿真设置

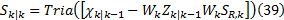
为验证本文算法ASSRCKF的有效性, 采用蒙特卡洛仿真, 将本文算法与ASEKF、ASUKF进行比较与分析。为仿真比较更为全面, 将基于容积卡尔曼滤波的扩维估计算法(Augmented state cubature Kalman filter, ASCKF)也进行了仿真, 其算法过程与ASSRCKF类似, 这里不再赘述。

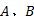
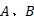
设定蒙特卡洛仿真次数为20次, 仿真步数设置为1000步。设置仿真环境如下:采用两部同步三坐标传感器 进行组网融合, 采样间隔均为T=1 s。设定 传感器的笛卡尔坐标分别为(0, 0, 0)km、(185.2, 0, 0)km; 各传感器的距离、方位角、俯仰角量测精度均分别设置为50 m、0.3° 、0.2° ; 而测距系统误差分别为2000 m、1500 m, 测方位角系统误差分别为0.4° 、0.3° , 俯仰角系统误差分别为0.3° 、0.2° 。

假设传感器公共探测区中的目标做匀速直线运动, 目标初始状态分别设置为:X(0)=[50 km, 250 m/s; -50 km, -200 m/s; 10 km, 10 m/s]。

各滤波器的初始化均采用文献[20]中所述的方法二进行设定。各算法的估计精度由均方根误差(Root mean square error, RMSE)曲线进行评价:

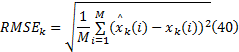
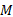
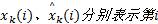
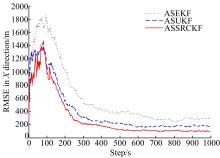
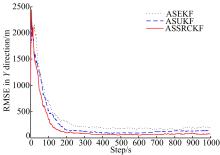
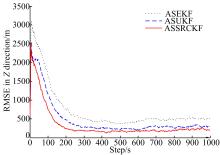
式中: 为蒙特卡洛仿真次数; 次仿真时的状态真值与估计值。

4.2 仿真结果及分析

传感器存在偏差的情况下, 图1给出了三种算法在 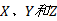轴方向上的目标状态估计RMSE曲线。需要说明的是, 从原理上分析, ASCKF与ASSRCKF的估计精度一致, 实际仿真结果也是如此, 故ASCKF的RMSE曲线不必在图中显示。

图1 X、Y、Z方向各算法的RMSE随时间变化曲线(a)X方向Fig.1 Time variation of RMSE in X, Y and Z direction

图1 X、Y、Z方向各算法的RMSE随时间变化曲线(b)Y方向Fig.1 Time variation of RMSE in X, Y and Z direction

图1 X、Y、Z方向各算法的RMSE随时间变化曲线(c)Z方向Fig.1 Time variation of RMSE in X, Y and Z direction

由图1可见, 3种实时扩维估计算法均能进行有效的目标状态估计。其中, 基于确定性采样滤波的两种算法ASUKF与ASSRCKF的扩维估计精度相对较高, 而ASSRCKF算法精度比ASUKF算法略优, 且仿真中更为稳定, 这也说明了SRCKF相对UKF更适合于高维系统滤波。

为进一步检测本文算法对传感器系统偏差的估计效果, 图2、图3分别给出了雷达A、雷达B在距离、方位角与俯仰角的偏差估计均方根误差随仿真步数变化图。由图2、图3可见, 3种扩维算法均能够在仿真步数大于200时基本实现估计收敛, 且精度较高, 说明了扩维思想在目标状态与系统偏差联合估计中的可行性。其中基于确定性采样滤波的两种算法具有相对较快的收敛速度, 且相对于ASEKF提高了偏差估计精度。尤其是ASSRCKF具有更佳的联合滤波性能, 在目标状态及偏差估计精度方面相对于ASUKF平均提高了2%~10%。

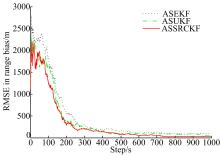图2 雷达A的距离、方位角、俯仰角系统偏差估计(a)距离系统偏差估计的均方根误差Fig.2 RMSE in range bias, azimuth bias and elevation bias(Radar A)

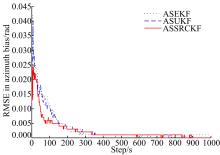图2 雷达A的距离、方位角、俯仰角系统偏差估计(b)方位角系统偏差估计
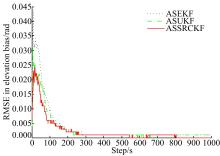RMSE in range bias, azimuth bias and elevation bias(Radar A)

图2 雷达A的距离、方位角、俯仰角系统偏差估计(c)俯仰角系统偏差估计Fig.2 RMSE in range bias, azimuth bias and elevation bias(Radar A)

ASEKF、ASUKF、ASCKF、ASSRCKF算法平均每次蒙特卡洛仿真的耗时为0.5753 s、0.2834 s、0.2226 s、0.2015 s(本文仿真中每次循环仿真具有1000步滤波过程)。

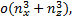
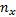
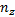
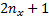
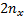
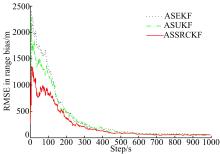可以看出, ASCKF与ASSRCKF的计算耗时明显低于前两种算法, 在算法实时性方面具有一定优势。从原理上分析, CKF与UKF的计算复杂度在同一个量级, 均为 其中 为状态维数, 为量测维数。UKF单次滤波需要采样 个不敏点, 而CKF只需采样 个容积点, 故CKF的计算代价略低于UKF。另一方面, ASSRCKF以平方根分解的形式降低了协方差矩阵运算的维度, 进一步节省了计算开销, 提高了算法的实时性。

图3 雷达B的距离、方位角、俯仰角系统偏差估计(a)距离系统偏差估计Fig.3 RMSE in range bias, azimuth bias and elevation bias(Radar B)

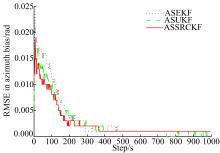图3 雷达B的距离、方位角、俯仰角系统偏差估计(b)方位角系统偏差估计Fig.3 RMSE in range bias, azimuth bias and elevation bias(Radar B)

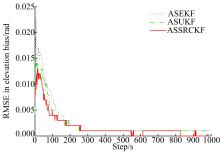图3 雷达B的距离、方位角、俯仰角系统偏差估计(c)俯仰角系统偏差估计Fig.3 RMSE in range bias, azimuth bias and elevation bias(Radar B)

此外, ASEKF基于扩展卡尔曼滤波理论, 其对系统模型的线性化误差往往会严重影响最终的估计精度, 甚至导致滤波发散, 且其需要计算雅各比矩阵, 在高维非线性系统中的计算耗时较大; ASUKF利用了确定性采样滤波技术UKF的优良特性, 可以避免滤波估计时非线性系统线性化所带来的影响, 但是其滤波性能是基于预先优化设置的系统参数, 影响了算法的可扩展性, 且UKF在高维系统中容易出现数值不稳定现象; 本文算法ASSRCKF基于CKF的滤波性能解决了UKF在高维系统中数值不稳定的缺点, 并采用协方差平方根的形式进行滤波计算, 保证了方差矩阵的正定性, 提高了算法的稳定性。

综合以上仿真与分析, 从估计精度、算法实时性、滤波稳定性等几个主要方面来看, ASSRCKF相对于已有的扩维算法具有明显的优势。

5 结束语

本文主要研究了传感器存在系统偏差条件下的三维目标跟踪问题。基于高斯求积规则与三阶球面-径向容积规则, 设计了基于平方根容积卡尔曼滤波的目标状态与传感器系统偏差扩维联合估计算法ASSRCKF。仿真分析表明:ASSRCKF在估计精度、算法实时性、滤波稳定性等方面均优于已有的扩维估计算法, 为带有系统误差的非线性状态估计问题提供了一种新的可行的解决方法。

The authors have declared that no competing interests exist.

参考文献
[1] Bar-Shalom Y, Li X R. Multitarget-Multisensor Tracking: Principles and Technique[M]. Stors C T: YBS Publishing, 1995. [本文引用:1]
[2] 何友, 王国宏, 关欣. 信息融合理论及应用[M]. 北京: 电子工业出版社, 2010. [本文引用:1]
[3] Farina A. Radar Data Processing (Vol. II)[M]. New York: Research Studies Press Ltd, 1985. [本文引用:1]
[4] Dana A M P. Registration: a prerequisite for multiple sensor tracking[C]∥Multitarget-multisensor Tracking, Advanced Applications, Bar-shalom Y Ed, Norwood: Artech House, 1990. [本文引用:1]
[5] Zhou Lin, Pan Quan, Liang Yan. Joint estimation of state and sensor systematic error in hybrid system[C]∥Proceedings of International Conference on Information Fusion, Singapore, 2012: 969-975. [本文引用:1]
[6] Burke J J. The SAGE real time quality control function and its interface with BUIC Ⅱ/BUIC Ⅲ[R]. MITRE Corporation Technical Report, No. 308, 1996. [本文引用:1]
[7] Dana M P. Registration: a prerequisite for multiple sensor tracking[C]∥Multitarget-Multisensor Tracking, Advanced Applications, Bar-Shalom Y Ed, Norwood: Artech House, 1990. [本文引用:1]
[8] Zhou Yi-feng, Henry L. An exact maximum likelihood registration algorithm for data fusion[J]. IEEE Trans on Signal Processing, 1997, 45(6): 1560-1572. [本文引用:1]
[9] Zhou L, Pan Q, Liang Y. Application of improved SA-PSO in the system error registration[J]. Opto-Electronic Engineering, 2010, 37(9): 27-31, 38. [本文引用:1] [CJCR: 0.476]
[10] Lin X D, Bar-shalom Y. Multisensor-multitarget bias estimaiton for general asynchronous sensors[J]. IEEE Transactions on Aerospace and Electronic Systems, 2006, 41(3): 899-919. [本文引用:1] [JCR: 1.299]
[11] He Y, Song Q, Xiong W. A track registration correlation algorithm based on Fourier transform[J]. Acta Aeronautica et Astronautica Sinica, 2010, 31(2): 362-365. [本文引用:1] [CJCR: 0.636]
[12] Nabaa N, Bishop R H. Solution to a multisensor tracking problem with sensor registration errors[J]. IEEE Trans on Aerospace and Electronic Systems, 1999, 35(1): 354-363. [本文引用:1]
[13] 宋强, 何友, 董云龙. 基于UKF的目标状态与系统偏差的联合估计算法[J]. 弹箭与制导学报, 2007, 27(3): 311-313, 316.
Song Qiang, He You, Dong Yun-long. An augmented state target tracking algorithm with systematic errors based on the unscented Kalman filter[J]. Journal of Projectiles, Rockets, Missiles and Guidance, 2007, 27(3): 311-313, 316. [本文引用:1] [CJCR: 0.2278]
[14] Li Z H, Chen S Y, Leung H. Joint data association, registration, and fusion using EM-KF[J]. IEEE Transactions on Aerospace and Electronic Systems, 2010, 46(2): 496-507. [本文引用:1] [JCR: 1.299]
[15] Julier S J, Uhlmann J K. Unscented filtering and nonlinear estimation[J]. IEEE Review, 2004, 92(3): 401-421. [本文引用:1]
[16] Duník J, Šimand l M, Straka O. Performance analysis of derivative-free filters[C]∥Proceedings of the 44th IEEE Conference on Decision and Control, and European Control Conference, Seville, 2005: 1941-1946. [本文引用:1]
[17] Arasaratnam I, Haykin S. Cubature Kalman filters[J]. IEEE Transactions on Automatic Control, 2009, 54(6): 1254-1269. [本文引用:3] [JCR: 2.718]
[18] 孙枫, 唐李军. Cubature 卡尔曼滤波与Unscented 卡尔曼滤波估计精度比较[J]. 控制与决策, 2013, 28(2): 303-308.
Sun Feng, Tang Li-jun. Estimation precision comparison of cubature Kalman filter and unscented Kalman filter[J]. Control and Decision, 2013, 28(2): 303-308. [本文引用:3] [CJCR: 0.907]
[19] 郝燕玲, 杨峻巍, 陈亮, 等. 基于SRCKF的水下航行器动基座初始对准技术[J]. 华中科技大学学报: 自然科学版, 2012, 40(2): 123-127.
Hao Yan-ling, Yang Jun-wei, Chen Liang, et al. Initial alignment method of the dynamic based for underwater vehicles using SRCKF[J]. Journal of Huazhong University of Science and Technology(Natural Science Edition), 2012, 40(2): 123-127. [本文引用:1] [CJCR: 0.502]
[20] 宋强, 何友, 董云龙. 一种目标状态与系统偏差的联合估计算法[J]. 弹箭与制导学报, 2007, 27(4): 312-315, 322.
Song Qiang, He You, Dong Yun-long. A joint estimation algorithm for state and systematic error[J]. Journal of Projectiles, Rockets, Missiles and Guidance, 2007, 27(4): 312-315, 322. [本文引用:1] [CJCR: 0.2278]