作者简介:贾洪飞(1969-),男,教授,博士生导师.研究方向:交通规划与管理,交通运输系统仿真.E-mail:jiahf@jlu.edu.cn
针对现有驾驶员行为模型对驾驶员特征因素考虑较少的不足,以快速路合流区为研究对象,运用模糊聚类方法与K-S检验法构建连续的驾驶员类型整合模型。在合流区换道过程中引入相互协作机制,并考虑驾驶特征差异对驾驶行为的影响,建立车道变换间隙接受模型。最后,以微观交通仿真系统MTSS为仿真平台,建立快速路合流区仿真模型,并进行了仿真验证,结果表明:仿真值与实测值的误差小于10%,表明构建的模型可以较好地表示驾驶员类型对驾驶行为的影响。
The existing driver model less considers the driver characteristic factors. To overcome this shortcoming, the expressway weaving area is chosen as the research object to build a gap acceptance model. First, a large number of vehicle trajectory data is generated using the video processing software VEVID. Second, a continuous driver type integration model is proposed using fuzzy clustering theory and K-S test method. Third, the mutual cooperation mechanism is introduced into the lane change process of the expressway weaving area, and the influence of driver characteristics on the driving behavior is considered to build the gap acceptance model. Finally, the microscopic traffic simulation system MTSS is taken as the simulation platform to build a merging simulation model to validate the gap acceptance model. Results show that the error between the simulation value and real measured value is less than 10%, which indicates that the proposed gap acceptance model can be used to describe the impact of driver type on driving behavior.
目前, 运用交通仿真技术分析快速路合流区运行特性已经在国内外得到了快速发展。快速路合流区的交通仿真可分为两大类:交通流动力学仿真和元胞自动机仿真。Hidas等[1]开发了道路交通微观仿真评估系统ARTEMis, 在该系统中将汇入换道划分为三类, 用最大速度下降值表示执行协同换道或强迫换道的可行性; 孙剑等[2]在传统的强制性车道变换模型中引入换道“ 协作” 机制、换道冲突“ 协商” 机制, 建立了相应的仿真模型TESS; Kondyli等[3]考虑了汇入车辆与主线车辆之间的相互作用以及参与者的性格特征, 建立合流区仿真模型; 熊胜辉等[4]考虑辅道交通流对交织区的影响, 以元胞自动机NS模型为基础, 通过设定跟车规则、换道规则, 对快速路交织区路网建立模型进行微观仿真。江金胜等[5]根据C型双侧交织区的车辆换道特征建立相应的换道规则, 采用多车道元胞自动机模型研究交织区系统的交通流特性。
综合以上分析, 目前针对快速路合流区交通流仿真方面的研究, 较好地考虑了交通流特征及交通流交互作用, 但对驾驶员特征因素考虑较少, 大都忽略了驾驶员自身特性差异对驾驶行为的影响。因此, 本文在驾驶员特征分析的基础上, 结合驾驶员类型划分的不确定性和模糊性, 在构建车道变换间隙接受模型时着重考虑驾驶员特征差异对驾驶行为的影响, 并引入相互协作机制, 以准确表示快速路合流区交通流特征。
根据国内外驾驶员特征的相关研究成果, 一般将驾驶员划分为保守型、普通型和激进型三种类型[6, 7]。不同类型的驾驶员在快速路合流区的行为存在显著差异。为了分析驾驶员特征, 首先采用行为量表方法对该问题进行研究。
根据Reason等[8]提出的标准化驾驶员行为问卷设计自填式量表, 进行驾驶员行为量表设计。量表由三部分组成, 第一部分是驾驶员的基本个人信息, 主要包括性别、年龄、驾龄、职业、开车频率等相关信息; 第二部分为驾驶风格的主观评估, 用1、2、3分别表示驾驶员风格“ 激进” 、“ 普通” 、“ 保守” ; 第三部分为潜在行为和影响因素评估, 用1、2、3分别表示驾驶员选择“ 不可能” 、“ 比较可能” 和“ 非常可能” 三种反应, 以及影响因素的“ 非常重要” 、“ 比较重要” 和“ 不重要” 三种等级。
为了保证驾驶员在不受干扰的情况下自主完成问卷, 驾驶员行为量表的测试采用电话访问的方式, 选择135位不同年龄和驾龄的驾驶员进行调查。通过调查数据统计分析, 驾驶员特征与其行为关系的统计结果如表1所示。
| 表1 驾驶员类型与其行为可能性关系表 Table 1 Relationship between driver types and their behaviors possibility |
通过以上驾驶员行为量表的统计分析, 三类不同驾驶员表现出不同的行为特征, 具体如下:
(1)激进型驾驶员
激进型驾驶员喜欢刺激和冒风险, 在行驶过程中主要考虑自身状态, 在汇入主线时发起强制汇入的概率最大; 在主线行驶时为汇入车辆减速协同的概率最小。
(2)普通型驾驶员
普通型驾驶员感知较为机敏、在汇入主线时会综合考虑自身及周边的交通状况, 倾向于选择协同汇入而非强迫汇入, 在主线行驶时一般会为汇入车辆减速进行协同。
(3)保守型驾驶员
保守型驾驶员善于忍耐、易低速行车且少超车, 在汇入主线时很少或根本不会尝试强制汇入, 他们会倾向于等待更大的汇入间距, 且不会对主线车辆产生干扰; 在主线行驶时为汇入车辆减速进行协同的可能性最大。
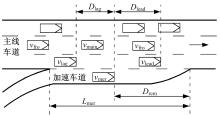
由于问卷可能使量表数据受到一定的主观因素和外界不确定因素的影响, 无法完全准确地反映真实驾驶员特性[9], 因此本文在以上驾驶员主观特征分析的基础上, 基于真实的驾驶员行为进行驾驶员类型的划分。首先, 选取广州市内环快速路一处典型的合流区作为数据观测点进行车辆运行视频的拍摄, 调查时间为连续2个工作日的早高峰时段(7∶ 00-9∶ 00), 调查区段示意图如图1所示。
利用车辆轨迹处理软件VEVID对采集的视频进行处理, 从而得到主线车辆与汇入车辆的速度、加速度和间隙等微观运行轨迹相关数据。通过视频处理得到的轨迹数据的主要特征如表2所示。
| 表2 调查数据特征 Table 2 Characteristics of investigated data |
快速路合流区驾驶行为特性受多重因素影响, 其中加速车道长度是一个重要的因素。由于加速车道长度是个相对固定值, 因此本文是在加速车道长度一定的情况下, 研究驾驶员类型特征的差异性。基于以上驾驶员类型特征的差异性分析, 并结合数据调查手段, 分别进行汇入车辆和主线车辆驾驶员特征指标的选取。为了保证分析结论的客观性和科学性, 特征指标的选取遵循:完备性、客观性、可操作性、可比性等原则。
2.2.1 汇入车辆驾驶员特征指标
选取加速车道长度的行驶距离比值、汇入车辆与主线后随车相对速度、后随车间距与前后总间距比值三个指标进行汇入车辆驾驶员类型分析。
(1)加速车道长度的行驶距离比值
驾驶员越激进, 汇入主线时加速车道行驶的距离越短; 反之, 驾驶员越保守, 由于不断寻找合适间隙, 完成汇入时, 加速车道行驶距离较长。该指标为反向指标, 其表达式如下:
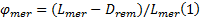
式中: 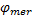
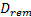
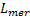
(2)汇入车辆与主线后随车相对速度
驾驶员越激进, 行驶速度越快; 反之, 则行驶速度越慢。为了反映汇入车辆的行驶速度相对于周围整体交通状态下的水平, 选择汇入车辆与主线后随车的相对速度, 而非汇入车辆取自身的速度。该指标为正向指标, 其表达式如下:

式中: 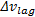
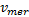
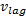
(3)后随车间距与前后总间距比值
驾驶员越激进, 在汇入主线过程中越易选择较小的前后间隙; 反之, 则越需要较大的间隙。由于后随车间隙不受自身控制, 因此相对前导车间隙是个更为重要的因素。选择该指标以全面反应前后间隙的影响, 并突出后随车间隙的重要性。该指标为反向指标, 其表达式如下:
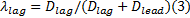
式中: 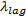
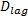
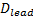
2.2.2 主线车辆驾驶员特征指标
选取主线车辆加速度、主线车辆速度与主线车辆平均速度的相对值、主线车辆与后随车辆相对距离这3个指标进行主线车辆驾驶员特征分析。
(1)主线车辆加速度
激进型驾驶员减速进行协同的概率较小, 他们倾向于保持原速度让汇入车辆在他们后面汇入。该指标为正向指标, 其表达式如下:
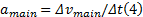
式中: 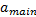
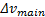

(2)主线车辆速度与主线平均速度的相对值
为了反应主线当前车辆在主线车道合流区段所有车辆中所处的相对水平, 选取主线车辆速度与主线平均速度的相对值作为反应驾驶员特征的变量, 该指标为正向指标, 驾驶员越激进, 其值越大, 表达式如下:
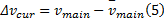
式中: 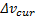
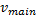
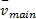
(3)主线车辆与后车相对距离
驾驶员类型越激进, 换道所需的间距越小, 如果主线车辆不换道, 则用后车最大间隙表示其换道间隙。该指标为反向指标, 表达式如下:
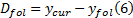
式中: 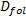
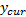
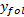
由于汇入车辆和主线车辆驾驶员特征指标各有不同的量纲。为了使不同量纲的数据也能进行比较, 采用平移-标准差变换与平移-极差变换的方法对数据进行标准化处理。
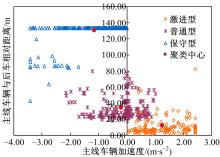
根据目前广泛采用的驾驶员类型划分方法, 将其划分为保守型、普通型和激进型三类。利用基于目标函数的模糊C均值(Fuzzy C-means, FCM)算法[10]分别对汇入车辆与主线车辆的驾驶员特征指标进行聚类分析, 汇入车辆驾驶员类型聚类结果如表3和图2、图3所示。
| 表3 汇入车辆驾驶员类型的聚类结果 Table 3 Clustering results of driver type at merging lane |
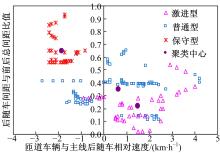 | 图2 后车相对速度与后车间距比值聚类关系Fig.2 Clustering relationship between relative speed of lag vehicle to merging vehicle and proportion of lag gap to total gap |
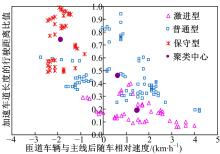 | 图3 后车相对速度与加速车道长度的行驶距离比值聚类关系Fig.3 Clustering relationship between relative speed of lag vehicle to merging vehicle and proportion of merging lane used by merging vehicle |
通过模糊聚类算法得到的主线车辆驾驶员类型聚类结果分别如表4和图4、图5所示。
| 表4 主线车辆驾驶员类型的聚类结果 Table 4 Clustering results of driver type at main lane |
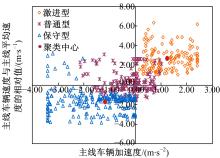 | 图4 主线车辆加速度和主线车辆速度与主线平均 速度的相对值聚类关系Fig.4 Clustering relationship between mainline vehicle acceleration and relative speed |
根据以上驾驶员类型的模糊聚类分析结果, 可以较好地依据调查数据进行驾驶员类型的判断, 但获取的每个驾驶员类别隶属度数值均位于[0, 1]区间, 不能直接依据数值大小进行驾驶员类型的判断, 因此不能为微观交通流仿真模型所用。此外, 驾驶员类型的划分本身具有不确定性和模糊性, 尤其是在类型划分的临界附近, 驾驶员之间并没有太过严格的区别, 生硬地进行几个类别的划分并不能较好地反应其差异性。因此有必要建立一个连续的驾驶员类型模型, 用数值大小直接表示驾驶员激进程度, 而不是简单地进行几个类别的划分。
对基于以上驾驶员类型模糊聚类分析得出的驾驶员类型及隶属度数值, 进行数据的连续化和标准化处理, 数据处理公式如下:
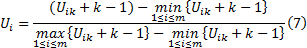
式中: 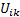
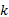
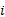
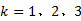
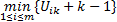
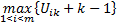
为了分析驾驶员类型的总体分布, 将以上经过连续化和标准化处理的驾驶员类型数据进行单个样本K-S检验, 检验结果如表5所示。
| 表5 驾驶员类型模型整合结果 Table 5 Clustering results of driver type models |
从检验结果可以看出, 在K-S检验中, 汇入车辆与主线车辆的P值(Sig 2-tailed)分别为0.70和0.56, 均大于0.05, 这说明数据呈近似正态分布。因此驾驶员类型可以用正态分布表示。
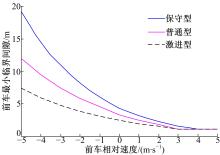
根据以上建立的驾驶员类型模型对3种驾驶员类型对应的换道间隙数据进行统计分析, 结果发现驾驶员类型对换道间隙有重要的影响。以汇入车辆的前车相对速度和前车间隙相互关系(见图6)为例, 可以看出:在前车相对速度低于4.0 m· s-1时, 驾驶员类型越激进, 换道所需的间隙越小; 随着前车相对速度的增加, 驾驶员类型的差异对换道间隙的影响逐步减小。
为了反映驾驶员特征差异对换道间隙的影响, 本文在构建间隙接受模型时, 除了考虑交通流相互作用机理(受篇幅限制, 主线车辆协同换道模型和汇入车辆强迫汇入模型不在此赘述), 还重点考虑驾驶员特征因素, 将驾驶员类型作为一个重要变量纳入到间隙接受模型中。
目前, 在绝大多数仿真模型中, 车道变换行为被划分为强制性车道变换和自主性车道变换两大类[11]。强制性车道变换是指车辆为了完成其正常行驶目的而必须采取的车道变换行为(如交织区的汇入车辆、地面交叉口的转向等); 自主性车道变换是指车辆为了追求更加理想的行驶方式而发生的车道变换行为。合流区车道变换行为显然属于强制性车道变换。
为了完成换道, 汇入车辆需要判断主线车道的交通状况是否满足换道要求。一旦交通状况满足要求就换道汇入; 反之, 则继续寻找合适的交通条件。由此可见, 该行为是一种典型的二元选择过程, 因此本文采用二元Logit模型估计间隙接受的概率, 其表达式如下:
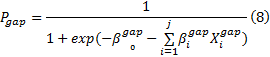
式中: 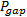

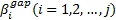
根据以上获取的大量车辆运行轨迹数据, 采用美国QMS公司开发的Eviews软件对以上构建的车道变换间隙接受概率模型的参数进行极大似然估计。首先通过 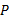
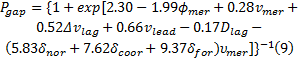
式中: 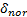
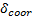
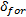
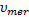
从表6可以看出, 间隙接受模型与加速车道长度的行驶距离比值、后车间隙、驾驶员激进程度成正比, 与汇入车辆速度、前车相对速度、后车相对速度成反比; 此外还可以看出, 在相同条件下, 激进型驾驶员比普通型和保守型驾驶员选择换道的概率要大。
| 表6 间隙接受模型标定结果 Table 6 Calibration results of gap acceptance model |
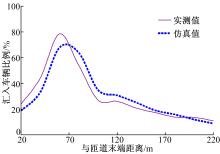
为了验证构建的间隙接受模型, 以吉林大学和上海交通大学开发的微观交通仿真系统MTSS为仿真平台, 选取获取驾驶员特征数据的广州市一处典型快速路合流区建立仿真模型。采用均方根偏差(RMSE)和平均百分比偏差(MPE)两个指标进行模型的验证, 其公式如下:
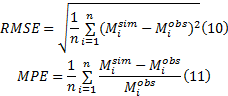
式中: 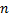
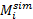
| 表7 驾驶员类型模型验证结果 Table 7 Validation results of driver type model |
结合驾驶员类型划分的不确定性和模糊性, 选取反应驾驶员特征的指标, 运用模糊聚类及数据整合方法, 建立了驾驶员类型整合模型; 将驾驶员类型分布作为一个重要参数纳入到快速路车道变换间隙接受模型中, 并建立了交通仿真模型予以验证, 结果表明:构建的基于驾驶员类型模型的间隙接受模型可以较好地表示驾驶员类型对驾驶行为的影响。因采集数据样本有限, 下一阶段将扩大数据的采集范围, 使模型标定结果更具有普遍性和广泛性。
The authors have declared that no competing interests exist.
| [1] |
|
| [2] |
|
| [3] |
|
| [4] |
|
| [5] |
|
| [6] |
|
| [7] |
|
| [8] |
|
| [9] |
|
| [10] |
|
| [11] |
|