本文不考虑交叉口设置左转短车道或左弯待转区的情况。假设所研究交叉口在高峰时段内采用定时信号控制方式; 某进口道早高峰时单车道左转流量明显大于单车道直行流量, 而晚高峰时单车道直行流量明显高于单车道左转流量。如果所研究交叉口某进口道交通流明显具有这种潮汐特性, 那么可以在该进口道上设置可变导向车道。这里认为车流与车道组一一对应, 将某股车流所能使用的所有车道称为该股车流对应的车道组。另外, 在进口道设置可变导向车道需要满足两个条件:①进口道车道数为3条或3条以上; ②左转车流与直行车流分别由独立的信号进行控制。

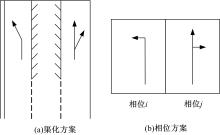
如图1(a)所示, 以含3条车道的进口道为例, 内侧车道为左转车道, 外侧车道为直右车道, 中间车道设为可变导向车道, 该车道随着交通流分布的变化可以让车辆直行或左转。这里假设右转车流比例较小。当左转流量明显高于直行流量时, 可变导向车道指示的行车方向为左转; 反之, 可变导向车道指示的行车方向为直行。如图1(b)所示, 该进口道的左转车流与直右车流在不同的相位内通行, 其通行顺序可以先左转后直行, 也可以先直行后左转。当研究整个交叉口时, 需要考虑与其他进口道各股车流之间的关系, 统筹考虑交叉口的相位相序设计方案。

图1

Fig.1

	Figure Option ViewDownloadNew Window
	图1 可变导向车道设置方案Fig.1 Setting scenario of a reversible approach lane

基于以上基本假设, 根据交叉口交通流分布, 各进口道都有可能设置可变导向车道。因此, 交叉口可能存在1条或1条以上的可变导向车道。

在信号控制交叉口, 当存在可变导向车道时, 一条车道组的饱和流率为:

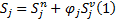
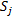
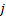
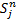
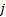
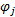
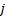
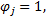
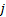
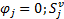
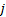
式中: 为第 条车道组的饱和流率(pcu/h); 为第 条车道组中固定导向车道的饱和流率(pcu/h); 为可变导向车道功能激活标识符, 当第 条车道组所含可变导向车道被激活时, 当第 条车道组所含可变导向车道没被激活或不存在可变导向车道时, 为第 条车道组中可变导向车道的饱和流率(pcu/h)。

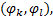
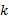
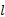
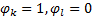
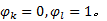
这里还需定义可变导向车道功能唯一性约束数对 这一约束数对的含义是第 条和第 条车道组中的可变导向车道不能同时被激活, 即 或者 这一数对保证进口道的可变导向车道在一个时段内只能有一种功能属性, 即允许车辆的行驶方向为左转或直行。

由一条车道组的饱和流率可得该车道组的通行能力为:

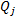
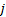
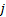
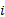
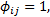
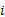
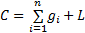
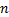
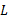
式中: 为第 条车道组的通行能力(pcu/h); 为车流与相位关联标识符, 当第 股车流在第 个相位内有通行权时, 否则, 为第 个相位的有效绿灯时间(s); 为周期时长(s); 为相位数; 为每周期总损失时间(s)。

根据美国《道路通行能力手册2000》^[12], 一条车道组的车均延误为:

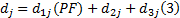
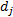
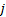
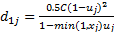
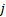
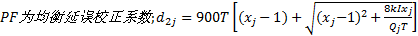
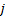
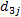
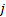
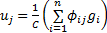
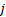
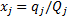
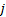
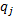
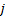
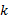
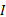
式中: 为第 条车道组的车均延误(s/pcu); 为第 条车道组的均衡控制延误(s/pcu); 为第 条车道组的增量延误(s/pcu); 为第 条车道组的初始排队延误(s/pcu); 为第 条车道组的绿信比; 为第 条车道组的饱和度; 为第 条车道组的流量(pcu/h); 为分析期持续时间(h); 为控制类型校正系数; 为上游分流或供给校正系数。

对进口道上每条车道组的车均延误进行集计处理, 可得交叉口车辆总延误为:

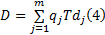
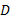
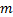
式中: 为交叉口车辆总延误(s); 为交叉口车道组数。

对于每一股车流, 车道组有效绿灯时间应大于或等于最小绿灯时间, 即:

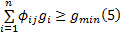
式中: 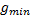为最小绿灯时间(s)。

这里车道组有效绿灯时间是指在一个信号周期内该车道组对应车流能够有效通行的绿灯时间。

对于交叉口, 所有相位有效绿灯时间之和加上一个信号周期内的总损失时间即为信号周期时长。根据文献[12], 这一信号周期时长应在临界的上、下限之间, 即

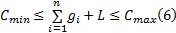
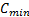
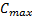
式中: 为最小周期时长(s); 为最大周期时长(s)。

相位有效绿灯时间应为非负数, 即

为了获得使交叉口总延误最小化的信号配时设计方案, 在满足约束条件(5)(6)(7)的情况下最小化目标函数(见式(4)), 则可得信号配时优化模型^[13]:

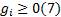
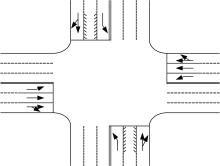
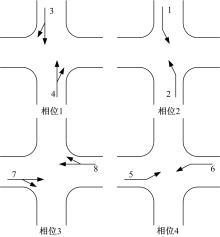
图2(a)为一个含可变导向车道的典型交叉口的渠化方案, 图2(b)为该交叉口的相位方案, 图中数字表示车流编号。

图2

Fig.2

	Figure Option ViewDownloadNew Window
	图2 典型交叉口渠化与相位设计方案(a) 渠化方案Fig.2 Channelization and signal phase plans for a typical intersection

图2

Fig.2

	Figure Option ViewDownloadNew Window
	图2 典型交叉口渠化与相位设计方案(b) 相位方案Fig.2 Channelization and signal phase plans for a typical intersection

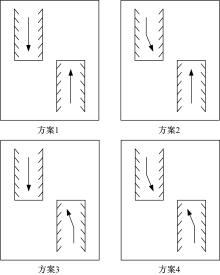
以该图所示交叉口为例, 高峰小时内该交叉口各进口道各流向的流量如表1所示。由图2可见, 该交叉口北进口道和南进口道的中间车道均为可变导向车道, 其车道功能在左转和直行之间进行切换。这两条可变导向车道的功能属性有四种组合方案, 如图3所示。

表1

Table 1

表1(Table 1)

表1 交叉口各流向流量 Table 1 Traffic volume for each movement at intersection 进口道 流量/(pcu· h-1) 左转 直行 右转 合计 北进口 400 700 100 1200 南进口 650 420 80 1150 西进口 300 600 50 950 东进口 260 580 60 900

表1 交叉口各流向流量 Table 1 Traffic volume for each movement at intersection

图3

Fig.3

	Figure Option ViewDownloadNew Window
	图3 可变导向车道功能组合方案Fig.3 Combination scenarios of functions of reversible approach lanes

针对图3所示各方案, 使用本文所建立的优化模型计算使交叉口总延误最小的信号配时参数及其相应的性能指标, 所得结果如表2所示。从表2中可以看出, 当北进口道可变导向车道为直行、南进口道可变导向车道为左转时, 按图2(b)所设计的四相位配时方案的最佳周期时长较其他三种方案短, 总延误和车均延误都最小, 饱和也最低, 且低于1, 交叉口通行能力第二大。因此, 方案3是该高峰小时内的最优方案。

表2

Table 2

表2(Table 2)

表2 不同方案对应的最佳配时参数及性能指标 Table 2 Optimal signal timing parameters and performance indices under different scenarios 参数或指标 方案1 方案2 方案3 方案4 有效绿灯 时间/s 相位1 31.69 47.06 31.10 57.30 相位2 49.45 37.86 24.70 25.21 相位3 26.41 25.26 20.92 25.96 相位4 22.45 19.82 18.34 21.53 周期时长/s 150.00 150.00 115.05 150.00 通行能力/(pcu· h-1) 4789.27 5016.06 4836.74 4604.11 总延误/s 474294.09 1418708.11 300959.32 621076.95 车均延误/(s· pcu-1) 112.93 337.79 71.66 147.88 饱和度 1.06 1.37 0.97 1.13

表2 不同方案对应的最佳配时参数及性能指标 Table 2 Optimal signal timing parameters and performance indices under different scenarios

为了进一步说明模型优化效果, 使用交通仿真软件VISSIM对交通流运行状况进行模拟, 采用多步运行模式, 仿真时间为3600 s, 运行次数为5。表3给出了不同方案下交叉口各流向车流的车均延误。图4给出了不同方案下各进口道的平均排队长度和最大排队长度。

从表3可以看出, 当可变导向车道采用方案3时, 大多数车流的车均延误较其他方案低, 仅有南进口直行和右转车流的车均延误比方案4略高。从图4可以看出, 当可变导向车道采用方案3时, 各进口道平均排队长度和最大排队长度都比其他方案短。综合考虑, 该时段内可变导向车道功能及信号配时参数的最优组合是方案3。

表3

Table 3

表3(Table 3)

表3 不同方案下各流向车流的车均延误 Table 3 Average delay per vehicle for each movement under different scenarios 方案 北进口 南进口 西进口 东进口 左转 直行 右转 左转 直行 右转 左转 直行 右转 左转 直行 右转 1 65.80 94.90 74.16 63.42 80.10 65.46 77.46 76.36 59.50 66.84 69.88 54.60 2 180.50 135.24 117.14 142.04 141.86 115.54 148.90 132.08 98.74 98.78 90.90 68.42 3 48.66 40.70 28.46 44.26 48.64 41.10 61.54 51.28 39.52 50.10 50.06 40.72 4 89.92 70.48 60.66 68.08 42.00 38.10 87.64 86.10 63.08 95.86 95.60 76.50

表3 不同方案下各流向车流的车均延误 Table 3 Average delay per vehicle for each movement under different scenarios

图4

Fig.4

	Figure Option ViewDownloadNew Window
	图4 不同方案下进口道平均排队长度和最大排队长度(a) 平均排队长度 (b)最大排队长度Fig.4 Average queue length and maximum queue length on each approach under different scenarios