管成(1968-),男,副教授,博士.研究方向:工程机械液压控制,挖掘机器人技术.E-mail:guan@zju.edu.cn
为提高挖掘机器人的工作效率,保证其运行轨迹平滑,提出了一种基于NURBS曲线的轨迹规划方法。利用5次NURBS曲线插值挖掘机器人关节位置,引入矢值函数,通过莱布尼茨公式求解NURBS曲线的高阶导矢,设定启停速度和加速度,得到经过指定关节位置加加速度连续的轨迹曲线。分析了NURBS曲线权因子在挖掘轨迹局部规划中的作用。采用序列二次规划方法求解约束条件下的非线性最小化问题,规划出时间最优轨迹曲线。仿真和试验表明:提出的轨迹规划方法能够得到满足物理约束的时间最优关节轨迹,且可进行轨迹局部优化。
In order to improve the efficiency of the robotic excavator meanwhile to obtain its smooth running trajectory, a new trajectory planning method based on Non-uniform Rational Basis Spline (NURBS) was proposed. A quintic NURBS curve was employed to interpolate joint positions of the robotic excavator. Using the vector-valued function, by Leibniz formula, higher order derivative vector of NURBS curve was obtained to set the start and stop speeds and accelerations; and to make up the trajectory curves with continuous jerk, which passes specified joint positions. The effect of NURBS weight factor in sectional trajectory planning was analyzed. Nonlinear minimization problems under constraints were solved using sequential quadratic programming; then time-optimal trajectories were planned. Simulation and experiment results show that the proposed trajectory planning method can provide time-optimal trajectories, which satisfy kinematic constraints and the sectional trajectory optimization is effective.
挖掘机器人大多工作在作业环境恶劣、作业对象和作业任务多变的条件下[1]。与普通液压挖掘机的多路阀相比, 挖掘机器人采用电磁伺服阀来实现包括挖掘、回转、卸料、返回的自主作业[2]。为提高挖掘机器人的工作性能, 减少液压系统和执行系统的冲击振动, 使挖掘机器人运行更加平稳, 提高工作装置节能效果, 以最优时间和平滑轨迹为目标的轨迹规划成为最优控制的研究焦点[3, 4, 5]。挖掘机器人的铲斗末端轨迹特性为复杂的空间曲线[6, 7], 现有的挖掘机器人轨迹规划方法大多基于多项式曲线或B样条曲线, 在全局大范围轨迹里难以应用单一的多项式来表达, 也难以胜任实际工况中挖掘机器人的局部复杂轨迹[8, 9]。近年来, 非均匀有理B样条曲线(NURBS)在工程应用领域逐渐得到重视。由于NURBS曲线具有局部修改性, 移动控制顶点、调整节点矢量或改变权因子仅影响NURBS曲线的局部形状, 而不会影响整体轨迹的性能[10, 11, 12]。利用NURBS曲线将挖掘机器人作业任务进行轨迹规划, 可以得到轨迹连续, 各关节无速度、加速度突变的轨迹曲线, 而且可进行局部轨迹调节, 适合挖掘机机器人化控制[12]。刘宇等[6]以3次NURBS曲线插值关节位置, 得到满足物理约束的时间、平滑性综合最优的轨迹曲线。但是, 没有给出具体的关节轨迹规划方法。同时, 基于3次NURBS曲线的时间最优轨迹规划方法只能保证关节速度、加速度连续, 而不能保证加速度平滑和加加速度连续[5], 得到的轨迹曲线关节位置跟踪误差较低, 造成挖掘机器人系统的过度损耗, 影响挖掘机器人的使用寿命。
本文采用C4连续的5次NURBS曲线插值挖掘机器人关节位置, 对挖掘机器人关节轨迹进行时间最优轨迹规划。引入矢值函数求解轨迹曲线在指定关节位置的高阶矢量, 得到关节的速度、加速度和加加速度轨迹曲线, 通过调整权因子实现挖掘机器人关节轨迹曲线的局部优化。提出一种基于NURBS曲线的全局时间最优、可进行局部优化的轨迹规划方法。
进行基于NURBS的挖掘机器人轨迹规划, 利用NURBS曲线的强凸包性和局部修改性, 以最优时间作为性能指标, 在满足各种约束条件的基础上进行挖掘机器人轨迹规划, 使挖掘机器人铲斗末端经过指定工作点的运动时间最短。同时, 基于NURBS曲线权因子调整铲斗位姿, 进行挖掘轨迹的局部优化。
挖掘机器人轨迹规划可描述为构造满足物理约束的曲轨迹线, 结合NURBS曲线的定义, 采用 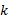

式中: 
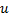



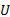
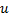


一般设定 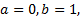
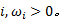
令:

则式(1)可以改写为:
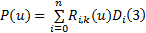
式中: 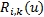
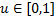
由式(3)可得:
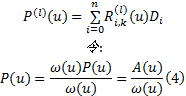
式中: 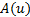
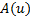


于是可得:
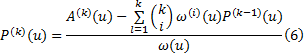
式(6)给出了计算 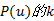
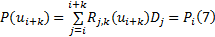
式中: 

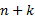
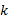

基于5次NURBS曲线的关节轨迹可以设定4个边界条件, 于是, 得到 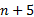
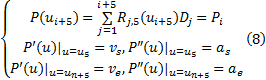
式中: 

根据控制顶点 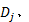


在基于NURBS的挖掘机器人轨迹规划中, 根据实际要求, 经常需要挖掘机器人调整铲斗位姿实现特定的挖掘曲线。除了通过对控制顶点的位置和节点矢量进行约束, 实现全局时间最优轨迹规划外, NURBS曲线在轨迹规划方面还具有另一优势, 可以通过调整控制顶点的权重因子实现对挖掘轨迹曲线的局部优化。
将权因子 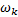
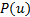
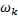
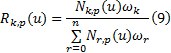
根据求导法则, 可得:

因此, 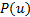

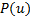
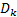
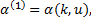


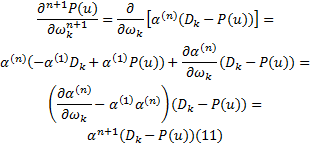
式中: 
这就完成了证明。由此可以推导出计算 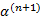
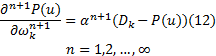
式中: 
以上证明了随着 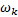

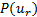

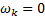
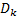
时间最优轨迹规划是指在挖掘机器人关节轨迹起点和终点间离散出一些中间点, 对两点间的时间间隔进行优化, 使得末端执行器从起点到终点的访问时间最短, 且要考虑末端执行器在运动过程中速度、加速度和加加速度的物理约束[3]。
设挖掘机器人的关节速度、加速度和加加速度约束分别为 
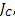
速度:
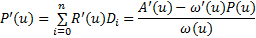
加速度:

加加速度:

物理约束:

基于NURBS曲线的挖掘机器人时间最优轨迹规划问题就是在满足物理约束并可根据实际工况通过权因子 
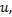
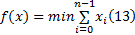
需满足以下物理约束条件:

式中: 

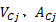


采用序列二次规划法(SQP)来求解式(13)所描述的非线性约束优化问题。在每一次迭代中, 收敛可以由用牛顿法(Quasi-Newton)得到的拉格朗日函数构成的Hessian矩阵来保证, 从而转化为一个二次规划(QP)子问题。
根据不等式约束条件, 可构造线性化非线性约束条件的拉格朗日函数为:

式中: 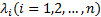
通过线性化非线性条件, 可以得到二次规划(QP)子问题:

通过QP算法来求解此子问题, 可形成如下新的迭代方程:

步长参数 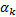

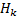
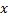
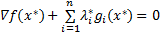
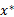
以如图1所示的挖掘机器人为研究对象, 对所提出的轨迹规划方法进行仿真和试验。该试验台功率为7.5 kW, 斗容量为0.02 m3, 转斗半径为0.4 m, 流量为25 L/min, 卸载高度为1.8 m, 最大挖远为3 m, 最大挖深为1.5 m。根据挖掘机器人的实际工作要求, 规划满足指定关节位置和物理约束的时间最优轨迹曲线。指定挖掘机器人的动臂、斗杆、铲斗、回转4个关节必须经过的关节位置序列如表1所示, 设定各个关节对应的速度、加速度、加加速度物理约束如表2所示。不同于一般的工业机器人, 挖掘机器人的铲斗位姿在实际挖掘过程中是非常关键的问题, 在进行挖掘机器人时间最优关节轨迹规划时, 参考已有挖掘机器人铲斗位姿规划规律[1, 8], 铲斗位姿通过指定铲斗的空间位置设定, 使得在挖掘过程中铲斗轨迹曲线连续平滑, 减少对铲斗缸和对应电磁换向阀的冲击。
| 表1 挖掘机器人各关节位置 Table 1 Joint positions of robotic excavator |
为保证挖掘机器人自主挖掘时的工作平稳性, 减少对机器人系统的冲击, 动臂、斗杆、铲斗和回转的启动与停止速度、加速度均取为0。根据表1和表2限定的关节位置序列和物理约束条件, 采用序列二次规划法进行轨迹规划运算, 求解约束条件下的时间最优解问题, 得到轨迹曲线的时间最优节点为 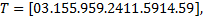

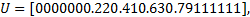
| 表2 挖掘机器人的物理约束条件 Table 2 Kinematic constraints of robotic excavator |
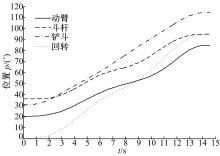
采用闭环控制方法, 将挖掘机器人的挖掘轨迹指令转化为驱动电磁伺服阀的电压指令, 通过控制液压缸的直线位移来实现各个关节的运动。本文主要研究轨迹规划方法, 轨迹控制方法在此不做详细讨论。根据以上获得的NURBS曲线参数, 可以规划出满足物理约束条件, 基于5次NURBS曲线的挖掘机器人时间最优轨迹曲线, 如图2所示。从图中可以看出:挖掘机器人的动臂、斗杆、铲斗和回转关节轨迹曲线平滑连续, 经过指定的关节位置, 角位移范围符合挖掘机器人的实际工作要求。关节速度曲线如图3(a)所示, 曲线平滑连续, 在启动、停止位置处, 各关节速度均为0, 运行过程中, 关节最大速度为11.04 (° )/s, 满足实际速度约束条件。关节加速度曲线如图3(b)所示, 曲线同样平滑连续, 各关节在启动、停止位置处加速度均为0 (° )/s2, 避免了挖掘机器人在启停位置处对关节的刚性冲击, 各关节加速度均在[-6 4] (° )/s2范围内, 变化区间较小。关节加加速度曲线如图3(c)所示, 加加速度曲线平滑连续, 在工作区间内, 加加速度均在[-5 12] (° )/s3范围内, 有效地减少了工作过程中挖掘机器人系统的冲击和振动。从图3可以看出:规划出的挖掘机器人各关节速度、加速度、加加速度曲线平滑连续, 均满足设定的物理约束, 变化幅度较小, 因而规划得到了明显优于约束数据且性能良好的轨迹曲线。
| 表3 时间最优轨迹控制顶点角度值 Table 3 Time-optimal trajectory control points |
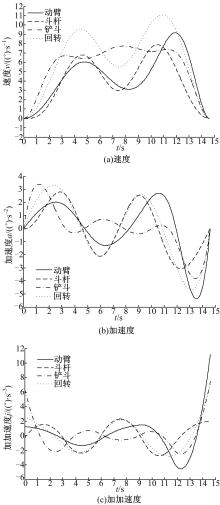 | 图3 挖掘机器人时间最优轨迹速度、加速度和加加速度曲线Fig.3 Time-optimal trajectory velocity, acceleration and jerk curves of robotic excavator |
在进行挖掘机器人时间最优轨迹规划的基础上, 通过基于NURBS的局部轨迹规划实现挖掘过程中对铲斗位姿的调整, 以满足特定工况条件下的具体工作要求。在图1所示的挖掘机器人上进行挖掘作业过程中的避障试验, 研究基于NURBS曲线的挖掘轨迹局部优化。在进行挖掘轨迹时间最优规划的基础上, 挖掘机器人进行沟槽挖掘, 指定铲斗斗齿尖轨迹曲线的7个控制顶点坐标为Di=[50 0; 150 -350; 400 -400; 600 -400; 800 -400; 1050 -350; 1150 0](i=1, 2, …, 7。下同), 5次NURBS轨迹曲线的节点为U=[0 0 0 0 0 0 0.2 0.4 0.6 0.8 1 1 1 1 1 1 ]。当设定各控制顶点权因子为ω i=[1 4 3 1 3 4 1]时, 铲斗末端轨迹曲线如图4所示, 挖掘轨迹经过设定的障碍区域。此时, 可以通过调整距离障碍最近的控制顶点D1的权因子ω 1来调整铲斗位姿, 进而改变铲斗斗齿尖轨迹和挖掘路径, 其他控制顶点的权因子不变, 当ω 1=3, 2, 1时, 挖掘机器人铲斗末端轨迹曲线变化如图5所示。可见, 随着ω 1的减小, 如图中箭头所示, 轨迹曲线上的点朝着背离控制顶点D1的方向运动, 当ω 1=1, 即ω i=[1 4 3 1 3 4 1]时, 挖掘轨迹完全离开障碍区域, 挖掘机器人成功避障。这样, 由于5次NURBS曲线同时具有局部修改性和C4连续性, 通过调整权因子可以改变挖掘机器人的局部挖掘轨迹, 并且轨迹曲线可以保持良好的平滑性和连续性, 使挖掘机器人在一些典型的挖掘过程中能够根据实际工作情况修正预期的挖掘轨迹, 保证了挖掘机器人的工作效率。
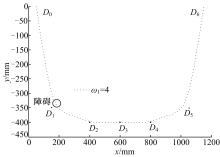 | 图4 ω i=[1 4 3 1 3 4 1]时挖掘机器人铲斗末端轨迹曲线Fig.4 Robotic excavator bucket end trajectory curvewith ω i=[1 4 3 1 3 4 1] |
基于挖掘机器人的物理基础和工作特征, 提出了一种基于NURBS曲线的挖掘机器人轨迹规划方法。分析了该轨迹规划方法的理论基础和用于挖掘机器人轨迹规划的优势, 采用5次NURBS曲线插值关节位置, 可以保证速度、加速度与加加速度在关节空间的连续。可设定关节启动和停止的速度与加速度对运动轨迹进行优化, 以实现对机器人工作系统振动和冲击的有效控制。充分利用了NURBS曲线的局部修改性, 采用序列二次规划方法求解物理约束下的时间最优轨迹规划问题, 得到时间最优、加加速度连续的轨迹曲线, 能够获得满足物理约束的理想轨迹, 使得挖掘机器人关节可以平稳且较快地经过规定空间位置, 可进行局部挖掘轨迹优化满足具体工况要求, 也验证了此轨迹规划方法的有效性。该轨迹规划方法对工程机械自动化和工业机器人技术有很好的参考和使用价值。
The authors have declared that no competing interests exist.
| [1] |
|
| [2] |
|
| [3] |
|
| [4] |
|
| [5] |
|
| [6] |
|
| [7] |
|
| [8] |
|
| [9] |
|
| [10] |
|
| [11] |
|
| [12] |
|