基于路面识别的汽车驱动力模糊滑模控制

引用本文

赵健, 张进, 朱冰. 基于路面识别的汽车驱动力模糊滑模控制. 2015, 45(4): 1036-1042
ZHAO Jian, ZHANG Jin, ZHU Bing. Fuzzy sliding mode traction control based on road friction coefficient estimation. Journal of Jilin University Engineering and Technology Edition, 2015, 45(4): 1036-1042 复制到剪切板

Permissions

基于路面识别的汽车驱动力模糊滑模控制

赵健¹, 张进¹, 朱冰^1,²

1.吉林大学汽车仿真与控制国家重点实验室, 长春 130022

2.吉林大学工程仿生教育部重点实验室, 长春 130022

朱冰(1982-),男,副教授,博士.研究方向:汽车地面系统分析与控制,工程仿生学.E-mail:zhubing@jlu.edu.cn

作者简介:赵健(1978-),男,副教授,博士.研究方向:汽车地面系统分析与控制.E-mail:zhaojian@jlu.edu.cn

基金:国家自然科学基金项目(51105169, 51175215, 51205156); 吉林省科技发展计划项目(20140204010GX)

摘要

为适应路面附着条件的变化对车辆驱动力控制系统的要求,设计了基于纵滑侧偏组合刷子轮胎模型的路面识别算法,采用卡尔曼滤波方式估算轮胎与路面间的附着力,应用最小二乘法估算路面附着系数,进而确定当前路面对应的最佳车轮滑转率;在此基础上,设计了基于路面自适应的驱动力模糊滑模控制算法,并在Matlab/Simulink与CarSim联合仿真环境下进行了仿真验证。结果表明,本文算法能快速准确地识别路面变化,并根据路面附着情况有效调节车轮滑转率,改善车辆驱动性能。

关键词: 车辆工程; 路面附着系数估算; 驱动力控制; 卡尔曼滤波; 最小二乘法; 模糊滑模控制

中图分类号:U461.2 文献标志码:A 文章编号:1671-5497(2015)04-1036-07

Fuzzy sliding mode traction control based on road friction coefficient estimation

ZHAO Jian¹, ZHANG Jin¹, ZHU Bing^1,²

1.State Key Laboratory of Automotive Simulation and Control, Jilin University, Changchun 130022, China

2.Key Laboratory of Bionic Engineering of Ministry of Education, Jilin University, Changchun 130022, China

Abstract

In order to meet the requirements of variable road conditions for vehicle traction control system, a road identification algorithm was proposed based on combined longitudinal and lateral brushed tire model. First, the tire-road forces were estimated by the Kalman filtering method; the road friction coefficient on each wheel was estimated using least square method, and its optimal slip ratio was obtained subsequently. Then, a fuzzy sliding mode based on traction controller was designed using the identified road information. Finally, the algorithm was verified using Matlab/Simulink and CarSim co-simulation. Results show that the proposed algorithm can identify the variation of road conditions and regulate the slip ratios of the driving wheels quickly and accurately, thus, the vehicle driving pe4rformance can be effectively improved.

Keyword: vehicle engineering; road friction coefficient estimation; traction control; Kalman filtering; least square method; fuzzy sliding mode control

Show Figures

0 引言

汽车驱动力控制系统在汽车起步、加速、爬坡过程中, 通过控制车轮滑转状态, 使车辆驱动轮在恶劣路面或复杂行驶条件下也能产生最佳的纵向驱动力, 并保证一定的转向能力^[1]。目前国内外学者对于驱动力控制系统研究已进行了大量的工作, 例如, 赵健等^[2]针对四轮驱动汽车, 应用模糊理论设计了牵引力控制系统的油门控制器和制动控制器。张晓兵等^[3]提出面向牵引力控制的自动变速器档位干预策略。

这些算法大都采用固定车轮最佳滑转率进行控制, 忽略了路面变化对控制系统的影响。而实际上, 车辆行驶路况复杂, 不但路面附着系数多变, 不同附着系数路面对应的最佳车轮滑转率也有很大差别。因此, 对路面条件的精确识别是保证驱动力控制精度和品质的关键。

对于路面识别算法, 国内外进行了大量的研究。李亮等^[4]提出了一种综合路面附着识别方法, 并引入了置信度的概念, 运用模糊逻辑算法实现了附着状态的判断。Takuro等^[5]提出了在转弯工况下利用回正力矩及卡尔曼滤波来估算前轮所在路面的附着系数的方法。Edoardo等^[6]介绍了倍耐力电子轮胎, 电子轮胎拥有内嵌的传感器和数字计算能力, 能实时地提供地面与轮胎的接触力、摩擦因数和附着系数的最大值。么鸣涛等^[7]提出了基于车辆振动加速度响应的路面识别方法, 通过路面不平度的特征信息将路面进行分类。Choi等^[8]提出了用线性递归最小二乘法来实时获取轮胎路面附着系数的方法。

虽然目前的路面附着系数估算方法很多, 但大部分都是面向车辆稳定性控制的, 而驱动力控制大多数采用固定的最佳滑转率控制, 难以在各种路面条件下均获得最佳的驱动性能。本文采用卡尔曼滤波和最小二乘法相结合的方式对路面附着系数进行估算, 自适应调节最佳车轮滑转率, 以此为基础, 设计模糊滑模控制器, 对汽车驱动力进行控制, 使之在不同的路面附着系数条件下, 都能获得最佳的驱动性能。

1 基于卡尔曼滤波的轮胎力估算

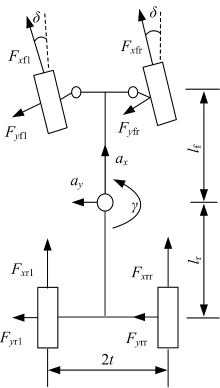
忽略空气阻力, 并将滚动阻力线性化, 汽车的受力分析如图1所示, 车轮的受力分析如图2所示。

	Figure Option View Download New Window
	图1 车辆受力分析图Fig.1 Force analysis in vehicle

	Figure Option View Download New Window
	图2 车轮受力分析图Fig.2 Force analysis in single wheel

车辆的力和力矩平衡方程为:

$\begin{matrix} \begin{matrix} m a_{x} = H_{x} \cdot F (1) \\ m a_{y} = H_{y} \cdot F (2) \\ I_{z} \cdot \overset{\cdot}{γ} = H_{γ} \cdot F (3) \end{matrix} \end{matrix}$

式中:F= $\begin{matrix} {[\begin{matrix} F_{xfl} & F_{xfr} & F_{xrl} & F_{xrr} & F_{yf} & F_{yr} \end{matrix}]}^{T} \end{matrix}$

$\begin{matrix} \{\begin{matrix} F_{yf} = F_{yfl} + F_{yfr} \\ F_{yr} = F_{yrl} + F_{yrr} \end{matrix} \end{matrix}$

H_x= $\begin{matrix} [\begin{matrix} cosδ & cosδ & 1 & 1 & - sinδ & 0 \end{matrix}] \end{matrix}$

H_y= $\begin{matrix} [\begin{matrix} sinδ & sinδ & 0 & 0 & cosδ & 1 \end{matrix}] \end{matrix}$

$\begin{matrix} \begin{matrix} H_{γ} = [\begin{matrix} l_{f} \cdot sinδ - t \cdot cosδ & l_{f} \cdot sinδ + t \cdot cosδ \end{matrix} \\ \begin{matrix} - t & t & l_{f} cosδ & - l_{r} \end{matrix}] \end{matrix} \end{matrix}$

式中:F_xi为车轮纵向力(i=fl, fr, rl, rr分别对应左前、右前、左后、右后轮, 下同); F_yi为车轮侧向力; F_y_f为前轴侧向力; F_y_r为后轴侧向力; δ 为前轮转角; m为整车质量; a_x为车辆纵向加速度; a_y为车辆侧向加速度; I_z为车辆横摆转动惯量; γ 为车辆横摆角速度; l_f为车辆质心到前轴距离; l_r为车辆质心到后轴距离; 2t为车辆轮距。

车轮力矩方程为:

$\begin{matrix} I_{w} \cdot {\overset{\cdot}{ω}}_{i} = T_{di} - T_{bi} - r \cdot F_{xi} - f_{ri} \cdot F_{zi} \cdot r (4) \end{matrix}$

式中:I_w为车轮转动惯量; ω _i为车轮轮速; T_d_i为车轮驱动力矩; T_b_i为车轮制动力矩; F_zi为车轮法向力; f_r_i为滚动阻力系数; r为车轮有效滚动半径; G为车轮法向载荷; F_p为车轴作用于车轮的水平力; T_f为滚动阻力矩。

根据式(1)~(4), 建立状态空间方程:

$\begin{matrix} \begin{matrix} \overset{\cdot}{x} (t) = A (t) x (t) + B (t) + w (t) \\ z (t) = H (t) x (t) + v (t) (5) \\ A (t) = [\begin{matrix} 0_{6 \times 6} & 0_{6 \times 5} \\ \begin{matrix} - \frac{r}{I_{w}} I_{4 \times 4} & 0_{4 \times 2} \end{matrix} & 0_{4 \times 5} \\ H_{γ} / I_{z} & 0_{1 \times 5} \end{matrix}] (6) \\ B (t) = [\begin{matrix} 0_{6 \times 1} \\ \frac{T_{dfl} - T_{bfl} - f_{rfl} \cdot F_{zfl} \cdot r}{I_{w}} \\ \frac{T_{dfr} - T_{bfr} - f_{rfr} \cdot F_{zfr} \cdot r}{I_{w}} \\ \frac{- T_{brl} - f_{rrl} \cdot F_{zrl} \cdot r}{I_{w}} \\ \frac{- T_{brr} - f_{rrr} \cdot F_{zrr} \cdot r}{I_{w}} \\ 0 \end{matrix}] (7) \\ H (t) = [\begin{matrix} H_{x} / m & 0_{1 \times 5} \\ H_{y} / m & 0_{1 \times 5} \\ 0_{5 \times 6} & I_{5 \times 5} \end{matrix}] (8) \end{matrix} \end{matrix}$

式中:11维系统状态向量x(t)=[F_x_fl, F_x_fr, F_x_rl, F_x_rr, F_y_f, F_y_r, ω _fl, ω _fr, ω _rl, ω _rr, γ ]^T; 7维测量矩阵z(t)=[a_x, a_y, ω _fl, ω _fr, ω _rl, ω _rr, γ ]^T; 系统过程噪声w(t)是11维零均值白噪声向量; 测量噪声v(t)为7维零均值白噪声向量, 且w(t)和v(t)互不相关。

采用零阶保持的方法, 将车辆连续系统状态空间方程进行离散化, 得到相应的离散系统的状态空间方程如下:

$\begin{matrix} \{\begin{matrix} x_{k + 1} = A_{k} x_{k} + B_{k} + w_{k} \\ z_{k} = H_{k} x_{k} + v_{k} \end{matrix} (9) \end{matrix}$

进行离散卡尔曼滤波的系统估计过程如下:

状态一步预测:

$\begin{matrix} {\hat{x}}_{k | k - 1} = A_{k | k - 1} {\hat{x}}_{k - 1} + B_{k | k - 1} (10) \end{matrix}$

状态估计:

$\begin{matrix} {\hat{x}}_{k} = {\hat{x}}_{k | k - 1} + K_{k} (z_{k} - H_{k} {\hat{x}}_{k | k - 1}) (11) \end{matrix}$

滤波增益矩阵:

$\begin{matrix} K_{k} = P_{k | k - 1} {H^{T}}_{k} / (H_{k} P_{k | k - 1} {H_{k}}^{T} + V) (12) \end{matrix}$

一步预测误差方差阵:

$\begin{matrix} P_{k | k - 1} = A_{k | k - 1} \cdot P_{k - 1} \cdot {A^{T}}_{k | k - 1} + W (13) \end{matrix}$

估计误差方差阵:

$\begin{matrix} P_{k} = (I - K_{k} H_{k}) P_{k | k - 1} (14) \end{matrix}$

式中:矩阵W和V分别为过程噪声和测量噪声的协方差矩阵。只要给定初值 $\begin{matrix} {\hat{x}}_{0} \end{matrix}$ 和P₀, 根据k时刻的测量值z_k, 就可以递推计算出k时刻的状态估计 $\begin{matrix} {\hat{x}}_{k} \end{matrix}$ , 得到相应车轮轮胎力的估计值。

2 路面附着系数估算

2.1 纵滑侧偏组合刷子轮胎模型

由于刷子模型的求解参数少于魔术公式等模型, 且能比较准确地描述如摩擦椭圆影响和饱和轮胎力等轮胎的非线性特征^{[9, 10]}, 本文采用纵滑侧偏组合刷子轮胎模型进行路面附着系数识别。

纵滑侧偏组合刷子轮胎模型的计算公式如下:

$\begin{matrix} \begin{matrix} F_{x} = \frac{C_{x} (\frac{κ}{1 + κ})}{f} \cdot F_{t} (15) \\ F_{y} = - \frac{C_{α} (\frac{tanα}{1 + κ})}{f} \cdot F_{t} (16) \\ 其中 : \\ F_{t} = \{\begin{matrix} f - \frac{1}{3 μ F_{z}} f^{2} + \frac{1}{27 μ^{2} F_{z}^{2}} f^{3}, & f \leq 3 μ F_{z} \\ μ F_{z}, & 其他 \end{matrix} \\ f = \sqrt[]{C_{x}^{2} {(\frac{κ}{1 + κ})}^{2} + C_{α}^{2} {(\frac{tanα}{1 + κ})}^{2}} \\ κ = (ωr - v_{w}) / v_{w} \end{matrix} \end{matrix}$

式中:C_x为轮胎纵滑刚度; C_α为轮胎侧偏刚度; μ 为路面附着系数; α 为轮胎侧偏角; κ 为实际纵向滑转率; v_w为轮心处的纵向速度。

刷子轮胎模型需要辨识的参数包括C_x、C_α和μ , 根据文献[8]可知, C_x、C_α与很多因素有关, 如轮胎尺寸、胎面宽度、胎面刚度、充气压力、负载等, 在短时间内变化很小, 可以近似看作趋近于定值, 而路面附着系数μ , 可以采用最小二乘法进行估算。

2.2 基于最小二乘法的路面附着系数估算

最小二乘估计使所有偏差的平方和达到最小, 可以有效抑制测量误差^[11]。

首先将刷子轮胎模型写成如下非线性形式:

$\begin{matrix} y (k) = f (k, θ) + v_{l} (17) \end{matrix}$

式中:y是测量值, 这里采用由卡尔曼滤波得到的轮胎力的数值, 即y=[F_x, F_y]^T; f(k, θ )为刷子轮胎模型的表达式, 其中, θ 是刷子轮胎模型参数, θ =[μ ]; v_l是相应的测量噪声。

为满足最小二乘法的需要, 将式(17)线性化, y(k)可以近似地写成:

$\begin{matrix} \begin{matrix} y (k) \approx F (k) (\hat{θ} (k) - \hat{θ} (k - 1)) + \\ f (k, \hat{θ} (k - 1)) (18) \end{matrix} \end{matrix}$

式中:F $\begin{matrix} (k) \end{matrix}$ = $\begin{matrix} \frac{\partial f (k, θ)}{\partial θ} \end{matrix} \begin{matrix} |_{θ = \hat{θ} (k - 1)} \end{matrix}$ 。

定义变量h(k):

$\begin{matrix} \begin{matrix} h (k) = y (k) + F (k) (\hat{θ} (k - 1)) - \\ f (k, \hat{θ} (k - 1)) (19) \end{matrix} \end{matrix}$

将y(k)的表达式带入上式, 得到:

$\begin{matrix} h (k) \approx F (k) \hat{θ} (k) (20) \end{matrix}$

将非线性的刷子轮胎模型进行线性化处理后, 即可以采用最小二乘法估算方法来进行路面附着系数估算。一般说来, 基于刷子模型的路面附着系数估算算法需要轮胎存在一定的滑转率才能获得较精确的测量结果, 而在低滑转工况下, 估算结果会有一些抖动, 为了避免因此而产生错误的估算结果, 本文算法只在滑转率大于5%时进行估算值的更新, 滑转率小于5%时, 则保持上一个时刻的估算值不变。

2.3 不同路面的最佳车轮滑转率

根据文献[10], 在驱动工况下, 轮胎的理论纵向滑转率s与实际纵向滑移率κ 存在如下关系:

$\begin{matrix} s = \frac{κ}{1 + κ} (21) \end{matrix}$

轮胎与路面间的附着系数随车轮滑转率变化, 由文献[12, 13]可知, 一般情况下, 峰值路面附着系数对应的最佳车轮滑转率在0.2左右, 而附着系数较高的路面对应的最佳车轮滑转率也较大。因此可以根据估算得到的路面附着系数通过查表的方式获得车轮的最佳滑转率s₀, 最佳滑转率与路面附着系数的关系如下:μ ≥ 0.4时, s₀=0.25; μ ≤ 0.1时, s₀=0.15; 0.1< μ < 0.4时, s₀=0.2。

3 汽车驱动力的模糊滑模控制

选取实际滑转率与最佳车轮滑转率的差值e及其导数作为状态变量:

$\begin{matrix} \{\begin{matrix} e = s - s_{0} \\ \overset{\cdot}{e} = \overset{\cdot}{s} \end{matrix} (22) \end{matrix}$

其切换函数δ _slide为:

$\begin{matrix} δ_{slide} = ce + \overset{\cdot}{e} = \overset{\cdot}{s} + c [s - s_{0}] (23) \end{matrix}$

式中:c为滑模面系数。

考虑到控制的快速性和平顺性的要求, 采用连续函数和模糊调节结合的方式对轮胎的滑转率进行滑模变结构控制, 取:

$\begin{matrix} {\overset{\cdot}{δ}}_{slide} = c \overset{\cdot}{e} + \overset{\cdot \cdot}{e} = - ε \cdot \tanh (δ_{slide} / Ω) (24) \end{matrix}$

式中:Ω 为滑模边界值, Ω > 0; ε 为趋近速率, ε > 0。

$\begin{matrix} \begin{matrix} 则有 : \\ δ_{slide} \cdot {\overset{\cdot}{δ}}_{slide} < 0 (25) \end{matrix} \end{matrix}$

满足滑模变结构控制的全局达到条件, 则滑动模态存在, 控制方法可行。

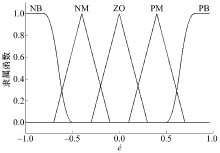
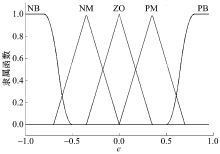
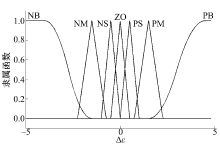
为了减少抖振, ε 采用模糊调节的方式取值。模糊调节的输入为e和 $\begin{matrix} \overset{\cdot}{e} \end{matrix}$ , 输出为Δ ε , 系统输入输出的模糊集分别定义为e={NB, NM, ZO, PM, PB}; $\begin{matrix} \overset{\cdot}{e} \end{matrix}$ ={NB, NM, ZO, PM, PB}; Δ ε ={NB, NM, NS, ZO, PS, PM, PB}。其中, NB为负大, NM为负中, NS为负小, ZO为零, PS为正小, PM为正中, PB为正大。其输入输出隶属函数如图3~图5所示。模糊规则设计如表1所示。

	Figure Option View Download New Window
	图3 输入 $\begin{matrix} \overset{\cdot}{e} \end{matrix}$ 的隶属函数Fig.3 Membership function of input $\begin{matrix} \overset{\cdot}{e} \end{matrix}$

	Figure Option View Download New Window
	图4 输入e的隶属函数Fig.4 Membership function of input e

	Figure Option View Download New Window
	图5 输出Δ ε 的隶属函数Fig.5 Membership function of output Δ ε

表1 模糊规则 Table 1 Fuzzy control rules

求式(21)的一阶和二阶导数, 将 $\begin{matrix} \overset{\cdot}{s} \end{matrix}$ 和 $\begin{matrix} \overset{\cdot \cdot}{s} \end{matrix}$ 代入式(24), 并略去高阶项, 可得:

$\begin{matrix} \overset{\cdot \cdot}{ω} = - c \overset{\cdot}{ω} + \frac{ωr}{v} [c \frac{\overset{\cdot}{v}}{r} + 2 \overset{\cdot}{s} \overset{\cdot}{ω} - ωε \cdot \tanh (δ_{slide} / Ω)] (26) \end{matrix}$

对式(4)两边求导, 得:

$\begin{matrix} {\overset{\cdot}{T}}_{b} = {\overset{\cdot}{T}}_{d} - ({\overset{\cdot}{F}}_{x} \cdot r + I_{w} \overset{\cdot \cdot}{ω}) (27) \end{matrix}$

假设车轮驱动力矩已知, 将式(26)代入上式, 即可得到所需的驱动轮制动力矩变化率 $\begin{matrix} {\overset{\cdot}{T}}_{b} \end{matrix}$ 。

4 仿真分析

在Matlab/Simulink和CarSim环境下建立联合仿真平台, 选择普通前驱D级轿车进行仿真, 对路面附着系数的估算结果和驱动力控制的效果进行分析验证。

仿真在附着系数为阶跃变化的路面上进行, 路面附着系数变化情况如下:行驶路程l=0~10 m时, μ =0.5; l=10~25时, μ =0.1; l=25~50时, μ =0.3。路面总长度为50 m, 初始车速为1 km/h, 油门开度在0.1 s内由0上升到100%, 仿真结果如图6~图11所示。

	Figure Option View Download New Window
	图6 轮胎纵向力估算对比图Fig.6 Curves of wheel longitudinal force

	Figure Option View Download New Window
	图7 路面附着系数估算对比图Fig.7 Curves of road friction coefficient

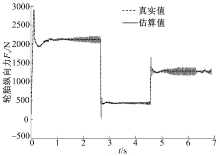
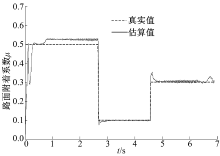
基于卡尔曼滤波算法得到的轮胎力估算值是路面附着系数估算算法的输入量, 因此路面附着系数估算的误差与轮胎力估算的误差有同样的变化趋势, 轮胎纵向力的估算精度越高, 路面附着系数的估算精度也越高。图6为实际的轮胎纵向力与估算的轮胎纵向力对比图, 由图可见, 估算的轮胎纵向力在真实值附近波动, 除路面跃变时有较大的瞬时估算误差外, 其余时刻的估算误差均在10%以下, 算法具有较高的估算精度。图7为实际路面附着系数与估算路面附着系数对比图, 由图可见, 采用本文算法, 在估算的最初阶段, 路面附着系数有一定偏差, 但估算值约在0.3 s内即趋于稳定, 而在路面发生跃变时, 估算值与实际值的最大瞬态偏差只有15%。在路面附着系数为0.5时, 估算结果与实际值之间约有6%的稳态误差, 这是由用于估算的刷子模型和CarSim中的轮胎模型的偏差造成的, 而在附着系数较低时, 估算值与真实值之间几乎没有稳态误差。可见算法可以快速适应路面条件的变化, 实现对轮胎力和路面附着系数的渐近无偏估计。

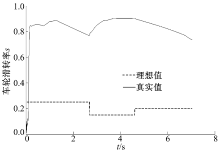
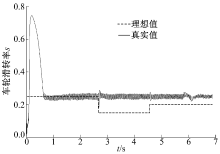
图8~图10分别为无驱动力控制、基于固定目标滑转率的普通滑模驱动力控制和基于本文设计的路面自适应模糊滑模驱动力控制条件下, 单侧驱动轮滑转率的变化曲线, 由于车辆在均一附着系数路面上行驶, 另一侧驱动轮滑转率曲线与图示曲线基本一致。由图8~图10可见, 无驱动力控制情况下, 驱动车轮迅速发生打滑, 严重影响车辆的起步性能, 而基于固定目标滑转率和固定滑动趋近率的滑模驱动力控制虽然可以较为有效地控制驱动轮的过度滑转, 但并不能将滑转率控制在最佳值, 且轮速存在较大抖动; 基于路面自适应识别的模糊滑模驱动力控制则可以快速有效地响应路面条件的变化, 平滑地将车轮滑转率控制在最佳值附近, 从而得到更佳的控制效果。本文设计的驱动力控制算法能将滑转率稳定控制在目标值附近(一般> 10%), 高于2.2小节中设置的更新估算值的滑转率门限(5%), 因此本文估算算法可以满足本文的驱动力控制算法的需求。

	Figure Option View Download New Window
	图8 无驱动力控制的车轮滑转率Fig.8 Slip ratio of wheel without traction control

	Figure Option View Download New Window
	图9 普通滑模驱动力控制的车轮滑转率Fig.9 Slip ratio of wheel with normal sliding mode traction control

	Figure Option View Download New Window
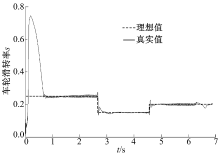	图10 基于路面识别的模糊滑模驱动力控制车轮滑转率Fig.10 Slip ratio of wheel with fuzzy sliding mode traction control based on road identification

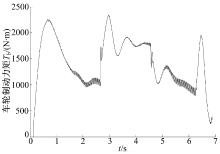
图11为本文设计的控制算法的车轮制动力矩曲线, 由图可见, 车轮制动力矩最大值达到了2350 N· m, 在轮速趋于稳定后, 制动力矩略有波动, 对照图10, 说明本文算法控制效果良好。

	Figure Option View Download New Window
	图11 基于路面识别的模糊滑模驱动力控制车轮制动力矩Fig.11 Braking torque of wheel with fuzzy sliding mod traction control based on road identification

5 结束语

建立了离散车辆观测模型, 采用卡尔曼滤波方法进行了轮胎力的估算, 据此基于纵滑侧偏组合刷子轮胎模型, 采用最小二乘法估算得到了路面附着系数, 仿真结果表明, 这一算法可以快速准确地识别路面附着系数的跃变, 实现对路面附着系数的渐近无偏估计。车辆在低附着系数路面上全力加速时, 车轮会发生明显打滑, 而本文所设计的驱动力控制算法可以快速适应路面附着条件的变化, 将驱动轮滑转率始终控制在最佳值附近, 有效提高了车辆驱动性能。同时, 采用模糊规则调节滑模控制趋近速率, 可以减少车轮波动, 提升控制品质。

The authors have declared that no competing interests exist.

参考文献

View Option

[1]	喻凡, 林逸. 汽车系统动力学[M]. 北京: 机械工业出版社, 2012: 120-122. [本文引用:1]
[2]	赵健, 李静, 李幼德, 等. 模糊控制在四轮牵引力控制系统中的应用[J]. 吉林大学学报: 工学版, 2005, 35(2): 111-115. Zhao Jian, Li Jing, Li You-de, et al. Applications of fuzzy control on four-wheel traction control system[J]. Journal of Jilin University(Engineering and Technology Edition), 2005, 35(2): 111-115. [本文引用:1]
[3]	张晓兵, 李宏刚, 荣睿, 等. 换档干预的牵引力控制系统硬件在环试验[J]. 吉林大学学报: 工学版, 2008, 38(5): 1006-1009. Zhang Xiao-bing, Li Hong-gang, Rong Rui, et al. Hardware-in-the-loop simulation of traction control system based on gear-shift intervention in automatic mechanical transmission[J]. Journal of Jilin University(Engineering and Technology Edition), 2008, 38(5): 1006-1009. [本文引用:1]
[4]	李亮, 冉旭, 李红志, 等. 用于汽车牵引力控制的复杂路面轮胎-道路附着状态判断[J]. 机械工程学报, 2012, 48(10): 109-114. Li Liang, Ran Xu, Li Hong-zhi, et al. Identification of tire-road adhesion state on complicated road surface for traction control system[J]. Journal of Mechanical Engineering, 2012, 48(10): 109-114. [本文引用:1]
[5]	Takuro Matsuda, Shin-ichiro Jo, Hikaru Nishira, et al. Instantaneous estimation of road friction based on front tire sat using Kalman filter[J]. SAE International Journal of Passenger Cars - Mechanical Systems, 2013, 6(1): 147-153. [本文引用:1]
[6]	Sabbioni E, Kakalis L, Cheli F. On the impact of the maximum available tire-road friction coefficient awareness in a brake-based torque vectoring system[C]∥SAE Paper, 2010-01-0116. [本文引用:1]
[7]	么鸣涛, 管继富, 顾亮. 基于车辆振动加速度响应的路面识别研究[J]. 拖拉机与农用运输车, 2011, 38(1): 28-31. Yao Ming-tao, Guan Ji-fu, Gu Liang. Research on road identification based on vehicle vibration acceleration response[J]. Tractor and Farm Transporter, 2011, 38(1): 28-31. [本文引用:1]
[8]	Choi M, Oh J J, Choi S B. Linearized recursive least squares methods for real-time identification of tire-road friction coefficient[J]. IEEE Transactions on Vehicular Technology, 2013, 62(7): 2906-2918. [本文引用:1]
[9]	Li Li, Wang Fei-yue, Zhou Qun-zhi. Integrated longitudinal and lateral tire/road friction modeling and monitoring for vehicle motion control[J]. IEEE Transactions on Intelligent Transportation Systems, 2006, 7(1): 1-18. [本文引用:1]
[10]	Pacejka Hans B. Tyre and Vehicle Dynamics[M]. 2nd ed, New York: Elsevier, 2006: 101-117. [本文引用:1]
[11]	赵琳, 王小旭, 李亮, 等. 非线性系统滤波理论[M]. 北京: 国防工业出版社, 2012: 11-13. [本文引用:1]
[12]	Singh K B, Arat M A, Taheri S. Enhancement of collision mitigation braking system performance through real-time estimation of tire-road friction coefficient by means of smart tires[C]∥SAE Paper, 2012-01-2014. [本文引用:1]
[13]	万家庆, 贺汉根, 陈杨, 等. 基于路面附着系数曲线的最佳滑移率计算方法[J]. 汽车科技, 2004(6): 13-16. Wan Jia-qing, He Han-gen, Chen Yang, et al. Best slip ratio calculation method based on road friction coefficient curves[J]. Automobile Science and Technology, 2004(6): 13-16. [本文引用:1]

2012

0.0

... 0 引言汽车驱动力控制系统在汽车起步、加速、爬坡过程中,通过控制车轮滑转状态,使车辆驱动轮在恶劣路面或复杂行驶条件下也能产生最佳的纵向驱动力,并保证一定的转向能力^[1] ...

2005

0.0

. 2005, 35(2):111-115 DOI:doi:10.3969/j.issn.1671-5497.2005.02.001

Applications of fuzzy control on four-wheel traction control system

模糊控制在四轮牵引力控制系统中的应用

Zhao Jian , Li Jing , Li You-de

赵健, 李静, 李幼德

摘　要：针对四轮驱动汽车，应用模糊理论设计了牵引力控制系统的油门控制器和制动控制器。建立了基于Matlab／Simulink的硬件在环开发平台，并选择分离路面和棋盘路面两种工况进行了硬件在环试验。结果表明，所设计的控制器能有效地消除驱动轮过度滑转，从而提高了车辆的牵引性能，且在路面条件突变时具有较强的适应性。

... 目前国内外学者对于驱动力控制系统研究已进行了大量的工作,例如,赵健等^[2]针对四轮驱动汽车,应用模糊理论设计了牵引力控制系统的油门控制器和制动控制器 ...

2008

0.0

. 2008, 38(5):1006-1009

Hardware-in-the-loop simulation of traction control system based on gear-shift intervention in automatic mechanical transmission

换档干预的牵引力控制系统硬件在环试验

Zhang Xiao-bing , Li Hong-gang , Rong Rui

张晓兵, 李宏刚, 荣睿

在已有牵引力控制系统的基础上，提出面向牵引力控制的自动变速器档位干预策略，搭建了软硬件在环试验平台，进行了典型附着路面台架试验。试验结果表明：基于发动机、变速器和制动联合调节的牵引力控制系统能够有效改善汽车在弱附着地面的加速性能。

... 张晓兵等^[3]提出面向牵引力控制的自动变速器档位干预策略 ...

2012

0.0

... 李亮等^[4]提出了一种综合路面附着识别方法,并引入了置信度的概念,运用模糊逻辑算法实现了附着状态的判断 ...

2013

0.0

... Takuro等^[5]提出了在转弯工况下利用回正力矩及卡尔曼滤波来估算前轮所在路面的附着系数的方法 ...

2010

0.0

... Edoardo等^[6]介绍了倍耐力电子轮胎,电子轮胎拥有内嵌的传感器和数字计算能力,能实时地提供地面与轮胎的接触力、摩擦因数和附着系数的最大值 ...

2011

0.0

. 2011, 38(1):28-31 DOI:doi:10.3969/j.issn.1006-0006.2011.01.008

Research on road identification based on vehicle vibration acceleration response

基于车辆振动加速度响应的路面识别研究

Yao Ming-tao , Guan Ji-fu , Gu Liang.

么鸣涛, 管继富, 顾亮

分别在土路与公路两种路况下, 对试验测试得到的车辆振动加速度响应分别从相关性、频域、时域进行信号分析,并对试验条件下的响应信号功率谱密度按照最大峰值进行归一化处理,进而提出路面识别算法。结果表明:路面识别算法可以在一定程度上对路面的频率结构作定性的判断;车辆振动加速度响应信号体现路面不平度特征的信息;分析结论能为路面识别的研究提供参考。

... 么鸣涛等^[7]提出了基于车辆振动加速度响应的路面识别方法,通过路面不平度的特征信息将路面进行分类 ...

2013

0.0

... Choi等^[8]提出了用线性递归最小二乘法来实时获取轮胎路面附着系数的方法 ...

2006

0.0

... 1 纵滑侧偏组合刷子轮胎模型由于刷子模型的求解参数少于魔术公式等模型,且能比较准确地描述如摩擦椭圆影响和饱和轮胎力等轮胎的非线性特征^[9,10],本文采用纵滑侧偏组合刷子轮胎模型进行路面附着系数识别 ...

2006

0.0

2012

0.0

... 2 基于最小二乘法的路面附着系数估算最小二乘估计使所有偏差的平方和达到最小,可以有效抑制测量误差^[11] ...

2012

0.0