基于分数阶PI λD μ的橡胶坝充排水恒流控制

引用本文

单泽彪, 石要武, 单泽涛, 石屹然, 史红伟. 基于分数阶PI ^λD ^μ的橡胶坝充排水恒流控制 . 2015, 45(4): 1219-1224
SHAN Ze-biao, SHI Yao-wu, SHAN Ze-tao, SHI Yi-ran, SHI Hong-wei. Constant current control of water filling and drainage system for rubber dam using fractional order PI ^λD ^μ . Journal of Jilin University Engineering and Technology Edition, 2015, 45(4): 1219-1224 复制到剪切板

Permissions

基于分数阶PI ^λD ^μ的橡胶坝充排水恒流控制

单泽彪¹, 石要武¹, 单泽涛², 石屹然¹, 史红伟³

1.吉林大学通信工程学院,长春 130022

2.诺博橡胶制品有限公司,河北保定 072550

3.长春理工大学电子信息工程学院,长春 130012

史红伟(1978-),男,讲师,博士.研究方向:测控技术与智能系统.E-mail:qitiand@qq.com

作者简介:单泽彪(1986-),男,博士研究生.研究方向:阵列信号处理,信号检测与自动控制.E-mail:zbshan@126.com

基金:国家自然科学基金项目(51075175); 吉林省科技发展计划项目(20140101078JC)

摘要

针对橡胶坝充排水这一变结构、大滞后、非线性实际控制系统,提出采用能满足系统稳定性和鲁棒性要求的分数阶PI ^λD ^μ控制策略对其进行恒流控制。首先建立了橡胶坝充排水系统的数学模型,从理论上证明了分数阶PI ^λD ^μ控制器对于该系统具有较好的鲁棒特性。然后把该分数阶PI ^λD ^μ控制器数字化后应用于橡胶坝充排水实际系统中,取得了较好的控制效果。最后给出了恒流量充水过程的实际控制运行曲线,表明本文PI ^λD ^μ控制器具有较强的抗干扰性和较好的鲁棒性,达到了恒流量充排水控制的设计目标及要求。

关键词: 自动控制技术; 恒流控制; 分数阶PI λD μ; 橡胶坝充排水; 变结构系统

中图分类号:TP273 文献标志码:A 文章编号:1671-5497(2015)04-1219-06

Constant current control of water filling and drainage system for rubber dam using fractional order PI ^λD ^μ

SHAN Ze-biao¹, SHI Yao-wu¹, SHAN Ze-tao², SHI Yi-ran¹, SHI Hong-wei³

1.College of Communication Engineering, Jilin University ,Changchun 130022, China

2.Nuobo Rubber Production Co, Ltd, Baoding 072550,China

3.School of Electronic and Information Engineering, Changchun University of Science and Technology, Changchun 130012,China

Abstract

Water filling and drainage system is a typical nonlinear, time varying, variable structure system. A fractional order PI ^λD ^μ control scheme for such system is proposed. First, the mathematical model of the water filling and drainage system of a rubber dam is established. It is proved in theory that the fractional order PI ^λD ^μ controller has better robust properties for the system. Then a fractional order PI ^λD ^μ controller is designed for the system in a practical project, which achieves good control effect. Finally, an actual control curve of constant current is given using the fractional order PI ^λD ^μ controller. Practice proves that the proposed control scheme is efficient and the system possesses good static and dynamic performance and certain robustness.

Keyword: automatic control technology; constant current control; fractional order PI λD μ; water filling and drainage system for rubber dam; variable structure system

Show Figures

0 引言

橡胶坝充排水控制系统的恒定流量充排水控制对橡胶坝工程设施具有重要的意义。工业过程控制中流量控制的方式一般都是采用交流变频调速器调节水泵电机的转速, 继而实现输出流量的平滑无级调节。当需要对这类由通用变频器加感应电机构成的变频调速系统进行控制时, 采用常规PID往往难以达到预定的控制效果^{[1, 2]}, 针对这类问题, 杜欣慧等^[1]提出了一种基于参数自调整模糊PID控制的交流闭环变频调速系统的设计方法; 戴先中等^[2]采用了一种神经网络逆控制的方法, 使得这种变频调速系统获得了更加优良的运行性能。然而上述研究都是基于系统结构不发生变化时的情况。

由于运行环境的复杂性和充排水系统结构设计的特点, 橡胶坝充排水系统不仅表现出强非线性和大滞后性, 而且还属于一种变结构、变参数的控制系统。针对此问题, 本文提出采用能满足系统稳定性和鲁棒性要求的分数阶PI^λD^μ对其进行充排水恒流控制。分数阶PI^λD^μ是把传统整数阶PID的阶次推广到分数阶领域, 它不仅仅是比整数阶PID控制器多了两个自由度— — 积分阶次和微分阶次, 使其具有更大的调节范围, 更重要的是它具有比整数阶PID更好的控制品质及更强的鲁棒性^[3]。目前已提出的几种重要的分数阶控制器有TID控制器^[4]、CRONE控制器^[5]、P(ID)^μ控制器^[6]以及PI^λD^μ控制器^[7]等。其中分数阶PI^λD^μ控制器在一定范围内对本身和被控对象的参数变化不敏感, 在稳定性和动态性能方面具有整数阶PID控制器不可比拟的优势。

在分数阶PI^λD^μ控制器应用研究方面, 人们也做了不少的工作, 如文献[8]针对二阶惯性系统的速度控制设计了一个分数阶PI^λD^μ控制器、文献[9]在一般时滞系统方面进行了分数阶鲁棒控制研究、文献[10]针对车辆方向控制进行了分数阶PD^μ控制器的研究。然而, 学者们的研究大多都是针对不同系统模型做的理论仿真研究, 在实际系统中真实运用却鲜见报道。

作者基于松花江壅水坝实际工程项目, 首先把实际系统中的通用变频器及其直接驱动的水泵电机看作一个整体— — 变频调速控流系统, 给出了相应的数学模型, 并从理论上证明了分数阶PI^λD^μ控制器对于该充排水系统具有较好的鲁棒特性; 然后把该分数阶PI^λD^μ控制器数字实现化后应用于充排水实际系统中进行恒流量控制与调节; 最后给出了恒流量充排水的实际控制运行曲线, 结果证明了本文方法的有效性。

1 橡胶坝充排水控制系统

1.1 充排水系统

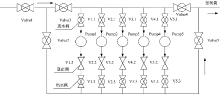
橡胶坝主要由橡胶坝袋、土建工程及充排水系统三部分组成, 其中充排水系统主要由远程监控系统、充排水泵、输水管路、变频器、电气控制装置、水位监测设备、坝袋高度及内压检测装置等组成。根据坝袋高度、坝袋内压以及上下游水位, 通过变频设备对水泵电机的启停/调速控制以及输水管路上的电动阀的开关控制等进行坝袋充排水自动控制, 图1为实际充排水系统结构图。

	Figure Option View Download New Window
	图1 橡胶坝充排水系统结构图Fig.1 System of filling and draining off water of rubber dam

上述充排水系统主要由5台水泵电机及各管路进出水阀门构成, 其中每台水泵电机又由一台变频器进行变频调速控制。充水过程:打开阀门1、阀门3及阀门5, 使之形成相应的充水通路(图1中箭头表示方向), 然后再启动相应数量的水泵进行充水, 各水泵出水先汇至同一管道, 最后通过阀门5后再流至橡胶坝袋方向。排水过程与之正好相反, 即打开阀门1、阀门2与阀门4及相应的进出口阀门, 形成相应排水通路, 然后再启动相应数量的水泵对坝袋进行排水调节。

此充排水系统的主要控制问题就是根据橡胶坝控制运行要求, 在橡胶坝总充排水量允许范围内, 启动相应数量的水泵对坝袋进行充排水, 并在此过程中通过变频器变频调节, 实现橡胶坝袋的总进、出水流量恒定, 即设计一个控制器通过变频器去调节水泵转速, 在因系统设定值改变导致泵启动数量和出水阀门开度的变化或受到其他干扰情况下使坝袋的总进、出水流量在较短的时间内稳定在预先设定的状态, 并满足一定的动态性能和允许的静态误差要求。同时还需满足各运行水泵出口压力均衡, 以防止某出口压力偏小造成其逆止阀关闭的情况发生。

1.2 系统模型的建立

橡胶坝充排水系统中每台水泵电机都由一台通用型变频器进行变频调速控制, 把每台变频器及其驱动的水泵电机看成一个整体, 称之为变频调速控流系统。如果忽略各水泵在整个充排水系统中的位置结构差异, 那么此充排水系统可以看成由5个相对独立且特性相同的变频调速控流子系统构成, 对于每个变频调速控流子系统来说, 给定变频器一个频率信号输入就能得到水泵的一个流量输出。

由充排水系统的特性可知, 水泵由初始状态向管道充排水的恒流状态过渡时, 可分为流量上升过程与恒流过程, 其中流量上升过程, 可近似为一个时间常数T₁比较大的惯性环节; 恒流过程中, 流量可认为基本不变, 是一个纯滞后过程, 则供水系统的模型可表示为:

$\begin{matrix} G_{1} (s) = \frac{K_{1}}{T_{1} s + 1} e^{- τs} (1) \end{matrix}$

式中:K₁为供水系统的增益; τ 为供水系统的时滞常数。

变频器和水泵电机可近似等效为时间常数为T₂的一阶惯性环节^[11], 表示为:

$\begin{matrix} G_{2} (s) = \frac{K_{2}}{T_{2} s + 1} (2) \end{matrix}$

式中:K₂为调速系统的增益。

系统中的其他控制或检查环节, 如继电器控制转换、流量测量转换等环节的惯性时间及延迟时间与供水系统的时间常数相比都可以忽略, 均可等效为比例环节, 故整个变频调速控流子系统的模型可表示为带滞后的两个惯性环节的串联, 如下式表示:

$\begin{matrix} G_{g} (s) = \frac{K}{(T_{1} s + 1) (T_{2} s + 1)} e^{- τs} (3) \end{matrix}$

式中:K为系统的总增益。

1.3 控制系统设计及其结构分析

根据橡胶坝充排水系统实际控制要求, 设计了如下双闭环控制方案, 其中外环采用的是流量反馈控制, 控制器应用分数阶PI^λD^μ控制; 内环采用的是压力反馈控制, 控制器应用PI控制, 由于该系统中含有5个相对独立的变频调速控流子系统, 故设计了5个并级形式的内环控制环节。主回路(外环)用来进行总进、出水流量的控制, 实现恒流量充排水; 副回路(内环)用来进行各水泵出口压力的调节, 保证各出口压力均衡。当总进、出水流量高于或低于给定值时, 流量控制器发出校正信号, 修正水泵控制系统的给定值, 使水泵减少或增加进、出水量, 经过校正过的进、出水量将等于给定值。控制系统框图如图2所示。

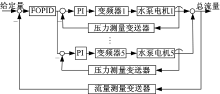	Figure Option View Download New Window
	图2 橡胶坝充排水双闭环控制系统框图Fig.2 Two closed loop control system of filling and draining off water of rubber dam

图2中, 压力PI控制器传递函数为C_p(s)=K_np+K_ni/s, 结合式(3)变频调速控流子系统的传递函数可知整个内环部分的闭环传递函数为:

$\begin{matrix} G (s) = \frac{C_{p} (s) G_{g} (s)}{1 + C_{p} (s) G_{g} (s)} (4) \end{matrix}$

再设分数阶PI^λD^μ控制器的传递函数为C_f $\begin{matrix} (s) \end{matrix}$ , 可得整个充排水系统的开环传递函数为:

$\begin{matrix} \begin{matrix} Φ (s) = C_{f} (s) \overset{N}{\sum_{i = 1}} G_{i} (s) (5) \\ N = 1, 2, \dots, 5 \end{matrix} \end{matrix}$

式中:N为实际水泵启动的数量, 可见, 当N取不同值时, 系统结构是变化的。

2 分数阶PI^λD^μ控制器

2.1 分数阶微积分

一般的分数阶微积分算子可用下式来表达:

$\begin{matrix} _{a}^{} D_{t}^{α} f (t) = \{\begin{matrix} \frac{d^{α}}{d t^{α}} f (t), Re (α) > 0 \\ f (t), Re (α) = 0 \\ \int_{a}^{t} f (τ) {(dτ)}^{- α}, Re (α) < 0 \end{matrix} (6) \end{matrix}$

式中 $\begin{matrix} :_{a}^{} \end{matrix} \begin{matrix} D_{t}^{α} \end{matrix}$ 为微分或积分操作算子; a和t为微积分上下限; α 可以是任意实数或复数。

从不同角度去考察分数阶微积分可以得到不同的定义, 其中最著名的是Riemann-Liouville(RL)定义, 其定义如下:

$\begin{matrix} _{a}^{} D_{t}^{α} f (t) = \frac{1}{Γ (n - α)} {(\frac{d}{dt})}^{n} \int_{a}^{t} \frac{f (τ)}{{(t - τ)}^{α - n + 1}} dτ (7) \end{matrix}$

式中:n-1≤ α ≤ n, n∈ N; Γ (· )为Gamma函数。

Laplace变换不仅适用于整数阶系统, 同样也适用于分数阶系统。根据RL定义, 分数阶微分的Laplace变换为:

$\begin{matrix} L [_{a} D_{t}^{α} f (t)] = s^{α} F (s) - {[_{a} D_{t}^{α - 1} f (t)]}_{t = 0} (8) \end{matrix}$

分数阶积分的Laplace变换为:

$\begin{matrix} L [_{a} D_{t}^{- α} f (t)] = s^{- α} F (s) (9) \end{matrix}$

2.2 分数阶PI^λD^μ控制器及其数字实现

整数阶PID控制器的传递函数描述为:

$\begin{matrix} C (s) = \frac{U (s)}{E (s)} = K_{P} + \frac{K_{I}}{s} + K_{D} s (10) \end{matrix}$

式中:U $\begin{matrix} (s) \end{matrix}$ 为控制器的输出; E $\begin{matrix} (s) \end{matrix}$ 为控制器的误差输入。

把上式中的微分与积分项的阶次推广到实数, 便可以得到分数阶PI^λD^μ控制器的传递函数, 即:

$\begin{matrix} C_{f} (s) = \frac{U (s)}{E (s)} = K_{P} + \frac{K_{I}}{s^{λ}} + K_{D} s^{u}, (λ, u > 0) (11) \end{matrix}$

式中:积分阶次λ 和微分阶次μ 可以是任意正实数, 而且积分项是s^λ, 也就是说在对数相频曲线图中, 它的斜率不再是-20 dB/dec, 而是-20λ dB/dec。式(11)所对应的时间域方程可以表示为:

$\begin{matrix} u (t) = K_{P} e (t) + K_{I} D^{- λ} e (t) + K_{D} D^{μ} e (t) (12) \end{matrix}$

与传统整数阶PID控制器相比, 分数阶PI^λD^μ控制器除了具有K_P、K_I、K_D三个可以用来调整系统性能的参数外, 还增加了一个积分阶次λ 和一个微分阶次μ 两个参数。通过合理的参数选择, 分数阶PI^λD^μ控制器在提高系统灵活性、鲁棒性以及总体控制性能等方面将起到很大的积极作用, 从而取得更好的控制效果。

分数阶控制器是无限阶次, 通过计算机具体实现时需要对微积分算子进行离散化。在此采用Tustin+CFE直接离散化方法^[12]对其进行数字实现, 把分数阶微积分s^α用Tustin算子来表示得到阶次为α 的生成函数为:

D^α $\begin{matrix} (z) \end{matrix}$ = $\begin{matrix} {[ω (z^{- 1})]}^{α} \end{matrix}$ = $\begin{matrix} {[\frac{2 (1 - z^{- 1})}{T (1 + z^{- 1})}]}^{α} \end{matrix}$ (13)

式中:T表示采样时间。

然后用连分式将式(CFE)近似展开, 形式如下:

$\begin{matrix} D^{α} (z) = a_{0} (z) + \frac{b_{1} (z)}{a_{1} (z) + \frac{b_{2} (z)}{a_{2} (z) + \frac{b_{3} (z)}{a_{3} (z) + \dots}}} (14) \end{matrix}$

式中:a_i $\begin{matrix} (z) \end{matrix}$ 和b_i $\begin{matrix} (z) \end{matrix}$ 为常量或z的有理函数。通过恰当的截断可以获得 $\begin{matrix} {[\frac{2 (1 - z^{- 1})}{T (1 + z^{- 1})}]}^{α} \end{matrix}$ 的近似有理函数, 其离散化模型为:

$\begin{matrix} \begin{matrix} D^{α} (z) = \frac{Y (z)}{F (z)} = \\ {(\frac{2}{T})}^{α} CFE {\{{(\frac{1 - z^{- 1}}{1 + z^{- 1}})}^{α}\}}_{p, q} = {(\frac{2}{T})}^{α} \frac{P_{p} (z^{- 1})}{Q_{q} (z^{- 1})} (15) \end{matrix} \end{matrix}$

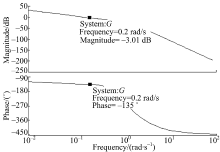
式中:P_p(z^-¹)、Q_q(z^-¹)均为变量z^-¹多项式; CFE $\begin{matrix} (\cdot) \end{matrix}$ 表示进行连分式展开。一般为计算方便取p=q=n, n为数字实现的近似阶次。

2.3 基于分数阶PI^λD^μ的系统鲁棒性分析

使用离散的分数阶PI^λD^μ控制器对前面所述的充排水系统进行鲁棒性分析, 其中变频调速控流子系统参数K=1.25, T₁=35 s, T₂=6 s, τ =65 s是由现场测试数据辨识而来, 并经现场调试整定确定分数阶PI^λD^μ控制器参数为K_P=0.42, K_I=0.002, K_D=10.5, λ =0.81, μ =0.92; 内环压力PI控制器参数K_n_P=0.24, K_n_I=0.05, 用Tustin+CFE直接离散方法, 采样周期T=1 s, 逼近阶次为3, 并取N=2, 即有两台水泵在运行工作状态时, 得到基于分数阶PI^λD^μ控制器的充排水系统开环传递函数Bode图如图3所示。由图3可知, 该控制器对于在有两台水泵工作时的该系统具有较好的频域特性, 即在截止频率ω _c处幅频特性比较平坦, 说明其闭环系统具有较好的鲁棒稳定性, 而且在截止频率ω _c附近其相频特性曲线亦比较平滑且相对平坦, 说明系统具有较好的增益鲁棒性。

	Figure Option View Download New Window
	图3 基于分数阶PI^λD^μ的充排水系统开环传递函数Bode图Fig.3 Bode diagram with fractional order PI^λD^μ controller

3 现场实际控制及运行效果分析

在松花江壅水坝工程项目中进行橡胶坝恒定流量充排水控制实验, 其中数据采集周期T_c=0.5 s, 其他控制器参数如同2.3节所述。该系统中硬件主要有ABB/ACS510-01型号变频器, 研华工业控制计算机, 实现数据传输功能的西门子系列S7-300PLC, 75 kW、Y315L2-10型三相异步电动机, 900ZLB-4型卧式离心泵, 压力及流量传感器等, 软件主要是进行监视及控制功能的WinCC组态软件, 其中分数阶PI^λD^μ控制率是在WinCC全局脚本编辑器中采用ANSI C实现。

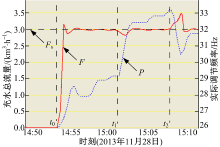
实验1:开启两台水泵, 进行开关阀实验; 实际运行曲线如图4所示。

	Figure Option View Download New Window
	图4 充水过程的实际控制曲线(开关阀实验)Fig.4 Actual control curve of filling water process with open or close values

图4中, F_s表示充水流量设定值, F表示实际充水流量值, P表示实际调节频率值。打开两个坝袋进口阀门, 并在t₀时刻启动1#、2#两台水泵, 从图4中可以看出, 经过一段时间调节, 实际流量稳定在设定值附近并保持基本恒定, 说明设计的控制器具有较好的控制性能; 在t₁时刻, 调整其中一台水泵出口阀门开度至30%, 在t₂时刻, 又重新完全打开该阀门, 可见, 流量稍微有点下调(t₁时刻)和超调(t₂时刻), 随后又很快回复到原设定值状态, 说明设计的控制器具有较强的抗干扰能力。另外从图4中可以看出, 此时控制输出(频率)基本保持不变且略高于最初状态时, 说明随着橡胶坝不断地充水, 坝袋中的压力也在不断变大, 体现出了坝袋充水过程中的非线性。

实验2:开启3台水泵, 进行加减泵实验。实际运行曲线如图5所示。

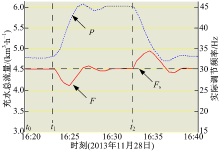	Figure Option View Download New Window
	图5 充水过程的实际控制曲线(加减泵实验)Fig.5 Actual control curve of filling water process with increase or decrease pumps

图5中, 初始运行状态是3台水泵(1#、2#与3#水泵)为三个坝袋进行充水, 即图中t₀~t₁时段, 此时段中流量实际值等于流量设定值4.5 km³/h且保持恒定; 在t₁时刻, 在保持流量设定值不变的情况下, 对其进行减少一泵(如关闭1#泵)实验, 从图5可以看出, 流量曲线经过几次振荡后又达到设定值, 可保持基本稳定, 而此时频率输出在45 Hz处基本保持不变; 在t₂时刻, 重新启动刚才关闭的1#泵, 流量又很快回到了原初始状态, 说明在系统结构发生变化时设计的控制器仍具有较好的控制性能。

从上面实际运行曲线可以看出, 不仅是在初始启泵过程中可以有效控制充水总流量达到橡胶坝恒流充水的目的, 而且在加减泵(系统结构变化)和开关阀(参数变化)情况下仍能有效达到流量调节的目的, 且都具有较好的控制效果。总体说明分数阶PI^λD^μ控制方法具有较好的控制性能和较强的鲁棒性, 采用该控制方法有效解决了该充排水系统中的结构变化、时变性及非线性等问题, 达到了在充水过程中的流量恒定的控制目的。另外经过现场运行试验, 在橡胶坝排水过程中同样可以达到流量恒定控制的设计要求。

4 结束语

针对橡胶坝充排水这一复杂的实际控制系统, 采用具有一定鲁棒特性的分数阶PI^λD^μ控制方法, 在对分数阶PI^λD^μ控制率进行数字实现后, 把其应用于该系统中进行恒定流量充排水控制与调节, 现场实际运行效果表明该分数阶PI^λD^μ控制方法具有较好的抗干扰性和较强的鲁棒性, 取得了良好的控制效果, 达到了恒流量充排水控制的设计目标及要求。

The authors have declared that no competing interests exist.

参考文献

View Option

[1]	杜欣慧, 刘娇, 王孝, 等. 模糊控制与恒压频比控制在水泵调速系统中的实现[J]. 电气技术, 2008, 9(1): 20-23. Du Xin-hun, Liu Jiao, Wang Xiao, et al. The implementation of fuzzy control and constant U/f control to speed-regulating system of pump[J]. Electrical Engineering, 2008, 9(1): 20-23. [本文引用:2]
[2]	戴先中, 刘国海, 张兴华. 恒压频比变频调速系统的神经网络逆控制[J]. 中国电机工程学报, 2005, 25(7): 109-114. Dai Xian-zhong, Liu Guo-hua, Zhang Xing-hua. Neural network inverse control of variable frequency speed-regulating system in V/F mode[J]. Proceedings of the CSEE, 2005, 25(7): 109-114. [本文引用:2]
[3]	吴振宇, 赵亮, 冯林. 基于分数阶PID控制器的智能车控制[J]. 控制工程, 2011, 18(3): 401-404. Wu Zhen-yu, Zhao Liang, Feng Lin. Control of intelligent vehicle based on fractional order PID[J]. Control Engineering of China, 2011, 18(3): 401-404. [本文引用:1]
[4]	Lurie J. Three-parameter tunable tilt-integral-derivative controller[P]. US Patent US5371670, 1994. [本文引用:1]
[5]	Oustaloup A, Melchior P. The great principles of CRONE control[C]∥System Engineering in the Service of Humans, Int Conf on Systems, Man and Cybernetics, Paris: Le Touquet, 1993: 118-129. [本文引用:1]
[6]	汪纪锋, 李元凯. 分数阶P(ID)^μ控制器和分数阶超前校正器的设计[J]. 电路与系统学报, 2006, 11(5): 21-25. Wang Ji-feng, Li Yuan-kai. Design for two types of fractional-order controllers: P(ID)^μ controller and lead-leg compensator[J]. Journal of Circuits and Systems, 2006, 11(5): 21-25. [本文引用:1]
[7]	Podlubny I. Fractional-order systems and PID controllers[J]. IEEE Transactions on Automation Control, 1999, 44(1): 208-214. [本文引用:1]
[8]	王瑞平, 皮佑国. 基于分数阶PD速度控制器的永磁同步电动机控制研究[J]. 中山大学学报: 自然科学版, 2013, 52(3): 34-39. Wang Rui-ping, Pi You-guo. Research on fractional-order PD speed controller for PMSM[J]. Acta Scientiarum Naturalium Universitatis Sunyatseni, 2013, 52(3): 34-39. [本文引用:1]
[9]	梁涛年, 陈建军. 时滞系统分数阶PI^λD^μ鲁棒控制[J]. 振动、测试与诊断, 2011, 31(3): 257-361. Liang Tao-nian, Chen Jian-jun. Fractional order PI^λD^μ robust control for time delay system[J]. Journal of Vibration, Measurement & Diagnosis, 2011, 31(3): 257-361. [本文引用:1]
[10]	庄德军, 喻凡, 林逸. 基于分数阶PI^μ控制器的车辆方向控制[J]. 上海交通大学学报, 2007, 41(2): 278-283. Zhuang De-jun, Yu Fan, Lin Yi. The vehicle directional control based on fractional order PI^μ controller[J]. Journal of Shanghai Jiaotong University, 2007, 41(2): 278-283. [本文引用:1]
[11]	汤跃, 张新鹏, 黄志攀, 等. 离心泵变压供水系统控制模型辨识的试验研究[J]. 农业工程学报, 2012, 26(7): 189-193. Tang Yue, Zhang Xin-peng, Huang Zhi-pan, et al. Experimental study on control model of centrifugal pomp variable-pressure water supply system[J]. Transactions of the Chinese Society of Agricultural Engineering, 2012, 26(7): 189-193. [本文引用:1]
[12]	聂冰, 赵慧敏, 郭永香, 等. 交流电机调速系统的分数阶PI^λ控制[J]. 大连交通大学学报, 2012, 33(2): 84-86. Nie Bing, Zhao Hui-min, Guo Yong-xiang, et al. Application of fractional order controller in speed adjustment system of AC motor[J]. Journal of Dalian Jiaotong University, 2012, 33(2): 84-86. [本文引用:1]

2008

0.0

... 当需要对这类由通用变频器加感应电机构成的变频调速系统进行控制时,采用常规PID往往难以达到预定的控制效果^[1,2],针对这类问题,杜欣慧等^[1]提出了一种基于参数自调整模糊PID控制的交流闭环变频调速系统的设计方法 ...

2005

0.0

... 戴先中等^[2]采用了一种神经网络逆控制的方法,使得这种变频调速系统获得了更加优良的运行性能 ...

2011

0.0

... 积分阶次和微分阶次,使其具有更大的调节范围,更重要的是它具有比整数阶PID更好的控制品质及更强的鲁棒性^[3] ...

0.0

... 目前已提出的几种重要的分数阶控制器有TID控制器^[4]、CRONE控制器^[5]、P(ID)^{#cod#x003bc ...}

1993

0.0

... 目前已提出的几种重要的分数阶控制器有TID控制器^[4]、CRONE控制器^[5]、P(ID)^{#cod#x003bc ...}

2006

0.0

... 控制器^[6]以及PI^{#cod#x003bb ...}

1999

0.0

... 控制器^[7]等 ...

2013

0.0

2011

0.0

2007

0.0

2012

0.0

... 变频器和水泵电机可近似等效为时间常数为T₂的一阶惯性环节^[11],表示为: ...

2012

0.0

... 在此采用Tustin+CFE直接离散化方法^[12]对其进行数字实现,把分数阶微积分s^{#cod#x003b1 ...}