面向制动踏板感觉的主缸动力学模型及其关键影响因素

引用本文

孟德建, 张立军, 方明霞, 余卓平. 面向制动踏板感觉的主缸动力学模型及其关键影响因素. 2015, 45(5): 1388-1394
MENG De-jian, ZHANG Li-jun, FANG Ming-xia, YU Zhuo-ping. Master cylinder dynamic model for brake pedal feeling and its key factors. Journal of Jilin University Engineering and Technology Edition, 2015, 45(5): 1388-1394 复制到剪切板

Permissions

面向制动踏板感觉的主缸动力学模型及其关键影响因素

孟德建^1,^2,³, 张立军^1,², 方明霞⁴, 余卓平^1,²

1.同济大学汽车学院,上海 201804

2.同济大学智能型新能源汽车协同创新中心,上海 201804

3.同济大学力学流动站,上海 200092

4.同济大学,航空航天与力学学院,上海 200092

张立军(1972-),男,教授,博士生导师.研究方向:汽车系统动力学,振动与噪声控制.E-mail:tjedu_zhanglijun@tongji.edu.cn

作者简介:孟德建(1982-),男,助理教授,博士.研究方向:汽车系统动力学,振动与噪声控制.E-mail:mdj0218@163.com

基金:中国博士后科学基金项目(2013M531208); 国家自然科学基金项目(51175380)

摘要

考虑回位弹簧的预紧力、系统摩擦力、阀口间隙以及制动液体积弹性模量的变化,建立了面向制动踏板感觉的制动主缸动力学模型。开展了不同推杆速度下的制动主缸特性试验,进而辨识了模型的关键参数。经过对比与分析发现,试验结果与仿真结果一致性较好。进而分析了影响制动踏板感觉的关键因素,结果表明:活塞内径、回位弹簧预紧力和刚度以及制动液气体含量对面向制动踏板感觉的制动主缸特性具有重要的影响。

关键词: 车辆工程; 制动主缸; 液压制动系统; 制动踏板感觉; 体积弹性模量

中图分类号:U463.5 文献标志码:A 文章编号:1671-5497(2015)05-1388-07

Master cylinder dynamic model for brake pedal feeling and its key factors

MENG De-jian^1,^2,³, ZHANG Li-jun^1,², FANG Ming-xia⁴, YU Zhuo-ping^1,²

1.School of Automotive Engineering,Tongji University,Shanghai 201804,China

2.Collaborative Innovation Center for Intelligent New Energy Vehicle,Tongji University,Shanghai 201804,China

3.Mechanics Post-doctoral Research Station,Tongji University,Shanghai 200092,China

4.School of Aerospace Engineering and Applied Mechanics,Tongji University,Shanghai 200092,China

Abstract

A brake master cylinder dynamic model for brake pedal feeling is proposed, in which the return spring preload, system friction forces, valve port clearance and changes in the brake fluid bulk modulus are considered. Experiments on the characteristics of the brake master cylinder are carried out under the condition of different pushrod speed, and then the key parameters of model are identified. By analysis and comparison, it is found that the test results and the simulation results have a good consistency. Further, the key factors of the brake master cylinder for brake pedal feel are analyzed, and results show that the piston diameter, spring preload and stiffness, and the brake fluid gas content significantly influence the brake pedal feel and master cylinder performance.

Keyword: vehicle engineering; brake master cylinder; hydraulic brake system; brake pedal feel; bulk modulus

Show Figures

0 引言

制动踏板感觉作为驾驶员与汽车之间交互的重要组成, 直接影响到消费者对车辆品质的评价。因此, 现在的汽车制动系统不仅要满足汽车制动安全性, 还需要具有良好的制动踏板感觉。主缸是将机械踏板力转化为制动液压力的关键部件, 在制动系统中起到“ 变压器” 的作用^{[1, 2]}。整车制动踏板感觉经常使用踏板行程与制动油压关系、踏板力与制动油压关系进行评价, 显然体现了主缸对制动踏板感觉的重要作用。因此, 面向制动踏板感觉的主缸建模与关键影响因素分析, 对考虑制动踏板感觉的制动系统正向开发与设计具有重要的意义。

中心阀式串列双腔主缸是现代汽车制动主缸的主要类型, 它主要包括第一活塞、第一活塞回位弹簧、第二活塞、第二活塞回位弹簧、中心阀、皮碗和缸体等结构, 制动液填充在活塞腔内。针对这一包含弹簧机械系统和黏性液体的机构, Khan等^[1]采用键合图的方法建立了机械系统的动力学模型, Gerdes和詹军等^{[2, 3]}则建立了机械系统动力学数学模型。Fisher^[4]考虑活塞回位弹簧的预紧力和系统受到的摩擦力, 利用液体体积弹性模量的定义, 建立了包含机械系统模型和制动液模型的制动主缸动力学数学模型。在此基础之上, Yamada等^[5]利用一维流体连续方程建立了制动液的数学模型, 刘晓^[6]重点考虑了补偿空位置建立了制动液的数学模型, 他们都使用Matlab/Simulink软件对机械系统和制动液数学模型进行了仿真。根据制动主缸的拓扑结构, Fortina和贺平等^{[7, 8]}分别利用AMEsim软件和Modelica/MWorks软件建立了制动主缸动力学模型。Day等^[9]进一步建立了AMEsim和Abaqus联合仿真的制动主缸动力学模型, 重点分析了橡胶皮腕变形对制动主缸特性的影响。方泳龙等^[10]建立了制动主缸行程知识库, 王兴东等^[11]利用分段函数建立了汽液混合型制动主缸动力学模型, 为笔者建立制动主缸动力学模型提供了借鉴。

通过分析发现:①现有的制动主缸模型均是针对制动性能而开发的, 它们往往关注制动速度、制动距离、制动减速度、制动热效能等整车制动性能指标^{[3, 4, 6]}, 或者是制动油压、推杆力和推杆行程的时域特性^{[1, 2, 7, 8, 10, 11]}。而制动踏板感觉往往考察主缸推杆力-行程、主缸油压-行程、主缸油压-推杆力的关系^[9]。②面向制动踏板感觉的制动主缸特性高度依赖于主缸推杆速度, 但是现有研究基本没有考虑推杆速度对制动踏板特性的影响。③现有的制动主缸的动力学模型存在不足。例如, 在建立机械系统模型时, 文献[6]忽略了系统摩擦力, 文献[1-3, 5-6]忽略了回位弹簧的预紧力, 而文献[4]未给出活塞开始工作的判定条件; 在建立制动液模型时, 往往忽略体积弹性模量的变化^{[5, 6]}; 而在使用AMEsim等软件建模时, 没能给出反应系统特性的数学表达式^{[7, 8, 9]}。

为了完成面向制动踏板感觉的制动系统设计与开发, 本文在考虑回位弹簧的预紧力、系统摩擦力、阀口间隙以及制动液体积弹性模量的变化的基础上, 建立了进程阶段面向制动踏板感觉的主缸动力学模型。基于试验辨识了模型的关键参数, 并在不同推杆速度下验证了模型的有效性。以推杆力-行程特性、主缸油压-行程特性和主缸油压-推杆力特性形成的3象限图为评价指标, 分析了影响制动主缸特性的关键因素。

1 试验方案

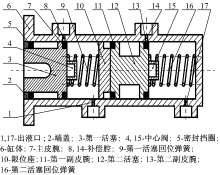
在制动踏板感觉试验台架上, 利用伺服电动缸对制动主缸施加推力, 使用拉压力传感器测量推杆力, 拉杆位移传感器测量推杆位移, 油压传感器测量活塞腔油压, 传感器的布置如图1所示。为了充分辨识回位弹簧刚度和活塞所受摩擦力, 分别在无制动液和有制动液两种情况下开展试验。这两种工况下推杆速度分为5个水平, 分别为4、6、8、10、20 mm/s。在无制动液工况时不测量油压, 有制动液时将出液口堵住。

	Figure Option View Download New Window
	图1 主缸试验传感器布置Fig.1 Sensors layout in master cylinder experiment

2 数学模型与参数辨识

2.1 研究对象与基本假设

中心阀式串列双腔制动主缸的典型结构及其关键零件如图2所示。为了建立制动主缸动力学模型, 作基本假设如下:①只考虑皮腕与缸体之间的摩擦力, 忽略制动液及其流动产生的摩擦力; ②工作过程中制动液温度保持不变且为室温; ③忽略制动液流动在活塞腔内造成的压力损失, 认为同一腔内压力处处相等。

	Figure Option View Download New Window
	图2 主缸结构示意图Fig.2 Structure schematic diagram of master cylinder

2.2 机械系统动力学模型

根据主缸结构和工作原理, 可以将其等效为图3所示的物理模型。主缸的运动过程包含3个阶段, 分别建立各个阶段的动力学方程, 模型中包含的关键零件及其参数说明如下:m_c1、m_c2分别为第一、第二活塞质量; x_c1、x_c2分别为第一、第二活塞位移; F_e为第一活塞推力; k_c1、k_c2分别为第一、第二活塞回位弹簧刚度; c_c1、c_c2分别为第一、第二活塞阻尼; F_m1、F_m2分别为第一、第二活塞回位弹簧预紧力; F_u1、F_u2分别为第一、第二活塞摩擦力; P₁、P₂分别为第一、第二活塞腔油压。

	Figure Option View Download New Window
	图3 主缸物理模型Fig.3 Physical model of master cylinder

第一阶段:主缸推杆力增加, 克服第二活塞回位弹簧预紧力后开始运动, 第二活塞回位弹簧开始被压缩, 直至第一活塞回位弹簧开始被压缩为止。该过程中可将第一活塞、第一活塞回位弹簧和第二活塞看作一个整体。制动主缸的动力学方程为:

$\begin{matrix} \begin{matrix} \{\begin{matrix} x_{c 1} = 0, F_{e} \leq F_{m 2} + F_{u 1} + F_{u 2} \\ (m_{c 1} + m_{c 2}) {\overset{\cdot \cdot}{x}}_{c 1} + c_{c 2} {\overset{\cdot}{x}}_{c 1} + k_{c 2} x_{c 1} = F_{e} - F_{m 2} - \\ F_{u 1} - F_{u 2} - P_{2} s_{c}, \\ F_{m 2} + F_{u 1} + F_{u 2} < F_{e} \leq F_{m 1} \end{matrix} (1) \\ 令 F_{N 1} = c_{c 2} {\overset{\cdot}{x}}_{c 11} + k_{c 2} x_{c 11} + P_{2} s_{c} (2) \end{matrix} \end{matrix}$

式中:x_c11为第一阶段末第一活塞的位移; F_N1为第二阶段第一活塞受到的初始力。

第二阶段:第一活塞回位弹簧开始被压缩, 直至第二活塞回位弹簧被压缩至极限。该过程中前、后活塞以不同的速度共同运动, 第一活塞动力学方程为:

$\begin{matrix} \begin{matrix} m_{c 1} {\overset{\cdot \cdot}{x}}_{c 1} + c_{c 1} ({\overset{\cdot}{x}}_{c 1} - {\overset{\cdot}{x}}_{c 2}) + k_{c 1} (x_{c 1} - x_{c 2}) = \\ F_{e} - F_{N 1} - F_{m 1} - P_{1} s_{c} (3) \\ F_{e} > F_{m 1} \end{matrix} \end{matrix}$

第二活塞动力学方程为:

$\begin{matrix} \begin{matrix} m_{c 2} {\overset{\cdot \cdot}{x}}_{c 2} + c_{c 2} {\overset{\cdot}{x}}_{c 2} + k_{c 2} x_{c 2} = (P_{1} - P_{2}) \cdot s_{c} + \\ c_{c 1} ({\overset{\cdot}{x}}_{c 1} - {\overset{\cdot}{x}}_{c 2}) + k_{c 1} (x_{c 1} - x_{c 2}) (4) \\ x_{c 2} \leq h_{2} \\ 令 F_{N 2} = c_{c 1} ({\overset{\cdot}{x}}_{c 12} - {\overset{\cdot}{x}}_{c 22}) + \\ k_{c 1} (x_{c 12} - x_{c 22}) + P_{1} s_{c} (5) \end{matrix} \end{matrix}$

式中:x_c12、x_c22分别为第二阶段末第一、第二活塞的位移, F_N2为第三阶段第一活塞受到的初始力。

第三阶段:第二活塞回位弹簧被压缩至极限, 直至第一活塞回位弹簧也被压缩至极限。该过程中只有第一活塞在运动, 制动主缸的动力学方程为:

$\begin{matrix} \begin{matrix} m_{c 1} {\overset{\cdot \cdot}{x}}_{c 1} + c_{c 1} {\overset{\cdot}{x}}_{c 1} + k_{c 1} x_{c 1} = \\ F_{e} - F_{N 2} - P_{1} s_{c} x_{c 1} \leq h_{1} (6) \end{matrix} \end{matrix}$

式中:h₁为第一活塞腔有效长度; s_c为活塞面积。

2.3 制动液动力学模型

由一维流体连续方程可得:

$\begin{matrix} \frac{1}{ρ} \frac{dρ}{dt} + \frac{\partial v_{x}}{\partial x} = 0 (7) \end{matrix}$

式中:ρ 为流体的密度; v_x为流体沿 $\begin{matrix} \vec{x} \end{matrix}$ 方向的流速; x为流体沿 $\begin{matrix} \vec{x} \end{matrix}$ 方向的位移; t为时间。

令Q为流体的体积流量, S为过流面积, 则式(7)可表达为:

$\begin{matrix} \frac{1}{ρ} \frac{dρ}{dt} + \frac{1}{S} \frac{\partial Q}{\partial x} = 0 (8) \end{matrix}$

对于具有规则形状的腔体, 假设流体的体积流量均匀降低, 则式(8)可表示为:

$\begin{matrix} \frac{1}{ρ} \frac{dρ}{dt} + \frac{Q_{in} - Q_{out}}{V} = 0 (9) \end{matrix}$

式中:Q_in为流进的流体流量; Q_out为流出的流体流量; V为腔体体积。

制动液是可压缩性液体, 其压缩能力用体积弹性模量K_e表示:

$\begin{matrix} K_{e} = - ρ \frac{dP}{dρ} (10) \end{matrix}$

式中:P为流体压力。

制动液动力学方程为:

$\begin{matrix} \frac{dP}{dt} = K_{e} \frac{(Q_{in} - Q_{out})}{V} (11) \end{matrix}$

由于实际试验过程中将主缸出液口堵住, 因此Q_out=0。所以, 第一阶段制动液动力学方程为:

$\begin{matrix} \frac{d P_{2}}{dt} = K_{e} \frac{{\overset{\cdot}{x}}_{c 1} s_{c}}{V}, x_{c 1} \geq h_{b 2} (12) \end{matrix}$

第二阶段制动液动力学方程为:

$\begin{matrix} \{\begin{matrix} \frac{d P_{1}}{dt} = K_{e} \frac{({\overset{\cdot}{x}}_{c 1} - {\overset{\cdot}{x}}_{c 2}) s_{c}}{V}, x_{c 1} \geq h_{b 1} \\ \frac{d P_{2}}{dt} = K_{e} \frac{{\overset{\cdot}{x}}_{c 2} s_{c}}{V}, x_{c 1} \geq h_{b 1} \end{matrix} (13) \end{matrix}$

第三阶段制动液动力学方程为:

$\begin{matrix} \frac{d P_{1}}{dt} = K_{e} \frac{{\overset{\cdot}{x}}_{c 1} s_{c}}{V}, x_{c 1} \leq h_{1} (14) \end{matrix}$

式中:h_b1、h_b2为初始状态下第一、第二中心阀口间隙。

制动液体积弹性模量K_e随着含气量和压力变化, 工程中制动液的体积弹性模量^{[12, 13]}为:

$\begin{matrix} \begin{matrix} K_{e} = \frac{K_{l}}{A α^{2} + Bα + 1} (15) \\ A = - 10 δ_{0} K_{l} {(\frac{P_{0}}{P})}^{\frac{1}{γ}} (16) \\ B = 10 δ_{0} K_{l} {(\frac{P_{0}}{P})}^{\frac{1}{γ}} + \\ \frac{K_{l} [1 - {(P_{0} / P)}^{\frac{1}{γ}}]}{P - P_{0}} - 1 (17) \end{matrix} \end{matrix}$

式中:K_l为纯制动液的体积弹性模量; δ ₀为标准大气压下空气的溶解度; γ 为气体绝热指数; α 为制动液中实际的气体含量; P₀为标准大气压。

2.4 基于试验的关键参数辨识

2.4.1 无制动液工况

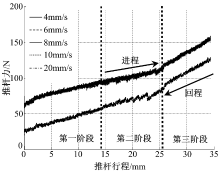
在无制动液工况下, 主要辨识前回位弹簧的刚度和预紧力以及活塞受到的摩擦力。图4为无制动液时主缸的推杆力-行程曲线。由图4可知:推杆力-行程特性可以分为0~14 mm、14~25 mm、25~35 mm三个阶段, 其中第三阶段中主要压缩第一活塞回位弹簧, 曲线的斜率即为该弹簧刚度; 第一阶段主要是压缩第二活塞回位弹簧, 曲线的斜率即为该弹簧刚度。

	Figure Option View Download New Window
	图4 无制动液工况主缸推杆力-行程曲线Fig.4 Master cylinder pushrod force-travel curves on condition of no brake fluid

推杆速度对其制动主缸机械特性影响可以忽略不计, 在相同推杆行程下进程和回程阶段的推杆力差值的一半即为摩擦力, 但不同推杆位置时摩擦力的大小不同, 这主要是由于在第一和第二阶段, 摩擦力包含推杆和橡胶密封圈摩擦力和3个皮碗与缸壁的摩擦力, 而在第三阶段摩擦力包含推杆和橡胶密封圈摩擦力和1个皮碗与缸壁的摩擦力。分别在0~25 mm、25~35 mm内计算各个行程下进程与回程推杆力的差值的平均值, 得到制动主缸摩擦力。

推杆进程中行程为零时的推杆力为第一阶段摩擦力和第二活塞回位弹簧的预紧力之和, 由于摩擦力已求, 从而可以计算出第二活塞回位弹簧的预紧力。在推杆行程为14 mm时, 第一阶段结束, 第二阶段开始, 此时的推杆力为第一活塞回位弹簧的预紧力。

2.4.2 有制动液工况

图5为有制动液工况制动主缸油压-行程曲线。由图5可知:当推杆行程为零时的油压为制动主缸的初始油压, 制动油压开始迅速增大时的推杆行程为制动主缸空行程, 即初始状态下第二中心阀口间隙。

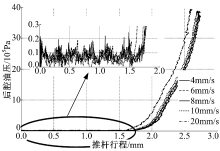	Figure Option View Download New Window
	图5 有制动液工况主缸油压-行程曲线Fig.5 Master cylinder pushrod force-travel curves on condition of with brake fluid

经试验辨识的主缸参数及数值如下:F_u1=14 N; F_u2=6 N; F_m1=94 N; F_m2=44 N; k_c1=4.5 N/m; k_c2=1.9 N/m; h_b1=1.6 mm; 初始油压P₀=8000 Pa。

3 模型有效性验证

图6为推杆速度为4 mm/s和20 mm/s且无制动液工况时制动主缸特性对比图。由图6可知:无制动液工况下制动主缸模型仿真结果与试验结果具有较好的一致性, 仅在起始位置处误差稍大, 这主要是由于皮碗在运动之处的不规则变形引起的。

	Figure Option View Download New Window
	图6 无制动液工况制动主缸推杆力-行程曲线对比Fig.6 Comparison of master cylinder pushrod force- travel curves on condition of no brake fluid

图7为推杆速度为4 mm/s和20 mm/s且有制动液工况时制动主缸特性对比图。由图7可知:有制动液时制动主缸动力学模型仿真结果与试验结果的一致性较好。

	Figure Option View Download New Window
	图7 有制动液工况制动主缸特性对比Fig.7 Comparison of master cylinder characteristics on condition of with brake fluid

4 关键影响因素

研究已经表明^{[1, 10, 14, 15]}, 主缸结构类型、阀口间隙、橡胶皮碗等因素对制动踏板感觉具有重要影响。本文重点针对活塞内径、弹簧预紧力和刚度、制动液气体含量等因素, 以推杆速度为4 mm/s工况为例, 分析它们对制动踏板感觉的影响。

	Figure Option View Download New Window
	图8 活塞内径对制动主缸特性的影响Fig.8 Influence of piston inner diameter on master cylinder characteristics

4.1 活塞内径

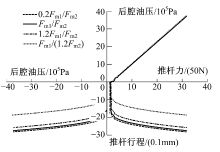
图8为活塞内径对制动主缸特性的影响, 其中, 20 mm特性曲线为实际制动主缸特性。由图8可知:随着活塞内径的增大, 主缸油压-行程曲线没有变化; 制动主缸推杆力-行程曲线变化较小, 只有在大行程时主缸推杆力-行程的刚度稍微增加, 这将会使制动踏板感觉有变硬的趋势; 主缸油压-推杆力曲线变化显著, 主缸油压-推杆力刚度明显减小, 从而导致制动踏板感觉有偏软的趋势, 这主要是由于活塞内径增大, 相同推杆力产生的压强降低。

4.2 弹簧预紧力和刚度

图9为回位弹簧预紧力对制动主缸特性的影响。其中, 前3个工况为第二活塞回位弹簧预紧力不变, 依次增大第一活塞回位弹簧预紧力。通过分析可知:弹簧预紧力对主缸油压-推杆力曲线特性影响较小, 对推杆力-行程曲线特性和主缸油压-行程曲线特性影响较大。随着第一活塞回位弹簧预紧力的增大, 主缸油压空行程减小, 推杆力-行程曲线拐点提前, 从而导致制动踏板感觉油压空行程减小, 制动踏板力-行程曲线拐点提前。

	Figure Option View Download New Window
	图9 回位弹簧预紧力对制动主缸特性的影响Fig.9 Influence of the return spring preload on master cylinder characteristics

在图9中, 第三和第四工况分别使第一、第二活塞回位弹簧预紧力增加相同倍数, 通过分析可知:改变第二活塞回位弹簧预紧力可以更加有效地改变推杆力-行程特性和主缸油压-行程特性, 进而说明主缸油压特性对第二活塞回位弹簧预紧力更加敏感。

图10为回位弹簧刚度对制动主缸特性的影响, 其中, 第一工况为第一活塞弹簧刚度增大, 第二活塞刚度不变; 第二、三、四工况为第一活塞弹簧刚度不变, 第二活塞弹簧刚度依次增大。由图10可知:弹簧刚度对主缸油压-推杆力曲线特性影响较小, 对推杆力-行程曲线特性和主缸油压-行程曲线特性影响较大。随着第二活塞回位弹簧刚度的增大, 主缸油压空行程减小, 推杆力-行程曲线拐点提前, 从而导致制动踏板感觉油压空行程减小, 制动踏板力-行程曲线拐点提前。增大第一活塞回位弹簧刚度时, 制动主缸特性变化较小。因此, 说明主缸油压特性对第二活塞回位弹簧刚度更加敏感。

	Figure Option View Download New Window
	图10 回位弹簧刚度对制动主缸特性的影响Fig.10 Influence of the return spring stiffness on master cylinder characteristics

4.3 制动液气体含量

图11为制动液气体含量对制动主缸特性的影响。由图11可知:制动液气体含量对主缸油压-推杆力特性的影响较小, 但是对推杆力-行程曲线特性和主缸油压-行程曲线特性影响较大。随着制动液气体含量的增加, 制动主缸推杆力-行程刚度和主缸油压-行程刚度减小, 从而导致制动踏板感觉有变软的趋势; 制动液气体含量增大到一定程度后, 制动主缸特性变化不明显。因此, 实际制动系统的排气效果对制动主缸和制动踏板感觉具有重要的影响。

	Figure Option View Download New Window
	图11 制动液气体含量对制动主缸特性的影响Fig.11 Influence of the brake fluid gas content on master cylinder characteristics

5 结束语

考虑回位弹簧预紧力、系统摩擦力以及关键结构参数建立了制动主缸机械动力学模型, 考虑制动液体积弹性模量的可变性建立了制动液动力学模型, 基于试验辨识了系统的关键参数, 进而建立了面向制动踏板感觉的制动主缸动力学模型。经不同推杆速度下的试验对比与分析, 该模型具有较好的有效性和准确性。活塞内径对主缸油压-推杆力刚度影响较大; 回位弹簧预紧力和刚度对推杆力-行程曲线拐点和主缸油压空行程影响较大, 第二活塞回位弹簧表现的更加敏感; 制动液气体含量对制动主缸特性具有重要的影响。

The authors have declared that no competing interests exist.

参考文献

View Option

[1]	Khan Y, Kulkarni P, Youceftoumi K. Modeling, experimentation and simulation of a brake apply system[J]. Journal of Dynamic Systems Measurement and Control, 1994, 116(1): 111-122. [本文引用:4]
[2]	Gerdes J C, Hedrick J K. Brake system modeling for simulation and control[J]. Journal of Dynamic Systems Measurement and Control, 1999, 121(3): 496-503. [本文引用:3]
[3]	詹军. 基于ACC的制动系统模型研究[J]. 中国机械工程, 2005, 16(5): 76-78. Zhan Jun. Research on model of brake system based on ACC system[J]. China Mechanical Engineering, 2005, 16(5): 76-78. [本文引用:2]
[4]	Fisher D K. Brake system component dynamic performance measurement and analysis[C]∥International Automobile Safety Conference, Detroit, Michigan, 1970. [本文引用:2]
[5]	Yamada T, Sawada M. Development and implementation of simulation tool for vehicle brake system[C]∥SAE 2001 World Congress, Detroit, Michigan, 2001. [本文引用:2]
[6]	刘晓. 基于特性的制动系统动态建模与分析[D]. 长春: 吉林大学汽车工程学院, 2012. Liu Xiao. Dynamic modeling and analysis of the braking system based on its characteristics[D]. Changchun: College of Automotive Engineering, Jilin University, 2012. [本文引用:3]
[7]	Fortina A, Velardocchia M, Sorniotti A. Braking system components modelling[C]∥21st Annual Brake Colloquium & Exhibition, Hollywood, Florida, 2003. [本文引用:3]
[8]	贺平. 基于Modelica的液压制动系统多领域建模与仿真[D]. 武汉: 华中科技大学机械科学与工程学院, 2011. He Ping. The multi-domain modeling and simulation of hydraulic brake system based on modelica[D]. Wuhan: School of Mechanical Science and Engineering, Huazhong University of Science & Technology, 2011. [本文引用:3]
[9]	Day A, Ho H, Hussain K, et al. Brake system simulation to predict brake pedal feel in a passenger car[C]∥SAE 2009 Brake Colloquium and Exhibition, Tampa, Florida, 2009. [本文引用:3]
[10]	方泳龙, 胥向欣, 刘玺. 制动主缸与踏板行程专家系统知识库的建立[J]. 江苏大学学报: 自然科学版, 2007, 28(6): 477-481. Fang Yong-long, Xu Xiang-xin, Liu Xi. Expert system knowledge base construction of brakemaster cylinder stroke and brake pedal stroke[J]. Journal of Jiangsu University (Natural Science Edition), 2007, 28(6): 477-481. [本文引用:3]
[11]	王兴东, 胡于进, 李成刚, 等. 气液混合型制动系的执行机构建模试验和仿真[J]. 汽车工程, 2002, 24(6): 516-519. Wang Xing-dong, Hu Yu-jin, Li Cheng-gang, et al. Modeling, experiment and simulation of a pneumatic-hydraulic brake system[J]. Automotive Engineering, 2002, 24(6): 516-519. [本文引用:2]
[12]	朱冬. 液压系统低压管路瞬态过程研究[D]. 哈尔滨: 哈尔滨工业大学机电工程学院, 2006. Zhu Dong. The research of fluid transients in low pressure hydraulic pipeline[D]. Harbin: Mechatronic Engineering, Harbin Institute of Technology, 2006. [本文引用:1]
[13]	冯斌, 龚国芳, 杨华勇. 液压油弹性模量提高方法与试验[J]. 农业机械学报, 2010, 41(3): 219-222. Feng Bin, Gong Guo-fang, Yang Hua-yong. Method and experiment for increasing effective fluid bulk modulus in hydraulic systems[J]. Transactions of the Chinese Society for Agricultural Machinery, 2010, 41(3): 219-222. [本文引用:1]
[14]	Goto Y, Yasuda A, Ishida S. Brake Master cylinder for secure brake feel and improved system failure performance[C]∥21st Annual Brake Colloquium & Exhibition, Hollywood, Florida, 2003. [本文引用:1]
[15]	Rajesh A T, Badal B, Pol S. Co-relating subjective and objective brake performance: a case study[C]∥24th Annual Brake Colloquium and Exhibition, Grapevine, Texas, 2006. [本文引用:1]

1994

0.0

... 的作用^[1,2] ...

... 针对这一包含弹簧机械系统和黏性液体的机构,Khan等^[1]采用键合图的方法建立了机械系统的动力学模型,Gerdes和詹军等^[2,3]则建立了机械系统动力学数学模型 ...

... 通过分析发现:①现有的制动主缸模型均是针对制动性能而开发的,它们往往关注制动速度、制动距离、制动减速度、制动热效能等整车制动性能指标^[3,4,6],或者是制动油压、推杆力和推杆行程的时域特性^{[1,2,7,8,10,11]} ...

... 4 关键影响因素研究已经表明^[1,10,14,15],主缸结构类型、阀口间隙、橡胶皮碗等因素对制动踏板感觉具有重要影响 ...

1999

0.0

... 的作用^[1,2] ...

2005

0.0

. 2005, 16(5):76-78 DOI:doi:10.3321/j.issn:1004-132X.2005.05.020

Research on model of brake system based on ACC system

基于ACC的制动系统模型研究

Zhan Jun.

詹军

介绍了汽车自适应巡航控制系统的原理和特点,以及该系统对制动系统模型的要求;建立了汽车纵向动力学模型,并在此基础上建立了包括真空助力器、液压系统、制动器的整个制动系统的数学模型.该模型能满足控制的需要,并且较简单又具有较高的精度.对该模型进行了计算机模拟仿真,获得了较好仿真效果.

1970

0.0

... Fisher^[4]考虑活塞回位弹簧的预紧力和系统受到的摩擦力,利用液体体积弹性模量的定义,建立了包含机械系统模型和制动液模型的制动主缸动力学数学模型 ...

2001

0.0

... 在此基础之上,Yamada等^[5]利用一维流体连续方程建立了制动液的数学模型,刘晓^[6]重点考虑了补偿空位置建立了制动液的数学模型,他们都使用Matlab/Simulink软件对机械系统和制动液数学模型进行了仿真 ...

... 在建立制动液模型时,往往忽略体积弹性模量的变化^[5,6] ...

2012

0.0

. 2012, :-

Dynamic modeling and analysis of the braking system based on its characteristics

基于特性的制动系统动态建模与分析[D]

Liu Xiao.

刘晓

现有的商业汽车动力学仿真软件可以实现整车制动性能的仿真。但是，商业软件中制动系统要么过于简单，要么需求的参数太多，不便于整车厂在产品设计阶段进行仿真对比验证。同时汽车动力学仿真软件中的整车动力学模型一般都需要很多结构参数和性能参数，这样的要求往往很难实现。为了解决这一问题，本文依托“长安-吉林大学产学研工程中心”的“乘用车制动系统设计匹配开发”项目，有针对性的开发带有简单整车动力学模型的制动系统动态仿真软件。本文的主要内容和相关结论如下： 1.本文调研了国内外制动系统和与制动系统相关的整车动力学模型的研究现状。通过对比分析，利用机械动力学、液压系统动力学、流体力学等力学原理，提出制动系统各个模块的建模原理，并在MATLAB环境下，实现制动系统的仿真开发。最后，以某款车为例，借助部件性能特性实验，获取制动系统和整车参数，并进行相应的软件调试和验证。 2.本文建立了基于特性的制动系统动态模型。忽略踏板惯量等因素的影响，建立了机械式制动踏板的静力学稳态模型。在真空助力器稳态输入输出特性的基础上，用一阶迟滞环节近似等效地表达了真空助力器的动态模型。从而减少了真空助力器动态模型对结构参数和性能参数的需求。为了更好地反映制动系统液压部分的动态特性，保留制动主缸和制动轮缸活塞惯量和制动主缸和制动器间隙的影响。同时，建立了考虑制动管路容性和制动液粘度的制动管路动态模型。借鉴KELVIN- VOIGT模型，建立了制动块和制动盘间的弹簧阻尼连续接触模型，既满足模块划分的需求，也更加准确地反映动态接触过程和制动块变形对踏板位移的影响。最后，用制动效能因数统一表达了制动器制动力矩计算模型。 3.本文还调研了国内外与制动性能评价相关的标准和企业评估项目，综合分析得出制动系统仿真对整车动力学模型的需求。根据模型的需求，建立了十四自由度整车动力学模型。整车动力学模型中，将车体看成是刚体建立了车体的完整六自由度；由于本文主要研究制动系统的建模，所以转向系统采用了较简单的模型，直接由方向盘转角和转向系统的角传动比计算车轮转角；将悬架中的弹性元件和减震器用线性刚度阻尼系统表示，假定车轮只有垂直于车体的自由度，而不考虑悬架导向机构造成的KC特性；为了减少参数，保证模型在汽车预开发阶段的应用，轮胎模型选取了UA理论轮胎模型 4.在MATLAB/Simulink软件环境中，搭建了带有制动系统的整车动力学模型。重点分析了制动系统的滞后特性。最后根据长安公司提供的某款车的实车参数，结合BOSCH和SABS两家机构的实车试验数据，验证了制动系统模型和简单整车动力学模型的精度。通过本文的研究，汽车制造厂商在前期产品设计阶段，只需要少量的制动系统和整车参数就可以实现制动系统性能和整车制动性能的预测和分解。缩短后期试验周期，提高系统集成能力，从而缩短开发时间，提高工作效率，节约生产成本。

... 在建立制动液模型时,往往忽略体积弹性模量的变化^[5,6] ...

2003

0.0

... 根据制动主缸的拓扑结构,Fortina和贺平等^[7,8]分别利用AMEsim软件和Modelica/MWorks软件建立了制动主缸动力学模型 ...

... 而在使用AMEsim等软件建模时,没能给出反应系统特性的数学表达式^[7,8,9] ...

2011

0.0

. 2011, :- DOI:doi:10.7666/d.d187080

The multi-domain modeling and simulation of hydraulic brake system based on modelica

基于Modelica的液压制动系统多领域建模与仿真[D]

He Ping.

贺平

汽车制动系统是当前汽车主动安全技术研究的热点。在目前生产的轿车当中,应用最广泛的是液压制动系统,液压制动系统的工作过程是一个非常复杂的动态过程,而目前很多的车辆动力学领域的研究往往只考虑液压制动系统的静态特性,这样不能够对车辆的动力学性能进行有效的分析,因此有必要建立详细的液压制动系统的动态模型,并在此基础上分析液压制动系统的动态响应。液压制动系统是典型的机械、液压、气压等多领域耦合的复杂系统。近年来国际上提出了一种工程建模语言Modelica,该语言支持多领域物理系统的统一建模与仿真求解,支持陈述式非因果建模与连续离散混合建模,已在工程分析中得到广泛应用。本文基于多领域物理系统统一建模与仿真分析平台MWorks,利用Modelica语言建立了制动踏板、真空助力器、制动主缸、制动轮缸等复杂部件的参数化模型,基于这些部件模型搭建了液压制动系统,并分析了液压制动系统的动态响应,同时研究了液压制动系统参数的变化对于系统动态性能的影响。为了研究液压制动系统的动态响应对于整车制动性能的影响,本文建立了某型号轿车多体动力学模型,其中主要包括轮胎模型、前悬架模型、后悬架模型、转向系统模型。并将整车多体动力学模型与液压制动系统模型集成为车辆多领域模型,进行了整车直线制动工况和转弯制动工况的仿真分析。仿真结果表明该车的制动性能良好,同时也表明MWorks平台能够有效处理多领域建模与仿真分析问题。

... 根据制动主缸的拓扑结构,Fortina和贺平等^[7,8]分别利用AMEsim软件和Modelica/MWorks软件建立了制动主缸动力学模型 ...

... 而在使用AMEsim等软件建模时,没能给出反应系统特性的数学表达式^[7,8,9] ...

2009

0.0

... Day等^[9]进一步建立了AMEsim和Abaqus联合仿真的制动主缸动力学模型,重点分析了橡胶皮腕变形对制动主缸特性的影响 ...

... 而制动踏板感觉往往考察主缸推杆力-行程、主缸油压-行程、主缸油压-推杆力的关系^[9] ...

... 而在使用AMEsim等软件建模时,没能给出反应系统特性的数学表达式^[7,8,9] ...

2007

0.0

. 2007, 28(6):477-481 DOI:doi:10.3969/j.issn.1671-7775.2007.06.005

Expert system knowledge base construction of brakemaster cylinder stroke and brake pedal stroke

制动主缸与踏板行程专家系统知识库的建立

Fang Yong-long , Xu Xiang-xin , Liu Xi.

方泳龙, 胥向欣, 刘玺

根据专家的经验知识和设计思路,分析了制动主缸和踏板行程计算中的各个影响因素.结合开发汽车制动专家系统的实践,采用C++编程语言,在Visual Studio.NET2005开发环境中,充分利用面向对象的知识表达方法和模块化程序设计方法,建立了制动主缸和踏板行程知识库.并利用已有的某车型参数对知识库的计算与分析功能进行了测试,结果显示汽车制动专家系统主缸与踏板行程知识库已达到预期设计目标.

... 方泳龙等^[10]建立了制动主缸行程知识库,王兴东等^[11]利用分段函数建立了汽液混合型制动主缸动力学模型,为笔者建立制动主缸动力学模型提供了借鉴 ...

... 4 关键影响因素研究已经表明^[1,10,14,15],主缸结构类型、阀口间隙、橡胶皮碗等因素对制动踏板感觉具有重要影响 ...

2002

0.0

. 2002, 24(6):516-519 DOI:doi:10.3321/j.issn:1000-680X.2002.06.014

Modeling, experiment and simulation of a pneumatic-hydraulic brake system

气液混合型制动系的执行机构建模试验和仿真

Wang Xing-dong , Hu Yu-jin , Li Cheng-gang

王兴东, 胡于进, 李成刚

分析了用于多轴车制动系气液混合型执行机构各元件的动态特性,结合其鼓式制动器,提出了一种鼓式制动器的弹性特征模型;将各元器件有机结合,建立了整个执行机构的动态特性分析的数学模型,应用Mat-lab工具进行仿真计算.将仿真计算和试验获得的压力建立过程进行对比分析,结果验证了仿真数学模型的正确性.

2006

0.0

. 2006, :-

The research of fluid transients in low pressure hydraulic pipeline[D]. Harbin: Mechatronic Engineering,

液压系统低压管路瞬态过程研究[D]

Zhu Dong.

朱冬

液压系统中,阀门的快速开启或关闭会在管路中发生压力瞬态脉动过程。当压力脉动发生在液压泵的吸油管路或液压系统的回油管路等低压管路中时,会引起气泡和气穴的产生及破灭。气泡和气穴的产生及破灭不仅破坏了流体的连续性、降低了介质的物理特性,而且还会影响压力脉动波的传播过程。因此,研究低压液压管路有气泡和气穴产生的瞬态压力脉动过程,对于液压泵的流量特性预测以及液压系统的正常工作有着重要的意义。本文通过流体力学分析方法,在连续性方程和运动方程基础上,建立了低压液压管路中伴随气泡和气穴产生的瞬态压力脉动数学模型,给出了动态摩擦力数学模型及气泡和气穴产生及破灭数学模型。采用有限差分及Matlab/Simulink仿真方法,提出了采用Simulink中selector模块求解空间域上积分的方法,对低压液压管路有气泡和气穴产生的瞬态压力脉动过程进行了时间域和空间域上的求解,对不同起始流量、不同液压油粘度和不同初始气泡量等条件下的瞬态压力脉动过程进行了仿真研究。本文对低压液压管路有气泡和气穴产生的瞬态压力脉动过程进行了实验研究。利用压电传感器测量了管路中的压力变化,并用高速摄像机记录了阀门处气泡和气穴的产生及破灭过程。对不同起始流量、不同液压油粘度和不同初始气泡量等条件下的瞬态压力脉动过程进行了实验研究。

... 制动液体积弹性模量K_e随着含气量和压力变化,工程中制动液的体积弹性模量^[12,13]为: ...

2010

0.0

. 2010, 41(3):219-222 DOI:doi:10.3969/j.issn.1000-1298.2010.03.045

Method and experiment for increasing effective fluid bulk modulus in hydraulic systems

液压油弹性模量提高方法与试验

Feng Bin , Gong Guo-fang , Yang Hua-yong.

冯斌, 龚国芳, 杨华勇

分析了液压系统中含气量、工作压力等参数对油液有效体积弹性模量的影响规律,在此基础上采用抽真空除气与弹性模量检测相结合的方法提高油液弹性模量至期望值,并试验于某大型液压泵站。应用结果表明:含气量对弹性模量值影响显著,利用抽真空能够有效减小油液的含气量,将弹性模量值由821.3 MPa提高至1 201 MPa;该方法在闭式液压系统中能够实现油液弹性模量的提高。

... 制动液体积弹性模量K_e随着含气量和压力变化,工程中制动液的体积弹性模量^[12,13]为: ...

2003

0.0

... 4 关键影响因素研究已经表明^[1,10,14,15],主缸结构类型、阀口间隙、橡胶皮碗等因素对制动踏板感觉具有重要影响 ...

2006

0.0

... 4 关键影响因素研究已经表明^[1,10,14,15],主缸结构类型、阀口间隙、橡胶皮碗等因素对制动踏板感觉具有重要影响 ...