超冗余多轴液压振动台的内力耦合控制

引用本文

魏巍, 杨志东, 曲志勇, 韩俊伟. 超冗余多轴液压振动台的内力耦合控制. 2015, 45(5): 1461-1467
WEI Wei, YANG Zhi-dong, QU Zhi-yong, HAN Jun-wei. Internal force coupling control for hyper-redundant multi-axis. Journal of Jilin University Engineering and Technology Edition, 2015, 45(5): 1461-1467 复制到剪切板

Permissions

超冗余多轴液压振动台的内力耦合控制

魏巍^1,², 杨志东², 曲志勇², 韩俊伟²

1.中国工程物理研究院机械制造工艺研究所,四川绵阳 621900

2.哈尔滨工业大学机电学院,哈尔滨 150001

作者简介:魏巍(1987-),男,博士研究生.研究方向:多轴振动台.E-mail:iamcoolweiwei@foxmail.com

基金:国家自然科学基金项目(51205077); 中央高校基本科研业务费专项项目(HITNSRIF.2015051)

摘要

针对传统多轴振动台内力耦合控制策略控制参数复杂、控制效果差的缺点,提出一种基于变形位移和变形力空间的内力耦合控制策略。给出超冗余振动台电液伺服系统的非线性方程及机械部分的单刚体动力学模型,在内力耦合空间分析的基础上,通过内力合成矩阵对合成内力进行闭环反馈补偿,由冗余变形分解矩阵将补偿量分配到各液压伺服阀的输入端。仿真结果显示该算法能有效降低超冗余液压振动台的液压缸出力及耦合内力。

关键词: 流体传动与控制; 超冗余振动台; 内力耦合; 电液伺服系统

中图分类号:TH137 文献标志码:A 文章编号:1671-5497(2015)05-1461-07

Internal force coupling control for hyper-redundant multi-axis

WEI Wei^1,², YANG Zhi-dong², QU Zhi-yong², HAN Jun-wei²

1.Institute of Machinery Manufacturing Technology,China Academy of Engineering Physics,Mianyang 621900,China

2.School of Mechatronic Engineering, Harbin Institute of Technology, Harbin 150001, China

Abstract

Traditional internal force coupling control for shaking table is complex and shows poor control performance because of the same control parameter numbers of the cylinders. In order to stabilize the internal force, a novel Internal Force Coupling (IFC) control strategy is proposed based on deformation displacement and force spaces. Nonlinear equations of electro-hydraulic servo system and single rigid body dynamic model of mechanical part of the hyper-redundant shaking table are established with hydraulic and parallel mechanism theory respectively. Under the analysis of internal force space, internal forces calculated by force synthesis matrix are compensated in closed loop and decomposed to the inputs of the servovalves through the redundant deformation matrix. Simulation results show that the IFC control strategy effectively reduces cylinder forces and internal coupling forces of the hyper-redundant multi-axis hydraulic shaking table.

Keyword: fluid power transmission and control; hyper-redundant shaking table; internal force coupling; electro-hydraulic servo system

Show Figures

超冗余多轴液压振动台主要用于大型结构件的地震及其他振动环境下的模拟试验^[1]。为了获得更大的出力, 这类多轴振动台的液压缸数量往往远多于其控制的自由度数^{[2, 3, 4, 5]}。虽然冗余驱动有良好的承载能力, 但是运动过程中各液压作动器参数和特性的不一致以及安装误差等因素会使得各个驱动器之间产生很大的内力纷争, 这种内力耦合会降低系统的性能, 减小激振系统的净出力, 严重时甚至会导致振动台根本无法动作^{[6, 7, 8]}。而超冗余振动台由于具有更多的冗余自由度, 因此其内力耦合的现象会更为严重。

内力耦合控制是指采用特定的控制策略来消除或减弱内力耦合, 它是其他控制策略有效的基础。关广丰^[9]提出压力镇定控制技术, 其控制思想为液压缸压力同步控制思想, 将液压缸间压力差别作为反馈量修正驱动信号, 以达到减弱内力耦合的目标。Underwood^[10]提出八自由度思想来解决冗余振动台的自由度控制问题, 在原有六自由度动作空间基础上再引入两个扭曲自由度, 通过抑制这两个自由度的输出, 达到抑制内力耦合的目的。这些方法在一定程度上起到了抑制内力耦合的效果, 但是只适用于驱动冗余度比较小(冗余度为2)的情况, 当冗余度较大时这些内力耦合抑制方法的效果将受到限制。传统的压力镇定控制没有对内力耦合空间进行分析, 需要调整的控制参数与所需要的激振器数目相同, 不适合驱动冗余度大的振动台。本文将对超冗余振动台的内力耦合空间进行分析, 并在此基础上对内力进行补偿控制。

1 超冗余多轴液压振动台模型

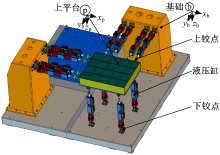
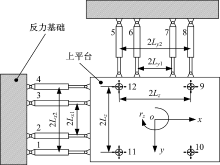
本文中研究的超冗余多轴液压振动台的结构如图1所示。12个液压缸均布在x、y、z三个互相垂直的方向。每个液压缸通过两个球铰分别与上平台和基础相连。该超冗余多轴液压振动台的冗余度为6, 其对应的俯视图如图2所示。

	Figure Option View Download New Window
	图1 超冗余振动台简图Fig.1 Hyper-redundant shaking table

	Figure Option View Download New Window
	图2 超冗余振动台的俯视示意图Fig.2 Top view of hyper-redundant shaking table

1.1 机械系统模型

如图1所示, 动坐标系{p}与上平台固连在一起, 并随着上平台一起运动, 而静坐标系{b}固连在基础上, 始终保持不变。上平台处于初始位置时, {p}与{b}的原点与上平台的质心重合。超冗余多轴振动台运动学的反解是通过给定上平台的位姿计算出液压缸的位移量, 液压缸的长度矢量为:

$\begin{matrix} l_{i} = T \cdot A_{i} - B_{i} + c (1) \end{matrix}$

式中:l_i为第i个液压缸的长度矢量; T∈ R³^×³为动坐标系{p}到静坐标系{b}之间的旋转变换矩阵; A_i∈ R³为第i个上铰点在动坐标系{p}下的坐标; c= $\begin{matrix} {[\begin{matrix} x & y & z \end{matrix}]}^{T} \end{matrix}$ ∈ R³为上平台的平动位移; B_i∈ R³为第i个下铰点在静坐标系{b}下的坐标。

对式(1)求导, 可得上铰点的运动速度v_ai为:

$\begin{matrix} v_{ai} = ω \times T A_{i} + \overset{\cdot}{c} (2) \end{matrix}$

式中:ω 为{p}相对于{b}的角速度; $\begin{matrix} \overset{\cdot}{c} \end{matrix}$ 为上平台中心的平动速度。

液压缸的速度 $\begin{matrix} {\overset{\cdot}{l}}_{i} \end{matrix}$ 为上铰点速度v_ai在液压缸矢量方向的投影, 结合式(2), $\begin{matrix} {\overset{\cdot}{l}}_{i} \end{matrix}$ 表示为:

$\begin{matrix} {\overset{\cdot}{l}}_{i} = {l^{T}}_{ni} v_{ai} = [\begin{matrix} {l^{T}}_{ni} & {(T A_{i} \times l_{ni})}^{T} \end{matrix}] [\begin{matrix} \overset{\cdot}{c} \\ ω \end{matrix}] (3) \end{matrix}$

式中:l_ni为第i个液压缸的单位方向矢量。

定义上平台的广义速度 $\begin{matrix} \overset{\cdot}{q} \end{matrix}$ = $\begin{matrix} {[\begin{matrix} {\overset{\cdot}{c}}^{T} & ω^{T} \end{matrix}]}^{T} \end{matrix}$ , 考虑到振动台的12个液压缸, 式(3)可写成:

$\begin{matrix} \overset{\cdot}{l} = J_{l} (Θ) \overset{\cdot}{q} (4) \end{matrix}$

式中:Θ = $\begin{matrix} {[\begin{matrix} x & y & z & φ & θ & ψ \end{matrix}]}^{T} \end{matrix}$ ∈ R⁶为上平台相对基础的位姿, 包括平动位移和欧拉旋转角; J_l $\begin{matrix} (Θ) \end{matrix}$ ∈ R¹²^×⁶为雅可比矩阵, 该矩阵和上平台的位姿Θ 相关, J_l $\begin{matrix} (Θ) \end{matrix}$ = $\begin{matrix} [\begin{matrix} {L^{T}}_{n} & {(TA \times L_{n})}^{T} \end{matrix}] \end{matrix}$ , 其中, L_n= $\begin{matrix} [\begin{matrix} l_{n 1} & \dots & l_{n 12} \end{matrix}] \end{matrix}$ , A= $\begin{matrix} [\begin{matrix} A_{1} & \dots & A_{12} \end{matrix}] \end{matrix}$ 。

多刚体并联机器人的动力学方程可以通过拉格朗日法、牛顿-欧拉法及虚功原理等不同的方法求解^[11]。由于多轴振动台的上平台及负载质量远大于各驱动缸的活塞杆质量, 因此在求解其动力学方程时可以按照单刚体求解, 本文采用凯恩法建立系统的单刚体动力学方程^{[12, 13]}:

$\begin{matrix} f_{q} = M (Θ) \overset{\cdot \cdot}{q} + C (Θ, \overset{\cdot}{q}) \overset{\cdot}{q} + G (Θ) (5) \end{matrix}$

式中:M(Θ )∈ R⁶^×⁶为上平台及负载的质量矩阵; C(Θ , $\begin{matrix} \overset{\cdot}{q} \end{matrix}$ )为离心力及科氏力系数矩阵; G(Θ )为重力项; f_q∈ R⁶为自由度空间的力系向量。

多轴振动台垂直方向的液压缸都有平衡缸系统, 通过平衡缸的预先加压来抵消上平台及负载重力的影响。另外, 多轴振动台一般仅在零位附近做小幅值的振动, 转角很小, 离心力及科氏力对系统的动态特性的影响可以忽略^[14]。同时考虑到自由度空间的力系矢量可以由关节空间的力(即液压缸的出力)转换得到, 式(5)可以变为:

$\begin{matrix} {J^{T}}_{l} (Θ) f_{a} = M (Θ) \overset{\cdot \cdot}{q} (6) \end{matrix}$

式中:f_a为12个液压缸出力构成的力向量。

1.2 液压系统模型

电液伺服系统由伺服阀和液压缸组成, 如图3所示^[15]。

	Figure Option View Download New Window
	图3 电液伺服系统Fig.3 Electro-hydraulic servo system

电液伺服阀的阀芯位移与给定电流之间可以用一个二阶传递函数表示^[16]:

$\begin{matrix} {\overset{\cdot \cdot}{x}}_{v} + 2 ζ_{v} ω_{v} {\overset{\cdot}{x}}_{v} + {ω_{v}}^{2} x_{v} = k_{v} {ω_{v}}^{2} u (7) \end{matrix}$

式中:x_v为伺服阀阀芯位移; ω _v、ζ _v分别为伺服阀的固有频率和阻尼比; u为输入电流信号; k_v为阀芯位移与电流信号之间的比例系数。

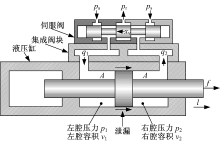
按照零开口四通滑阀建立伺服阀的流量方程, 流入液压缸左腔的流量q₁和右腔的流量q₂分别为:

$\begin{matrix} \begin{matrix} q_{1} = \{\begin{matrix} c_{d} w x_{v} \sqrt[]{\frac{2}{ρ} (p_{s} - p_{1})}, x_{v} \geq 0 \\ c_{d} w x_{v} \sqrt[]{\frac{2}{ρ} (p_{1} - p_{r})}, x_{v} < 0 \end{matrix} (8) \\ q_{2} = \{\begin{matrix} c_{d} w x_{v} \sqrt[]{\frac{2}{ρ} (p_{2} - p_{r})}, x_{v} \geq 0 \\ c_{d} w x_{v} \sqrt[]{\frac{2}{ρ} (p_{s} - p_{2})}, x_{v} < 0 \end{matrix} (9) \end{matrix} \end{matrix}$

式中:c_d为流量系数; w为伺服阀节流窗口的面积梯度; p₁、p₂分别为液压缸左腔压力与右腔压力; p_s、p_r分别为供油压力与回油压力; ρ 为液压油密度。

图3中所示的液压缸为双作用对称液压缸, 其左腔与右腔的流量连续性方程分别为:

$\begin{matrix} \begin{matrix} q_{1} = A \overset{\cdot}{l} + \frac{v_{1}}{β_{e}} {\overset{\cdot}{p}}_{1} + c_{tc} (p_{1} - p_{2}) (10) \\ q_{2} = A \overset{\cdot}{l} - \frac{v_{2}}{β_{e}} {\overset{\cdot}{p}}_{2} + c_{tc} (p_{1} - p_{2}) (11) \end{matrix} \end{matrix}$

式中:A为液压缸有效作用面积; l为液压缸的伸长量; β _e为液压弹性模量; c_tc为液压缸的总泄漏系数; v₁和v₂分别为左腔与右腔的容积, 表示为:

$\begin{matrix} \begin{matrix} v_{1} = v + Al (12) \\ v_{2} = v - Al (13) \end{matrix} \end{matrix}$

式中:v为液压缸处于中位时腔室的容积。

液压缸的输出力f_a为:

$\begin{matrix} f_{a} = A (p_{1} - p_{2}) - B_{c} \overset{\cdot}{l} (14) \end{matrix}$

式中:B_c为液压缸的黏性摩擦因数。

2 内力耦合空间分析

2.1 位移变换分析

对于冗余的多轴振动台, 系统的给定信号一般为负载在自由度空间的位姿信号Θ , 包括平动位移和转动位移。除了这部分自由度位移外, 冗余自由度上的位移λ 则体现在上平台的柔性变形上, 这部分的变形是由系统的内力造成的。对于小位移的运动, 由上平台的位移(包括刚体自由度位移及变形位移)到液压缸的位移可以由下面的线性公式表示^[6]:

$\begin{matrix} CΘ + Dλ = l (15) \end{matrix}$

式中:λ = $\begin{matrix} {[\begin{matrix} λ_{1} & λ_{2} & \dots & λ_{6} \end{matrix}]}^{T} \end{matrix}$ ∈ R⁶为变形位移; C∈ R¹²^×⁶、D∈ R¹²^×⁶分别为刚体位移与变形位移到液压缸位移的变化矩阵, 对于零位附近的小位移运动, 由式(4)可以得到:

$\begin{matrix} C = J_{l} (Θ_{0}) (16) \end{matrix}$

式中:Θ ₀= $\begin{matrix} {[\begin{matrix} 0 & 0 & 0 & 0 & 0 & 0 \end{matrix}]}^{T} \end{matrix}$ 为零位时上平台的刚性位移。

选择S∈ R⁶^×¹²为液压缸位移到上平台刚性位移之间的变换矩阵, 则对于任意λ 有^[5]:

$\begin{matrix} Θ = Sl (17) \end{matrix}$

式(17)对于任意λ 均成立, 将式(17)及λ =0代入式(15)则有:

$\begin{matrix} CS = I_{12} (18) \end{matrix}$

式中:I₁₂∈ R¹²^×¹²为单位方阵。

由于变换矩阵C不是方阵, 因此, 式(18)中S的解不唯一。本文选择C的最小二乘伪逆作为S的解:

$\begin{matrix} S = {(C^{T} C)}^{- 1} C^{T} (19) \end{matrix}$

将式(15)左乘S, 结合式(19), 并考虑到一般情况下λ ≠ 0可以得到:

$\begin{matrix} SD = 0 (20) \end{matrix}$

式(20)表明D由S矩阵零空间的基底组成, 矩阵D不唯一。本文采用Matlab的命令函数null(S), 通过奇异值分解的方法, 以S矩阵零空间的单位正交基底作为D的解。

2.2 力变换分析

根据能量守恒原理, 液压缸驱动力所做的功等于上平台刚体自由度空间力做的功与冗余自由度空间内力所做的功之和, 即:

$\begin{matrix} {f^{T}}_{q} Θ + {f^{T}}_{λ} λ = {f^{T}}_{a} l (21) \end{matrix}$

式中:f_λ= $\begin{matrix} {[\begin{matrix} f_{λ 1} & f_{λ 2} & \dots & f_{λ 6} \end{matrix}]}^{T} \end{matrix}$ ∈ R⁶为冗余内力组成的向量。

定义矩阵P∈ R⁶^×¹²为液压缸位移到变形位移的转换矩阵, 将式(17)及P代入式(21), 得到:

$\begin{matrix} S^{T} f_{q} + P^{T} f_{λ} = f_{a} (22) \end{matrix}$

定义矩阵Q∈ R⁶^×¹²为液压缸出力到内力的转换矩阵, 则对任意f_q有^[5]:

$\begin{matrix} f_{λ} = Q f_{a} (23) \end{matrix}$

式(23)对于任意f_q均成立, 将式(23)及f_q=0代入式(22)则有:

$\begin{matrix} P^{T} Q = I_{12} (24) \end{matrix}$

将式(22)左乘Q, 结合式(23)得到:

$\begin{matrix} Q S^{T} = 0 或 S Q^{T} = 0 (25) \end{matrix}$

与式(20)比较可得:

$\begin{matrix} Q = D^{T} (26) \end{matrix}$

矩阵Q即为液压缸出力到冗余内力的变换矩阵。

3 内力耦合控制策略

由第2节得到内力变换矩阵, 引入控制量U:

$\begin{matrix} U = - D \cdot diag \{k_{f 1}, k_{f 2}, \dots, k_{f 6}\} \cdot Q P_{L} (27) \end{matrix}$

由于矩阵D和Q均为正交向量组成, 内力空间的基底互相垂直, 且均为单位长度。各液压缸的出力通过该矩阵合成的冗余内力为同一个度量空间。因此, k_f1=k_f2=…=k_f6。式(27)变为:

$\begin{matrix} U = - k_{f} \cdot DQ P_{L} (28) \end{matrix}$

12个液压作动器在上平台的布置方式如图2所示, 其中1号与4号液压缸之间的距离为1 m; 2号与3号液压缸之间的距离为0.5 m; 5号与8号液压缸之间的距离为1 m; 6号与7号液压缸之间的距离为0.5 m; 9号与10号液压缸之间的距离为1 m。由此得到内力耦合控制策略中的各变换矩阵分别如下。

自由度分解矩阵C为:

C= $\begin{matrix} [\begin{matrix} 1 & 0 & 0 & 0 & 0 & - 0.5 \\ 1 & 0 & 0 & 0 & 0 & - 0.25 \\ 1 & 0 & 0 & 0 & 0 & 0.25 \\ 1 & 0 & 0 & 0 & 0 & 0.5 \\ 0 & 1 & 0 & 0 & 0 & - 0.5 \\ 0 & 1 & 0 & 0 & 0 & - 0.25 \\ 0 & 1 & 0 & 0 & 0 & 0.25 \\ 0 & 1 & 0 & 0 & 0 & 0.5 \\ 0 & 0 & - 1 & 0.5 & 0.5 & 0 \\ 0 & 0 & - 1 & - 0.5 & 0.5 & 0 \\ 0 & 0 & - 1 & - 0.5 & - 0.5 & 0 \\ 0 & 0 & - 1 & 0.5 & - 0.5 & 0 \end{matrix}] \end{matrix}$

自由度合成矩阵S为:

S^T=

$\begin{matrix} [\begin{matrix} 0.25 & 0 & 0 & 0 & 0 & - 0.4 \\ 0.25 & 0 & 0 & 0 & 0 & - 0.2 \\ 0.25 & 0 & 0 & 0 & 0 & 0.2 \\ 0.25 & 0 & 0 & 0 & 0 & 0.4 \\ 0 & 0.25 & 0 & 0 & 0 & - 0.4 \\ 0 & 0.25 & 0 & 0 & 0 & - 0.2 \\ 0 & 0.25 & 0 & 0 & 0 & 0.2 \\ 0 & 0.25 & 0 & 0 & 0 & 0.4 \\ 0 & 0 & - 0.25 & 0.5 & 0.5 & 0 \\ 0 & 0 & - 0.25 & - 0.5 & 0.5 & 0 \\ 0 & 0 & - 0.25 & - 0.5 & - 0.5 & 0 \\ 0 & 0 & - 0.25 & 0.5 & - 0.5 & 0 \end{matrix}] \end{matrix}$

冗余位移分解矩阵D为:

$\begin{matrix} [\begin{matrix} 0.4 & 0.53 & - 0.07 & - 0.22 & - 0.21 & - 0.06 \\ - 0.46 & - 0.5 & 0.19 & - 0.07 & - 0.42 & - 0.16 \\ 0.53 & 0.03 & 0.45 & 0.21 & 0.34 & 0.58 \\ 0.003 & - 0.07 & - 0.57 & 0.08 & 0.29 & - 0.36 \\ - 0.21 & - 0.17 & - 0.35 & - 0.26 & 0.42 & 0.32 \\ - 0.04 & 0.15 & 0.2 & 0.7 & 0.1 & - 0.39 \\ 0.65 & - 0.44 & 0.08 & - 0.15 & - 0.24 & 0.002 \\ - 0.4 & 0.47 & 0.07 & - 0.28 & - 0.29 & 0.06 \\ 0 & 0 & 0.25 & - 0.25 & 0.25 & - 0.25 \\ 0 & 0 & - 0.25 & 0.25 & - 0.25 & 0.25 \\ 0 & 0 & 0.25 & - 0.25 & 0.25 & - 0.25 \\ 0 & 0 & - 0.25 & 0.25 & - 0.25 & 0.25 \end{matrix}] \end{matrix}$

内力变换矩阵Q为:Q=D^T。

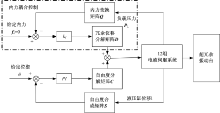
多轴振动台的控制一般采用的是自由度零位线性化控制^[7], 液压缸的位移经过自由度合成矩阵变换为位姿反馈信号参与自由度闭环, 自由度控制信号则经过自由度分解矩阵变换为电液伺服系统的伺服阀输入信号。将内力耦合控制策略加入自由度零位线性化控制结构中, 可以得到图4所示的超冗余振动台的整体控制框图。液压缸的压力信号经内力变换矩阵转为冗余内力参与内力闭环控制, 内力控制信号经过冗余位移分解矩阵变为伺服阀输入信号, 将其与自由度零位线性化控制策略得到的伺服阀输入信号进行合成, 实现冗余内力的解耦控制。

	Figure Option View Download New Window
	图4 超冗余振动台的整体控制策略Fig.4 Overall control system of hyper-redundant shaking table

4 仿真分析

在Simulink下, 根据液压系统模型和机械系统模型建立超冗余多轴振动台的仿真模型, 并搭建图4所示的振动台整体控制策略。由于本文超冗余振动台的频宽为40 Hz, 因此选择1 ms的定步长为模型及控制算法的仿真周期, 仿真采用Runge-Kutta解算器。仿真模型中的参数如下:上平台及负载质量为1000 kg; 伺服阀固有频率为628 rad/s; 伺服阀阻尼比为0.5; 液压缸黏性阻尼系数为10000 N/(m· s^-1); 液压缸有效作用面积为18.849 cm²; 供油压力为1.8× 10⁷ Pa; 油液弹性模量为6.9× 10⁸ Pa; 油液密度为845 kg/m³; 流量系数为0.64; 液压缸总泄漏系数为4× 10^-12 m³· s^-1· Pa^-1。

在x方向给定幅值5 mm, 频率5 Hz的正弦信号进行仿真分析。当各个液压缸参数相同时, x方向四组液压缸的出力及合成的内力如图5所示。x向各缸的出力相同, 内力空间合成的内力很小, 这时的内力是由于系统零位线性化控制误差造成的。

将x方向的4个液压伺服系统分别设置不同的增益(k₁=1.02、k₂=0.98、k₃=0.99、k₄=1.01)来模拟液压缸在工作过程中的不一致。不采用内力耦合控制策略时, x向各液压缸的出力及合成的内力如图6所示。与图5对比可知, 各液压缸之间动作的不一致使得超冗余振动台产生了内力, 在同一给定位移下, 液压缸需要更大的出力来平衡内力的作用, 液压缸的最大出力由1100 N提高到了2000 N, 增大了近一倍。

	Figure Option View Download New Window
	图5 相同参数下液压缸出力及合成内力Fig.5 Cylinder and internal forces under same parameters

	Figure Option View Download New Window
	图6 不同参数下液压缸出力及合成内力Fig.6 Cylinder and internal forces under different parameters

	Figure Option View Download New Window
	图7 内力耦合控制下液压缸出力及合成内力Fig.7 Cylinder and internal forces under IFC control

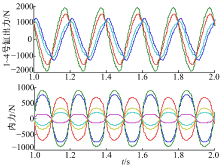
采用本文提出的内力耦合控制策略时, x方向各液压缸出力及合成的内力如图7所示。对比图6和图7可以看出:采用了内力耦合控制策略后, 内力矩阵合成的内力有了显著的减低, 最大内力降到了未采用耦合控制策略时的10%以下, x方向各液压作动器的出力也趋于一致, 并且降低到各缸参数一致时的出力大小。

5 结束语

提出了一种改进的内力耦合控制策略, 用来降低超冗余液压振动台在运动过程中由于液压作动器参数不一致导致的内力耦合现象。通过对上平台自由度空间和冗余度空间的分析, 得到了内力耦合空间的正交基底, 并在此基础上给出了只有一个控制参数的内力补偿控制策略, 与传统的压力镇定方式相比, 该控制策略显著简化了参数调整过程, 更容易实现内力耦合的最优控制。基于液压系统非线性和机械系统动力学模型的仿真试验也表明, 采用该内力耦合控制策略可以有效减小系统的内力, 增大系统的净出力, 提高超冗余振动台的运动能力。

The authors have declared that no competing interests exist.

参考文献

View Option

[1]	袁立鹏, 崔淑梅, 卢红影, 等. 基于定理反馈理论迭代学习的液压角振动台控制策略[J]. 吉林大学学报: 工学版, 2011, 41(3): 676-682. Yuan Li-peng, Cui Shu-mei, Lu Hong-ying, et al. QFT iteration-learning based control strategy of hydraulic angular vibration table[J]. Journal of Jilin University(Engineering and Technology Edition), 2011, 41(3): 676-682. [本文引用:1]
[2]	Shen Gang, Zhu Zhen-cai, Zhang Lei, et al. Adaptive feed-forward compensation for hybrid control with acceleration time waveform replication on electro-hydraulic shaking table[J]. Control Engineering Practice, 2013, 21(8): 1128-1142. [本文引用:1]
[3]	Severn R T. The development of shaking tables—A historical note[J]. Earthquake Engineering and Structural Dynamics, 2011, 40(2): 195-213. [本文引用:1]
[4]	Plummer A R. A detailed dynamic model of a six-axis shaking table[J]. Journal of Earthquake Engineering, 2008, 12(4): 631-662. [本文引用:1]
[5]	Tagawa Y, Kajiwara K. Controller development for the E-Defense shaking table[J]. Proceedings of the Institution of Mechanical Engineers, Part I: Journal of Systems and Control Engineering, 2007, 221(2): 171-181. [本文引用:3]
[6]	Plummer A R. A general coordinate transformation framework for multi-axis motion control with applications in the testing industry[J]. Control Engineering Parctice, 2010, 18(6): 598-607. [本文引用:2]
[7]	Saglia J A, Tsagarakis N G, Dai J S, et al. Inverse-kinematics-based control of a redundantly actuated platform for rehabilitation[J]. Proceedings of the Institution of Mechanical Engineers, Part I: Journal of Systems and Control Engineering, 2009, 223(1): 53-70. [本文引用:2]
[8]	何景峰, 李保平, 佟志忠, 等. 液压驱动冗余振动台自由度控制及内力协调[J]. 振动与冲击, 2011, 30(3): 74-78. He Jing-feng, Li Bao-ping, Tong Zhi-zhong, et al. DoF control and inner force balancing of hydraulically redundant actuated shaking table[J]. Journal of Vibration and Shock, 2011, 30(3): 74-78. [本文引用:1]
[9]	关广丰, 熊伟, 王海涛, 等. 6自由度电液振动台控制策略研究[J]. 振动与冲击, 2010, 29(4): 200-203. Guan Guang-feng, Xiong Wei, Wang Hai-tao, et al. Control strategy of a 6-DOF hydraulic shaker[J]. Journal of Vibration and Shock, 2010, 29(4): 200-203. [本文引用:1]
[10]	Underwood Marcos A, Keller Tony. Applying coordinate transformations to multi-DOF shaker control[J]. Sound and Vibration, 2006, 40(1): 22-27. [本文引用:1]
[11]	Jiang Hong-zhou, He Jing-feng, Tong Zhi-zhong. Characteristics analysis of joint space inverse mass matrix for the optimal design of a 6-DOF parallel manipulator[J]. Mechanism and Machine Theory, 2010, 45(5): 722-739. [本文引用:1]
[12]	Chen Yi-xin, Mclnroy John E. Decoupled control of flexure-jointed hexapods using estimated joint-space mass-inertia matrix[J]. IEEE Transactions on Control Systems Technology, 2004, 12(3): 413-421. [本文引用:1]
[13]	Dasgupta B, Mruthyunjaya T S. Closed-form dynamic equation of the general Stewart platform through the Newton-Euler approach[J]. Mechanism and Machine Theory, 1998, 33(7): 993-1012. [本文引用:]
[14]	Jiang Hong-zhou, He Jing-feng, Tong Zhi-zhong. Modal space control for a hydraulically driven Stewart platform[J]. Journal of Control Engineering and Technology, 2012, 2(3): 106-115. [本文引用:1]
[15]	Merritt H E. Hydraulic Control Systems[M]. New York: John Wiley & Sons, 1967. [本文引用:1]
[16]	Li H R. Hydraulic Control Systems[M]. Beijing: National Defense Industry Press, 1990. [本文引用:1]

2011

0.0

. 2011, 41(3):676-682

QFT iteration-learning based control strategy of hydraulic angular vibration table

基于定理反馈理论迭代学习的液压角振动台控制策略

Yuan Li-peng , Cui Shu-mei , Lu Hong-ying

袁立鹏, 崔淑梅, 卢红影

To achieve the robustness of a control system and the convergence of the control strategy, a Quantitive Feedback Theory (QFT) iteration learning-control strategy was designed, and the convergence criterion was given from viewpoint of frequency-domain. Both experiment and simulation results show that the compound iterationlearning-control strategy can increase the bandwidth and improve the precision of the system while tracking the expected input. At the same time, the random vibration signal can also be tracked well by using the control strategy. It was demonstrated that the compound iteration-learning-control is a new way in high performance real-time control of hydraulic angular vibration table.

针对控制系统的鲁棒性以及迭代学习的收敛性，进行了定量反馈理论（Quantitative feedback theory,QFT）复合迭代学习控制算法设计，并从频域角度给出了其收敛性条件。将仿真结果与实验数据进行对比分析，验证了此控制策略的有效性。该QFT迭代学习控制策略不仅拓宽了系统频带，改善了系统输出对期望信号输入的跟踪精度，同时可以很好地跟踪随机振动信号功率谱，为液压角振动台高性能实时控制开辟了新途径。

... 超冗余多轴液压振动台主要用于大型结构件的地震及其他振动环境下的模拟试验^[1] ...

2013

0.0

... 为了获得更大的出力,这类多轴振动台的液压缸数量往往远多于其控制的自由度数^[2,3,4,5] ...

2011

0.0

... 为了获得更大的出力,这类多轴振动台的液压缸数量往往远多于其控制的自由度数^[2,3,4,5] ...

2008

0.0

... 为了获得更大的出力,这类多轴振动台的液压缸数量往往远多于其控制的自由度数^[2,3,4,5] ...

2007

0.0

... 为了获得更大的出力,这类多轴振动台的液压缸数量往往远多于其控制的自由度数^[2,3,4,5] ...

... 有^[5]: ...

... ¹²为液压缸出力到内力的转换矩阵,则对任意f_q有^[5]: ...

2010

0.0

... 虽然冗余驱动有良好的承载能力,但是运动过程中各液压作动器参数和特性的不一致以及安装误差等因素会使得各个驱动器之间产生很大的内力纷争,这种内力耦合会降低系统的性能,减小激振系统的净出力,严重时甚至会导致振动台根本无法动作^[6,7,8] ...

... 对于小位移的运动,由上平台的位移(包括刚体自由度位移及变形位移)到液压缸的位移可以由下面的线性公式表示^[6]: ...

2009

0.0

... 多轴振动台的控制一般采用的是自由度零位线性化控制^[7],液压缸的位移经过自由度合成矩阵变换为位姿反馈信号参与自由度闭环,自由度控制信号则经过自由度分解矩阵变换为电液伺服系统的伺服阀输入信号 ...

2011

0.0

. 2011, 30(3):74-78 DOI:doi:10.3969/j.issn.1000-3835.2011.03.016

DoF control and inner force balancing of hydraulically redundant actuated shaking table

液压驱动冗余振动台自由度控制及内力协调

He Jing-feng , Li Bao-ping , Tong Zhi-zhong

何景峰, 李保平, 佟志忠

A shaking table is an important facility for earthquake damage testing of large scale structures like high buildings, large bridges and infrastructural systems. To improve the payload capacity for the test for large-scale structures or real-scale structures, hydraulically redundant actuated parallel mechanisms are usually adopted. In the present paper, by exploring the interactions between the mechanical parts and the hydraulic actuated systems, an integrated model of hydraulically redundant actuated shaking table is obtained. Then, a framework of Degree-of-Freedom (DoF) control for the shaking table of this type is put forward. To regulate forces among the redundant actuated systems and to reduce force couplings, an inner force balancing control method based on pseudo-inverse of Jacobian matrix is also employed. Simulation validated the proposed DoF control and inner force balancing method.

振动台是一种对高层建筑、大型桥梁和基础设施等大型结构进行抗震性能试验的重要设备。为了提高振动台有效载荷，以便进行大尺寸或全尺寸结构试验，振动台通常采用液压驱动冗余并联机构。本文首先根据液压驱动冗余振动台机液作用机理，建立了冗余振动台的整体机液动力学模型，并提出一种适用于液压驱动冗余振动台的自由度控制结构。之后，针对冗余驱动内力耦合问题，采用基于雅克比矩阵伪逆的内力协调控制方法，协调控制各激振器间的出力，减少各个激振器间的内力耦合。最后，通过仿真分析，验证了本文提出的自由度控制和内力协调控制的有效性。

2010

0.0

. 2010, 29(4):200-203 DOI:doi:10.3969/j.issn.1000-3835.2010.04.045

Control strategy of a 6-DOF hydraulic shaker

6自由度电液振动台控制策略研究

Guan Guang-feng , Xiong Wei , Wang Hai-tao

关广丰, 熊伟, 王海涛

Torsion control strategy of 6 DOF (degree-of-freedom) hydraulic shaker is presented to improve the control precision of the system. Two torsion control loops are added to the original 6 DOF control loops. The force balance controller is improved based on the torsion control strategy. The number of controller parameters is reduced from eight to two, and the two parameters are independent and can be adjusted individually. Sine vibration tests are run in one 6 DOF hydraulic shaker with the new algorithm. Test results show that the torsion control strategy is favorable to improve the performance indices of acceleration evenness degree and transverse components in the low-frequency band of the system. The improved force balance controller can reduce the inner force among the eight cylinders effectively.

为提高6自由度电液振动台的控制精度，在传统6自由度控制回路中增加两路扭曲控制回路，采用扭曲控制策略控制平台振动。基于扭曲控制策略，对传统压力镇定控制器进行改进，将相互关联的8个参数缩减为2个相互独立的参数。正弦振动试验结果表明，采用扭曲控制策略能够明显改善振动台系统低频段的加速度均匀度和横向分量指标，改进后的压力镇定控制器能够有效削弱系统中各液压缸之间的内力。

... 关广丰^[9]提出压力镇定控制技术,其控制思想为液压缸压力同步控制思想,将液压缸间压力差别作为反馈量修正驱动信号,以达到减弱内力耦合的目标 ...

2006

0.0

... Underwood^[10]提出八自由度思想来解决冗余振动台的自由度控制问题,在原有六自由度动作空间基础上再引入两个扭曲自由度,通过抑制这两个自由度的输出,达到抑制内力耦合的目的 ...

2010

0.0

... 多刚体并联机器人的动力学方程可以通过拉格朗日法、牛顿-欧拉法及虚功原理等不同的方法求解^[11] ...

2004

0.0

... 由于多轴振动台的上平台及负载质量远大于各驱动缸的活塞杆质量,因此在求解其动力学方程时可以按照单刚体求解,本文采用凯恩法建立系统的单刚体动力学方程^[12,13]: ...

1998

2012

0.0

... 另外,多轴振动台一般仅在零位附近做小幅值的振动,转角很小,离心力及科氏力对系统的动态特性的影响可以忽略^[14] ...

1967

0.0

... 2 液压系统模型电液伺服系统由伺服阀和液压缸组成,如图3所示^[15] ...

1990

0.0

... 电液伺服阀的阀芯位移与给定电流之间可以用一个二阶传递函数表示^[16]: ...