传统的下肢康复训练设备必须在理疗师的辅助下才能进行训练, 耗时费力, 因此新型智能下肢运动康复护理设备的开发与临床应用已备受关注。近年来, 已经有很多涉及机器人协助下肢功能障碍者进行康复训练^{[1, 2, 3]}、使其重获独立步行能力方面的研究。文献[4]中给出一种卧式下肢康复训练设备, 虽然可以满足重复稳定地训练, 但是训练者用力主动性不强, 训练过程枯燥, 并且其机械系统中的仿生机械腿结构复杂、成本昂贵, 不利于批量化生产。哈尔滨工程大学研究的采用AVR单片机的机器人训练控制系统成本低、易于产品化, 但也存在重力平衡问题以及机器人与患者肢体功能干涉的问题^[5], 虽然其机械结构简易, 仅由两根绳索通过定滑轮悬吊训练者使其保持直立状态, 但是并不能提供从坐姿到站立的站起训练。该课题组设计了另一种用于站起训练的机械结构^[6], 虽然可以实现站起训练, 但是不能按照正常人体重心轨迹变化进行重复稳定的训练, 并且该结构没有保护装置, 当下肢毫无支撑力的训练者处于站姿时, 体重完全作用于上肢, 反复训练会加重上肢疲劳, 存在安全隐患。德国Fraunhofer研究所采用最新的机器人技术、计算机技术和虚拟现实技术开发了Haptic Walker康复机器人^[7], 虽然可模拟出任意步态运动轨迹, 但体积过大, 结构复杂, 拆装运输不便。临床经验表明^[8], 下肢康复训练只有通过符合正常人体运动模式的重复性特定训练任务, 才能使重组中的大脑皮质通过深刻的体验来学习和存储正确的运动模式。

基于目前的社会背景与研究现状, 本文设计一种减重式康复训练系统的机械结构, 使训练者可以在重复的站起训练过程中模拟健康人体站起时重心轨迹的变化, 使下肢肌肉在健康模式下得到恢复训练。该结构价格低廉、操作简单、使用安全, 承重受力合理, 安装拆卸、包装运输方便, 易于加工生产, 适于家用和产品化推广。

根据临床研究^[9], 当人体从坐姿状态向上站起时, 其重心轨迹是一条向前向上的运动曲线。根据重心轨迹曲线, 为了保证正常人体站起过程中有自由的站立空间, 本文设计了减重式下肢智能康复训练系统的机械结构, 使其既能安装电控装置, 又能稳定承载足够的负荷, 在最大形变和许用应力等力学参数方面满足要求, 当训练对象的下肢不能提供足够支撑力时, 可通过系统悬吊装置提供能够抵消人体部分甚至全部重力的拉力, 从而减轻患者腿部承受的负荷。当训练者穿着专用承重背心处于坐姿时, 该训练系统进行工作, 系统电控部分中的伺服电机会根据预置程序控制悬吊绳索, 使训练者按照健康人体站起轨迹完成站起训练动作。

图1

Fig.1

	Figure Option ViewDownloadNew Window
	图1 康复训练系统机械结构示意图Fig.1 Mechanical structure of rehabilitation training system

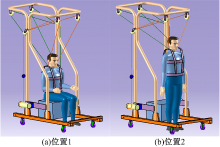
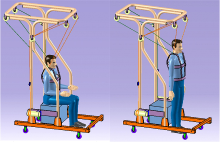
图1为本文初步设计的可以使训练者实现减重式站起智能康复训练系统机械结构示意图。为适合通常身高体型范围内的训练者实现站起康复训练, 整个机械结构高度和宽度分别设计为2 m和0.75 m。为了满足安装提拉绳索和转向滑轮要求, 并且满足最大形变和许用应力要求, 机械结构顶部设计为圆角矩形梁形式。为了使机械结构力学承重分布更加合理, 双侧竖直梁设计成双管分跨支撑形式。为了分析该结构动态承载负荷时的稳定状态, 首先给出两个边界参考位置:训练者处于坐姿, 调整落座点, 使其重心处于顶部圆角矩形面几何中心点正下方, 称为位置1(图1(a)所示); 训练者按健康人体站起轨迹被绳索提拉到站姿, 重心位于顶部矩形面几何中心下方前侧, 称为位置2(图1(b)所示)。假设训练者下肢毫无支撑能力, 身体完全由绳索提拉, 则在位置2时机械结构处于最大负荷状态, 机械结构与人体的整体重心比在位置1时靠前, 根据稳定性零力矩原理(ZMP)^[10], 双侧竖直支撑梁中前梁设计成向前弯曲后再竖直向下与底座方管梁连接的承力状态, 如图1所示。为了防止两侧支撑梁在动态承重情况下发生侧向失稳, 在底座两条方管梁之间加方管横梁紧固。

该系统在运行过程中主要通过伺服电机带动绳索, 经过双侧竖直支撑梁和顶部前后圆角直梁上的6个滑轮改变方向后对训练者施力, 因此在该机械结构各梁的合适位置通过螺栓固定滑轮, 并作为力学分析时力的加载点。为了节省有限元分析和优化设计的运算时间, 并提高计算精度, 把该机械结构简化为薄壳结构, 并在Catia软件中用二维面结构建立模型, 采用壳单元类型将其以10 mm边长的单元格进行网格划分, 在螺栓孔之间用rbe2单元进行刚性连接, 同时用hypermesh中bolt(washer)功能在螺孔周围进行局部刚化模拟螺栓垫片效果, 对其进行力学分析, 计算中所用材料参数如下:弹性模量为210 GPa, 材料密度为7850 kg/m³, 泊松比为0.3。

为保证动态加载人体实验时整个机械结构在受力允许范围内满足力学要求, 对其进行最大受力状态的静力学分析。图2给出了机械结构中各受力点所加载力的计算示意图。本文以最大可满足体重为100 kg, 身高为190 cm的训练者(定为系统额定对象)进行康复训练为标准, 对其加载竖直向下G=980 N(m=100 kg, g=9.8 m/s²)的载荷进行受力分析。因为机械结构左右对称, 所以由顶部前后圆角横梁上A、B、G、H四点滑轮引出的左右两组牵引绳索受力情况相同, 本文只分析单侧一组绳索张力F_AE、F_GE即可, 在圆角矩形梁坐标系O-XYZ内A、B、G、H四处加载力。当进行康复训练初始时刻, 训练者坐在位置1。当训练系统开始工作后, 前绳和后绳相互配合提拉训练者站起到站姿的位置2, 整个机械结构处于最大负荷状态, 绳索在训练者肩上的两个施力点(E、F点)在Y方向上与前梁和后梁的距离比均为1∶ 5(以系统额定对象为参考), 如果此额定情况下能够满足力学要求, 则其他情况下也能满足力学要求。参考图2机械结构中各点的几何关系, 可以得出:

2FAEcosα+2FGEcosβ=G1FAEsinαcosγ=FGEsinβcosφ2

图2

Fig.2

	Figure Option ViewDownloadNew Window
	图2 载荷计算示意图Fig.2 Schematic of load calculation

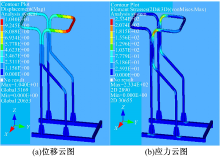
该设计方案机械结构中双侧竖直支撑梁选用外径⌀=50 mm、壁厚d=2.5 mm的45#钢管材进行加工, 底座采用45#钢2.5 mm厚的50 mm四方管加工, 各接触管件之间选用焊接关系, 其屈服强度为355 MPa, 安全系数为n=1.4, 则整个机械结构的许用应力为253.5 MPa, 设计要求管件最大形变位移不超过20 mm。根据对前述模型受力情况的分析, 在软件中对机械结构中各受力点加载上述方法计算出的载荷做受力分析, 分析其刚度、强度情况。图3(a)为机械结构在上述受力情况下的位移云图, 可见最大位移发生在顶部前横梁位置, 最大值为10.4 mm, 所以刚度满足本文设定的最大形变位移不超过20 mm的设计要求, 并且实际设计的整个机械结构高度为2 m, 最大形变值也远小于该结构的整体尺寸, 不会对训练者造成影响。图3(b)为机械结构所受应力状况, 最大应力发生在双侧竖直支撑梁顶部的前弯曲处, 最大值为233.4 MPa, 实际最大应力值小于许用应力, 所以该设计在强度方面也满足要求。但是该设计下整个机械结构所用管材壁厚达2.5 mm, 使得总质量为46.6 kg, 耗材较多。因此在满足设计要求的前提下, 需要对机械结构进行优化设计。

图3

Fig.3

	Figure Option ViewDownloadNew Window
	图3 焊接关系的机械结构静力学分析结果Fig.3 Analysis of the structure with welding relationship

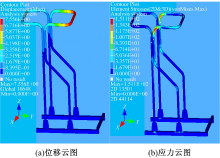
前述机械结构各接触管件采用了焊接关系, 但是本着开发可实际应用产品以方便运输与安装的目的, 在不改变设计结构的情况下将各管件焊接关系改进为可拆装的螺栓栓接关系, 各点受力(6个滑轮处)与所用管材(⌀=50 mm、d=2.5 mm、45#)保持不变, 其静力学分析结果如图4(a)(b)所示。其中机械结构的最大形变位移减至7.56 mm, 最大应力减至151.1 MPa, 仍满足设计要求, 即小于本文设定的最大形变位移20 mm, 小于许用应力253 MPa, 因此本改进方案可行。

图4

Fig.4

	Figure Option ViewDownloadNew Window
	图4 栓接关系的机械结构静力学分析结果Fig.4 Analysis of the structure with bolted relationship

在改进了管件连接关系后, 本着开发可实际应用产品时少用材料以降低成本的目的, 在不改变设计结构的基础上, 对管件厚度做尺寸优化设计, 以减小整体质量。将管壁厚度作为设计变量, 将整体质量作为优化目标, 将最大许用应力(253 MPa)和最大允许形变位移(20 mm)作为约束条件。其数学形式如下:

Minmx1, x2, …, xnf≤20σmax≤2533

式中:m(x_i)为优化目标函数; x_i为管壁厚度; i为迭代次数; f为最大形变位移; σ _max为最大应力。

对机械结构进行3次迭代优化计算后, 圆管管壁厚度为1.842 mm, 整体质量由46.6 kg减为37.9 kg, 比原设计减少18.67%, 说明优化后能够最大限度地减少用料, 从而提高经济效益。

以上优化都是在不改变结构设计的基础上进行的, 尽管管件连接结构由焊接关系改为栓接关系, 方便了拆装与运输, 在设计要求的力学性能允许范围内所做管壁厚度尺寸优化减薄了管壁, 但是由于材料刚度和强度的限制, 此结构下的管件连接关系的改进仅使用料质量减少了18.67%, 可见在该结构下只通过改进为栓接关系并优化管壁厚度减少用料量还是有限的。因此, 为了进一步减少材料用量并进一步减小单个管件尺寸以提高拆装和包装运输的方便性, 本文从几何结构设计上对以上设计进行再次优化。通过图4(b)看出:最大应力发生在双侧竖直支撑梁的前弯曲处, 那么考虑在侧梁顶部加直梁固定, 应该会减少弯曲处的应力并降低顶部前后横梁的最大位移。根据前述力学分析的经验, 保持原有管材选型(⌀=50 mm、d=2.5 mm、45#)不变并对机械结构做改进设计, 如图5所示。将双侧竖直支撑梁的前后梁去掉, 使双侧竖直支撑梁主要起支撑作用, 再在其上安装圆角矩形梁, 之前设计结构中顶部4个滑轮改安装在圆角矩形梁的前后梁上。在该改进的机械结构上相同位置施加相同载荷后, 其力学分析结果如图6所示。通过观察可以看出, 整个机械结构的最大形变位移减为4.807 mm, 最大应力减为138.8 MPa, 完全满足设计要求, 在保持该设计结构和设计要求力学性能范围内, 应用式(3)再次对管壁做尺寸优化, 管壁厚度减小到1.275 mm, 整体质量降低为33.2 kg。通过与图4中的计算结果对比发现:改进设计结构之后用料进一步减少, 其总质量比前一次设计再次减少12.4%, 并且该设计各管件都通过螺栓栓接, 拆卸后每一个管件尺寸更小, 更利于安装前的包装和运输。

图5

Fig.5

	Figure Option ViewDownloadNew Window
	图5 改进设计后系统机械结构示意图Fig.5 Improved mechanical mechanism

图6

Fig.6

	Figure Option ViewDownloadNew Window
	图6 改进设计后的机械结构静力学分析结果Fig.6 Analysis of the improved structure

尽管以上设计在满足设计要求的前提下已经最大限度地降低了整体质量, 并且兼顾了方便包装运输和安装拆卸, 但是在整体结构设计上并未有质的变化, 各管件形状仍然存在弯曲, 不便于加工生产, 而且拆卸后单个管件尺寸仍然较大, 所以, 仍希望通过结构设计优化来进一步降低质量, 并减小拆卸后各管件尺寸。因此, 依据对前述机械结构力学分析的经验和三角形结构稳定性原理, 重新设计了另外一种可实现减重式训练系统的机械结构, 如图7中左图所示。该结构可为使用者提供的活动空间与之前的设计结构相同, 上下采用50 mm方管梁(厚度1.5 mm, 45#钢), 左右两侧各两根交叉栓接的支撑圆管梁(外径为40 mm, 厚度4.5 mm, 45#钢), 与上下方管梁交接部分直接通过打孔插入并用螺栓固定, 更加利于拼装拆卸, 各管件均为支线型, 尺寸更小。

图7

Fig.7

	Figure Option ViewDownloadNew Window
	图7 采用侧向交叉梁的改进设计方案示意图Fig.7 Lateral cross-beam structure with or without top beam

对此改进结构再次做有限元分析。因为该设计除了结构有所变化外, 安装滑轮数量和空间位置与之前的设计结构完全相同, 因此仍按前述计算的施力关系进行静力学分析, 两组交叉圆管处螺栓孔用刚性单元进行连接并释放其轴向的旋转自由度实现栓接效果, 计算结果如图8所示。整个机械结构的最大形变位移为18.25 mm, 发生在受力较大的后梁; 最大应力为131.2 MPa, 发生在底部四方管的螺栓孔处。从计算结果来看, 此机械结构的最大变形位移小于所规定的20 mm, 最大应力小于许用应力253 MPa, 所以该设计方案同样满足设计要求。但是从产品角度考虑, 虽然该设计结构下具备了各部件更加适合拆卸、组合、包装、运输的优点, 但是用料质量陡增为54.6 kg, 成为本设计的最大缺点。为了进一步保持本设计结构的优点并降低用料质量, 通过分析其应力云图和位移云图(见图8)可知, 结构中较大位移都发生在顶部前后梁位置, 致使应力大部分集中在侧向支撑梁栓接部位。因此在此设计基础上, 在顶部前后梁之间再加一根圆管拉梁, 如图7中右图所示, 从而限制顶部前后梁位移, 改善侧梁栓接位置的应力集中现象, 在承受与前述结构同样载荷下的受力分析如图9所示, 可见在应力满足要求的情况下最大位移得到了极大改善, 最后整个机械结构的质量从54.6 kg降为27.6 kg。通过分析该结构的最大位移和最大应力可知, 在满足最大设计要求条件下管壁厚度还可进一步优化, 经过4次迭代计算, 得到优化结果:顶部两个方管厚度为1.5 mm, 底座方管厚度为0.8 mm, 侧向4根圆管厚度为1.1 mm, 所添加的顶部拉梁圆管厚度为1.35 mm, 最后, 整个机械结构的质量优化为19.2 kg。

图8

Fig.8

	Figure Option ViewDownloadNew Window
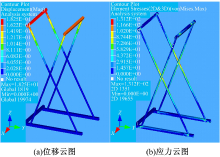	图8 顶部无拉梁的侧梁交叉式机械结构静力学分析结果Fig.8 Analysis of the structure with lateral cross-beam and without top-beam

图9

Fig.9

	Figure Option ViewDownloadNew Window
	图9 顶部添加拉梁的侧梁交叉式机械结构静力学分析结果Fig.9 Analysis of the structure with lateral cross-beam and top-beam

基于前述对各机械结构力学分析与优化设计, 得出表1中的结果。第一种设计方案在满足设计要求的情况下, 管件采用焊接关系的力学性能和栓接关系的力学性能是接近的, 但是从方便拆卸运输的角度出发, 采用栓接关系较为合理, 并在设计要求内对管件进行尺寸优化, 其质量从46.6 kg降到了37.9 kg。进一步改进设计(方案二)后, 继续在设计要求范围内对其优化, 对比发现, 方案二中单个管件的几何尺寸不仅比方案一中小, 满足管件拆卸后更加方便包装、运输的目的, 而且在满足设计要求的力学性能下, 质量也进一步减小到33.2 kg。为了进一步改进机械结构中单个管件的几何尺寸, 使其更加方便加工、组装和包装运输, 试探性地给出了方案三, 通过力学分析发现, 该结构要满足设计要求的力学性能, 需要增大侧向支撑管件的厚度, 主要是因为侧向管件交叉栓接后, 只有下半部分与底部横梁形成稳定的三角结构, 但是上半部分却处于开放状态, 而且顶部前后横梁又是主要的承力梁, 这就使得同样受力条件下, 各侧梁的顶部发生较大形变位移, 而栓接点处承受较大力矩作用, 出现应力比较集中的问题, 因此为了满足力学要求, 需要尽量增大管壁厚度, 导致结构的总体质量陡增, 使得该设计方案不够理想。但该机构的力学分析结果却给改进设计带来启发, 在顶部加入拉梁, 使得侧梁上半部分也构成三角稳定结构, 给出方案四并做优化分析。

表1

Table 1

表1(Table 1)

表1 各机械结构设计下的分析结果 Table 1 Results of each design 机械结构 设计说明 编号 管件关系 与取值状态 圆管壁厚度/mm 最大应力 /MPa 最大位移 /mm 质量/kg 初始设计方案一 图1 1 全焊接+自定值 2.5 233.4 10.4 46.6 2 栓接+优化值 1.8 253 20 37.9 改进设计方案二 图5 3 栓接+自定值 1.5 234.4 9.93 36.6 4 栓接+优化值 1.3 253 20 33.2 双侧支撑管交叉栓接设计 无顶拉梁设 计方案三 图7左 5 自定值 4.5 131.2 18.3 54.6 6 5方4圆全优 顶部两方管1.0 底座3方管0.7 侧向4圆管4.3 253 20 46.7 加顶拉梁设 计方案四 图7右 7 自定值 1.5 232.1 6.23 27.6 8 管件优化值 顶部方管1.5 底座方管0.8 双侧圆管1.1 顶拉梁圆管1.31 253 20 19.2

表1 各机械结构设计下的分析结果 Table 1 Results of each design

图10

Fig.10

	Figure Option ViewDownloadNew Window
	图10 各设计方案下机械结构质量变化曲线图Fig.10 Graph of qualities of each mechanical structure

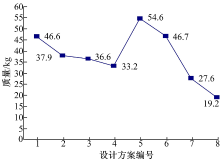
从结果可以发现, 顶部拉梁的加入极大地改善了该结构的力学性能, 在满足设计要求的前提下, 整个机械结构的质量得到极大的降低, 变为19.2 kg。参考图10中给出的各种设计方案下的质量变化曲线可以看出, 在各结构满足文中制定的设计要求的前提下, 最后一种设计方案用料质量是最少的, 并且其机械结构较之前的设计又是最为简单的, 从产品角度考虑, 不仅单个管件方便加工, 而且都是直线型管件, 非常方便包装运输, 管件间又是栓接固定, 非常便于安装拆卸。

为开发一套智能人体站起运动康复训练系统, 实现减重式站起训练, 减轻训练者腿部承受的负荷, 并使其能按照正常人体站起的重心轨迹进行反复训练, 本文设计并分析了几种机械结构, 不仅可以在几何结构上为训练系统预留恰当位置安装电气控制设备, 又能在力学结构上满足额定载荷设计要求下使训练者完成稳定的训练。通过对几种设计结构的分析、改进与优化, 可以看出每种设计结构都有很好的力学性能, 但是从开发可实际应用产品的角度出发, 参照表1中的各设计方案下的数据说明及之前给出的设计结构示意图可以看出:在满足力学要求的前提下, 每次对设计方案的改进都会使其各部件更加适合加工、拆卸、组合、包装、运输。在4种设计方案下, 机械结构在满足力学要求的前提下, 质量逐步减小。虽然对比之前的设计方案三质量有所增加, 但恰恰为方案四提供了直接的参考依据, 在其顶部前后梁间安装了拉梁, 改进后结构的力学性能得到极大改善, 材料的使用量减少, 降低了设备的重量和制造成本, 采用直线型管件进行简单栓接安装, 便可满足整个系统的承力要求。本文最后给出的设计方案与之前设计相比较, 不涉及到管材的焊接成型, 只需对所选型号管材进行切割打孔、栓接拼装即可, 也使其更利于产品化加工、推广和家庭化应用。