基于多虚拟元件的直腿四足机器人Trot步态控制

引用本文

李满天, 蒋振宇, 王鹏飞, 孙立宁. 基于多虚拟元件的直腿四足机器人Trot步态控制. 2015, 45(5): 1502-1511
LI Man-tian, JIANG Zhen-yu, WANG Peng-fei, SUN Li-ning. Trotting gait control of quadruped robot with straight legs based on virtual elements. Journal of Jilin University Engineering and Technology Edition, 2015, 45(5): 1502-1511 复制到剪切板

Permissions

基于多虚拟元件的直腿四足机器人Trot步态控制

李满天, 蒋振宇, 王鹏飞, 孙立宁

哈尔滨工业大学机器人技术与系统国家重点实验室,哈尔滨 150080

王鹏飞(1977-),男,副教授,博士.研究方向:仿生机器人.E-mail:wangpengfei1007@163.com

作者简介:李满天(1974-),男,副教授,博士.研究方向:仿生机器人.E-mail:limt@hit.edu.cn

基金:“863”国家高技术研究发展计划项目(2011AA040701); 国家自然科学基金项目(61375097,61175107)

摘要

为了提高四足机器人在未知复杂地形下的快速平稳通过能力,基于直腿四足机器人模型对机器人着地相控制方法进行了研究。首先,针对在复杂路面下的运动工况,建立了直腿四足机器人的运动学和动力学模型。其次,基于弹簧负载倒立摆动力学特性,在机身多个自由度上引入弹性阻尼等虚拟元件,在着地相过程中实现了对包括前进等在内的多个机身运动自由度的控制。最后,在虚拟样机仿真中实现了机器人在平坦路面和复杂路面下的运动,验证了控制方法的正确性和有效性。通过对仿真结果的分析,总结出两种控制策略在运动平稳性、能耗水平和耦合运动等方面的优劣,为提高机器人在不同运行工况下的综合运动性能奠定了基础。

关键词: 自动控制技术; 四足机器人; 运动控制; 对角小跑步态

中图分类号:TP273 文献标志码:A 文章编号:1671-5497(2015)05-1502-10

Trotting gait control of quadruped robot with straight legs based on virtual elements

LI Man-tian, JIANG Zhen-yu, WANG Peng-fei, SUN Li-ning

State Key Laboratory of Robotics and System, Harbin Institute of Technology, Harbin 150080, China

Abstract

To enhance the capability of fleet and smooth navigation of quadruped robot in unknown and complex terrain, a control method of quadruped robot with straight legs in stance phase is proposed. First, in terms of the motion condition on the complex terrain, the kinematics and dynamics models of the quadruped robot with straight legs are established. Then, on the basis of the dynamic characteristics of the Spring Loaded Inverted Pendulum (SLIP), virtual elastic and damping elements are introduced to the multi-DoFs of the torso to realize the control of these DoFs during stance phase, especially, in the forward movement. Finally, the control method is verified in simulation of the robot navigating on flat or complex ground. The performances of two control strategies developed are discussed in simulation to improve the synthesized performance of quadruped under different conditions.

Keyword: automatic control technology; quadruped robot; locomotion control; trotting gait

Show Figures

0 引言

四足哺乳动物在复杂环境中表现出的高机动性一直是机器人研究追求的目标。其中, Trot步态^{[1, 2]}是四足哺乳动物以中等速度运动时广泛采用的一种运动形式。目前, 四足机器人的应用已经逐渐扩展到野外环境, 而其中的关键问题之一是提高机器人在复杂地形下的快速平稳通过能力并降低系统能耗水平。为提高机器人的运动性能, 很多研究人员都对Trot步态的控制方法进行了研究。MIT腿实验室的Raibert等^[3]基于弹簧负载倒立摆模型(Spring loaded inverted pendulum, SLIP)实现了直腿单足和四足机器人的跑跳运动。该方法基于SLIP的被动动力学特性, 从原理上保证了系统运行的低能耗, 但其缺少着地相内的前进速度控制, 因此在复杂地形运动中, 机器人行走速度可能会有较大波动。Buchli等^[4]开发了基于逆动力学的控制算法并将其运用到LittleDog机器人, 使之可以通过比较大的障碍, 但目前这种方法常运用在静步态。在Trot步态的控制研究中, 还有很多基于智能算法^{[5, 6, 7]}和CPG^{[8, 9]}的尝试, 但都不够完善。美国波士顿动力公司研制的BigDog四足机器人实现了以Trot步态在复杂路面上的行走^[10], 但机器人的本体设计和控制方法细节尚未公开。

虚拟模型控制(VMC)是提高足式机器人运动性能的另一种有效手段, ScarlETH应用这种控制策略控制单腿跳跃运动^{[11, 12]}。在Trot步态着地相运动过程中要实现对机身6个运动自由度的调节, 需要控制机身上受到的3个合力和3个合力矩。直腿四足机器人的两条对角着地腿共有6个相互独立的力或力矩作为控制输出, 但机身期望的合力和合力矩与6个控制输出的转换矩阵并不总是满秩矩阵, 这不仅限制了VMC的应用, 还可能给机身的多个运动自由度带来耦合运动现象, 为此需要对VMC方法在四足机器人上的应用做深入的分析和探讨。为了解决这一问题, 本文在前期研究^[13]的基础上, 结合Trot步态运动特点, 通过改进虚拟模型控制策略, 提出一种基于3个虚拟元件的四足机器人Trot步态着地相运动控制策略, 解决了机器人在平坦路面上的机身位姿控制问题, 并能有效地简化控制参数的整定过程。为了提高复杂路面上的运动平稳性, 本文进一步提出了基于5个虚拟元件的控制策略。最后, 通过仿真对控制算法加以验证, 并分析了这两种控制策略对机身前进速度的控制效果、能耗水平和多自由度耦合的影响。

1 模型的建立

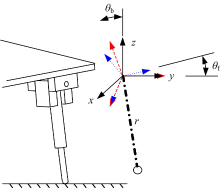
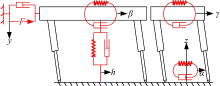
直腿四足机器人模型如图1(a)所示。机器人有4条可伸缩的腿, 每条腿有一个前摆关节和一个侧摆关节, 两个关节的中心线相交。前摆关节和侧摆关节受作用其上的力矩控制, 而腿部的伸缩由腿部的轴向力控制。机器人机身质心位于其几何中心。机身姿态角和腿部摆角转动正方向的定义如图1(b)所示, α 、β 、γ 分别为机身的偏航角、俯仰角和横滚角, x_b、y_b、z_b分别为机身质心在世界坐标系下3个方向的位移, θ _f、θ _b分别为腿的前摆角和侧摆角。机器人沿x_b、y_b轴的运动分别称为侧移运动和前进运动, 相应的速度为侧移速度和前进速度。机器人的机身和腿部都有质量和转动惯量。

	Figure Option View Download New Window
	图1 机器人模型Fig.1 Model of robot

1.1 模型运动学分析

在对四足机器人进行控制时, 需要了解机器人当前的运动状态。本文采用Z-X-Y欧拉角的形式描述机身连体坐标系(Ox_by_bz_b)在世界坐标系中的位置和姿态, 变换矩阵如下:

$\begin{matrix} \begin{matrix} _{b}^{w} T =_{w_{0}}^{w} T \cdot_{b_{1}}^{w_{0}} T \cdot_{b_{2}}^{b_{1}} T \cdot_{b}^{b 2} T = \\ [\begin{matrix} cαcγ - sαsβsγ & - cβsα & cαsγ + cγsαsβ & x_{b} \\ cγsα - cαsβsγ & cαcβ & sαsγ - cαsγsβ & y_{b} \\ - cβsγ & sβ & cβcγ & z_{b} \\ 0 & 0 & 0 & 1 \end{matrix}] (1) \end{matrix} \end{matrix}$

式中:c和s分别为cos和sin的简化符号。

为了获得足端在机身连体坐标系中的坐标以在控制过程中规划足端的运动和了解地面的状况, 建立如图2所示的腿部运动学模型。

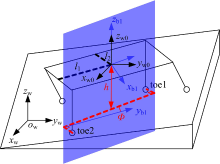
	Figure Option View Download New Window
	图2 腿部运动学模型Fig.2 Model of leg

图2中实线的t₀号坐标系固连在机身上, 虚线的t₁号坐标系固连在连接块上, 点线的t₂号坐标系固连在腿上部, 它们的原点都位于前摆关节和侧摆关节中心线的交点处。r是足端到关节中心线交点的距离。通过坐标变换可以得到足端在t₀号坐标系中的坐标表示式:

$\begin{matrix} ^{t_{0}} {[\begin{matrix} x \\ y \\ z \\ 1 \end{matrix}]}_{toe} = [\begin{matrix} - rs θ_{b} c θ_{f} \\ rs θ_{f} \\ - rc θ_{b} c θ_{f} \\ 1 \end{matrix}] (2) \end{matrix}$

每条腿对应的t₀号坐标系与机身质心处的坐标系(Ox_by_bz_b)存在平移关系。利用式(1)和式(2), 不仅可以确定各个足端的位置, 还可以利用着地的对角腿的足端位置确定地面的倾角和机身质心处的高度。如图3所示, 将地面倾角φ 定义为在坐标系(Ox_b1y_b1z_b1)中两着地腿的足端向OYZ平面内投影的连线与y_b1轴的夹角, 将机身质心处高度h定义为在坐标系(Ox_b1y_b1z_b1)中两着地腿的足端向z_b1轴投影的平均值。其中z_b1轴与世界坐标系的z_w同向, y_b1轴指向机身偏航方向。

	Figure Option View Download New Window
	图3 地面倾角和机身质心处高度定义图Fig.3 Definitions of land’ s slope and the body height

利用式(1)和式(2)可以得到两着地腿足端toe1和toe2在坐标系(Ox_b1y_b1z_b1)中的坐标^b1z₁ $\begin{matrix} 、^{b 1} \end{matrix}$ z₂ $\begin{matrix} 、^{b 1} \end{matrix}$ y₁、^b1y₂, 进而得到地面倾角为:

$\begin{matrix} φ = \arctan (\frac{_{}^{b 1} z_{2} -_{}^{b 1} z_{1}}{_{}^{b 1} y_{2} -^{b 1} y_{1}}) (3) \end{matrix}$

机身质心处高度为:

$\begin{matrix} h = \frac{_{}^{b 1} z_{1} +_{}^{b 1} z_{2}}{2} (4) \end{matrix}$

将计算得到的地面倾角和机身质心处高度值作为机器人在复杂路面行走时的反馈信息, 实现在运动过程中依照地面情况进行机身俯仰角和跳跃高度的调节。

1.2 模型动力学分析

为使机器人机身能够依循虚拟元件的特性实现预期的运动, 首先对着地腿的关节力矩和轴向力对机身的作用加以分析, 以便施加合适的控制力矩和力。由于模型中腿部质量远小于机身的质量, 因此机器人在着地相的运动主要由着地足的力和力矩进行调节, 并且在分析中忽略腿部惯性力的影响。

由足端在t₀号坐标系中的坐标可以得到关于速度[ $\begin{matrix} \overset{\cdot}{x} \end{matrix}$ , $\begin{matrix} \overset{\cdot}{y} \end{matrix}$ , $\begin{matrix} \overset{\cdot}{z} \end{matrix}$ ]和[ $\begin{matrix} \overset{\cdot}{r} \end{matrix}$ , $\begin{matrix} {\overset{\cdot}{θ}}_{b} \end{matrix}$ , $\begin{matrix} {\overset{\cdot}{θ}}_{f} \end{matrix}$ ]的雅可比矩阵J:

$\begin{matrix} [\begin{matrix} \overset{\cdot}{x} \\ \overset{\cdot}{y} \\ \overset{\cdot}{z} \end{matrix}] = J [\begin{matrix} \overset{\cdot}{r} \\ {\overset{\cdot}{θ}}_{b} \\ {\overset{\cdot}{θ}}_{f} \end{matrix}] = [\begin{matrix} - s θ_{b} c θ_{f} & - rc θ_{b} c θ_{f} & rs θ_{b} s θ_{f} \\ s θ_{f} & 0 & rc θ_{f} \\ - c θ_{b} c θ_{f} & rs θ_{b} c θ_{f} & rc θ_{b} s θ_{f} \end{matrix}] [\begin{matrix} \overset{\cdot}{r} \\ {\overset{\cdot}{θ}}_{b} \\ {\overset{\cdot}{θ}}_{f} \end{matrix}] (5) \end{matrix}$

根据虚功原理, 可以得到关节力矩和腿部轴向力与足底力的关系。在忽略腿部惯性力时, 足底力与腿部对机身的作用力大小相等, 方向相反。因此得到关节力矩和腿部轴向力与腿部对机身的作用力的关系如下式所示:

$\begin{matrix} [\begin{matrix} F_{x} \\ F_{y} \\ F_{z} \end{matrix}] = - (J^{T})^{- 1} [\begin{matrix} F \\ τ_{b} \\ τ_{f} \end{matrix}] (6) \end{matrix}$

式中:F_x、F_y、F_z表示腿部对机身的3个方向作用力; F为腿部滑动关节输出力; τ _f和τ _b分别为腿部前摆和侧摆关节的输出力矩。

由受力分析可知, 腿部对机身t₀号坐标系的作用力矩与关节力矩存在如下关系:

$\begin{matrix} [\begin{matrix} T_{x} \\ T_{y} \\ T_{z} \end{matrix}] = - [\begin{matrix} 0 & c θ_{b} \\ 1 & 0 \\ 0 & - s θ_{b} \end{matrix}] [\begin{matrix} τ_{b} \\ τ_{f} \end{matrix}] (7) \end{matrix}$

综合式(6)和式(7), 可以得到着地腿对机身的作用力和力矩:

$\begin{matrix} \begin{matrix} [\begin{matrix} F_{x} \\ F_{y} \\ F_{z} \\ T_{x} \\ T_{y} \\ T_{z} \end{matrix}] = [\begin{matrix} s θ_{b} c θ_{f} & c θ_{b} / (rc θ_{f}) & - s θ_{b} s θ_{f} / r \\ - s θ_{f} & 0 & - c θ_{f} / r \\ c θ_{b} c θ_{f} & - s θ_{b} / (rc θ_{f}) & - c θ_{b} s θ_{f} / r \\ 0 & 0 & - c θ_{b} \\ 0 & - 1 & 0 \\ 0 & 0 & s θ_{b} \end{matrix}] \cdot \\ [\begin{matrix} F \\ τ_{b} \\ τ_{f} \end{matrix}] = T_{F} [\begin{matrix} F \\ τ_{b} \\ τ_{f} \end{matrix}] (8) \end{matrix} \end{matrix}$

机身质心处的合力和合力矩如下式所示:

$\begin{matrix} \begin{matrix} {[\begin{matrix} F_{cx} & F_{cy} & F_{cz} & T_{cx} & T_{cy} & T_{cz} \end{matrix}]}^{T} = \\ [\begin{matrix} F_{x 1} + F_{x 2} \\ F_{y 1} + F_{y 2} \\ F_{z 1} + F_{z 2} \\ - 2 (F_{z 1} - F_{z 2}) l_{1} + T_{x 1} + T_{x 2} \\ 2 (F_{z 1} - F_{z 2}) l_{2} + T_{y 1} + T_{y 2} \\ 2 (F_{x 1} - F_{x 2}) l_{1} - 2 (F_{y 1} - F_{y 2}) l_{2} + T_{z 1} + T_{z 2} \end{matrix}] = \\ AF {[\begin{matrix} F_{1} & τ_{b 1} & τ_{f 1} & F_{2} & τ_{b 2} & τ_{f 1} \end{matrix}]}^{T} (9) \\ 其中 : \\ A = \\ {[\begin{matrix} 1 & 0 & 0 & 0 & 0 & 0 & 1 & 0 & 0 & 0 & 0 & 0 \\ 0 & 1 & 0 & 0 & 0 & 0 & 0 & 1 & 0 & 0 & 0 & 0 \\ 0 & 0 & 1 & 0 & 0 & 0 & 0 & 0 & 1 & 0 & 0 & 0 \\ 0 & 0 & - 2 l_{1} & 1 & 0 & 0 & 0 & 0 & 2 l_{1} & 1 & 0 & 0 \\ 0 & 0 & 2 l_{2} & 0 & 1 & 0 & 0 & 0 & - 2 l_{2} & 0 & 1 & 0 \\ 2 l_{1} & - 2 l_{2} & 0 & 0 & 0 & 1 & - 2 l_{1} & 2 l_{2} & 0 & 0 & 0 & 1 \end{matrix}]}_{6 \times 12} \\ F = {[\begin{matrix} T_{F_{1}} & 0_{6 \times 3} \\ 0_{6 \times 3} & T_{F_{2}} \end{matrix}]}_{12 \times 6} \end{matrix} \end{matrix}$

式中:F_x、τ _b_x、τ _f_x的下标x的1, 2分别代表腿1和腿2; l₁、l₂的定义见图3。

由式(9)可知, 机身质心处的3个合力和3个合力矩是两着地腿6个控制力和控制力矩的函数。分析发现, 对角着地腿上的轴向力、前摆力矩和侧摆力矩并不能在任意情况下使质心处的3个合力和3个合力矩为任意值。下面以当r₁=r₂=r₀, θ _b1=θ _b2=0, θ _f1=θ _f2=0时为例进行说明, 此时对角着地腿对机身的作用力和作用力矩为:

$\begin{matrix} [\begin{matrix} F_{xi} \\ F_{yi} \\ F_{zi} \\ T_{xi} \\ T_{yi} \\ T_{zi} \end{matrix}] = [\begin{matrix} 0 & 1 / r_{0} & 0 \\ 0 & 0 & - 1 / r_{0} \\ 1 & 0 & 0 \\ 0 & 0 & - 1 \\ 0 & - 1 & 0 \\ 0 & 0 & 0 \end{matrix}] [\begin{matrix} F_{i} \\ τ_{bi} \\ τ_{fi} \end{matrix}], i = 1, 2 (10) \end{matrix}$

将式(10)代入式(9)可得机身质心处所受的合力和合力矩为:

$\begin{matrix} \begin{matrix} {[\begin{matrix} F_{cx} & F_{cy} & F_{cz} & T_{cx} & T_{cy} & T_{cz} \end{matrix}]}^{T} = \\ [\begin{matrix} 0 & \frac{1}{r_{0}} & 0 & 0 & \frac{1}{r_{0}} & 0 \\ 0 & 0 & - \frac{1}{r_{0}} & 0 & 0 & - \frac{1}{r_{0}} \\ 1 & 0 & 0 & 1 & 0 & 0 \\ - 2 l_{1} & 0 & - 1 & 2 l_{1} & 0 & - 1 \\ 2 l_{2} & - 1 & 0 & - 2 l_{2} & - 1 & 0 \\ 0 & \frac{2 l_{1}}{r_{0}} & \frac{2 l_{2}}{r_{0}} & 0 & - \frac{2 l_{1}}{r_{0}} & - \frac{2 l_{2}}{r_{0}} \end{matrix}] \cdot \\ {[\begin{matrix} F_{1} & τ_{b 1} & τ_{f 1} & F_{2} & τ_{b 2} & τ_{f 2} \end{matrix}]}^{T} (11) \end{matrix} \end{matrix}$

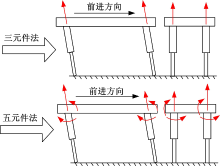
对于上式所示的以 $\begin{matrix} {[F_{1}, τ_{b 1}, τ_{f 1}, F_{2}, τ_{b 2}, τ_{f 2}]}^{T} \end{matrix}$ 为未知数的非齐次线性方程组, 要使对于任意的合力和合力矩 $\begin{matrix} {[F_{cx}, F_{cy}, F_{cz}, T_{cx}, T_{cy}, T_{cz}]}^{T} \end{matrix}$ 有解, 需要使矩阵T为满秩矩阵, 而此时矩阵T的秩为5, 不满足要求。即关节驱动力与机身驱动力没有严格的一一对应关系, 因此无法依据动力学反解的方法来设计控制器, 着地相的控制策略需要进一步的分析和探讨。

2 控制方法设计

本文作者在基于SLIP模型的简化直腿四足机器人的运动控制方法研究^[13]中发现, 机器人在地形扰动下行走性能不尽理想, 并且姿态控制参数整定较为繁琐。而虚拟模型控制方法则假想机身处存在一些虚拟元件, 由这些虚拟元件产生机身处期望的受力, 再通过关节雅可比矩阵转换得到的腿部控制力和力矩以产生虚拟元件的效果。本文主要针对四足机器人在崎岖路面上的着地相控制策略, 为此结合前期研究, 在文献[11-12]的基础上发展出了两种基于虚拟模型的着地相控制方法。控制策略依照虚拟元件数量分别称为“ 三元件法” 和“ 五元件法” 。

四足机器人的动态平稳行走首先需要维持机

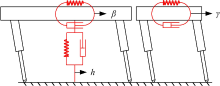
身姿态的稳定, 为此首先在机身的俯仰和横滚运动自由度上各加入一个弹簧阻尼虚拟元件。同时, 为了减小运动过程中的地面冲击, 在机身高度方向上增加一个弹簧阻尼虚拟元件。该方法称为“ 三元件法” , 其虚拟元件分布如图4所示。

	Figure Option View Download New Window
	图4 三元件法的虚拟元件分布Fig.4 Virtual elements in 3-element method

机身质心处的合力和合力矩应符合下式:

$\begin{matrix} [\begin{matrix} F_{cz} \\ T_{cx} \\ T_{cy} \end{matrix}] \end{matrix}$ = $\begin{matrix} [\begin{matrix} - k_{p h} (h - h_{0} - Δ h) - k_{d h} \overset{\cdot}{z} \\ - k_{pβ} (β - β_{d}) - k_{dβ} \overset{\cdot}{β} \\ - k_{pγ} (γ - γ_{d}) - k_{dγ} \overset{\cdot}{γ} \end{matrix}] \end{matrix}$ (12)

式中:k_p_x为虚拟元件的弹性系数; k_d_x为虚拟元件的阻尼系数; β _d、γ _d为期望的俯仰角和横滚角; h为当前高度; h₀为初始高度; Δ h为期望的高度变化。

当质心处的合力和合力矩满足式(12)时, 机器人在垂直机身方向会呈现弹簧阻尼的特性。此外, 选择合理的阻尼参数能够使俯仰角和横滚角跟随期望角度, 而阻尼系数可以根据着地时长和机身转动惯量计算得到, 由此可以避免前期方法^[13]中机身俯仰和横滚运动的PD参数调节过程。利用式(12)所示的方程组不能将两条着地腿的4个关节力矩和两个轴向力都解算出来, 还需要3个附加方程。出于平衡各驱动器负载以及减小对单驱动器的输出要求的考虑, 添加如下的方程组:

$\begin{matrix} \{\begin{matrix} F_{1} - F_{2} = 0 \\ τ_{f 1} - τ_{f 2} = 0 \\ τ_{b 1} - τ_{b 2} = 0 \end{matrix} (13) \end{matrix}$

综合式(9)(12)(13), 可以得出各关节力矩和轴向力:

$\begin{matrix} \begin{matrix} [\begin{matrix} F_{1} \\ τ_{b 1} \\ τ_{f 1} \\ F_{2} \\ τ_{b 2} \\ τ_{f 2} \end{matrix}] = {[\begin{matrix} P_{1} \\ P_{2} \end{matrix}]}^{- 1} [\begin{matrix} 0 \\ 0 \\ 0 \\ - k_{p h} (h - h_{0} - Δ h) - k_{d h} \overset{\cdot}{z} \\ - k_{pβ} (β - β_{d}) - k_{dβ} \overset{\cdot}{β} \\ - k_{pγ} (γ - γ_{d}) - k_{dγ} \overset{\cdot}{γ} \end{matrix}] (14) \\ P_{1} = [\begin{matrix} 1 & 0 & 0 & - 1 & 0 & 0 \\ 0 & 1 & 0 & 0 & - 1 & 0 \\ 0 & 0 & 1 & 0 & 0 & - 1 \end{matrix}] \\ P_{2} = {[\begin{matrix} A (3, :) \\ A (4, :) \\ A (5, :) \end{matrix}]}_{3 \times 12} {[\begin{matrix} T_{F_{1}} & 0_{6 \times 3} \\ 0_{6 \times 3} & T_{F_{2}} \end{matrix}]}_{12 \times 6} \end{matrix} \end{matrix}$

式中:A(i, :)为式(9)中矩阵A的第i行。

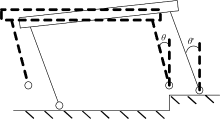
利用式(14)获得的着地腿的关节力矩和轴向力用于调节机身的俯仰、横滚和竖直方向的运动。对四足机器人的前进速度、侧移速度和偏航角的控制则是通过选择着地角的方式加以实现。但在阶梯和斜坡等复杂路面上运动时, 机器人的运动可能会受到地形的剧烈影响。如图5所示, 台阶导致着地后着地角发生变化, 即θ '≠ θ 。在这种情况下, 若不在着地后对速度进行控制, 将导致速度偏离期望值, 甚至使机器人失去平衡。

	Figure Option View Download New Window
	图5 复杂地形对着地角的影响Fig.5 Influence on touch down angle caused by rough terrain

为了弥补着地角调节策略的不足并提高模型在复杂地形下的快速通过能力, 本文在三元件法的基础上进一步在机身前进方向上添加一个力和阻尼并联的虚拟元件。由上文分析可知, 质心处的6个合力/力矩, 只能选取其中的5个作为控制输出。因此在偏航角处添加一个弹簧阻尼虚拟元件, 而侧移速度仍采用着地角控制方法。此时机器人有5个虚拟元件, 分布如图6所示。在着地相运动中, 机器人的前进速度会跟随期望速度, 在竖直方向呈现弹簧阻尼的特性, 同时3个姿态角也会跟随期望角度。由虚拟元件可以得到机身质心处的合力和合力矩的5个方程, 如下式所示:

$\begin{matrix} [\begin{matrix} F_{cy} \\ F_{cz} \\ T_{cx} \\ T_{cy} \\ T_{cz} \end{matrix}] = [\begin{matrix} - k_{y} (\overset{\cdot}{y} - {\overset{\cdot}{y}}_{d}) + mgsinβ \\ - k_{p h} (h - h_{0} - Δ h) - k_{d h} \overset{\cdot}{z} \\ - k_{pβ} (β - β_{d}) - k_{dβ} \overset{\cdot}{β} \\ - k_{pγ} (γ - γ_{d}) - k_{dγ} \overset{\cdot}{γ} \\ - k_{pαs} (α - α_{d}) - k_{dαs} \overset{\cdot}{α} \end{matrix}] (15) \end{matrix}$

式中:mgsinβ 为用于补偿沿机身前进方向的重力分量; $\begin{matrix} \overset{\cdot}{y} \end{matrix}$ 、α _d分别为期望的前进速度和俯仰角。

	Figure Option View Download New Window
	图6 五元件法的虚拟元件Fig.6 Virtual elements in 5-element method

为了将6个控制力和控制力矩解出, 增加一个附加方程:

$\begin{matrix} τ_{b 1} - τ_{b 2} = 0 (16) \end{matrix}$

将式(9)(15)(16)联立, 可以得出各关节力矩和轴向力:

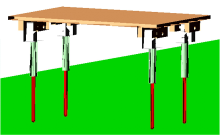
$\begin{matrix} \begin{matrix} [\begin{matrix} F_{1} \\ τ_{b 1} \\ τ_{f 1} \\ F_{2} \\ τ_{b 2} \\ τ_{f 2} \end{matrix}] = {[\begin{matrix} P_{1} \\ P_{2} \end{matrix}]}^{- 1} [\begin{matrix} 0 \\ - k_{y} (\overset{\cdot}{y} - {\overset{\cdot}{y}}_{d}) \\ - k_{p h} (h - h_{0} - Δ h) - k_{d h} \overset{\cdot}{z} \\ - k_{pβ} (β - β_{d}) - k_{dβ} \overset{\cdot}{β} \\ - k_{pγ} (γ - γ_{d}) - k_{dγ} \overset{\cdot}{γ} \\ - k_{pαs} (α - α_{d}) - k_{dαs} \overset{\cdot}{α} \end{matrix}] (17) \\ P_{2} = {[\begin{matrix} A (2, :) \\ A (3, :) \\ A (4, :) \\ A (5, :) \\ A (6, :) \end{matrix}]}_{5 \times 12} {[\begin{matrix} T_{F_{1}} & 0_{6 \times 3} \\ 0_{6 \times 3} & T_{F_{2}} \end{matrix}]}_{12 \times 6} \\ P_{1} = [\begin{matrix} 0 & 1 & 0 & 0 & - 1 & 0 \end{matrix}] \end{matrix} \end{matrix}$

3 仿真实验与分析

本文采用ADAMS和MATLAB联合仿真手段对控制方法的性能加以分析。仿真模型如图7所示, 结构参数如下:机身质量为12.14 kg, 机身沿x方向、y方向和z方向的转动惯量分别为0.23、0.09、0.32 kg· m², 连接块质量为0.2 kg, 腿上部和下部质量分别为0.08和0.03 kg, 前后腿和左右腿之间跨距分别为0.36和0.18 m, 腿部伸展长度为0.25 m。分析内容包括前进速度跟踪性能、前摆关节能量消耗、前进速度与侧移速度耦合影响等方面。

	Figure Option View Download New Window
	图7 ADAMS中的仿真模型Fig.7 Simulation model in ADAMS

3.1 前进速度跟踪性能分析

由于三元件法和五元件法的不同主要在于前进速度上虚拟元件的有无, 而五元件法设计的初衷是加强复杂路面上前进速度的控制, 所以首先要研究和比较的是这两种方法在前进速度上的跟踪性能。

三元件法对机器人速度的控制是通过着地角在一个着地相过程中影响机体平动速度的总效果来实现的^[13], 如图8所示。三元件法在着地相不能对速度进行实时的反馈控制, 速度必然会有波动。同时, 由于着地角与速度之间的关系是非线性的, 且难以获得准确的表达式, 所以用着地角对速度进行控制很难在一个跳跃周期达到目标值, 需要在跳跃多步后才能调整到目标值。

	Figure Option View Download New Window
	图8 着地角对速度的影响图Fig.8 Influence on forward speed caused by touch down angle

五元件法中前进速度处存在由阻尼和力组成的虚拟元件, 在着地相中前向驱动力符合下式:

$\begin{matrix} F_{y} = - k_{y} (\overset{\cdot}{y} - {\overset{\cdot}{y}}_{d}) = m \overset{\cdot \cdot}{y} (18) \end{matrix}$

式中:F_y为前进速度方向上的合力; $\begin{matrix} \overset{\cdot}{y} \end{matrix}$ , $\begin{matrix} {\overset{\cdot}{y}}_{d} \end{matrix}$ 分别为当前速度和期望速度; k_y为系数。

速度会在着地时以指数收敛至目标速度, 如下式所示:

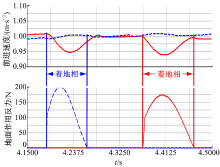
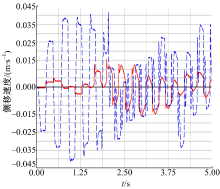
$\begin{matrix} v = {\overset{\cdot}{y}}_{d} + ({\overset{\cdot}{y}}_{0} - {\overset{\cdot}{y}}_{d}) e^{- \frac{k_{y}}{m} t} (19) \end{matrix}$

为验证上面的分析, 在ADAMS虚拟样机中利用两种方法控制机器人的前进速度稳定到1 m/s, 图9是两种方法的仿真结果。

	Figure Option View Download New Window
	图9 前进速度控制仿真结果Fig.9 Simulation result of forward velocity control

图中的实线和虚线分别对应三元件法和五元件法。从图中可以看出与前面分析的结果一致, 在着地相时三元件法中的前进速度会有一个先减速后加速的过程, 前进速度会出现波动, 而五元件法中前进速度紧紧跟随目标速度, 准确性更高。

复杂地形会给机器人的运动带来扰动。例如, 在过台阶时机身俯仰角会因地形扰动而发生变化, 并且腿部着地点的位置与预想的位置发生偏差。台阶的出现会对前进速度的控制产生较大的扰动。为对比两种方法的控制性能, 在ADAMS虚拟样机中分别用两种方法控制四足机器人以0.6 m/s的期望速度通过一个2 cm高的台阶。图10是在过台阶时两种方法的仿真结果。图中实线和虚线分别对应三元件法和五元件法。相比三元件法, 五元件法在过台阶时前进速度的波动要小得多。五元件法能很好地稳定住前进速度, 对地形变化具有较强的抗干扰能力。

	Figure Option View Download New Window
	图10 过台阶仿真结果Fig.10 Simulation result of crossing a step

在生物和足式机器人研究中, 一般采用无量纲数FR来衡量不同体型的生物或机器人的行走速度, 其计算公式如下:

$\begin{matrix} FR = v^{2} / (gl) (20) \end{matrix}$

式中:v为前进速度; g为重力加速度; l为腿长; Bigdog机器人Trot步态的最大FR为0.26或0.41^[14], 通过计算, 机器人在平坦路面和台阶跨越仿真中所能达到的FR分别为0.41和0.15。

综上, 两种方法都具备四足机器人在未知地形下快速行走控制的应用潜力。但五元件法对地面的适应能力更强, 运动平稳性更为理想。

3.2 前摆关节能量消耗分析

两种方法对前进速度控制效果的不同是由前摆力矩的输出不同引起的, 因此其能耗水平也有差异。而能量利用率也是评价机器人性能的一个重要指标。为此本节将两种策略的电机驱动器在输出前摆力矩过程中的热能损耗进行比较。

在三元件法中, 速度的控制是通过着地角来实现的, 而在着地时前摆力矩并不用于控制速度, 而是主要用于控制机身的俯仰角, 它近似符合下式:

$\begin{matrix} τ_{f} = - k_{p} (β - β_{d}) - k_{d} \overset{\cdot}{β} (21) \end{matrix}$

当机器人平稳运动时, 俯仰角波动很小, 因此在三元件法中前摆力矩很小, 前摆关节近似是一个被动关节, 而五元件法中的前摆力矩和腿部轴向力共同用于控制前进速度。为便于分析, 将矢状面内的机器人模型依照“ 虚拟腿” 方法^[3]进一步简化为弹簧负载倒立摆, 如图11所示。

	Figure Option View Download New Window
	图11 五元件法力矩分析Fig.11 Analysis on torque in 5-element method

在前进速度平面内, 五元件法为保证机身前进速度的恒定和竖直方向的弹簧质量特性, 需满足:

$\begin{matrix} \{\begin{matrix} - \frac{τ_{f}}{r} cosθ - Fsinθ = m \overset{\cdot \cdot}{y} = 0 \\ - \frac{τ_{f}}{r} sinθ + Fcosθ = - K (z - z_{0}) = Psin (\frac{t}{T_{s}} π) \end{matrix} (22) \end{matrix}$

式中:T_s为着地相时间; K为与腿部期望的弹簧刚度有关的常量。

将两式联立可得:

τ _f=-rsinθ Psin( $\begin{matrix} \frac{t}{T_{s}} \end{matrix}$ π )=yPsin( $\begin{matrix} \frac{t}{T_{s}} \end{matrix}$ π ) (23)

设前进速度为 $\begin{matrix} {\overset{\cdot}{y}}_{0} \end{matrix}$ , 则:

$\begin{matrix} y_{0} = {\overset{\cdot}{y}}_{0} T_{s} / 2, y = (t - T_{s} / 2) {\overset{\cdot}{y}}_{0} (24) \end{matrix}$

将式(24)代入式(23)中, 可得:

$\begin{matrix} τ_{f} = {\overset{\cdot}{y}}_{0} P (t - T_{s} / 2) \sin (\frac{t}{T_{s}} π) (25) \end{matrix}$

由式(25)可知, τ _f在着地相的前半段为负值, 先从零变小后又增大为零, 在着地相的后半段为正值, 先从零增大后又减小为零(如图11所示)。并且τ _f的幅值随着当前速度的增大而增大。

为了衡量控制力矩的能耗水平, 本文采用电机能耗模型加以模拟。电机输出力矩的大小与电枢电流成正比, 而热损耗的功率与电枢电流的二次方成正比。由此获得控制力矩能耗如下:

$\begin{matrix} \begin{matrix} J = \int_{0}^{T_{s}} (τ_{f})^{2} dt = \\ \int_{0}^{T_{s}} {({\overset{\cdot}{x}}_{0} P (T_{s} / 2 - t) \sin (\frac{t}{T_{s}} π))}^{2} dt = \\ {\overset{\cdot}{x}}_{0}^{2} P^{2} T_{s} (\frac{1}{24} - \frac{1}{4 π^{2}}) > 0 (26) \end{matrix} \end{matrix}$

五元件法的前摆力矩在一个着地相所消耗的能量大于零, 且随着速度的增大而增大。为了做量化对比, 进一步利用仿真手段对能耗水平进行分析。两种方法分别控制机器人在2 s内加速至1 m/s, 并维持该前进速度。在仿真中获得右后腿前摆力矩, 并按式(26)计算消耗的能量。仿真结果如图12所示。

	Figure Option View Download New Window
	图12 关节的力矩和能耗Fig.12 Torque and power consumption of joint

图中的实线和虚线分别对应三元件法和五元件法。其中, 五元件法的前摆力矩曲线形状与前面计算的结果一致, 并且三元件法的前摆力矩和能耗都比五元件法小得多。

3.3 侧移耦合运动分析

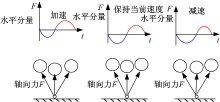
在三元件法中, 机器人的运动类似于一个三维的弹簧负载倒立摆, 前进速度和侧移速度都是通过着地角进行控制, 在机器人平稳运行, 机身姿态角很小时, 可以认为前进速度和侧移速度都只受轴向力影响, 它们之间的相互影响很小。而在五元件法中, 机器人的前摆关节施加力矩调节前进速度保持恒定, 通过对角腿的不对称轴向力调节机身俯仰。侧摆关节应该施加一个相应的力矩以抑制非对称轴向力对横滚角的影响, 如图13所示。在五元件法中这个侧摆力矩会通过着地腿在机身的侧移方向产生一个侧移力, 进而影响侧移速度。

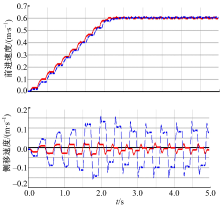
	Figure Option View Download New Window
	图13 稳定运动时机身受力分析Fig.13 Force analysis when stable running

在仿真研究中, 两种方法分别控制机器人在2 s时间内加速至1 m/s, 并维持该前进速度, 观察侧移速度。仿真结果如图14所示。图中, 实线和虚线分别对应三元件法和五元件法, 三元件法侧移速度波动的幅值比五元件法要小, 而且在五元件法中, 由于加速过程中的前摆力矩波动比较大, 相应的侧摆力矩的波动比较大, 导致此时的侧移速度波动也比较大。

	Figure Option View Download New Window
	图14 两种策略的侧移速度比较图Fig.14 Comparison of lateral velocity in two methods

另一方面, 着地腿的侧摆力矩为了平衡非对称轴向力的影响, 其大小和腿部在前进方向与侧移方向的跨距的比值有关, 比值越大, 侧摆力矩的值越小, 对侧移运动的影响也越小。由机器人的结构尺寸可知, 机器人前后腿的跨距为0.36 m, 左右腿的跨距为0.18 m, 它们的比值为2。如果将机器人的前进方向当作侧移方向, 而将侧移方向当作前进方向, 则此时腿部在前进方向的跨距与在侧移方向的跨距的比值为0.5。针对上述比值为2和0.5两种情况, 如图15所示的仿真中, 采用五元件法控制机器人在2 s时间内加速至0.6 m/s, 并维持该前进速度, 比较它们在侧移方向上速度的波动。图中实线和虚线分别对应腿部在前进方向与侧移方向的跨距的比值为2和0.5的情况, 两种情况下前进速度的曲线相差不大, 而比值为0.5时的侧移速度波动的幅值比比值为2时大得多。这说明比值越大对侧移运动的影响越小的观点是正确的, 同时也指出在比值较小时不宜采用五元件法。

	Figure Option View Download New Window
	图15 不同尺寸比值下侧移速度比较图Fig.15 Comparison of lateral velocity with different size

4 结束语

针对基于SLIP模型的Raibert方法所存在的对地形扰动反应比较敏感等问题, 本文在前期研究的基础上, 通过改进虚拟模型控制策略, 提出了着地相过程的机身位姿调节策略。机器人在仿真环境中维持了自身的平稳运行, 由此验证了控制策略的正确性。通过两种方法的对比分析可以看出, 机身前进自由度上加入虚拟元件, 尽管可以提高前进速度控制的准确性和机器人对地形变化的抗干扰能力, 但需要付出能耗加大和耦合运动增强的代价。根据环境和运行工况的变化, 通过合理选择这两种控制策略能够有效地提高机器人的综合运动性能。

通过本文对控制策略的研究和分析可以得知, 该算法的成功应用依赖于腿部关节的力和力矩伺服控制以及机身姿态和速度的反馈信息。本文作者在前期开展了机器人关节力/力矩伺服控制和包括机身速度信息在内的本体状态感知算法研究, 但目前该感知算法仍不尽完善。因此为了将本文所提出的控制算法应用于具有多关节腿部结构的四足机器人, 在下一阶段的工作主要包括:①对仿生腿部机构的运动学和动力学开展相关研究; ②完善机器人本体状态感知算法, 为本文提出的控制算法提供必要的准确的反馈信息。

The authors have declared that no competing interests exist.

参考文献

View Option

[1]	Hoyt D F, Taylor C R. Gait and the energetics of locomotion in horses[J]. Nature, 1981, 292(5820): 239-240. [本文引用:1]
[2]	Nanua P, Waldron K J. Energy comparison between trot, bound, and gallop using a simple model[J]. Journal of Biomechanical Engineering, 1995, 117(4): 466-473. [本文引用:1]
[3]	Raibert M H. Legged Robots that Balance[M]. Massachusetts: MIT Press, 1986. [本文引用:2]
[4]	Buchli J, Kalakrishnan M, Mistry M, et al. Compliant quadruped locomotion over rough terrain[C]∥IEEE Intelligent Robots and Systems, St. Louis, USA, 2009: 814-820. [本文引用:1]
[5]	Palmer III L R, Orin D E. Intelligent control of high-speed turning in a quadruped[J]. Journal of Intelligent and Robotic Systems, 2010, 58(1): 47-68. [本文引用:1]
[6]	Shkolnik A, Levashov M, Manchester I R, et al. Bounding on rough terrain with the LittleDog robot[J]. The International Journal of Robotics Research, 2011, 30(2): 192-215. [本文引用:1]
[7]	Kalakrishnan M, Buchli J, Pastor P, et al. Learning, planning, and control for quadruped locomotion over challenging terrain[J]. The International Journal of Robotics Research, 2011, 30(2): 236-258. [本文引用:1]
[8]	Maufroy C, Nishikawa T, Kimura H. Stable dynamic walking of a quadruped robot “Kotetsu” using phase modulations based on leg loading/unloading[C]∥IEEE International Conference on Robotics and Automation, Anchorage, USA, 2010: 5225-5230. [本文引用:1]
[9]	Maufroy C, Kimura H, Takase K. Integration of posture and rhythmic motion controls in quadrupedal dynamic walking using phase modulations based on leg loading/unloading[J]. Autonomous Robots, 2010, 28(3): 331-353. [本文引用:1]
[10]	Buehler M, Playter R, Raibert M. Robots step outside[C]∥Adaptive Motion of Animals and Machines, Ilmenau, Germany, 2005: 1-4. [本文引用:1]
[11]	Pratt J, Chew C M, Torres A, et al. Virtual model control: An intuitive approach for bipedal locomotion[J]. The International Journal of Robotics Research, 2001, 20(2): 129-143. [本文引用:1]
[12]	Hutter M, Remy C D, Hoepflinger M A, et al. Scarleth: design and control of a planar running robot[C]∥IEEE/RSJ International Conference on Intelligent Robots and Systems, San Francisco, USA, 2011: 562-567. [本文引用:1]
[13]	Jiang Zhen-yu, Li Man-tian, Guo Wei. Running control of a quadruped robot in trotting gait[C]∥IEEE Conference on Robotics, Automation and Mechatronics, Qingdao, China, 2011: 172-177. [本文引用:4]
[14]	Spröwitz A, Tuleu A, Vespignani M, et al. Towards dynamic trot gait locomotion: design, control, and experiments with cheetah-cub, a compliant quadruped robot[J]. The International Journal of Robotics Research, 2013, 32(8): 932-950. [本文引用:1]

1981

0.0

... 其中,Trot步态^[1,2]是四足哺乳动物以中等速度运动时广泛采用的一种运动形式 ...

1995

0.0

... 其中,Trot步态^[1,2]是四足哺乳动物以中等速度运动时广泛采用的一种运动形式 ...

1986

0.0

... MIT腿实验室的Raibert等^[3]基于弹簧负载倒立摆模型(Spring loaded inverted pendulum,SLIP)实现了直腿单足和四足机器人的跑跳运动 ...

... 方法^[3]进一步简化为弹簧负载倒立摆,如图11所示 ...

2009

0.0

... Buchli等^[4]开发了基于逆动力学的控制算法并将其运用到LittleDog机器人,使之可以通过比较大的障碍,但目前这种方法常运用在静步态 ...

2010

0.0