基于“三步法”的柴油机urea-SCR系统控制设计

引用本文

赵靖华, 陈志刚, 胡云峰, 陈虹. 基于“三步法”的柴油机urea-SCR系统控制设计. 2015, 45(6): 1913-1923
ZHAO Jing-hua, CHEN Zhi-gang, HU Yun-feng, CHEN Hong. Design of diesel engine's urea-SCR system controller using triple-step method. Journal of Jilin University Engineering and Technology Edition, 2015, 45(6): 1913-1923 复制到剪切板

Permissions

基于“三步法”的柴油机urea-SCR系统控制设计

赵靖华^1,², 陈志刚¹, 胡云峰¹, 陈虹¹

1.吉林大学汽车仿真与控制国家重点实验室,长春 130022

2.吉林师范大学计算机学院,吉林四平 136002

陈虹(1963-),女,教授,博士生导师.研究方向:非线性控制应用及汽车电子控制.E-mail:chenh@jlu.eud.cn

作者简介:赵靖华(1980-),男,讲师,博士.研究方向:发动机尾气排放控制.E-mail:zhaojh08@mails.jlu.edu.cn

基金:国家自然科学基金重点项目(61034001); 吉林省科技发展计划、吉林省公共计算平台基金资助项目(20130101179JC-16)

摘要

为了同时实现较高的NO _x转化率和较低的氨逃逸,提出了一种新颖的面向控制的urea-SCR模型,基于三步非线性控制方法——“三步法”设计了控制器。该控制器能够调节时变参数的非线性系统,跟踪理想的氨覆盖率目标。针对测量噪声和系统的不确定性,研究分析了该闭环系统的稳定性。研究基于精确enDYNA模型,在FTP75瞬态测试循环条件下,与蒙特卡罗随机参数法选取的最优PID控制器对比表明,所提出的控制策略具有很大优势。

关键词: 自动控制技术; 尿素选择性催化还原系统控制; 三步非线性控制方法(“三步法”); 输入状态稳定性理论

中图分类号:TP273 文献标志码:A 文章编号:1671-5497(2015)06-1913-11

Design of diesel engine's urea-SCR system controller using triple-step method

ZHAO Jing-hua^1,², CHEN Zhi-gang¹, HU Yun-feng¹, CHEN Hong¹

1.State Key Laboratory of Automotive Simulation and Control, Jilin University, Changchun 130022,China

2.Computer College, Jilin Normal University, Siping 136002, China

Abstract

For simultaneously achieving NOx conversion efficiency and low ammonia slip, a new control-oriented model of urea-SCR systems and novel nonlinear controller based on triple-step nonlinear method are presented. The proposed controller could drive the parameter-varying nonlinear system to track the desired ammonia coverage ratio. The robustness of the controller against the measurement noises and system uncertainties are analyzed. Based on validated enDYNA model, transient FTP75 driving cycle simulation is conducted to evaluate the effectiveness of the proposed strategy. Comparisons with Monte Carlo methods' optimal PID controller are presented to show the advantages of the proposed strategy.

Keyword: automation technology; urea-SCR systems control; triple-step method; input-to-state stable

Show Figures

0 引言

与汽油机相比, 柴油机具有更高的燃油经济性和更高的动力输出。尽管柴油机已经并且仍将继续在中-重型车辆领域占统治地位, 近些年来, 在轻型车辆领域柴油机也在迅速扩张, 但柴油机的排放问题对其发展一直是个挑战, 特别是NO_x排放。研究人员提出了很多降低NO_x排放的方法^{[1, 2]}。其中, 尿素选择性催化还原(urea-SCR)技术具备一定优势^[2]。该技术利用氨(NH₃)还原发动机产生的NO_x, 这些氨一般都来源于32.5%的尿素溶液(添蓝溶液), 但储存尿素的罐会增加车辆的重量^[3]。虽然氨能够还原NO_x, 但其本身也是对人体有害的, 并且有着刺鼻的气味。尽管在当前的排放法规中没有明文规定, 但是较高的氨逃逸被认为是对身体有害的, 并且气味十分难闻^[4]。所以, 同时实现较低的NO_x排放与氨逃逸成为了urea-SCR系统研究的主要问题。

为满足上述目标, 有学者提出了一些硬件改进措施。但在实际应用中, 大多数都是以增加成本和所占空间为代价^[5]。目前, 人们已经普遍认识到, 通过改进尿素喷射技术达到上述控制目标是一种较便捷且经济的方法^[6]。当前的一些尿素喷射控制方法, 主要集中在反馈控制设计和基于线性urea-SCR系统模型的控制设计上^{[3, 7]}。其中, 一部分反馈控制是基于NO_x传感器的^[8], 但NO_x传感器对氨有交叉敏感性^[9]。最近, 德尔福公司推出了NH₃传感器^[7], 但由于其还未被量产, 在实际的工业应用中很少用到。这就使得单独的NO_x和NH₃反馈都很难达到理想的控制目的^[10]。于是, 有学者提出了一种综合的反馈方法, 即以氨覆盖率为反馈控制目标。此外, 由于urea-SCR系统化学反应本身具有较强的复杂性和非线性, 逐渐使得非线性控制方法成为了研究热点^[11]。因此, 有学者提出了以理想氨覆盖率作为反馈控制目标的非线性控制方法^{[10, 12, 13]}。文献[12]提出了一种基于backstepping的非线性氨覆盖率反馈控制技术, 能够获得较好的排放控制效果。文献[14, 15]还提出了一些氨覆盖率的估计方法。

与此同时, 一些先进的非线性控制方法也在不断发展, 这其中就包括反馈线性化^{[16, 17]}和backstepping技术^{[18, 19]}。但是, 对大多数非线性方法来讲, 设计过程中复杂的推导会使得理论研究与工业实践之间存在一定障碍。为了简化推导过程和降低MAP标定成本, 文献[20]提出了三步非线性控制方法— — “ 三步法” , 并将其应用于直喷汽油机的轨压控制中。该方法借鉴了广泛应用于工业实践的基于MAP的前馈反馈结构。文献[21]将这种方法扩展应用于两输入两输出的车用轮上电机控制系统中。在urea-SCR系统中, 化学反应对废气温度和NO_x排放量等参数非常敏感, 而且, 这些参数都是时变的。因此, 本文研究结合urea-SCR系统非线性特点并且考虑到低车重和低成本问题, 提出一种新颖的面向控制的模型表述方法, 将“ 三步法” 扩展应用于时变参数的非线性系统控制中, 设计了一种氨覆盖率跟踪控制器。

1 问题描述及系统建模

1.1 问题描述

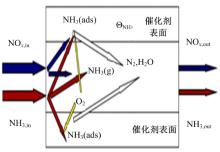
如图1所示, urea-SCR系统中的化学反应主要包括下面几个过程。首先, 发动机排出的NO_x_{, in}和添蓝溶液产生的NH_{3, in}进入系统。

	Figure Option View Download New Window
	图1 urea-SCR化学反应示意图Fig.1 Schematic presentation of the urea-SCR reactions

在催化器内, 部分NH₃被吸附在催化剂表面, 变成吸附态的氨(NH₃(ads)), 其余部分仍为气态氨(NH₃(g)), 并且这两部分可以相互转化, 反应方程式如下:

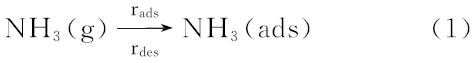
吸附态的氨能够在催化剂的作用下选择性地与NO_x反应生成N₂和H₂O, 当温度高于200 ℃时, 该反应主要按照Eley-Rideal机制进行^[22], 反应方程式如下所示:

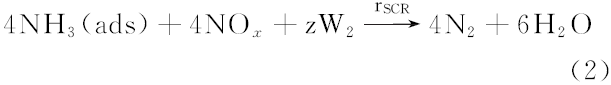
同时, 吸附态的氨也能够被氧化成N₂和H₂O, 反应方程式如下:

经过上述几步化学反应, 剩余的NO_x(NO_x_{, out})和氨(NH_{3, out})从urea-SCR系统排出。此外, urea-SCR系统的氨贮存能力与吸附态的NH₃(ads)之比被定义为氨覆盖率( $\begin{matrix} Θ_{N H_{3}} \end{matrix}$ )。

Urea-SCR系统的控制目标是要同时实现较高的NO_x转化效率和较低的氨逃逸。文献[10, 12, 13, 14]提出了一种氨覆盖率反馈控制方法, 并取得了良好效果。而理想的氨覆盖率目标可以从相对应的发动机urea-SCR系统实验数据及分析中获取。在urea-SCR系统中, 化学反应对废气温度和NO_x排放量等参数非常敏感, 且这些参数都是时变的, 这是一项非常具有挑战性的控制需求。本文的控制问题就是, 考虑到系统时变参数非线性的氨覆盖率跟踪控制问题。

研究以欧6(EURO 6)的NO_x排放标准为参考, 提出的控制目标为:NO_x排放平均水平在0.3 g/kWh以下, 并且氨逃逸在平均80× 10⁶以下。由陈虹等人提出的“ 三步法” 控制策略, 具有简洁和标准化的结构^{[20, 21]}, 本文将该方法扩展应用于时变参数系统上, 解决上述urea-SCR系统控制问题。为此, 建立了urea-SCR系统的集中参数模型, 并且根据该系统的非线性特点, 提出了一种新颖的面向控制的urea-SCR系统模型。

1.2 集中参数模型

根据阿列纽斯方程, 研究对化学反应过程的反应速率进行建模。方程(1)中的吸附(r_ads)和解吸附r_des速率由如下公式表示:

$\begin{matrix} \begin{matrix} r_{ads} = c_{s} S_{c} α_{prob} \sqrt{\frac{RT}{2 π M_{N H_{3}}}} C_{N H_{3}} (1 - Θ_{N H_{3}}) \\ r_{des} = c_{s} k_{des} e^{- \frac{E_{a, des}}{RT}} Θ_{N H_{3}} (4) \end{matrix} \end{matrix}$

方程(2)中的还原速率r_SCR由如下公式表示:

$\begin{matrix} r_{SCR} = c_{s} RT k_{SCR} e^{- \frac{E_{a, red}}{RT}} C_{N O_{x}} Θ_{N H_{3}} (5) \end{matrix}$

方程(3)对应的反应速率(r_ox)由如下公式表示:

$\begin{matrix} r_{ox} = c_{c} k_{ox} e^{- \frac{E_{a, ox}}{RT}} Θ_{N H_{3}} (6) \end{matrix}$

需要指出的是, 在柴油机废气中氧浓度总是很高的, 相比于其他气体成分来说十分充足。所以, 大多数的urea-SCR反应速率对氧浓度的变化都不敏感, 可以忽略。

研究假设上述催化反应是一个连续搅拌釜式反应器(CSTR), 即催化系统的所有状态是均质的。基于上述假设, 根据质量平衡以及热量平衡原则, urea-SCR系统模型的常微分方程(ODEs)表示如下:

$\begin{matrix} \begin{matrix} \{\begin{matrix} {\overset{\cdot}{C}}_{N O_{x}} = a_{1} (n_{N O_{x}, in}^{*} - n_{N O_{x}, out}^{*}) - r_{SCR} \\ {\overset{\cdot}{C}}_{N H_{3}} = a_{1} (n_{N H_{3}, in}^{*} - n_{N H_{3}, out}^{*}) - r_{ads} + r_{des} \\ c_{s} {\overset{\cdot}{Θ}}_{N H_{3}} = r_{ads} - r_{des} - r_{SCR} - r_{ox} \\ \overset{\cdot}{T} = a_{6} m_{EG}^{*} (T_{in} - T) - a_{7} (T^{4} - T_{amb}^{4}) \end{matrix} \\ (7) \end{matrix} \end{matrix}$

考虑到urea-SCR系统中, 气体成分的流量与浓度之间的关系为:

$\begin{matrix} n_{x}^{*} = \frac{R_{S, EG}}{P_{amb}} m_{EG}^{*} T C_{x} (8) \end{matrix}$

并且, 将公式(4)(5)(6)以及(8)代入公式(7)中, 得到:

$\begin{matrix} \{\begin{matrix} {\overset{\cdot}{C}}_{N O_{x}} = a_{1} n_{N O_{x}, in}^{*} - C_{N O_{x}} (a_{0} a_{1} m_{EG}^{*} T + \\ a_{4} (T) Θ_{N H_{3}}); \\ {\overset{\cdot}{C}}_{N H_{3}} = a_{1} n_{N H_{3}, in}^{*} - C_{N H_{3}} [a_{0} a_{1} m_{EG}^{*} T + \\ a_{4} (T) (1 - Θ_{N H_{3}})] + a_{3} (T) Θ_{N H_{3}}; \\ c_{s} Θ_{N H_{3}} = a_{2} (T) (1 - Θ_{N H_{3}}) C_{N H_{3}} - \\ [a_{3} (T) + a_{4} (T) C_{N O_{x}} + a_{5} (T)] Θ_{N H_{3}}; \\ T = a_{6} m_{EG}^{*} (T_{in} - T) - a_{7} (T^{4} - T_{amb}^{4}) \end{matrix} (9) \end{matrix}$

其中, 上述公式中的参数定义如下:

$\begin{matrix} \{\begin{matrix} a_{0} = \frac{R_{S, EG}}{Pamb}, \\ a_{1} = \frac{1}{ε V_{c}}, \\ a_{2} (T) = c_{s} S_{c} αProb \sqrt{\frac{RT}{2 π M_{N H_{3}}}}, \\ a_{3} (T) = c_{s} k_{Des} e^{(\frac{- E_{a, Des}}{RT})}, \\ a_{4} (T) = c_{s} RT k_{Des} e^{(\frac{- E_{a, SCR}}{RT})}, \\ a_{5} (T) = c_{s} k_{Ox} e^{(\frac{- E_{a, Ox}}{RT})}, \\ a_{6} = \frac{c_{p, EG}}{c_{p, c} m_{c}}, \\ a_{7} = \frac{ε_{rad, scr} σ_{sb} A_{rad, scr}}{c_{p, c} m_{c}} \end{matrix} (10) \end{matrix}$

上述建模过程中的假设和简化都参考了文献[3, 23, 24]。表1和表2分别显示了模型中常量和变量的相关定义及参数。

表1 常量命名法 Table 1 Constants nomendature

符号	描述	数值/单位
S_c	1 mol活性原子的表面积	581[m²/mol]
α _prob	粘着率	1.11× 10^-3
c_s	单位体积气体中活性原子浓度	7.30[mol/m³]
c_{p, EG}	排气定压比热	1060[J/(kg· K)]
c_{p, c}	催化器比热	1054[J/(kg· K)]
$\begin{matrix} M_{N H_{3}} \end{matrix}$	NH₃的摩尔质量	17 [g/mol]
R	气体常数	8.3145[J/(mol· K)]
R_{S, EG}	排气气体常数	288 [J/(kg· K)]
k_Des	解吸附速率因子	0.514[1/s]
k_SCR	urea-SCR反应速率因子	2.6776[m²/s]
k_Ox	NH₃氧化反应速率因子	3.34× 10⁶[1/s]
E_{a, Des}	解吸附活性能	15.2 [J/mol]
E_{a, SCR}	urea-SCR反应活性能	28471[J/mol]
E_a,_Ox	NH₃氧化反应活性能	1.16× 10⁵[J/mol]
P_amb	大气压	101325[Pa]
V_c	urea-SCR系统的总容积	0.01 [m³]
m_c	催化器质量	19[kg]
ε	空隙比	0.81
ε _{rad, scr}	黑度	0.507
σ _sb	气体辐射常数	5.67× 10^-8
A_{rad, scr}	催化器辐射表面积	0.9044[m²]

表1 常量命名法 Table 1 Constants nomendature

表2 变量命名法 Table 2 Variables nomendature

符号	描述	单位
C_x	物质x的摩尔浓度	[mol/m³]
$\begin{matrix} n_{x}^{*} \end{matrix}$	物质x的摩尔质量流量	[mol/s]
$\begin{matrix} m_{EG}^{*} \end{matrix}$	废气质量流量	[kg/s]
T, T_in, T_amb	温度, 废气温度, 环境温度	[K]
$\begin{matrix} Θ_{N H_{3}} \end{matrix}$	NH₃的表面覆盖率	[-]

表2 变量命名法 Table 2 Variables nomendature

1.3 一种新颖的面向控制的urea-SCR系统模型

为了实现氨覆盖率控制, 将T, $\begin{matrix} C_{N O_{x}} \end{matrix}$ 等看做可测量变量, 考虑的状态量仅为 $\begin{matrix} Θ_{N H_{3}} \end{matrix}$ 和 $\begin{matrix} {C_{N H_{3}}}^{[25]} \end{matrix}$ 。定义状态变量x:=[ $\begin{matrix} Θ_{N H_{3}} \end{matrix}$ $\begin{matrix} C_{N H_{3}} \end{matrix}$ ], 时变参数p=[T $\begin{matrix} C_{N O_{x}} \end{matrix}$ $\begin{matrix} m_{EG}^{*} \end{matrix}$ ]^T, 控制输入变量u:= $\begin{matrix} n_{N H_{3}, in}^{*} \end{matrix}$ , 被控输出为 $\begin{matrix} Θ_{N H_{3}} \end{matrix}$ 。基于SCR模型(9), 得到系统面向控制模型:

${\overset{\cdot}{x}}_{1} = f_{11} (x, p) + f_{12} (x, p) x_{2} {\overset{\cdot}{x}}_{2} = f_{21} (x, p) + a_{1} u (11)$

其中,

$\begin{matrix} \begin{matrix} \{\begin{matrix} f_{11} (x, p) = - \frac{1}{c_{s}} [a_{3} (T) + a_{4} (T) C_{N O_{x}} + \\ a_{5} (T)] x_{1} \\ f_{12} (x, p) = \frac{1}{c_{s}} a_{2} (T) (1 - x_{1}) \\ f_{21} (x, p) = - x_{2} [a_{0} a_{1} m_{EG}^{*} T + \\ a_{2} (T) (1 - x_{1})] + a_{3} (T) x_{1} \end{matrix} (12) \end{matrix} \end{matrix}$

该系统为非线性且时变参数系统。设被控输出为y=x₁, 控制器的目标为驱动参数依赖的非线性系统跟踪给定参考量y^*。此外, 根据表1中的常量、表2中的变量以及公式(10)中的变量定义, 同时基于吸附态的氨与urea-SCR系统最大氨贮存能力之比小于1的实际情况(0≤ x₁< 1), 可知f₁₂(x, p)≠ 0。

为了设计一款非线性的氨覆盖率的跟踪控制器, 研究对上述模型进行适当简化。根据公式(11)(12), 对y求导可得:

$\overset{\cdot}{y} = {\overset{\cdot}{x}}_{1} = f_{11} (x, p) + f_{12} (x, p) x_{2} (13)$

以及

$\begin{matrix} \begin{matrix} \overset{\cdot \cdot}{y} = A_{1} (x, p) \overset{\cdot}{y} + f_{12} (x, p) f_{21} (x, p) + \\ a_{1} f_{12} (x, p) u + d_{1} (14) \end{matrix} \end{matrix}$

式中:A₁(x, p)= $\begin{matrix} \frac{\partial f_{11} (x, p)}{\partial x_{1}} \end{matrix}$ + $\begin{matrix} \frac{\partial f_{12} (x, p)}{\partial x_{1}} \end{matrix}$ x₂,

A₂(x, p)= $\begin{matrix} \frac{\partial f_{11} (x, p)}{\partial p} \end{matrix}$ + $\begin{matrix} \frac{\partial f_{12} (x, p)}{\partial p} \end{matrix}$ x₂,

并且将A₂(x, p) $\begin{matrix} \overset{\cdot}{p} \end{matrix}$ 看作建模误差, 用d₁=A₂(x, p) $\begin{matrix} \overset{\cdot}{p} \end{matrix}$ 表示。由此, 公式(14)给出了一种新的面向控制的urea-SCR系统模型表述方法, 并且a₁≠ 0, f₁₂(x, p)≠ 0

2 氨覆盖率控制器设计

在本章中, 首先忽略建模误差d₁, 基于文献[20]所提出的“ 三步法” 非线性控制策略, 设计了一款氨覆盖率跟踪控制器。设计过程分为三个阶段, 其中前两个阶段顺次推导出稳态控制器和一个参考可变的前馈控制。经过这两步, 得到了明确的误差动态仿射表达式, 主要可简化误差状态反馈设计。因此, 最终的控制法则由三部分组成:稳态控制、参考可变的前馈控制以及跟踪误差反馈控制。需要特别指出的是, 这种方法的优点在于, 系统参数的特性并没有使控制器的推导过程过于复杂化。

2.1 稳态控制(步骤1)

以公式(14)所示的新的系统表述为研究起始, 暂且假定d₁=0, 首先设计类稳态控制器。通过设定 $\begin{matrix} \overset{\cdot \cdot}{y} \end{matrix}$ =0, $\begin{matrix} \overset{\cdot}{y} \end{matrix}$ =0, 得到的稳态控制法则f_s(x)如下:

$\begin{matrix} f_{s} (x) = \frac{1}{a_{1}} f_{21} (x, p) (15) \end{matrix}$

该控制法则叫类稳态控制, 原因是这部分的获取是基于假设系统处于稳态前提下, 且该法则与当前测量或估计状态x相关, 而不是参照真实的稳态x。该控制法则的设计思想基于MAP的控制方法, 该方法广泛应用于汽车工程领域。MAP的获取可通过大量的稳态实验标定完成, 并且, MAP的执行可根据当前的测量或估计状态。采用上述状态依赖类稳态控制方法的优点, 将会在后续推导过程中逐步体现。

2.2 参考可变的前馈控制(步骤2)

事实上, 面对如此复杂的系统, 仅仅凭借一个稳态控制是远远不够的。为了获取足够的闭环控制性能, 将另外一些附加的控制信息u₁引入控制系统。将

$\begin{matrix} u = f_{s} (x) + u_{1} (16) \end{matrix}$

代入公式(14)中, 得到

$\begin{matrix} \overset{\cdot \cdot}{y} = A_{1} (x, p) \overset{\cdot}{y} + a_{1} f_{12} (x, p) u_{1} (17) \end{matrix}$

令 $\begin{matrix} \overset{\cdot \cdot}{y} \end{matrix}$ = $\begin{matrix} {\overset{\cdot \cdot}{y}}^{*} \end{matrix}$ 及 $\begin{matrix} \overset{\cdot}{y} \end{matrix}$ = $\begin{matrix} {\overset{\cdot}{y}}^{*} \end{matrix}$ , 得到的与参考动态相关的前馈控制u₁如下:

$\begin{matrix} \begin{matrix} u_{1} = \frac{1}{a_{1} f_{12} (x, p)} {\overset{\cdot \cdot}{y}}^{*} - \frac{A_{1} (x, p)}{a_{1} f_{12} (x, p)} {\overset{\cdot}{y}}^{*} = \\ f_{f} (x, p, {\overset{\cdot}{y}}^{*}, {\overset{\cdot \cdot}{y}}^{*}) (18) \end{matrix} \end{matrix}$

由于公式(18)具有 $\begin{matrix} {\overset{\cdot \cdot}{y}}^{*} \end{matrix}$ 和 $\begin{matrix} {\overset{\cdot}{y}}^{*} \end{matrix}$ 的仿射形式, 故称之为参考动态的前馈控制, 并将其定义为f_f(x, p, $\begin{matrix} {\overset{\cdot}{y}}^{*} \end{matrix}$ , $\begin{matrix} {\overset{\cdot \cdot}{y}}^{*} \end{matrix}$ )。

2.3 非线性反馈控制(步骤3)

在前两步控制器设计中, 没有考虑到跟踪偏移。为了处理最后的跟踪偏移误差, 定义一个新的控制量u₂, 并将其加入到类稳态控制和参考动态的前馈控制中, 且定义的跟踪误差如下:

$e_{1} : = y^{*} - y (19)$

将

$\begin{matrix} \begin{matrix} u = f_{s} (x) + u_{f} (x, {\overset{\cdot}{y}}^{*}, {\overset{\cdot \cdot}{y}}^{*}) + u_{2} (20) \end{matrix} \end{matrix}$

代入公式(14)中, 得到的跟踪误差动态形式如下:

$\begin{matrix} {\overset{\cdot \cdot}{e}}_{1} = A_{1} (x, p) {\overset{\cdot}{e}}_{1} - a_{1} f_{12} (x, p) u_{2} (21) \end{matrix}$

很明显, 公式(21)是e和u的仿射形式。相比基于原系统(11)的控制设计, 这样一种特殊形式, 对于推导渐进稳定的反馈控制器来说, 具有简化控制算法的重要意义。定义e₂= $\begin{matrix} {\overset{\cdot}{e}}_{1} \end{matrix}$ , 上式被重写为:

$\begin{matrix} \{\begin{matrix} {\overset{\cdot}{e}}_{1} = e_{2} \\ {\overset{\cdot}{e}}_{2} = A_{1} (x, p) {\overset{\cdot}{e}}_{2} - a_{1} f_{12} (x, p) u_{2} \end{matrix} (22) \end{matrix}$

为保证跟踪误差动态是渐进稳定的, 采用backstepping技术推导u₂。将e₂看做是虚拟控制, 定义V₁= $\begin{matrix} \frac{1}{2} \end{matrix} \begin{matrix} e_{1}^{2} \end{matrix}$ + $\begin{matrix} \frac{1}{2} \end{matrix}$ k₀χ ², 且k₀> 0, χ =∫ e₁dt, 经推导得到:

$\begin{matrix} {\overset{\cdot}{V}}_{1} = e_{1} {\overset{\cdot}{e}}_{1} + k_{0} e_{1} χ = e_{1} e_{2} + k_{0} e_{1} χ (23) \end{matrix}$

选择虚拟控制为:

$\begin{matrix} e_{2}^{*} = - k_{1} e_{1} - k_{0} χ (24) \end{matrix}$

在假定k₁> 0的条件下, 设e₂= $\begin{matrix} e_{2}^{*} \end{matrix}$ , 得到:

$\begin{matrix} \{\begin{matrix} {\overset{\cdot}{V}}_{1} = - k_{1} e_{1}^{2} \\ {\overset{\cdot}{e}}_{1} = - k_{1} e_{1} - k_{0} χ \end{matrix} (25) \end{matrix}$

但事实上, e₂≠ $\begin{matrix} e_{2}^{*} \end{matrix}$ 。因此, 定义e₃= $\begin{matrix} e_{2}^{*} \end{matrix}$ -e₂, 上式变为:

$\begin{matrix} \{\begin{matrix} {\overset{\cdot}{V}}_{1} = - k_{1} e_{1}^{2} - e_{1} e_{3} \\ {\overset{\cdot}{e}}_{1} = - k_{1} e_{1} - k_{0} χ - e_{3} \end{matrix} (26) \end{matrix}$

并且结合公式(22), 推导 $\begin{matrix} {\overset{\cdot}{e}}_{2}^{*} \end{matrix}$ =-k₁ $\begin{matrix} {\overset{\cdot}{e}}_{1} \end{matrix}$ -k₀e₁以及e₂= $\begin{matrix} {\overset{\cdot}{e}}_{1} \end{matrix}$ 得到:

$\begin{matrix} \begin{matrix} {\overset{\cdot}{e}}_{3} = {\overset{\cdot}{e}}_{2}^{*} - {\overset{\cdot}{e}}_{2} = \\ - k_{1} {\overset{\cdot}{e}}_{1} - k_{0} e_{1} - A_{1} (x, p) e_{2} + a_{1} f_{12} (x, p) u_{2} = \\ - k_{1} {\overset{\cdot}{e}}_{1} - k_{0} e_{1} - A_{1} (x, p) {\overset{\cdot}{e}}_{1} + a_{1} f_{12} (x, p) u_{2} = \\ - (k_{1} + A (x_{1}, p)) {\overset{\cdot}{e}}_{1} - k_{0} e_{1} + a_{1} f_{12} (x_{1}, p) u_{2} (27) \end{matrix} \end{matrix}$

定义V₂=V₁+ $\begin{matrix} \frac{1}{2} \end{matrix} \begin{matrix} e_{3}^{2} \end{matrix}$ , 结合公式(26)经推导得到:

$\begin{matrix} \begin{matrix} {\overset{\cdot}{V}}_{2} = {\overset{\cdot}{V}}_{1} + e_{3} {\overset{\cdot}{e}}_{3} = \\ - k_{1} e_{1}^{2} - e_{1} e_{3} + e_{3} (- (k_{1} + A_{1} (x, p)) {\overset{\cdot}{e}}_{1} - \\ k_{0} e_{1} + a_{1} f_{12} (x, p) u_{2}) = \\ - k_{1} e_{1}^{2} + e_{3} (- e_{1} - (k_{1} + A_{1} (x, p)) {\overset{\cdot}{e}}_{1} - \\ k_{0} e_{1} + a_{1} f_{12} (x, p) u_{2}) = \\ - k_{1} e_{1}^{2} + e_{3} (- (1 + k_{0}) e_{1} - \\ (k_{1} + A_{1} (x, p)) {\overset{\cdot}{e}}_{1} + a_{1} f_{12} (x, p) u_{2}) (28) \end{matrix} \end{matrix}$

选择控制器:

在k₃> 0的条件下, 能够得到:

$\begin{matrix} {\overset{\cdot}{V}}_{2} = - k_{1} e_{1}^{2} - k_{3} e_{3}^{2} (30) \end{matrix}$

能够保证误差动态是渐进稳定的。再将公式(24)和e₂= $\begin{matrix} {\overset{\cdot}{e}}_{1} \end{matrix}$ 代入u₂中, 经推导得到:

$\begin{matrix} \begin{matrix} u_{2} = \frac{1 + k_{0}}{a_{1} f_{12} (x, p)} e_{1} + \frac{k_{1} + A_{1} (x, p)}{a_{1} f_{12} (x, p)} {\overset{\cdot}{e}}_{1} - \\ \frac{k_{2}}{a_{1} f_{12} (x, p)} e_{3} = \frac{1 + k_{0}}{a_{1} f_{12} (x, p)} e_{1} + \\ \frac{k_{1} + A_{1} (x, p)}{a_{1} f_{12} (x, p)} {\overset{\cdot}{e}}_{1} - \frac{k_{2}}{a_{1} f_{12} (x, p)} (e_{2}^{*} - e_{2}) = \\ \frac{1 + k_{0}}{a_{1} f_{12} (x, p)} e_{1} + \frac{k_{1} + A_{1} (x, p)}{a_{1} f_{12} (x, p)} {\overset{\cdot}{e}}_{1} - \\ \frac{k_{2}}{a_{1} f_{12} (x, p)} (- k_{1} e_{1} - k_{0} χ - {\overset{\cdot}{e}}_{1}) = \\ \frac{1 + k_{0} + k_{1} k_{2}}{a_{1} f_{12} (x, p)} e_{1} + \frac{k_{1} + k_{2} + A_{1} (x, p)}{a_{1} f_{12} (x, p)} {\overset{\cdot}{e}}_{1} + \\ \frac{k_{0} k_{2}}{a_{1} f_{12} (x, p)} e_{1} dt (31) \end{matrix} \end{matrix}$

再结合公式(15)(18)(31), 得到最终的控制法则如下:

$\begin{matrix} \begin{matrix} u = - \frac{1}{a_{1}} f_{21} (x, p) - \\ \frac{A_{2} (x, p)}{a_{1} f_{12} (x, p)} \overset{\cdot}{p} + \frac{1}{a_{1} f_{12} (x, p)} {\overset{\cdot \cdot}{y}}^{*} - \\ \frac{A_{1} (x, p)}{a_{1} f_{12} (x, p)} {\overset{\cdot}{y}}^{*} + \frac{1 + k_{0} + k_{1} k_{2}}{a_{1} f_{12} (x, p)} e_{1} + \\ \frac{k_{1} + k_{2} + A_{1} (x, p)}{a_{1} f_{12} (x, p)} {\overset{\cdot}{e}}_{1} + \frac{k_{0} k_{2}}{a_{1} f_{12} (x, p)} e_{1} dt \\ (32) \end{matrix} \end{matrix}$

将上述控制法则重写为:

$u = f_{s} (x, p) + f_{f} (x, p, {\overset{\cdot}{y}}^{*}, {\overset{\cdot \cdot}{y}}^{*}) + f_{P} (x, p) e_{1} + f_{I} (x, p) \int e_{1} dt + f_{D} (x, p) {\overset{\cdot}{e}}_{1} (33)$

式中：

$\begin{matrix} \begin{matrix} \{\begin{matrix} f_{s} (x, p) = - \frac{1}{a_{1}} f_{21} (x, p); \\ f_{f} (x, p, {\overset{\cdot}{y}}^{*}, {\overset{\cdot \cdot}{y}}^{*}) = \\ \frac{1}{a_{1} f_{12} (x, p)} {\overset{\cdot \cdot}{y}}^{*} - \frac{A_{1} (x, p)}{a_{1} f_{12} (x, p)} {\overset{\cdot}{y}}^{*}; \\ f_{P} (x, p) = \frac{1 + k_{0} + k_{1} k_{2}}{a_{1} f_{12} (x, p)}; \\ f_{I} (x, p) = \frac{k_{0} k_{2}}{a_{1} f_{12} (x, p)}; \\ f_{D} (x, p) = \frac{k_{1} + k_{2} + A_{1} (x, p)}{a_{1} f_{12} (x, p)} \end{matrix} (34) \end{matrix} \end{matrix}$

显然, 本文究所提出的非线性控制器具有简洁的结构。f_s(x, p)部分代表了广泛应用的MAP形式的类稳态控制。f_f(x, p, $\begin{matrix} {\overset{\cdot}{y}}^{*} \end{matrix}$ , $\begin{matrix} {\overset{\cdot \cdot}{y}}^{*} \end{matrix}$ )作为前馈控制, 考虑了跟踪参考的动态性能。反馈控制部分是由参考误差动态的李雅普诺夫方法推导的, 并且最终整理得到状态且参数依赖的PID控制器形式。当前, 广泛应用于工业实践的是标准2自由度结构, 这种结构一般都包含PID反馈控制、前馈MAP, 可能还包括一些纠正MAP。研究采用的控制器与上述标准2自由度结构具有可比性。尽管MAP标定工作耗时、耗费用, 但所提方法能够降低标定工作的难度, 而且能够改善动态性能, 具体原因如下:

(1)稳态控制能反映系统的一些固有特性, 且当系统接近于稳态时, 稳态控制器起主动作用。

(2)前馈部分根据参考动态给出矫正动作。并且这部分是状态且参数依赖的, 有利于改善瞬态性能。

(3)在稳态和前馈控制的协调下, 最终的误差反馈控制具有仿射线性系统的形式。参数依赖的PID控制具有增益可调的特性, 这一特性能够免除增益调节的试验过程。

3 实际执行的控制器简化

3.1 从氨喷射量到实际的添蓝溶液喷射控制阀信号

在本研究所提出的控制模型中, 氨喷射量 $\begin{matrix} n_{N H_{3}, in}^{*} \end{matrix}$ 是作为控制输入的, 但在实际应用中, 该物理量很难直接得到, 它来源于进入系统前的添蓝溶液喷射阀信号。并且, 添蓝溶液转化为氨需要经过蒸发、分解以及水解三步复杂的化学反应过程^[26], 这些过程在参数漂移时不可避免地引入误差。

3.2 信号处理和高阶导数的计算

输入信号整形技术, 也称之为动态表面控制技术, 是用来抑制指令信号突然变化的。而且, 通常有必要用低通滤波器来衰减测量噪声。研究为获得有效执行控制法则(见式(33)), 利用上述信号处理技术对所需的 $\begin{matrix} {\overset{\cdot}{y}}^{*} \end{matrix}$ 和 $\begin{matrix} {\overset{\cdot \cdot}{y}}^{*} \end{matrix}$ 进行处理。假设参考轨迹不会频繁振动(事实也是如此), 并且忽略了参考轨迹的二阶导数 $\begin{matrix} {\overset{\cdot \cdot}{y}}^{*} \end{matrix}$ 。

用 $\begin{matrix} {\bar{y}}^{*} \end{matrix}$ 代表被跟踪的参考量(或是测量量y_m)。 $\begin{matrix} {\bar{y}}^{*} \end{matrix}$ 或y_m经过一个二阶过滤器处理后(如果在执行过程中忽略 $\begin{matrix} {\overset{\cdot \cdot}{y}}^{*} \end{matrix}$ , 则是一个一阶过滤器)

$\begin{matrix} \frac{y^{*}}{{\bar{y}}^{*}} = \frac{ω_{n}^{2}}{s^{2} + 2 ξ ω_{n} s + ω_{n}^{2}} (35) \end{matrix}$

过滤器输出为y^*或y, 并且由 $\begin{matrix} {\overset{\cdot}{e}}_{1} \end{matrix}$ = $\begin{matrix} {\overset{\cdot}{y}}^{*} \end{matrix}$ - $\begin{matrix} \overset{\cdot}{y} \end{matrix}$ 得到 $\begin{matrix} {\overset{\cdot}{e}}_{1} \end{matrix}$ 。在仿真过程中, 用起始阶段的氨覆盖率目标去初始化过滤器, 该目标是根据工况条件获得的。尽管系统输出的微分不是由状态观测器, 而是由过滤器得到的, 但在ω _n和ξ 选取合理的前提下, 计算精度是可以保证的。

3.3 最终的控制器实施法则

控制器的最终实施法则为:

$\begin{matrix} \begin{matrix} u_{im} = f_{s} (x, p) + f_{fim} (x, p, {\overset{\cdot}{y}}^{*}, {\overset{\cdot \cdot}{y}}^{*}) \\ f_{P} (x, p) e_{1} + f_{I} (x, p) \int e_{1} dt + f_{D} (x, p) {\overset{\cdot}{e}}_{1} (36) \end{matrix} \end{matrix}$

式中：

$f_{fim} (x, p, {\overset{\cdot}{y}}^{*}, {\overset{\cdot \cdot}{y}}^{*}) = \frac{A_{2} (x, p)}{a_{1} f_{12} (x, p)} {\overset{\cdot}{y}}^{*} (37)$

4 鲁棒分析

在上述控制规则的实施中, 包括f_f(x, p, $\begin{matrix} {\overset{\cdot}{y}}^{*} \end{matrix}$ , $\begin{matrix} {\overset{\cdot \cdot}{y}}^{*} \end{matrix}$ )中 $\begin{matrix} {\overset{\cdot \cdot}{y}}^{*} \end{matrix}$ 在内的高阶导数被忽略了, 这会将误差和干扰引入到系统中。在控制输入信号由添蓝溶液喷射信号到 $\begin{matrix} n_{N H_{3, in}}^{*} \end{matrix}$ 的转化过程中, 也存在不确定性。将上述误差和不确定性看做一个附加的干扰项d₂, 可得:

$\begin{matrix} u = u_{im} + d_{2} (38) \end{matrix}$

事实上, 其他的一些不确定性可能也被包括在d₂中, 将上述控制法则应用到系统(式(36))中, 相应的误差动态系统如下:

$\begin{matrix} \{\begin{matrix} \overset{\cdot}{χ} = e_{1} \\ {\overset{\cdot}{e}}_{1} = - k_{0} χ - k_{1} e_{1} - e_{3} \\ {\overset{\cdot}{e}}_{3} = e_{1} - k_{2} e_{3} + d \end{matrix} (39) \end{matrix}$

式中:d=d₁-a₁f₁₂(x, p)d₂。

上述公式将控制执行过程中的不确定性d₂(如公式(38)所示)和模型转化过程中的误差d₁(如公式(14)所示), 都包含在一起。

取同样的李雅普诺夫函数V₂=V₁+ $\begin{matrix} \frac{1}{2} \end{matrix} \begin{matrix} e_{3}^{2} \end{matrix}$ , 对V₂求导可得:

$\begin{matrix} \begin{matrix} {\overset{\cdot}{V}}_{2} = {\overset{\cdot}{V}}_{1} + {\overset{\cdot}{e}}_{3} e_{3} = - k_{1} e_{1}^{2} - k_{2} e_{3}^{2} + e_{3} d \\ (40) \end{matrix} \end{matrix}$

由杨氏不等式可得:

$\begin{matrix} \begin{matrix} {\overset{\cdot}{V}}_{2} \leq - k_{1} e_{1}^{2} - k_{2} e_{3}^{2} + \frac{1}{2} e_{3}^{2} + \frac{1}{2} d^{2} = \\ - k_{1} e_{1}^{2} - (k_{2} - \frac{1}{2}) e_{3}^{2} + \frac{1}{2} d^{2} (41) \end{matrix} \end{matrix}$

定义W(e)=k₁ $\begin{matrix} e_{1}^{2} \end{matrix}$ +(k₂- $\begin{matrix} \frac{1}{2} \end{matrix}$ ) $\begin{matrix} e_{3}^{2} \end{matrix}$ , 选择k₂> $\begin{matrix} \frac{1}{2} \end{matrix}$ 。由e₂=∫ e₁dt关系式可知, W(e)是连续正定的。因此, 误差系统(式(39))是关于d的输入到状态稳定的(input-state stable, ISS)。同样, 误差系统对考虑到的不确定性具有鲁棒性。

而且, 从系统(式(39))中能够观察到, k₁可以控制跟踪误差e₁的衰减问题, 并且k₂可以控制e₃的衰减。从这一点来看, k₁和k₂的取值应该大一些。然而, 从系统(式(34))中可以看到, 较大的k₁和k₂会导致控制器的高增益, 这一点在实际应用中是应该避免的。更值得注意的是, 大的k₂会导致e₃的快速响应。参考e₃= $\begin{matrix} {\overset{\cdot}{e}}_{1} \end{matrix}$ - $\begin{matrix} e_{2}^{*} \end{matrix}$ , 从跟踪虚拟控制目标 $\begin{matrix} e_{2}^{*} \end{matrix}$ 的角度来说, 应该选择一个大的k₂, 然而 $\begin{matrix} {\overset{\cdot}{e}}_{1} \end{matrix}$ 的快速响应可能会导致系统强烈的欠阻尼性。基于研究所提出的urea-SCR系统模型表述, 在仿真阶段控制参数调节过程中, 保证了上述参数的选取原则。

在细节上讨论了一些跟踪误差的偏移, 并对系统(式(39))进行拉普拉斯转化以及一些简单推导之后, 得到:

$\begin{matrix} E_{1} (s) = \frac{1}{(s + k_{1} + \frac{k_{0}}{s}) (s + k_{2}) + 1} D (s) (42) \end{matrix}$

由终值定理可得跟踪误差为:

$\begin{matrix} e_{1} (\infty) = \lim_{s \to 0} s [\frac{1}{(s + k_{1} + \frac{k_{0}}{s}) (s + k_{2}) + 1} D (s)] (43) \end{matrix}$

在d为脉冲和阶跃信号的前提下, 可得e₁(∞ )=0。从引入积分项的作用来看, 这一点确实很有好处。而且, 如果干扰d是一个有范围 $\begin{matrix} \bar{d} \end{matrix}$ 的信号 $\begin{matrix} \bar{d} \end{matrix}$ , 偏移可表示为:

$\begin{matrix} e_{1} (\infty) = \frac{\bar{d}}{k_{0} k_{2}} (44) \end{matrix}$

大体来说, 关于干扰的信息量较少, 为了降低跟踪误差的偏移, 建议选择足够大的k₀和k₂。

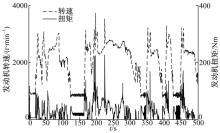
综上, 研究给出的控制参数调节规则为:①根据所需的跟踪误差衰减率选择k₁, 较大的k₁意味着跟踪误差的快速衰减; ②根据可以接受的跟踪误差, 选择大的k₀; ③考虑到控制器的高增益问题, 选择k₂> $\begin{matrix} \frac{1}{2} \end{matrix}$ (可能k₂≤ k₁), 以平衡快速响应和较少的欠阻尼之间的矛盾。

5 仿真结果

仿真在TESIS公司开发的enDYNA^[27]发动机精确建模软件平台上进行, 基于某款确定类型的轻型柴油机建立了enDYNA发动机模型。该发动机有四个缸, 排量为1.9 L, 配备涡轮增压和进气中冷系统, 并且最大转速为4500 r/min。为了充分验证所提控制方法的性能, 仿真在瞬态测试循环FTP75环境下进行, 该瞬态测试循环可以评价连续可变工况条件下的控制系统性能。所选enDYNA发动机模型在FTP75测试循环下, 前500 s的工况变化过程如图2所示。

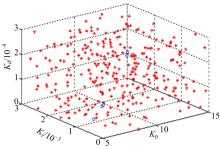
	Figure Option View Download New Window
	图2 FTP75部分瞬态工况条件Fig.2 Part of working conditions of FTP75

在“ 三步法” 控制器参数选取之前, 首先进行了最优PID控制器参数的选取。该最优PID控制器参数的选取采用了蒙特卡罗方法^[28], 该方法的难点是如何选取一个较好的随机数发生器^[29]。研究采用了线性同余发生器, 在K_p∈ [5, 15], K_i∈ [0, 3× 10^-3]以及K_d∈ [0, 3× 10^-4]的范围内, 产生了300个均匀分布的样本。通过将排放水平限定在NO_x平均水平低于0.27 g/kWh; 氨平均逃逸量在77.8× 10^-6以下; 最大逃逸量不超过114× 10^-6, K_p, K_i以及K_d参数被划分为“ 优集” 和“ 差集” 。如图3所示, “ °” 代表“ 优集” ; 而“ × ” 代表“ 差集” 。根据上述参数选取仿真结果, 选择了较小的一组作为最优PID控制器参数, 即K_p=6.278, K_i=8.4× 10^-4以及K_d=2.4× 10^-5, 排放结果如表3所示。

	Figure Option View Download New Window
	图3 PID参数随机样本的分布与划分Fig.3 Distribution and division of random samples of PID parameters

表3 最优PID控制器的参数选取和排放结果 Table 3 Controller parameters selection and emission result of the optimal PID controller

以上述最优PID控制器排放水平为参考, 结合上述理论分析, 研究进行了“ 三步法” 控制器参数的选取。6组“ 三步法” 控制器参数选取的数值及排放结果如表4所示。在这些组参数中, 三项排放指标都比最优PID控制器要好。而且, “ 三步法” 控制器的参数选取范围相对更大。研究所采用的“ 三步法” 控制器参数如下:

$\begin{matrix} k_{0} = 5000, k_{1} = 1000, k_{2} = 100 (45) \end{matrix}$

表4 “ 三步法” 控制器的参数选取和排放结果 Table 4 Controller parameters selection and emission result of the triple-step method controller

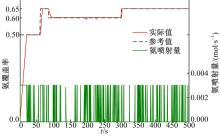
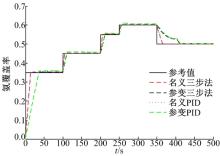
代表性的仿真结果如图4所示。氨覆盖率在初始阶段设置值为0.5; 在第60 s时刻阶跃到0.65; 在第85 s时刻该值阶跃下降到0.6; 最后, 在第300 s时刻再次阶跃回到0.65。

	Figure Option View Download New Window
	图4 氨覆盖率阶跃跟踪控制Fig.4 Ammonia coverage ratios step track control

上述目标值的改变能够测试控制器的瞬态跟踪性能。该控制输入氨的摩尔流量被限定为0.003 mol/s, 并且喷射器的执行情况也显示在图4中。除个别工况以外, 氨覆盖率跟踪效果较好。在测试循环的初始阶段出现了25 s左右的调节时间, 原因是在FTP75测试循环下, 车辆是从第20 s开始启动的, 之前没有NO_x输出, 氨主要经历了吸附反应, 氨覆盖率缓慢上升; 在60~70 s之间的调节时间, 一方面是由于控制目标阶跃变化, 另一方面是由于此刻转速和扭矩也处在剧烈变化之中, 随后的一段时间内废气温度以及发动机NO_x排放等参数都非常不稳定, 强烈的非线性对控制器控制效果有干扰; 此外, 200 s和230 s左右时刻的震荡也是上述工况的剧烈变化造成的。85~95 s之间阶跃下降阶段的调节时间, 一方面是由于控制器控制受到约束, 氨喷射量只能是正值, 即只能增加氨覆盖率, 不能减少; 另一方面原因是, 氨覆盖率下降速度受到此工况下NO_x排放量的限制。

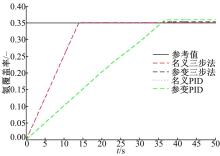
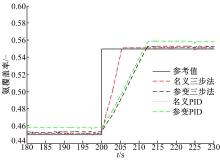
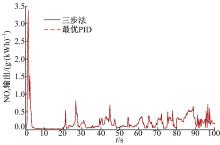
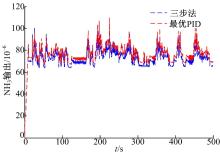
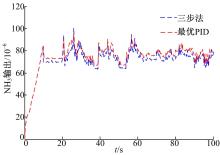
本文提出的“ 三步法” 控制器与最优PID控制器对比结果如图5~图11所示, 所有实验都是具有相同的urea-SCR系统总容积和长度。由于系统标定误差和废气温度等外部状态的可变性, urea-SCR系统参数将会在一定范围内变化。针对参数c_s的100%的可变范围, 图5~图7显示了“ 三步法” 控制器与最优PID控制器之间的跟踪效果对比结果。很明显, 两个控制器在该参数的不确定性的影响下, 调节时间都增加了, 且对“ 三步法” 控制器影响较小。而且, 参数可变对最优PID控制器造成了较大的静差。因此, 相比于最优PID, “ 三步法” 控制器对参数不确定性具有更强的鲁棒性。

	Figure Option View Download New Window
	图5 参数可变的跟踪相应对比Fig.5 Tracking response with parameter variation

	Figure Option View Download New Window
	图6 图5中0~50 s部分的放大Fig.6 Zoom-in of Fig.5(0-50 s)

	Figure Option View Download New Window
	图7 图5中180~230 s部分的放大Fig.7 Zoom-in of Fig.5(180-230 s)

	Figure Option View Download New Window
	图8 NO_x排放对比Fig.8 Comparison of NO_x emission

	Figure Option View Download New Window
	图9 图8中0~100 s部分的放大Fig.9 Zoom-in of Fig.8(0-100 s)

	Figure Option View Download New Window
	图10 NH₃排放对比Fig.10 Comparison of ammonia emission

	Figure Option View Download New Window
	图11 图10中0~100 s部分的放大Fig.11 Zoom-in of Fig.10(0-100 s)

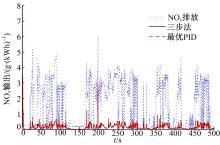
研究提出的“ 三步法” 控制器与最优PID控制器, 排放控制效果对比结果如图8~图11所示。排放控制目标为:控制NO_x排放的平均水平在0.3 g/kWh以下, 并且氨逃逸在平均80× 10^-6以下。由发动机排出, 进入urea-SCR后处理系统的NO_x输入量与两个控制器的输出排放控制效果比较, 如图8、图9所示, 两种控制方法的转化效率都能达到90%以上, 并且控制效果基本一致。两种控制器的氨逃逸量如图10、图11所示, 所采用的“ 三步法” 控制器的控制效果明显要好很多, 相比于研究所提出的控制器, PID控制器的平均氨逃逸量要高出7%以上。并且, PID控制器的震荡更为强烈, 表明“ 三步法” 控制器具有更好的排放效果和鲁棒性。

6 结论

为了同时实现较高NO_x转化效率以及较低的氨逃逸率, 研究采用“ 三步法” 非线性控制技术, 设计了一款非线性控制器跟踪氨覆盖率。基于一款配有urea-SCR系统的精确的enDYNA柴油机模型, 在FTP75瞬态测试循环下, 验证了该控制器良好的跟踪性能。与最优PID控制的实验对比结果表明, 在参数不确定性的影响下, 对“ 三步法” 控制器调节时间影响较小, 且对最优PID控制器造成了较大的静差; 在NO_x转化效率基本一致的条件下; PID控制器的平均氨逃逸量要高出7%以上, 并且震荡更为强烈, 本文所采用的“ 三步法” 控制器具有更好的鲁棒性。

The authors have declared that no competing interests exist.

参考文献

View Option

[1]	刘忠长, 孙士杰, 田径, 等. 瞬态工况下喷油参数对柴油机排放及燃烧特性的影响[J]. 吉林大学学报: 工学版, 2014, 44(6): 1639-1646. Liu Zhong-chang, Sun Shi-jie, Tian Jing, et al. Influences of fuel injection parameters on emissions and combustion of diesel engine under transient conditions[J]. Journal of Jilin University(Engineering and Technology Edition), 2014, 44(6): 1639-1646. [本文引用:1]
[2]	Johnson T V. Diesel emission control in review[J]. SAE Int J Fuels Lubr, 2009, 1(1): 68-81. [本文引用:2]
[3]	Sch`ar C M, Onder C H, Geering H P. Control of an SCR catalytic converter system for a mobile heavy-duty application[J]. IEEE Transactions on Control Systems Technology, 2006, 14(4): 641-653. [本文引用:2]
[4]	Johnson T V. Review of diesel emissions and control[J]. International Journal of Engine Research, 2009, 10(5): 275-285. [本文引用:1]
[5]	Gabrielsson P L T. Urea SCR in automotive applications[J]. Topics in Catalysis, 2004, 28(1-4): 177-184. [本文引用:1]
[6]	Chiang C J, Kuo C L, Huang C C, et al. Model predictive control of SCR aftertreatment system[C]∥IEEE Conference on Industrial Electronics and Applications, 2010: 2058-2063. [本文引用:1]
[7]	Devarkonda M, Parker G, Johnson J H. Model-based control system design in a urea-SCR aftertreatment system based on NH₃ sensor feedback[J]. International Journal of Automotive Technology, 2009, 10(6): 653-662. [本文引用:2]
[8]	Zhao J, Yang T L, Lu G Y. Enhancement of NO₂ gas sensing response based on ordered mesoporous fe-doped In₂O₃[J]. In Sensors and Actuators B, 2014, 191: 806-812. [本文引用:1]
[9]	侯洁, 颜伏伍, 胡杰, 等. Urea-SCR系统NO_x传感器的NH₃交叉感应研究[J]. 内燃机学报, 2014, 32(3): 249-253. Hou Jie, Yan Fu-wu, Hu Jie, et al. Ammonia cross-sensitivity of NO_x sensor for Urea-SCR system[J]. Transactions of CSICE, 2014, 32(3): 249-253. [本文引用:1]
[10]	Hsieh M, Wang J. Diesel engine selective catalytic reduction ammonia surface coverage control using a computationally-efficient model predictive control assisted method[J]. Proceedings of the ASME Dynamic Systems and Control Conference, 2009, 1: 865-872. [本文引用:2]
[11]	Westerlund C, Westerberg B. Model predictive control of a combined EGR/SCR HD diesel engine[C]∥SAE Technical Papers, 2010-01-1175. [本文引用:1]
[12]	Hsieh M, Wang J. A two-cell backstepping-based control strategy for diesel engine selective catalytic reduction systems[J]. IEEE Transactions on Control Systems Technology, 2011, 19(6): 1504-1515. [本文引用:1]
[13]	Hsieh M, Wang J. Backstepping based nonlinear ammonia surface coverage ratio control for diesel engine selective catalytic reduction systems[J]. In Proceedings of the ASME Dynamic Systems and Control Conference, 2009, 1: 1-8. [本文引用:1]
[14]	Zhang H, Wang J, Wang Y Y. Robust filtering for ammonia coverage estimation in diesel engine selective catalytic reduction systems[J]. Journal of Dynamic Systems, Measurement, and Control, 2013, 064504. [本文引用:1]
[15]	Bonfils A, Creff Y, Lepreux O, et al. Closed-loop control of a SCR system using a NO_x sensor cross-sensitive to NH₃[J]. Journal of Process Control, 2014, 24: 368-378. [本文引用:1]
[16]	Bin Y, Li K Q, Ukawa H, et al. Modelling and control of a non-linear dynamic system for heavy-duty trucks[J]. Journal of Automobile Engineering, 2006, 220(10): 1423-1435. [本文引用:1]
[17]	Li T H S, Huang C J, Chen C C. Novel fuzzy feedback linearization strategy for control via differential geometry approach[J]. ISA Transactions, 2010, 49: 348-357. [本文引用:1]
[18]	Ma M M, Chen H, Cong Y F. Backstepping based constrained control of nonlinear hydraulic active suspensions[C]∥in Proceedings of the 26th Chinese Control Conference. Hunan China, 2007: 463-466. [本文引用:1]
[19]	Gao B Z, Chen H, Sanada K, et al. Design of clutch slip controller for automatic transmission using backstepping[J]. IEEE/ASME Transactions on Mechatronics, 2011, 16(3): 498-508. [本文引用:1]
[20]	Chen H, Gong X, Liu Q F, et al. Triple-step method to design non-linear controller for rail pressure of gasoline direct injection engines[J]. IET Control Theory and Applications, 2014, 8(11): 948-959. [本文引用:1]
[21]	Zhao H Y, Gao B Z, Ren B T, et al. Integrated control of in-wheel motor electric vehicles using a triple-step nonlinear method[J]. Journal of the Franklin Institute-Engineering and Applied Mathematics, 2015, 352(2): 519-540. [本文引用:1]
[22]	Willi R. Low-temperature selective catalytic reduction of catalytic behavior and kinetic modeling[D]. Switzerland : ETH Zurich, 1996. [本文引用:1]
[23]	Heiredal M L, Jensen A D, Thogersen J R, et al. Pilot-scale investigation and cfd modeling of particle deposition in low-dust monolithic SCR deNO_x catalysts[J]. AIChE Journal, 2013, 59(6): 1919-1933. [本文引用:1]
[24]	Kota A S, Luss D, Balakotaiah V. Modeling studies of low-temperature aerobic NO_x reduction by a sequence of LNT-SCR catalysts[J]. AIChE Journal, 2013, 59(9): 3421-3431. [本文引用:1]
[25]	Hsieh M. Control of diesel engine urea selective catalytic reduction systems[D]. Ohio: Ohio State University, 2010. [本文引用:1]
[26]	Piazzesi G, Devadas M, Krocher O, et al. Isocyanic acid hydrolysis over fe-zam5 in urea SCR[C]∥Catalysis Communications, 2006, : 600-602. [本文引用:1]
[27]	Philipp O, Huber M. Development and test of ECU functions for OBD with enDYNA[C]∥Proc JSAE Annual Congress, 2004. [本文引用:1]
[28]	Wang P, Chen H, Yang X P, et al. Design and analysis of a model predictive controller for active queue management[J]. ISA Transactions, 2012, 51: 120-131. [本文引用:1]
[29]	Tempo R, Calafiore G, Dabbene F. Rand omized Algorithms for Analysis and Control of Uncertain Systems[M]. New York: Springer-Verlag, 2005. [本文引用:1]

2014

0.0

. 2014, 44(6):1639-1646 DOI:doi:10.13229/j.cnki.jdxbgxb201406017

Influences of fuel injection parameters on emissions and combustion of diesel engine under transient conditions

瞬态工况下喷油参数对柴油机排放及燃烧特性的影响

Liu Zhong-chang , Sun Shi-jie , Tian Jing

刘忠长, 孙士杰, 田径

To explore new ways to optimize combustion under transient conditions, the influences of fuel injection parameters on the emission and combustion characteristics in a high-pressure common-rail diesel engine were investigated. The engine speed of 1650r/min was selected, and at this speed the engine torque was increased from 10% to 90% of the maximum torque within five seconds. Results show that, under transient condition, the smoke surges and NO x is below that under steady-state condition, CA50 delays. When the injection timing is advanced, the smoke emission and NO x emission increase, CA10, CA50 and CA90 are in advance. When the injection pressure is higher, the smoke emission decreases, NO x emission increases, CA10 and CA50 are in advance. The feasibility of reducing distortion between transient-state and steady-state by adjusting the fuel injection parameters was also discussed. Results show that adjusting the injection pressure can reduce the performance difference between the transient-state and steady-state.

为了探究瞬态工况下燃烧优化的新方法,在一台高压共轨柴油机上研究了瞬态工况下喷油参数对排放及燃烧特性的影响,试验工况点选择在柴油机转速为1650 r/min,在5 s内使柴油机转矩从该转速最大转矩的10%达到90%。结果表明:瞬态工况下柴油机的燃烧和排放特性明显有别于稳态工况,具体表现为:瞬态工况下烟度激增,NO x 排放低于稳态工况,CA50后移;瞬态工况下随着喷油正时的提前,烟度排放增加,NO x 排放量增加,CA10、CA50和CA90均提前;随着喷油压力的加大,烟度排放降低,NO x 排放量增加,CA10、CA50提前。此外,还探讨了通过调整喷油参数减小瞬态工况下柴油机性能畸变的可行性,结果表明:通过调整喷油压力可以有效地减少柴油机瞬态与稳态性能上的差异。

... 研究人员提出了很多降低NO_x排放的方法^[1,2] ...

2009

0.0

... 研究人员提出了很多降低NO_x排放的方法^[1,2] ...

... 其中,尿素选择性催化还原(urea-SCR)技术具备一定优势^[2] ...

2006

0.0

... 5%的尿素溶液(添蓝溶液),但储存尿素的罐会增加车辆的重量^[3] ...

... 当前的一些尿素喷射控制方法,主要集中在反馈控制设计和基于线性urea-SCR系统模型的控制设计上^[3,7] ...

2009

0.0

... 尽管在当前的排放法规中没有明文规定,但是较高的氨逃逸被认为是对身体有害的,并且气味十分难闻^[4] ...

2004

0.0

... 但在实际应用中,大多数都是以增加成本和所占空间为代价^[5] ...

2010

0.0

... 目前,人们已经普遍认识到,通过改进尿素喷射技术达到上述控制目标是一种较便捷且经济的方法^[6] ...

2009

0.0

... 当前的一些尿素喷射控制方法,主要集中在反馈控制设计和基于线性urea-SCR系统模型的控制设计上^[3,7] ...

... 最近,德尔福公司推出了NH₃传感器^[7],但由于其还未被量产,在实际的工业应用中很少用到 ...

2014

0.0

... 其中,一部分反馈控制是基于NO_x传感器的^[8],但NO_x传感器对氨有交叉敏感性^[9] ...

2014

0.0

... 其中,一部分反馈控制是基于NO_x传感器的^[8],但NO_x传感器对氨有交叉敏感性^[9] ...

2009

0.0

... 这就使得单独的NO_x和NH₃反馈都很难达到理想的控制目的^[10] ...

... 因此,有学者提出了以理想氨覆盖率作为反馈控制目标的非线性控制方法^[10,12,13] ...

0.0

... 此外,由于urea-SCR系统化学反应本身具有较强的复杂性和非线性,逐渐使得非线性控制方法成为了研究热点^[11] ...

2011

0.0

... 因此,有学者提出了以理想氨覆盖率作为反馈控制目标的非线性控制方法^[10,12,13] ...

2009

0.0

... 因此,有学者提出了以理想氨覆盖率作为反馈控制目标的非线性控制方法^[10,12,13] ...

2013

0.0

2014

0.0

2006

0.0

... 与此同时,一些先进的非线性控制方法也在不断发展,这其中就包括反馈线性化^[16,17]和backstepping技术^[18,19] ...

2010

0.0

... 与此同时,一些先进的非线性控制方法也在不断发展,这其中就包括反馈线性化^[16,17]和backstepping技术^[18,19] ...

2007

0.0

... 与此同时,一些先进的非线性控制方法也在不断发展,这其中就包括反馈线性化^[16,17]和backstepping技术^[18,19] ...

2011

0.0

... 与此同时,一些先进的非线性控制方法也在不断发展,这其中就包括反馈线性化^[16,17]和backstepping技术^[18,19] ...

2014

0.0

... 控制策略,具有简洁和标准化的结构^[20,21],本文将该方法扩展应用于时变参数系统上,解决上述urea-SCR系统控制问题 ...

2015

0.0

... 控制策略,具有简洁和标准化的结构^[20,21],本文将该方法扩展应用于时变参数系统上,解决上述urea-SCR系统控制问题 ...

1996

0.0

... 吸附态的氨能够在催化剂的作用下选择性地与NO_x反应生成N₂和H₂O,当温度高于200 ℃时,该反应主要按照Eley-Rideal机制进行^[22],反应方程式如下所示: ...

2013

0.0

2013

0.0

2010

0.0

2006

0.0

... 并且,添蓝溶液转化为氨需要经过蒸发、分解以及水解三步复杂的化学反应过程^[26],这些过程在参数漂移时不可避免地引入误差 ...

2004

0.0

... 5 仿真结果仿真在TESIS公司开发的enDYNA^[27]发动机精确建模软件平台上进行,基于某款确定类型的轻型柴油机建立了enDYNA发动机模型 ...

2012

0.0

... 该最优PID控制器参数的选取采用了蒙特卡罗方法^[28],该方法的难点是如何选取一个较好的随机数发生器^[29] ...

2005

0.0

... 该最优PID控制器参数的选取采用了蒙特卡罗方法^[28],该方法的难点是如何选取一个较好的随机数发生器^[29] ...