基于重复-自抗扰控制的航空光电稳定平台控制系统设计

引用本文

魏伟, 戴明, 李嘉全, 毛大鹏, 王昊. 基于重复-自抗扰控制的航空光电稳定平台控制系统设计. 2015, 45(6): 1924-1932
WEI Wei, DAI Ming, LI Jia-quan, MAO Da-peng, WANG Hao. Design of airborne opto-electric platform control system based on ADRC and repetitive control theory. Journal of Jilin University Engineering and Technology Edition, 2015, 45(6): 1924-1932 复制到剪切板

Permissions

基于重复-自抗扰控制的航空光电稳定平台控制系统设计

魏伟^1,², 戴明¹, 李嘉全¹, 毛大鹏¹, 王昊^1,²

1.中国科学院长春光学精密机械与物理研究所航空光学成像与测量重点实验室,长春 130033

2.中国科学院大学长春光学精密机械与物理研究所研究生部,长春 130033

戴明(1965-),男,研究员,硕士.研究方向:动机座稳定技术.E-mail:daim@vip.163.com

作者简介:魏伟(1987-),男,博士.研究方向:航空光电稳定平台视轴稳定技术.E-mail:451123977@qq.com

基金:“973”国家重点基础研究发展计划项目(2009CB72400603B); “863”国家高技术研究发展计划项目(2008AA121803)

摘要

分析了航空光电稳定平台模型并利用电流环使平台模型简化为K/s。阐述了影响平台稳定性的扰动以及抑制扰动的方法。介绍了平方滞后超前控制原理及其优缺点。根据重复控制器以及自抗扰控制器的优点,将它们组合搭建控制系统,并在振动平台上进行速度稳定和目标跟踪试验。结果表明:与传统的控制器相比,用本文控制方法得出的扰动隔离度至少提高了6.28 dB;所设计的系统在符合工程需求的范围内,具有很强的实用性和鲁棒性,对实际工程控制器设计具有一定的参考价值。

关键词: 飞行器控制系统; 平方滞后超前控制; 重复控制; 自抗扰控制; 扰动隔离度

中图分类号:TP273 文献标志码:A 文章编号:1671-5497(2015)06-1924-09

Design of airborne opto-electric platform control system based on ADRC and repetitive control theory

WEI Wei^1,², DAI Ming¹, LI Jia-quan¹, MAO Da-peng¹, WANG Hao^1,²

1.Key Laboratory of Airborne Optical Imaging and Measurement, Changchun Institute of Optics, Fine Mechanics and Physics, Chinese Academy of Sciences, Changchun 130033,China

2.Postgraduate Department of Changchun Institute of Optics,Fine Mechanicsand Physics, University of Chinese Academy of Sciences, Changchun 130033,China

Abstract

The airborne opto-electric stable platform model was analyzed and simplified to K/s with current loop. The disturbance to the platform stability and the disturbance rejection method were illustrated. The traditional square lag-lead compensation method, its strengths and weaknesses were introduced. The repetitive controller and Active Disturbance Rejection Controller (ADRC) were described. A repetitive controller and a two stage ADRC were designed, which were integrated into a new controller system taking the advantages of both. Speed stability experiment and target tracking experiment were carried out on a vibration platform. Results show that compared with conventional controllers, the proposed controller improves the disturbance isolation by 6.28 dB at least. On all accounts, the proposed control system has strong robustness, observably improves the disturbance isolation of the opto-electric platform and can provide guide for engineering applications.

Keyword: aircraft control system; square lag-lead control; repetitive control; auto/active disturbance rejection control(ADRC); isolation degree of disturbance

Show Figures

0 引言

高精度机载光电稳定平台是由多级框架、光电红外系统以及激光瞄准系统组成的综合航空遥感器, 其主要作用是隔离载体对光电平台的扰动^[1], 使光电系统视轴能够快速、稳定地跟踪目标, 且使激光功率通过长距离传输后仍能集中于目标上, 具有机动性高、鲁棒性强、实时性好等特点, 因而被广泛应用于地质测绘、军事侦察、军事打击引导等领域。

造成机载光电稳定平台视轴不稳定的因素有很多, 例如飞机姿态的变化, 飞机的振动, 轴系间的摩擦、耦合, 传感器噪声等; 而平台采用的是力矩电机直接驱动方式驱动平台, 因此载体上的干扰源对平台的速度扰动最为明显, 其通过平台和负载间的摩擦影响光学镜头视轴的稳定性。目前消除扰动的方法主要还是PID理论以及平方滞后超前等方法, 这些方法利用提高开环系统的型别和低频段的增益来降低扰动对平台稳定性的影响^[2], 属于被动抗扰方法, 被动抗扰方法的优点是理论简单、易于调节、适应性强, 仍是绝大多数控制过程中最常采用的控制方法。不过, 由于被动抗扰受到机械谐振频率的影响, 系统开环剪切频率不能无限制提高, 因而限制了被动抗扰方法抑制扰动的能力。

重复控制^{[3, 4]}是依据内膜原理发展而来的控制方法, 它可以周期性地跟踪输入信号, 也可以周期性地抑制扰动, 从系统框图来看, 它仍属于被动抗扰的范畴。从傅里叶变换原理可知, 扰动信号可以认为是正弦信号的叠加, 而基于内膜原理的控制方法对周期信号可以做到完全跟踪和抑制^[5], 因此从理论上该方法具有一定的先进性, 从系统波特图以及试验结果分析, 重复控制理论可以有效提高系统的扰动隔离度。

自抗扰控制方法^[6]是一种不依赖于系统模型的控制方法, 它不必对控制对象建模, 而是直接将系统的未建模动态和未知外界扰动都归结为对系统的总和扰动而进行估计和补偿。采用自抗扰控制器的机载光电侦察平台伺服系统, 阶跃响应速度快、无超调, 对模型摄动和测量噪声不敏感, 对外界扰动的抑制能力强, 能够有效克服摩擦扰动对平台低速运动性能的影响^[7], 各项性能均优于传统控制器。

本文设计了基于重复控制方法和自抗扰控制方法的控制器。控制结果表明:此控制器与单一使用重复控制或者自抗扰控制, 以及传统的控制方法相比, 在速度稳定性和目标跟踪精度上都有非常显著的提高, 且控制系统的鲁棒性仍能满足工程需求, 具有一定的理论研究和工程应用价值。

1 光电稳定平台数学模型分析及简化

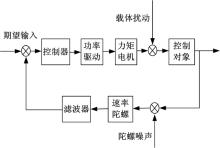
本文分析的光电稳定平台为两轴四框架结构, 由大功率力矩电机直接驱动, 控制过程如图1所示, 当光电平台受到载体扰动时, 通过陀螺敏感得到平台相对于惯性空间的角速度, 并与指令速度信号作差得到速度误差信号, 误差信号通过控制器, 由控制算法得到控制电压信号, 再通过功率驱动器驱动电机产生驱动力矩, 使控制对象反向运动, 从而达到抑制误差的目的。

	Figure Option View Download New Window
	图1 平台控制系统结构简图Fig.1 Structure diagram of platform control system

由于两轴四框架中方位轴和俯仰轴互相正交, 所以他们之间的耦合作用基本可以忽略, 且它们的控制过程大致相似, 又因为方位轴控制系统结构内, 位置环与速度环的控制方法大致类似, 所以取方位轴速度环作为控制研究对象。

速度环控制对象由二阶惯性环节和一阶振荡环节串联构成, 属于高阶控制对象。试验证明, 控制这样的高阶对象时, 容易产生严重的相位滞后, 对这一现象可以通过引入电流环加以简化。

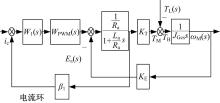
电流环控制就是在速度环内再加一个电流反馈传感器和电流反馈校正网络, 采用双级模式脉冲宽度调制(Pulse width modulation, PWM)设计, 构成电流闭环控制系统, 改变速度回路控制对象的特性, 降低控制对象的阶次, 其原理图如图2所示。

	Figure Option View Download New Window
	图2 电流环的工作原理Fig.2 Principle of current loop

图2中, i_c为电枢电流; R_a为电枢回路总电阻; L_a为电枢回路总电感; T_M为电动机转矩; T_L为扰动折算到电动机转轴上的负载转矩; T_B为加速转矩; J_Ges为折算到电动机上总的转动惯量; ω _M为电动机角速度; E_g为反电势。

可以设计电流反馈校正网络W₁(s), 使得在一定的带宽内电流环的闭环传递函数G_i(s)=1, 则图2可简化为图3, 由于电流环的设计采用模拟电路, 因而W₁(s)能实时对电流进行校正, 这时i_c的动态过程变化很快, 而反电势E_g的变化过程相对来说是缓慢的, 因此可以忽略反电势对电流环的影响^[8], 简化后的电机模型框图如图3所示。

	Figure Option View Download New Window
	图3 简化后的直流力矩电机结构图Fig.3 Simplified structure diagram of dc torque motor

电流环能够最大程度地简化电机模型, 从而为分析系统扰动提供非常方便和直观的条件, 同时使电机模型变得更加精确, 而且精确电机模型和外部扰动模型使得伺服控制器的设计更有针对性。利用上述电流环原理对光电稳定平台的控制对象进行简化, 得到模型如式(1)所示:

$\begin{matrix} G_{0} (s) = K / s (1) \end{matrix}$

式中:K为可测常数。

2 扰动分析及扰动抑制方法

光电稳定平台的扰动主要来源于载体姿态变化对平台的速度扰动, 其作用原理如图4所示, 图中d₁, d₂, d₃为传递过程中的扰动。

	Figure Option View Download New Window
	图4 扰动传递过程Fig.4 Transfer process of disturbance

由此可见, 扰动使载体姿态变化, 首先引起外框架的晃动, 由于外框架带宽较低, 对扰动的抑制能力很弱, 载体的扰动几乎未经衰减, 完全传递至内框架, 进而影响视轴的稳定精度。由此可见, 如何突破带宽的限制, 同时提高内、外框架对扰动的抑制能力, 使得载体的扰动在传递的过程中逐次得到外框架、内框架的衰减是减小载体姿态变化对视轴稳定精度影响的关键。

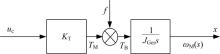
由于内、外框架的驱动方式相同, 其扰动的作用原理也基本一致, 所以本文仅以内框架为例来分析扰动在框架中的作用原理(见图5), 图5中f为承载体对系统的速度扰动。

	Figure Option View Download New Window
	图5 扰动作用原理Fig.5 Principle of disturbance in system

图5中:

$ω_{M} (s) = x (s) = \frac{K_{T} u_{c} (s) - f (s)}{J_{Ges} s} (2)$

从而得到：

$\begin{matrix} \begin{matrix} x (s) = \frac{K_{T}}{J_{Ges} s} [u_{c} (s) + \frac{J_{Ges} s}{K_{T}} f (s)] (3) \end{matrix} \end{matrix}$

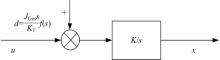
这样得到的等效扰动如图6所示。

	Figure Option View Download New Window
	图6 经等效处理后系统中扰动的作用原理Fig.6 Principle of disturbance by equivalent processing

图6中, x为平台方位轴的角速率; k=J_Ges/K_T为经电流环简化后的参数; u为控制量; d为外界对系统的扰动总和。结合平台具体参数, 得到内框架被控制对象的传递函数如式(4)所示:

$\begin{matrix} G (s) = 32 / s (4) \end{matrix}$

3 平方滞后超前控制

在传统的控制方法中, 平方滞后超前控制是非常经典和常用的一种方法, 其中平方滞后环节使得校正后的系统开环低频段斜率为-60 dB, 从而大幅度提高开环增益, 进而抑制干扰力矩。同时在平方滞后的基础上加入超前环节, 提高系统的带宽和动态性能。本文试验中采用的光电稳定平台, 其内框架的平方滞后超前环节的参数如式(5)所示:

$\begin{matrix} G_{c_in} (s) = \frac{1400 (0.0095 s + 1) {(0.0556 s + 1)}^{2}}{(0.0052 s + 1) {(s + 1)}^{2}} (5) \end{matrix}$

经试验验证, 校正后内框架系统的闭环带宽为26.8 Hz。单位阶跃响应如图7所示, 超调量σ =11.3%, 上升时间t_r=10.9 ms。

	Figure Option View Download New Window
	图7 内模理论对正弦扰动的抑制原理Fig.7 Principle of sine wave disturbance rejection by internal model theory

平方滞后超前控制器的核心思想是依靠提高开环系统的型别, 从而提高低频段的增益来抑制载体扰动。然而, 提高开环增益将使得系统相位裕量减小, 进而使稳定性变差。同时, 由于受系统机械谐振和开环剪切频率的影响, 低频段增益不能无限制提高, 因此带宽很难做到更高水平, 所以其扰动抑制能力难以得到本质上的提高。

4 基于重复控制和自抗扰的控制器

4.1 重复控制

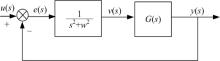
重复控制是日本的Inoue于1981年根据内模原理的思想提出来的^{[9, 10]}, 以正弦扰动信号为例, 介绍内膜原理的抑制扰动原理。设扰动为频率为w的正弦函数, 那么该信号可以由传递函数1/(s²+w²)产生, 如果要跟踪单一频率的正弦信号, 那么根据内膜原理, 需要在控制器内植入模型1/(s²+w²)。

这样, 误差传递函数为:

$E (s) = \frac{e (s)}{u (s)} = \frac{1}{1 + \frac{G (s)}{s^{2} + w^{2}}} (6)$

则误差为：

$\begin{matrix} \begin{matrix} e (s) = \frac{1}{1 + \frac{G (s)}{s^{2} + w^{2}}} u (s) = \frac{1}{s^{2} + w^{2} + G (s)} \times \\ [(s^{2} + w^{2}) \frac{1}{s^{2} + w^{2}}] = \frac{1}{s^{2} + w^{2} + G (s)} (7) \end{matrix} \end{matrix}$

推导过程中发生了s²+w²的零极点对消, 这样, 只需要判断特征方程s²+w²+G(s)=0的特征根分布情况, 只要根都分布在左半s-平面, 那么就可以判断跟踪误差渐进收敛到零。正弦信号的跟踪问题就简化成内部稳定问题。

利用内模原理的思想, 在稳定的闭环系统内设置一个可以产生与参考输入同周期的内部模型, 从而使系统实现对外部周期性参考信号的渐近跟踪, 即叠加到被控对象的输入信号除偏差信号外, 还叠加了上一周期该时刻的控制偏差。把上一周期的偏差和当前的偏差一起叠加到被控对象进行控制, 形成所谓的重复控制。

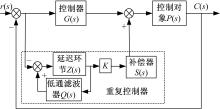
重复控制本身属于开环补偿控制^[11], 并不是闭环控制, 在实际应用中, 为了得到较好的动态性能, 通常把重复控制器嵌入到常规的PID闭环控制环内以形成复合控制, 系统框图如图8所示。

	Figure Option View Download New Window
	图8 重复控制器原理Fig.8 Principle of repetitive controller

图8中, 虚线框内为重复控制器, 其中延时环节的正反馈环节设计关键问题是系统的稳定。只有当对象正则但不严格正则时系统才能稳定, 对此设计低通滤波器Q(s), 且为了满足非最小相位系统的带宽要求, 设计动态补偿器K× S(s), 其中K为补偿系数。补偿器可以改造控制对象, 使系统在中低频段为单位增益, 增加系统的稳定裕度, 这样, 当满足式(8)时系统稳定:

$\begin{matrix} ‖ Q (s) [1 - F (s) G_{0} (s)] ‖_{\infty} < 1 (8) \end{matrix}$

式中:G₀为广义被控对象, G₀=P(s)/[1+P(s)]。

在平台控制过程中, 输入信号不一定是周期信号, 但是可以运用重复控制的思想, 利用延迟环节, 周期性补偿误差信号, 逐周期减小误差, 加快误差收敛速度, 因而能够大大降低控制系统的稳态误差。这种方法不但能够降低周期性给定信号的控制误差, 而且还能抑制负载的周期性扰动。

4.2 自抗扰控制器

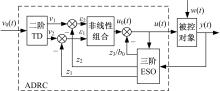
自抗扰控制器(ADRC)由跟踪微分器(TD)、扩张状态观测器(ESO)、状态偏差组合(SEF)组成, 系统结构如图9所示。

	Figure Option View Download New Window
	图9 自抗扰控制器的工作原理Fig.9 Principle of ADRC

其中, 跟踪微分器的主要作用有两个:一是给参考信号安排过渡过程; 二是获取参考信号微分的估计且不会放大噪声。扩张状态观测器主要作用也有两个:一是跟踪控制对象的输出信号并估计其微分; 二是估计控制系统的扰动总和。状态偏差组合为一非线性函数, 其具体形式可根据系统的不同进行调整^{[12, 13]}。由自抗扰原理, 在u₀中加入对系统扰动的补偿, 可得自抗扰控制量为:

$\begin{matrix} u = u_{0} - z_{3} / b_{0} (9) \end{matrix}$

它对扰动进行了实时的估计和补偿, 与被动抗扰方式相比, 自抗扰控制方法可以估计所有扰动的总和, 使一些未预料到的扰动也能得到补偿, 而且省去了很多控制作用带来的不足, 例如积分环节的饱和作用等。

4.3 基于自抗扰和重复控制理论的控制器设计

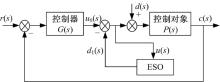
利用自抗扰理论的思想, 设计扩张状态观测器ESO^{[14, 15]}, 并引入扰动前馈补偿算法进行主动抗扰。如图10所示。

	Figure Option View Download New Window
	图10 扰动前馈型自抗扰控制器的工作原理Fig.10 Principle of ADRC based disturbance feed-forward

图10中, ESO为扩张状态观测器; r(s)为期望输入; C(s)为系统输出; d(s)为等效总和扰动; d₁(s)为扰动观测值。由此系统框图得出输入以及误差到输出的传递函数为:

$\begin{matrix} \begin{matrix} C (s) = \frac{G (s) P (s)}{1 + G (s) P (s)} r (s) + \\ \frac{P (s)}{1 + G (s) P (s)} [d (s) - d_{1} (s)] (10) \end{matrix} \end{matrix}$

由式(10)可以看出, 扰动观测器观测到的d₁(s)越接近于误差d₁(s), 那么误差对系统的影响就越小。

设计扩张状态观测器ESO, 由前文得到的被控对象等效传递函数G(s), 将式(4)改写成状态方程:

$\begin{matrix} \{\begin{matrix} {\overset{\cdot}{x}}_{1} = 32 u + d \\ y = x_{1} \end{matrix} (11) \end{matrix}$

式中:u为控制量; x₁为系统角速度; y为系统输出; d为式(5)中的扰动总和, 将d作为一个新的被扩张的状态加入到系统中, 即令:x₃=d, 由此式(11)可以改写为:

$\begin{matrix} \{\begin{matrix} {\overset{\cdot}{x}}_{1} = x_{2} + 32 u \\ {\overset{\cdot}{x}}_{2} = a (t) \\ y = x_{1} \end{matrix} (12) \end{matrix}$

式(13)是基于式(12)设计二阶非线性扩张状态观测器, 对扰动d进行实时估计, 用z₁观测系统角速度; z₂观测扰动d; β ₀₁和β ₀₂为扩张状态观测器的可调参数。

$\begin{matrix} \{\begin{matrix} e_{1} = z_{1} - y \\ {\overset{\cdot}{z}}_{1} = z_{2} - β_{01} e_{1} + bu \\ {\overset{\cdot}{z}}_{2} = - β_{02} fal (e_{1}, 1 / 2, δ) \\ y = z_{1} \end{matrix} (13) \end{matrix}$

式中:fal函数的形式为:

$\begin{matrix} fal (e, α, δ) = \{\begin{matrix} \frac{e}{δ^{α - 1}}, |e| \leq δ \\ |e| sign (e), |e| > δ \end{matrix} (14) \end{matrix}$

其中[-δ , δ ]为fal(e, α , δ )函数中线性段区间长度, 它可以避免状态观测器在原点附近发生高频振荡。由于本次试验中陀螺噪声峰值为0.27/s, δ 取值应大于此值, 取δ =0.37° /s, 满足试验条件。

在本试验中采用基于带宽的单参数化方法来设计扩张状态观测器的参数。设β ₀₁=2ω 、β ₀₂=ω ², 取ω =200。这样就可以根据自抗扰控制的思想, 令u=u₀-z₂/32, 设计自抗扰控制器如下式所示:

$\begin{matrix} \{\begin{matrix} {\overset{\cdot}{x}}_{1} = 32 u_{0} + d - z_{2} \\ y = x_{1} \end{matrix} (15) \end{matrix}$

由此得出:只要合理设计状态观测器, 便可以使(d-z₂)→ 0, 达到消除扰动的目的。

从上文知道, 重复控制对周期性扰动的抑制方面具有其他算法不可比拟的优势^[16], 而自抗扰控制器不需要知道控制对象的具体参数和形式, 可以对控制器施加重复控制补偿, 而利用自抗扰控制器主动隔离扰动, 在主动抗扰和被动抗扰的双重作用下, 对系统中的扰动进行抑制, 大大提高了系统的扰动隔离度。

结合重复控制原理与自抗扰控制原理, 发挥其各自优势, 设计控制器如图11所示。

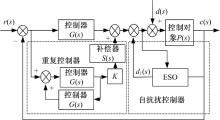	Figure Option View Download New Window
	图11 基于重复控制和自抗扰原理的控制器工作原理Fig.11 Principle of control system based on ADRC and repetitive control theory

其中, 设计低通滤波器通带为50 Hz的巴特沃兹滤波器, 取延迟环节延迟一个采样周期, 补偿系数K为10, 补偿器S(s)的传递函数为:

$\begin{matrix} S (s) = \frac{s^{2}}{s + 0.826} (16) \end{matrix}$

5 试验及结果分析

为了验证本文设计的控制器的控制效果, 将光电稳定平台安装在振动平台上, 振动平台在2 Hz的频率范围内任意振动, 对稳定平台分别进行速度稳定试验、目标跟踪试验以及控制器的鲁棒性性能分析。并与经典的平方滞后超前控制器控制结果进行对比。

5.1 速度稳定试验

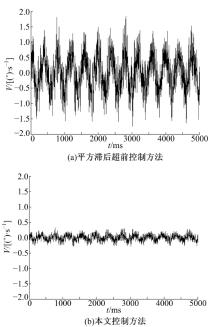
在速度稳定试验中, 振动平台在0~2 Hz内以任意频率摇摆, 稳定平台期望转速为0, 通过测量陀螺信号中的速度残差来判断平台速度环稳定方法对扰动的隔离程度, 图12(a)和图12(b)为振动平台以1° , 2 Hz做正弦运动时, 稳定平台分别采用平方滞后超前控制器和本文设计控制器时的速度残差。

	Figure Option View Download New Window
	图12 平方滞后超前控制和本文控制方法的扰动残差Fig.12 Disturbance remains of traditioral method and the designed method

由图12可以看出, 与传统的平方滞后超前控制方法相比, 本文设计的控制器对扰动残差的隔离效果非常明显, 扰动峰值大约为0.4 ° /s, 由于平台在关机状态下的陀螺噪声峰值为0.27 ° /s, 即所设计系统几乎完全隔离扰动。

对2 Hz下扰动残差数据进行频谱分析, 频谱曲线如图13所示。从图中可以看到, 本文设计控制器隔离扰动后的残差量大约为采用平方滞后超前控制器残差量的1/7, 即对2 Hz的扰动隔离度提高了20.6 dB。而对由其他非线性因素引起的倍频速度分量扰动, 本文所设计的方法也有很明显的抑制效果。

	Figure Option View Download New Window
	图13 扰动残差对比Fig.13 Remains of disturbance

表1为振动平台在幅值为1° 、频率为0.1~2.0 Hz之间振动时, 采用本文所设计方法后相比于传统方法的扰动隔离度提高程度, 可以看出, 在各个频率处, 本文所设计方法对扰动的抑制能力都有明显提高。

表1 本文方法相比于平方滞后超前控制器扰动隔离度的提高程度 Table 1 Improvement of disturbance isolation degree by the designed controller compared with square lag-lead controller

5.2 目标跟踪试验

设计光路模拟光电稳定平台的高空工作环境:将光电稳定平台的跟踪器置于最长焦距, 模拟其对无限远的固定目标进行跟踪。其中跟踪器在最长焦距时, 角度值量纲为53 μ rad; 再控制振动平台使其在1° 、2 Hz做正弦运动, 模拟光电稳定平台载体对它的扰动。

图14(a)为采用平方滞后超前控制时的角度偏差, 变化范围是± 1.412 mrad; 图14(b)为采用本文所设计方法控制时的角度偏差, 变化范围是± 0.265 rad, 从图中可以看出, 本文方法对目标的跟踪效果比传统方法提高了5倍之多。

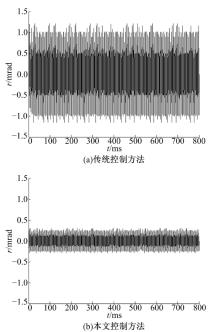	Figure Option View Download New Window
	图14 采用传统控制方法和本文控制方法的视轴晃动范围Fig.14 Range of visual axis sloshing with troditionnal method and the designed method

表2为摇摆台以1° 、0.1~2.0 Hz之间每隔0.5 Hz的频率进行摇摆, 分别使用两种方法时, 稳定平台视轴相对于目标中心点的角度运动范围。从表中可以看出, 在0~2 Hz的每个频率点, 本文所设计控制器的跟踪效果都优于平方滞后超前控制器的跟踪效果。

表2 平台处于跟踪状态时视轴的晃动范围 Table 2 Range of visual axis sloshing when the platform is in tracking state

5.3 鲁棒性分析

为了验证本文所设计控制器的鲁棒性, 改变控制对象的参数, 使其在± 15%的范围内变化, 并保持控制器的参数不变, 重新进行速度稳定和目标跟踪试验, 得到在0~2 Hz内的稳定和跟踪结果如表3和表4所示。

表3 模型参数变化± 15%时扰动隔离度的提高程度 Table 3 Improvement of disturbance isolation degree by using the designed controller when the model parameters change in 15%

表4 模型参数变化± 15%时视轴的晃动范围 Table 4 Range of visual axis sloshing by using the designed controller when the model parameters change in 15%

对比表1~表4可以看出, 当系统参数变化± 15%时, 本文所设计控制器, 在速度稳定性能和跟踪精度上, 依然明显优于平方滞后超前控制器。

当系统参数的变化超过± 15%时, 速度稳定性能和跟踪精度虽有提高, 但提高程度已低于6.02 dB(即1倍于传统方法的提高程度); 当系统参数的变化超过± 17%时, 自抗扰控制器的速度稳定性能和跟踪精度已不如平方滞后超前控制器的性能。由于± 15%的参数变化范围已经很好地符合实际工程的需要。所以, 本文设计控制器相对于传统控制器, 具有更好的稳定性能和跟踪性能, 在实际工程应用中, 具有很强的实用性和鲁棒性。

6 结束语

通过对光电稳定的平台模型以及对影响其性能的扰动分析, 结合平台模型特点, 提出了一种基于重复控制和自抗扰理论的控制器设计方案。在系统前端通过重复控制对误差信号周期性补偿, 在系统后端, 设计了基于扰动频率自适应的扩张状态观测器。然后在重复控制策略的基础上, 引入扰动前馈补偿算法进行主动抗扰。试验结果表明:针对1° 、0.1~2.0 Hz的载体扰动, 相比于传统的平方滞后超前控制器, 采用基于重复控制和自抗扰控制方法设计的控制器, 系统扰动隔离度至少提高了6.28 dB, 且随着扰动频率增大, 扰动隔离度提高程度更明显, 最好的情况达到13.06 dB。本文控制器对被控对象参数在15%的范围内任意变化, 仍然能达到非常好的速度稳定性和目标跟踪精度, 具有很强的鲁棒性。综上所述, 基于重复控制和自抗扰控制方法设计的控制器对比于经典控制方法, 大大提高了光电稳定平台对扰动的抑制能力。这为进一步提高航空光电稳定平台的扰动隔离度提供了新方法, 具有较高的参考价值和实用价值。

The authors have declared that no competing interests exist.

参考文献

View Option

[1]	Hua Chang-chun, Wang Qing-guo, Guan Xin-ping, et al. Robust adaptive controller design for nonlinear time-delay systems via T-S fuzzy approach[J]. IEEE Transactions on Fuzzy Systems, 2008, 17(4): 901-910. [本文引用:1]
[2]	李嘉全, 丁策, 孔德杰, 等. 基于速度信号的扰动观测器及在光电稳定平台的应用[J]. 光学精密工程, 2011, 19(5): 998-1004. Li Jia-quan, Ding Ce, Kong De-jie, et al. Velocity based disturbance observer and its application to photoelectric stabilized platform[J]. Optics and Precision Engineering, 2011, 19(5): 998-1004. [本文引用:1]
[3]	李翠艳, 张东纯, 庄显义. 重复控制综述[J]. 电机与控制学报, 2005, 1(9): 37-44. Li Cui-yan, Zhang Dong-chun, Zhuang Xian-yi. Repetitive control a survey[J]. Electric Machines and Control, 2005, 1(9): 37-44. [本文引用:1]
[4]	Lei Po, Liu Zhu-mu, Fu Xiao-na, et al. Sliding mode control with disturbance observer for a class of nonlinear systems[J]. International Journal of Automation & Computing, 2012, 5(1): 301-309. [本文引用:1]
[5]	Chen Mou, Wu Qin-xian, Jiang Chang-sheng, et al. Guaranteed transient performance based control with input saturation for near space vehicles[J]. Science China Information Sciences, 2014, 57(5): 1-12. [本文引用:1]
[6]	赖爱芳, 郭毓, 郑立君. 航天器姿态机动及稳定的自抗扰控制[J]. 控制理论与应用, 2012, 29(3): 401-407. Lai Ai-fang, Guo Yu, Zheng Li-jun. Active disturbance rejection control for spacecraft attitude maneuver and stability[J]. Control Theory & Applications, 2012, 29(3): 401-407. [本文引用:1]
[7]	高志强. 控制工程的抗扰范式[C]∥29届中国控制会议, 北京, 2010: 29-31. Gao Zhi-qiang. On disturbance rejection paradigm in control engineering[C]∥Proceedings of the 29th Chinese Control Conference, Beijing, 2010: 29-31. [本文引用:1]
[8]	张黎黎, 黄一, 吕俊芳. 机载光电跟瞄平台伺服系统中电流环的设计与仿真[J]. 航空计测技术, 2003, 23(6): 15-21. Zhang Li-li, Huang Yi, Lü Jun-fang. Design and simulation of current-loop for servo of airborne electro-optical pointing and tracking platform[J]. Aviation Metrology & Measurement Technology, 2003, 23(6): 15-21. [本文引用:1]
[9]	张东纯, 曾鸣, 苏宝库. 基于重复控制的动态补偿器及其在恒速调节系统中的应用[J]. 中国电机工程学报, 2001, 21(7): 95-97. Zhang Dong-chun, Zeng Ming, Su Bao-ku. Dynamic compensator based on repetitive control and its application to constant speed regulating system[J]. Proceedings of the CSEE, 2001, 21(7): 95-97. [本文引用:1]
[10]	曹正才, 金艳艳. 基于重复控制的高精度平台控制系统设计[J]. 雷达与对抗, 2005(4): 57-59. Cao Zheng-cai, Jin Yan-yan. Design of a highly precise platform control system based on repetitive control[J]. Radar & Ecm, 2005(4): 57-59. [本文引用:1]
[11]	杨松, 曾鸣, 苏宝库. 一种新的重复自适应摩擦补偿方法及其在高精度伺服系统中的应用[J]. 东南大学学报: 自然科学版, 2006, 36(增刊1): 74-78. Yang Song, Zeng Ming, Su Bao-ku. New repetitive adaptive friction compensation scheme in high-precise servo system[J]. Journal of Southeast University (Natural Science Edition), 2006, 36(Sup. 1): 74-78. [本文引用:1]
[12]	韩京清. 自抗扰控制技术-估计补偿不确定因素的控制技术[M]. 北京: 国防工业出版社, 2009. [本文引用:1]
[13]	张绍德, 陈主成. 一种基于干扰观测器的伺服系统设计[J]. 电子科技大学学报, 2005, 34(1): 85-88. Zhang Shao-de, Chen Zhu-cheng. Design method for servo-system based on disturbance observer[J]. Journal of UEST of China, 2005, 34(1): 85-88. [本文引用:1]
[14]	李贤涛, 张葆, 赵春蕾, 等. 基于自适应的自抗扰控制技术提高扰动隔离度[J]. 吉林大学学报: 工学版, 2015, 45(1): 202-208. Li Xian-tao, Zhang Bao, Zhao Chun-lei, et al. Improve isolation degree based on adaptive ADRC[J]. Journal of Jilin University(Engineering and Technology Edition), 2015, 45(1): 202-208. [本文引用:1]
[15]	Richard J P, Time-delay systems: an overview of some recent advances and open problems[J]. Automatic, 2003, 39(10): 1667-1694. [本文引用:1]
[16]	佘锦华, 大山恭弘. 重复控制系统中非周期扰动的抑制[J]. 控制理论与应用, 2001, 18(增刊1): 7-10. She Jin-hua, Yasuhiro Ohyama. Rejection of non-periodic disturbances in repetitive control systems[J]. Control Theory and Applications, 2001, 18(Sup. 1): 7-10. [本文引用:1]

2008

0.0

... 0 引言高精度机载光电稳定平台是由多级框架、光电红外系统以及激光瞄准系统组成的综合航空遥感器,其主要作用是隔离载体对光电平台的扰动^[1],使光电系统视轴能够快速、稳定地跟踪目标,且使激光功率通过长距离传输后仍能集中于目标上,具有机动性高、鲁棒性强、实时性好等特点,因而被广泛应用于地质测绘、军事侦察、军事打击引导等领域 ...

2011

0.0

. 2011, 19(5):998-1004 DOI:doi:10.3788/OPE.20111905.0998

Velocity based disturbance observer and its application to photoelectric stabilized platform

基于速度信号的扰动观测器及在光电稳定平台的应用

Li Jia-quan , Ding Ce , Kong De-jie

李嘉全, 丁策, 孔德杰

The disturbance estimation and compensation was introduced into close loop control systems to improve the low speed performance and disturbance rejected ability of photoelectric stabilized platforms. An original Velocity based Disturbance Observer (VDOB) was proposed and its characteristics were studied. The working principle of regular Disturbance Observer (DOB) was introduced and its drawbacks in applications to stabilized platforms were pointed out. By introducing a nominal model of stabilized platforms, the VDOB was established based on velocity signals, the structure of closed loop control system with VDOB was given, and its transfer behavior, disturbance rejected ability and robustness were analyzed. Finally, some simulations and experiments were carried out. Experiment results show that the PI controller with VDOB can overcome the speed creeping problem existed in traditional PI controllers when the platform does sinusoidal movement. Furthermore, the velocity disturbance isolation level of the platform after using PI controller with VDOB is increased by about 14 dB, Correspondingly, the stabilization precision of platform is increased from 0.03°(RMS) to 0.0044°(RMS) when the vehicle on platform is moved in sinusoidal manner at 1 Hz and 6.3(°)/s. In conclusion, the proposed VDOB is effective and valuable.

在闭环控制系统中引入了扰动估计和补偿来改善光电稳定平台低速性能,并提高其扰动抑制能力。提出了基于速度信号的扰动观测器,并对其各项性能进行了研究。介绍了常规的基于加速度的扰动观测器的工作原理,指出了它在光电稳定平台应用中存在的问题;通过引入平台的标称模型,构建了基于平台速度信号的扰动观测器,给出了相应的闭环控制系统结构,分析了它的输入输出特性、扰动抑制能力和鲁棒性;最后,对本文方法进行了仿真和物理实验。实验结果表明:当平台按0.5 Hz,0.6(°)/s做正弦运动时,引入本文提出的带扰动观测器的PI控制基本克服了常规PI控制存在的低速爬坡现象;对于1 Hz,6.3(°)/s的载体正弦速度扰动,平台的扰动隔离度提高了约14 dB,稳定精度从0.03°(RMS)提高到了0.0044°(RMS)。实验结果证明了本文方法的有效性。

... 目前消除扰动的方法主要还是PID理论以及平方滞后超前等方法,这些方法利用提高开环系统的型别和低频段的增益来降低扰动对平台稳定性的影响^[2],属于被动抗扰方法,被动抗扰方法的优点是理论简单、易于调节、适应性强,仍是绝大多数控制过程中最常采用的控制方法 ...

2005

0.0

. 2005, 1(9):37-44 DOI:doi:10.3969/j.issn.1007-449X.2005.01.009

Repetitive control a survey

重复控制综述

Li Cui-yan , Zhang Dong-chun , Zhuang Xian-yi.

李翠艳, 张东纯, 庄显义

重复控制方法在反馈系统中对于周期性外激励信号的跟踪/抑制具有很高的控制性能.介绍了连续和离散时延内模重复控制、有限维重复控制以及非线性系统重复控制方法的主要理论和研究成果,并给出了重复控制的一些典型应用,最后指出了该方法亟待解决的一些难点问题.

... 重复控制^[3,4]是依据内膜原理发展而来的控制方法,它可以周期性地跟踪输入信号,也可以周期性地抑制扰动,从系统框图来看,它仍属于被动抗扰的范畴 ...

2012

0.0

2014

0.0

... 从傅里叶变换原理可知,扰动信号可以认为是正弦信号的叠加,而基于内膜原理的控制方法对周期信号可以做到完全跟踪和抑制^[5],因此从理论上该方法具有一定的先进性,从系统波特图以及试验结果分析,重复控制理论可以有效提高系统的扰动隔离度 ...

2012

0.0

. 2012, 29(3):401-407

Active disturbance rejection control for spacecraft attitude maneuver and stability

航天器姿态机动及稳定的自抗扰控制

Lai Ai-fang , Guo Yu , Zheng Li-jun.

赖爱芳, 郭毓, 郑立君

针对航天器动力学参数不确定性以及系统存在外部持续干扰的问题，提出了一种自抗扰姿态控制器的设计方法．在为期望姿态安排过渡过程的基础上，设计了扩张状态观测器，对参数不确定性和外部干扰进行估计，并实时补偿．为抑制跟踪误差，设计了非线性状态误差反馈律．仿真结果表明，该控制器不仅能很好地估计并补偿系统受到的持续干扰，而且对航天器动力学参数的不确定性具有较强的鲁棒性，满足航天器姿态快速机动和高稳定度的控制要求，性能指标明显优于PD控制．

... 自抗扰控制方法^[6]是一种不依赖于系统模型的控制方法,它不必对控制对象建模,而是直接将系统的未建模动态和未知外界扰动都归结为对系统的总和扰动而进行估计和补偿 ...

2010

0.0

. 2010, :29-31

On disturbance rejection paradigm in control engineering

控制工程的抗扰范式

Gao Zhi-qiang.

高志强

控制工程的内容可归纳于三个范式:工业范式,模型范式,抗扰范式。本文围绕怎样抗扰这个问题将控制设计的现有方法进行了归类、比较。工业范式反映了近百年来,人们在实践中寻找有效控制手段的途径;模型范式适合思维严谨的学者,在一个公理系统的框架内,基于给定的数学模型和控制目标,推演反馈控制律;抗扰范式则回到控制问题的本质,即控制问题就是抗扰问题,为怎样抗扰这个基本问题,为怎样看待、理解自抗扰控制技术,提供了一个新的思路。自抗扰的"自"英文翻译为"主动",又有"自然而然"之意,这在理论和实践上都很有意义。

... 采用自抗扰控制器的机载光电侦察平台伺服系统,阶跃响应速度快、无超调,对模型摄动和测量噪声不敏感,对外界扰动的抑制能力强,能够有效克服摩擦扰动对平台低速运动性能的影响^[7],各项性能均优于传统控制器 ...

2003

0.0

. 2003, 23(6):15-21 DOI:doi:10.3969/j.issn.1674-5795.2003.06.005

Design and simulation of current-loop for servo of airborne electro-optical pointing and tracking platform

机载光电跟瞄平台伺服系统中电流环的设计与仿真

Zhang Li-li , Huang Yi , L#cod#x000fc; Jun-fang.

张黎黎, 黄一, 吕俊芳

主要叙述了机载光电跟瞄平台伺服系统中电流环的组成并对电流调节器这一关键环节的设计进行了重点分析,在MATLAB的环境下对建好的电流环模型进行了仿真.

... 可以设计电流反馈校正网络W₁(s),使得在一定的带宽内电流环的闭环传递函数G_i(s)=1,则图2可简化为图3,由于电流环的设计采用模拟电路,因而W₁(s)能实时对电流进行校正,这时i_c的动态过程变化很快,而反电势E_g的变化过程相对来说是缓慢的,因此可以忽略反电势对电流环的影响^[8],简化后的电机模型框图如图3所示 ...

2001

0.0

. 2001, 21(7):95-97 DOI:doi:10.3321/j.issn:0258-8013.2001.07.021

Dynamic compensator based on repetitive control and its application to constant speed regulating system

基于重复控制的动态补偿器及其在恒速调节系统中的应用

Zhang Dong-chun , Zeng Ming , Su Bao-ku.

张东纯, 曾鸣, 苏宝库

随位置呈周期性变化的扰动经常存在于恒速调节系统中，限制了系统速率稳定度的进一步提高。该文分析了这类周期性扰动对系统速率稳定度的影响，提出了一种基于重复控制原理的动态补偿方案，给出了重复补偿器的设计方法和应用条件，并在一高精度转台系统中予以实现，收到了良好的效果，实验证明该补偿方案提高了转台系统的速率稳定度。

... 1 重复控制重复控制是日本的Inoue于1981年根据内模原理的思想提出来的^[9,10],以正弦扰动信号为例,介绍内膜原理的抑制扰动原理 ...

2005

0.0

. 2005, (4):57-59

Design of a highly precise platform control system based on repetitive control

基于重复控制的高精度平台控制系统设计

Cao Zheng-cai , Jin Yan-yan.

曹正才, 金艳艳

针对传统PID控制算法的局限性,本文提出了一种基于重复控制的雷达平台控制系统的设计,给出了将重复控制算法引入PID闭环控制系统的实现方法。应用结果表明,在雷达平台控制系统中引入重复控制算法,可改善系统的控制品质,使系统的跟踪控制精度能有很大的提高。

... 1 重复控制重复控制是日本的Inoue于1981年根据内模原理的思想提出来的^[9,10],以正弦扰动信号为例,介绍内膜原理的抑制扰动原理 ...

2006

0.0

. 2006, 36(增刊1):74-78

New repetitive adaptive friction compensation scheme in high-precise servo system

一种新的重复自适应摩擦补偿方法及其在高精度伺服系统中的应用

Yang Song , Zeng Ming , Su Bao-ku.

杨松, 曾鸣, 苏宝库

针对高精度转台直流力矩电机系统中存在的非线性动态摩擦及周期性波动力矩扰动,为提高转台位置的跟踪精度,提出了一种新的重复自适应摩擦补偿方法,将重复控制机制引入到基于自适应控制的摩擦补偿策略中.电机中摩擦模型采用摩擦参数非一致性变化的LuGre动态模型.该方法的控制律包含一个参数自适应律、等效PD控制律和一个重复控制律.其中,参数自适应律用来估计未知模型参数并予以补偿,而插入的重复控制器用来提高系统运动曲线的跟踪性能.Lyapunov方法证明该补偿方法保证了闭环系统全局稳定性和对期望位置信号的渐近跟踪.最后,通过对高精度伺服系统的仿真研究证明了该改进补偿方法的有效性.

... 重复控制本身属于开环补偿控制^[11],并不是闭环控制,在实际应用中,为了得到较好的动态性能,通常把重复控制器嵌入到常规的PID闭环控制环内以形成复合控制,系统框图如图8所示 ...

2009

0.0

... 状态偏差组合为一非线性函数,其具体形式可根据系统的不同进行调整^[12,13] ...

2005

0.0

. 2005, 34(1):85-88 DOI:doi:10.3969/j.issn.1001-0548.2005.01.023

Design method for servo-system based on disturbance observer

一种基于干扰观测器的伺服系统设计

Zhang Shao-de , Chen Zhu-cheng.

张绍德, 陈主成

将摩擦力的Stribeck曲线作为伺服系统的摩擦模型,提出用干扰观测器来补偿摩擦力对伺服系统低速运行的影响.在对象的名义模型正确条件下,干扰观测器和反馈控制器的设计可以分开独立进行.低频时,产生的系统特性类似名义模型的特性,并从理论上保证了被控对象参数不确定时的鲁棒性,同时摩擦对伺服系统输出的影响等于零.仿真实验表明了该控制策略的有效性.

... 状态偏差组合为一非线性函数,其具体形式可根据系统的不同进行调整^[12,13] ...

2015

0.0

. 2015, 45(1):202-208 DOI:doi:10.13229/j.cnki.jdxbgxb201501030

Improve isolation degree based on adaptive ADRC

基于自适应的自抗扰控制技术提高扰动隔离度

Li Xian-tao , Zhang Bao , Zhao Chun-lei

李贤涛, 张葆, 赵春蕾

摘　要：针对扩张状态观测器对二阶及二阶以上系统的扰动观测值存在相位滞后的问题,提出了一种基于扰动频率自适应的自抗扰控制的新方法,并在直线型倒立摆装置中进行了实验验证。实验结果表明：本文方法解决了扩张状态观测器对二阶及二阶以上系统的扰动观测值存在相位滞后的问题;在2 Hz以内随机扰动的作用下,对比传统状态反馈控制器,它将扰动隔离度至少提高了7.85 d B,同时,自抗扰控制器具有很强的鲁棒性,允许被控对象参数在15%的范围内浮动。

... 3 基于自抗扰和重复控制理论的控制器设计利用自抗扰理论的思想,设计扩张状态观测器ESO^[14,15],并引入扰动前馈补偿算法进行主动抗扰 ...

2003

0.0

... 3 基于自抗扰和重复控制理论的控制器设计利用自抗扰理论的思想,设计扩张状态观测器ESO^[14,15],并引入扰动前馈补偿算法进行主动抗扰 ...

2001

0.0

. 2001, 18(增刊1):7-10 DOI:doi:10.3969/j.issn.1000-8152.2001.z1.002

Rejection of non-periodic disturbances in repetitive control systems

重复控制系统中非周期扰动的抑制

She Jin-hua , Yasuhiro Ohyama.

佘锦华, 大山恭弘

为了改善重复控制系统中的扰动抑制性能,提出一种基于曲率模型的扰动估计新方法.该方法的主要特点是扰动的估计值直接与重复控制规则结合也不影响重复控制系统的稳定性.仿真结果显示该方法可以有效地抑制扰动.

... 从上文知道,重复控制对周期性扰动的抑制方面具有其他算法不可比拟的优势^[16],而自抗扰控制器不需要知道控制对象的具体参数和形式,可以对控制器施加重复控制补偿,而利用自抗扰控制器主动隔离扰动,在主动抗扰和被动抗扰的双重作用下,对系统中的扰动进行抑制,大大提高了系统的扰动隔离度 ...