新的闭式通用浮雕变换解算法在三维表面检测中的应用

引用本文

林欣堂, 李艳东, 吴攀超. 新的闭式通用浮雕变换解算法在三维表面检测中的应用. 2015, 45(6): 1987-1993
LIN Xin-tang, LI Yan-dong, WU Pan-chao. Novel closed-form GBR solution in application of three-dimensional surface detection. Journal of Jilin University Engineering and Technology Edition, 2015, 45(6): 1987-1993 复制到剪切板

Permissions

新的闭式通用浮雕变换解算法在三维表面检测中的应用

林欣堂¹, 李艳东², 吴攀超¹

1.哈尔滨工程大学自动化学院,哈尔滨 150001

2.齐齐哈尔大学计算机与控制工程学院,齐齐哈尔 161001

作者简介:林欣堂(1982-),男,博士研究生.研究方向:计算机视觉三维重建.E-mail:work_lxt@126.com

基金:国家自然科学基金青年基金项目(61100103)

摘要

使用光度立体视觉法对物体表面形状进行检测时,往往需要解决通用浮雕变换(Generalized bas-relief, GBR)中参数解算及含有镜面、阴影等干扰的非朗伯目标表面这两个主要问题。针对非标定光度立体视觉中GBR参数的解算问题,提出了一种基于局部极大灰度值点的闭式解算法。与已有GBR解算方法相比,本文提出的算法只需要进行二元二次方程组的闭式计算,无需寻优或迭代过程,在计算速度及精度上有较大提高。对于非朗伯表面问题本文主要采用分割方法,还引入了主要成分分析法进一步去除干扰,使本文提出的闭式解算法能够满足使用条件。最后通过对实物目标的三维检测验证了本文算法的高效性。

关键词: 信息处理技术; 三维重建; 非标定光源; 光度立体视觉

中图分类号:TP391.4 文献标志码:A 文章编号:1671-5497(2015)06-1987-07

Novel closed-form GBR solution in application of three-dimensional surface detection

LIN Xin-tang¹, LI Yan-dong², WU Pan-chao¹

1.College of Automation, Harbin Engineering University, Harbin 150001,China

2. Computer and Control Engineering, Qiqihar University, Qiqihar 161001,China

Abstract

In object surface detection using photometric stereo algorithm, two main issues need to be solved; unknown Generalized Bas-Relief (GBR) parameters and surface containing mirror point, shadows and other interference. To solve incalibrated photometric stereo, a novel closed-form algorithm based on local maxima points is proposed to solve GBR parameters. The algorithm, which only solves group of dual quadratic equation without optimization or iterative process, greatly improves the speed and accuracy compared with the existing GBR solutions. To solve non-Lambertian surface issue, image segment and PCA technology are used to segment and remove interference to ensure the algorithm satisfying the application conditions. Higher accuracy and efficiency are proved by experiments.

Keyword: information processing technology; 3D reconstruction; non-calibrated light source; photometric stereo

Show Figures

光度立方体视觉算法(Photometric stereo, PS)是固定相机与物体通过不同位置的光源在物体表面反射得到的灰度域信息解算得到表面法向量域信息, 进而完成对物体表面的三维检测算法^[1]。因其检测结构简单且适用于弱纹理表面形状的检测, 近年来越来越受到重视。

在标定的远距离点光源下, 早期的研究主要假设物体表面为朗伯表面, 因此只需要3幅图像就可以完成对物体表面的三维形状检测^[1]。但是在现实环境中绝大多数物体表面都是非朗伯表面, 同时缺乏表面反射模型等相关信息, 给表面的三维检测带来了困难。另一方面在实际应用过程中往往光源是非标定的, 即光源、相机与物体表面间的几何信息未知。这会使得寻优得到的光源及表面法向量与真实值间相差一个变换矩阵, 即通用浮雕变换(Generalized bas-relief, GBR)矩阵。如何在物体表面未知的条件下完成对物体表面的三维检测, 即非标定光源光度立体视觉问题, 成为本文需要解决的又一难题。

本文针对上述两个问题提出了一种新的闭式GBR参数解算方法实现对非标定光源方向的解算。使用分块分别处理的方法, 实现对含有镜面及阴影等干扰的非朗伯表面在非标定光源下的三维检测。

1 非朗伯非标定光源

1.1 非朗伯表面光度立体视觉

现有PS算法针对非朗伯表面的三维形状检测大体可分为去除镜面点、理论或经验双向反射分布函数(Bidirectional reflectance distribution function, BRDF)模型及组合、利用反射模型的几何特性及PS算法与其他方法的结合4大类。

去除镜面点算法的基本思路是把镜面点与漫反射点进行区分, 将其中的镜面点当成孤立干扰点去除, 对余下部分作为朗伯表面处理^[2]。利用镜面点亮度呈现强烈的极性^[3]、光谱在镜面点的独立性^[4]来区分镜面点与漫反射点。还有些文献引入了其他数学工具, 如RANSAC^[5]、中值滤波法^[6]、最小秩法^[7]及期望极值法^[8]等。文献[9]使用主要成分分析法(Principal component analysis, PCA)去除干扰点, 对少量干扰点有很好的鲁棒性, 但是光源必需是标定的。

有些文献用BRDF模型重建非朗伯表面, 常见的有Lambertian模型、Phong模型、Torrance-Sparrow模型及Ward模型等^[10]。同时文献[11]研究出的物体表面每个像素可以用1、2种反射模型的混合来表示, 如文献[12]等。这类算法往往需要标定过的光源信息, 还需要提供模型选择及其参数相关信息。通用性及鲁棒性较差, 且需要参数较多, 计算较复杂。

有些文献避开BRDF本身, 利用BRDF中各参数之间具有的几何特性关系完成对物体表面的三维形状检测, 如文献[13]利用参数间的互换性、文献[14]利用BRDF函数的对称性及文献[14]利用特殊的光源与相机位置关系等。这一类算法需要特殊的光源与相机相互位置关系, 采用近似算法, 精度和实际应用性受到限制。

还有一类文献把PS算法与其他的三维检测算法结合^[15]。这类算法能够实现各算法的互补, 得到的结果往往更精确。但是由于需要处理的数据量大, 且需要融合不同检测方法的结果, 因此计算复杂、速度慢。

上述各方法都需要提供标定的光源信息, 无法实现对非标定光源下的表面检测。

1.2 非标定光源光度立体视觉

上述算法大部分都是使用离线标定的光源与相机位置的关系, 这限制了其实际应用。为了解决这一问题, 有些算法使用了标准镜面和糙面球体来实现对光源方向及强度的标定^[12]; 还有些文献不需要对光源进行标定, 但仍然要求光源与相机间有特定的位置关系^[14]。

在远距点光源下, 可积朗伯表面在不同位置光源下的灰度可以得到表面法向量与光源方向间的关系, 但是这一结果与真实结果相差一个通用浮雕变换^[16], 因此在远距点光源下必需要对GBR造成的多义性进行去除。对这一变换中参数的计算, 文献[17]使用镜面点而文献[18]发现镜面反射点及朗伯点都能提供光源的信息。这类闭式计算方法最大的优点是速度快、稳定、精度高, 但是需要表面法向量已知。还有些文献使用寻优的方法得到各参数值, 如文献[19]假设错误的GBR使得反射率分散, 利用反射率的最小熵(Entropy minimization, EM)完成了对GBR的参数计算; 文献[20]利用图像中的彩色及强度信息实现光度立体视觉的自标定(SCPS), 完成对GBR各参数的计算。

这些算法只针对朗伯表面, 且采用寻优、迭代等非闭式解算方法, 计算复杂。

2 新的GBR闭式解算法

2.1 GBR解算问题的产生

在远距点光源下, 朗伯表面灰度值满足:

$\begin{matrix} I = N^{T} L (1) \end{matrix}$

式中:N为物体表面各像素上的法向量, N= $\begin{matrix} [N_{1}, \dots, N_{P}] \end{matrix}$ ∈ R³^{× P}; P为图像中像素点的总数; L为不同光源位置下光源方向向量, L= $\begin{matrix} [L_{1}, \dots, L_{K}] \end{matrix}$ ∈ R³^{× K}; K为光源方向总数。

当光源方向未知时, 由上式得到的灰度值对应的法向量和光源方向不是唯一的, 存在可逆变换矩阵G, 如下式所示:

$\begin{matrix} I = N^{T} G^{- 1} GL = {\hat{N}}^{T} \hat{L} (2) \end{matrix}$

因此通过图像灰度值寻优得到的法向量及光源方向估计值不唯一, 其中的矩阵G就是通用浮雕变换(GBR)矩阵。根据文献[16]证明, 当物体表面可积时存在固定的变换矩阵G, 且满足下式:

$\begin{matrix} G = [\begin{matrix} 1 & 0 & 0 \\ 0 & 1 & 0 \\ μ & ν & λ \end{matrix}] (3) \end{matrix}$

式中:参数满足λ > 0; μ , ν ∈ R。

由此可知估计法向量矩阵 $\begin{matrix} \hat{N} \end{matrix}$ 与真实法向量矩阵N间有 $\begin{matrix} \hat{N} \end{matrix}$ =G^-^TN, 同理估计光源矩阵与真实光源方向矩阵间有 $\begin{matrix} \hat{L} \end{matrix}$ =GL。因此在光源方向及物体表面法向量信息未知时, 想要通过估计值得到光源方向及法向量的真实值, 必需对GBR解算, 即对矩阵G中λ 、μ 、ν 三个参数进行求解。

2.2 本文提出的GBR解算方法

针对GBR参数解算问题, 文献[18]通过寻找已知法向量的镜面点直接计算光源的方向。这一算法可以直接通过像素位置进行计算, 不需要优化过程, 具有速度快的优点。但其前提是表面各像素法向量已知, 不适合本文。因此本文提出了利用朗伯表面区域上局部极大灰度值点作为种子点, 使用其中任意两个不同光源下的种子点可以解算出GBR变换中各参数的值, 具体证明如下:在朗伯表面上光源位置k下, 选取局部灰度值最大点p作为种子点。则有该种子点上真实的法向量与光源方向的内积值< N_p· L_k> 最大。带入GBR参数则有:

$\begin{matrix} (μ, ν, λ) \in argmax < \frac{G^{T} {\hat{N}}_{p}}{‖ G^{T} {\hat{N}}_{p} ‖}, \frac{G^{- 1} {\hat{L}}_{k}}{‖ G^{- 1} {\hat{L}}_{k} ‖} > (4) \end{matrix}$

式(4)等价于:

$\begin{matrix} (μ, ν, λ) \in argmin ‖ G^{T} {\hat{N}}_{p} ‖‖ G^{- 1} {\hat{L}}_{k} ‖ (5) \end{matrix}$

定义式(5)为要求解的最小能量函数, 带入式(3)可得:

$\begin{matrix} \begin{matrix} \min \frac{1}{λ^{2}} [{({\hat{n}}_{1, p} + μ {\hat{n}}_{3, p})}^{2} + ({\hat{n}}_{2, p} + \\ ν {\hat{n}}_{3, p})^{2} + λ^{2} {\hat{n}}_{3, p}^{2}] [λ^{2} ({\hat{l}}_{1, k}^{2} + {\hat{l}}_{2, k}^{2}) + \\ {(- μ {\hat{l}}_{1, k} - ν {\hat{l}}_{2, k} + {\hat{l}}_{3, k})}^{2}] (6) \end{matrix} \end{matrix}$

式中: $\begin{matrix} {\hat{L}}_{k} \end{matrix}$ = $\begin{matrix} {[\begin{matrix} {\hat{l}}_{1, k} & {\hat{l}}_{2, k} & {\hat{l}}_{3, k} \end{matrix}]}^{T} \end{matrix}$ 为位置k下估计的光源方向; $\begin{matrix} {\hat{N}}_{p} \end{matrix}$ = $\begin{matrix} {[\begin{matrix} {\hat{n}}_{1, p} & {\hat{n}}_{2, p} & {\hat{n}}_{3, p} \end{matrix}]}^{T} \end{matrix}$ 为像素p的估计法向量方向。

当式(6)取极值时, 对变量λ 取一阶偏导数为零, 得出下式:

$\begin{matrix} \begin{matrix} ({\hat{l}}_{1, k}^{2} + {\hat{l}}_{2, k}^{2}) {\hat{n}}_{3, p}^{2} λ^{4} = [{({\hat{n}}_{1, p} + μ {\hat{n}}_{3, p})}^{2} + \\ {({\hat{n}}_{2, p} + ν {\hat{n}}_{3, p})}^{2}] {({\hat{l}}_{3, k} - μ {\hat{l}}_{1, k} - ν {\hat{l}}_{2, k})}^{2} (7) \end{matrix} \end{matrix}$

由此可以得出λ 值:

$\begin{matrix} \begin{matrix} λ = {[({\hat{n}}_{1, p} + μ {\hat{n}}_{3, p})^{2} + ({\hat{n}}_{2, p} + \\ ν {\hat{n}}_{3, p})^{2}] ({\hat{l}}_{3, k} - μ {\hat{l}}_{1, k} - \\ ν {\hat{l}}_{2, k})^{2} / ({\hat{l}}_{1, k}^{2} + {\hat{l}}_{2, k}^{2}) {\hat{n}}_{3, p}^{2}}^{\frac{1}{4}} (8) \end{matrix} \end{matrix}$

带入式(6), 则要求解的最小能量函数变为:

$\begin{matrix} \begin{matrix} argmin \sqrt{{\hat{l}}_{1, k}^{2} + {\hat{l}}_{2, k}^{2}} \\ \sqrt{{({\hat{n}}_{1, p} + μ {\hat{n}}_{3, p})}^{2} + {({\hat{n}}_{2, p} + ν {\hat{n}}_{3, p})}^{2}} + \\ |{\hat{n}}_{3, p}| |{\hat{l}}_{3, p} - μ {\hat{l}}_{1, k} - ν {\hat{l}}_{2, k}| (9) \end{matrix} \end{matrix}$

同上, 将μ , ν 两个参数分别对能量函数式(6)求一阶偏导为零, 可以得到:

$\begin{matrix} \begin{matrix} μ \in [\min (μ_{0}, μ_{1}), \max (μ_{0}, μ_{1})] \\ ν \in [\min (ν_{0}, ν_{1}), \max (ν_{0}, ν_{1})] \end{matrix} \end{matrix}$

其中:

$\begin{matrix} \{\begin{matrix} μ_{0} = - {\hat{n}}_{1, p} / {\hat{n}}_{3, p} \\ μ_{1} = \frac{{\hat{l}}_{1, k} {\hat{l}}_{2, k} {\hat{n}}_{2, p} - {\hat{l}}_{2, k}^{2} {\hat{n}}_{1, p} + {\hat{l}}_{3, k} {\hat{l}}_{1, k} {\hat{n}}_{3, p}}{{\hat{n}}_{3, p} ({\hat{l}}_{1, k}^{2} + {\hat{l}}_{2, k}^{2})} \\ ν_{0} = - {\hat{n}}_{2, p} / {\hat{n}}_{3, p} \\ ν_{1} = \frac{{\hat{l}}_{1, k} {\hat{l}}_{2, k} {\hat{n}}_{1, p} - {\hat{l}}_{1, k}^{2} {\hat{n}}_{2, p} + {\hat{l}}_{2, k} {\hat{l}}_{3, k} {\hat{n}}_{3, p}}{{\hat{n}}_{3, p} ({\hat{l}}_{1, k}^{2} + {\hat{l}}_{2, k}^{2})} \end{matrix} (10) \end{matrix}$

因为要同时满足对μ , ν 两个参数的一阶偏导为零, 可以得到下式:

$\begin{matrix} μ / ν = (μ_{1} - μ_{0}) / (ν_{1} - ν_{0}) = {\hat{l}}_{1, k} / {\hat{l}}_{2, k} = α (11) \end{matrix}$

式中:α ∈ $\begin{matrix} [0, 1] \end{matrix}$ 。

因此可以得出点 $\begin{matrix} (μ, ν) \end{matrix}$ 在线段 $\begin{matrix} ([\begin{matrix} μ_{0} & ν_{0} \end{matrix}], [\begin{matrix} μ_{1} & ν_{1} \end{matrix}]) \end{matrix}$ 上, 即满足:

$\begin{matrix} [\begin{matrix} μ \\ ν \end{matrix}] = [\begin{matrix} μ_{0} \\ ν_{0} \end{matrix}] + (1 - α) ([\begin{matrix} μ_{1} \\ ν_{1} \end{matrix}] - [\begin{matrix} μ_{0} \\ ν_{0} \end{matrix}]) (12) \end{matrix}$

上述推导只是针对一个种子点, 对于两个不同的种子点存在下式:

$\begin{matrix} \begin{matrix} [\begin{matrix} μ_{0, a} \\ ν_{0, a} \end{matrix}] + α ([\begin{matrix} μ_{1, a} \\ ν_{1, a} \end{matrix}] - [\begin{matrix} μ_{0, a} \\ ν_{0, a} \end{matrix}]) = \\ [\begin{matrix} μ_{0, b} \\ ν_{0, b} \end{matrix}] + β ([\begin{matrix} μ_{1, b} \\ ν_{1, b} \end{matrix}] - [\begin{matrix} μ_{0, b} \\ ν_{0, b} \end{matrix}]) (13) \end{matrix} \end{matrix}$

进一步可以得到:

$\begin{matrix} [\begin{matrix} {\hat{l}}_{1, ka} A & - {\hat{l}}_{1, kb} B \\ {\hat{l}}_{2, ka} A & - {\hat{l}}_{2, kb} B \end{matrix}] [\begin{matrix} α \\ β \end{matrix}] = [\begin{matrix} μ_{1, b} - μ_{1, a} \\ ν_{1, b} - ν_{1, a} \end{matrix}] (14) \end{matrix}$

式中:A= $\begin{matrix} ({\hat{N}}^{T}_{pa} {\hat{L}}_{ka}) \end{matrix}$ /[ $\begin{matrix} {\hat{n}}_{3, pa}^{2} \end{matrix} \begin{matrix} ({\hat{l}}_{1, ka}^{2} + {\hat{l}}_{2, ka}^{2}) \end{matrix}$ ]; B= $\begin{matrix} ({\hat{N}}^{T}_{pb} {\hat{L}}_{kb}) \end{matrix}$ /[ $\begin{matrix} {\hat{n}}_{3, pb}^{2} \end{matrix} \begin{matrix} ({\hat{l}}_{1, kb}^{2} + {\hat{l}}_{2, kb}^{2}) \end{matrix}$ ]。

两个不同的种子点可以解得唯一GBR参数解的条件是前边的2× 2矩阵满秩, 即满足:

$\begin{matrix} {\hat{l}}_{1, ka} / {\hat{l}}_{2, ka} \neq {\hat{l}}_{1, kb} / {\hat{l}}_{2, kb} (15) \end{matrix}$

由式(15)可知, 如果获得光源方向和表面法向量的初始估计, 选取在不同的光源方向下取得的两个种子点利用式(14)可以对GBR各参数值进行闭式解算。

2.3 本文解算法的优点

这种闭式解算方法与最小熵算法^[19]、彩色和强度优化法^[20]相比, 直接对方程组进行计算, 没有寻优或迭代过程, 因此在速度上具有明显的优势; 只要物体表面不是平面, 则在不同光源位置下一定存在多个局部极大灰度值种子点, 因此保证了这一算法的鲁棒性; 对于一对种子点则可以计算出对应的一组 $\begin{matrix} [λ, μ, ν] \end{matrix}$ 参数, 对于多组种子点对可以得到多组参数值。本文对得到的多组参数值选取不同组间距离值最小的一组:

$\begin{matrix} (λ, μ, ν) \equiv {\hat{y}}_{\min} = argmin \overset{S}{\sum_{i = 1}} ‖ \hat{y} - y_{i} ‖^{2} (16) \end{matrix}$

式中:S为不同光源种子点对的总数; $\begin{matrix} \hat{y} \end{matrix}$ 为S组结果中的任意一组。

通过这一简单的优化步骤可以去除干扰点, 对得到的结果进行筛选, 进一步提高了本文算法的精度及鲁棒性。

3 本文的三维重建过程

3.1 近似朗伯区域分割

为了得到近似朗伯表面区域同时考虑到计算速度, 本文使用了极化度域值^[3]进行分割。但是由于低灰度值区域会被误判为高极化度, 因此本文选用基于极化度与灰度的双域值方法去除干扰。根据文献[3]极化度的计算方法为:

DOP $\begin{matrix} (x, y) \end{matrix}$ = $\begin{matrix} \frac{I_{\max} (x, y) - I_{\min} (x, y)}{I_{\max} (x, y) + I_{\min} (x, y)} \end{matrix}$ (17)

式中:0≤ DOP $\begin{matrix} (x, y) \end{matrix}$ ≤ 1; I_max $\begin{matrix} (x, y) \end{matrix}$ 、I_min $\begin{matrix} (x, y) \end{matrix}$ 为像素在一系列不同的光源与相机位置关系下, 得到的不同的像素值中最大及最小值。

虽然极化度算法计算简单, 但是由于极化度方法易受到阴影等低灰度值像素的干扰, 使得I_min $\begin{matrix} (x, y) \end{matrix}$ 虽然很小, 但被误判为高极化度值。因此本文同时使用灰度域值及极化值, 用式(18)把原始图像分成3个部分。

$\begin{matrix} \{\begin{matrix} α_{1} \geq \max (I (x, y)) ⋂ \min (I (x, y)) \geq \\ α_{2} ⋂ DOP (x, y) \leq β \\ \max (I (x, y)) > α_{1} ⋂ DOP (x, y) > β \\ 其他 \end{matrix} (18) \end{matrix}$

式中:α ₁、α ₂和β 分别为灰度、极化度域值。

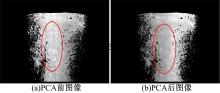
这些域值把原始表面分成三个部分:满足低极化度和灰度值限定范围内的近似朗伯表面的部分; 满足高灰度、高极化度的近似镜面部分; 满足低灰度值低极化度部分。图1(a)为12幅金属圆管原始图像中的一幅, 图1(b)为对原始图像分割得到的近似朗伯表面区域, 其中参数取α ₁=0.9, α ₂=0.4, β =0.4。

	Figure Option View Download New Window
	图1 原始图像双域值分割Fig.1 Dual threshold segmentation of original image

上述分割后的近似朗伯表面部分只能把原始图像中的高度镜面性成份分离出来, 余下部分还是含有镜面、阴影及周围光源等引起的干扰, 而这些干扰在实际图像中是不可避免的。因此为了提高图像处理过程的鲁棒性, 本文引入文献[21]提出的PCA算法:

$\begin{matrix} \{\begin{matrix} \min ‖ A ‖_{f} + γ ‖ E ‖_{1} \\ s.t I = A + E \end{matrix} (19) \end{matrix}$

式中:参数γ 的选择参照文献[22], γ =3/ $\begin{matrix} \sqrt{P} \end{matrix}$ , P为单幅图像的像素总数。

对该区域的原始图像进一步去除干扰, 得到图像中的主要成分A, 使得去除干扰后的该区域更接近朗伯表面, 如图2中圈中部分所示。

	Figure Option View Download New Window
	图2 PCA去干扰Fig.2 PCA remove interference

3.2 近似朗伯区域重建

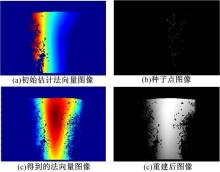
为了使用本文GBR闭式解算法, 先使用文献[23]对该区域表面法向量及光源方向进行初始估计, 如图3(a)所示。其中由红到蓝代表像素法向量与光轴方向的接近程度由大到小。对于种子点的检测使用文献[18]的方法, 但是要删除其中在不同光源位置下都被选为预备点的像素, 余下的像素作为种子点, 如图3(b)所示。

	Figure Option View Download New Window
	图3 朗伯区域重建Fig.3 Lambertian zone reconstruction

选择出两个不同光源下种子点组成的种子点对, 使用式(16)对这多组点对进行筛选。再使用本文第2节结论可以解算GBR中各参数值, 同时利用文献[23]得到的光源方向及表面法向量估计值可以得到表面法向量及光源方向的真实值, 如图3(c)所示。对这一近似朗伯表面区域得到的法向量域, 使用泊松表面重建算法^[24], 完成该区域的三维重建, 如图3(d)所示。

3.3 其余部分表面重建

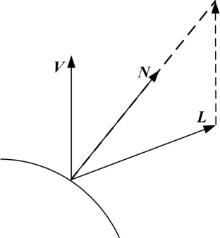
余下部分由式(18)可知分为高镜面性部分及低灰度、低极化度部分。本文利用3.2节得到的光源方向信息, 对这两部分各像素的法向量进行计算。对高镜面性像素选取不同光源位置下最大灰度值及其对应的光源方向L_k, 令相机方向为Z轴上的单位向量, 即V= $\begin{matrix} {[0, 0, 1]}^{T} \end{matrix}$ , 如图4所示。

	Figure Option View Download New Window
	图4 镜面点法向量计算Fig.4 Calculation of mirror point normal

此时可以用下式对法向量进行计算:

$\begin{matrix} N = (V + L_{k}) / ‖ V + L_{k} ‖ (20) \end{matrix}$

对低灰度、低极化度部分像素法向量进行计算, 为了避免阴影干扰, 本文选择每个像素最大的3个灰度值及对应光源方向, 用式(21)对其法向量进行计算:

$\begin{matrix} N = [\begin{matrix} l_{11} & l_{12} & l_{13} \\ l_{21} & l_{22} & l_{23} \\ l_{31} & l_{32} & l_{33} \end{matrix}] \times [\begin{matrix} I_{1} \\ I_{2} \\ I_{3} \end{matrix}] (21) \end{matrix}$

式中:(l₁_k, l₂_k, l₃_k)为k位置光源方向; I_k为光源k下像素的灰度值。

至此完成余下部分的法向量估计, 结合前面已经得到的近似朗伯表面部分的法向量结果, 再次使用泊松表面重建算法^[24]得到最终的目标表面深度信息, 如图5所示。

	Figure Option View Download New Window
	图5 全局重建Fig.5 Global reconstruction

4 对比试验及分析

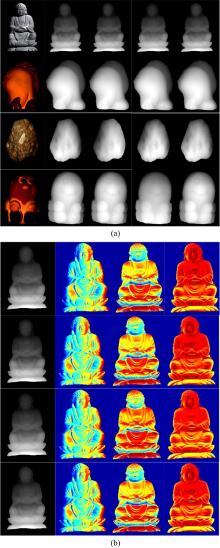
为了进一步证明本文提出的基于局部极大灰度值点的闭式GBR解算法的高效性, 使用Neil Alldrin提供的物体图像及三维实值对本文提出的GBR解算方法进行评估。比较了本文检测算法与EM^[19]算法、SCPS^[20]算法对相同目标在检测精度及速度方面的差异, 结果如图6所示。

	Figure Option View Download New Window
	图6 表面重建试验Fig.6 Surface reconstruction experiment

图6(a)中从左至右各列是各组实物图中的一幅、目标的深度实值、EM算法结果、SCPS算法结果、本文结果。为了更明确地展示各算法检测结果的不同, 图6(b)的各行分别是深度实值、EM算法、SCPS算法及本文算法, 从左到右各列分别是深度图、表面法向量的x分量、y分量及z分量分布图。为了进一步量化各算法在检测速度及准确性上的区别, 根据检测结果列出表1, 其中ε 为检测结果与实值之间的平均差值, σ 为方差。

表1 试验结果对比表 Table 1 Comparison results of experiment

通过对比试验的结果分析可以得出, 由于使用了基于局部极大灰度值点的闭式GBR解算法, 使得本文算法比全局寻优或间接寻优算法的计算速度大幅提高。同时, 由于直接使用了目标表面上的各像素点进行解算, 比寻优后三维重建算法的精度有所提高。

5 结束语

(1)本文提出的基于局部极大灰度值点的闭式GBR解算法可以实现对非郎伯表面非标定光源下的GBR矩阵参数的解算, 计算简单, 精度较高。

(2)本文提出的非标定光源下非朗伯表面的三维重建算法可以实现对非标定光源下非朗伯表面目标的三维重建。试验证明本文算法具有精度高、计算速度快的优点。

The authors have declared that no competing interests exist.

参考文献

View Option

[1]	Woodham R. Photometric method for determining surface orientation from multiple images[J]. Optical Engineering, 1980, 19(1): 139-144. [本文引用:2]
[2]	Barsky S, Petrou M. The 4-source photometric stereo method for three-dimensional surfaces in the presence of highlights and shadows[J]. PAMI, 2003, 25(10): 1239-1252. [本文引用:1]
[3]	Wolff L B, Boult T E. Constraining object features using a polarization reflectance model[J]. PAMI, 1991, 13(7): 635-657. [本文引用:2]
[4]	Tan P, Mallick S P, Quan L, et al. Isotropy, reciprocity and the generalized bas-relief ambiguity[C]∥IEEE Conference on Computer Vision and Pattern Recognition, Minneapolis, MN, 2007: 1-8. [本文引用:1]
[5]	Mukaigawa Y, Ishii Y, Shakunaga T. Analysis of photometric factors based on photometric linearization[J]. Journal of the Optical Society of America, 2007, 24(10): 3326-3334. [本文引用:1]
[6]	Miyazaki D, Hara K, Ikeuchi K. Median photometric stereo as applied to the segonko tumulus and museum objects[J]. International Journal of Computer Vision, 2010, 86(2-3): 229-242. [本文引用:1]
[7]	Wu L, Ganesh A, Shi B, et al. Robust photometric stereo via low-rank matrix completion and recovery[C]∥Lecture Notes in Computer Science, Queenstown, New Zealand , 2011, 6494: 703-717. [本文引用:1]
[8]	Wu T P, Tang C K. Photometric stereo via expectation maximization[J]. IEEE Trans Pattern Anal Mach Intell, 2010, 32(3): 546-560. [本文引用:1]
[9]	Lin Z, Chen M, Wu L, et al. The augmented lagrange multiplier method for exact recovery of corrupted low-rank matrices[DB/OL]. [2014-02-07]. http://arxiv.org/pdf/1009.5055.pdf. [本文引用:1]
[10]	Ward G J. Measuring and modeling anisotropic reflection[C]∥Proceedings of the 19th Annual Conference on Computer Graphics and Interactive Techniques, New York, NY, USA, 1992: 265-272. [本文引用:1]
[11]	Lensch H, Kautz J, Goesele M, et al. Image-based reconstruction of spatial appearance and geometric detail[J]. ACM Transactions on Graphics, 2003, 22(2): 234-257. [本文引用:1]
[12]	Goldman D B, Curless B, Hertzmann A, et al. Shape and spatially-varying BRDFs from photometric stereo[J]. Pattern Analysis and Machine Intelligence, 2010, 32(6): 1060-1071. [本文引用:1]
[13]	Zickler T, Belhumeur P, Kriegman D. Helmholtz stereopsis: exploiting reciprocity for surface reconstruction[J]. IJCV, 2003, 49(2-3): 1215-1227. [本文引用:1]
[14]	Chand raker M, Bai J M, Ramamoorthi R. On differential photometric reconstruction for unknown, isotropic BRDFs[J]. IEEE Transactions on Pattern Analysis and Machine Intelligence, 2013, 35(12): 2941-2955. [本文引用:1]
[15]	Wöhler C, d'Angelo P. Stereo image analysis of non-Lambertian surfaces[J]. International Journal of Computer Vision, 2009, 81(2): 529-540. [本文引用:1]
[16]	Belhumeur P N, Kriegman D J, Yuille A L. The bas-relief ambiguity[J]. International Journal of Computer Vision, 1999, 35(1): 33-44. [本文引用:1]
[17]	Kato Y, Horiuchi T, Tominaga S. Estimation of multiple light sources from specular highlights[C]∥21st International Conference on Pattern Recognition, Tsukuba, 2012: 2033-2086. [本文引用:1]
[18]	Lagger P, Fua P. Retrieving multiple light sources in the presence of specular reflections and texture[J]. Computer Vision and Image Understand ing, 2008, 111(2): 207-218. [本文引用:1]
[19]	Alldrin N G, Mallick S P, Kriegman D. Resolving the generalized bas-relief ambiguity by entropy minimization[C]∥IEEE Conference on Computer Vision and Pattern Recognition, Minneapolis, MN, 2007: 1-7. [本文引用:2]
[20]	Shi B, Matsushita Y, Wei Y, et al. Self-calibrating photometric stereo[C]∥2010 IEEE Conference on Computer Vision and Pattern Recognition, San Francisco, CA, 2010, 1118-1125. [本文引用:2]
[21]	吴仑, 王涌天, 刘越. 一种鲁棒的基于光度立体视觉的表面重建方法[J]. 自动化学报, 2013, 39(8): 1-10. Wu Lun, Wang Yong-tian, Liu Yue. A robust approach based on photometric stereo for surface reconstruction[J]. Acta Automatica Sinica, 2013, 39(8): 1-10. [本文引用:1]
[22]	Wright J, Ganesh A, Rao S, et al. Robust principal component analysis: exact recovery of corrupted low-rank matrices by convex optimization[C]∥In proceedings of Neural Information Processing Systems (NIPS), Vancouver B C, Canada, 2009: 2080-2088. [本文引用:1]
[23]	Yuille A, Snow D. Shape and albedo from multiple images using integrability[C]∥Computer Vision and Pattern Recognition, San Juan, 1997: 158-164. [本文引用:1]
[24]	Simchony T, Chellappa R, Shao M. Direct analytical methods for solving poisson equations in computer vision problems[J]. IEEE Transactions on Pattern Analysis and Machine Intelligence, 1990, 12(5): 435-446. [本文引用:2]

1980

0.0

... 光度立方体视觉算法(Photometric stereo,PS)是固定相机与物体通过不同位置的光源在物体表面反射得到的灰度域信息解算得到表面法向量域信息,进而完成对物体表面的三维检测算法^[1] ...

... 在标定的远距离点光源下,早期的研究主要假设物体表面为朗伯表面,因此只需要3幅图像就可以完成对物体表面的三维形状检测^[1] ...

2003

0.0

... 去除镜面点算法的基本思路是把镜面点与漫反射点进行区分,将其中的镜面点当成孤立干扰点去除,对余下部分作为朗伯表面处理^[2] ...

1991

0.0

... 利用镜面点亮度呈现强烈的极性^[3]、光谱在镜面点的独立性^[4]来区分镜面点与漫反射点 ...

... 1 近似朗伯区域分割为了得到近似朗伯表面区域同时考虑到计算速度,本文使用了极化度域值^[3]进行分割 ...

2007

0.0

... 利用镜面点亮度呈现强烈的极性^[3]、光谱在镜面点的独立性^[4]来区分镜面点与漫反射点 ...

2007

0.0

... 还有些文献引入了其他数学工具,如RANSAC^[5]、中值滤波法^[6]、最小秩法^[7]及期望极值法^[8]等 ...

2010

0.0

... 还有些文献引入了其他数学工具,如RANSAC^[5]、中值滤波法^[6]、最小秩法^[7]及期望极值法^[8]等 ...

2011

0.0

... 还有些文献引入了其他数学工具,如RANSAC^[5]、中值滤波法^[6]、最小秩法^[7]及期望极值法^[8]等 ...

2010

0.0

... 还有些文献引入了其他数学工具,如RANSAC^[5]、中值滤波法^[6]、最小秩法^[7]及期望极值法^[8]等 ...

0.0

1992

0.0

... 有些文献用BRDF模型重建非朗伯表面,常见的有Lambertian模型、Phong模型、Torrance-Sparrow模型及Ward模型等^[10] ...

2003

0.0

2010

0.0

... 为了解决这一问题,有些算法使用了标准镜面和糙面球体来实现对光源方向及强度的标定^[12] ...

2003

0.0

2013

0.0

... 还有些文献不需要对光源进行标定,但仍然要求光源与相机间有特定的位置关系^[14] ...

2009

0.0

... 还有一类文献把PS算法与其他的三维检测算法结合^[15] ...

1999

0.0

... 在远距点光源下,可积朗伯表面在不同位置光源下的灰度可以得到表面法向量与光源方向间的关系,但是这一结果与真实结果相差一个通用浮雕变换^[16],因此在远距点光源下必需要对GBR造成的多义性进行去除 ...

2012

0.0

2008

0.0

2007

0.0

... 3 本文解算法的优点这种闭式解算方法与最小熵算法^[19]、彩色和强度优化法^[20]相比,直接对方程组进行计算,没有寻优或迭代过程,因此在速度上具有明显的优势 ...

... 比较了本文检测算法与EM^[19]算法、SCPS^[20]算法对相同目标在检测精度及速度方面的差异,结果如图6所示 ...

2010

0.0

... 比较了本文检测算法与EM^[19]算法、SCPS^[20]算法对相同目标在检测精度及速度方面的差异,结果如图6所示 ...

2013

0.0

2009

0.0

1997

0.0

1990

0.0

... 对这一近似朗伯表面区域得到的法向量域,使用泊松表面重建算法^[24],完成该区域的三维重建,如图3(d)所示 ...

... 至此完成余下部分的法向量估计,结合前面已经得到的近似朗伯表面部分的法向量结果,再次使用泊松表面重建算法^[24]得到最终的目标表面深度信息,如图5所示 ...