改进的粒子滤波重采样算法

引用本文

李娟, 刘晓龙, 卢长刚, 左英泽. 改进的粒子滤波重采样算法. 2015, 45(6): 2069-2074
LI Juan, LIU Xiao-long, LU Chang-gang, ZUO Ying-ze. Improvement of resampling algorithm of particle filter. Journal of Jilin University Engineering and Technology Edition, 2015, 45(6): 2069-2074 复制到剪切板

Permissions

改进的粒子滤波重采样算法

李娟¹, 刘晓龙¹, 卢长刚², 左英泽¹

1.吉林大学通信工程学院,长春 130012

2.吉林大学汽车工程学院,长春 130022

作者简介:李娟(1970-),女,副教授,博士.研究方向:信号与信息处理.E-mail:ljuan@jlu.edu.cn

基金:吉林省科技厅重点科技攻关项目(20140204044GX)

摘要

针对粒子滤波算法粒子退化的问题,提出了分类重采样(CR)算法。根据重采样时筛选出粒子数目的多少采用不同类型的复制方案,并在有效粒子减少的情况下,及时补充新粒子。仿真结果表明:当选取的粒子数目较少或者仿真周期较长时,该算法相比较多项式重采样(MR)算法和系统重采样(SR)算法具有较小的均方根误差,且多次仿真得到的均方根误差(RMSE)的方差也相对较小,说明该算法在鲁棒性、持久性和稳定性方面有所改善。

关键词: 信息处理技术; 粒子滤波; 粒子退化; 重采样算法; 分类重采样

中图分类号:TN911.7 文献标志码:A 文章编号:1671-5497(2015)06-2069-06

Improvement of resampling algorithm of particle filter

LI Juan¹, LIU Xiao-long¹, LU Chang-gang², ZUO Ying-ze¹

1.College of Communication Engineering, Jilin University, Changchun 130012, China

2.College of Automotive Engineering, Jilin University, Changchun 130022, China

Abstract

To solve the problem of particles degeneracy in the particle filter algorithms, a Classified Resampling (CR) algorithm is proposed. This algorithm adopts different duplication schemes according to the quantity of selected particles; furthermore, it replenishes new particles in the case that the number of effective particles is reduced. Simulation results demonstrate that, with smaller number of particles or longer simulation period, the proposed algorithm has minor Root Mean Square Error (RMSE) compared with Multinomial Resampling (MR) and Systematic Resampling (SR), and with multiple simulations the variance of RMSE is smaller, which indicates that the robustness, durability and stability of the proposed algorithm are improved.

Keyword: information processing; particle filters; particles degeneracy; resampling algorithm; classified resampling

Show Figures

粒子滤波(Particle filter, PF)是一种基于Monte Carlo仿真的递推贝叶斯估计方法, 它是在序贯重要性采样(SIS)的基础上, 再进行重采样的一个递推过程。粒子滤波可以有效地处理非线性、非高斯噪声环境下的状态估计问题, 被广泛用于在目标跟踪^[1]、导航定位^[2]等领域。

自从1993年Gordon等^[3]提出重采样算法以来, 出现了很多重采样算法, 比较经典的有多项式重采样(Multinomial resampling, MR)^[3], 系统重采样(Systematic resampling, SR)^[4]和残差重采样(Residual resampling, RR)^[5]。以上算法在一定程度上解决了样本退化的问题, 但随着时间的延长, 大权值粒子多次被复制, 粒子集的多样性丧失。为此, Li和Sattar等提出Deterministic Resampling算法^[6], 通过划分网格并逐步裂变的方法保持了粒子的多样性, 但由于计算量过大不适宜做实时处理。此外, 结合最新观测值的辅助粒子滤波算法^[7]增加了一步重采样过程, 因此更接近真实状态值, 但当过程噪声较大时, 滤波性能急剧下降。基于观测似然重要性采样粒子滤波^[8]直接根据观测似然函数进行采样, 保证大多数粒子点都分布在高观测似然区域, 提高了粒子的利用效率, 但只适合于观测精度高的场合。

本文提出了一种改进的重采样算法— — 分类重采样(Classified resampling, CR), 该算法使大权值粒子全部保留, 小权值粒子被舍弃, 在按权值由大到小的顺序依次进行相应次数复制的过程中, 根据筛选出粒子个数的不同采用不同的复制方案。若采样粒子的权重分布极其恶劣时, 及时补充新粒子, 保持了粒子的多样性。

1 粒子滤波算法

粒子滤波是通过寻找一组在状态空间中传递的随机样本对概率密度函数p(x_t|y_1:_t)进行近似, 并以样本均值代替积分运算, 从而获得状态最小方差的估计过程。随着粒子数的增加, 粒子的概率密度函数逐渐逼近状态的概率密度函数, 即达到了最优贝叶斯估计的效果^[9]。

假设动态系统的目标状态转移方程和目标观测方程分别为:

$\begin{matrix} \begin{matrix} x_{t} = f_{t} (x_{t - 1}, n_{t - 1}) (1) \\ y_{t} = h_{t} (x_{t}, v_{t}) (2) \end{matrix} \end{matrix}$

式中:n_t-₁和v_t分别为过程噪声和观测噪声; x_t为目标状态值, 具有马尔可夫特性; y_t为目标观测值, 各时刻的值具有独立性。

由式(1)(2)可以看出, 系统模型没有对系统作线性和非线性以及对噪声作高斯或非高斯的假设, 因此适用于非线性非高斯状态下的跟踪滤波。

传统的粒子滤波方法^[4]就是用前一时刻状态值x_t-₁和现在的观测值y_t来递推估计现在的状态值x_t。其算法步骤如下所示:

(1)初始化:由先验概率密度p(x₀)随机抽取N个粒子 $\begin{matrix} x_{0}^{i} \end{matrix}$ , i=1, 2, …, N。

(2)重要性采样:将p(x_t $\begin{matrix} |x_{t - 1}^{i} \end{matrix}$ )作为重要密度函数^[4]进行采样, $\begin{matrix} x_{t}^{i} \end{matrix}$ ~p(x_t $\begin{matrix} |x_{t - 1}^{i} \end{matrix}$ ), i=1, 2, …, N, 根据当前的观测值y_t, 更新粒子的权值 $\begin{matrix} w_{t}^{i} \end{matrix}$ = $\begin{matrix} w_{t - 1}^{i} \end{matrix}$ p(y_t| $\begin{matrix} x_{t}^{i} \end{matrix}$ ), $\begin{matrix} w_{t}^{i} \end{matrix}$ 为t时刻第i个采样粒子的权重, 并归一化权值: $\begin{matrix} {\tilde{w}}_{t}^{i} \end{matrix}$ = $\begin{matrix} w_{t}^{i} \end{matrix} \begin{matrix} (\overset{N}{\sum_{j = 1}} w_{t}^{j}) \end{matrix}$

(3)重采样:通过对比阈值N_th和有效粒子数N_eff=1 $\begin{matrix} (\overset{N}{\sum_{i = 1}} {({\tilde{w}}_{t}^{i})}^{2}) \end{matrix}$ 的大小, 来判定是否需要重采样:若N_eff≤ N_th, 说明开始出现退化现象, 则对粒子集{ $\begin{matrix} x_{t}^{i} \end{matrix}$ }进行重采样, 得到新的粒子集{ $\begin{matrix} {\hat{x}}_{t}^{i} \end{matrix}$ }, 并将所有粒子的权值设为 $\begin{matrix} {\tilde{w}}_{t}^{i} \end{matrix}$ =1/N; 若N_eff> N_th, 跳到下一步。

(4)状态输出:根据Monte Carlo思想, 通过对采样粒子进行加权来近似表示当前状态值。若无重采样: $\begin{matrix} {\tilde{x}}_{t} \end{matrix}$ ≈ $\begin{matrix} \overset{N}{\sum_{i = 1}} \end{matrix} \begin{matrix} x_{t}^{i} \end{matrix} \begin{matrix} {\tilde{w}}_{t}^{i} \end{matrix}$ ; 若有重采样: $\begin{matrix} {\tilde{x}}_{t} \end{matrix}$ ≈ $\begin{matrix} \frac{1}{N} \end{matrix} \begin{matrix} \overset{N}{\sum_{i = 1}} \end{matrix} \begin{matrix} {\hat{x}}_{t}^{i} \end{matrix}$

(5)令t=t+1, 返回到步骤(2), 进行下一时刻的状态估计, 直到滤波结束。

2 分类重采样算法

2.1 分类重采样算法的原理

粒子退化现象是SIS的主要缺点, 具体表现为经过若干次迭代后, 重要性权值的方差会随着时间递增, 即最后只有少数粒子具有很大的权值, 而其余粒子的权值几乎可以忽略不计, 从而使得粒子集不能有效地表达状态的后验概率密度分布^[10]。为了防止这一现象, 本文提出的分类重采样方案通过直接方式对粒子进行筛选, 保留大权值粒子, 去除小权值粒子, 然后按权值大小顺序对大权值粒子进行复制, 使粒子总数恢复原有总数。这样直接改善了粒子退化的现象, 使得新产生的粒子集能更有效地表达状态的后验概率密度分布。下面将本文在粒子筛选和复制时采用的方案做出详细说明。

(1)粒子的筛选方案

首先选取区间0~1/N中的内的任一随机数u, 然后将此时刻每个粒子的权重 $\begin{matrix} w_{t}^{i} \end{matrix}$ 与u进行对比, 将权重 $\begin{matrix} w_{t}^{i} \end{matrix}$ ≥ u的粒子留下, 将权重 $\begin{matrix} w_{t}^{i} \end{matrix}$ < u的粒子舍弃。筛选结束后, 统计出被筛选出的粒子个数C, 将粒子按权重大小进行排序, 并计算出权重和sum, 以及这些粒子的平均权重:

means=sum/C

粒子滤波重采样算法的原则就是剔除小权值粒子、复制大权值粒子, 本文直接将粒子的权重与一个小于1/N的数字相比较, 保大舍小。筛选的标准选定为0~1/N中的一个随机数, 1/N是所有粒子权重的平均值, 也就是说舍去的粒子的权重全部小于粒子权重的平均值。

(2)粒子的复制方案

为了恢复粒子总数为N, 必须对筛选出的粒子进行复制。复制过程是从权值大的粒子开始直至粒子总数达到N为止。选取一个粒子数目的门限值N_p, 每个粒子复制的个数要根据筛选出的粒子数C与门限值N_p的比较结果选取不同复制方案:①当筛选出的粒子数大于或等于门限值, 即C≥ N_p时, 每个粒子复制的次数为小于或等于 $\begin{matrix} w_{t}^{i} \end{matrix}$ /means的最大整数; ②当筛选出的粒子数小于门限值, 即C< N_p时, 粒子的复制次数为大于或等于 $\begin{matrix} w_{t}^{i} \end{matrix}$ /means的最小整数。

根据粒子权重越大, 复制次数越多的原则, 将复制次数选择为一个接近 $\begin{matrix} w_{t}^{i} \end{matrix}$ /means的数值。情况一, 所筛选出的粒子数较多, 说明这一时刻粒子权重分布较为平均, 即粒子权重特别大和特别小的粒子数量较少。这种情况下, 选择尽可能更多的大权值粒子进行复制, 而不是将少数大权值粒子多次复制, 因此复制次数选为小于或等于 $\begin{matrix} w_{t}^{i} \end{matrix}$ /means的最大整数。情况二, 所筛选出的粒子数量较少, 说明粒子权重分布不均匀, 一定出现了较大权值的粒子。这种情况下, 为了体现大权值粒子的权重, 将粒子复制次数选为大于或等于 $\begin{matrix} w_{t}^{i} \end{matrix}$ /means的最小整数。

(3)新粒子产生方案

若采样粒子的权重分布极其恶劣, 即权重方差过大时, 容易出现将C个粒子复制相应次数后, 粒子总数仍不足N的情况。为了增加粒子的多样性, 而不是将原有大权值粒子多次复制, 采用了产生新粒子的方案。将大权值的粒子 $\begin{matrix} x_{t}^{i} \end{matrix}$ 加上一个噪声级别的随机数, 得到相应的新粒子 $\begin{matrix} {\tilde{x}}_{t}^{i} \end{matrix}$ 。新粒子的产生是从权值最大的粒子开始的, 按照粒子权重由大到小的顺序依次产生, 直至粒子总数为N个为止。

产生新粒子时, 要给原有粒子加上一个噪声级别的随机数, 这个随机数也可以称之为扰动。本文根据状态噪声的统计特性来确定扰动的数值范围。由于状态噪声的分布是确定的, 因而噪声的数字特征可以根据具体分布得出。当状态噪声的均值为E(n_t)方差为D(n_t)时, 扰动的取值为:

-E(n_t)+ $\begin{matrix} \sqrt{D (n_{t})} \end{matrix}$ × X

式中:X为-1到1之间任一随机数。

以状态噪声n_t-₁~N(0, 1)为例, 扰动即为-1到1之间任一随机数。根据概率分布原理:

$\begin{matrix} \frac{1}{\sqrt{2 π}} \end{matrix} \begin{matrix} \int_{-}^{1} \end{matrix}$ exp $\begin{matrix} (- \frac{x^{2}}{2}) \end{matrix}$ dx=0.6826

此时扰动的取值范围占状态噪声分布的68.26%, 数值取得过大, 所占噪声分布比例大, 但造成扰动也较大, 综合衡量扰动大小和所占噪声分布比例的扰动取值与状态噪声比例较为合理。

新粒子只有在粒子集的权重方差较大的时候才需要产生, 新粒子一方面保持了与原状态值的近似, 另一方面又不同于原本己多次复制的大权值粒子, 达到了粒子集的优化。这只是在粒子的权重分布极其恶劣的条件下采取的一种补救方法。通过新粒子的产生增加了粒子的多样性, 防止了粒子的枯竭。

2.2 分类重采样算法的步骤

(1)粒子筛选;

(2)计算筛选出粒子的个数、权重和、均值;

(3)粒子的复制, 采用分类复制方案, 必要时产生新粒子;

(4)均分权重, 将所有粒子的权值重置为1/N。改进算法伪代码如表1所示。

表1 分类重采样算法的伪代码 Table 1 Pseudo-code of CR algorithm

产生随机数:u=rand(1)/N, c=0
For i=1:N
if $\begin{matrix} w_{t}^{i} \end{matrix}$ ≥ u
$\begin{matrix} x_{t}^{c} \end{matrix}$ = $\begin{matrix} x_{t}^{i} \end{matrix}$ , $\begin{matrix} w_{t}^{c} \end{matrix}$ = $\begin{matrix} w_{t}^{i} \end{matrix}$ , c=c+1
End if
End for
权重和sum₀=0
For j=1:c
排序 sort{ $\begin{matrix} w_{t}^{c} \end{matrix}$ }, 求和sum_i=sum_i-1+ $\begin{matrix} w_{t}^{i} \end{matrix}$
End for
平均权值为means=sum/c
If N> c≥ 2N/3
将{ $\begin{matrix} x_{t}^{c} \end{matrix}$ }按大小顺序复制floor[ $\begin{matrix} w_{t}^{i} \end{matrix}$ /means]次
直至粒子总数为N
Else
将{ $\begin{matrix} x_{t}^{c} \end{matrix}$ }按大小顺序复制ceil[ $\begin{matrix} w_{t}^{i} \end{matrix}$ /means]次,
直至粒子总数为N;
若复制后总数仍小于N,
将大权值的粒子 $\begin{matrix} x_{t}^{i} \end{matrix}$ 增加扰动得到tⁱ,
用tⁱ补足N个。
End if
所有权重设为:1/N

表1 分类重采样算法的伪代码 Table 1 Pseudo-code of CR algorithm

3 仿真分析

将本文提出的分类重采样算法与多项式重采样算法和系统重采样算法进行分析和比较, 通过在相同条件下对3种算法的仿真, 得出各算法的优劣性。

3.1 仿真条件

仿真采用了一种广泛使用的非线性系统模型。状态方程为:

$\begin{matrix} x_{t} = \frac{x_{t - 1}}{2} + \frac{25 x_{t - 1}}{1 + x_{t - 1}^{2}} + 8 \cos [1.2 (t - 1)] + n_{t - 1} (3) \end{matrix}$

观测方程为:

$\begin{matrix} y_{t} = \frac{x_{t}^{2}}{20} + v_{t} (4) \end{matrix}$

仿真参数设置:状态初始条件为x₀~N(0, 5); 状态噪声n_t-₁~N(0, 1); 观测噪声v_t~N(0, 1); 门限值N_p=2N/3。为了观测不同粒子数目和不同仿真周期情况下各算法的性能, 仿真采用的粒子数N分别为10、20、50; 仿真周期T分别为100、1000、10000。

3.2 评价指标

(1)均方根误差(RMSE)为:

$\begin{matrix} RMSE = \sqrt{\frac{1}{T} \overset{T}{\sum_{t = 1}} {(x_{t} - {\tilde{x}}_{t})}^{2}} (5) \end{matrix}$

式中:x_t为状态真实值; $\begin{matrix} {\tilde{x}}_{t} \end{matrix}$ 为估计值; T为仿真周期。

(2)RMSE的均值和方差

进行M次蒙特卡罗仿真后, RMSE的均值为:

$\begin{matrix} \bar{RMSE} = \frac{1}{M} \overset{M}{\sum_{i = 1}} RMS E_{i} (6) \end{matrix}$

RMSE的方差为:

$\begin{matrix} σ^{2} = \frac{1}{M} \overset{M}{\sum_{i = 1}} {(RMS E_{i} - \bar{RMSE})}^{2} (7) \end{matrix}$

3.3 仿真结果分析

为了更清晰地对比这3种重采样算法, 本文进行了3次实验。在3次实验中, 采用不同粒子数的目的是评价算法的鲁棒性, 采用不同仿真周期的目的是评价算法的持久性, 计算RMSE的方差是为了评价算法的稳定性。

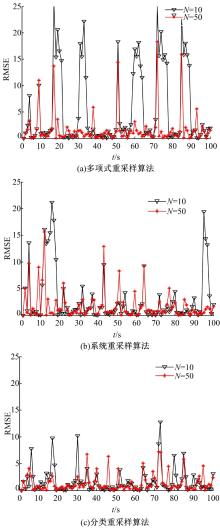
实验1 当T=100时, 选取粒子数目不同的情况下, 各种重采样算法均方根误差的对比结果如图1所示。

	Figure Option View Download New Window
	图1 三种重采样算法取不同粒子数时的RMSEFig.1 RMSE of three resampling algorithms with different particle numbers

增加粒子数可以减小结果的RMSE, 但计算量却随之成级数增加。因此当系统计算条件有限时, 就需要在较少的粒子数目下, 保持算法的准确性。从图1(a)可看出, MR算法在粒子数为10和50时, RMSE相差很大。这说明该算法对粒子数的多少很敏感, 在粒子数较少的情况下, 算法的估计精度和稳定性都会急剧下降; 从图1(b)可看出, SR算法在粒子数较少时, RMSE较大, 虽然没有MR算法的那么突出, 但反应出的估计效果并不理想。从图1(c)可看出, CR算法在粒子数不同时, RMSE均较小, 尤其在粒子数少时, 比前两种算法具有较高的估计精度, 证明了该算法有较好的鲁棒性。

实验2 进行100次仿真后, 在不同粒子数和不同仿真周期的情况下各种算法性能对比, 结果如表2和表3所示。

表2 N=10时不同仿真周期情况下3种算法的

\begin{matrix} \bar{RMSE} \end{matrix}

Table 2

\begin{matrix} \bar{RMSE} \end{matrix}

of three algorithms with different period at N=10

算法	T=100	T=1000	T=10000
MR	6.5627	6.6082	6.6848
SR	5.9198	5.9129	5.9767
CR	5.5390	5.3261	5.3182

表2 N=10时不同仿真周期情况下3种算法的

\begin{matrix} \bar{RMSE} \end{matrix}

Table 2

\begin{matrix} \bar{RMSE} \end{matrix}

of three algorithms with different period at N=10

表3 N=20时不同仿真周期情况下3种算法的

\begin{matrix} \bar{RMSE} \end{matrix}

Table 3

\begin{matrix} \bar{RMSE} \end{matrix}

of three algorithms with different period at N=20

算法	T=100	T=1000	T=10000
MR	4.9827	5.3772	5.3995
SR	4.3713	4.7722	4.8234
CR	4.6163	4.5527	4.5558

表3 N=20时不同仿真周期情况下3种算法的

\begin{matrix} \bar{RMSE} \end{matrix}

Table 3

\begin{matrix} \bar{RMSE} \end{matrix}

of three algorithms with different period at N=20

由表2和表3可以明显看出, 在T=100时, 3种重采样算法的 $\begin{matrix} \bar{RMSE} \end{matrix}$ 相差不大; 当仿真周期延长时, MR和SR这两种算法的 $\begin{matrix} \bar{RMSE} \end{matrix}$ 呈现增大的趋势。因此MR和SR算法在仿真周期较长的情况下性能明显降低。CR算法的 $\begin{matrix} \bar{RMSE} \end{matrix}$ 随着仿真周期的延长变化并不明显。当时间延长到T=10000时, CR算法的 $\begin{matrix} \bar{RMSE} \end{matrix}$ 明显小于其他两种算法。当N=10、T=10000时, CR算法的 $\begin{matrix} \bar{RMSE} \end{matrix}$ 比SR算法降低11%, 比MR算法降低20%, 说明了CR算法具有良好的估计持久性能。

从表4中可以明显地看出, 随着重采样粒子数的增多, 3种算法RMSE的方差都明显减小。其中分类重采样的方差在不同粒子数情况下都是最小的, 尤其是粒子数越少时, 分类重采样的优势越大。由图1也可以验证该结论。这说明该方法具有稳定的估计性能。

表4 T=1000时3种算法在不同粒子数的σ ² Table 4 σ ² of three algorithms with different particle numbers when T=1000

实验3 各种算法估计效果仿真。

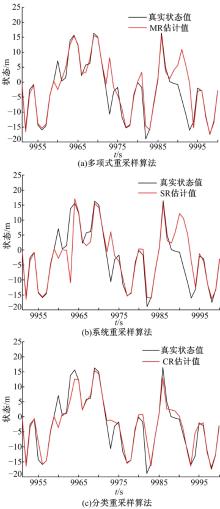
图2(a)(b)(c)分别是3种重采样算法在N=20; T=10000时, 对前述非线性系统模型跟踪的结果。为了清晰起见, 图中只展示了后50个时间点。从图中可以看出, CR算法比另两种算法更接近真实值。

	Figure Option View Download New Window
	图2 基于三种重采样算法的估计结果Fig.2 Estimation result with three resampling algorhtms

4 结束语

SIS算法会出现退化现象, 而重采样算法虽然可以解决退化现象, 但又带来了样本枯竭的问题, 一个好的重采样算法应该在减少小权值粒子数目和保持粒子多样性之间进行合理权衡。本文提出的CR算法, 根据筛选出的粒子的多少采用不同复制方案, 必要时通过扰动产生新的粒子。算法原理简单, 易于实现, 在解决粒子退化的同时, 预防了粒子的枯竭。仿真结果显示:RMSE在粒子数目较少时较之MR和SR算法有明显优势, 此外RMSE随着仿真周期的延长变化不明显。在N=10, T=10000时, $\begin{matrix} \bar{RMSE} \end{matrix}$ 比SR算法的低11%, 尽管该算法计算量比SR算法略有增加, 但在鲁棒性、持久性、稳定性方面有较大的改善。

The authors have declared that no competing interests exist.

参考文献

View Option

[1]	陈飞. 基于粒子滤波的无线传感器网络目标跟踪算法研究[D]. 长春: 吉林大学通信工程学院, 2009. Chen Fei. The target tracking algorithm research based on particle filtering in wireless sensor network[D]. Changchun: College of Communication Engineering, Jilin University, 2009. [本文引用:1]
[2]	Gustafsson F, Gunnarsson F, Bergman N, et al. Particle filters for positioning, navigation, and tracking[J]. IEEE Transactions on Signal Processing, 2002, 50(2): 425-437. [本文引用:1]
[3]	Gordon N, Salmond D. Novel approach to nonlinear and non-Gaussian Bayesian state estimation[J]. IEE Proc of Institute Electric Engineering, 1993, 140(2): 107-113. [本文引用:2]
[4]	Arulampalam M S, Maskell S, Gordon N, et al. A tutorial on particle filters for online nonlinear/non-Gaussian Bayesian tracking[J]. IEEE Proceedings on Signal Processing, 2002, 50(2): 174-188. [本文引用:3]
[5]	Liu J S, Chen R. Sequential monte carlo methods for dynamic systems[J]. Journal of the American Statistical Association, 1998, 93(443): 1032-1044. [本文引用:1]
[6]	Li T C, Sattar T P, Sun S D. Deterministic resampling: unbiased sampling to avoid sample impoverishment in particle filters[J]. Signal Process, 2012, 92(7): 1637-1645. [本文引用:1]
[7]	Pitt M K, Shephard N. Filtering via simulation: auxiliary particle filters[J]. Journal of the American Statistical Association, 1999, 94(446): 590-599. [本文引用:1]
[8]	高建坡, 韦志辉, 孟迎军, 等. 基于观测似然重要性采样的粒子滤波算法[J]. 系统仿真学报, 2009, 21(12): 3705-3709. Gao Jian-po, Wei Zhi-hui, Meng Ying-jun, et al. Particle filter based on observation likelihood importance sampling[J]. Journal of System Simulation, 2009, 21(12): 3705-3709. [本文引用:1]
[9]	胡士强, 敬忠良. 粒子滤波算法综述[J]. 控制与决策, 2005, 20(4): 361-365. Hu Shi-qiang, Jing Zhong-liang. Overview of particle filter algorithm[J]. Control and Decision, 2005, 20(4): 361-365. [本文引用:1]
[10]	胡研研. 基于粒子滤波的目标跟踪算法研究[D]. 长春: 吉林大学通信工程学院, 2012. Hu Yan-yan. Research on target tracking algorithm based on particle filter[D]. Changchun: College of Communication Engineering, Jilin University, 2012. [本文引用:1]

2009

0.0

. 2009, :- DOI:doi:10.7666/d.y1072744

The target tracking algorithm research based on particle filtering in wireless sensor network

基于粒子滤波的无线传感器网络目标跟踪算法研究[D]

Chen Fei.

陈飞

随着通信技术、嵌入式技术、微机电系统、传感器技术的迅速发展，具有一定感知能力、计算能力和通信能力的无线传感器开始出现，其应用受到业界的广泛关注。目标跟踪被广泛应用于军事、民用各个方面，如监控、导航、障碍规避系统等。它的主要目的是确定目标的位置，个数，运动方向等。随着无线传感器的发展，基于无线传感器网络实现目标跟踪成为了一个研究热点。本文针对传感器节点之间数据融合的问题，引入了粒子滤波算法。在解决目标跟踪这种非线性非高斯噪声问题中，粒子滤波算法具有很好的表现。本文同时将目标跟踪的问题模型化，并将滤波算法应用其中，给出了目标跟踪的算法。针对该模型的各个节点存在的协作问题，本文分析了一种分布式的网络模型。同时讨论了无线传感器节点的功耗问题。如何建模目标跟踪问题、以及构架目标跟踪系统是本文研究的主要工作。本文的主要研究工作包括：首先，针对粒子滤波算法进行了系统的分析，讨论了粒子滤波存在的问题及解决方案，并分析比较了几种常见的粒子滤波算法。其次，分析目标跟踪问题中目标移动的几何特性，根据这些几何特性，将目标跟踪问题转化为线性规划问题，即给出了几个约束条件，在这些约束条件下运用粒子滤波算法实现目标跟踪。再次，从无线传感器网络实现的角度，讨论了无线传感器节点各个模块的功耗问题，针对各个模块的特点给出了相应的解决方案；同时分析了无线传感器网络实现目标跟踪算法的网络模型。最后，给出了各个算法的模拟与仿真，并对仿真结果进行分析验证。基于无线传感器网络的目标跟踪应用具有很大的潜力，有待进一步的研究和探索。在本文的结尾部分，对基于无线传感器网络的目标跟踪进行了总结和展望。

... 粒子滤波可以有效地处理非线性、非高斯噪声环境下的状态估计问题,被广泛用于在目标跟踪^[1]、导航定位^[2]等领域 ...

2002

0.0

... 粒子滤波可以有效地处理非线性、非高斯噪声环境下的状态估计问题,被广泛用于在目标跟踪^[1]、导航定位^[2]等领域 ...

1993

0.0

... 自从1993年Gordon等^[3]提出重采样算法以来,出现了很多重采样算法,比较经典的有多项式重采样(Multinomial resampling,MR)^[3],系统重采样(Systematic resampling,SR)^[4]和残差重采样(Residual resampling,RR)^[5] ...

2002

0.0

... 传统的粒子滤波方法^[4]就是用前一时刻状态值x_t-₁和现在的观测值y_t来递推估计现在的状态值x_t ...

... (2)重要性采样:将p(x_txt-1i)作为重要密度函数^[4]进行采样, xti~p(x_txt-1i),i=1,2,…,N,根据当前的观测值y_t,更新粒子的权值 wti=wt-1ip(y_t|xti), wti为t时刻第i个采样粒子的权重,并归一化权值: w~ti=wti∑j=1Nwtj ...

1998

0.0

2012

0.0

... 为此,Li和Sattar等提出Deterministic Resampling算法^[6],通过划分网格并逐步裂变的方法保持了粒子的多样性,但由于计算量过大不适宜做实时处理 ...

1999

0.0

... 此外,结合最新观测值的辅助粒子滤波算法^[7]增加了一步重采样过程,因此更接近真实状态值,但当过程噪声较大时,滤波性能急剧下降 ...

2009

0.0

. 2009, 21(12):3705-3709

Particle filter based on observation likelihood importance sampling

基于观测似然重要性采样的粒子滤波算法

Gao Jian-po , Wei Zhi-hui , Meng Ying-jun

高建坡, 韦志辉, 孟迎军

摘　要：针对粒子滤波中如何来设计重要性采样函数进行动态粒子传播这个重要问题,提出了一种新的基于观测似然重要性采样的粒子滤波算法,该算法打破了常规粒子滤波先按某一重要性采样函数进行采样,再用观测似然进行粒子权重更新的思路,而是直接根据观测似然进行采样,然后再用先验转移概率进行粒子权重更新。由于算法在采样的过程中用到了观测似然函数,这样保证大多数粒子点都分布在高观测似然区域,极大提高了粒子的利用效率,实验证明基于观测似然重要性采样粒子滤波的性能明显优于当今流行的标准粒子滤波,扩展Kalman粒子滤波以及unscented粒子滤波。

... 基于观测似然重要性采样粒子滤波^[8]直接根据观测似然函数进行采样,保证大多数粒子点都分布在高观测似然区域,提高了粒子的利用效率,但只适合于观测精度高的场合 ...

2005

0.0

. 2005, 20(4):361-365 DOI:doi:10.3321/j.issn:1001-0920.2005.04.001

Overview of particle filter algorithm

粒子滤波算法综述

Hu Shi-qiang , Jing Zhong-liang.

胡士强, 敬忠良

对粒子滤波算法的原理和应用进行综述. 首先针对非线性非高斯系统的状态滤波问题, 阐述粒子滤波的原理; 然后在分析采样- 重要性-重采样算法基础上, 讨论粒子滤波算法存在的主要问题和改进手段; 最后从概率密度函数的角度出发, 将粒子滤波方法与其他非线性滤波算法进行比较, 阐明了粒子滤波的适应性, 给出了粒子滤波在一些研究领域中的应用, 并展望了其未来发展方向.

... 随着粒子数的增加,粒子的概率密度函数逐渐逼近状态的概率密度函数,即达到了最优贝叶斯估计的效果^[9] ...

2012

0.0

. 2012, :-

Research on target tracking algorithm based on particle filter[D]. Changchun: College of Communication Engineering,

基于粒子滤波的目标跟踪算法研究[D]

Hu Yan-yan.

胡研研

近年来随着计算机处理能力的快速发展，使得粒子滤波器作为序列信号处理的一种非常有效的方法成为研究领域的一个热点。它在处理复杂的非线性或非高斯问题的潜力，引起了信号处理，统计学，经济计量学等不同领域的专家学者的关注。尤其是来自国防的关注，因为它已经成为研究目标跟踪问题的一个十分有效的方法。　　本文首先讨论了几种经典的滤波（卡尔曼滤波、网格滤波、扩展卡尔曼滤波和近似网格滤波）所存在的问题。接着针对非线性非高斯系统的状态滤波问题，阐述了粒子滤波的原理；然后在分析采样-重要性- 重采样算法的基础上，讨论了粒子滤波算法存在的主...

... 1 分类重采样算法的原理粒子退化现象是SIS的主要缺点,具体表现为经过若干次迭代后,重要性权值的方差会随着时间递增,即最后只有少数粒子具有很大的权值,而其余粒子的权值几乎可以忽略不计,从而使得粒子集不能有效地表达状态的后验概率密度分布^[10] ...