基于云模型的地铁换乘枢纽拥挤度辨识方法

引用本文

周继彪, 陈红, 闫彬, 张文, 冯微. 基于云模型的地铁换乘枢纽拥挤度辨识方法. 吉林大学学报: 工学版, 2016, 46(1): 100-107
ZHOU Ji-biao, CHEN Hong, YAN Bin, ZHANG Wen, FENG Wei. Identification of pedestrian crowding degree in metro transfer hub based on normal cloud model. Journal of Jilin University Engineering and Technology Edition, 2016, 46(1): 100-107 复制到剪切板

Permissions

基于云模型的地铁换乘枢纽拥挤度辨识方法

周继彪¹, 陈红², 闫彬³, 张文⁴, 冯微²

1.宁波工程学院交通学院,浙江宁波 315211

2.长安大学公路学院,西安 710064

3.蚌埠汽车士官学校司训勤务系, 安徽蚌埠 233011

4.广州市城市规划勘测设计研究院交通规划室,广州 510060

陈红(1963-),女,教授,博士生导师.研究方向:综合交通规划.E-mail:hongchen82@126.com

作者简介:周继彪(1986-),男,讲师,博士.研究方向:综合交通规划.E-mail:zhoujb2014@nbut.edu.cn

基金:国家自然科学基金项目(51308311); 浙江省社会科学基金项目(15NDJC078YB); 宁波市自然科学基金项目(2015A610298)

摘要

针对地铁换乘枢纽拥挤状态划分中的模糊性和随机性,提出了一种基于云模型的地铁换乘枢纽行人拥挤度辨识方法。首先分析行人拥挤度的内涵和度量标准,根据它们在不同服务水平下边界值计算云的数字特征。其次利用云的合成理论建立不同服务水平对应的模板云模型,同时将采集到的行人交通特性基本参数输入到枢纽内各基础设施的云发生器中,建立待识别云模型。然后根据云相似度计算模板云和待识别云的相似度并引入拥挤度定义,给出拥挤度辨识的具体实现过程。最后以西安市北大街地铁换乘枢纽为例对其进行了试验验证。结果表明:通过实际采集的数据建立待识别云模型,并与模板云作相似度分析,得出通道该时刻的行人拥挤度为100.095,处于拥挤状态;楼梯该时刻的行人拥挤度为100.273,处于拥挤状态。该方法不仅能够较准确地定量辨别枢纽内行人拥挤度状态,而且能够反映行人拥挤的程度和拥挤的变化过程,有较强的实用性。

关键词: 交通运输系统工程; 拥挤度; 云模型; 地铁换乘枢纽; 基础设施

中图分类号:U491 文献标志码:A 文章编号:1671-5497(2016)01-0100-08

Identification of pedestrian crowding degree in metro transfer hub based on normal cloud model

ZHOU Ji-biao¹, CHEN Hong², YAN Bin³, ZHANG Wen⁴, FENG Wei²

1.School of Transportation, Ningbo University of Technology, Ningbo 315211, China

2.School of Highway, Chang'an University, Xi'an 710064, China

3.Department of Driver Training Service, Bengbu Automobile Sergeant's School, Bengbu 233011, China

4.Guangzhou Urban Planning & Design Survey Research Institute, Transport Planning & Design Studio, Guangzhou 510060, China

Abstract

In order to solve the problems of fuzziness and randomness in the division of congestion state in metro transfer hub, an identification method of pedestrian crowding degree factor is proposed based on normal cloud model. First, the connotation and the measure standard of the pedestrian crowding degree are analyzed, and according to their boundary value under different service level the digital characteristics of the cloud are calculated. Second, the cloud synthesis theory is applied to establish the template cloud corresponding to different service levels, and the survey data (pedestrian speed, flow etc.) are input into the cloud generator in order to set up the identification cloud model. Third, according the definition of cloud similarity, the similarity between the identified cloud and the template cloud in the infrastructure (e.g. channel, stairs) is calculated. Moreover, the crowding degree is defined independently, which is described in a quantificational level under the state of crowding degree in the metro transfer hub, and the method to identify the pedestrian crowding degree is given. The method is verified by a case study in a metro transfer hub in Xi'an. Results show that the pedestrian crowding degree in the channel 100.095, which is in the crowding state, the pedestrian crowding degree in the stair is 100.273, which is also in the crowded state. This method can not only accurately identify the crowded state quantificationally, but also reflect the change process of pedestrian crowding degree, which has strong practicality.

Keyword: engineering of communications and transportation system; crowding degree; cloud model; metro transfer hub; infrastructure

Show Figures

0 引言

地铁换乘枢纽作为城市运输体系的关键节点和中心环节, 是轨道交通大客流的汇聚点和集散地^[1]。行人拥挤度反映了地铁换乘枢纽内某设施(水平通道、楼梯等)乘客疏散时行人聚集的时间特征和乘客在枢纽内安全疏散过程中的便捷性和舒适性。建立地铁换乘枢纽内行人拥挤度自动辨识模型, 能够进一步明确不同拥挤状态的临界值, 为地铁换乘枢纽的安全预警提供必要的数据支持和理论依据。

目前国内外城市地铁换乘枢纽行人拥挤理论主要集中在数学模型和仿真、实验研究与社会心理研究等3个方面。在数学模型和仿真方面, 主要集中研究常态下行人拥挤动力学或者恐慌状态下的疏散过程^[2], 建立了在数学逻辑框架下的行人拥挤恐慌数学模型^{[3, 4]}, 并利用元胞自动机模型、格子气模型、社会力模型、流体动力学模型、智能体模型等^[5]数学方法对拥挤疏散进行检验。通过仿真评估常态下基础设施的服务水平, 改进设计方案, 建立有效的交通组织预案, 降低行人由于恐慌而造成的拥挤^{[6, 7]}, 预防拥挤事故灾难的发生。在实验研究方面, 主要分为现场观测、疏散演习、有控实验、动物群体实验和真实紧急事件的分析等5大方面。结合视频数据观察发现了几种典型的行人交通自组织现象, 包括瓶颈行为、自动渠化行为、徘徊行为等^{[8, 9]}。在行人紧急疏散并产生拥挤时, 加速自己的行进运动并不一定会产生较高的疏散通行率, 反而降低疏散效率, 产生“ 快即是慢效应” ^[10]。在社会心理研究方面, 其主要研究点主要集中在群体的拥挤特点(集体行为), 以及在给定情况下的心理状态^[11]。

综上所述, 目前的研究内容涉及交通工程学、疏散动力学、社会力模型、连续介质模型等, 呈现出多学科交叉的趋势, 但大多数是单因素、单层次, 一些成果的实用性不强。针对地铁换乘枢纽拥挤度方面的研究成果较少, 且较少运用复杂性理论和系统方法。鉴于此, 本文以行人速度、空间占有率、流量等参数作为交通状态识别模型输入, 以枢纽内行人拥挤状态的定量描述为模型输出, 采用行人拥挤度云辨识方法, 剖析地铁换乘枢纽行人拥挤度辨识问题, 探索地铁换乘枢纽拥挤度自动辨识问题。

1 行人拥挤度内涵分析

1.1 拥挤度基本内涵

(1)行人拥挤行为

拥挤是行人个体在聚集过量人群的空间内反映出来的主观感受, 是由行人流密度、空间环境、个体特征等多因素造成的。行人拥挤行为则是在高密度环境下行人通过心理判断、认知后采取的个人交通行为。行人在不同时空环境、出行目的和出行需求下表现出不同的拥挤行为。在拥挤情况下, 行人主观上感受到拥挤而造成心理压力上升, 随即产生急切、焦躁的情绪, 想迫切脱离拥挤环境。因此, 行人会提高步行速度、步幅, 并极力想超越对方。同向人群行人走行行为主要表现为靠右侧超越和跟随慢走行为, 对向人群行人走行行为主要表现为靠右侧行走、停留和随机选择路径等行为, 相比而言更加复杂。

(2)行人拥挤度特性分析

空间特性:行人在地铁换乘枢纽环境下, 随着行人空间的转移, 行人走行在枢纽入口、楼梯、通道、站台等设施上的行为特性都有所不同。如在枢纽出入口处, 由于出行目的的不同, 行人会提高步速、步幅, 但随着出入口人流密度的增加, 行人步行速度会逐渐降低。

时间特性:地铁换乘枢纽内行人出行一般具有早、晚两个高峰时段, 早高峰行人多以上班、上学为出行目的, 晚高峰则是回家、访友和聚餐为主, 高峰时段大约能持续1~2 h。因此, 由于时间的紧迫性、强刚性和严格性, 行人的步速、步幅、步频都较平时有所提高。

心理特性:当行人交通流密度增大时, 个体可使用公共资源空间变小, 拥挤现象就会出现, 随着客流量的继续增大, 行人心理的拥挤感及脱离意愿会随之增强。行人会比较容易对枢纽内部的拥挤环境产生反感情绪, 如性格急躁、鲁莽、不友好、身心压抑等, 同时行人会主动提高步速、在拥挤环境中穿行、碰撞或其他一些不文明的交通行为等。相反, 行人在行人交通流密度较低时, 个体可使用公共资源空间增大, 行人心理上的压力较为舒缓, 对枢纽内环境的主观感知相对不敏感, 行人在步速、步幅上自然会放慢减缓。

1.2 拥挤度度量标准

目前, 针对地铁换乘枢纽行人拥挤度的衡量指标, 国内外并没有统一的量化标准。《公共交通通行能力和服务水平手册》^[12]中给出了步行通道和楼梯处的服务水平分级情况, 如表1所示。

表1 手册中通道和楼梯处的服务水平分级 Table 1 Service level classification of channel and stairs in manual

行人服务水平是评估行人活动空间的通行能力和舒适性的有效手段, 计算与步行相关的行人服务水平(临界值)将基于以下两点:行人选择期望步行速度的自由度和绕过走得较慢的步行者的可能性。不同行人对于自由度、舒适度、可能性的选择不同, 同一行人在不同环境下的选择也不一致, 这种定性的主观感受造成了枢纽内服务水平评价必然具有模糊性与随机性。行人服务水平的模糊性和随机性主要有2类:指标定量化的模糊随机性、评价标准的模糊随机性。

(1)指标定量化的模糊随机性

影响行人服务水平的指标主要有行人自身特征指标、行人交通特征指标和设施特征指标3类。设施特征如长宽高可以通过测量得到数值, 而对于多数处于运动状态下的行人, 其交通特征值是随机动态变化的。如测量某时刻人均占用面积, 由于测量员的反应不同, 处于测量范围临界处的动态行人有时会被考虑进去, 有时会被忽略, 进而表现出一种模糊随机性。

(2)评价标准的模糊随机性

由于每项设施都至少有2个评价指标, 采用上述具体的数字对服务水平进行强制性划分, 在枢纽内服务水平划分过程中会产生不一致的现象。如针对通道处, 若行人占据空间为0.619 m²/人, 平均步行速度为59.966 m/min, 单位宽度行人流率为83.000 人/(m· min), 其服务水平的判定就表现出不一致性。根据表1可知, 由第一个指标判定的服务水平为E级, 由第二个指标判定的服务水平为E级, 第三个指标判定的服务水平为F级。因此, 这种服务水平判定结果是具有模糊性的, 导致行人拥挤状态的判断也具有模糊性。同时, 行人具有主观能动性, 行人的到达与离去具有很强的随机性, 任何时刻任何地点, 行人的决策都是难以准确预测的, 也使得交通参数难以确定。鉴于上述分析, 本文借用云模型^[13], 来进一步对地铁换乘枢纽内部行人拥挤度进行自动辨识。

2 行人拥挤度辨识方法

云模型将模糊理论中的模糊性和概率统计思想中的随机性有机结合, 描述自然语言中概念的不确定性。云模型^[13]由李德毅院士首次提出并应用于人工智能领域^[14], 先后经历了理论形成期、理论完成期和应用拓展期等3大时期^[15]。由于云模型是结合模糊数学和随机理论建立的不确定模型, 而交通流又具有很强的时变性、离散型、模糊性和非线性, 故云模型在交通领域也有一定的应用。将云模型引入到地铁换乘枢纽行人拥挤度自动辨识中, 进一步拓展了云模型的应用领域。

2.1 云辨识建模过程

(1)基本定义

定义1:设U是一个用精确数值表示的定量论域(研究的范围), C是论域U上的定性概念, 若定量值x∈ U, 且x是定性概念C的一次随机实现, x对C的确定度是有稳定倾向的随机数μ (x):U→ [0, 1], ∀ x∈ U, x→ μ (x), 则x在论域U上的分布称为云(Cloud), 每一个x称为一个云滴^[14]。“ 随机实现” 是基于概率论与数据统计学下的实现过程, “ 确定度” 是基于模糊理论下的隶属度(Membership), 云的特性一般用3个数字特征值来表示, 即:期望Ex(Expected value)、熵En(Entropy)和超熵He(Hyper entropy)。三个数字特征值的具体含义为:期望(Ex)表示云滴在论域空间分布的中心值, 是最能代表定性概念的点, 熵(En)表示定性概念的模糊性度量, 反映论域空间中可被概念接受的云滴取值范围, 超熵(He)表示熵的不确定性度量, 反映云滴的离散程度及云的厚度。

定义2:云的3En规则:论域U中的所有元素对定性语言值C的总贡献为1, 但有99.7%是落在区间[Ex-3En, Ex+3En]上。因此, 对于一个定性语言值概念, 其相应的云对象中对于[Ex-3En, Ex+3En]之外的云滴元素是小概率事件, 一般可忽略不计。

定义3:若云中x满足:x~NORM(Ex, En'), En'~NORM(En, He²), 且x对C的确定度满足:

$\begin{matrix} μ (x) = Exp \frac{- {(x - Ex)}^{2}}{2 {(En')}^{2}} (1) \end{matrix}$

则x在论域U上的分布称为正态云^[14]。正态云发生器是求解正态云模型的特定算法, 包括正向云发生器和逆向云发生器。正向云发生器是根据云的数字特征来产生云滴, 逆向云发生器是有云滴得到云的数字特征值。如果给定论域U中的一个特定点x₀, 通过云发生器生成x₀属于概念C的确定度分布, 此时的云发生器称为X条件云发生器。正向正态云发生器的具体实现算法如下:

Step1 生成以En为期望值、He²为方差的正态随机数En'_i。

Step2 生成以Ex为期望值、En $\begin{matrix} {'_{i}}^{2} \end{matrix}$ 为方差的正态随机数x_i。

Step3 计算μ _i(x)=exp[- $\begin{matrix} (x_{i} {- Ex)}^{2} \end{matrix}$ /2 $\begin{matrix} (En'_{i})^{2} \end{matrix}$ ]。

Step4 重复步骤Step1到Step3, 直到产生预定的n个云滴为止。

定义4:设论域中存在n个具有相同性质的子云C₁(Ex₁, En₁, He₁), C₂(Ex₂, En₂, He₂), …, C_n(Ex_n, En_n, He_n), 则n个子云合成为父云C(Ex, En, He)过程用C=C₁◦C₂◦…◦C_n表示, 其中“ ◦” 表示云的合成。若各子云的权值为ω _i, 父云的数字特征Ex、En、He的计算公式为:

$\begin{matrix} \{\begin{matrix} Ex = \frac{\overset{n}{\sum_{i = 1}} E x_{i} \times E n_{i} \times ω_{i}}{\overset{n}{\sum_{i = 1}} E n_{i} \times ω_{i}} \\ En = \overset{n}{\sum_{i = 1}} E n_{i} \times ω_{i} \\ He = \frac{\overset{n}{\sum_{i = 1}} H e_{i} \times E n_{i} \times ω_{i}}{\overset{n}{\sum_{i = 1}} E n_{i} \times ω_{i}} \end{matrix} (2) \end{matrix}$

(2)选择度量指标

根据《公共交通通行能力和服务水平手册》^[12]可确定各类设施服务水平度量指标。例如对于通道设施, 采用行人占据空间、平均步行速度和单位宽度的行人流量作为地铁换乘枢纽通道行人服务水平的指标, 一方面避免了单一评价指标的片面性, 另一方面又可以克服行人交通流基本参数采集误差的影响。在识别枢纽内行人拥挤状态过程中, 假设各个指标占有同等重要的作用, 对于通道和楼梯设施, 假设度量指标具有相同的权值。

(3)确定云的数字特征

设某度量指标的阈值向量为X=(x₁, x₂, x₃, x₄, x₅), x_i表示某度量指标在不同服务水平等级划分下的临界值。由于云的合成需在同一论域中实现, 因此在确定云的数字特征前, 需将指标值标准化。

对越大越优型指标的标准化处理如下式:

$\begin{matrix} \begin{matrix} x_{j}^{*} = \frac{x_{j} - \min {x_{j}}}{\max {x_{j}} - \min {x_{j}}} (3) \\ j = 1, 2, 3, 4, 5 \end{matrix} \end{matrix}$

对越小越优型指标的标准化处理如下式:

$\begin{matrix} \begin{matrix} x_{j}^{*} = \frac{\max {x_{j}} - x_{j}}{\max {x_{j}} - \min {x_{j}}} (4) \\ j = 1, 2, 3, 4, 5 \end{matrix} \end{matrix}$

式中:max{x_j}、min{x_j}分别为第j个阈值的最大值和最小值; $\begin{matrix} x_{j}^{*} \end{matrix}$ 为x_j的标准化值。

A和F服务水平分别用半升正态云和半降正态云表示, 可由式(5)得出云的3个基本数字特征:

$\begin{matrix} E x_{x 1} = x_{1}^{*}, E n_{x 1} = E n_{x 2}, E x_{x 6} = x_{5}^{*}, E n_{x 6} = E n_{x 5} (5) \end{matrix}$

B、C、D、E服务水平用全正态云表示, 可由式(6)计算得出云的3个基本数字特征:

$\begin{matrix} \{\begin{matrix} E x_{xj} = (x_{j - 1}^{*} + x_{j}^{*} \frac{)}{2} \\ E n_{xj} = (x_{j - 1}^{*} - x_{j}^{*} \frac{)}{6} \\ He = 0.01 (j = 2, 3, 4, 5) \end{matrix} (6) \end{matrix}$

(4)建立模板云模型

将6种服务水平下各指标的子云合成的父云称为模板云或标准云, 模板云(标准云)是识别枢纽内拥挤状态的标准云图。设某设施有3个度量指标, 各指标的子云记为R_j、S_j和T_j, 则父云U_j由R_j、S_j和T_j合成, 即U_j=R_j◦S_j◦T_j(j=1, 2, 3, 4, 5, 6), 具体计算如式(2)所示。

(5)建立待识别云模型的步骤

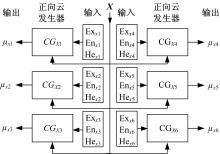
Step1 根据枢纽内设施服务水平度量指标的数字特征和正向正态云发生器的实现算法, 利用子云的数字特征和用Matlab软件建立某度量指标的正向正态云发生器CG_Xj。

Step2 将该指标实际采集的真实值x进行标准化处理后记为x^*。这里规定:对于x≤ min{x_j}范围内的指标值, 标准化结果为0, 对于x≥ max{x_j}范围内的指标值, 标准化结果为1。

Step3 将实际采集到的指标参数x输入到正向正态云发生器CG_X₁、CG_X₂、CG_X₃、CG_X₄、CG_X₅和CG_X₆中, 如图1所示。图1中每个云发生器的输出值μ _X₁、μ _X₂、μ _X₃、μ _X₄、μ _X₅和μ _X₆表示输入参数x隶属于X_j的程度。由云模型的模糊性和随机性可知, μ _Xj是具有稳定倾向的随机数, 而非一个特定定值。将μ _Xj归一化后得到X_j的权重ω _Xj, 如式(7)所示:

$\begin{matrix} ω_{Xj} = μ_{Xj} / \overset{6}{\sum_{j = 1}} μ_{Xj} (7) \end{matrix}$

利用子云的数字特征, 根据式(2)计算输入参数x的云的特征数字, 得到云X_x(Ex_X, En_X, He_X)。

	Figure Option View Download New Window
	图1 X条件下云发生器及输出Fig.1 Cloud generator under X and output

Step4 通过Step1和Step2的计算, 得到设施内其他各度量指标的待识别云的3个特征值。

Step5 合成待识别云。假设某设施有3个度量指标, 记各指标计算得到云分别为R_r、S_s和T_t, 利用式(2)合成得到待识别云U'=R_r◦S_s◦T_t=(Ex, En, He)。

(6)确定待识别云和模板云的相似度

行人拥挤状态识别需计算待识别云U'与各模板云U_j之间的相似度, 云相似度定义为:设有两朵云U'和云U, 云滴x_i(i=1, 2, …, N)由云发生器U'产生, 设x_i在云U中隶属度为β _i, 定义δ = $\begin{matrix} \frac{1}{N} \end{matrix} \begin{matrix} \overset{N}{\sum_{i = 1}} \end{matrix}$ β _i为U'和U的相似度。

根据云相似度定义, 计算待识别云U'与各模板云U_j之间的相似度, 具体过程如下:

Step1 在待识别云U'中生成以En为期望值, He²为方差的一个正态随机数En'_i=NORM(En, He²)。

Step2 在待识别云U'中生成以Ex为期望值, En $\begin{matrix} '_{i}^{2} \end{matrix}$ 为方差的一个正态随机数x_i=NORM(Ex, En $\begin{matrix} '_{i}^{2} \end{matrix}$ )。

Step3 在模板云U_j中生成以En_j为期望值, H $\begin{matrix} e_{j}^{2} \end{matrix}$ 为方差的一个正态随机数En'_j=NORM(En_j, H $\begin{matrix} e_{j}^{2} \end{matrix}$ )。

Step4 计算第j级服务水平的隶属度β _ij, 即β _ij=exp[- $\begin{matrix} (x_{i} - E x_{j})^{2} \end{matrix}$ /2En $\begin{matrix} '_{j}^{2} \end{matrix}$ ]。

Step5 重复步骤(1)~(4)直至产生满足要求的n个云滴为止。

Step6 计算待识别云U'与各模板云U_j之间的相似度δ _j:

$\begin{matrix} δ_{j} = \frac{1}{n} \overset{n}{\sum_{i = 1}} β_{ij} (8) \end{matrix}$

Step7 将δ _j归一化后得到待识别云归属于第j种服务水平的可能程度λ _j。

$\begin{matrix} λ_{j} = δ_{j} / \overset{6}{\sum_{j = 1}} δ_{j} (9) \end{matrix}$

显然, 待识别云U'的云滴x_i落在某个模板云U_j范围内越多, 则相似度δ _j越大, 可能程度λ _j也越大, 表明枢纽内待识别状态与第j种服务水平越接近。进一步强调的是云辨识的结果并不是把待识别状态强制性地划归为某种服务水平里, 而是辨识它归属于6种服务水平的可能程度。

2.2 行人拥挤度辨识

最大值判定法是利用可能程度最大值来确定待识别状态对应的服务水平等级, 但这很难体现行人拥挤程度。不同拥挤程度的交通条件及行人对拥挤的感受直接影响着行人的行为, 而行人的行为又直接关系到换乘枢纽设施的服务水平。因此引入行人拥挤度, 计算公式如式(10)所示:

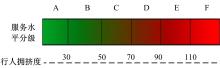
$\begin{matrix} γ = \overset{6}{\sum_{j = 1}} λ_{j} \times ξ_{j} (10) \end{matrix}$

式中:ξ _j表示不同服务水平的拥挤系数, 为了进一步体现出枢纽内服务水平的等级性和层次性, 这里假设拥挤系数分别为20、40、60、80、100、120。拥挤度越大, 表明枢纽内越拥挤, 行人的满意度越低, 其枢纽内的服务质量越低。6种服务水平对应的拥挤度范围是:非常畅通(γ < 30), 畅通(30≤ γ < 50), 一般畅通(50≤ γ < 70), 一般拥挤(70≤ γ < 90), 拥挤(90≤ γ < 110), 严重拥挤(γ ≥ 110)。具体如图2所示。

	Figure Option View Download New Window
	图2 基于行人拥挤度的服务水平划分Fig.2 Division of service level based on the crowding degree

3 实例验证

以西安市北大街地铁枢纽换乘站为例, 分别采集通道、楼梯、站台某时刻的交通数据。通道处实际采集的行人占据空间为0.619 m²/人, 平均步行速度为59.966 m/min, 单位宽度的行人流率为83.000人/(m· min); 楼梯处实际采集的行人占据空间为0.778 m²/人, 单位宽度的行人流率为49.555人/(m· min); 站台处实际采集的行人占据面积为0.486 m²/人, 平均人间距为0.398 m。首先按照式(3)和式(4)对各度量指标值进行标准化处理, 按照式(5)和式(6)计算得到通道和楼梯设施6种状态下各指标云的数字特征列于表2中。

表2 行人服务水平下各指标的云的数字特征 Table 2 Digital features of cloud of indicators

记U₁、U₂、U₃、U₄、U₅和U₆分别为A、B、C、D、E、F服务水平的模板云, 父云的数值特征具体计算如式(2)所示, 从而计算得到通道、楼梯的模板云U_j的数字特征, 具体如表3所示。

表3 模板云的数字特征 Table 3 Digital features of templated cloud

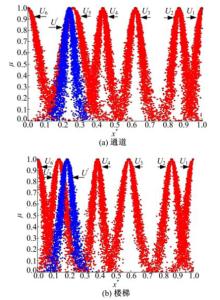
枢纽内各类基础设施以5000个云滴为基准, 结合2.1小节中关于正向正态云发生器的具体实现算法, 生成模板云图形, 具体如图3所示。

	Figure Option View Download New Window
	图3 通道和楼梯的模板云云图Fig.3 Templated cloud in channel and stairs

图3即是各类设施模板云的云图, 即模板云图或标准云图。通过实测数据建立待识别云模型, 并与模板云作相似度分析, 从而实现枢纽内行人拥挤度的判别。根据正向正态云发生器运算, 可以得到实测行人交通数据生成的待识别云的数字特征值, 如表4~表6所示。

表4 实例中采集得到的原始数据 Table 4 Original data in the case

表5 待识别云的数字特征值 Table 5 Digital characteristics of identified cloud

表6 合成后的待识别云的数字特征 Table 6 Digital features of identified cloud after synthesis

在建立待识别云模型过程中, 利用子云的数字特征及Matlab程序求解通道、楼梯处云发生器的输出值μ _Xj。将云发生器的输出值μ _Xj归一化后得到X_j的权重ω _Xj值。在第四步建立待识别云模型中, 利用Step1和Step2的计算, 得到设施内各度量指标的待识别云的3个数字特征值, 结果如表5所示。

利用模板云的数字特征, 合成待识别云, 即计算合成后待识别云的数字特征, 其结果如表6所示。

枢纽内各类基础设施以5000个云滴为基准, 结合2.1小节中关于正向正态云发生器的具体实现算法, 生成待识别云图形, 具体如图4所示。

	Figure Option View Download New Window
	图4 通道和楼梯处待识别云和模板云的相似度示意图Fig.4 Identified cloud and templated cloud in channel and stairs

通道处:根据模板云和待识别云相似度计算公式(8)以及待识别云归属可能程度的计算公式(9)可以得出:实际状态与6种服务水平的相似度分别为[0.000, 0.000, 0.000, 0.570, 508.020, 3.009], 实际状态归属于6种服务水平的可能程度分别为[0.000, 0.000, 0.000, 0.001, 0.993, 0.006]。显然, 该状态介于D和E级服务水平之间, 更多地倾向于E级, 归属于其他服务水平的可能性极小, 基本上都趋向于零。根据式(10)计算出:通道处该时刻的行人拥挤度为100.095, 处于拥挤状态。

楼梯处:根据模板云和待识别云相似度计算公式(8)以及待识别云归属可能程度的计算公式(9)可以得出:实际状态与6种服务水平的相似度分别为[0.000, 0.000, 0.002, 7.080, 2518.855, 42.088], 实际状态归属于6种服务水平的可能程度分别为[0.000, 0.000, 0.000, 0.003, 0.981, 0.016]。显然, 该状态介于E和F级服务水平之间, 更多地倾向于E级, 归属于其他服务水平的可能性极小, 基本上都趋向于零。根据公式(10)计算出:楼梯该时刻的行人拥挤度为100.273, 处于拥挤状态。

4 结论

(1)基于云模型将模糊理论中的模糊性和概率统计思想中的随机性有机结合, 辨识城市地铁换乘枢纽行人拥挤度问题是可行的。

(2)通过西安北大街轨道交通枢纽站实际采集的数据建立待识别云模型, 并与模板云作相似度分析, 从而实现行人拥挤度判别。通道该时刻的行人拥挤度为100.095, 处于拥挤状态。楼梯该时刻的行人拥挤度为100.273, 处于拥挤状态。

(3)下一步旨在根据行人占据空间、平均步行速度和单位宽度的行人流率作为地铁换乘枢纽通道行人服务水平的指标, 对未来可能发生的拥挤状态或者对己发生拥挤的时空扩散范围进行预测, 根据预测结果启动不同等级的预警机制, 以便管理部门制定合理的调控预案, 确保高峰时期大客流的高效、安全、便捷疏散, 预防集体踩踏事故的发生, 使被动调控转化成主动预警。

The authors have declared that no competing interests exist.

参考文献

View Option

[1]	周继彪, 陈红, 闫彬, 等. 地铁换乘枢纽行人交通特性实证研究[J]. 武汉理工大学学报, 2014, 36(4): 92-99. Zhou Ji-biao, Chen Hong, Yan Bin, et al. Pedestrian traffic characteristics analysis in the metro transfer hub[J]. Journal of Wuhan University of Technology, 2014, 36(4): 92-99. [本文引用:1]
[2]	Helbing D, Farkas I J, Molnar P, et al. Simulation of pedestrian crowds in normal and evacuation situations[J]. Pedestrian and Evacuation Dynamics, 2002, 21(1): 21-58. [本文引用:1]
[3]	Miguel A F. The emergence of design in pedestrian dynamics: locomotion, self-organization, walking paths and constructal law[J]. Physics of Life Reviews, 2013, 10(2): 168-180. [本文引用:1]
[4]	Ma J, Song W G, Lo S M, et al. New insights into turbulent pedestrian movement pattern in crowd-quakes[J]. Journal of Statistical Mechanics: Theory and Experiment, 2013(2): 28-36. [本文引用:1]
[5]	Zheng X, Zhong T, Liu M. Modeling crowd evacuation of a building based on seven methodological approaches[J]. Building and Environment, 2009, 44(3): 437-445. [本文引用:1]
[6]	Shiwakoti N, Sarvi M. Enhancing the panic escape of crowd through architectural design[J]. Transportation Research Part C: Emerging Technologies, 2013, 37(1): 260-267. [本文引用:1]
[7]	杨丽丽, 贾洪飞, 隽志才. 轨道交通枢纽换乘系统可靠性及其影响因素[J]. 吉林大学学报: 工学版, 2011, 41(4): 944-949. Yang Li-li, Jia Hong-fei, Juan Zhi-cai. Transfer system reliability and its influencing factors of rail transit terminal[J]. Journal of Jilin University (Engineering and Technology Edition), 2011, 41(4): 944-949. [本文引用:1]
[8]	Helbing D, Buzna L, Johansson A, et al. Self-organized pedestrian crowd dynamics: experiments, simulations, and design solutions[J]. Transportation Science, 2005, 39(1): 1-24. [本文引用:1]
[9]	Antonini G, Bierlaire M, Weber M. Discrete choice models of pedestrian walking behavior[J]. Transportation Research Part B: Methodological, 2006, 40(8): 667-687. [本文引用:1]
[10]	Helbing D, Johansson A. Pedestrian, Crowd and Evacuation Dynamics[M]. Berlin: Springer, 2009. [本文引用:1]
[11]	Mawson A R. Mass Panic and Social Attachment: the Dynamics of Human Behavior[M]. Farnham: Ashgate Publishing, Ltd, 2012. [本文引用:1]
[12]	Transportation Research Board. Transit Capacity and Quality of Service Manual[M]. Washington, D C: Transportation Research Board, 2003. [本文引用:2]
[13]	Li D Y, Meng H J, Shi X M. Membership clouds and membership cloud generators[J]. Journal of Computer Research and Development, 1995, 32(6): 15-20. [本文引用:2]
[14]	李德毅, 刘常昱. 论正态云模型的普适性[J]. 中国工程科学, 2004, 6(8): 28-34. Li De-yi, Liu Chang-yu. Study on the universality of the normal cloud model[J]. Engineering Science, 2004, 6(8): 28-34. [本文引用:3]
[15]	孟晖, 王树良, 李德毅. 基于云变换的概念提取及概念层次构建方法[J]. 吉林大学学报: 工学版, 2010, 40(3): 782-787. Meng Hui, Wang Shu-liang, Li De-yi. Concept extraction and concept hierarchy constructionbased on cloud transformation[J]. Journal of Jilin University (Engineering and Technology Edition), 2010, 40(3): 782-787. [本文引用:1]

2014

0.0

... 0 引言地铁换乘枢纽作为城市运输体系的关键节点和中心环节,是轨道交通大客流的汇聚点和集散地^[1] ...

2002

0.0

... 在数学模型和仿真方面,主要集中研究常态下行人拥挤动力学或者恐慌状态下的疏散过程^[2],建立了在数学逻辑框架下的行人拥挤恐慌数学模型^[3,4],并利用元胞自动机模型、格子气模型、社会力模型、流体动力学模型、智能体模型等^[5]数学方法对拥挤疏散进行检验 ...

2013

0.0

2009

0.0

2013

0.0

... 通过仿真评估常态下基础设施的服务水平,改进设计方案,建立有效的交通组织预案,降低行人由于恐慌而造成的拥挤^[6,7],预防拥挤事故灾难的发生 ...

2011

0.0

. 2011, 41(4):944-949

Transfer system reliability and its influencing factors of rail transit terminal

轨道交通枢纽换乘系统可靠性及其影响因素

Yang Li-li , Jia Hong-fei , Juan Zhi-cai.

杨丽丽, 贾洪飞, 隽志才

College of Transportation, Jilin University, Changchun 130022, China

Taking the rail transit terminal as the research object, the effects of the reliability of the serial units and the parallel units in the system on the reliability of the global system were analyzed through the establishment of the serial and parallel systems in the transfer facility. The reliability of the facility was defined as the probability that the passenger delay time is 0, and a reliability function model was built for the facility. The effects of parameters on the reliability were analyzed based on the reliability function versus parameters curves. The results indicate that the more serial units are in the system, the lower the system reliability is, and the parallel units are on the contrary. The reliability of the connection facility is affected by the width of facility and the passenger arrival rate, and the reliability of the service facility is affected by the average service rate of facility and the passenger arrival rate.

以轨道交通枢纽为研究对象，通过建立换乘设施串并联系统，分析了系统中串联、并联单元的可靠性对系统整体可靠性的影响。定义某一设施的可靠性是乘客在该设施上延误时间为0的概率，据此建立可靠性函数模型。并根据可靠性函数值随各参数变化曲线分析各参数对可靠性的影响。研究结果表明:系统中串联设施越多,可靠性越低，并联的数量越多,可靠性越高。连接类设施的可靠性受设施宽度及乘客到达率的影响，服务类设施的可靠性受设施平均服务率及乘客到达率的影响。

... 通过仿真评估常态下基础设施的服务水平,改进设计方案,建立有效的交通组织预案,降低行人由于恐慌而造成的拥挤^[6,7],预防拥挤事故灾难的发生 ...

2005

0.0

... 结合视频数据观察发现了几种典型的行人交通自组织现象,包括瓶颈行为、自动渠化行为、徘徊行为等^[8,9] ...

2006

0.0

... 结合视频数据观察发现了几种典型的行人交通自组织现象,包括瓶颈行为、自动渠化行为、徘徊行为等^[8,9] ...

2009

0.0

... ^[10] ...

2012

0.0

... 在社会心理研究方面,其主要研究点主要集中在群体的拥挤特点(集体行为),以及在给定情况下的心理状态^[11] ...

2003

0.0

... 《公共交通通行能力和服务水平手册》^[12]中给出了步行通道和楼梯处的服务水平分级情况,如表1所示 ...

... 根据《公共交通通行能力和服务水平手册》^[12]可确定各类设施服务水平度量指标 ...

1995

0.0

... 鉴于上述分析,本文借用云模型^[13],来进一步对地铁换乘枢纽内部行人拥挤度进行自动辨识 ...

... 云模型^[13]由李德毅院士首次提出并应用于人工智能领域^[14],先后经历了理论形成期、理论完成期和应用拓展期等3大时期^[15] ...

2004

0.0

... 云模型^[13]由李德毅院士首次提出并应用于人工智能领域^[14],先后经历了理论形成期、理论完成期和应用拓展期等3大时期^[15] ...

... (x),则x在论域U上的分布称为云(Cloud),每一个x称为一个云滴^[14] ...

... 则x在论域U上的分布称为正态云^[14] ...

2010

0.0

. 2010, 40(3):782-787

Concept extraction and concept hierarchy constructionbased on cloud transformation

基于云变换的概念提取及概念层次构建方法

Meng Hui , Wang Shu-liang , Li De-yi.

孟晖, 王树良, 李德毅

1.Institute of Beijing Information Technology, Beijing 100093,China;2.International School of Software, Wuhan University, Wuhan 430079, China;3.Institute of Beijing Electronic System Engineering, Beijing 100141, China

A method for extraction of qualitative concepts and construction of concept hierarchy is proposed. First, the cloud transformation is used to extract qualitative concept from database. Then, the former algorithm for pan concept tree generation is modified. When processing the cloud synthesization, the new algorithm takes the influence of the magnitude coefficient into consideration, which makes the output concept hierarchy more close to reality. As a case study, this method is used to extract qualitative concept and construct the concept hierarchy from car price data. Results demonstract that this method can extract qualitative concepts exactly. The concept center extracted by the proposed method is in good agreeement with that obtained by conventional clustering algorithm. The proposed method can also describe the concepts with uncertainty, thus the ontology based on these concepts could give better specification of the conceptualization.

提出了一种基于云变换的概念提取及概念层次构建方法。首先通过云变换从数据库中提取定性概念，然后对原有概念跃升算法进行改进，使其在处理概念云合并时考虑幅度系数的影响，从而使得算法输出的概念层次能够更符合实际。最后用该方法对汽车价格数据进行分析，从中提取定性概念，并构建概念层次。实验表明，该方法能够较准确地提取和表征定性概念，所提取的概念中心与传统聚类算法得到的概念中心吻合较好，且基于云模型的概念表示能同时体现概念的随机性和模糊性，从而使得基于这些概念构建的本体能更准确地描述概念模型。

... 云模型^[13]由李德毅院士首次提出并应用于人工智能领域^[14],先后经历了理论形成期、理论完成期和应用拓展期等3大时期^[15] ...