具有关节限位的7R仿人机械臂逆运动学优化

引用本文

霍希建, 刘伊威, 姜力, 夏晶, 刘宏. 具有关节限位的7R仿人机械臂逆运动学优化. 吉林大学学报: 工学版, 2016, 46(1): 213-220
HUO Xi-jian, LIU Yi-wei, JIANG Li, XIA Jing, LIU Hong. Inverse kinematic optimization of 7R humanoid arm with joint limits. Journal of Jilin University Engineering and Technology Edition, 2016, 46(1): 213-220 复制到剪切板

Permissions

具有关节限位的7R仿人机械臂逆运动学优化

霍希建, 刘伊威, 姜力, 夏晶, 刘宏

哈尔滨工业大学机器人技术与系统国家重点实验室,哈尔滨 150080

刘伊威(1977-),男,副教授,博士.研究方向:仿人机器人,仿人型灵巧手.E-mail:lyw@hit.edu.cn

作者简介:霍希建(1986-),男,博士研究生.研究方向:仿人机器人,机械臂设计与控制.E-mail:huoxijian@163.com

基金:“973”国家重点基础研究发展计划项目(2011CB013306); 国家自然科学基金项目(51175106)

摘要

针对7R仿人机械臂运动优化问题,建立了基于臂角参数的逆运动学封闭解,并采用解析法确定了关节限位约束下臂角参数的有效范围。此外,定义了一种新的关节位置评价函数,将避关节限位的优化指标转化为虚拟转矩。在此基础上,提出一种自寻优方法,用于解决机械臂避关节限位的运动优化问题。仿真结果表明:本文方法能准确地确定臂角的有效范围,同时能快速有效地完成机械臂运动学优化任务。

关键词: 自动控制技术; 冗余自由度机械臂; 封闭解; 有效臂角; 自寻优方法

中图分类号:TP242.6 文献标志码:A 文章编号:1671-5497(2016)01-0213-08

Inverse kinematic optimization of 7R humanoid arm with joint limits

HUO Xi-jian, LIU Yi-wei, JIANG Li, XIA Jing, LIU Hong

State Key Laboratory of Robotics and System, Harbin Institute of Technology, Harbin 150080, China

Abstract

To solve the kinematic optimization problem of the 7R humanoid arm, the closed-form solutions to the inverse kinematics based on the arm angle parameter were established. The range of the feasible arm angle corresponding to joint limits was determined using analytical methods. Besides, a new function was defined, which is used to evaluate the joint angles, and the optimal indexes of joint limits avoidance were transformed into virtual torques. Based on this, the self-optimizing method was proposed to solve the kinematic optimization problem of joint limits avoidance. Simulations demonstrate that the proposed method can determine the feasible range of the arm angle accurately and implement the kinematic optimization of the humanoid arm efficiently.

Keyword: automatic control technology; redundant manipulator; closed-form solution; feasible arm angle; self-optimizing method

Show Figures

0 引言

7R仿人机械臂为冗余自由度机械臂, 其逆运动学问题通常伴随有二次任务的优化。由于机械结构的限制和仿人特性的要求, 机械臂各关节的运动范围都会受到一定程度的限制^[1]。因此, 避关节限位成为七自由度机械臂运动优化的一个重要问题。

七自由度机械臂运动优化方法很多, 其中, 微分逆运动方法是将运动优化任务投影到雅克比矩阵零空间, 在速度/加速度水平实现的运动控制方法^{[2, 3]}。该类方法无法确定逆运动学的全部可行解, 且在奇异点附近的数值稳定性与计算精度难以同时获得最佳效果。运动学逆变换方法是在位置水平直接对运动学方程进行求解, 包括参数化封闭解方法和数值方法。前者是通过引入一个附加参数(如参数化关节^[4]、臂角^[1]等), 建立机械臂逆运动学的参数化解析解, 在此基础上采用代数法或搜索算法完成运动优化任务^{[5, 6]}。该方法计算简单, 可以快速确定所有可行的关节位置解。但该方法只适用于具有特殊构型的七自由度机械臂。数值方法是采用迭代法^[7]或智能算法^{[8, 9]}在运动方程约束下对二次优化任务进行求解。该方法适用于任意构型的机械臂, 但计算精度与复杂性之间难以同时获得最佳效果。人工神经网络^[10]凭借其较强的并行计算与数值逼近能力常用于解决机械臂的运动优化问题, 但该方法计算精度较低, 不适用于精细任务操作。此外, 由上述不同方法组合而成的混合算法也常用于解决机械臂运动优化问题, 以弥补单一方法的不足^{[11, 12]}。

本文以七自由度仿人机械臂为研究对象, 建立了臂角有效范围的求解方法, 并采用自寻优方法实现了机械臂避关节限位的运动优化。

1 仿人机械臂正运动学

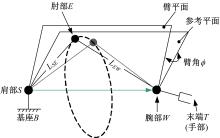
七自由度仿人机械臂通常采用S-R-S(spherical-roll-spherical)构型, 该构型在消除内部奇异、运动学计算及结构复杂性等方面具有诸多优势。本文所述7R(revolute joint)机械臂由7个独立的旋转关节构成, 前3个关节轴线交于一点等效为球型肩关节, 以模拟人体肩部的外展-内收运动、屈-伸运动、上臂的内-外旋运动。后3个关节构成虚拟球型腕关节, 实现腕部的外展-内收运动、屈-伸运动及反掌运动, 如图1所示。在此基础上, 参考人体运动学, 确定了机械臂各连杆的尺寸及关节活动范围。

	Figure Option View Download New Window
	图1 仿人机械臂DH坐标系Fig.1 DH coordinates frames of humanoid arm

为了描述机械臂末端的运动, 建立了机械臂DH坐标系, DH参数如表1所示。

表1 仿人机械臂DH参数 Table 1 DH parameters of humanoid arm

机械臂关节空间到笛卡尔空间的映射关系可由正运动学方程表示为:

$\begin{matrix} _{}^{0} A_{7} = {\overset{7}{\prod_{i = 1}}}_{}^{i - 1} A_{i} (1) \end{matrix}$

式中 $\begin{matrix} :_{}^{i - 1} \end{matrix}$ A_i∈ SE $\begin{matrix} (3) \end{matrix}$ 为坐标系Σ _i相对于坐标系Σ _i-₁的齐次变化矩阵。因此, 已知各关节角度, 机械臂末端位姿即可由方程(1)唯一确定。

2 逆运动学封闭解

2.1 机械臂自运动分析

给定三维空间内期望的末端位姿, S-R-S构型机械臂存在自运动。定义前3个关节轴线的交点为肩部S, 后3个关节轴线的交点为腕部W, 第3、4关节轴线交点为肘部E。则机械臂的自运动表现为:在基坐标系Σ ₀内机械臂绕 $\begin{matrix} \vec{SW} \end{matrix}$ 的旋转运动, 如图2所示。因此, 为了获得特定的机械臂运动学逆解, 需要引入一个附加参数来约束肘部的位置。本文定义第2、4关节轴线平行时(文中取θ ₃=0)肩-肘-腕三点所确定的平面为参考平面, 机械臂处于其他位形时, 肩-肘-腕三点所确定的平面为臂平面。沿 $\begin{matrix} \vec{SW} \end{matrix}$ 方向参考平面与臂平面之间的夹角定义为臂角ϕ , ϕ ∈ $\begin{matrix} [- π, π) \end{matrix}$ 。因此, 坐标系Σ _i在臂平面与参考平面之间的相对关系可以表示为:

$\begin{matrix} \begin{matrix} _{}^{0} A_{i} = [\begin{matrix} R (\vec{SW}, ϕ) & O \\ O^{T} & 1 \end{matrix}]_{}^{0} A_{i}^{r} (2) \\ R (\vec{SW}, ϕ) = \\ [\begin{matrix} k_{x}^{2} v + cϕ & k_{y} k_{x} v - k_{z} sϕ & k_{z} k_{x} v + k_{y} sϕ \\ k_{x} k_{y} v + k_{z} sϕ & k_{y}^{2} v + cϕ & k_{z} k_{y} v - k_{x} sϕ \\ k_{x} k_{z} v - k_{y} sϕ & k_{y} k_{z} v + k_{x} sϕ & k_{z}^{2} v + cϕ \end{matrix}] \end{matrix} \end{matrix}$

式中:O为3× 1零向量 $\begin{matrix} ;_{}^{0} \end{matrix} \begin{matrix} A_{i}^{r} \end{matrix}$ 为参考平面内坐标系Σ _i相对Σ ₀的位姿; sϕ =sinϕ , cϕ =cosϕ , v=1-cϕ (以下同); k_x、k_y和k_z分别为基坐标系内 $\begin{matrix} \vec{SW} \end{matrix}$ 在x、y和z方向上的分量。

	Figure Option View Download New Window
	图2 臂角定义Fig.2 Definitions of arm angle

2.2 逆运动学封闭解计算

设 $\begin{matrix} _{}^{0} \end{matrix}$ X₇∈ R³ $\begin{matrix} ,_{}^{0} \end{matrix}$ R₇∈ SO $\begin{matrix} (3) \end{matrix}$ 分别为机械臂末端相对基坐标系的位置与姿态, 定义 $\begin{matrix} _{}^{K} \end{matrix}$ X_MN为 $\begin{matrix} \vec{MN} \end{matrix}$ 在坐标系Σ _K中的向量表示。由运动学方程(1)可得:

$\begin{matrix} _{}^{0} \end{matrix}$ X_SW $\begin{matrix} =_{}^{0} \end{matrix}$ X_BT $\begin{matrix} -_{}^{0} \end{matrix}$ X_BS $\begin{matrix} -_{}^{0} \end{matrix} \begin{matrix} R_{7}_{}^{7} \end{matrix}$ X_WT

由图2可知, 关节4的角度θ ₄与机械臂自运动无关, 即θ ₄由Δ SEW唯一确定。

$\begin{matrix} \cos θ_{4} = - \frac{{L_{SE}}^{2} + {L_{EW}}^{2} - ‖_{}^{0} X_{SW} ‖^{2}}{2 \times L_{SE} \times L_{EW}} (3) \end{matrix}$

此外, 机械臂腕部W的位置与姿态是解耦的, 即前4个关节确定腕部位置 $\begin{matrix} _{}^{0} \end{matrix}$ X_SW, 后3个关节仅影响腕部姿态。因此, 参考平面内前2个关节的位置可根据腕部位置方程确定, 即

$\begin{matrix} \begin{matrix} _{}^{0} X_{SW} =_{}^{0} R_{1}^{r}_{}^{1} R_{2}^{r}_{}^{2} R_{3} |_{θ_{3} = 0} (_{}^{3} X_{SE} +_{}^{3} R_{4}_{}^{4} X_{EW}) \\ (4) \end{matrix} \end{matrix}$

根据方程(2)可知, 在臂角为ϕ 的臂平面内, 坐标系Σ ₃相对基坐标系Σ ₀的姿态可通过参考平面内的旋转矩阵 $\begin{matrix} _{}^{0} \end{matrix} \begin{matrix} R_{3}^{r} \end{matrix}$ 绕向量 $\begin{matrix} _{}^{0} \end{matrix}$ X_SW旋转得到, 即

$\begin{matrix} \begin{matrix} _{}^{0} R_{3} = R {(\vec{SW}, ϕ)}_{}^{0} R_{3}^{r} = A_{s} sinϕ + B_{s} cosϕ + C_{s} \\ (5) \end{matrix} \end{matrix}$

在此基础上, 将矩阵R $\begin{matrix} (\vec{SW}, ϕ) \end{matrix}$ 代入方程(5)中, 则系数矩阵A_s、B_s和C_s可表示为:

A_s= $\begin{matrix} [^{0} U_{SW} \times] \end{matrix} \begin{matrix} \cdot_{}^{0} \end{matrix} \begin{matrix} R_{3}^{0} \end{matrix}$

B_s=- $\begin{matrix} {[^{0} U_{SW} \times]}^{2} \end{matrix} \begin{matrix} \cdot_{}^{0} \end{matrix} \begin{matrix} R_{3}^{0} \end{matrix}$

C_s= $\begin{matrix} [^{0} {U_{SW}}^{0} {U_{SW}}^{T}] \end{matrix}$ · ⁰ $\begin{matrix} R_{3}^{0} \end{matrix}$

式中:⁰U_SW为 $\begin{matrix} _{}^{0} \end{matrix}$ X_SW的单位向量; $\begin{matrix} [^{0} U_{SW} \times] \end{matrix}$ 为⁰U_SW的反对称矩阵。

由于 $\begin{matrix} _{}^{0} \end{matrix}$ R₃ $\begin{matrix} =_{}^{0} \end{matrix} \begin{matrix} R_{1}_{}^{1} \end{matrix} \begin{matrix} R_{2}_{}^{2} \end{matrix}$ R₃, 结合方程(5)可得肩部关节位置解与臂角ϕ 的函数关系:

$\begin{matrix} \begin{matrix} θ_{1} = \arctan 2 \{- sign (\sin θ_{2}) (a_{s 22} sϕ + b_{s 22} cϕ + c_{s 22}), \\ - sign (\sin θ_{2}) (a_{s 12} sϕ + b_{s 12} cϕ + c_{s 12})\} (6) \\ θ_{2} = \pm \arccos (- a_{s 32} sϕ - b_{s 32} cϕ - c_{s 32}) (7) \\ θ_{3} = \arctan 2 \{sign (\sin θ_{2}) (a_{s 33} sϕ + b_{s 33} cϕ + c_{s 33}), \\ - sign (\sin θ_{2}) (a_{s 31} sϕ + b_{s 31} cϕ + c_{s 31})\} (8) \end{matrix} \end{matrix}$

式中:a_sij、b_sij、c_sij分别是矩阵A_s、B_s和C_s中的第(i, j)元素。

根据方程(1)和(5), 坐标系Σ ₇相对基坐标系Σ ₀的姿态可表示为:

$\begin{matrix} _{}^{0} \end{matrix}$ R₇=R $\begin{matrix} {(\vec{SW}, φ)}_{}^{0} \end{matrix} \begin{matrix} R_{3}^{r}_{}^{3} \end{matrix} \begin{matrix} R_{4}_{}^{4} \end{matrix}$ R₇

将A_s、B_s和C_s代入上述方程 $\begin{matrix} ,_{}^{4} \end{matrix}$ R₇可表示为:

$\begin{matrix} _{}^{4} \end{matrix}$ R₇=A_wsinϕ +B_wcosϕ +C_w

式中:A_w=³R₄^T· A_s^T· ⁰R₇;

B_w $\begin{matrix} =_{}^{3} \end{matrix}$ R $\begin{matrix} {_{4}}^{T} \end{matrix}$ · B_s^T· ⁰R₇;

C_w $\begin{matrix} =_{}^{3} \end{matrix}$ R $\begin{matrix} {_{4}}^{T} \end{matrix}$ · C_s^T· ⁰R₇。

在此基础上, 腕部各关节角度与臂角ϕ 的函数关系为:

$\begin{matrix} \begin{matrix} θ_{5} = \arctan 2 \{- sign (\sin θ_{6}) (a_{w 23} sϕ + b_{w 23} cϕ + c_{w 23}), \\ - sign (\sin θ_{6}) (a_{w 13} sϕ + b_{w 13} cϕ + c_{w 13})\} (9) \\ θ_{6} = \pm \arccos (- a_{w 33} sϕ - b_{w 33} cϕ - c_{w 33}) (10) \\ θ_{7} = \arctan 2 \{sign (\sin θ_{6}) (a_{w 32} sϕ + b_{w 32} cϕ + c_{w 32}), \\ - sign (\sin θ_{6}) (a_{w 31} sϕ + b_{w 31} c ϕ + c_{w 31})\} (11) \end{matrix} \end{matrix}$

式中:a_wij、b_wij、c_wij分别是矩阵A_w、B_w和C_w中的第(i, j)元素。

至此, 确定了仿人机械臂基于臂角ϕ 的参数化逆运动学封闭解。该封闭解引入双变量反正切函数, 简化了计算过程中运动学逆解的判断过程, 避免了可行解的丢失。因此, 给定工作空间内期望末端位姿及臂角ϕ , 根据封闭解方程可以快速地确定机械臂的各关节位置。

3 臂角可行性分析

3.1 必要性分析

理论上, 对应机械臂工作空间内的一个末端位姿, S-R-S机械臂可绕 $\begin{matrix} \vec{SW} \end{matrix}$ 作整周旋转运动。在实际应用中, 由于机械结构的限制及仿人特性的要求, 机械臂各关节的运动范围都会受到一定程度的限制, 进而导致自运动表现为机械臂绕 $\begin{matrix} \vec{SW} \end{matrix}$ 在部分区域内的连续旋转运动。即对应机械臂工作空间内的一个末端位姿, 臂角的有效取值范围受关节限位的影响。只有确定臂角的取值范围, 才能保证臂角所对应的运动学逆解的可行性。因此, 确定臂角的有效范围是机械臂逆运动学计算的前提。下面采用解析法求解关节限位与臂角参数之间的对应关系。

3.2 臂角的有效范围

机械臂逆运动学封闭解包含3种形式:θ ₂与θ ₆为关于ϕ 的余弦函数形式; θ ₁、θ ₃、θ ₅和θ ₇均为关于ϕ 的反正切函数形式; θ ₄是关于末端位置的函数, 与臂角参数无关。首先定义如下参数:θ _{i_}_max和θ _{i_}_min分别为关节i活动范围的上、下极限, 关节活动范围θ _{i_}_min≤ θ _i≤ θ _{i_}_max, 关节i对应的臂角有效范围为Ψ _i。下面分别对不同的函数形式进行分析, 确定关节限位与臂角有效范围之间的映射关系。

(1)余弦函数形式

根据方程(7)和(10), θ ₂、θ ₆与臂角ϕ 之间的函数关系可统一写成如下形式:

$\begin{matrix} \cos θ_{i} = asinϕ + bcosϕ + c (12) \end{matrix}$

若 $\begin{matrix} \sqrt[]{a^{2} + b^{2}} \end{matrix}$ ≠ 0, 则方程(12)转化为

sin $\begin{matrix} (ϕ + φ) \end{matrix}$ = $\begin{matrix} \frac{cosθ - c}{\sqrt[]{a^{2} + b^{2}}} \end{matrix}$ ∈ $\begin{matrix} [H_{\min}, H_{\max}] \end{matrix}$

式中:φ =arctan2 $\begin{matrix} (b, a) \end{matrix}$ ; $\begin{matrix} [H_{\min}, H_{\max}] \end{matrix}$ 可由θ _{i_}_max和θ _{i_}_min确定。

因此, 确定臂角ϕ 的有效范围问题转化为求解不等式:

$\begin{matrix} H_{\min} \leq \sin (ϕ + φ) \leq H_{\max} (13) \end{matrix}$

令hϕ =ϕ +φ , 则hϕ 的最大值与最小值可以表示为:

$\begin{matrix} \begin{matrix} h ϕ_{\min} = \{\begin{matrix} \arcsin (H_{\min}), |H_{\min}| \leq 1 \\ π / 2, H_{\min} > 1 \\ - π / 2, H_{\min} < - 1 \end{matrix} \\ h ϕ_{\max} = \{\begin{matrix} \arcsin (H_{\max}), |H_{\max}| \leq 1 \\ π / 2, H_{\max} > 1 \\ - π / 2, H_{\max} < - 1 \end{matrix} \end{matrix} \end{matrix}$

不等式(13)的解集存在以下情况:

(a)H_min> 1或H_max< -1, 则Ψ _i=∅;

(b)H_min=-1且H_max=1, 则Ψ _i= $\begin{matrix} [- π, π] \end{matrix}$ ;

(c)H_min≥ 0且H_max≥ 0, 则

hϕ ∈ $\begin{matrix} [\begin{matrix} h ϕ_{\min} & h ϕ_{\max} \end{matrix}] \end{matrix}$ ∪ $\begin{matrix} [π - h ϕ_{\max}, π - h ϕ_{\min}] \end{matrix}$ ;

(d)H_min≤ 0且H_max≥ 0, 则

hϕ ∈ $\begin{matrix} [h ϕ_{\min}, h ϕ_{\max}] \end{matrix}$ ∪ $\begin{matrix} [π - h ϕ_{\max}, π] \end{matrix}$ ∪ $\begin{matrix} [- π, - π - h ϕ_{\min}] \end{matrix}$ ;

(e)H_min< 0且H_max< 0, 则

hϕ ∈ $\begin{matrix} [h ϕ_{\min}, h ϕ_{\max}] \end{matrix}$ ∪ [-π -hϕ _max, -π -hϕ _min]。因此, 根据hϕ 的范围, 可确定关节运动约束下臂角的有效范围Ψ _i。

若 $\begin{matrix} \sqrt[]{a^{2} + b^{2}} \end{matrix}$ =0, 则cosθ _i=c, 关节角θ _i为常数, 此时机械臂处于奇异位型, Ψ _i= $\begin{matrix} [- π, π] \end{matrix}$ 。

(2)反正切函数形式

根据方程(6)(8)(9)和(11), θ ₁、θ ₃、θ ₅和θ ₇与臂角ϕ 之间的函数关系可统一写成双变量反正切函数形式:

$\begin{matrix} \begin{matrix} θ_{i} = \arctan 2 \{sign (sinθ') (a_{m} sinϕ + b_{m} cosϕ + c_{m}), \\ sign (sinθ') (a_{n} sinϕ + b_{n} cosϕ + c_{n})\} (14) \end{matrix} \end{matrix}$

式中:θ '是与θ _i有关的关节变量, 文中指θ ₂或θ ₆。

鉴于正切函数特性, 将关节活动范围投影至4个象限。 $\begin{matrix} [θ_{i_\min_I}, θ_{i_\max_I}] \end{matrix}$ 、 $\begin{matrix} [θ_{i_\min_II}, θ_{i_\max_II}] \end{matrix}$ 、 $\begin{matrix} [θ_{i_\min_III}, θ_{i_\max_III}] \end{matrix}$ 和 $\begin{matrix} [θ_{i_\min_IV}, θ_{i_\max_IV}] \end{matrix}$ 分别为关节i在I、II、III和IV象限的分量, 其所对应的臂角有效范围分别为Ψ _i_{_I}、Ψ _i_{_II}、Ψ _i_{_III}和Ψ _i_{_IV}。此外, 为了确定方程(14)中sign $\begin{matrix} (sinθ') \end{matrix}$ 的符号, 关节变量θ '分别投影至 $\begin{matrix} [0, π] \end{matrix}$ 和 $\begin{matrix} [- π, 0] \end{matrix}$ 两个区间上。定义h_{tan_max}、h_{tan_min}分别为关节变量θ 在单一象限内所对应tanθ 的最大值与最小值, $\begin{matrix} [θ'_{\min_U}, θ'_{\max_U}] \end{matrix}$ 、 $\begin{matrix} [θ'_{\min_L}, θ'_{\max_L}] \end{matrix}$ 分别为关节θ '在 $\begin{matrix} [0, π] \end{matrix}$ 和 $\begin{matrix} [- π, 0] \end{matrix}$ 区间上的分量。

若a_nsinϕ +b_ncosϕ +c_n≠ 0, 则求解关节i在第K $\begin{matrix} (K = I, II, II, IV) \end{matrix}$ 象限内关节活动范围对应的臂角有效范围问题等效为求解不等式:

(I): $\begin{matrix} \{\begin{matrix} a_{n} sinϕ + b_{n} cosϕ + c_{n} > 0 \\ A_{1} \sin (ϕ + φ_{1}) + C_{1} \leq 0 \\ A_{2} \sin (ϕ + φ_{2}) + C_{2} \geq 0 \end{matrix} \end{matrix}$

θ '∈ $\begin{matrix} [θ'_{\min_U}, θ'_{\max_U}] \end{matrix}$

和

(II): $\begin{matrix} \{\begin{matrix} a_{n} sinϕ + b_{n} cosϕ + c_{n} < 0 \\ A_{1} \sin (ϕ + φ_{1}) + C_{1} \geq 0 \\ A_{2} \sin (ϕ + φ_{2}) + C_{2} \leq 0 \end{matrix} \end{matrix}$

θ '∈ $\begin{matrix} [θ'_{\min_L}, θ'_{\max_L}] \end{matrix}$

式中:

A₁= $\begin{matrix} \sqrt[]{(a_{m} - h_{\tan_\max} a_{n})^{2} + (b_{m} - h_{\tan_\max} b_{n})^{2}} \end{matrix}$ ,

A₂= $\begin{matrix} \sqrt[]{(a_{m} - h_{\tan_\min} a_{n})^{2} + (b_{m} - h_{\tan_\min} b_{n})^{2}} \end{matrix}$ ,

C₁=c_m-h_{tan_max}c_n, C₂=c_m-h_{tan_min}c_n,

φ ₁=arctan2 $\begin{matrix} (b_{m} - h_{\tan_\max} b_{n}, a_{m} - h_{\tan_\max} a_{n}) \end{matrix}$ ,

φ ₂=arctan2 $\begin{matrix} (b_{m} - h_{\tan_\min} b_{n}, a_{m} - h_{\tan_\min} a_{n}) \end{matrix}$ 。

设上述不等式I与不等式II对应的解集分别为 $\begin{matrix} Ψ_{i_K}^{U} \end{matrix}$ 和 $\begin{matrix} Ψ_{i_K}^{L} \end{matrix}$ , 则关节i对应的臂角有效范围表示为:

$\begin{matrix} Ψ_{i} = (\overset{IV}{⋃_{K = I}} Ψ_{i_K}^{U}) ⋃ (\overset{IV}{⋃_{K = I}} Ψ_{i_K}^{L}) (15) \end{matrix}$

若a_nsinϕ +b_ncosϕ +c_n=0, 则关节角θ _i为常数, 机械臂处于奇异位型, Ψ _i= $\begin{matrix} [- π, π] \end{matrix}$ 。

3.3 公共臂角计算

根据方程(14)(15)可知, θ ₂会影响肩部关节变量θ ₁、θ ₃与臂角有效范围的关系, 即肩部3个关节与臂角有效范围之间存在耦合关系。设sinθ ₂≥ 0时, 肩部3个关节对应的臂角ϕ 的有效范围分别为 $\begin{matrix} Ψ_{1}^{+} \end{matrix}$ 、 $\begin{matrix} Ψ_{2}^{+} \end{matrix}$ 和 $\begin{matrix} Ψ_{3}^{+} \end{matrix}$ ; sinθ ₂< 0时, 肩部3个关节对应的臂角有效范围分别为 $\begin{matrix} Ψ_{1}^{-} \end{matrix}$ 、 $\begin{matrix} Ψ_{2}^{-} \end{matrix}$ 和 $\begin{matrix} Ψ_{3}^{-} \end{matrix}$ , 则肩部3个关节对应的臂角有效范围Ψ _S可以表示为:

$\begin{matrix} \begin{matrix} Ψ_{S} = (\overset{3}{⋂_{i = 1}} Ψ_{i}^{+}) ⋃ (\overset{3}{⋂_{i = 1}} Ψ_{i}^{-}) = \\ (Ψ_{1}^{+} ⋂ (\overset{IV}{⋃_{K = I}} Ψ_{2_K}^{U}) ⋂ \\ (\overset{IV}{⋃_{K = I}} Ψ_{3_K}^{U})) ⋃ (Ψ_{1}^{-} ⋂ (\overset{IV}{⋃_{K = I}} Ψ_{2_K}^{L}) ⋂ (\overset{IV}{⋃_{K = I}} Ψ_{3_K}^{L})) \end{matrix} \end{matrix}$

同理, 腕部3个关节对应的臂角有效范围可以表示为:

$\begin{matrix} \begin{matrix} Ψ_{W} = (\overset{7}{⋂_{i = 5}} Ψ_{i}^{+}) ⋃ (\overset{7}{⋂_{i = 5}} Ψ_{i}^{-}) = \\ (Ψ_{5}^{+} ⋂ (\overset{IV}{⋃_{K = I}} Ψ_{6_K}^{U}) ⋂ \\ (\overset{IV}{⋃_{K = I}} Ψ_{7_K}^{U})) ⋃ (Ψ_{1}^{-} ⋂ (\overset{IV}{⋃_{K = I}} Ψ_{6_K}^{L}) ⋂ (\overset{IV}{⋃_{K = I}} Ψ_{7_K}^{L})) \end{matrix} \end{matrix}$

因此, 对应机械臂期望的末端位姿点, 臂角的有效范围Ψ 可以表示为

$\begin{matrix} Ψ = Ψ_{S} ⋂ Ψ_{W} (16) \end{matrix}$

4 运动学优化

对应工作空间内机械臂末端的一个期望位姿, 给定任意臂角ϕ ∈ Ψ , 即可根据逆运动学封闭解方程确定机械臂各关节角度。由于机械臂关节处于远离关节限位时具有较好的操作能力, 而臂角ϕ 与关节θ 映射关系非常复杂, 如何在臂角有效范围内确定最优的臂角值以避开关节限位, 显得非常必要。

机械臂避关节限位的运动优化问题通常等效为远离关节限位的运动优化问题, 即运动优化过程中, 关节位置距离极限位置越远, 关节位置的适应度越高。这种评价指标计算量大, 并且影响其他任务的优化效果。针对这一弊端, 本文在传统人工势场的基础上, 将关节活动范围划分为工作区和危险区, 将关节极限位置视为“ 斥力源” 。危险区与关节极限位置相连, 该区域内的关节位置与关节极限位置之间的距离均小于预设的安全阈值, 关节位置会受到远离关节限位的斥力作用, 且距离极限位置越近, 斥力作用越显著。在关节危险区内需要进行避关节限位的运动优化。而工作区内的关节位置距离关节限位均大于预设的安全裕度, 关节位置不受虚拟力作用, 无需进行运动优化。关节活动范围划分方式如图3所示。

	Figure Option View Download New Window
	图3 关节工作区与危险区Fig.3 Workable space and danger space of joint

在此基础上, 本文将关节活动范围内关节位置的评价指标等效为虚拟转矩, 其函数形式表示为:

$\begin{matrix} M_{i} = \{\begin{matrix} \frac{(θ_{i_\max} - θ_{i}) - ρ_{U, i}}{ρ_{U, i}}, (θ_{i_\max} - θ_{i}) < ρ_{U, i} \\ 0, (θ_{i_\min} + ρ_{L, i}) \leq θ_{i} \leq (θ_{i_\max} - ρ_{U, i}) \\ \frac{ρ_{L, i} - (θ_{i} - θ_{i_\min})}{ρ_{L, i}}, (θ_{i} - θ_{i_\min}) < ρ_{L, i} \end{matrix} \end{matrix}$

式中:ρ _L_,_i为关节i的工作区下边界距离关节活动范围下限的距离; ρ _U_,_i为关节i的工作区上边界距离关节活动上限的距离。

实质上, ρ _L_,_i和ρ _U_,_i代表机械臂关节运动优化的安全裕度。ρ _L_,_i和ρ _U_,_i的取值需要根据机械臂操作任务、工作环境及关节活动范围等因素综合确定。例如, 关节运动速度较大、关节活动范围较大或运动优化任务较少时, 安全裕度可以取较大值, 反之, 则应该取较小值。

对于7R仿人机械臂, 由于肘部关节(第4关节)不参与机械臂的自运动, 因此, 机械臂运动优化过程中不考虑肘部关节的影响。综合其他各关节对应的虚拟转矩, 机械臂在基坐标系中的等效转矩M及其沿 $\begin{matrix} \vec{SW} \end{matrix}$ 方向上的等效转矩M_eq分别表示为:

$\begin{matrix} \begin{matrix} M = ({\sum_{i = 1, 2, 3, 5, 6, 7}}_{}^{0} R_{i} {[00 k_{i} M_{i}]}^{T}) / (\overset{3}{\sum_{i = 1}} k_{i} + \overset{7}{\sum_{i = 5}} k_{i}) \\ M_{eq} = ‖ M ‖ cosγ \end{matrix} \end{matrix}$

式中:γ 为 $\begin{matrix} \vec{SW} \end{matrix}$ 与向量M之间的夹角; k_i为关节i的加权系数, 通常0≤ k_i≤ 1, k_i的相对取值越大, 则关节i的优化程度越高, 如k_i=0, 则不针对关节i进行优化。

机械臂在等效转矩M_eq驱动下, 臂角ϕ 会向着 $\begin{matrix} |M_{eq}| \end{matrix}$ 减小的方向变化。由于虚拟转矩是在避关节限位的过程中产生的, $\begin{matrix} |M_{eq}| \end{matrix}$ 减小的过程实质是机械臂避关节限位的优化过程。设期望的允许误差值为M_err≥ 0, 通过数值迭代方式, 当 $\begin{matrix} |M_{eq}| \end{matrix}$ ≤ M_err时, 机械臂结束运动优化过程。这种在虚拟转矩驱动下通过机械臂自运动实现的运动优化方法称作自寻优方法。

设当前臂角值及下一时刻的臂角值分别为ϕ $\begin{matrix} (k) \end{matrix}$ 和ϕ $\begin{matrix} (k + 1) \end{matrix}$ , 则自寻优方法的数值迭代过程具体表现为:

ϕ $\begin{matrix} (k + 1) \end{matrix}$ =ϕ $\begin{matrix} (k) \end{matrix}$ +λ M_eq

式中:λ > 0为优化步长或优化速率, λ 越小, 运动优化速度越慢, 数值稳定性也越好。

5 运动仿真与验证

为了验证上述逆运动学方法的有效性, 本文以哈尔滨工业大学自主研制的7R仿人机械臂为研究对象, 通过数值仿真加以验证。

5.1 参数化封闭解验证

在关节活动范围内任选一组关节解, 则对应的机械臂末端位置 $\begin{matrix} _{}^{0} \end{matrix}$ P₇与姿态 $\begin{matrix} _{}^{0} \end{matrix}$ R₇可根据正运动学方程来确定。

$\begin{matrix} _{}^{0} \end{matrix}$ P₇= $\begin{matrix} [\begin{matrix} 0.4754 & 0.4131 & 0.4312 \end{matrix}] \end{matrix} \begin{matrix} (m) \end{matrix}$

$\begin{matrix} _{}^{0} \end{matrix}$ R₇= $\begin{matrix} [\begin{matrix} 0.5789 & - 0.8153 & - 0.0129 \\ - 0.5653 & - 0.4127 & 0.7143 \\ - 0.5876 & - 0.4063 & - 0.6998 \end{matrix}] \end{matrix}$

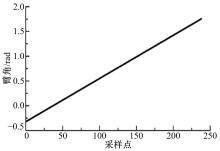
不考虑关节限位, 任取一个臂角ϕ =π /10 $\begin{matrix} (rad) \end{matrix}$ , 由逆运动学封闭解方程可以得到8组可行解, 如表2所示。每组可行解所对应的机械臂实际末端位姿可由正运动学方程(1)确定。经计算, 8组可行解所对应的实际末端位姿与期望位姿之间的绝对误差均小于1× 10^-10, 从而验证了所得逆运动学封闭解算法的正确性。

表2 运动学逆解 Table 2 Inverse kinematic solutions (rad)

5.2 臂角有效范围验证

对应上述 $\begin{matrix} _{}^{0} \end{matrix}$ R₇与 $\begin{matrix} _{}^{0} \end{matrix}$ P₇, 根据各关节的活动范围, 计算得到肩关节与腕关节的公共臂角分别为:

Ψ _S= $\begin{matrix} [- π, - 2.4946] \end{matrix}$ ∪ $\begin{matrix} [- 0.3205, π] \end{matrix} \begin{matrix} (rad) \end{matrix}$

Ψ _W= $\begin{matrix} [- 0.3205, 1.7608] \end{matrix} \begin{matrix} (rad) \end{matrix}$

则机械臂整体的臂角有效范围为:

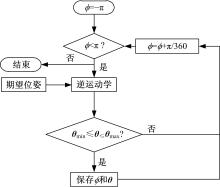
$\begin{matrix} Ψ = Ψ_{S} ⋂ Ψ_{W} = [- 0.3205, 1.7608] (rad) (17) \end{matrix}$

为了验证所得结果的正确性, 本文采用数值方法获得臂角ϕ 与逆运动学可行解之间的关系, 具体计算流程如图4所示。所得臂角的有效范围如图5所示。可以发现, 式(17)表示的臂角有效范围与图5所示结果完全一致, 从而验证了本文方法的有效性。

	Figure Option View Download New Window
	图4 臂角计算流程图Fig.4 Flow chart of computations for arm angle

	Figure Option View Download New Window
	图5 可行臂角范围Fig.5 Range of feasible arm angle

5.3 机械臂运动优化验证

考虑机械臂各关节限位, 从表2所示运动学逆解中任取一组可行解θ _init, 采用自寻优方法进行避关节限位的运动优化。

θ _init= $\begin{matrix} [\begin{matrix} 3.1410 & 2.6193 & 2.6277 & 1.0472 \end{matrix} \end{matrix}$

$\begin{matrix} \begin{matrix} - 0.4907 & 1.3159 & 1.3105 \end{matrix}] \end{matrix} \begin{matrix} (rad) \end{matrix}$

鉴于机械臂关节活动范围较大, 各关节的安全裕度设置为同一值, 即ρ _U=ρ _L=π /6 $\begin{matrix} (rad) \end{matrix}$ 。此外, 定义运动优化过程中各关节权重相同, 即k_i=1 $\begin{matrix} (i = 1, 2, 3, 5, 6, 7) \end{matrix}$ , 优化步长与允许误差分别设置为:λ =0.5, M_err=0.005。

在此基础上, 以θ _init为初始状态, 采用自寻优方法, 经过26步迭代计算, 最终完成机械臂的运动优化。优化后的运动学逆解为:

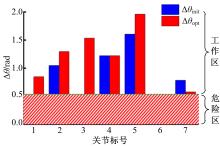
θ _opt= $\begin{matrix} [\begin{matrix} - 0.1996 & - 2.5156 & - 1.0113 & 1.0472 \end{matrix} \end{matrix}$

$\begin{matrix} \begin{matrix} - 0.1360 & 1.2512 & 1.5182 \end{matrix}] \end{matrix} \begin{matrix} (rad) \end{matrix}$

在此基础上, 根据式(18)分别计算初始解θ _init、优化解θ _opt与关节极限位置之间的最小距离Δ θ , 计算结果如图6所示。

$\begin{matrix} Δ θ_{i} = \min (|θ_{i} - θ_{i_\max}|, |θ_{i} - θ_{i_\min}|) (18) \end{matrix}$

Δ θ _init= $\begin{matrix} [\begin{matrix} 0.0006 & 1.0485 & 0.0097 & 1.2217 \end{matrix} \end{matrix}$

$\begin{matrix} \begin{matrix} 1.6037 & 0.2549 & 0.7839 \end{matrix}] \end{matrix} \begin{matrix} (rad) \end{matrix}$

Δ θ _opt= $\begin{matrix} [\begin{matrix} 0.8476 & 1.2939 & 1.5349 & 1.2217 \end{matrix} \end{matrix}$

$\begin{matrix} \begin{matrix} 1.9584 & 0.3196 & 0.5762 \end{matrix}] \end{matrix} \begin{matrix} (rad) \end{matrix}$

	Figure Option View Download New Window
	图6 初始解与优化解性能评价Fig.6 Evaluations of initial solutions and optimal solutions

对比Δ θ _init和Δ θ _opt, 可以得出如下结论:

(1)机械臂位于初始位形时, 关节1、关节3均位于关节活动范围的危险区, 且关节位置距离极限位置较近。采用自寻优方法完成运动优化之后, 关节1、关节3均由关节危险区转化至关节工作区, 且距离关节极限位置较远。

(2)优化后的关节2、关节5仍处于关节工作区, 并且与初始解相比, 优化解至关节限位的距离变大。

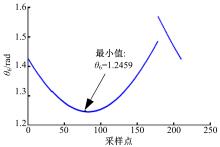
(3)在运动优化前、后, 关节6都位于关节危险区, 但与初始解相比, 优化解至关节限位的距离有所增加。由图4计算流程可以得到对应该末端位姿的关节6的全部可行解, 且关节最小值(θ ₆=1.2459 rad)至关节限位的距离最大, 如图7所示。由于优化后的关节位置非常接近关节6的最小值, 因此, 优化后的关节6已实现最大程度的避关节限位的优化。

	Figure Option View Download New Window
	图7 关节6的全部可行解Fig.7 Feasible angles of 6th joint

(4)与初始解相比, 优化后的关节7至关节限位的距离有所减小, 这是为了实现关节6的避极限目标所进行的折中。但是, 优化后的关节7仍处于关节工作区内, 并且该关节的工作性能未受影响。

(5)关节4不参与机械臂的自运动, 因此在运动优化过程中, 关节4的位置保持不变。

综上可以看出, 自寻优方法有效地实现了7R仿人机械臂避关节限位的运动优化。

6 结论

(1)建立了基于臂角参数的7R仿人机械臂逆运动学封闭解。引入双变量反正切函数, 简化了计算过程中逆解的判断过程, 避免了可行解的丢失。

(2)建立了关节限位约束下臂角有效范围的求解方法。与现有方法相比, 避免了复杂的函数求导运算, 简化了计算过程。

(3)构建了一种新的避关节限位的评价指标, 并提出一种自寻优方法, 可以快速有效地实现仿人机械臂的运动优化。

The authors have declared that no competing interests exist.

参考文献

View Option

[1]	Shimizu M, Kakuya H, Yoon W K, et al. Analytical inverse kinematic computation for 7-DOF redundant manipulators with joint limits and its application to redundancy resolution[J]. IEEE Transactions on Robotics, 2008, 24(5): 1131-1142. [本文引用:2]
[2]	Chan T F, Dubey R V. A weighted least-norm solution based scheme for avoiding joint limits for redundant joint manipulators[J]. IEEE Transactions on Robotics and Automation, 1995, 11(2): 286-292. [本文引用:1]
[3]	孙奎, 谢宗武, 黄建斌, 等. 基于连续比例因子的冗余度机器人梯度投影算法[J]. 吉林大学学报: 工学版, 2009, 39(5): 1257-1261. Sun Kui, Xie Zong-wu, Huang Jian-bin, et al. Gradient projection method of kinematic redundant manipulator based on continues scale factor[J]. Journal of Jilin University (Engineering and Technology Edition), 2009, 39(5): 1257-1261. [本文引用:1]
[4]	吴伟国. 冗余度机器人运动学基本理论与七自由度仿人手臂的研究[D]. 哈尔滨: 哈尔滨工业大学, 1995. Wu Wei-guo. Study of the redundant freedom robot kinematics basic theory and the seven degree-of-freedom bionics arm[D]. Harbin: Harbin Institute of Technology, 1995. [本文引用:1]
[5]	Moradi H, Lee S. Joint Limit Analysis and Elbow Movement Minimization for Redundant Manipulators Using Closed form Method[M]. Advances in Intelligent Computing, Berlin, Heidelberg: Springer, 2005: 423-432. [本文引用:1]
[6]	陈鹏, 刘璐, 余飞, 等. 一种仿人机械臂的运动学逆解的几何求解方法[J]. 机器人, 2012, 34(2): 211-216. Chen Peng, Liu Lu, Yu Fei, et al. A geometrical method for inverse kinematics of a kind of humanoid manipulator[J]. Robot, 2012, 34(2): 211-216. [本文引用:1]
[7]	Wang P, Li D, Zhang D, et al. Practical algorithm for solving real time inverse kinematics of industrial 7R robot[C]∥IEEE International Conference on Automation and Logistics, China: Inst of Elec and Elec Eng Computer Society, 2007: 1963-1967. [本文引用:1]
[8]	Huang H C, Chen C P, Wang P R. Particle swarm optimization for solving the inverse kinematics of 7-DOF robotic manipulators[C]∥IEEE International Conference on Systems, Man, and Cybernetics, Seoul, 2012: 3105-3110. [本文引用:1]
[9]	周友行, 何清华, 邓伯禄. 一种改进的爬山法优化求解冗余机械手运动学逆解[J]. 机器人, 2003, 25(1): 35-38. Zhou You-hang, He Qing-hua, Deng Bo-lu. An ameliorative “mountain climbing” arithmetic to solve inverse kinematics of redundant manipulator[J]. Robot, 2003, 25(1): 35-38. [本文引用:1]
[10]	Assal S F M, Watanabe K, Izumi K. Neural network-based kinematic inversion of industrial redundant robots using cooperative fuzzy hint for the joint limits avoidance[J]. IEEE/ASME Transactions on Mechatronics, 2006, 11(5): 593-603. [本文引用:1]
[11]	祖迪, 吴镇炜, 谈大龙. 一种冗余机器人逆运动学求解的有效方法[J]. 机械工程学报, 2005, 41(6): 71-75. Zu Di, Wu Zhen-wei, Tan Da-long. Efficient inverse kinematic solution for redundant manipulators[J]. Chinese Journal of Mechanical Engineering, 2005, 41(6): 71-75. [本文引用:1]
[12]	Park S S, Chung W K. Combined method of weighted least norm and gradient projection for avoiding joint limit[C]∥The 8th International Conference on Ubiquitous Robots and Ambient Intelligence, Incheon, 2011: 798-799. [本文引用:1]

2008

0.0

... 由于机械结构的限制和仿人特性的要求,机械臂各关节的运动范围都会受到一定程度的限制^[1] ...

... 前者是通过引入一个附加参数(如参数化关节^[4]、臂角^[1]等),建立机械臂逆运动学的参数化解析解,在此基础上采用代数法或搜索算法完成运动优化任务^[5,6] ...

1995

0.0

... 七自由度机械臂运动优化方法很多,其中,微分逆运动方法是将运动优化任务投影到雅克比矩阵零空间,在速度/加速度水平实现的运动控制方法^[2,3] ...

2009

0.0

. 2009, 39(5):1257-1261

Gradient projection method of kinematic redundant manipulator based on continues scale factor

基于连续比例因子的冗余度机器人梯度投影算法

Sun Kui , Xie Zong-wu , Huang Jian-bin

孙奎, 谢宗武, 黄建斌

1.Robot Research Institute, Harbin Institute of Technology, Heilongjiang, Harbin, 150080, China；2.Institute of Robotics and Mechatronics, German Aerospace Center, DLR, 82230 Wessling, Germany

The status of gradient projection method of redundant manipulator is analysed, the effect and selection methods of the scale factor of the homogeneous solution is expatiated. A new method to calculate the scale factor is proposed which will make it changed continuously in real time. Computer simulation has been conducted to compare the new scheme with the other two typical ones, the results show that the new algorithm with the continuous scale factor can make the joints angle, joints velocity and joints acceleration of the manipulator more smoothly and continuously, it also can overcome the shortcoming of two traditional gradient projection methods. Experiment results with a 4 DOF manipulator verify the validity of the proposed algorithm.

分析了冗余度机器人梯度投影法的研究现状，阐述了齐次解的比例因子的作用及其选择方法，提出了一种实时连续变化的比例因子计算方法。通过计算机仿真将所提出的逆运动学解方案同两个典型方案进行了比较。仿真结果表明，所提出的连续比例因子算法可以使机器人各关节角、角速度和角加速度的变化更加平滑和连续，克服了两种传统梯度投影法的缺陷。最后利用4自由度机械臂进行了实验，证明了算法的有效性。

... 七自由度机械臂运动优化方法很多,其中,微分逆运动方法是将运动优化任务投影到雅克比矩阵零空间,在速度/加速度水平实现的运动控制方法^[2,3] ...

1995

0.0

2005

0.0

2012

0.0

2007

0.0

... 数值方法是采用迭代法^[7]或智能算法^[8,9]在运动方程约束下对二次优化任务进行求解 ...

2012

0.0

... 数值方法是采用迭代法^[7]或智能算法^[8,9]在运动方程约束下对二次优化任务进行求解 ...

2003

0.0

... 数值方法是采用迭代法^[7]或智能算法^[8,9]在运动方程约束下对二次优化任务进行求解 ...

2006

0.0

... 人工神经网络^[10]凭借其较强的并行计算与数值逼近能力常用于解决机械臂的运动优化问题,但该方法计算精度较低,不适用于精细任务操作 ...

2005

0.0

... 此外,由上述不同方法组合而成的混合算法也常用于解决机械臂运动优化问题,以弥补单一方法的不足^[11,12] ...

2011

0.0

... 此外,由上述不同方法组合而成的混合算法也常用于解决机械臂运动优化问题,以弥补单一方法的不足^[11,12] ...