基于无迹卡尔曼滤波的轮毂电机驱动车辆状态观测

引用本文

宋传学, 肖峰, 刘思含, 李少坤, 段亮, 彭思仑. 基于无迹卡尔曼滤波的轮毂电机驱动车辆状态观测.吉林大学学报:工学版, 2016, 46(2): 333-339
SONG Chuan-xue, XIAO Feng, LIU Si-han, LI Shao-kun, DUAN Liang, PENG Si-lun. State estimation of electric vehicle with in-wheel motors based on UKF. Journal of Jilin University Engineering and Technology Edition, 2016, 46(2): 333-339 复制到剪切板

Permissions

基于无迹卡尔曼滤波的轮毂电机驱动车辆状态观测

宋传学¹, 肖峰¹, 刘思含², 李少坤¹, 段亮¹, 彭思仑¹

1.吉林大学汽车仿真与控制国家重点实验室,长春 130022

2.吉林大学机械科学与工程学院,长春 130022

通讯作者:彭思仑(1987-),男,工程师.研究方向:汽车系统动力学.E-mail:pengsilun@126.com

作者简介:宋传学(1959-),男,教授,博士生导师.研究方向:汽车系统动力学.E-mail:songchx@126.com

基金:科技部国际合作计划项目(2010DFB83650)

摘要

针对车辆质心(CG)侧偏角和轮胎附着力等参数无法用传感器直接测量得到的情况,本文设计了一种基于无迹卡尔曼滤波的车辆状态观测器.该方法考虑了车辆运行工况变化时的非线性因素,引入了非线性动态轮胎模型来提高轮胎侧向力的估算精度.与动力学软件AMESim建立的参考模型进行了对比仿真,仿真结果表明:本文建立的观测器能够准确估算出轮毂电机驱动汽车的状态参数.

关键词: 车辆工程; 轮毂电机驱动汽车; 状态观测; 无迹卡尔曼滤波

中图分类号:U461 文献标志码:A 文章编号:1671-5497(2016)02-0333-07

State estimation of electric vehicle with in-wheel motors based on UKF

SONG Chuan-xue¹, XIAO Feng¹, LIU Si-han², LI Shao-kun¹, DUAN Liang¹, PENG Si-lun¹

1.State Key Laboratory of Automotive Simulation and Control, Jilin University, Changchun 130022, China

2.College of Mechanical Science and Engineering, Jilin University, Changchun 130022, China

Abstract

For four-wheel independently drive in-wheel motors electric vehicle, the dynamic control systems, such as direct yaw moment control, can be easily achieved. Accurate estimation of vehicle state variables and uncertain parameters can improve the robustness of the vehicle dynamic control system. Various sensors are generally equipped to acquire the vehicle dynamics. For both technical and economic reasons, some fundamental vehicle parameters, such as the sideslip angle and tire-road forces can hardly be obtained directly by sensors. Therefore, a state observer is developed to estimate these parameters based on Unscented Kalman Filter (UKF). In addition, a nonlinear dynamics tire model is utilized to improve the accuracy of tire lateral force estimation. Compared to the reference model built in AMEsim, the simulation results show that the proposed observer can provide the precision values of the vehicle state.

Keyword: vehicle engineering; in-wheel-motor vehicle; state estimation; unscented kalman filter

Show Figures

0 引言

随着科技的进步, 电动汽车的驱动系统也在不断的发展革新, 基于轮毂电机驱动的四轮独立驱动电动汽车就是一种突破性的驱动结构形式^[1].轮毂电机驱动电动汽车可以通过对4个车轮的驱动转矩进行独立控制来实现车辆的直接横摆力矩控制(DYC).由于电机具有响应快, 控制精度高等特点, 相对于主动制动的DYC系统, 轮毂电机驱动汽车的的DYC更容易实现^{[2, 3]}.对于轮毂电机驱动汽车的DYC, 通常选择横摆角速度与质心侧偏角为受控对象, 而4个电机的驱动转矩可以作为控制输入量, 所以控制系统的输入有4个, 因此轮毂电机的DYC系统可以看成一种过自由度控制系统.过自由度控制系统能够合理地分配电机转矩, 充分利用轮胎的附着极限, 避免出现车轮滑动或抱死的现象^[4].

实时而准确地获得状态变量是DYC系统研究的关键, 它能够帮助控制单元确定控制系统的控制目标, 作出合理的判断.但是由于经济, 技术等条件的限制, 质心侧偏角, 轮胎侧偏力主要通过建立观测器估算获得.建立车辆状态观测器需要考虑车辆模型的非线性因素以及车辆参数不断变化的问题, 尤其轮胎的非线性力学特性使车辆的状态在非线性区间转弯时变化非常剧烈.车辆是一个非线性系统, 因此车辆状态参数的预测多采用滑模观测, 鲁棒观测和卡尔曼滤波等算法.其中, 扩展卡尔曼滤波(EKF)应用最为广泛, 常见于对轮胎模型的辨识^{[5, 6]}.但是在实际应用中, 由于EKF主要是通过泰勒展开将非线性系统近似线性化, 引入了截断误差, 使参数的估计难以达到理想的高精度, 此外扩展卡尔曼滤波器中的Jacobian矩阵计算起来非常复杂.为了克服EKF的缺点, 牛津大学的Julier等^[7]建立了无迹卡尔曼滤波(UKF)算法.无迹卡尔曼滤波是一种基于确定性采样进行变量估计的新型卡尔曼滤波器, 它的非线性性能优于卡尔曼滤波器.有学者应用UKF对车辆的轮胎侧向力, 车速等状态参数进行了估计并与EKF观测器进行了对比^{[8, 9, 10]}.但应用UKF对轮毂电机驱动汽车的状态参数进行估计的研究还比较少.基于此, 本文针对轮毂电机驱动车辆多信息源的特点, 应用UKF算法为其设计状态观测器, 并引入了非线性动态轮胎模型, 提高轮胎侧向力的估算精度.最后, 本文通过仿真试验验证了所提出的观测算法的准确性.

1 动力学模型

1.1 车辆模型

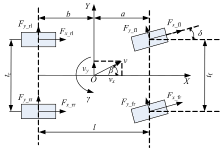
估算模型采用具有纵向, 侧向和横摆运动的三自由度双轨车辆模型.该模型可以模拟匀速转弯, 弯道加速/制动等复杂工况, 并且计算速度较快, 如图1所示.根据牛顿力学建立x、y、z三个方向上力的平衡方程:

$a_{x} = {\overset{\cdot}{v}}_{x} - r v_{y}$ (1)

$a_{y} = {\overset{\cdot}{v}}_{y} - r v_{x}$ (2)

$I_{z} \overset{\cdot}{γ} = M_{z}$ (3)

$\begin{matrix} \begin{matrix} M_{z} = a (F_{x_{-} fl} sinδ + F_{y_{-} fl} cosδ + \\ F_{x_{-} f r} sinδ + F_{y_{-} fr} cosδ) - \\ \frac{t_{f}}{2} (F_{x_{-} fr} cosδ - F_{y_{-} fr} sinδ - \\ F_{x_{-} fl} cosδ + F_{y_{-} fl} sinδ) - \\ b (F_{y - rl} + F_{y - rr}) + \frac{t_{r}}{2} (F_{x - rr} - F_{x - rl}) \end{matrix} \end{matrix}$ (4)

式中: $\begin{matrix} v_{x} \end{matrix}$ 为纵向车速; $\begin{matrix} v_{y} \end{matrix}$ 为侧向车速; $\begin{matrix} γ \end{matrix}$ 为横摆角速度; $\begin{matrix} a_{x} \end{matrix}$ 为纵向加速度; $\begin{matrix} a_{y} \end{matrix}$ 为侧向加速度; $\begin{matrix} a 、 b \end{matrix}$ 分别为质心至前, 后轴的距离; $\begin{matrix} t_{f} 、 t_{r} \end{matrix}$ 分别为前, 后轮距; $\begin{matrix} F_{x_ij} \end{matrix}$ 为纵向力, $\begin{matrix} F_{y_ij} \end{matrix}$ 为侧向力, $\begin{matrix} ij = fl, fr, rl, rr \end{matrix}$ 分别代表左前轮, 右前轮, 左后轮, 右后轮; $\begin{matrix} M_{z} \end{matrix}$ 为横摆力矩; $\begin{matrix} δ \end{matrix}$ 为前轮转角.

车辆的侧偏角定义为:

$\begin{matrix} β = \arctan \frac{v_{y}}{v_{x}} \end{matrix}$ (5)

	Figure Option View Download New Window
	图1 车辆模型Fig.1 Vehicle model

1.2 车轮旋转动力学模型

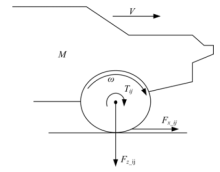
电动轮受力分析如图2所示.可以得出车轮旋转动力学方程为:

$\begin{matrix} (F_{x_ij} + F_{z_{-} ij} f_{ij}) r_{ij} = T_{ij} - J_{ij} {\overset{\cdot}{ω}}_{ij} \end{matrix}$ (6)

式中: $\begin{matrix} T_{ij} \end{matrix}$ 为各轮驱/制动力矩; $\begin{matrix} J_{ij} \end{matrix}$ 为各轮转动惯量; $\begin{matrix} ω_{ij} \end{matrix}$ 为各轮角速度; $\begin{matrix} F_{z_{-} ij} \end{matrix}$ 为各车轮的地面垂直载荷; $\begin{matrix} f_{ij} \end{matrix}$ 为各车轮的滚动阻力系数; $\begin{matrix} r_{ij} \end{matrix}$ 为车轮滚动半径.

	Figure Option View Download New Window
	图2 四分之一车辆模型Fig.2 Quarter vehicle model

由方程可以得到轮胎的纵向力为:

$\begin{matrix} F_{x_ij} = \frac{1}{r} (T_{ij} - J_{ij} {\overset{\cdot}{ω}}_{ij}) - F_{z_{-} ij} f_{ij} \end{matrix}$ (7)

轮胎垂直载荷可用下式表示:

$\begin{matrix} \{\begin{matrix} F_{z_{-} fl} = M (g \frac{a}{2 l} - a_{x} \frac{h_{g}}{2 l} - a_{y} \frac{h_{g} b}{t_{f} l}) \\ F_{z_{-} fr} = M (g \frac{b}{2 l} - a_{x} \frac{h_{g}}{2 l} - a_{y} \frac{h_{g} b}{t_{f} l}) \\ F_{z_{-} rl} = M (g \frac{a}{2 l} + a_{x} \frac{h_{g}}{2 l} - a_{y} \frac{h_{g} b}{t_{f} l}) \\ F_{z_{-} rr} = M (g \frac{b}{2 l} + a_{x} \frac{h_{g}}{2 l} + a_{y} \frac{h_{g} b}{t_{f} l}) \end{matrix} \end{matrix}$ (8)

式中: $\begin{matrix} h_{g} \end{matrix}$ 为质心高度.

1.3 轮胎模型

本文还需要选择合适的轮胎模型来进行侧向力估算.轮胎的侧向力受载荷, 胎压, 附着系数, 车速等多种因素影响.因此, 基于轮胎物理特性或者半经验公式的Pacejka模型, Dugoff模型等被建立来精确描述轮胎的力学特性^{[11, 12]}, 其中应用最广泛的就是Pacejka的魔术公式.但是由于魔术公式所需的参数太多, 而且有些参数不容易获得, 所以本文选择了另外一种Dugoff模型来估算轮胎侧偏力.

不考虑纵向力, 轮胎的侧偏力可用以下公式描述:

$\begin{matrix} F_{y_{-} ij} = - C_{ij} \tan α_{ij} f (λ) \end{matrix}$ (9)

式中: $\begin{matrix} C_{ij} \end{matrix}$ 为侧偏刚度; $\begin{matrix} α_{ij} \end{matrix}$ 为各车轮的侧偏角.

$α_{fl, fr} = - (δ - \arctan (\frac{v_{y} + aγ}{v_{x} \mp \frac{t_{f}}{2} γ}))$ (10)

$α_{rl, rr} = \arctan (\frac{v_{y} - bγ}{v_{x} \mp \frac{t_{r}}{2} γ})$ (11)

$\begin{matrix} f (λ) \end{matrix}$ 可用下式表示:

$\begin{matrix} f (λ) = \{\begin{matrix} (2 - λ) λ, ifλ < 1 \\ 1, ifλ \geq 1 \end{matrix} \end{matrix}$ (12)

式中: $\begin{matrix} λ = \frac{μ F_{z_ij}}{2 C_{ij} |\tan α_{i, j}|}; μ \end{matrix}$ 为路面附着系数.

原始Dugoff模型的刚度值是不随垂直载荷变化而变化的, 但是实际上载荷的转移会影响侧偏刚度的变化^[13], 所以侧偏刚度可以用一个以垂直载荷为变量的二阶多项式来表示:

$\begin{matrix} C_{y_ij} (F_{z}) = (m F_{z_ij} - n F_{z_ij}^{2}) \end{matrix}$ (13)

式中: $\begin{matrix} m 、 n \end{matrix}$ 分别为多项式的一阶和二阶系数.

侧偏刚度随着载荷的变化而变化, 可以修正Dugoff轮胎模型.

在瞬态工况下, 相对于侧偏角的变化, 轮胎侧偏力的产生会有一个迟滞效应, 这种瞬态特性可以引入一个松弛长度 $\begin{matrix} τ_{ij} \end{matrix}$ 来进行阐述^[14].轮胎动力学侧向力可以用下式来表示:

$\begin{matrix} {\overset{\cdot}{F}}_{y_{-} ij} = \frac{v}{τ_{ij}} (- F_{y_{-} ij} + {\bar{F}}_{y_{ij}}) \end{matrix}$ (14)

式中: $\begin{matrix} {\bar{F}}_{y_{-} ij} \end{matrix}$ 为Dugoff轮胎模型在准静态工况下的侧偏力.式(14)适用于在车速变化时对轮胎侧向力进行描述.

2 观测器设计

非线性系统的状态估计模型可以通过状态空间方程的形式来描述:

$\begin{matrix} \{\begin{matrix} \overset{\cdot}{x} (t) = f (x (t), u (t)) + w (t) \\ y (t) = h (x (t), u (t)) + v (t) \end{matrix} \end{matrix}$ (15)

$\begin{matrix} w (t) 、 v (t) \end{matrix}$ 分别为过程噪声和测量噪声, 符合Gaussian分布.

需要观测的状态变量包括纵向速度, 侧向速度, 横摆角速度和各车轮侧向力, 定义状态变量:

$\begin{matrix} \begin{matrix} x = {[x_{1} x_{2} x_{3} x_{4} x_{5} x_{6} x_{7}]}^{T} = \\ {[v_{x} v_{y} ω_{r} F_{x_fl} F_{x_fr} F_{x_rl} F_{x_rr}]}^{T} \end{matrix} \end{matrix}$ (16)

测量变量包括纵向加速度, 侧向加速度和横摆角速度, 定义测量变量 $\begin{matrix} y : \end{matrix}$

$\begin{matrix} y = {[y_{1} y_{2} y_{3}]}^{T} = {[ω_{r} a_{x} a_{y}]}^{T} \end{matrix}$ (17)

车轮的纵向力可以通过轮胎旋转动力学方程(6)计算得到, 由于驱动电机的力矩和转速能够精确得到, 所以认为车轮纵向力是已知的.定义状态方程的输入变量由前轮转角和各车轮纵向力组成:

$\begin{matrix} u = {[u_{1} u_{2} u_{3} u_{4} u_{5}]}^{T} = {[δ F_{x_fl} F_{x_fr} F_{x_rl} F_{x_rr}]}^{T} \end{matrix}$ (18)

观测器的状态方程表达式为:

$\begin{matrix} \{\begin{matrix} {\overset{\cdot}{x}}_{1} = [u_{2} \cos (u_{1}) - x_{4} \sin (u_{1}) + u_{3} \cos (u_{1}) - \\ x_{5} \sin (u_{1}) + u_{4} + u_{5} - F_{w}] / m + x_{3} x_{2} \\ {\overset{\cdot}{x}}_{2} = [u_{2} \sin (u_{1}) + x_{4} \cos (u_{1}) + u_{3} \sin (u_{1}) + \\ x_{5} \cos (u_{1}) + x_{6} + x_{7}] / m + x_{3} x_{1} \\ {\overset{\cdot}{x}}_{3} = \{a [u_{2} \sin (u_{1}) + x_{4} \cos (u_{1}) + \\ \begin{matrix} u_{3} \sin (u_{1}) - u_{5} \cos (u_{1})] - \frac{t_{f}}{2} [u_{3} \cos (u_{1}) - \\ x_{5} \sin (u_{1}) - u_{2} \cos (u_{1}) + x_{4} \sin (u_{1})] - \end{matrix} \\ b (x_{6} + x_{7}) + \frac{t_{r}}{2} (u_{5} - u_{4})} I_{z} \\ {\overset{\cdot}{x}}_{4} = \frac{v}{τ_{fl}} [- x_{4} + {\bar{F}}_{y_fl} (α_{fl}, F_{z_fl})] \\ {\overset{\cdot}{x}}_{5} = \frac{v}{τ_{fr}} [- x_{5} + {\bar{F}}_{y_fr} (α_{fr}, F_{z_fr})] \\ {\overset{\cdot}{x}}_{6} = \frac{v}{τ_{rl}} [- x_{6} + {\bar{F}}_{y_rl} (α_{rl}, F_{z_rl})] \\ {\overset{\cdot}{x}}_{7} = \frac{v}{τ_{rr}} [- x_{7} + {\bar{F}}_{y_rr} (α_{rr}, F_{z_rr})] \end{matrix} \end{matrix}$ (19)

测量方程表达式为:

$\begin{matrix} \begin{matrix} \{\begin{matrix} h_{1} = ω_{r} = x_{3} \\ h_{2} = a_{x} = u_{2} \cos (u_{1}) - x_{4} \sin (u_{1}) + \\ u_{3} \cos (u_{1}) - x_{5} \sin (u_{1}) + u_{4} + u_{5} - F_{w} \\ h_{3} = a_{y} = u_{2} \sin (u_{1}) + x_{4} \cos (u_{1}) + \\ u_{3} \sin (u_{1}) + x_{5} \cos (u_{1}) + x_{6} + x_{7} \end{matrix} \end{matrix} \end{matrix}$ (20)

状态变量将应用UKF技术进行估计.

3 UKF滤波器设计

UKF是在卡尔曼滤波框架下运用采样方法来近似非线性函数, 因为近似非线性函数的概率密度分布比近似非线性函数更容易.UT变换是UKF的核心思想, 它采用固定数量的参数去近似一个高斯分布, 即在原状态分布中按某一规则取一些点, 使这些点的均值和协方差等于原状态分布的均值和协方差, 然后将这些点代入非线性函数中, 得到相应非线性函数值点集, 通过这些点集求取变换后的均值和协方差.利用UKF估计轮毂电机驱动车辆状态的步骤如下:

(1)状态方程离散化.将状态方程式(15)离散化后得到的离散状态方程如下所示:

$\begin{matrix} \{\begin{matrix} x_{k + 1} = f (x_{k}, u_{k}) + w_{k} \\ y_{k} = h (x_{k}, u_{k}) + v_{k} \end{matrix} \end{matrix}$ (21)

式中: $\begin{matrix} x_{k} \end{matrix}$ 为 $\begin{matrix} k \end{matrix}$ 时刻的状态矢量; $\begin{matrix} u_{k} \end{matrix}$ 为输入矢量; $\begin{matrix} y_{k} \end{matrix}$ 为输出矢量; 过程噪声 $\begin{matrix} w_{k} \end{matrix}$ 的协方差为Q测量噪声 $\begin{matrix} v_{k} \end{matrix}$ 的协方差为R; w_k与 $\begin{matrix} v_{k} \end{matrix}$ 的互协方差为0; Q, R均为对称正定矩阵.

(2)初始化滤波器

考虑系统噪声和测量噪声, 定义扩展矢量 $\begin{matrix} x_{k}^{a} = {[\begin{matrix} x_{k} & w_{k} & v_{k} \end{matrix}]}^{T}, \end{matrix}$ 初始条件满足:

$\begin{matrix} \{\begin{matrix} {\bar{x}}_{0} = E (x_{0}) \\ P_{0} = E [(x_{0} - {\bar{x}}_{0}) (x_{0} - {\bar{x}}_{0})^{T}] \\ {\bar{x}}_{0}^{a} = E [x^{a}] = [{\bar{x}}^{T}_{0} {00]}^{T} \\ P_{0}^{a} = E [(x_{0}^{a} - {\bar{x}}_{0}^{a}) (x_{0}^{a} - {\bar{x}}_{0}^{a})^{T}] \end{matrix} \end{matrix}$ (22)

(3)Sigma点采样

$\begin{matrix} \{\begin{matrix} χ_{0, k | k}^{a} = {\bar{x}}_{k | k}^{a} \\ χ_{i, k | k}^{a} = {\bar{x}}_{k | k}^{a} + \sqrt[]{(n_{a} + λ) P_{k | k}^{a}}, \\ i = 1, \dots, n \\ χ_{i, k | k}^{a} = {\bar{x}}_{k | k}^{a} - \sqrt[]{(n_{a} + λ) P_{k | k}^{a}}, \\ i = n + 1, \dots, 2 n \end{matrix} \end{matrix}$ (23)

Sigma点权值:

$\begin{matrix} \{\begin{matrix} W_{0}^{(m)} = λ / (n_{a} + λ) \\ W_{0}^{(c)} = λ / (n_{a} + λ) + (1 - α^{2} + β_{t}) \\ W_{i}^{(m)} = W_{i}^{(c)} = 1 / 2 (n_{a} + λ) \\ i = 1, \dots, 2 n \end{matrix} \end{matrix}$ (24)

式中: $\begin{matrix} n_{a} = 2 n + n_{v}; λ = α^{2} (n_{a} + e) - n_{a} \end{matrix}$ ; n为状态矢量的维数; $\begin{matrix} n_{v} \end{matrix}$ 为测量噪声维数.

选择合适的变量 $\begin{matrix} α 、 β_{t} \end{matrix}$ 和 $\begin{matrix} e 。 e \end{matrix}$ 通常取0, 保证协方差矩阵的半正定性; $\begin{matrix} α \end{matrix}$ 决定Sigma点在 $\begin{matrix} {\bar{x}}^{a}_{0} \end{matrix}$ 附近的密集程度, 通常取值范围为 $\begin{matrix} 10^{- 4} \leq α \leq 1, \end{matrix}$ 本文选择a=0.005若随机变量服从高斯分布, $\begin{matrix} β_{t} = 2 \end{matrix}$ 最合适.

(4)UKF递推滤波计算

时间更新:

$\begin{matrix} \{\begin{matrix} χ_{i, k + 1 | k}^{a} = f (χ_{i, k | k}^{a}, u_{k}) \\ {\bar{x}}_{k + 1 | k}^{a} = \overset{2 n_{a}}{\sum_{i = 0}} W_{i}^{(m)} χ_{i, k + 1 | k}^{a} \\ y_{i, k + 1 | k}^{a} = h (χ_{i, k + 1 | k}^{a}, u_{k}) \\ {\bar{y}}_{k + 1 | k}^{a} = \overset{2 n_{a}}{\sum_{i = 0}} {W_{i}}^{(m)} y_{i, k + 1 | k}^{a} \\ P_{k + 1 | k}^{a} = \overset{2 n_{a}}{\sum_{i = 0}} W_{i}^{(c)} (χ_{i, k + 1 | k}^{a} - {\bar{X}}_{k + 1 | k}^{a}) \\ {(χ_{i, k + 1 | k}^{a} - {\bar{X}}_{k + 1 | k}^{a})}^{T} \end{matrix} \end{matrix}$ (25)

测量更新:

$\begin{matrix} \{\begin{matrix} P_{(y, y), k + 1 | k}^{a} = \overset{2 n_{a}}{\sum_{i = 0}} W_{i}^{(c)} (y_{k + 1 | k}^{a} - \\ y_{k + 1 | k}^{a}) (y_{k + 1 | k}^{a} - y_{k + 1 | k}^{a})^{T} \\ P_{(x, y), k + 1 | k}^{a} = \overset{2 n_{a}}{\sum_{i = 0}} W_{i}^{(c)} (x_{k + 1 | k}^{a} - \\ {\bar{x}}_{k + 1 | k}^{a}) (y_{k + 1 | k}^{a} - {\bar{y}}_{k + 1 | k}^{a})^{T} \\ K_{k + 1} = P_{(x, y), k + 1 | k}^{a} (P_{(y, y), k + 1 | k}^{a})^{- 1} \\ P_{k + 1 | k + 1}^{a} = P_{k + 1 | k}^{a} - K_{k + 1} P_{(y, y), k + 1 | k}^{a} {K^{T}}_{k + 1} \\ {\bar{x}}_{k + 1 | k + 1}^{a} = {\bar{x}}_{k + 1 | k} + K_{k + 1} ({y^{a}}_{k} - {\bar{y}}_{k + 1 | k}^{a}) \end{matrix} \end{matrix}$ (26)

4 仿真验证

为了验证UKF算法的观测效果, 本文在车辆动学软件AMEsim中进行仿真试验.车辆模型中输出的车辆状态可以作为真实值.车辆横摆角速度, 车辆侧向加速度与纵向加速度可以作为输入量传递至观测器, 最后将观测器中估计的轮胎侧向力, 质心侧偏角等状态参数值与车辆模型中的真实值进行对比, 验证UKF算法的观测效果.本文分别在附着系数为0.9和0.3的高, 低附着路面上进行双移线试验, 仿真试验步长为1 ms.

4.1 高附着路面试验

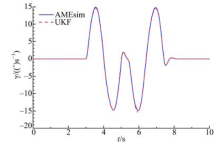
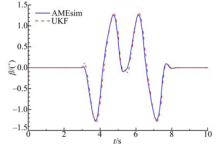
车速为80 km/h, 路面附着系数为0.9.图3为横摆角速度的估计结果, 由于横摆角速度可以直接在传感器中获取, 所以有很高的估计精度, 收敛非常快.图4为质心侧偏角的估计结果, 从图中可以看出, 估计值与参考值趋势一致, 吻合良好, 侧向激励较大时, 估计值会略有误差.图5为轮胎侧向力的估计结果.观测值与参考值的误差很小, 只有在波峰和波谷处会略有增大.

	Figure Option View Download New Window
	图3 横摆角速度估计结果(高附着)Fig.3 Estimation of the yaw rate(high adhesion)

	Figure Option View Download New Window
	图4 侧偏角估计结果(高附着)Fig.4 Estimation of the sideslip angle at CG(high adhesion)

	Figure Option View Download New Window
	图5 侧向力估计结果(高附着)Fig.5 Lateral force of tire(high adhesion)

4.2 低附着路面试验

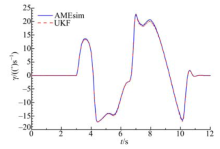
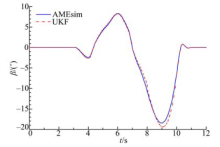
车速为80 km/h, 路面附着系数为0.3, 此路况下进行双移线工况试验, 车辆会处于非线性运动阶段.图6中, 在低附着路面下, 横摆角速度的估计值仍具有很高的精度, 为质心侧偏角的准确估计奠定了良好基础.由图7可以看出, 质心侧偏角的观测值能很好地跟踪车辆模型的输出值, 在8~10 s, 质心侧偏角最高达到了19° , 车辆已经进入了非线性区间.

	Figure Option View Download New Window
	图6 横摆角速度估计结果(低附着)Fig.6 Estimation of the yaw rate(low adhesion)

	Figure Option View Download New Window
	图7 侧偏角估计结果(低附着)Fig.7 Estimation of the sideslip angle at CG(low adhesion)

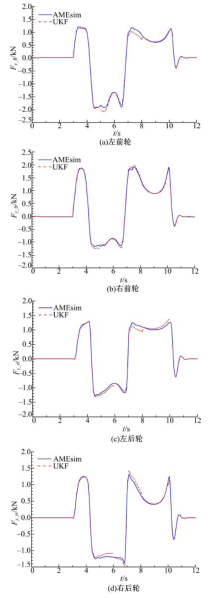
图8为轮胎侧偏力的观测结果.误差较大的地方出现在质心侧偏角较大区域, 此时轮胎与地面关系进入非线性区间, 轮胎受力趋势发生了改变, 所以影响了观测结果.

	Figure Option View Download New Window
	图8 侧向力估计结果(低附着)Fig.8 Lateral force of tire on(low adhesion)

5 结束语

利用轮毂电机驱动汽车的特点, 建立了车辆动力学模型, 应用非线性性能更优秀的UKF算法设计了车辆状态观测器.仿真结果表明, 观测器能够有效估计车辆在非线性区间内的质心侧偏角和横摆角速度, 并达到了较好的精度.轮胎力计算的精确度是车辆状态观测的重要因素, 本文在侧向力的观测计算中, 引入了考虑动态特性的修正Dugoff轮胎模型, 对运动状态下的轮胎侧向力可以进行有效估计.

The authors have declared that no competing interests exist.

参考文献

View Option

[1]	Hori Y. Future vehicle driven by electricity and control-research on four-wheel-motored "UOT Electric March II"[J]. IEEE Transactions on Industrial Electronics, 2004, 51(5): 954-962. [本文引用:1]
[2]	Sakai S, Hori Y. Advanced motion control of electric vehicle with fast minor feedback loops: basic experiments using the 4-wheel motored EV "UOT Electric March II"[J]. JSAE Review, 2001, 22(4): 527-536. [本文引用:1]
[3]	李刚, 宗长富, 陈国迎, 等. 线控转向四轮独立驱动电动车的AFS/DYC集成控制[J]. 华南理工大学学报: 自然科学版, 2012, 40(3): 150-155. Li Gang, Zong Chang-fu, Chen Guo-ying, et al. Integrated AFS/DYC control of steering-by-wire 4WID electric vehicle[J]. Journal of South China University of Technology (Natural Science Edition), 2012, 40(3): 150-155. [本文引用:1]
[4]	He P, Hori Y. Resolving actuamr redundancy for 4WD electric vehicle bysequential quadratic optimum method[DB/OL]. [2013-12-16]. http://www.hori.k.u-tokyo.ac.jp/hori_lab/paper_2009/old-papers/ka/hukui_ka.pdf. [本文引用:1]
[5]	Wenzel T A, Burnham K J, Blundell M V. Dual extended Kalman filter for vehicle state and parameter estimation[J]. Vehicle System Dynamics, 2006, 44(2): 153-171. [本文引用:1]
[6]	Kim J. Identification of lateral tyre force dynamics using an extended Kalman filter from experimental road test data[J]. Control Engineering , 2009, 17(3): 357-367. [本文引用:1]
[7]	Julier S J, Uhlmann J K. A new extension of the kalman filter to nonlinear systems[C]//Proceedings of the International Symposium on Aerospace/Defense Sensing, Simulation and Controls, Orland o, Florida, USA, 1997: 182-193. [本文引用:1]
[8]	Doumiati M, Victorino A, Charara A, et al. Estimation of vehicle lateral tire-road forces: a comparison between extended and unscented kalman filtering[C]//European Control Conference, Budapest, Hungary, 2009: 4804-4809. [本文引用:1]
[9]	解少博, 林程. 基于无迹卡尔曼滤波的车辆状态与参数估计[J]. 农业机械学报, 2011, 42(12): 6-12. Xie Shao-bo, Lin Cheng. State and parameters estimation of vehicle based on UKF[J]. Transactions of the Chinese Society for Agricultural Machinery, 2011, 42(12): 6-12. [本文引用:1]
[10]	邓永停, 李洪文, 王建立, 等. 基于卡尔曼滤波器的交流伺服系统自适应滑模控制[J]. 光学精密工程, 2014, 22(8): 2088-2095. Deng Yong-ting, Li Hong-wen, Wang Jian-li, et al. Adaptive sliding mode control for AC servo system based on Kalman filter[J]. Optics and Precision Engineering, 2014, 22(8): 2088-2095. [本文引用:1]
[11]	Pacejka H B. Tire and Vehicle Dynamics[M]. Oxford : Elsevier, 2012: 172-215. [本文引用:1]
[12]	Dugoff H, Fanches P, Segel L. An analysis of tire properties and their influence on vehicle dynamic performance[C]//SAE Paper, 1970. [本文引用:1]
[13]	Gillespie T D. Fundamental of vehicle dynamics[C]//SAE Paper, 1992. [本文引用:1]
[14]	Rajamani R. Vehicle Dynamics and Control[M]. Berlin, Germany: Springer-Verlag, 2005: 389-393. [本文引用:1]

2004

0.0

... 0 引言随着科技的进步,电动汽车的驱动系统也在不断的发展革新,基于轮毂电机驱动的四轮独立驱动电动汽车就是一种突破性的驱动结构形式^[1] ...

2001

0.0

. , :527-536

Advanced motion control of electric vehicle with fast minor feedback loops: basic experiments using the 4-wheel motored EV “UOT Electric March II”

... 由于电机具有响应快,控制精度高等特点,相对于主动制动的DYC系统,轮毂电机驱动汽车的的DYC更容易实现^[2,3] ...

2012

0.0

. 2012, 40(3):150-155 DOI:doi:10.3969/j.issn.1000-565X.2012.03.024

Integrated AFS/DYC control of steering-by-wire 4WID electric vehicle

线控转向四轮独立驱动电动车的AFS/DYC集成控制

Li Gang , Zong Chang-fu , Chen Guo-ying

李刚, 宗长富, 陈国迎

针对线控转向四轮独立驱动电动车的主动前轮转向(AFS)与直接横摆力矩控制(DYC)的集成控制问题,提出了一种基于模型预测控制的、采用分层集成控制结构的集成控制算法,设计了模型预测控制器,研究了基于二次规划的驱动力分配方法,并通过仿真实验对算法进行验证.结果表明:基于模型预测控制理论的集成控制算法能够使车辆有效地跟踪期望运动轨迹,提高车辆稳定性和主动安全性.

... 由于电机具有响应快,控制精度高等特点,相对于主动制动的DYC系统,轮毂电机驱动汽车的的DYC更容易实现^[2,3] ...

2013

0.0

... 过自由度控制系统能够合理地分配电机转矩,充分利用轮胎的附着极限,避免出现车轮滑动或抱死的现象^[4] ...

2006

0.0

... 其中,扩展卡尔曼滤波(EKF)应用最为广泛,常见于对轮胎模型的辨识^[5,6] ...

2009

0.0

. , :357-367

Identification of lateral tyre force dynamics using an extended Kalman filter from experimental road test data

... 其中,扩展卡尔曼滤波(EKF)应用最为广泛,常见于对轮胎模型的辨识^[5,6] ...

1997

0.0

... 为了克服EKF的缺点,牛津大学的Julier等^[7]建立了无迹卡尔曼滤波(UKF)算法 ...

2009

0.0

... 有学者应用UKF对车辆的轮胎侧向力,车速等状态参数进行了估计并与EKF观测器进行了对比^[8,9,10] ...

2011

0.0

. 2011, 42(12):6-12

State and parameters estimation of vehicle based on UKF

基于无迹卡尔曼滤波的车辆状态与参数估计

Xie Shao-bo , Lin Cheng.

解少博, 林程

Accurate estimation of vehicle state variables and uncertain parameters can improve the robustness of vehicle dynamic control system. The concept of uncertain vehicle parameter-set was proposed. The state space model for the estimation system was established. The estimation of the state variables and uncertain parameter-set were completed based on the UKF theory. The comparison with the reference model showed that the estimation method was effective and could get the precise results. A transformed magic formula tire model was also proposed to calculate the cornering force in the estimation process. The tire model reduced the parameters and could realize the precise estimation of tire lateral force. 

准确获取车辆运动过程中的状态变量和时变模型参数可以提高动力学控制的鲁棒性。引入了车辆模型时变参数的概念，建立了车辆动力学状态空间模型，应用无迹卡尔曼滤波(UKF)算法对车辆状态变量和参数进行了估计。与车辆动力学软件CarMaker建立的参考模型对比表明，该估计方法具有可行性和准确性。在估计系统中，提出含自适应参数的简化魔术公式来表达轮胎侧偏力，减少了模型参数，并且实现了对轮胎侧向力的准确估计。

... 有学者应用UKF对车辆的轮胎侧向力,车速等状态参数进行了估计并与EKF观测器进行了对比^[8,9,10] ...

2014

0.0

. 2014, 22(8):2088-2095 DOI:doi:10.3788/OPE.20142208.2088

Adaptive sliding mode control for AC servo system based on Kalman filter

基于卡尔曼滤波器的交流伺服系统自适应滑模控制

Deng Yong-ting , Li Hong-wen , Wang Jian-li

邓永停, 李洪文, 王建立

An adaptive sliding mode controller based on Kalman filter was proposed to reduce load torque ripples and the influence of varying system parameters on the Permanent Magnet Synchronous Motor (PMSM) system. The varying system parameters were evaluated by the adaptive law, and the external disturbance was evaluated by the Kalman filter. The integral action contained in the sliding surface was designed to ensure the steady state error of tracking velocity zero, and the exponential reaching law was employed to increase the reaching speed and to suppress the chattering of sliding mode control. The external disturbance obtained by the Kalman filter was used for feed-forward compensation for the controller output, so the chattering caused by high sliding mode gains was decreased effectively. Experimental results demonstrate that the speed fluctuation is 卤1 r/min when the motor reaches the steady state of 600 r/min. Compared with the traditional PI controller, the proposed controller decreases the speed fluctuation by 2% when the torque disturbance of 1.6 N路m is added at the steady speed of 600 r/min. These data verified by simulation and experimental results indicate that the adaptive sliding mode controller based on Kalman filter has anti-disturbance performance and robustness to the AC servo control systems and shows excellent stability.

... 有学者应用UKF对车辆的轮胎侧向力,车速等状态参数进行了估计并与EKF观测器进行了对比^[8,9,10] ...

2012

0.0

... 因此,基于轮胎物理特性或者半经验公式的Pacejka模型,Dugoff模型等被建立来精确描述轮胎的力学特性^[11,12],其中应用最广泛的就是Pacejka的魔术公式 ...

1970

0.0

... 因此,基于轮胎物理特性或者半经验公式的Pacejka模型,Dugoff模型等被建立来精确描述轮胎的力学特性^[11,12],其中应用最广泛的就是Pacejka的魔术公式 ...

1992

0.0

... 原始Dugoff模型的刚度值是不随垂直载荷变化而变化的,但是实际上载荷的转移会影响侧偏刚度的变化^[13],所以侧偏刚度可以用一个以垂直载荷为变量的二阶多项式来表示: ...

2005

0.0

... 在瞬态工况下,相对于侧偏角的变化,轮胎侧偏力的产生会有一个迟滞效应,这种瞬态特性可以引入一个松弛长度 τij来进行阐述^[14] ...