四轮转向车辆的径向基函数神经网络复合控制器设计

引用本文

高琳琳, 金立生, 郑义, 李科勇. 四轮转向车辆的径向基函数神经网络复合控制器设计.吉林大学学报:工学版, 2016, 46(2): 366-372
GAO Lin-lin, JIN Li-sheng, ZHENG Yi, LI Ke-yong. Design of radial basis function neural network compound controller for four wheel steering vehicle. Journal of Jilin University Engineering and Technology Edition, 2016, 46(2): 366-372 复制到剪切板

Permissions

四轮转向车辆的径向基函数神经网络复合控制器设计

高琳琳, 金立生, 郑义, 李科勇

吉林大学交通学院,长春 130022

通讯作者:金立生(1975-),男,教授,博士生导师.研究方向:智能车辆导航技术.E-mail:jinls@jlu.edu.cn

作者简介:高琳琳(1985-),女,博士研究生.研究方向:车辆稳定性控制.E-mail:lingyunzhi1046@126.com

基金:吉林省科技厅国际合作项目(20130413056GH); 长春市科技局重大科技攻关计划项目(长科技合(2013021)号-13KG05); 清华大学汽车安全与节能国家重点实验室开放基金项目(KF14182); 吉林大学国家杰出青年基金后备人选培育计划项目

摘要

建立了四轮转向车辆的八自由度动力学模型,并设计了四轮转向车辆的径向基函数神经网络控制器,该控制器采用直接闭环训练法以离线的方式进行训练.为了克服离线训练导致控制系统适应性差的缺点,本文同时设计了一个单神经元自适应PSD控制器,它与径向基函数神经网络控制器组成复合控制系统共同完成对四轮转向车辆的控制.结合建立的八自由度车辆动力学模型对设计的复合控制器进行仿真实验分析,结果表明,无论匀速工况还是变速工况,径向基函数神经网络复合控制器均可有效地改善四轮转向车辆的操作稳定性.

关键词: 车辆工程; 四轮转向; 稳定性控制; 径向基函数神经网络; 单神经元自适应PSD控制

中图分类号:U461.91 文献标志码:A 文章编号:1671-5497(2016)02-0366-07

Design of radial basis function neural network compound controller for four wheel steering vehicle

GAO Lin-lin, JIN Li-sheng, ZHENG Yi, LI Ke-yong

College of Transportation, Jilin University, Changchun 130022, China

Abstract

The dynamic model of eight Degrees of Freedom (8D) Four-wheel Steering (4WS) vehicle was established. Using the theory of artificial neural network, a Radial Basis Function Neural Network (RBFNN) controller was designed and it was trained by the direct close-loop training method off-line. In order to overcome the shortcomings of poor adaptability caused by off-line training, a single neuron adaptive PSD controller was also designed. The RBFNN controller and the single neuron adaptive PSD controller composed a compound control system to jointly complete the steering control of 4WS vehicle. Simulation experiments were carried out by combining the RBFNN compound controller with the 8D 4WS vehicle dynamic model. Results show that the designed RBFNN compound controller can effectively improve the steering stability of 4WS vehicle both in constant speed and variable speed conditions.

Keyword: vehicle engineering; four-wheel steering; stability control; radial basis function neural network; single neuron adaptive PSD control

Show Figures

0 引言

随着汽车性能以及汽车动力学技术的发展, 后轮随前轮一同参与转向的四轮转向(4WS)系统应运而生.4WS控制系统根据当前的车辆状态和驾驶员意图控制后轮进行转向.低速时, 后轮与前轮转向方向相反, 增加汽车的机动性; 高速时, 后轮与前轮转向方向相同, 提高汽车的转向稳定性^[1].自4WS技术出现以来, 如鲁棒控制^[2], 内模控制^[3], 非线性解耦控制^[4], 模糊控制^[5]等控制方法都被应用于4WS车辆的转向控制.其中, 由于神经网络具有强大的自适应, 自学习能力, 因此受到了更为广泛的关注.李静等^[6]利用BP神经网络实现PID控制器参数的自动调整, 进而利用该PID控制器实现车辆操作稳定性控制; Nagai等^[7]运用复合控制理论, 将线性控制与BP神经网络结合构造复合辨识和控制系统, 实现4WS车辆的动力学模型辨识与控制; Lu等^[8]建立了包括统一轮胎模型在内的4WS车辆二自由度动力学模型, 并利用径向基函数(RBF)神经网络辨识该模型, 最后利用该神经网络模型设计RBF神经网络控制器.

考虑到BP网络具有收敛速度慢, 易陷入局部极小等缺点, 本文选用逼近能力强, 收敛速度快的RBF网络, 设计4WS车辆的RBF神经网络控制器.为避免文献^[8]中由于离线训练导致控制器适应性差的缺点, 本文同时设计一个单神经元自适应PSD控制器, 并将其与RBF神经网络控制器结合构造4WS车辆的复合控制系统, 以此提高系统的控制精度与自适应性.将设计的RBF神经网络复合控制器与4WS车辆的八自由度动力学模型结合进行仿真实验, 同时与前轮转向, 前后轮转角比例控制^{[9, 10]}, 前馈反馈组合控制^[7]进行比较, 证明了该复合控制器的有效性.

1 4WS车辆动力学模型

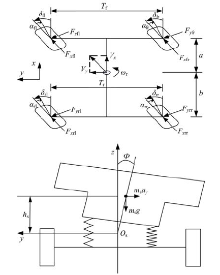
为了便于后文中RBF神经网络复合控制器的设计和分析, 文中建立包括车辆纵向, 侧向, 横摆, 侧倾以及车轮旋转在内的4WS车辆的八自由度动力学模型, 相应的力学分析示意图如图1所示.

	Figure Option View Download New Window
	图1 4WS车辆受力分析Fig.1 Scheme of 4WS vehicle mechanical analysis

根据图1, 可得车辆运动方程如下:

纵向运动平衡方程为:

$\begin{matrix} \begin{matrix} m ({\overset{\cdot}{V}}_{x} - ω_{r} V_{y}) + m_{s} h_{s} ω_{r} \overset{\cdot}{φ} = \\ F_{xfl} \cos δ_{fl} - F_{yfl} \sin δ_{fl} + \\ F_{xfr} \cos δ_{fr} - F_{yfr} \sin δ_{fr} + \\ F_{xrl} \cos δ_{rl} - F_{yrl} \sin δ_{rl} + \\ F_{xrr} \cos δ_{rr} - F_{yrr} \sin δ_{rr} \end{matrix} \end{matrix}$ (1)

侧向运动平衡方程为:

$\begin{matrix} \begin{matrix} m (\overset{\cdot}{V_{y}} + ω_{r} V_{x}) - m_{s} h_{s} \overset{\cdot \cdot}{φ} = \\ F_{xfl} \sin δ_{fl} + F_{yfl} \cos δ_{fl} F_{xfr} \sin δ_{fr} + \\ F_{yfr} \cos δ_{fr} + F_{xrl} \sin δ_{rl} + F_{yrl} \cos δ_{rl} + \\ F_{xrr} \sin δ_{rr} + F_{yrr} \cos δ_{rr} \end{matrix} \end{matrix}$ (2)

横摆运动平衡方程为:

$\begin{matrix} \begin{matrix} I_{zz} \overset{\cdot}{ω_{r}} - I_{xz} \overset{\cdot \cdot}{φ} = a (F_{xfl} \sin δ_{fl} + F_{yfl} \cos δ_{fl} + \\ F_{xfr} \sin δ_{fr} + F_{yfr} \cos δ_{fr}) - b (F_{xrl} \sin δ_{rl} + F_{yrl} \\ \cos δ_{r l} + F_{xrr} \sin δ_{rr} + F_{yrr} \cos δ_{rr}) - \\ \frac{T_{f}}{2} (F_{xfl} \cos δ_{fl} - F_{yfl} \sin δ_{fl} - F_{xfr} \cos δ_{fr} + \\ F_{yfr} \sin δ_{fr}) - \frac{T_{r}}{2} (F_{xrl} \cos δ_{rl} - F_{yrl} \sin δ_{rl} - \\ F_{xrr} \cos δ_{rr} + F_{yrr} \sin δ_{rr}) \end{matrix} \end{matrix}$ (3)

侧倾运动平衡方程为:

$\begin{matrix} \begin{matrix} I_{xx} \overset{\cdot \cdot}{φ} - I_{x z} \overset{\cdot}{ω_{r}} = m_{s} h_{s} (\overset{\cdot}{V_{y}} + V_{x} ω_{r}) + m_{s} h_{s} gφ - \\ (K_{φf} + K_{φr}) φ - (C_{φf} + C_{φr}) \overset{\cdot}{φ} \end{matrix} \end{matrix}$ (4)

车轮旋转平衡方程为:

$\begin{matrix} I_{w} \overset{\cdot}{ω_{ij}} = - R_{w} F_{xij} + T_{dij} - T_{bij} \end{matrix}$ (5)

式中: $\begin{matrix} ij = fl, fr, rl, rr 。 \end{matrix}$

车轮纵向速度计算方程为:

$\begin{matrix} \{\begin{matrix} V_{wxfl} = (V_{x} - \frac{T_{f}}{2} ω_{r}) \cos δ_{fl} + (V_{y} + a ω_{r}) \sin δ_{fl} \\ V_{wxfr} = (V_{x} + \frac{T_{f}}{2} ω_{r}) \cos δ_{fr} + (V_{y} + a ω_{r}) \sin δ_{fr} \\ V_{wxrl} = (V_{x} - \frac{T_{r}}{2} ω_{r}) \cos δ_{rl} + (V_{y} - b ω_{r}) \sin δ_{rl} \\ V_{wxrr} = (V_{x} + \frac{T_{r}}{2} ω_{r}) \cos δ_{rr} + (V_{y} - b ω_{r}) \sin δ_{rr} \end{matrix} \end{matrix}$ (6)

车轮侧偏角计算方程为:

$\begin{matrix} \begin{matrix} \{\begin{matrix} α_{fl} = \arctan (\frac{V_{y} + a ω_{r}}{V_{x} - 0.5 T_{f} ω_{r}}) - E_{fl} φ - δ_{fl} \\ α_{fr} = arcta n (\frac{V_{y} + a ω_{r}}{V_{x} + 0.5 T_{f} ω_{r}}) - E_{fr} φ - δ_{fr} \\ α_{rl} = \arctan (\frac{V_{y} - b ω_{r}}{V_{x} - 0.5 T_{r} ω_{r}}) - E_{rl} φ - δ_{rl} \\ α_{rr} = \arctan (\frac{V_{y} - b ω_{r}}{V_{x} + 0.5 T_{r} ω_{r}}) - E_{rr} φ - δ_{rr} \end{matrix} \end{matrix} \end{matrix}$ (7)

车轮垂直载荷计算方程为:

$\begin{matrix} \{\begin{matrix} F_{zfl} = \frac{mgb}{2 L} - \frac{m a_{x} h}{2 L} - \frac{m a_{y} b h}{L T_{f}} - \frac{1}{T_{f}} (K_{φf} φ + C_{φf} \overset{\cdot}{φ}) \\ F_{z fr} = \frac{mgb}{2 L} - \frac{m a_{x} h}{2 L} + \frac{m a_{y} b h}{L T_{f}} + \frac{1}{T_{f}} (K_{φf} φ + C_{φf} \overset{\cdot}{φ}) \\ F_{zrl} = \frac{mga}{2 L} + \frac{m a_{x} h}{2 L} - \frac{m a_{y} a h}{L T_{r}} - \frac{1}{T_{r}} (K_{φr} φ + C_{φr} \overset{\cdot}{φ}) \\ F_{zrr} = \frac{mga}{2 L} + \frac{m a_{x} h}{2 L} + \frac{m a_{y} a h}{L T_{r}} + \frac{1}{T_{r}} (K_{φr} φ + C_{φr} \overset{\cdot}{φ}) \end{matrix} \end{matrix}$ (8)

式(1)~(8)中主要车辆参数定义如下: $\begin{matrix} m 、 m_{s} \end{matrix}$ 分别为整车质量和簧载质量; $\begin{matrix} h 、 h_{s} \end{matrix}$ 分别为质心高度和侧倾力臂; $\begin{matrix} ω_{r} \end{matrix}$ 为横摆角速度; $\begin{matrix} φ \end{matrix}$ 为车身侧倾角; $\begin{matrix} β \end{matrix}$ 为质心侧偏角; $\begin{matrix} I_{zz} \end{matrix}$ 为横摆转动惯量; $\begin{matrix} I_{xx} \end{matrix}$ 为侧倾转动惯量; $\begin{matrix} I_{xz} \end{matrix}$ 为簧载质量转动惯量积; $\begin{matrix} a 、 b \end{matrix}$ 分别为质心到前, 后轴轴距; $\begin{matrix} T_{f} 、 T_{r} \end{matrix}$ 分别为前, 后轴轮距; $\begin{matrix} K_{φf} 、 K_{φr} \end{matrix}$ 分别为前, 后轴侧倾刚度; $\begin{matrix} C_{φf} 、 C_{φr} \end{matrix}$ 分别为前, 后轴侧倾阻尼; $\begin{matrix} I_{w} \end{matrix}$ 为车轮转动惯量; $\begin{matrix} ω_{ij} \end{matrix}$ 为车轮转速; $\begin{matrix} T_{dij} 、 T_{bij} \end{matrix}$ 分别为驱动力矩和制动力矩; $\begin{matrix} F_{xij} 、 F_{yij} \end{matrix}$ 分别为纵向力和侧向力; $\begin{matrix} δ_{ij} \end{matrix}$ 为车轮转角, 其中ij=fl, fr, rl, rr分别表示左前, 右前, 左后, 右后车轮.此外, 文中忽略转向机构的影响, 直接以车轮转角作为整车动力学模型的输入, 同时近似认为两前轮, 两后轮转角相等, 即有:δ _fl=δ _fr=δ _f, δ _rl=δ _rr=δ _r.

由于GIM理论轮胎模型^[11]具有公式简洁, 计算速度快, 不需要进行参数拟合的优点, 为此文中选用GIM轮胎模型计算轮胎的纵向力和侧向力.

2 RBF神经网络复合控制器结构

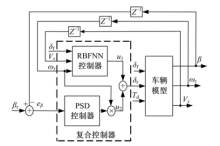
车辆的质心侧偏角和横摆角速度是描述车辆转向运动状态的重要因素, 它们从侧面反映了车辆的操作稳定性和转向安全, 大多数4WS控制器会选取二者之一作为控制目标.本文选取零质心侧偏角作为控制目标进行4WS车辆的RBF神经网络复合控制器设计, 该复合控制器的结构如图2所示.从图2中可以看出, 所设计的复合控制器包括一个RBF神经网络控制器和一个单神经元PSD控制器, 二者相互配合共同完成4WS车辆的转向控制.

	Figure Option View Download New Window
	图2 RBF神经网络复合控制器结构Fig.2 Structure of RBFNN compound controller

3 RBF神经网络控制器设计

3.1 RBF神经网络控制器的结构

RBF神经网络控制器的本质是一个三层前向RBF神经网络, 其网络输出可以描述如下:

$h_{j} (z) = \exp (- \frac{‖ z - c_{j} ‖^{2}}{2 {σ_{j}}^{2}}), j = 1, 2, \dots, p$ (9)

$u_{1} = \overset{p}{\sum_{j = 1}} w_{j} h_{j} (z)$ (10)

式中: $\begin{matrix} z \end{matrix}$ 为控制器的输入, 文中分别为当前时刻的前轮转角 $\begin{matrix} δ_{f} (k) 、车速 V_{x} (k) \end{matrix}$ 以及车辆的横摆角速度 $\begin{matrix} ω_{r} (k); h_{j} (z) \end{matrix}$ 为隐含层节点的输出; $\begin{matrix} c_{j} \end{matrix}$ 和 $\begin{matrix} σ_{j} \end{matrix}$ 分别为第j个隐含层节点的中心和宽度; $\begin{matrix} p \end{matrix}$ 为隐含层节点的数目; $\begin{matrix} u_{1} \end{matrix}$ 为控制器的输出; $\begin{matrix} w_{j} (j = 1, 2, \dots, p) \end{matrix}$ 为网络输出层的权值.

3.2 RBF神经网络控制器的训练

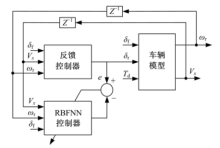
神经网络控制器的训练方法主要包括直接法和间接法.由于间接法需要训练额外的正模型或者逆模型, 过程繁琐且结构复杂, 因此文中尝试采用相对简单的直接法训练RBF神经网络控制器.然而, 由于实际控制中很难确定控制量的工作范围, 这便导致了以直接法训练控制器并非"目标指引".为了解决这个问题, 本文将被控对象引入一个反馈控制系统中构成闭环直接训练系统, 如图3所示.

	Figure Option View Download New Window
	图3 闭环直接训练系统结构Fig.3 Structure of the closed-loop direct training system

在训练系统中引入反馈控制器的目的是使控制系统能够稳定工作.选用文献[7]中的线性控制器作为反馈控制器, 其表达式可以描述为:

$\begin{matrix} δ_{r} = - (\frac{k_{f}}{k_{r}}) δ_{f} + (\frac{m V_{x} + 2 (- a k_{f} + b k_{r})}{- 2 k_{r} V_{x}}) ω_{r} \end{matrix}$ (11)

式中: $\begin{matrix} k_{f} 、 k_{r} \end{matrix}$ 分别为前, 后轮的侧偏刚度, 取负值.

RBF神经网络控制器的待训练参数包括隐含层节点数目 $\begin{matrix} p 、 \end{matrix}$ 中心 $\begin{matrix} c_{j} 、 \end{matrix}$ 宽度 $\begin{matrix} σ_{j} \end{matrix}$ 以及输出层权值 $\begin{matrix} w_{j}, 其中 j = 1, 2, \dots, p 。 \end{matrix}$ 文中采用最小二乘法确定隐含层的节点数目和中心, 采用伪逆法确定输出层权值.隐含层节点的宽度设定为相同值, 该值通过仿真实验试凑, 最终定为4.3.

RBF神经网络控制器以离线方式进行训练.选取2000组前轮转角与初始车速值作为输入样本, 样本数据应尽可能覆盖整个工作空间.具体地, 前轮转角选为零信号和[-0.15 rad, 0.15 rad]之间的随机信号; 考虑高速公路车速上限为120 km/h, 为保证一定余量, 初始车速选为(0 km/h, 144 km/h]之间符合正弦规律变化的信号.利用上述输入样本和图3所示直接闭环训练系统采集相应的输出样本数据, 采样周期为4 s.每个周期开始时都有一组前轮转角与初始车速作用于直接闭环训练系统.车速跟踪控制器计算转向过程中施加在车轮上的转矩, 保证采样周期内车速恒定, 关于车速跟踪控制器本文不做详细描述.采样周期结束时, 最终的后轮转角, 横摆角速度和实际车速被记录下来, 得到一组输出样本.

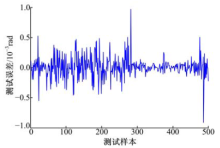
利用上述方法采集训练样本数据2000组, 其中1500组用于控制器的训练, 直至训练误差达到1× 10^-7训练停止, 剩余500组用于对控制器进行测试, 其测试误差如图4所示.对测试误差进行统计分析, 测试误差的绝对值均值为1.2168× 10^-4, 均方差为1.0862× 10^-4, 最大值为9.6505× 10^-4.

	Figure Option View Download New Window
	图4 测试误差Fig.4 Test error

4 单神经元自适应PSD控制器设计

由于RBF神经网络采用离线的方式进行训练, 训练结束后控制器参数保持固定, 这便导致系统的自适应能力较差.为了进一步提高系统的自适应性和控制精度, 本文同时设计了一个单神经元自适应PSD控制器, 该控制器以零质心侧偏角为控制目标, 其输出可以描述为:

$\{\begin{matrix} a_{1} (k) = r (k) - a (k) = e (k) \\ a_{2} (k) = e (k) - e (k - 1) = Δe (k) \\ a_{3} (k) = e (k) - 2 e (k - 1) + e (k - 2) = Δ^{2} e (k) \end{matrix}$ (12)

$\{\begin{matrix} u_{2} (k) = u_{2} (k - 1) + K (k) \overset{3}{\sum_{s = 1}} \bar{g_{s}} (k) a_{s} (k) \\ \bar{g_{s}} (k) = g_{s} (k) / \overset{3}{\sum_{s = 1}} |g_{s} (k)| \end{matrix}$ (13)

式中: $\begin{matrix} a \end{matrix}$ 为被控对象的状态反馈量, 同时也是单神经元PSD控制器的输入, 文中为车辆的质心侧偏角; $\begin{matrix} r \end{matrix}$ 为状态反馈量的期望值, 文中为0; $\begin{matrix} u_{2} (k) \end{matrix}$ 为控制器的输出, 文中为横摆角速度的反馈增益系数; $\begin{matrix} g_{1} 、 g_{2} 、 g_{3} \end{matrix}$ 为单神经元的权值; $\begin{matrix} K (k) \end{matrix}$ 为控制器增益系数.

控制器的权值学习算法可以描述为:

$\begin{matrix} \{\begin{matrix} g_{1} (k + 1) = g_{1} (k) + d_{I} z (k) u_{2} (k) [e (k) + Δe (k)] \\ g_{2} (k + 1) = g_{2} (k) + d_{P} z (k) u_{2} (k) [e (k) + Δe (k)] \\ g_{3} (k + 1) = g_{3} (k) + d_{D} z (k) u_{2} (k) [e (k) + Δe (k)] \end{matrix} \end{matrix}$ (14)

式中: $\begin{matrix} d_{I}, d_{P}, d_{D} \end{matrix}$ 分别为积分, 比例, 微分的学习速率; $\begin{matrix} z (k) \end{matrix}$ 为教师信号, 取 $\begin{matrix} z (k) = e (k) 。 \end{matrix}$

单神经元PSD控制器采用动态增益系数, 其调整算法可以描述为:

$\begin{matrix} \begin{matrix} T_{v} (k) = T_{v} (k - 1) + \\ L \cdot sgn [|Δe (k)| - T_{v} (k - 1) |Δ^{2} e (k)|] \end{matrix} \end{matrix}$ (15)

当 $\begin{matrix} sgn (e (k)) = sgn (e (k - 1)) \end{matrix}$ 时, 有:

$\begin{matrix} K (k) = K (k - 1) + CK (k - 1) / [T_{v} (k - 1)] \end{matrix}$ (16)

当 $\begin{matrix} sgn (e (k)) \neq sgn (e (k - 1)) \end{matrix}$ 时, 有:

$\begin{matrix} K (k) = 0.75 K (k - 1) \end{matrix}$ (17)

式中: $\begin{matrix} 0.025 \leq C \leq 0.05; 0.05 \leq L \leq 0.1 。 \end{matrix}$

5 仿真实验与分析

将本文设计的RBF神经网络复合控制器与前文建立的4WS车辆的八自由度动力学模型结合进行仿真实验分析, 车辆主要参数如下:整车质量m=1704.7 kg; 质心至前轴距离a=1.035 m; 质心至后轴距离b=1.655 m; 前轴轮距T_f=1.535 m; 后轴轮距T_r=1.535 m; 质心高度h=0.542 m; 前轴侧偏刚度k_f=-31106.98 N/rad; 后轴侧偏刚度k_r=-29584.56 N/rad.

本文选取匀速工况正弦响应实验和变速工况(包括驱动工况和制动工况)阶跃响应实验分析所设计的RBF神经网络复合控制器.仿真实验中, 单神经元自适应PSD控制器的权值初始值取为0~1之间的随机值, $\begin{matrix} d_{P} 、 d_{I} 、 d_{D} 、 C 、 L \end{matrix}$ 分别取为60, 1, 0.1, 0.05和0.1, 增益系数 $\begin{matrix} K \end{matrix}$ 的初始值取为0.6.

为了对RBF神经网络复合控制器的有效性进行验证, 本文同时利用前轮转向, 前馈反馈组合控制^[7], 前后轮转角比例控制^[9]与所设计的复合控制器进行对比分析.前馈反馈组合控制的控制律见式(11), 前后轮转角比例控制的控制律为:

$\begin{matrix} δ_{r} = \frac{- b - \frac{ma {V_{x}}^{2}}{2 k_{r} (a + b)}}{a - \frac{mb {V_{x}}^{2}}{2 k_{f} (a + b)}} δ_{f} \end{matrix}$ (18)

匀速工况正弦响应实验中, 前轮转角为幅值0.15 rad, 频率0.25 Hz的单个正弦信号, 初始车速分别取为20 km/h和120 km/h.不同控制策略下车辆质心侧偏角和横摆角速度的对比曲线如图5所示.

图5(a)表明, 低速时, RBF神经网络复合控制下的车辆质心侧偏角在[-0.0013 rad, 0.0015 rad]之间作小范围波动, 控制效果较前轮转向, 前后轮转角比例控制和前馈反馈组合控制更好.图5(b)则表明, 低速时, RBF神经网络复合控制下的横摆角速度与前后轮转角比例控制和前馈反馈组合控制效果相当, 大于前轮转向, 这说明低速条件下, 上述几种策略控制下的车辆机动性要优于前轮转向.

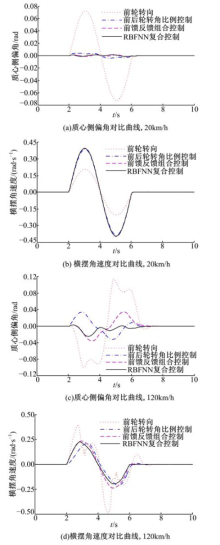	Figure Option View Download New Window
	图5 正弦响应实验对比曲线(匀速工况)Fig.5 Comparison curve of sinusoidal response experiment(constant speed condition)

图5(c)(d)表明, 高速时, 前轮转向的质心侧偏角峰值超过0.1 rad, 横摆角速度无规律变化, 表明车辆失去控制.相同条件下的前后轮转角比例控制, 前馈反馈组合控制和RBF神经网络复合控制仍能保持车辆稳定.RBF神经网络复合控制下的车辆质心侧偏角波动最小, 控制效果最好; 横摆角速度响应时间与前馈反馈组合控制相当, 小于前后轮转角比例控制; 横摆角速度幅值与前后轮转角比例控制近似, 低于前馈反馈组合控制, 且较低速时有所减小, 说明高速时横摆角速度对前轮转角的增益减小, 车辆的安全性得到了提高.

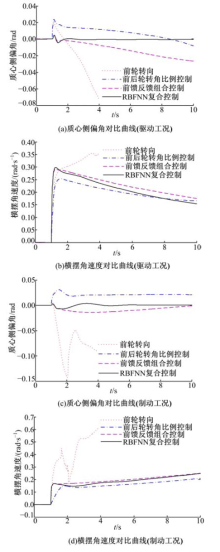
变速工况(包括驱动工况和制动工况)阶跃响应实验中, 在第1 s时输入前轮转角为0.1 rad的阶跃信号.驱动工况下, 初始车速为40 km/h, 通过驱动力矩作用使车辆10 s内加速至120 km/h, 不同控制策略下的车辆质心侧偏角和横摆角速度对比曲线如图6(a)(b)所示.制动工况下, 初始车速为120 km/h, 通过制动力矩作用使车辆10 s内减速至60 km/h, 不同控制策略下的车辆质心侧偏角和横摆角速度对比曲线如图6(c)(d)所示.

从图6(a)中可以看出, 驱动转向工况下, RBF神经网络复合控制下的车辆质心侧偏角经过短暂的调整后进入稳定状态, 其稳态值近似为0, 驱动转向时的行车安全得到了一定保证.相同条件下, 前后轮转角比例控制和前馈反馈组合控制下的车辆质心侧偏角随车速的变化而变化, 无法进入稳定状态; 前轮转向车辆则已失去控制.从图6(c)中可以看出, 制动转向工况下, RBF神经网络复合控制和前后轮转角比例控制下的车辆质心侧偏角均可进入稳定状态, RBF神经网络复合控制的调整时间较前后轮转角比例控制长, 但其稳态值近似为0, 小于前后轮转角比例控制的0.0212 rad.相同条件下, 前馈反馈组合控制下的车辆质心侧偏角随车速发生变化, 无法进入稳定状态, 前轮转向车辆则已失去控制.

	Figure Option View Download New Window
	图6 阶跃响应实验对比曲线(变速工况)Fig.6 Comparison curve of step response experiment (variable speed condition)

从图6中可以看出, 无论驱动转向工况还是制动转向工况, RBF神经网络复合控制, 前后轮转角比例控制和前馈反馈组合控制下的车辆横摆角速度均随车速的增加而减小, 说明随着车速的增加, 横摆角速度对前轮转角的增益减小, 车辆的机动性减小, 稳定性提高.

6 结论

(1)匀速转向工况下, 无论在低速还是高速时, RBF神经网络复合控制器的综合控制效果优于前轮转向, 前后轮转角比例控制和前馈反馈组合控制, 高速时尤为显著.

(2)驱动转向工况下, RBF神经网络复合控制器控制下的车辆质心侧偏角可不受车速变化的影响, 经过短暂的调整后进入稳定状态, 且稳态值近似为0.同等条件下, 前后轮转角比例控制和前馈反馈组合控制下的车辆质心侧偏角均随车速的变化而变化, 无法进入稳定状态.

(3)制动转向工况下, 前后轮转角比例控制和RBF神经网络复合控制器控制下的车辆质心侧偏角均可不受车速变化的影响进入稳定状态, RBF神经网络复合控制器控制下的车辆质心侧偏角稳态值近似为0, 小于前后轮转角比例控制.同等条件下, 前馈反馈组合控制下的车辆质心侧偏角随车速发生变化, 无法进入稳定状态.

(4)变速转向工况下, 无论驱动还是制动工况, RBF神经网络复合控制, 前后轮转角比例控制和前馈反馈组合控制下的车辆横摆角速度均随车速的增加而减小, 说明随着车速的增加, 车辆的机动性降低, 稳定性提高.

由此可见, 利用RBF神经网络理论和复合控制策略实现4WS车辆的转向控制是一种很有潜力的方法, 低速时可以提高车辆的机动性, 高速时可以提高车辆的稳定性.

The authors have declared that no competing interests exist.

参考文献

View Option

[1]	Ozatay E, Unlusoy S Y, Yildirim A M. Enhancement of vehicle hand ling using four wheel steering control strategy[C]//SAE Technical Paper, 2006-01-0942. [本文引用:1]
[2]	Yin Guo-dong, Chen Nan, Wang Jin-xiang, et al. Robust control for 4WS vehicles considering a varying tire-road friction coefficient[J]. International Journal of Automotive Technology, 2010, 11(1): 33-40. [本文引用:1]
[3]	Men Jin-lai, Wu Bo-fu, Chen Jie. Comparisons of 4WS and Brake-FAS based on IMC for vehicle stability control[J]. Journal of Mechanical Science and Technology, 2011, 25(5): 1265-1277. [本文引用:1]
[4]	Chen Chang-fang, Jia Ying-min. Nonlinear decoupling control of four-wheel-steering vehicles with an observer[J]. International Journal of Control, Automation and Systems, 2012, 10(4): 697-702. [本文引用:1]
[5]	El Hajjaji A, Ciocan A, Hamad D. Four wheel steering control by fuzzy approach[J]. Journal of Intelligent and Robotic Systems, 2005, 41(2/3): 141-156. [本文引用:1]
[6]	李静, 徐斌, 张英锋, 等. 车辆电子稳定性程序神经网络PID控制算法[J]. 吉林大学学报: 工学版, 2007, 37(4): 741-744. Li Jing, Xu Bin, Zhang Ying-feng, et al. Control algorithm based on neural network PID controller for vehicle electronic stability program[J]. Journal of Jilin University (Engineering and Technology Edition), 2007, 37(4): 741-744. [本文引用:1]
[7]	Nagai M. Non-linear design approach to four wheel steering system using neural networks[J]. Vehicle System Dynamics, 1995, 24(4/5): 329-342. [本文引用:3]
[8]	Lu Qiang, Wang Hui-yi, Guo Kong-hui. Identification and control of four-wheel-steering vehicles based on neural network[C]//Proceedings of the IEEE International Vehicle Electronics Conference, Changchun, 1999: 250-253. [本文引用:2]
[9]	Sano S, Furukawa Y, Shiraishi S. Four wheel steering system with rear wheel steer angle controlled as a function of steering wheel angle[C]//SAE Technical Paper, 860625. [本文引用:2]
[10]	王一光, 陈兴林, 李晓杰. 光刻机工件台宏动三自由度建模及自适应神经网络控制[J]. 光学精密工程, 2015, 23(1): 132-140. Wang Yi-guang, Chen Xing-lin, Li Xiao-jie. Three degrees of freedom modeling and adaptive neural network control for long-stroke wafer stage[J]. Optics and Precision Engineering, 2015, 23(1): 132-140. [本文引用:1]
[11]	Gim G, Nikravesh P. An analytical model of pneumatic tyres for vehicle dynamic simulations. part 2: comprehensive steps[J]. International Journal of Vehicle Design, 1991, 12(1): 19-39. [本文引用:1]

2006

0.0

... 高速时,后轮与前轮转向方向相同,提高汽车的转向稳定性^[1] ...

2010

0.0

... 自4WS技术出现以来,如鲁棒控制^[2],内模控制^[3],非线性解耦控制^[4],模糊控制^[5]等控制方法都被应用于4WS车辆的转向控制 ...

2011

0.0

... 自4WS技术出现以来,如鲁棒控制^[2],内模控制^[3],非线性解耦控制^[4],模糊控制^[5]等控制方法都被应用于4WS车辆的转向控制 ...

2012

0.0

... 自4WS技术出现以来,如鲁棒控制^[2],内模控制^[3],非线性解耦控制^[4],模糊控制^[5]等控制方法都被应用于4WS车辆的转向控制 ...

2005

0.0

... 自4WS技术出现以来,如鲁棒控制^[2],内模控制^[3],非线性解耦控制^[4],模糊控制^[5]等控制方法都被应用于4WS车辆的转向控制 ...

2007

0.0

. 2007, 37(4):741-744 DOI:doi:10.3969/j.issn.1671-5497.2007.04.002

Control algorithm based on neural network PID controller for vehicle electronic stability program

车辆电子稳定性程序神经网络PID控制算法

Li Jing , Xu Bin , Zhang Ying-feng

李静, 徐斌, 张英锋

摘　要：设计了面向车辆操纵稳定性控制的车轮制动神经网络PID控制器参数自调整算法,介绍了自行研制的车辆ESP硬件在环试验平台,采用该平台进行了控制算法的台架试验.结果表明：ESP神经网络PID控制算法能有效防止极限工况下车辆丧失操纵稳定性,显著改善车辆的主动安全性.

... 李静等^[6]利用BP神经网络实现PID控制器参数的自动调整,进而利用该PID控制器实现车辆操作稳定性控制 ...

1995

0.0

... Nagai等^[7]运用复合控制理论,将线性控制与BP神经网络结合构造复合辨识和控制系统,实现4WS车辆的动力学模型辨识与控制 ...

... 将设计的RBF神经网络复合控制器与4WS车辆的八自由度动力学模型结合进行仿真实验,同时与前轮转向,前后轮转角比例控制^[9,10],前馈反馈组合控制^[7]进行比较,证明了该复合控制器的有效性 ...

... 为了对RBF神经网络复合控制器的有效性进行验证,本文同时利用前轮转向,前馈反馈组合控制^[7],前后轮转角比例控制^[9]与所设计的复合控制器进行对比分析 ...

1999

0.0

... Lu等^[8]建立了包括统一轮胎模型在内的4WS车辆二自由度动力学模型,并利用径向基函数(RBF)神经网络辨识该模型,最后利用该神经网络模型设计RBF神经网络控制器 ...

... 为避免文献^[8]中由于离线训练导致控制器适应性差的缺点,本文同时设计一个单神经元自适应PSD控制器,并将其与RBF神经网络控制器结合构造4WS车辆的复合控制系统,以此提高系统的控制精度与自适应性 ...

0.0

2015

0.0

. 2015, 23(1):132-140 DOI:doi:10.3788/OPE.20152301.0132

Three degrees of freedom modeling and adaptive neural network control for long-stroke wafer stage

光刻机工件台宏动三自由度建模及自适应神经网络控制

Wang Yi-guang , Chen Xing-lin , Li Xiao-jie.

王一光, 陈兴林, 李晓杰

摘　要：提出了一种工件台宏动三自由度建模方法以解决光刻机工件台宏动部分在X和Y方向的运动耦合问题并实现它的超精密长行程微米精度的跟踪定位.该建模方法将X方向电机的偏转角度作为被控对象并且在模型中包含了耦合效应对X方向运动的影响.基于此模型提出了一种自适应神经网络控制策略,该策略采用径向基函数（Radial BasisFunction,RBF）神经网络对模型参数信息及外界非线性扰动进行实时在线估计,以减小未建模动态、电机齿槽力波动、端部效应、摩擦等扰动对控制系统性能的影响.通过对控制策略的理论推导和稳定性分析,保证了闭环控制系统的收敛性.最后在光刻机工件台上进行了S曲线跟踪定位试验,验证了宏动三自由度建模方法和控制策略的效果.试验结果显示：X和Y方向的位置跟踪误差均小于3μm,X方向电机偏转角度小于1 μrad,满足工件台宏动部分跟踪定位精度的要求.

1991

0.0

... 由于GIM理论轮胎模型^[11]具有公式简洁,计算速度快,不需要进行参数拟合的优点,为此文中选用GIM轮胎模型计算轮胎的纵向力和侧向力 ...