功率分流混合动力车辆多目标优化分层控制方法

引用本文

张东好, 项昌乐, 韩立金, 郑海亮. 功率分流混合动力车辆多目标优化分层控制方法.吉林大学学报:工学版, 2016, 46(2): 373-382
ZHANG Dong-hao, XIANG Chang-le, HAN Li-jin, ZHENG Hai-liang. Multi-objective optimization hierarchic control method for power-split hybrid electric vehicles. Journal of Jilin University Engineering and Technology Edition, 2016, 46(2): 373-382 复制到剪切板

Permissions

功率分流混合动力车辆多目标优化分层控制方法

张东好¹, 项昌乐^1,², 韩立金^1,², 郑海亮¹

1.北京理工大学机械与车辆学院,北京 100081

2.北京理工大学车辆传动国家重点实验室,北京 100081

通讯作者:项昌乐(1963-),男,教授,博士生导师.研究方向:车辆动力学与控制.E-mail:xiangcl@bit.edu.cn

作者简介:张东好(1986-),男,博士研究生.研究方向:车辆控制.E-mail:zhdonghao@163.com

基金:国家自然科学基金项目(51305026)

摘要

混合动力车辆的最优控制是一个多目标优化问题.根据发动机,电动/发电机和蓄电池的工作特征及各部件的功率耦合特性建立了多目标优化模型,将最优控制问题划分为能量管理,动力分配和协调控制3个层次,进而利用分层控制方法将优化结果应用到了实时控制过程.搭建了混合动力系统的动态仿真模型,并利用dSPACE平台进行了在线测试试验.试验结果验证了分层控制方法的实时性和有效性,与基于规则的方法相比,其动力性提高了22.2%,燃油经济性提高了10.6%,供电性能提高了15.5%.

关键词: 车辆工程; 分层控制; 多目标优化; 混合动力车辆; 最优控制

中图分类号:U469.72 文献标志码:A 文章编号:1671-5497(2016)02-0373-10

Multi-objective optimization hierarchic control method for power-split hybrid electric vehicles

ZHANG Dong-hao¹, XIANG Chang-le^1,², HAN Li-jin^1,², ZHENG Hai-liang¹

1.School of Mechanical Engineering, Beijing Institute of Technology, Beijing 100081, China

2.National Key Lab of Vehicular Transmission, Beijing Institute of Technology, Beijing 100081, China

Abstract

The optimal control of Hybrid Electric Vehicles (HEV) is a problem of multi-objective optimization. An optimization model was built based on the working characteristics of the engine, the Motor/Generator (MG) and the battery pack, and their interactions. The optimal control problem was divided into three levels, the energy management, power distribution, and coordinated control. The optimal results were applied in the real-time control process using the hierarchic control method. The dynamic simulation model was built and the on-line test was carried out on dSPACE platform. The results verify the feasibility and effectiveness of the hierarchic control method. Compared with the rule-based method, the proposed method can improve the drivability by 22.2%, the fuel consumption by 10.6% and the electricity supply performance by 15.5%, respectively.

Keyword: vehicle engineering; hierarchic control; multi-objective optimization; hybrid electric vehicle; optimal control

Show Figures

汽车带给人们便利的同时, 也带来了日益严重的环境污染和资源短缺问题^[1].混合动力车辆能够有效地缓解资源和环境的压力, 并且具有更优异的动力性, 经济性等综合性能, 已经成为了研究热点.由于混合动力车辆具有多个能量源和多个动力部件, 如何进行能量管理和动力分配成为控制策略需要解决的关键问题.现有的控制策略主要有基于规则的策略和基于优化的策略^{[2, 3]}两大类.前者依赖于工程师的经验, 非常直观而且计算量较小, 在控制策略的开发初期得到了广泛应用^{[4, 5, 6]}.但是, 仅依靠工程师的直觉很难充分挖掘出系统的潜能, 需要一种能够在理论上保证最优或近似最优的控制方法, 因此逐渐产生了各种基于优化的方法^{[7, 8, 9, 10]}.然而, 由于优化模型的求解需要大量的迭代计算, 在当前的技术条件下还很难满足实时控制的要求.

为了解决上述问题, 本文将基于规则的方法和基于优化的方法结合起来, 提出了一种基于多目标优化的分层控制方法.首先, 利用优化的方法建立了功率分流混合动力车辆的多目标优化模型; 然后, 利用规则的方法将最优控制问题划分为多个层次, 并且将优化结果应用于实时控制过程; 最后, 利用建模工具与试验平台对控制算法的实时性和有效性进行了检验.

1 多目标优化模型

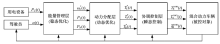
本文以一种双模式功率分流的混合动力车辆为研究对象, 其基本结构和功率分流情况如图1所示.

	Figure Option View Download New Window
	图1 双模式功率分流混合动力车辆基本结构和功率分流情况Fig.1 Basic strucutre and power flow state of the dual-mode power-split hybrid electric vehicle

发动机经过前减速齿轮与输入轴相连, 输出轴经过后减速齿轮与车轮相连.电机A和电机B具有四象限工作能力, 根据工况的需要既可以当作发电机, 也可以当作电动机.根据离合器C和制动器D的状态(结合或者分离), 可以将车辆的运行情况划分为EVT1和EVT2两种模式, 如表1所示.

表1 工作模式对照表 Table 1 HEV modes

在EVT1模式下, 发动机的功率流经过k2排的行星架分成两路, 一路经过k2排的齿圈和k1排的行星架再分成两路, 另一路经过k2排的太阳轮传递到k3排; k1排的齿圈与电机A相连, 它的功率流传递到电机A, 并且转化成电功率(发电); k1排的太阳轮与k2排的太阳轮以及电机B(电动状态)相连, 它们的功率流在电机B的输出端进行汇合后传递到k3排, 并经过k3排的行星架传递到输出轴.

在EVT2模式下, 发动机的功率流也经过k2排的行星架分成两路, 不过此时电机A工作在电动状态, 来自k2排的功率流与电机A的功率流在k1排的行星架进行汇合, 并且经过离合器C(结合)传递到输出轴; k2排太阳轮的功率流一部分经过k1排传递到输出轴, 另一部分直接传递到电机B, 并且转化为电功率, 即电机B工作在发电状态.

综上, 在EVT1模式电机A发电, 电机B驱动, 在EVT2模式电机B发电, 电机A驱动, 理想情况下两个电机之间可以实现电功率平衡, 即不需要附加动力电池组.但是, 为了更加充分地发挥出混合动力系统的优势, 本课题在两个电机之间配置了小功率的动力电池组, 它主要用于补偿两个电机之间的功率偏差, 并且满足一些特殊工况(发动机反拖启动等)下的用电功率需求.此外, 根据功率需求和控制策略的需要, 两个电机还可以同时处于电动状态或者发电状态, 而图1代表了最常用的工况.整车的基本参数如下:整车质量为15 000 kg, 最高车速为110 km/h; 柴油机额定功率为300 kW, 最高转速为2200 r/min, 最高转矩为1427 N· m; 电机A/B额定功率为90 kW, 额定转速为3200 r/min, 最高转速为6000 r/min; 锂电池组母线电压为550 V, 容量为15 Ah; 耦合机构参数 $\begin{matrix} k_{1} = 2.13, k_{2} = 2.13, k_{3} = 2.33; \end{matrix}$ 前传动比为i_f=1.41, 后传动比为i_r=4.15.其中, 发动机配备了冷却风扇, 额定功率为30 kW.此外, 电机A/B的最优匹配功率分别为75 kW和88 kW, 由于两者相差不大, 本课题从工程的角度考虑, 为了降低设计成本并且保证互换性, 选择了两个相同的电机.

1.1 优化目标

现有的控制策略主要以燃油经济性和排放性能作为优化目标^{[7, 8]}, 一部分考虑了车辆的驾驶性能和蓄电池的使用寿命^{[9, 10]}.本文的研究对象是一款重型车, 它对动力性能的要求非常高, 而且采用了大量的电子设备, 因此需要混合动力系统具备良好的供电能力.在此基础上, 还需要尽量提高其燃油经济性, 从而降低使用成本并且保证行驶里程.

基于研究对象的上述特点, 本文选择动力性, 燃油经济性和供电性能作为优化目标.

(1)动力性能

驾驶员的踏板开度体现了其对车辆加速, 匀速, 减速等行驶状态的期望, 可以解释成车轮上的需求功率.车轮上的实际功率与需求功率的差值越小, 车辆的实际状态越接近于驾驶员的期望状态, 车辆的动力性能越好, 其目标函数为:

$\begin{matrix} L_{D} (t) = |P_{α} (t) - P_{d} (t)| \end{matrix}$ (1)

式中: $\begin{matrix} P_{α} (t) \end{matrix}$ 为驾驶员的需求功率; $\begin{matrix} P_{d} (t) \end{matrix}$ 为车轮上的实际功率.

驾驶员的踏板包括加速踏板和制动踏板, 两者的状态可以用统一的变量 $\begin{matrix} α \end{matrix}$ 来表示. $\begin{matrix} α = 0 \end{matrix}$ 表示加速踏板和制动踏板都处于初始位置; $\begin{matrix} α > 0 \end{matrix}$ 表示驾驶员踩下加速踏板, 其数值代表了加速踏板的开度, 最大值为1; $\begin{matrix} α < 0 \end{matrix}$ 表示驾驶员踩下制动踏板, 其数值代表了制动踏板的开度, 最小值为-1.

驾驶员的需求功率为:

$\begin{matrix} P_{α} (t) = f_{α} (α, v) = \{\begin{matrix} α P_{dmax}, α \geq 0 \\ α F_{bmax} v, α < 0 \end{matrix} \end{matrix}$ (2)

式中: $\begin{matrix} P_{dmax} \end{matrix}$ 为车轮上的最大驱动功率; $\begin{matrix} F_{bma x} \end{matrix}$ 为车轮上的最大制动力; $\begin{matrix} v \end{matrix}$ 为传感器采集的车速信息.

车轮上的实际功率为:

$\begin{matrix} P_{d} (t) = T_{D} ω_{D} = (d_{1} T_{A} + d_{2} T_{B}) ω_{D} \end{matrix}$ (3)

式中: $\begin{matrix} T_{D} \end{matrix}$ 为车轮的总驱动转矩; $\begin{matrix} ω_{D} \end{matrix}$ 为车轮的实际角速度; $\begin{matrix} T_{A} 、 T_{B} \end{matrix}$ 分别为电机A, B的输出转矩.

转矩系数 $\begin{matrix} d_{1} 、 d_{2} \end{matrix}$ 与工作模式有关, 表示为:

EVT1: $\begin{matrix} \begin{matrix} d_{1} = \frac{(1 + k_{1} + k_{2}) (1 + k_{3}) i_{h}}{k_{1} k_{2}}, \\ d_{2} = - (1 + k_{3}) i_{h} \end{matrix} \end{matrix}$

EVT2: $\begin{matrix} d_{1} = - \frac{(1 + k_{1} + k_{2}) i_{h}}{k_{1}}, d_{2} = k_{2} i_{h} \end{matrix}$

式中: $\begin{matrix} k_{1} 、 k_{2} 、 k_{3} \end{matrix}$ 为3个行星排的特性参数; $\begin{matrix} i_{h} \end{matrix}$ 为输出轴到车轮的传动比.

(2)燃油经济性

单位时间内, 发动机的燃油消耗量越少, 燃油经济性能越好, 其目标函数为:

$\begin{matrix} L_{F} (t) = T_{E} (t) ω_{E} (t) f_{E} (T_{E}, ω_{E}) \end{matrix}$ (4)

式中: $\begin{matrix} T_{E} (t) \end{matrix}$ 为发动机的输出转矩; $\begin{matrix} ω_{E} (t) \end{matrix}$ 为发动机的输出转速; $\begin{matrix} f_{E} (T_{E}, ω_{E}) \end{matrix}$ 为发动机的燃油消耗率, 可以由万有特性试验数据插值得到.

(3)供电性能

两个电机可以对外供电, 从而满足用电设备和蓄电池的电能需求.两个电机的供电功率与总需求功率的差值越小, 供电性能越好, 其目标函数为:

$\begin{matrix} L_{E} (t) = |P_{N} (t) - P_{AB} (t)| \end{matrix}$ (5)

式中: $\begin{matrix} P_{N} (t) \end{matrix}$ 为用电设备的总需求功率; $\begin{matrix} P_{AB} (t) \end{matrix}$ 为两个电机的净供电功率.

在图1所示的混合动力系统中, 两个电机可能处于发电状态, 也可能处于电动状态.为了符号的统一, 取电动状态时功率为正, 发电状态时功率为负, 则两个电机对外输出的净电功率为:

$\begin{matrix} P_{AB} (t) = - T_{A} (t) ω_{A} (t) η_{A} - T_{B} (t) ω_{B} (t) η_{B} \end{matrix}$ (6)

式中: $\begin{matrix} ω_{A} (t) 、 ω_{B} (t) \end{matrix}$ 为两个电机的角速度; $\begin{matrix} η_{A} 、 η_{B} \end{matrix}$ 为两个电机的机械功率与电功率的比例系数, 发电状态时等于效率, 电动状态时等于效率的倒数.

1.2 约束条件

为了保证混合动力系统的正常运行, 发动机, 电机和蓄电池都必须在其特性范围内工作, 则:

$\begin{matrix} ω_{Emin} \leq ω_{E} (t) \leq ω_{Emax} \end{matrix}$ , $\begin{matrix} T_{Emin} (ω_{E}) \leq T_{E} (t) \leq T_{Emax} (ω_{E}) \end{matrix}$

$\begin{matrix} ω_{Amin} \leq ω_{A} (t) \leq ω_{Amax} \end{matrix}$ , $\begin{matrix} T_{Amin} (ω_{A}) \leq T_{A} (t) \leq T_{Ama x} (ω_{A}) \end{matrix}$

$\begin{matrix} ω_{Bmin} \leq ω_{B} (t) \leq ω_{Bmax} \end{matrix}$ , $\begin{matrix} T_{Bmin} (ω_{B}) \leq T_{B} (t) \leq T_{Bmax} (ω_{B}) \end{matrix}$

$\begin{matrix} S_{\min} \leq S (t) \leq S_{\max} \end{matrix}$ , $\begin{matrix} P_{bmin} (S) \leq P_{b} (t) \leq P_{bmax} (S) \end{matrix}$

式中: $\begin{matrix} S (t) \end{matrix}$ 为蓄电池的荷电状态; $\begin{matrix} P_{b} (t) \end{matrix}$ 为蓄电池的功率, 放电为正.

发动机, 电机和车轮之间存在速度耦合, 即:

$ω_{A} (t) = a_{1} ω_{E} (t) + a_{2} ω_{D} (t)$ (7)

$ω_{B} (t) = b_{1} ω_{E} (t) + b_{2} ω_{D} (t)$ (8)

EVT1模式: $\begin{matrix} a_{1} = \frac{(1 + k_{1}) (1 + k_{2})}{k_{1} k_{2} i_{q}}, \end{matrix}$

$\begin{matrix} \begin{matrix} a_{2} = - \frac{(1 + k_{1} + k_{2}) (1 + k_{3}) i_{h}}{k_{1} k_{2}}, \\ b_{1} = 0, b_{2} = (1 + k_{3}) i_{h} \end{matrix} \end{matrix}$

EVT2模式: $\begin{matrix} a_{1} = - \frac{1 + k_{2}}{k_{1} i_{q}} \end{matrix}$ , $\begin{matrix} a_{2} = \frac{1 + k_{1} + k_{2}}{k_{1} i_{h}}, \end{matrix}$

$\begin{matrix} b_{1} = \frac{1 + k_{2}}{i_{q}} \end{matrix}$ , $\begin{matrix} b_{2} = - k_{2} i_{h} \end{matrix}$

式中: $\begin{matrix} i_{q} \end{matrix}$ 为发动机到输入轴的传动比.

角速度 $\begin{matrix} ω_{D} (t) \end{matrix}$ 与车速 $\begin{matrix} v (t) \end{matrix}$ 的关系为:

$\begin{matrix} v (t) = ω_{D} (t) r_{w} \end{matrix}$ (9)

式中: $\begin{matrix} r_{w} \end{matrix}$ 为车轮的半径.

蓄电池, 电机和用电设备通过直流母线实现了电功率耦合, 即:

$\begin{matrix} P_{b} (t) = T_{A} (t) ω_{A} (t) η_{A} + T_{B} (t) ω_{B} (t) η_{B} + P_{r} (t) \end{matrix}$ (10)

式中: $\begin{matrix} P_{r} (t) \end{matrix}$ 为用电设备的功率.

根据蓄电池的内阻模型, 其荷电状态为:

$\begin{matrix} S (t) = \int_{0}^{t} \frac{\sqrt[]{U_{oc}^{2} - 4 P_{b} (t) R_{b}} - U_{oc}}{2 C_{b} R_{b}} dt + S_{0} \end{matrix}$ (11)

式中: $\begin{matrix} U_{oc} \end{matrix}$ 为开路电压; $\begin{matrix} R_{b} \end{matrix}$ 为内阻; $\begin{matrix} C_{b} \end{matrix}$ 为容量; $\begin{matrix} S_{0} \end{matrix}$ 为初始荷电状态.

式(7)~(11)体现了状态变量之间的耦合关系, 属于等式约束条件.

2 分层控制方法

前面建立了混合动力车辆的多目标优化模型, 通过求解模型就可以得到最优的控制变量.然而, 由于优化目标和约束条件具有显著的非线性特征, 如果直接采用优化算法进行求解, 其计算量太大, 无法应用于实时的控制过程.为了解决这个问题, 本文提出了一种基于多目标优化的分层控制方法.

2.1 基本控制框架

根据控制问题的时间尺度, 可以将其划分为3个层次:能量管理层, 动力分配层和协调控制层.能量管理层属于稳态时间尺度, 主要解决发动机和蓄电池的能量管理问题; 动力分配层属于动态时间尺度, 主要解决发动机和两个电机的动力分配问题; 协调控制层属于瞬态时间尺度, 主要解决发动机和两个电机的协调控制问题.

图2给出了分层控制方法的基本框架.首先, 根据驾驶员的踏板开度, 用电设备的需求功率以及反馈得到的状态信息, 基于规则的方法确定发动机和蓄电池的需求功率, 并利用稳态优化得到发动机的最优转速; 然后, 根据发动机和两个电机的转矩范围, 利用动态优化得到各部件的最优转矩; 最后, 利用反馈得到的状态偏差对发动机和两个电机的转矩进行实时修正, 得到各部件的转矩控制命令.

	Figure Option View Download New Window
	图2 基于多目标优化的分层控制框架Fig.2 Structure of Hierarchic control based on multi-objective optimization

2.2 能量管理算法

混合动力车辆有发动机和蓄电池两个能量源.为了满足用电设备的电能需求, 既可以由发动机带动发电机供电, 也可以由蓄电池直接供电; 为了满足车辆行驶的机械能需求, 既可以由发动机来提供, 也可以由电动机把蓄电池的电能转化为机械能.可见, 在混合动力系统中存在能量管理问题.本文的研究对象为重型车辆, 受制于蓄电池的技术水平, 其功率远远低于发动机.为了保证蓄电池的使用寿命, 本文采用了基于发动机功率跟随的能量管理策略, 即整车的需求功率主要来自于发动机.

能量管理算法的计算步骤如下:

(1)根据驾驶员的踏板开度 $\begin{matrix} α (t) \end{matrix}$ 和反馈得到的车速信息 $\begin{matrix} v (t), \end{matrix}$ 确定驱动需求功率为:

$\begin{matrix} P_{α} (t) = f_{α} (α, v) = \{\begin{matrix} α P_{dmax}, α \geq 0 \\ α F_{bmax} v, α < 0 \end{matrix} \end{matrix}$

(2)为了保证蓄电池的使用寿命, 应当尽量将其荷电状态维持在期望值附近.根据反馈得到的SOC信息, 确定蓄电池的需求功率为:

$\begin{matrix} P_{b} (t) = f_{b} (S) \end{matrix}$ (12)

如果蓄电池的SOC高于期望值, 则其需求功率为负, 即蓄电池需要放电; 如果SOC低于期望值, 则其需求功率为正, 即蓄电池需要充电.

(3)根据蓄电池的需求功率 $\begin{matrix} P_{b} (t) \end{matrix}$ 和用电设备的需求功率 $\begin{matrix} P_{r} (t), \end{matrix}$ 得到总的用电需求功率为:

$\begin{matrix} P_{N} (t) = P_{b} (t) + P_{r} (t) \end{matrix}$ (13)

其中, $\begin{matrix} P_{r} (t) \end{matrix}$ 来自于电气设备的管理, 这不是本文的研究重点, 下文以用电循环工况的形式给出.

根据总用电需求功率 $\begin{matrix} P_{N} (t) \end{matrix}$ 和驱动需求功率 $\begin{matrix} P_{α} (t), \end{matrix}$ 得到整车的总需求功率为:

$\begin{matrix} P_{T} (t) = P_{α} (t) + P_{N} (t) \end{matrix}$ (14)

发动机的功率等于总需求功率, 即:

$\begin{matrix} P_{E} (t) = P_{T} (t) / η_{E} \end{matrix}$ (15)

式中: $\begin{matrix} η_{E} \end{matrix}$ 为发动机功率的传递效率.

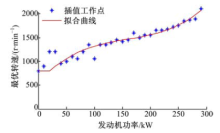
(4)根据发动机的需求功率 $\begin{matrix} P_{E} (t) \end{matrix}$ , 利用燃油经济性优化得到发动机的最优转速为:

$\begin{matrix} ω_{E}^{*} (t) = \min [L_{E} (ω_{E})] \end{matrix}$ (16)

式(4)为燃油经济性的目标函数.在发动机功率已知的条件下, 燃油经济性仅取决于发动机的转速.根据发动机的燃油经济性曲线, 可以得到每个功率下的最优转速, 如图3所示.

	Figure Option View Download New Window
	图3 发动机最优转速曲线Fig.3 Engine's optimal speed map

图3中离散点为试验数据插值得到的若干功率下的最优转速点, 实线为二项式拟合得到的最优转速曲线, 其表达式为:

$ω_{E 0}^{*} (t) = 558 + 13.2 P_{E} (t) - 0.07 P_{E}^{2} (t)$ (17)

$ω_{E}^{*} (t) = \min \{\max [ω_{E 0}^{*} (t), ω_{Emin}], ω_{Emax}\}$ (18)

式中: $\begin{matrix} ω_{E}^{*} (t) \end{matrix}$ 为功率 $\begin{matrix} P_{E} (t) \end{matrix}$ 对应的最优转速.

为了保证发动机的转速不超过约束范围, 利用式(18)加以限制.可见, 根据发动机的需求功率 $\begin{matrix} P_{E} (t), \end{matrix}$ 利用式(17)(18)就可以得到其最优转速.

2.3 动力分配算法

混合动力车辆有发动机, 电机A和电机B三个动力部件.前面通过对燃油经济性进行稳态优化得到了发动机的最优转速, 则发动机的最优转矩为:

$\begin{matrix} T_{E}^{*} (t) = \frac{P_{E} (t)}{ω_{E}^{*} (t)} \end{matrix}$ (19)

由式(3)(6)可知, 动力性能和供电性能都是电机转矩的函数.因此, 通过对两者进行动态优化就可以得到电机的最优转矩.由于电机的转矩可以通过行星齿轮机构传递到发动机的输出轴, 从而对发动机的调速造成影响.因此, 在进行动态优化前, 必须对两个电机的转矩加以约束.

发动机的动力学方程为:

$\begin{matrix} J_{E} {\overset{\cdot}{ω}}_{E} (t) = T_{E} (t) - \frac{T_{I} (t)}{i_{q}} \end{matrix}$ (20)

式中: $\begin{matrix} J_{E} \end{matrix}$ 为等效到发动机输出轴的总转动惯量; $\begin{matrix} T_{I} (t) \end{matrix}$ 为行星耦合机构输入轴的转矩.

输入轴的转矩 $\begin{matrix} T_{I} (t) \end{matrix}$ 是电机转矩 $\begin{matrix} T_{A} (t) 、 T_{B} (t) \end{matrix}$ 的函数, 即:

$\begin{matrix} T_{I} (t) = e_{1} T_{A} (t) + e_{2} T_{B} (t) \end{matrix}$ (21)

转矩系数 $\begin{matrix} e_{1} 、 e_{2} \end{matrix}$ 与工作模式有关, 如下:

EVT1: $\begin{matrix} e_{1} = - \frac{(1 + k_{1}) (1 + k_{2})}{k_{1} k_{2}} \end{matrix}$ , $\begin{matrix} e_{2} = 0 \end{matrix}$

EVT2: $\begin{matrix} e_{1} = \frac{1 + k_{2}}{k_{1}} \end{matrix}$ , $\begin{matrix} e_{2} = - (1 + k_{2}) \end{matrix}$

把式(21)代入式(20), 可得:

$\begin{matrix} {\overset{\cdot}{ω}}_{E} (t) = \frac{T_{E} (t) i_{q} - [e_{1} T_{A} (t) + e_{2} T_{B} (t)]}{J_{E} i_{q}} \end{matrix}$ (22)

如果 $\begin{matrix} ω_{E} (t) < ω_{E}^{*} (t), \end{matrix}$ 为了保证发动机的转速朝着最优方向移动, 即 $\begin{matrix} {\overset{\cdot}{ω}}_{E} (t) > 0, \end{matrix}$ 则必须满足:

$\begin{matrix} e_{1} T_{A} (t) + e_{2} T_{B} (t) < T_{E} (t) i_{q} \end{matrix}$ (23)

同理, 如果 $\begin{matrix} ω_{E} (t) > ω_{E}^{*} (t) \end{matrix}$ , 为了保证发动机的转速朝着最优方向移动, 即 $\begin{matrix} {\overset{\cdot}{ω}}_{E} (t) < 0, \end{matrix}$ 则必须满足:

$\begin{matrix} e_{1} T_{A} (t) + e_{2} T_{B} (t) > T_{E} (t) i_{q} \end{matrix}$ (24)

动力分配算法的计算步骤如下:

(1)利用约束条件(23)和(24)计算电机B的转矩范围, 并且与其外特性求交集, 即:

EVT1: $\begin{matrix} T'_{Bmin} = T_{Bmin} (ω_{A}), T'_{Bmax} = T_{Bmax} (ω_{A}) \end{matrix}$

EVT2:

$\begin{matrix} \begin{matrix} T'_{Bmin} = \\ \{\begin{matrix} \max [\frac{T_{E} i_{q} - e_{1} T_{Amin}}{e_{2}}, T_{Bmin} (ω_{A})], ω_{E} < ω_{E}^{*} \\ T_{Bmin} (ω_{B}), ω_{E} > ω_{E}^{*} \end{matrix} \end{matrix} \end{matrix}$

$\begin{matrix} \begin{matrix} T'_{Bmax} = \\ \{\begin{matrix} T_{Bmax} (ω_{B}), ω_{E} < ω_{E}^{*} \\ \min [\frac{T_{E} i_{q} - e_{1} T_{Amax}}{e_{2}}, T_{Bmax} (ω_{A})], ω_{E} > ω_{E}^{*} \end{matrix} \end{matrix} \end{matrix}$

(2)假设两个电机的供电功率等于用电设备和蓄电池的总需求功率, 则:

$\begin{matrix} T_{B} (t) = - \frac{P_{N} (t) + T_{A} (t) ω_{A} (t) η_{A}}{ω_{B} (t) η_{B}} \end{matrix}$ (25)

由于电机的效率是其转矩的函数, 因此方程(25)是电机转矩的隐函数.为了简化计算, 在动态优化时采用电机的平均效率, 在协调控制层再进行修正.

(3)根据电机A的外特性, 利用式(25)计算电机 B的转矩范围, 即:

$\begin{matrix} \begin{matrix} T ″_{Bmin} = \{\begin{matrix} \frac{P_{N} + T_{Amin} ω_{A} η_{A}}{- ω_{B} η_{B}}, ω_{A} ω_{B} < 0 \\ \frac{P_{N} + T_{Amax} ω_{A} η_{A}}{- ω_{B} η_{B}}, ω_{A} ω_{B} > 0 \\ - \frac{P_{N}}{ω_{B} η_{B}}, ω_{A} = 0 \\ T_{Bmin} (ω_{B}), ω_{B} = 0 \end{matrix} \\ T ″_{Bmax} = \{\begin{matrix} \frac{P_{N} + T_{Amin} ω_{A} η_{A}}{- ω_{B} η_{B}}, ω_{A} ω_{B} < 0 \\ \frac{P_{N} + T_{Amax} ω_{A} η_{A}}{- ω_{B} η_{B}}, ω_{A} ω_{B} > 0 \\ - \frac{P_{N}}{ω_{B} η_{B}}, ω_{A} = 0 \\ T_{Bmax} (ω_{B}), ω_{B} = 0 \end{matrix} \end{matrix} \end{matrix}$

(4)对步骤(1)和步骤(3)得到的电机B的转矩范围求交集, 即:

$\begin{matrix} \begin{matrix} T_{Bmin} = \max (T'_{Bmin}, T ″_{Bmin}), \\ T_{Bmax} = \min (T'_{Bmax}, T ″_{Bmax}) \end{matrix} \end{matrix}$

如果 $\begin{matrix} T_{Bmin} \leq T_{Bmax}, \end{matrix}$ 说明方程(25)有解, 此时再以动力性能为目标进行优化, 即:

$\begin{matrix} [T_{A}^{*} (t), T_{B}^{*} (t)] = \min [L_{D} (T_{A}, T_{B})] \end{matrix}$ (26)

如果 $\begin{matrix} T_{Bmin} > T_{Bmax}, \end{matrix}$ 说明方程(25)无解, 此时以供电性能为目标进行优化, 即:

$\begin{matrix} [T_{A}^{*} (t), T_{B}^{*} (t)] = \min [L_{E} (T_{A}, T_{B})] \end{matrix}$ (27)

式(5)为供电性能的目标函数, 它是 $\begin{matrix} (T_{A}, T_{B}) \end{matrix}$ 的二次函数.因此, 发电性能优化属于二次规划问题.

由于 $\begin{matrix} L_{D} = 0 \end{matrix}$ 无解, 即 $\begin{matrix} L_{D} \neq 0, \end{matrix}$ 可以将其划分为两种情况, 即 $\begin{matrix} P_{AB} (t) > P_{N} (t) \end{matrix}$ 或 $\begin{matrix} P_{AB} (t) < P_{N} (t) 。 \end{matrix}$ 因此, 只需要找出 $\begin{matrix} P_{AB} (t) \end{matrix}$ 的最大值和最小值, 并将其代入目标函数(5), 再找出函数值较小的一个, 即为上述优化问题的最优解.由于 $\begin{matrix} P_{AB} (t) \end{matrix}$ 是 $\begin{matrix} (T_{A}, T_{B}) \end{matrix}$ 的一次函数, 这样就把二次规划转化成了线性规划问题.

2.4 协调控制算法

前面通过稳态优化和动态优化得到了各部件的最优控制命令.由于优化的结果依赖于模型的精度, 而且不具备抗干扰能力.为了补偿模型误差对实时控制的影响, 并且提高控制算法的鲁棒性, 本文在多目标优化的基础上, 利用反馈得到的状态偏差对优化结果进行了实时修正.

协调控制算法包含的内容如下:

(1)根据发动机最优转速与实际转速的偏差, 利用PID控制器对其目标转速进行实时修正, 使得发动机的实际转速尽可能地接近最优转速.

发动机转速的反馈修正算法为:

$\begin{matrix} Δ ω_{E} (t) = ω_{E}^{*} (t) - ω_{E} (t), \end{matrix}$

$\begin{matrix} \begin{matrix} κ_{E} (t) = K_{P} [Δ ω_{E} (t) + \frac{1}{T_{I}} \int_{0}^{t} Δ ω_{E} (t) dt + T_{D} \frac{d}{dt} Δ ω_{E} (t)], \end{matrix} \end{matrix} \begin{matrix} ω_{E}^{com} (t) = ω_{E}^{*} (t) + κ_{E} (t) \end{matrix}$

式中: $\begin{matrix} Δ ω_{E} (t) \end{matrix}$ 为最优转速与实际转速的偏差; $\begin{matrix} κ_{E} (t) \end{matrix}$ 为PID控制器输出的转速增量; $\begin{matrix} K_{P} 、 T_{I} 、 T_{D} \end{matrix}$ 为PID参数, 在线调试得到; $\begin{matrix} ω_{E}^{com} (t) \end{matrix}$ 为修正后的发动机目标转速.

(2)根据直流母线的实际电压与其期望值的偏差, 对发电机的最优转矩进行实时修正, 以补偿电机效率的模型误差, 并且保证电气系统的稳定性.

前面得到了蓄电池的功率 $\begin{matrix} P_{b} (t), \end{matrix}$ 利用内阻模型可以得到直流母线的期望电压为:

$\begin{matrix} U_{\exp} (t) = \frac{\sqrt[]{E_{b}^{2} - 4 P_{b} (t) R_{b}} + E_{b}}{2} \end{matrix}$

为了保证车辆的动力性能, 这里不改变电动机的转矩, 只是对发电机的转矩进行修正, 其算法为:

$\begin{matrix} \begin{matrix} ΔU (t) = U_{\exp} (t) - U_{act} (t), \\ Δ P_{M} (t) = f_{p} [Δ U (t)], \end{matrix} \end{matrix}$

$\begin{matrix} κ_{M} (t) = \frac{Δ P_{M} (t)}{ω_{M} (t)} \end{matrix}$ , $\begin{matrix} T_{M}^{com} (t) = T_{M}^{opt} (t) + κ_{M} (t) \end{matrix}$

式中: $\begin{matrix} U_{act} (t) \end{matrix}$ 为直流母线的实际电压, 由电压传感器采集得到; $\begin{matrix} Δ P_{M} (t) \end{matrix}$ 为发电机的功率修正量, 根据经验制定其与电压偏差的函数关系曲线; $\begin{matrix} κ_{M} (t) \end{matrix}$ 为发电机的转矩修正量; $\begin{matrix} T_{M}^{com} (t) \end{matrix}$ 为修正后的发电机转矩.

(3)根据发动机最优转矩与实际转矩的偏差, 对其目标转矩进行实时修正, 以补偿发动机的动态响应特性, 并且保证机械系统的稳定性.

本文同样采用PID控制器对发动机的目标转矩进行修正, 算法的关键在于如何获取发动机的实际转矩.对发动机的动力学方程(22)进行变换, 有:

$\begin{matrix} T_{E} (t) = J_{E} {\overset{\cdot}{ω}}_{E} (t) + \frac{e_{1} T_{A} (t) + e_{2} T_{B} (t)}{i_{q}} \end{matrix}$ (28)

由于两个电机的动态响应较快, 其实际转矩近似等于目标转矩, 即 $\begin{matrix} T_{A} (t) \approx T_{A}^{com} (t) 、 T_{B} (t) \approx T_{B}^{com} (t) 。 \end{matrix}$ 由于 $\begin{matrix} T_{A}^{com} (t) 、 T_{B}^{com} (t) \end{matrix}$ 为控制变量, 可以由其控制器实时存储下来.因此, 只要获得了发动机的加速度 $\begin{matrix} {\overset{\cdot}{ω}}_{E} (t), \end{matrix}$ 就可以得到其实际转矩.而发动机的加速度可以由卡尔曼滤波算法得到, 相关的技术已经比较成熟, 这里不过多介绍.

(4)针对多模式混合动力系统, 根据模式切换的要求对发动机的目标转速进行修正, 尽量减小离合器主, 被动端的速差, 保证切换过程中的平顺性.

在图1的行星耦合机构中, 离合器主, 被动端的速差可以表示成发动机和车轮转速的函数, 即:

$ω_{C} (t) = c_{1} ω_{E} (t) + c_{2} ω_{D} (t)$ (29)

$ω_{D} (t) = d_{1} ω_{E} (t) + d_{2} ω_{D} (t)$ (30)

式中: $\begin{matrix} ω_{C} (t) \end{matrix}$ 为离合器C主, 被动端速差; $\begin{matrix} ω_{D} (t) \end{matrix}$ 为制动器D主, 被动端速差; $\begin{matrix} c_{1} 、 c_{2} 、 d_{1} 、 d_{1} \end{matrix}$ 为转速系数.

下面以EVT1模式切换到EVT2模式为例进行说明.根据模式切换策略, 可以得到切换点的车速 $\begin{matrix} v_{12}, \end{matrix}$ 把它代入到式(9)可以得到车轮的转速为:

$\begin{matrix} ω_{1, 2} = \frac{v_{12}}{r_{w}} \end{matrix}$ (31)

EVT1模式切换到EVT2模式之前, 需要降低离合器C主, 被动端的速差, 令 $\begin{matrix} ω_{C} = 0, \end{matrix}$ 并把式(31)代入到式(29), 可以得到发动机的目标转速为:

$\begin{matrix} ω_{E}^{com} (t) = - \frac{c_{2}}{c_{1}} ω_{1, 2} \end{matrix}$ (32)

为了减小模式切换过程中离合器的冲击, 本文在模式切换之前预先对发动机进行调速.

3 建模与试验分析

3.1 动态仿真模型

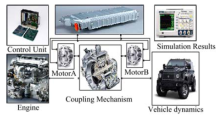
在Matlab/Simulink平台下, 搭建了机电复合传动车辆的动态仿真模型, 如图4所示.模型中充分考虑了各部件的实际工作特征, 例如发动机的启动工况, 怠速工况, 外特性, 动态响应特性, 燃油消耗特性以及辅助系统等, 能够比较真实地反映了物理系统的运行情况.

	Figure Option View Download New Window
	图4 混合动力车辆的动态仿真模型Fig.4 HEV's simulation model

在控制单元中, 利用嵌入式Matlab函数编写了控制算法, 输入为传感器采集的状态变量, 输出为决策变量.由于Matlab函数可以转化成C代码, 显著地提高了控制算法的运行速率.

3.2 在线测试试验

文献^{[11, 12]}介绍了dSPACE平台在控制策略开发中的应用价值, 为本文的在线测试试验提供了参考.dSPACE是由德国开发的一款实时仿真系统, 它具有强大的控制算法开发和测试功能, 并且可以实现与Matlab/Simulink平台的无缝连接.ControlDesk是一款基于dSPACE的综合试验和测试软件, 主要应用于快速控制原型(RCP)和半实物仿真(HIL)过程的在线控制.

首先, 在Simulink仿真模型的基础上, 利用RTI模型库分别搭建了控制单元和整车的CAN通信接口, 如图5所示.其中, 控制单元和车辆模型分别通过CAN1和CAN2发送和接收数据, CAN1发送(接收)的数据与CAN2接收(发送)的数据类型一致.

	Figure Option View Download New Window
	图5 在线测试平台的通信接口Fig.5 Communication interface of the on-line test platform

然后, 利用嵌入到Matlab的代码生成工具分别将控制单元和整车模型转化成C代码, 并下载到MicroAutoBox的两块芯片(分别模拟整车和综合控制器), 两者通过外部的CAN总线连接在一起, 可以实现实时的数据通信.

最后, 利用ControlDesk创建试验界面, 并且进行在线测试试验.整车模型通过CAN总线接收控制器的决策信号, 并且将状态信息发送回CAN总线.控制器根据CAN总线上的状态信息进行最优决策, 并且将控制信号发送到CAN总线.

由上可见, 控制器和整车模型通过CAN总线实现了实时的数据通信, 两者的运行情况实时显示在ControlDesk试验界面上, 试验数据可以自动保存, 便于进行分析和处理.

图6为在线测试的试验结果.为了与分层控制方法的结果进行对比, 本文基于规则的方法进行了相同的测试试验.图6(a)为两种控制方法下车速的跟踪情况, 图6(b)为蓄电池荷电状态的仿真结果.可见, 两种控制方法都达到了很好的车速跟踪效果, 而且蓄电池的始末状态基本相同, 为两种控制方法的对比提供了相同的前提条件.

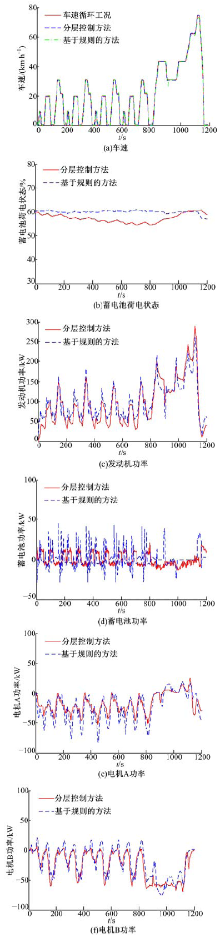	Figure Option View Download New Window
	图6 在线测试试验结果对比分析(分层控制方法和基于规则的方法)Fig.6 Experiment results comparison between hierarchic control method and rule-based method

图6(c)~(f)给出了两种控制方法下发动机, 蓄电池以及两个电机的功率状态.可见, 在相同的车速和蓄电池始末条件下, 各部件还可以工作在不同的功率状态.这是由于混合动力系统具有多个自由度, 即使车速和蓄电池始末条件完全相同, 各部件的功率状态也可以不同, 这就为功率流的分配提供了一个优化空间.

为了进一步比较两种方法的控制效果, 这里把在线测试结果分别代入动力性能, 燃油经济性和供电性能的目标函数(见式(1)(4)(5)), 得到其随着时间的变化关系, 如图8所示.

从图7可以看出:分层控制方法对应的性能函数整体上低于基于规则的方法, 这也说明前者实现了更好的动力性能, 供电性能和燃油经济性.

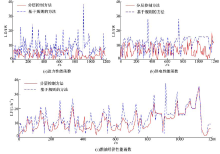	Figure Option View Download New Window
	图7 性能指标的对比分析(分层控制方法和基于规则的方法)Fig.7 Cost functions comparison between hierarchic control method and rule-based method

由于模型误差和反馈控制的原因, 某些工况下分层控制方法得到性能指标可能高于基于规则的方法, 这里为了衡量两者综合控制效果, 对其性能函数在整个循环工况内进行积分, 则有:

$J_{D} = \int_{0}^{T} L_{D} (t) dt = \overset{N}{\sum_{k = 1}} L_{D} (k) Δt$ (33)

$J_{E} = \int_{0}^{T} L_{E} (t) dt = \overset{N}{\sum_{k = 1}} L_{E} (k) Δt$ (34)

$J_{F} = \int_{0}^{T} L_{F} (t) dt = \overset{N}{\sum_{k = 1}} L_{F} (k) Δt$ (35)

式中: $\begin{matrix} J_{D} 、 J_{E} 、 J_{F} \end{matrix}$ 分别为动力性能, 供电性能及燃油经济性的积分目标函数; $\begin{matrix} T 、 Δt \end{matrix}$ 分别为循环工况的仿真时间和仿真步长; $\begin{matrix} N \end{matrix}$ 为循环工况的离散点个数, $\begin{matrix} N = T / Δt + 1 。 \end{matrix}$

根据式(33)(34)(35)的计算结果, 可以得到两种控制方法的定量比较, 如表2所示.

表2 不同控制方法的定量比较 Table 2 Quantitative comparison of different methods

动力性能和供电性能的单位都是kWh, 燃油经济性的单位是L, 它们都代表了能量的概念, 具有一定的可比性.从表2可以看出:与基于规则的方法相比, 分层控制方法的动力性能, 供电性能, 燃油经济性均有提高.此外, 在dSPACE在线测试试验中, CAN总线信号通讯正常, 这验证了分层控制方法的实时性, 为后续的台架试验和实车道路试验奠定了基础.

4 结束语

多目标优化模型兼顾了车辆的动力性, 燃油经济性和供电性能, 并且充分考虑了各部件的工作范围及其相互耦合作用, 从而确保了优化结果的可行性.分层控制方法将混合动力车辆的最优控制问题划分为能量管理, 动力分配和协调控制3个层次, 并且在每个层次内将多目标优化的结果转化成解析式和逻辑规则, 从而保证了控制算法的实时性.基于dSPACE平台进行了在线测试试验, 与基于规则的方法相比, 分层控制方法下的综合性能得到了显著提升.

The authors have declared that no competing interests exist.

参考文献

View Option

[1]	韩立金. 功率分流混合驱动车辆性能匹配与控制策略研究[D]. 北京: 北京理工大学机械与车辆学院, 2010. Han Li-jin. A study on performance matching and control strategy for power-split hybrid electric vehicles[D]. Beijing: School of Mechanical Engineering, Beijing Institute of Technology, 2010. [本文引用:1]
[2]	Salmasi F R. Control strategies for hybrid electric vehicles: Evolution, classification, comparison, and future trends[J]. Vehicular Technology, Transactions on, 2007, 56(5): 2393-2404. [本文引用:1]
[3]	Wirasingha S G, Emadi A. Classification and review of control strategies for plug-in hybrid electric vehicles[J]. Vehicular Technology, IEEE Transactions on, 2011, 60(1): 111-122. [本文引用:1]
[4]	王伟达, 项昌乐, 韩立金. 机电复合传动系统综合控制策略[J]. 机械工程学报, 2011, 47(20): 152-158. Wang Wei-da, Xiang Chang-le, Han Li-jin. Integrated control strategy of electro-mechanical transmission system[J]. Journal of Mechanical Engineering, 2011, 47(20): 152-158. [本文引用:1]
[5]	陈健, 李彦, 吴亚祥. 混合动力电动汽车模糊逻辑控制策略的研究与仿真[J]. 汽车工程, 2006, 28(4): 322-326. Chen Jian, Li Yan, Wu Ya-xiang. Study and simulation on fuzzy logic control strategy for hybrid electric vehicle[J]. Automotive Engineering, 2006, 28(4): 322-326. [本文引用:1]
[6]	Banvait H, Anwar S, Chen Y. A rule-based energy management strategy for plug-in hybrid electric vehicle (PHEV)[C]//American Control Conference, IEEE, 2009: 3938-3943. [本文引用:1]
[7]	Kim N, Cha S, Peng H. Optimal control of hybrid electric vehicles based on Pontryagin's minimum principle[J]. Control Systems Technology, IEEE Transactions on, 2011, 19(5): 1279-1287. [本文引用:2]
[8]	Johnson V H, Wipke K B. HEV control strategy for real-time optimization of fuel economy and emissions[C]//SAE Technical Paper, 2000-01-1543. [本文引用:2]
[9]	Ebbesen S, Elbert P, Guzzella L. Battery state-of-health perceptive energy management for hybrid electric vehicles[J]. Vehicular Technology, IEEE Transactions on, 2012, 61(7): 2893-2900. [本文引用:2]
[10]	Opila D F, Wang X, McGee R, et al. An energy management controller to optimally trade off fuel economy and drivability for hybrid vehicles[J]. Control Systems Technology, IEEE Transactions on, 2012, 20(6): 1490-1505. [本文引用:2]
[11]	郑海亮, 项昌乐, 王伟达, 等. 双模式机电复合传动系统综合控制策略[J]. 吉林大学学报 : 工学版, 2014, 44(2): 311-317. Zheng Hai-liang, Xiang Chang-le, Wang Wei-da, et al. Design and validation of control strategy for Dual-mode Electro-mechanical Transmission[J]. Journal of Jilin University (Engineering and Technology Edition), 2014, 44(2): 311-317. [本文引用:1]
[12]	王俊, 王庆年, 曾小华. 混合动力客车能量管理设计及硬件在环试验验证[J]. 吉林大学学报 : 工学版, 2014, 44(5): 1225-1232. Wang Jun, Wang Qing-nian, Zeng Xiao-hua. Hybrid buses energy management design and hardware in the loop test verification[J]. Journal of Jilin University (Engineering and Technology Edition), 2014, 44(5): 1225-1232. [本文引用:1]

2010

0.0

... 汽车带给人们便利的同时,也带来了日益严重的环境污染和资源短缺问题^[1] ...

2007

0.0

... 现有的控制策略主要有基于规则的策略和基于优化的策略^[2,3]两大类 ...

2011

0.0

... 现有的控制策略主要有基于规则的策略和基于优化的策略^[2,3]两大类 ...

2011

0.0

... 前者依赖于工程师的经验,非常直观而且计算量较小,在控制策略的开发初期得到了广泛应用^[4,5,6] ...

2006

0.0

... 前者依赖于工程师的经验,非常直观而且计算量较小,在控制策略的开发初期得到了广泛应用^[4,5,6] ...

2009

0.0

... 前者依赖于工程师的经验,非常直观而且计算量较小,在控制策略的开发初期得到了广泛应用^[4,5,6] ...

2011

0.0

... 但是,仅依靠工程师的直觉很难充分挖掘出系统的潜能,需要一种能够在理论上保证最优或近似最优的控制方法,因此逐渐产生了各种基于优化的方法^[7,8,9,10] ...

... 1 优化目标现有的控制策略主要以燃油经济性和排放性能作为优化目标^[7,8],一部分考虑了车辆的驾驶性能和蓄电池的使用寿命^[9,10] ...

2000

0.0

... 1 优化目标现有的控制策略主要以燃油经济性和排放性能作为优化目标^[7,8],一部分考虑了车辆的驾驶性能和蓄电池的使用寿命^[9,10] ...

2012

0.0

... 1 优化目标现有的控制策略主要以燃油经济性和排放性能作为优化目标^[7,8],一部分考虑了车辆的驾驶性能和蓄电池的使用寿命^[9,10] ...

2012

0.0

... 1 优化目标现有的控制策略主要以燃油经济性和排放性能作为优化目标^[7,8],一部分考虑了车辆的驾驶性能和蓄电池的使用寿命^[9,10] ...

2014

0.0

. 2014, 44(2):311-317 DOI:10.13229/j.cnki.jdxbgxb201402006

Design and validation of control strategy for Dual-mode Electro-mechanical Transmission

双模式机电复合传动系统综合控制策略

Zheng Hai-liang , Xiang Chang-le , Wang Wei-da

郑海亮, 项昌乐, 王伟达

School of Mechanical Engineering, Beijing Institute of Technology, Beijing 100081, China

In order to achieve the energy management and control of the dual-mode electro-mechanical transmission system, a comprehensive control strategy is studied. After the analysis of the structural characteristics of the dual-mode electro-mechanical transmission system, a control strategy for improving the fuel economy is proposed. This strategy can realize the operating mode judgment of transmission system and the coordinated control between the different energy sources. Based on dSPACE system, the hardware-in-loop simulation platform is developed to evaluate the control strategy of the dual-mode electro-mechanical transmission. The simulation results indicate that the proposed control strategy can realize the energy management and control of hybrid vehicles, the optimization of the engine operating point and the improvement of the vehicle fuel economy.

为了实现双模式机电复合传动系统的能量管理与控制，开展了系统综合控制策略的研究。在分析双模式机电复合传动系统机构特点的基础上，提出了在保证动力性的前提下改善燃油经济性为主要目标的控制策略，实现传动系统工作模式判断与切换以及系统不同能量源间的协调控制。开发了基于dSPACE的双模式机电复合传动控制策略硬件在环仿真平台，对该控制策略下的车辆性能进行了评价。仿真结果表明，开发的双模式机电复合传动系统控制策略实现了整车系统的能量管理与控制，优化了发动机的工作点，改善了车辆的燃油经济性。

... 2 在线测试试验文献^[11,12]介绍了dSPACE平台在控制策略开发中的应用价值,为本文的在线测试试验提供了参考 ...

2014

0.0

. 2014, 44(5):1225-1232 DOI:10.7964/jdxbgxb201405001

Hybrid buses energy management design and hardware in the loop test verification

混合动力客车能量管理设计及硬件在环试验验证

Wang Jun , Wang Qing-nian , Zeng Xiao-hua.

王俊, 王庆年, 曾小华

State Key Laboratory of Automotive Simulation and Control, Jilin University,Changchun 130022,China

A simulation model of electric hybrid buses was proposed, which is downloaded into the DSAPCE/Simulator using the Cruise real-time simulation modules as the simulation platform of the underlying vehicle model. Energy management control strategy based on the stateflow multi-mode operation control algorithm was established. The optimized algorithm was used to acquire high efficiency working areas as the control rules among the different modes, which were downloaded into TTC200 controller through automatic code generation technique. Then real-time loop test was carried out between TTC200 controller and Simulator hardware platform. The results show that, compared with offline simulation, the vehicle control strategy has good performance in real-time control and CAN bus communication works well, which reduces the subsequent vehicle debug cycle.

构建了混合动力客车的仿真模型,利用Cruise的实时仿真模块下载车辆模型至dSAPCE/Simulator作为整车的底层仿真平台。构建了基于stateflow的多模式整车能量管理控制策略,通过算法优化得到各模式最佳工作区域,从而确定多模式之间切换规则;利用自动代码生成技术生成代码并将其下载至TTC200控制器中,进行TTC200控制器与Simulator实时的硬件在环试验。试验结果与离线的仿真结果对比表明:整车控制策略的实时性较好,CAN总线通讯良好,减少了后续的实车调试周期。

... 2 在线测试试验文献^[11,12]介绍了dSPACE平台在控制策略开发中的应用价值,为本文的在线测试试验提供了参考 ...