基于6<em> σ</em>稳健性的电动汽车断开式转向梯形优化设计

引用本文

史天泽, 王登峰, 陈书明, 邓兆祥, 董红亮. 基于6 σ稳健性的电动汽车断开式转向梯形优化设计 .吉林大学学报:工学版, 2016, 46(3): 700-705
SHI Tian-ze, WANG Deng-feng, CHEN Shu-ming, DENG Zhao-xiang, DONG Hong-liang. Robustness optimization of divided steering linkage for electric vehicles based on 6 σ design . Journal of Jilin University Engineering and Technology Edition, 2016, 46(3): 700-705 复制到剪切板

Permissions

基于6 σ稳健性的电动汽车断开式转向梯形优化设计

史天泽¹, 王登峰¹, 陈书明¹, 邓兆祥^2,³, 董红亮^2,³

1.吉林大学汽车仿真与控制国家重点实验室,长春 130022

2.中国汽车工程研究院股份有限公司车辆NVH工程技术研究中心,重庆 401122

3.中国汽车工程研究院股份有限公司汽车噪声振动和安全技术国家重点实验室,重庆 401122

通讯作者:王登峰(1963-),男,教授,博士生导师.研究方向:汽车系统动力学与控制.E-mail:caewdf@jlu.edu.cn

作者简介:史天泽(1989-),男,博士研究生.研究方向:汽车系统动力学与控制.E-mail:stzjldx@163.com

基金:“863”国家高技术研究发展计划项目(2012AA111803)

摘要

建立了某电动轿车断开式转向梯形的数学解析模型并进行了相应的试验验证。以转向系实际内、外轮转角关系与理想阿克曼转角关系之差最小为优化目标,根据转向梯形运动特点推导出了约束条件,结合蒙特卡洛方法和6 σ稳健性优化设计技术,分别对梯形底角、横拉杆长度、直拉杆长度及齿条长度进行确定性优化和稳健性优化设计分析与比较,分析了不稳定因素对优化结果的影响。结果表明:优化后的转向梯形更接近理想内、外轮转角关系;稳健性优化结果比确定性优化结果具有更高的稳健性和可靠性。

关键词: 车辆工程; 电动轿车; 断开式转向梯形; 数学解析; 6 σ稳健性设计; 阿克曼转向

中图分类号:U463.45 文献标志码:A 文章编号:1671-5497(2016)03-0700-06

Robustness optimization of divided steering linkage for electric vehicles based on 6 σ design

SHI Tian-ze¹, WANG Deng-feng¹, CHEN Shu-ming¹, DENG Zhao-xiang^2,³, DONG Hong-liang^2,³

1.State Key Laboratory of Automotive Simulation and Control, Jilin University, Changchun 130022,China

2.China Automotive Engineering Research Institude Co.,Ltd., CAERI NVH Engineering R&D Center, Chongqing 401122, China

3.China Automotive Engineering Research Institude Co.,Ltd.,State Key Laboratory of Vehicle NVH and Safety Control, Chongqing 401122, China

Abstract

A mathematical model of divided steering linkage for electric vehicles is built and validated. Aiming at minimizing the difference between Ackerman steering angle and the practical steering angle, a robust optimization method is proposed based on theory and Monte Carlo simulation. The constraints are deduced by the characteristics of the steering linkage. The influences of uncertain factors on the optimization results are analyzed. The results demonstrate that the optimal linkage has a better Ackerman performance, and the robust design shows better reliability against the uncertain factors.

Keyword: vehicle engineering; electric vehicle; divided steering linkage; mathematical model; 6 σ robust design; ackerman angle

Show Figures

0 引言

轿车转向梯形机构的功能是通过对汽车内、外转向轮转角的合理匹配, 保证转向过程中所有车轮均绕同一瞬时中心转动, 以减少轮胎的磨损和动力消耗^[1]。近年来, 国内外学者们做了大量研究工作, 主要集中在运用作图法、直接搜索法、遗传算法、代理模型法^{[1, 2]}等确定性优化方法来改善汽车转向系统的性能。Simionescu等^[3]对平面四连杆机构的阿克曼关系进行了研究和优化。Má ntaras等^[4]建立了一种带有转向机构的麦弗逊悬架空间运动学模型, 并进行了检验。Hanzaki等^[5]对齿轮齿条转向机构进行了运动学描述和优化, 并指出了对转向误差灵敏度影响较大的因素。这些研究都是基于确定性优化方法进行的。

在实际生产及应用中, 零部件制造误差、运动副间隙、使用磨损等不确定性因素会对转向系统的性能产生一定影响。需要对这些因素进行稳健性设计, 以满足转向系统的使用性能要求。稳健性设计方法主要包括Taguchi方法、6σ 、双响应面法等。文献^[6]采用Taguchi方法对车门系统进行了稳健设计。文献^{[7, 8]}运用6σ 稳健性优化设计思想, 对泡沫填充的锥形薄壁结构及汽车行驶平顺性进行了研究。

目前, 针对转向系统结构性能稳健性优化的研究相对较少, 本文以某电动汽车断开式转向梯形机构为例, 建立其数学模型, 结合蒙特卡洛模拟技术及 $\begin{matrix} 6 σ \end{matrix}$ 稳健优化方法, 探讨了确定性优化和稳健性优化方法的优劣, 并验证了稳健性优化方法在汽车转向系统设计开发中的实用性。

1 6σ 稳健性设计理论

稳健性是指在参数的不确定性影响下相应的目标最优稳定性, 稳健性优化是在搜索目标函数最优解的同时, 控制设计变量的波动对优化目标的影响, 以提高目标函数最优解的可靠性。

确定性优化数学模型可以表示为:

$\begin{matrix} \{\begin{matrix} minf (x) \\ s . t . g_{i} (x) \leq 0, i = 1, 2, \dots, k \\ x^{L} \leq x \leq x^{U} \end{matrix} \end{matrix}$ (1)

式中: $\begin{matrix} x \end{matrix}$ 为设计变量; $\begin{matrix} f (x) \end{matrix}$ 为目标函数; $\begin{matrix} g_{i} (x) \end{matrix}$ 为约束; $\begin{matrix} x^{L} 、 x^{U} \end{matrix}$ 分别为设计变量的上、下界限。

典型的稳健性优化问题可以表示为^[8]:

$\begin{matrix} \{\begin{matrix} minf (μ_{Y} (X), σ_{Y} (X)) \\ s . t . g_{i} (μ_{Y} (X), σ_{Y} (X)) \leq 0 \\ i = 1, 2, \dots, k \\ X^{L} + ΔX \leq X \leq X^{U} - ΔX \end{matrix} \end{matrix}$ (2)

式中: $\begin{matrix} X \end{matrix}$ 为设计变量集; $\begin{matrix} Y \end{matrix}$ 为性能参数集; $\begin{matrix} μ_{Y} 、 σ_{Y} \end{matrix}$ 分别为 $\begin{matrix} Y \end{matrix}$ 的平均值和标准差; $\begin{matrix} ΔX \end{matrix}$ 为随机设计变量 $\begin{matrix} X \end{matrix}$ 的变化量。

对于稳健性优化, 其目标函数既要有能最小化目标函数平均值的性能, 又要有能最小化目标函数的波动性能, 因此可以表示为^[9]:

$\begin{matrix} f = \overset{k}{\sum_{i = 1}} [\pm \frac{W_{1 i}}{S_{1 i}} {(μ_{i} - M_{i})}^{2} + \frac{W_{2 i}}{S_{2 i}} σ_{i}^{2}] \end{matrix}$ (3)

式中: $\begin{matrix} W_{1 i} 、 W_{2 i} \end{matrix}$ 为权重系数; $\begin{matrix} S_{1 i} 、 S_{2 i} \end{matrix}$ 分别为目标函数平均值和最小波动对象的比例因子; $\begin{matrix} M_{i} \end{matrix}$ 为响应的目标值; $\begin{matrix} k \end{matrix}$ 为性能的相应数量。

同时, 式(2)中的约束可以修改为包括平均值和标准差的质量约束:

$\begin{matrix} \{\begin{matrix} μ - nσ \geq x^{L} \\ μ + nσ \leq x^{U} \end{matrix} \end{matrix}$ (4)

为了使设计变量在6σ 波动范围内满足稳健性设计要求, 可将约束范围 $\begin{matrix} n \end{matrix}$ 的值设定为6。于是6σ 稳健优化可以表示为:

$\begin{matrix} \{\begin{matrix} minf = \pm μ [f] + 6 σ [f] \\ s . t . g_{i} = \pm μ [g_{i}] + 6 σ [g_{i}] \leq 0 \\ x^{L} + 6 σ \leq μ \leq x^{U} - 6 σ \end{matrix} \end{matrix}$ (5)

若优化目标为极小值, 式(5)中目标函数均值取正; 若优化目标为极大值, 目标函数均值取负。目标函数(式(3))中的均值 $\begin{matrix} μ_{i} \end{matrix}$ 和均方差 $\begin{matrix} σ_{i} \end{matrix}$ 通过蒙特卡罗模拟得到。蒙特卡罗模拟的过程为:首先依据一定的分布规则对设计变量进行抽样, 抽样方法可选择随机抽样和描述抽样, 使用描述抽样可以有效减少所需的抽样数据点数; 然后将抽样得到的设计变量值代入数学模型中, 得到相应的蒙特卡罗分布, 相应的均值和均方差可通过蒙特卡罗分布云图计算得出。通过 $\begin{matrix} 6 σ \end{matrix}$ 稳健性优化设计, 使设计结果以极高概率( $\begin{matrix} 6 σ \end{matrix}$ 水平接近100%)处于可行域内, 使最优解远离约束边界且波动量很小。

2 转向系数学解析及试验验证

2.1 断开式转向系统的数学解析

两轴汽车以低速转弯行驶时, 可忽略离心力的影响; 假设轮胎是刚性的, 可忽略轮胎侧偏刚度的影响。若各车轮绕同一瞬时转向中心进行转弯行驶, 则两转向轮轴线的延长线相交于后轴延长线上, 这一几何关系称为阿克曼几何学^[1]。

满足阿克曼几何的前轮转向汽车应满足下述关系式:

$\begin{matrix} \cot θ_{o} - \cot θ_{i} = K / L \end{matrix}$ (6)

式中: $\begin{matrix} θ_{o} \end{matrix}$ 为外轮转角; $\begin{matrix} θ_{i} \end{matrix}$ 为内轮转角; $\begin{matrix} K \end{matrix}$ 为两主销轴线与转向梯形平面交点间的距离; $\begin{matrix} L \end{matrix}$ 为汽车轴距。

若转向轮外轮转角 $\begin{matrix} θ_{o} \end{matrix}$ 已知, 由此可得内轮转角 $\begin{matrix} θ_{i} \end{matrix}$ 的理想值为:

$\begin{matrix} θ_{i} = f_{ideal} (θ_{o}) = arccot (\cot θ_{o} - K / L) \end{matrix}$ (7)

满足式(7)的转向系统, 可以使汽车在转向过程中车轮作无侧滑纯滚动。事实上, 现有的汽车转向梯形结构不能保证在整个前轮转角的转向范围内均满足阿克曼几何, 只是近似地满足。

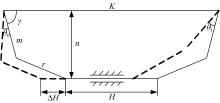
对于断开式转向梯形机构, 由于主销内倾角和主销后倾角对转向连杆机构的影响非常小, 因此可以近似地将转向梯形视为平面连杆机构进行分析。轿车上常用的后置式齿轮齿条转向机构的杆系布置如图1所示。图1中, $\begin{matrix} γ \end{matrix}$ 为梯形底角; $\begin{matrix} K \end{matrix}$ 为两主销与转向梯形平面交点的距离; $\begin{matrix} H \end{matrix}$ 为齿条长度; $\begin{matrix} m \end{matrix}$ 为转向横拉杆长度; $\begin{matrix} r \end{matrix}$ 为转向梯形臂长度; $\begin{matrix} n \end{matrix}$ 为齿条与 $\begin{matrix} K \end{matrix}$ 线距离; $\begin{matrix} ΔH \end{matrix}$ 为齿条移动距离。

	Figure Option View Download New Window
	图1 齿轮齿条转向系杆系机构布置Fig.1 Pinion rack steering linkages

根据图1所示杆系的几何关系, 在已知转向系各杆件长度的条件下, 可以得出实际内、外轮转角 $\begin{matrix} θ_{i} \end{matrix}$ 与 $\begin{matrix} θ_{o} \end{matrix}$ 之间的关系为:

$θ'_{i} = f_{actual} (θ_{o}) = γ - \arctan \frac{n}{ΔH + \frac{K - H}{2}} - \arccos \frac{n^{2} + {(\frac{K - H}{2} + ΔH)}^{2} + m^{2} - r^{2}}{2 m \sqrt[]{n^{2} + {(\frac{K - H}{2} + ΔH)}^{2}}}$ (8a)

$ΔH = \frac{K - H}{2} - m \times \sin (\frac{π}{2} - θ_{o} - γ) - r \times \cos [\arcsin \frac{n - m \times \cos (π / 2 - θ_{o} - γ)}{r}]$ (8b)

$γ = \arctan \frac{2 n}{K - H} + \arccos \frac{m^{2} + n^{2} + {(\frac{K - H}{2})}^{2} - r^{2}}{2 m \sqrt[]{n^{2} + {(\frac{K - H}{2})}^{2} - r^{2}}}$ (8c)

2.2 试验验证

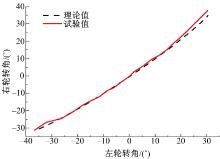
为了验证式(8)对内、外轮转角关系描述的准确性, 对某电动汽车转向系内、外轮转角关系进行了试验研究。将试验车安装在K& C试验台架上, 将转向轮置于滑盘上, 如图2所示。将滑盘解锁, 使车轮可自由转动, 利用试验台加载系统将前轮加载到半载状态下进行试验。试验时, 转向盘由中间位置向左转动至极限角度附近, 转动过程中每隔一定角度记录一组方向盘转角、左前轮转角和右前轮转角的数据, 等间距记录10组数据; 在方向盘回正至中间位置的过程中再等间距记录10组数据; 然后反向转动转向盘至另一极限角度附近并转回, 每个转动过程记录10组数据, 总共记录40组数据, 方向盘转速为30 ° /s。将该车转向系主要参数K=1362 mm, L=2389 mm, m=101 mm, n=145 mm, r=338 mm, H=670 mm代入式(8)计算得到公式推导的内、外轮转角曲线, 并与试验测得的内、外轮转角曲线进行对比, 结果如图3所示。由图3可见, 转向系内、外轮转角关系曲线的理论计算和K& C台架试验结果吻合较好, 可见式(8)能很好地表达转向系统在转向过程中内、外轮转角的关系。

	Figure Option View Download New Window
	图2 内、外轮转角关系试验Fig.2 Test on steering angle relationship between inner and outer wheel

	Figure Option View Download New Window
	图3 数学解析模型的验证Fig.3 Validation of mathematical model

3 转向梯形优化模型的建立

3.1 目标函数

汽车弯行驶时转向梯形的实际内侧车轮转角 $\begin{matrix} θ'_{i} \end{matrix}$ 应尽可能接近理想值 $\begin{matrix} θ_{i}, \end{matrix}$ 设计目标函数使理想转角与实际转角差的绝对值最小。考虑到汽车在实际使用中多数工况下转向轮转角一般均小于20° , 且大部分在10° 以内。在小转角下保证阿克曼转角可以有效地减少汽车高速行驶时轮胎的磨损, 而在不常使用的较大转角时可以适当放宽要求。因此引入加权因子 $\begin{matrix} ω (θ_{oi}), \end{matrix}$ 构成评价设计优劣的目标函数 $\begin{matrix} F_{obj} (X) \end{matrix}$ 为:

$\begin{matrix} F_{obj} (X) = \overset{θ_{omax}}{\sum_{θ_{oi = 1}}} ω (θ_{oi}) |θ'_{i} (θ_{oi}) - θ_{i} (θ_{oi})| \end{matrix}$ (9)

根据不同转向角度的实际使用频率, 加权因子取值为:

$\begin{matrix} ω (θ_{i}) = \{\begin{matrix} 1.5, 0 ° < θ_{i} \leq 10 ° \\ 1.0, 10 ° < θ_{i} \leq 20 ° \\ 0.5, 20 ° < θ_{i} \leq θ_{\max} \end{matrix} \end{matrix}$ (10)

3.2 设计变量

转向杆系中, 主销与转向梯形平面交点距离 $\begin{matrix} K \end{matrix}$ 和汽车轴距 $\begin{matrix} L \end{matrix}$ 为汽车整车参数, 若进行变动则会对汽车其他性能产生较大影响, 故选取转向梯形各杆长度及梯形底角 $\begin{matrix} H 、 m 、 n 、 r 、 γ \end{matrix}$ 为设计变量。根据实车结构确定其变化范围。

综合考虑加工误差、运动副的间隙、杆件和连接件的磨损等不确定因素来确定各变量的波动范围。加工过程中, 尺寸误差一般符合正态分布, 且转向系杆件属于配合件, 按标准公差IT13来确定其加工制造产生的波动; 关于运动副间隙, 根据文献[10]选取运动副配合为φ 15H8/g8的间隙分布为: $\begin{matrix} r ~ N (0.017, 0 . 003^{2}); \end{matrix}$ 由于转向系统的磨损涉及较多的因素和零件, 难以进行确定性描述, 采用参考文献[11]给出的四连杆机构杆系磨损量经验值来估计转向系统磨损量。最终确定优化的设计变量及其变化范围和分布如表1所示。

表1 设计变量及其变化范围 Table 1 Design variables and value range

设计变量	下限	上限	分布类型	均方差
$\begin{matrix} H \end{matrix}$ /mm	615	725	正态分布	2.5
$\begin{matrix} m \end{matrix}$ /mm	90	145	正态分布	1.5
$\begin{matrix} n \end{matrix}$ /mm	150	180	正态分布	1.5
$\begin{matrix} r \end{matrix}$ /mm	295	370	正态分布	2.0
$\begin{matrix} γ \end{matrix}$ /(° )	65	80	正态分布	1.0

表1 设计变量及其变化范围 Table 1 Design variables and value range

3.3 约束条件

汽车转向过程中梯形底角和齿条运动距离都应为非负数^[9], 且杆件长度必须满足构成梯形的几何约束, 因此转向梯形优化的约束条件为:

$\begin{matrix} \{\begin{matrix} g_{1} (X) = [m^{2} + n^{2} + r^{2} + {(\frac{K - H}{2})}^{2}] / \\ m^{2} - {(K - H)}^{2} - 4 n^{2} \leq 0 \\ g_{2} (X) = [m^{2} + n^{2} - r^{2} + {(\frac{K - H}{2} + ΔH)}^{2}] / \\ m^{2} - 4 n^{2} - {(K - H + 2 ΔH)}^{2} \leq 0 \\ g_{3} (X) = m^{2} si n^{2} θ_{o} + n^{2} - 2 mnsin θ_{o} - r^{2} \leq 0 \end{matrix} \end{matrix}$ (11)

3.4 转向梯形确定性优化模型

以转向系实际内、外轮转角关系与理想关系的差别最小为目标, 以各杆件长度及梯形底角的角度为设计变量, 构建确定性优化模型如下:

$\begin{matrix} \{\begin{matrix} \min f_{obj} (H, m, n, r, γ) \\ s . t . g_{1} (H, m, n, r, γ) \leq 0 \\ g_{2} (H, m, n, r, γ) \leq 0 \\ g_{3} (H, m, n, r, γ) \leq 0 \\ H \in (615, 725) \\ m \in (90, 145) \\ n \in (150, 180) \\ r \in (295, 370) \\ γ \in (65, 80) \end{matrix} \end{matrix}$ (12)

3.5 转向梯形稳健性优化模型

根据上文优化参数及 $\begin{matrix} 6 σ \end{matrix}$ 稳健性优化理论, 考虑各设计变量的波动, 以内外轮实际转角与理想值的差别 $\begin{matrix} Δ_{obj} \end{matrix}$ 的期望值最小、波动量最小为目标函数, 构建转向系稳健性优化数学模型如下:

$\begin{matrix} \{\begin{matrix} minF = λ μ^{2} (Δ_{obj}) + (1 - λ) σ^{2} (Δ_{obj}) \\ s . t . μ [g_{i}] + 6 σ [g_{i}] \leq 0 \\ H \in (615 + 6 σ (H), 725 - 6 σ (H)) \\ m \in (90 + 6 σ (m), 145 - 6 σ (m)) \\ n \in (150 + 6 σ (n), 180 - 6 σ (n)) \\ r \in (295 + 6 σ (r), 370 - 6 σ (r)) \\ γ \in (65 + 6 σ (γ), 80 - 6 σ (γ)) \end{matrix} \end{matrix}$ (13)

4 优化结果蒙特卡罗对比分析

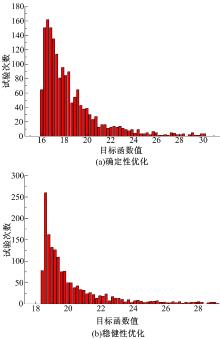
转向梯形确定性优化和稳健性优化结果及设计变量的取值如表2所示。图4为初始内外轮转角曲线、理想阿克曼转角曲线、确定性优化内外轮转角曲线和稳健性优化内外轮转角曲线对比。对确定性优化和稳健性优化结果分别作蒙特卡罗模拟试验进行稳健性验证, 根据表1确定的各设计变量的方差, 经过2000次随机试验分析, 得到目标函数概率分布如图5所示。对模拟结果进行正态分布拟合, 得到相应的分布函数, 其均值和均方差如表2所示。根据其均值和均方差分别绘制确定性优化和稳健性优化后转向系内、外轮转角关系误差带如图6所示, 为了表达清晰, 图中的偏差增大了一倍。

	Figure Option View Download New Window
	图4 优化前、后内外轮转角关系Fig.4 Comparisons of angle relationship between inner and outer wheel

	Figure Option View Download New Window
	图5 确定性和稳健性优化目标函数概率分布Fig.5 Objective distribution of deterministic and robust optimization

	Figure Option View Download New Window
	图6 确定性和稳健性优化误差带分布Fig.6 Error band of deterministic and robust optimization

表2 转向梯形优化结果比较 Table 2 Comparison of optimal results of steering linkages

参数	初始方案	确定性优化	稳健性优化
$\begin{matrix} H \end{matrix}$	670	670.11	672.69
$\begin{matrix} m \end{matrix}$	101	128.30	129.90
$\begin{matrix} n \end{matrix}$	145	167.71	167.46
$\begin{matrix} r \end{matrix}$	338	322.12	319.38
$\begin{matrix} γ \end{matrix}$	81	71.02	71.65
$\begin{matrix} μ (Δ_{obj}) \end{matrix}$	—	18.61	19.81
$\begin{matrix} σ (Δ_{obj}) \end{matrix}$	—	2.7518	1.7593
$\begin{matrix} σ \end{matrix}$ 水平	—	0.927	6.547

表2 转向梯形优化结果比较 Table 2 Comparison of optimal results of steering linkages

结合表2和图3~图6(a)进行分析, 相比初始方案, 经过确定性优化, 转向系性能较好地贴近了理想阿克曼转角, 目标函数期望值降低至18.61, 均方差为2.7931。稳健性优化目标函数的期望值为19.94, 均方差为1.760。这意味着稳健性优化方案的转向系性能略低于确定性优化, 但其优化结果的均方差则比确定性方案低36.99%, 说明稳健性设计结果波动性大大低于确定性优化。对比图6(a)和图6(b)可知, 稳健性优化的误差带分布明显窄于确定性优化的误差带分布, 也说明了稳健性设计的内、外轮转角关系具有更高的稳健性。

5 结束语

建立了断开式转向梯形的数学解析模型并进行了相应的试验验证, 在已知转向系各杆件长度的条件下, 即可推导出转向系统内、外轮实际转角间的关系。通过 $\begin{matrix} 6 σ \end{matrix}$ 稳健性优化, 转向系内、外轮转角关系得到显著改善。蒙特卡罗模拟试验结果表明:在优化参数产生波动的情况下, 该方法仍能保持最优的内、外轮转角关系, 即改善了优化目标的稳健性。可以在汽车的初始设计阶段就引入稳健性设计方法, 从而有效地提高产品性能的稳健性, 为汽车结构零部件或整车性能优化提供新思路。

The authors have declared that no competing interests exist.

参考文献

View Option

[1]	姚明龙, 王福林. 车辆转向梯形优化设计及其求解方法的研究[J]. 机械设计与制造, 2007(5): 24-26. Yao Ming-long, Wang Fu-lin. The optimal design of steering trapezoidal mechanism of vehicle and the research of solution method[J]. Machinery Design & Manufacture, 2007(5): 24-26. [本文引用:3]
[2]	唐应时, 朱彪, 朱位宇, 等. 基于响应面方法的转向梯形优化设计[J]. 中南大学学报: 自然科学版, 2012, 43(7): 2601-2606. Tang Ying-shi, Zhu Biao, Zhu Wei-yu, et al. Optimization of ackerman steering lingkage based on RSM[J]. Journal of Central South University(Science and Technology), 2012, 43(7): 2601-2606. [本文引用:1]
[3]	Simionescu P A, Beale D. Optimum synthesis of the four-bar function generator in its symmetric embodiment: the Ackermann steering linkage[J]. Mechanism and Machine Theory, 2002, 37(12): 1487-1504. [本文引用:1]
[4]	Mántaras D A, Luque P, Vera C. Development and validation of a three-dimensional kinematic model for the McPherson steering and suspension mechanisms[J]. Mechanism and Machine Theory, 2004, 39(6): 603-619. [本文引用:1]
[5]	Hanzaki A R, Rao P V M, Saha S K. Kinematic and sensitivity analysis and optimization of planar rack-and -pinion steering linkages[J]. Mechanism and Machine Theory, 2009, 44(1): 42-56. [本文引用:1]
[6]	黄金陵, 崔岸, 陈晓华, 等. 稳健设计方法用于车门系统设计[J]. 汽车工程, 2006, 28(11): 1011-1014. Huang Jin-ling, Cui An, Chen Xiao-hua, et al. Robust design of automotive door system[J]. Automotive Engineering, 2006, 28(11): 1011-1014. [本文引用:1]
[7]	高伟钊, 莫旭辉, 付锐, 等. 基于Kriging的泡沫填充锥形薄壁结构耐撞性6σ稳健性优化设计[J]. 固体力学学报, 2012, 33(4): 370-378. Gao Wei-zhao, Mo Xu-hui, Fu Rui, et al. 6σ robustness optimization design of the crashworthiness for foam-filled tapered thin-walled structure based on kriging method[J]. Chinese Journal of Solid Mechanics, 2012, 33(4): 370-378. [本文引用:1]
[8]	莫旭辉, 赵宇航, 钟志华, 等. 基于6 σ稳健性方法的汽车行驶平顺性优化[J]. 中南大学学报: 自然科学版, 2012, 43(11): 4286-4292. Mo Xu-hui, Zhao Yu-hang, Zhong Zhi-hua, et al. Robustness optimization of ride comfort for vehicle based on 6σ method[J]. Journal of Central South University (Science and Technology), 2012, 43(11): 4286-4292. [本文引用:2]
[9]	Durstine J. The truck steering system from hand wheel to road wheel[C]//SAE Technical Paper, 1973, 730039. [本文引用:2]
[10]	刘汪洋, 宋小文, 王晓晖. 断开式转向梯形机构的稳健优化设计模型[J]. 机电工程, 2011, 28(4): 429-431, 443. Liu Wang-yang, Song Xiao-wen, Wang Xiao-hui. Robust design model of vehicle divided steering linkage[J]. Journal of Mechanical & Electrical Engineering, 2011, 28(4): 429-431, 443. [本文引用:1]
[11]	孟宪举, 张策, 师忠秀, 等. 连杆机构稳健性优化设计[J]. 机械设计, 2004, 21(6): 31-33. Meng Xian-ju, Zhang Ce, Shi Zhong-xiu, et al. Optimization design for robustness of linkages[J]. Journal of Machine Design, 2004, 21(6): 31-33. [本文引用:1]

2007

0.0

. 2007, (5):24-26 DOI:doi:10.3969/j.issn.1001-3997.2007.05.010

The optimal design of steering trapezoidal mechanism of vehicle and the research of solution method

车辆转向梯形优化设计及其求解方法的研究

Yao Ming-long , Wang Fu-lin.

姚明龙, 王福林

在现有文献研究的基础上,对车辆转向梯形优化设计模型的求解方法进行了探讨.通过对该模型的研究分析,用一般方法求解该模型,计算速度偏慢且容易陷入局部最优解.通过对实数遗传算法进一步研究,提出了一种改进算法.结合轮式车辆转向梯形机构的实例计算并与一般方法计算比较,证明该方法不仅可提高运算速度,而且增大了求得全局最优解的可能性.

... 0 引言轿车转向梯形机构的功能是通过对汽车内、外转向轮转角的合理匹配,保证转向过程中所有车轮均绕同一瞬时中心转动,以减少轮胎的磨损和动力消耗^[1] ...

... 近年来,国内外学者们做了大量研究工作,主要集中在运用作图法、直接搜索法、遗传算法、代理模型法^[1,2]等确定性优化方法来改善汽车转向系统的性能 ...

... 若各车轮绕同一瞬时转向中心进行转弯行驶,则两转向轮轴线的延长线相交于后轴延长线上,这一几何关系称为阿克曼几何学^[1] ...

2012

0.0

. 2012, 43(7):2601-2606

Optimization of ackerman steering lingkage based on RSM

基于响应面方法的转向梯形优化设计

Tang Ying-shi , Zhu Biao , Zhu Wei-yu

唐应时, 朱彪, 朱位宇

在考虑悬架跳动时前束角变化的情况下,为实现对车辆转向运动学的最优化,以某小型皮卡车为研究对象,利用ADAMS/CAR软件建立前悬架和转向总成虚拟样机模型,进行转向和轮跳仿真实验.以内、外球头的空间坐标为优化变量,分别以阿克曼误差的均方根和前束角的变化范围为目标,运用DOE方法进行2次试验设计;根据实验结果分别对影响阿克曼误差和前束角的影响因素进行灵敏度分析,运用响应面方法(RSM)拟合出回归模型.利用MATLAB优化工具箱在约束前束角的情况下,对阿克曼误差进行优化,得到硬点的最优值.研究结果表明:在前束角的变化范围减少10％的前提下,转向机构在0°～25°常用转向角度,阿克曼误差减少51.27％.优化后的结果明显地改善了转向的运动学特性,并且避免了单独优化转向,对前束角造成的影响.

2002

0.0

... Simionescu等^[3]对平面四连杆机构的阿克曼关系进行了研究和优化 ...

2004

0.0

... ntaras等^[4]建立了一种带有转向机构的麦弗逊悬架空间运动学模型,并进行了检验 ...

2009

0.0

... Hanzaki等^[5]对齿轮齿条转向机构进行了运动学描述和优化,并指出了对转向误差灵敏度影响较大的因素 ...

2006

0.0

. 2006, 28(11):1011-1014 DOI:doi:10.3321/j.issn:1000-680X.2006.11.012

Robust design of automotive door system

稳健设计方法用于车门系统设计

Huang Jin-ling , Cui An , Chen Xiao-hua

黄金陵, 崔岸, 陈晓华

将Taguchi稳健设计方法应用于车门系统设计.通过将试验设计与计算分析结合获取产品设计质量特性信息;通过实例说明将结构参数优化组合,提高车门铰接系统稳健性的方法.此方法的优点是可以从许多试验条件中选择出最有代表性的少数几项试验,获得可靠的试验结果,且分析计算简单,适用于多参数的产品优化设计.

... 文献^[6]采用Taguchi方法对车门系统进行了稳健设计 ...

2012

0.0

. 2012, 33(4):370-378 DOI:doi:10.3969/j.issn.0254-7805.2012.04.004

6#cod#x003c3; robustness optimization design of the crashworthiness for foam-filled tapered thin-walled structure based on kriging method

基于Kriging的泡沫填充锥形薄壁结构耐撞性6#cod#x003c3;稳健性优化设计

Gao Wei-zhao , Mo Xu-hui , Fu Rui

高伟钊, 莫旭辉, 付锐

锥形薄壁结构的耐撞性设计过程中,其设计变量和噪声因素都具有一定的波动性,都存在不确定性.传统的优化设计方法由于忽略不确定因素的影响,当设计变量产生波动时,往往会引起设计最优目标超出约束界限或者目标函数对设计变量的波动极为敏感,从而导致设计失效.为了考虑参数的不确定影响,论文提出了一种结合试验设计技术、Kriging近似建模技术、蒙特卡罗模拟技术和 6σ质量控制理念的稳健优化设计方法,并应用该方法对泡沫填充锥形薄壁结构的耐撞性进行了优化设计.优化结果表明,该方法提高了锥形薄壁结构的耐撞性,同时也提高了设计变量的可靠性和目标函数的稳健性.由于在优化过程中调用的是Kringing模型,该方法比传统的优化方法具有更高的优化设计效率.算例表明,该方法具有非常强的工程实用性,能大幅提高产品的设计质量.

... 文献^[7,8]运用6#cod#x003c3 ...

2012

0.0

... 文献^[7,8]运用6#cod#x003c3 ...

... 典型的稳健性优化问题可以表示为^[8]: ...

1973

0.0

... 对于稳健性优化,其目标函数既要有能最小化目标函数平均值的性能,又要有能最小化目标函数的波动性能,因此可以表示为^[9]: ...

... 3 约束条件汽车转向过程中梯形底角和齿条运动距离都应为非负数^[9],且杆件长度必须满足构成梯形的几何约束,因此转向梯形优化的约束条件为: ...

2011

0.0

. 2011, 28(4):429-431,443 DOI:doi:10.3969/j.issn.1001-4551.2011.04.011

Robust design model of vehicle divided steering linkage

断开式转向梯形机构的稳健优化设计模型

Liu Wang-yang , Song Xiao-wen , Wang Xiao-hui.

刘汪洋, 宋小文, 王晓晖

摘　要：为解决传统优化设计方法中存在的最优解的函数值波动过大且容易违反约束的问题,将稳健设计运用于汽车断开式转向梯形机构的优化设计中。首先分别分析了稳健设计和转向机构的数学模型;其次在目标函数与约束中同时考虑运动副间隙的影响,建立了稳健优化设计模型。实例分析表明,与传统的优化方法相比较,该模型不仅可以得到较小的误差还具有较高的稳健性。研究结果表明,该方法有较好的可行性与实用性。

2004

0.0

. 2004, 21(6):31-33 DOI:doi:10.3969/j.issn.1001-2354.2004.06.010

Optimization design for robustness of linkages

连杆机构稳健性优化设计

Meng Xian-ju , Zhang Ce , Shi Zhong-xiu

孟宪举, 张策, 师忠秀

将设计变量作为随机变量,建立了连杆机构稳健性优化设计的数学模型,并以一个四杆机构为例进行了说明,将传统的确定性优化设计的结果与稳健性优化设计的结果进行了对比.