数控拉弯工艺中型材变形量的影响因素

引用本文

谷诤巍, 吕萌萌, 李欣, 徐虹. 数控拉弯工艺中型材变形量的影响因素.吉林大学学报:工学版, 2016, 46(4): 1190-1196
GU Zheng-wei, LYU Meng-meng, LI Xin, XU Hong. Influence factors of profile deformation in NC stretch bending. Journal of Jilin University Engineering and Technology Edition, 2016, 46(4): 1190-1196 复制到剪切板

Permissions

数控拉弯工艺中型材变形量的影响因素

谷诤巍, 吕萌萌, 李欣, 徐虹

吉林大学材料科学与工程学院,长春 130022

通讯作者：徐虹(1972-),女,副教授,博士.研究方向:金属塑性成形技术.E-mail:xuhong20141011@163.com

作者简介:谷诤巍(1970-),男,教授,博士.研究方向:金属板材成形技术.E-mail:gzweii@163.com

基金:国家自然科学基金项目(51301074); 吉林省科技发展计划项目(20130102021JC)

摘要

以某轨道车辆双曲率弯梁构件数控拉弯成形为例,推导了基于数控代码计算型材变形量的公式,分析了型材数控拉弯成形过程中伸长量及转角的变化规律及影响因素,将所得的变形量数据导入数值模拟模型中,对弯梁构件因伸长量设置不合理导致的拉裂缺陷进行了分析,并通过试验进行了验证。结果表明:数控拉弯成形过程中,型材总伸长量显著小于数控代码所给拉伸缸总伸长量,型材总转角大于数控代码所给支臂总转角;滑块位置对型材数控拉弯成形影响显著;型材长度、夹钳深度、预拉量不影响型材弯曲拉伸阶段伸长量,但影响型材伸长率。

关键词: 材料合成与加工工艺; 拉弯; 数控代码; 型材变形量

中图分类号:TG306 文献标志码:A 文章编号:1671-5497(2016)04-1190-07

Influence factors of profile deformation in NC stretch bending

GU Zheng-wei, LYU Meng-meng, LI Xin, XU Hong

College of Materials Science and Engineering, Jilin University,Changchun 130022,China

Abstract

Based on the NC stretch bending of a double curvatures beam of a railway vehicle, the formulae to calculate the profile deformation according to NC codes were developed. The variation trend and the influence factors of the elongation and rotation angle of the profile in NC stretch bending were analyzed. Besides, by importing the real deformation data into the numerical simulation model, the crack defect due to unreasonable elongation was analyzed and the corresponding tests were carried out. Results show that in NC stretch bending, the total elongation of the profile is significantly smaller than that of the tensile cylinder provided by the NC code, and the total rotation angle of the profile is larger than that of the arm. The position of the sliding block has a significant influence on the NC stretch bending of profile. The profile length, jig depth and pre-elongation do not affect the profile elongation in the wrap-stretching stage, but influence the elongation ratio.

Keyword: materials synthesis and processing technology; stretch bending; NC code; profile deformation

Show Figures

0 引言

轨道交通运输具有高效、节能和环保的特点, 一直是大规模交通运输的主要方式^[1]。近年来随着高铁技术的发展及推广, 轨道交通运输越来越受到人们的关注^[2]。轨道车辆车体构件尺寸大、精度要求高, 大多采用型材拉弯成形技术进行制造。拉弯技术可以在成形的同时对型材施加轴向拉力, 有利于减小回弹, 保证零件的高精度成形。拉弯有位移控制和力控制两种模式。位移控制模式可以直接控制材料变形, 控制精度较高, 应用更为广泛, 尤其在大尺寸零件的成形方面优势更为突出。位移控制拉弯主要在张臂式数控拉弯机上进行, 成形过程中, 型材在拉弯机两臂上夹钳的带动下弯曲成形。

近年来, 已有学者对型材拉弯成形开展了多方面的研究。刁可山和周贤宾等^{[3, 4]}对闭截面型材的拉弯成形的工艺参数影响规律及零件成形性能进行了研究。金朝海等^{[5, 6]}对铝合金矩形管拉弯成形的成形缺陷进行了数值模拟研究。万敏等^[7]给出了避免大型异型材拉弯成形模拟过程中的动态效应的夹钳轨迹设计方法。刘振宇等^[8]基于CATIAV5平台, 利用其二次开发工具CAA开发了相关系统, 对某一典型型材零件拉弯成形夹钳轨迹进行了设计。张晓丽等^[9]利用数学解析法给出了一种夹钳轨迹计算方法。金朝海和谷诤巍等^{[10, 11]}利用数控拉弯机配套软件PS2F(Profile stretch 2D forming)提供了一种由数控代码反求出夹钳运动轨迹的方法。

以上研究大多利用数值模拟技术研究了型材拉弯成形的工艺参数优化、成形性能及缺陷控制等技术并给出了许多建设性的结论。拉弯成形数值模拟中, 夹钳轨迹的确定是其关键所在。以上研究也给出了多种夹钳轨迹的设计方法, 但除PS2F方法外, 其他均需要在已知型材变形量的基础上进行计算, 而目前尚缺乏型材在数控拉弯过程中变形量的研究资料。生产中因材料波动和拉弯设备等原因经常出现需要对数控代码进行调整的情况, 而型材的变形量与生产中拉弯机运行所依据的数控代码并不一致, 无依据地对数控代码进行调整很容易使型材过量拉伸导致拉裂, 或拉伸不足而导致成形件轮廓精度差。因此, 有必要对型材在数控拉弯过程中的变形量进行研究, 找出数控代码与变形量之间的对应关系, 以对拉弯成形数值模拟及生产中数控代码调整提供帮助。

1 基于数控代码的型材变形量计算

1.1 张臂式拉弯成形机理

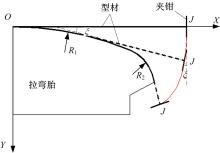
图1为张臂式数控拉弯机及其结构简图。如图1所示, 拉弯胎固定在工作台上; 型材置于拉弯胎中, 型材两端由夹钳夹持; 夹钳安装于拉伸缸中, 可以轴向伸缩; 拉伸缸通过滑块安装在支臂上, 滑块可沿支臂轴向移动; 滑块上安装有转轴, 拉伸缸可绕该转轴转动。拉弯过程中, 确定滑块位置后将拉伸缸固定, 然后将型材两端插于拉伸缸上的夹钳中, 拉伸缸的伸缩带动夹钳运动, 从而使型材伸长; 支臂的转动带动型材旋转, 从而包绕拉弯胎弯曲成形。

一般的拉弯过程分为预拉、弯曲拉伸和补拉三个阶段。预拉过程中, 支臂不动, 夹钳后移使型材伸长并达到屈服状态; 随后进入弯曲拉伸阶段, 该阶段, 夹钳和支臂同时运动, 使型材边拉伸边弯曲以至型材完全包绕拉弯胎完成弯曲成形; 最后施加一定程度的补拉, 进一步控制成形件卸载后的回弹, 补拉过程中支臂不再转动, 仅夹钳运动。

	Figure Option View Download New Window
	图1 数控拉弯机及其结构简图Fig.1 NC stretch bending machine and structure sketches

1.2 数控代码分析

典型的拉弯机数控代码主体(Part program body)如图2所示, 代码主体由多个组块(Block)构成, 每个组块给出一组拉伸缸伸缩量和支臂转角数据。图2中param ID“ 1087” 和“ 108A” 代表拉弯机两端拉伸缸的伸缩量, param ID“ 1088” 和“ 108B” 代表两端支臂的转角。

	Figure Option View Download New Window
	图2 数控代码Fig.2 NC codes

1.3 夹钳轨迹计算

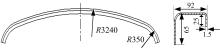
生产中, 轨道车辆车体构件大多为等曲率或双曲率弯曲件。本文以某轨道车辆车体上双曲率弯梁构件为对象开展研究。零件结构特征如图3所示。该件轮廓由中部R3240的大弧和两端R350的小弧构成, 大弧角度 $\begin{matrix} θ = 38 °, \end{matrix}$ 小弧角度 $\begin{matrix} θ' = 57 °, \end{matrix}$ 故弯曲件单侧弯曲总角度为76° 。该件数控代码主体由68个组块构成, 其拉伸缸伸总伸长量Δ S_总=427.6 mm, 支臂总转角α _总=64.57° , 可以看出数控代码所给转角角度与弯曲件的角度并不对应。

	Figure Option View Download New Window
	图3 双曲率弯梁构件结构特征Fig.3 Structural characteristics of a double curvatures beam

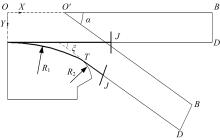
拉弯过程三个阶段中, 预拉及补拉阶段型材仅伸长不弯曲, 弯曲拉伸阶段型材同时完成拉伸和弯曲。夹钳轨迹设计的关键是弯曲拉伸阶段夹钳运动路径的确定。图4为双曲率弯曲件拉弯过程中夹钳运动轨迹示意图。由于零件结构对称, 只取一半进行分析。由图4可知, 型材转动 $\begin{matrix} ξ \end{matrix}$ 角度的同时, 夹钳相对原始位置也转动 $\begin{matrix} ξ \end{matrix}$ 角度; 型材沿轴向伸长, 夹钳则在 $\begin{matrix} X 、 Y \end{matrix}$ 方向分别移动一定的距离。因此, 在已知型材伸长量和转动角度的情况下, 即可通过几何关系计算得出夹钳的运动轨迹。

	Figure Option View Download New Window
	图4 夹钳轨迹示意图Fig.4 Schematic diagram of jig’ s trajectory

弯曲拉伸阶段, 型材包绕第一段的过程中, 夹钳坐标 $\begin{matrix} (X_{J}, Y_{J}) \end{matrix}$ 的计算公式如下:

$\begin{matrix} \{\begin{matrix} X_{J} = (R_{1} + t / 2) sinξ + \\ [L_{0} + L_{pre} - h + ΔL - (R_{1} + t / 2) ξ] cosξ \\ Y_{J} = (R_{1} + t / 2) (1 - cosξ) + \\ [L_{0} + L_{pre} - h + ΔL - (R_{1} + t / 2) ξ] sinξ \end{matrix} (1) \end{matrix}$

式中: $\begin{matrix} R_{1} 为第一段圆弧的半径和角度; t 为型材厚度; ΔL 和 ξ 分别为型材弯曲拉伸阶段伸长量和转角的累计值; L_{0} 为型材原始长度; L_{pre} 为预拉量; h \end{matrix}$ 为夹钳深度。

型材包绕第二段的过程中, 夹钳坐标的计算公式如下:

$\begin{matrix} \{\begin{matrix} X_{J} = X_{2} + (R_{2} + t / 2) sinξ + [L_{0} + L_{pre} - h + \\ ΔL - (R_{1} + t / 2) θ - (R_{2} + t / 2) (ξ - θ)] cosξ \\ Y_{J} = Y_{2} - (R_{2} + t / 2) cosξ + [L_{0} + L_{pre} - h + \\ ΔL - (R_{1} + t / 2) θ - (R_{2} + t / 2) (ξ - θ)] sinξ \end{matrix} (2) \end{matrix}$

计算过程中, 角度使用弧度制, 型材伸长量和转角均为累计值。

1.4 型材变形量计算

由夹钳轨迹计算式(2)可知, 测得相关数据后, 只需型材的伸长量和转角, 即可算出夹钳轨迹。然而, 拉弯机运行的数控代码与型材的变形量并不一致。为计算拉弯过程中型材的变形量, 对张臂式数控拉弯机的运行机理进行简化, 如图5所示。其中, 支臂转轴简化为 $\begin{matrix} O' 点, 滑块简化为 B 点, 滑块转轴简化为 D 点, 夹钳简化为 J \end{matrix}$ 点。

	Figure Option View Download New Window
	图5 拉弯机运动机理示意图Fig.5 Schematic diagram of movement mechanism of stretch bending machine

首先计算型材包绕第一段圆弧时的变形量。当支臂旋转 $\begin{matrix} α 角度后, 可得 D \end{matrix}$ 点坐标:

$\begin{matrix} \{\begin{matrix} X_{D} = X_{O'} + L_{OB} cosα - H_{BD} sinα \\ Y_{D} = L_{OB} \sin α + H_{BD} cosα \end{matrix} (3) \end{matrix}$

式中: $\begin{matrix} L_{OB} 为 OB 段长度, 即滑块与拉弯胎中心的距离; L_{BD} 为 BD 段长度, 即拉伸缸距支臂的垂直距离; X_{O'} 为 O' \end{matrix}$ 横坐标。根据几何关系可得:

$\begin{matrix} \begin{matrix} tanξ = \frac{Y_{D} - H_{BD}}{X_{D} - (R_{1} + t / 2) \tan (ξ / 2)} (4) \\ 又 \\ tanξ = \frac{2 \tan (ξ / 2)}{1 - ta n^{2} (ξ / 2)} (5) \\ 故 \\ \tan (ξ / 2) = \\ \frac{\sqrt[]{X_{D}^{2} - (Y_{D} - H_{BD} - 2 (R_{1} + t / 2)) (H_{BD} - Y_{D})} - X_{D}}{Y_{D} - H_{B D} - 2 (R_{1} + t / 2)} (6) \end{matrix} \end{matrix}$

由此, 可计算出型材转角 $\begin{matrix} \end{matrix}$ ξ。根据型材转角可得型材包绕拉弯胎时的切点T坐标:

$\begin{matrix} \{\begin{matrix} X_{T} = (R_{1} + t / 2) sinξ \\ Y_{T} = H_{BD} + (R_{1} + t / 2) (1 - cosξ) \end{matrix} (7) \end{matrix}$

于是, 根据相应几何关系, 可得型材伸长量的累计值:

$\begin{matrix} \begin{matrix} ΔL = Δs - [X_{O'} + L_{OB} - (R_{1} + t / 2) ξ - \\ \sqrt[]{{(X_{D} - X_{T})}^{2} + {(Y_{D} - Y_{T})}^{2}}] (8) \end{matrix} \end{matrix}$

型材包绕第二段圆弧过程中, $\begin{matrix} T \end{matrix}$ 点坐标计算式更新为:

$\begin{matrix} \{\begin{matrix} X_{T} = (R_{1} + t / 2) sinθ - (R_{2} + t / 2) sinθ + \\ (R_{2} + t / 2) sinξ \\ Y_{T} = H + (R_{1} + t / 2) (1 - cosθ) + \\ (R_{2} + t / 2) (cosθ - cosξ) \end{matrix} (9) \end{matrix}$

$\begin{matrix} \end{matrix}$ D点坐标计算式同式(3),因D、T共线,则:

$\begin{matrix} tanξ = \frac{Y_{D} - Y_{T}}{X_{D} - X_{T}} = \frac{sinξ}{cosξ} (10) \end{matrix}$

联合式(3)(9)(10), 并设中间变量 $\begin{matrix} A 、 B, \end{matrix}$ 令:

$\begin{matrix} \begin{matrix} A = L_{OB} sinα + H_{BD} cosα - H_{BD} - (R_{1} + \\ t / 2) (1 - cosθ) - (R_{2} + t / 2) cosθ (11) \\ B = X_{O'} + L_{OB} cosα - H_{BD} sinα - (R_{1} + \\ t / 2) sinθ + (R_{2} + t / 2) sinξ (12) \\ 可得 \\ \frac{A + (R_{2} + t / 2) cosξ}{B - (R_{2} + t / 2) sinξ} = \frac{sinξ}{cosξ} (13) \\ 又 \\ si n^{2} ξ + co s^{2} ξ = 1 (14) \\ 故 \\ cosξ = \frac{- A (R_{2} + t / 2)}{A^{2} + B^{2}} + \\ \frac{\sqrt[]{A^{2} (R_{2} {+ t / 2)}^{2} - (A^{2} + B^{2}) [(R_{2} {+ t / 2)}^{2} - B^{2}]}}{A^{2} + B^{2}} (15) \end{matrix} \end{matrix}$

从而可得型材转角。进而可得型材包绕第二段圆弧时伸长量的累计值:

$\begin{matrix} \begin{matrix} ΔL = Δs - [X_{O'} + L_{OB} - (R_{1} + t / 2) θ - (R_{2} + \\ t / 2) (ξ - θ) - \sqrt[]{{(X_{D} - X_{T})}^{2} + {(Y_{D} - Y_{T})}^{2}}] (16) \end{matrix} \end{matrix}$

利用型材各步变形量的累计值减去上一步变形量的累计值, 即可得到型材变形量的分步值。

2 型材变形量分析

2.1 型材变形量特征分析

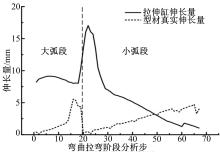
将计算得出的型材各步的伸长量与数控代码所给的拉伸缸伸长量进行对比, 如图6所示。由图6可知, 型材包绕大弧段过程中, 虽然各步的拉伸缸伸长量变化不大, 但型材变形量逐步增大; 由大弧段向小弧段过渡时, 拉伸缸伸长量和型材变形量变化剧烈, 二者均急剧增大后迅速减小; 型材包绕小弧段过程中, 型材的伸长量随拉伸缸伸长量的减小而增大, 二者变化趋势相反。此外, 计算得到型材的总伸长量为157.74 mm, 明显小于拉伸缸总伸长量427.6 mm。

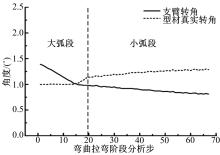
	Figure Option View Download New Window
	图6 型材伸长量与拉伸缸伸长量对比Fig.6 Comparison between elongation of profile and that of tensile cylinder

将计算得出的型材各步的转角与数控代码所给的支臂转角进行对比, 如图7所示。可以看出, 弯曲过程中, 支臂转角缓慢减小, 型材转角缓慢增大, 但二者的变化幅度均不大; 型材包绕大弧段时支臂转角大于型材的转角, 型材包绕小弧段时支臂转角小于型材转角。此外, 计算得到型材总转角为75.98° , 大于支臂总转角64.57° 。

	Figure Option View Download New Window
	图7 型材转角与支臂转角对比Fig.7 Comparison between rotation angle of profile and that of arm

2.2 型材变形量影响因素

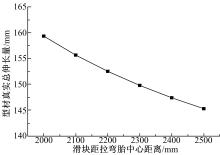
由上文型材变形量计算公式(15)(16)可知, 要计算型材变形量, 除需输入数控代码数据外, 还需输入的数据有滑块距拉弯胎中心距离 $\begin{matrix} L_{OB} 、拉伸缸距支臂距离 L_{BD} 、支臂转轴坐标 X_{O'} 、型材厚度 t 、弯曲件半径 R 。 \end{matrix}$ 对于给定的弯曲件, 除滑块位置可调外, 数控代码、拉弯机和弯曲件等数据均为确定值, 因此滑块位置是影响型材变形量的主要因素。对于给定的弯梁零件, 计算其总伸长量和转角随滑块位置的变化曲线, 分别如图8和图9所示。由图8、图9可知, 滑块位置对型材变形量影响显著, 型材伸长量和转角均随滑块距拉弯胎中心距离的减小而增大。因此, 生产中应注意合理设置滑块的位置:若滑块距拉弯胎中心过近, 容易导致型材过量拉伸而拉裂; 若滑块距拉弯胎中心过远, 容易导致型材弯曲和拉伸均不充分, 严重影响成形件的轮廓精度。

	Figure Option View Download New Window
	图8 型材总伸长量与滑块位置的关系Fig.8 Relationship between total elongation of profile and position of slide block

	Figure Option View Download New Window
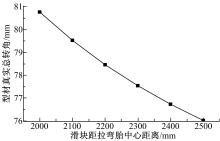	图9 型材总转角与滑块位置的关系Fig.9 Relationship between total rotation angle of profile and position of slide block

此外, 由型材变形量计算公式(15)(16)可知, 虽然型材初始长度 $\begin{matrix} L_{0} 、预拉量 L_{pre} 、夹钳深度 h \end{matrix}$ 对型材弯曲拉伸阶段变形量没有影响, 但这些参数影响型材的伸长率, 生产时也应注意。

3 拉弯成形模拟及试验

生产中因型材伸长量调整不合理经常出现轮廓精度差和拉裂等缺陷, 其中最严重的是拉裂(见图10), 因型材拉裂后不可调修。对于给定弯曲件, 导致其拉裂的最主要原因为滑块位置设置不合理而导致型材伸长量过大而拉裂。下面将利用数值模拟技术对该情况进行分析。

	Figure Option View Download New Window
	图10 拉裂缺陷Fig.10 Rack defect

利用式(15)(16)计算出型材变形量, 并将变形量数据代入式(2)中计算出夹钳轨迹, 利用所得数据构建拉弯成形模拟模型, 如图11所示。分两种情况进行模拟, 并开展相应的成形试验。一种设置合理滑块位置, 一种减小滑块距拉弯胎中心的距离。模拟成形件厚度分布云图及相应试验结果分别如图12和图13所示。由图12可知, 滑块距拉弯胎中心过近时, 型材拉伸过量导致厚度减小过大而拉裂; 由图13可知,

	Figure Option View Download New Window
	图11 拉弯模拟模型Fig.11 Stretch bending simulation model

	Figure Option View Download New Window
	图12 滑块距拉弯胎中心过近时模拟及试验结果Fig.12 Results of simulation and test when slide block is too close to center of dies

	Figure Option View Download New Window
	图13 滑块位置合理时模拟及试验结果Fig.13 Results of simulation and test when slide block is properly placed

滑块位置合理时, 零件成形质量良好。试验与模拟结果的一致性也证明了本文型材变形量相关研究的正确性。

4 结论

(1)数控拉弯成形过程中, 型材伸长量和转角与数控代码所给拉伸缸伸长量和支臂转角并不一致, 型材总伸长量显著小于拉伸缸总伸长量, 型材总转角大于支臂总转角。对本文研究的双曲率弯梁构件而言, 型材总伸长量仅为拉伸缸总伸长量的37%, 型材总转角为支臂总转角的118%。

(2)双曲率弯曲件数控拉弯成形过程中, 型材包绕各圆弧段时伸长量均随弯曲程度增大而逐步增大; 在大弧段向小弧段过渡时型材伸长量急剧增大后迅速减小。

(3)滑块位置对型材数控拉弯成形影响显著。若滑块距拉弯胎中心过近, 容易导致型材过量拉伸而拉裂; 若滑块距拉弯胎中心过远, 容易导致型材弯曲和拉伸均不充分, 严重影响成形件的轮廓精度。

(4)型材长度、夹钳深度、预拉量不影响型材数控拉弯成形弯曲拉伸阶段的伸长量, 但影响型材伸长率, 生产时应合理设置。

The authors have declared that no competing interests exist.

参考文献

View Option

[1]	王胜满. 用于地铁车辆的不锈钢型材拉弯成形缺陷[J]. 吉林大学学报: 工学版, 2013, 43(6): 1546-1550. Wang Sheng-man. Stretch bend forming defects of stainless steel profiles of metro vehicles[J]. Journal of Jilin University (Engineering and Technology Edition), 2013, 43(6): 1546-1550. [本文引用:1]
[2]	王胜满. 高速动车组端角柱构件的弯曲成形缺陷[J]. 吉林大学学报: 工学版, 2010, 40(增刊1): 247-251. Wang Sheng-man. Forming defects of outside profile pillar parts of CRH train[J]. Journal of Jilin University (Engineering and Technology Edition), 2010, 40(Sup. 1): 247-251. [本文引用:1]
[3]	刁可山, 周贤宾, 李晓星, 等. 矩形截面型材拉弯成形[J]. 北京航空航天大学学报, 2005, 31(2): 134-137. Diao Ke-shan, Zhou Xian-bin, Li Xiao-xing, et al. Stretch bending of aluminum extrusion[J]. Journal of Beijing University of Aeronautics and Astronautics, 2005, 31(2): 134-137. [本文引用:1]
[4]	周贤宾, 刁可山, 李晓星, 等. 闭截面型材的拉弯成形性[J]. 北京航空航天大学学报, 2006, 32(10): 1168-1173. Zhou Xian-bin, Diao Ke-shan, Li Xiao-xing, et al. Stretch bending formability of profile[J]. Journal of Beijing University of Aeronautics and Astronautics, 2006, 32(10): 1168-1173. [本文引用:1]
[5]	金朝海, 周贤宾, 刁可山, 等. 铝合金矩形管拉弯成形过程的数值模拟[J]. 材料科学与工艺, 2004, 12(6): 572-575. Jin Chao-hai, Zhou Xian-bin, Diao Ke-shan, et al. Numerical simulation of a stretch bending process for extruded aluminum rectangular tubes[J]. Materials Science and Technology, 2004, 12(6): 572-575. [本文引用:1]
[6]	金朝海, 周贤宾, 刁可山, 等. 铝合金型材拉弯成形回弹的有限元模拟[J]. 材料科学与工艺, 2004, 12(4): 394-397. Jin Chao-hai, Zhou Xian-bin, Diao Ke-shan, et al. Springback analysis for stretch bending of aluminum profile[J]. Materials Science and Technology, 2004, 12(4): 394-397. [本文引用:1]
[7]	万敏, 洪振军, 李卫东, 等. 大型异型材拉弯成形有限元模拟技术研究[J]. 锻压技术, 2008, 33(5): 160-164. Wan Min, Hong Zhen-jun, Li Wei-dong, et al. FEM simulation technology on stretch bending of long profile with complex section[J]. Forging and Stamping Technology, 2008, 33(5): 160-164. [本文引用:1]
[8]	刘振宇, 金朝海, 李小强, 等. 基于CATIA的型材拉弯夹钳加载轨迹设计系统[J]. 材料科学与工艺, 2010, 18(S1): 158-161. Liu Zhen-yu, Jin Chao-hai, Li Xiao-qiang, et al. Development of trajectory design of jaws in profile stretch-bending based on CATIA[J]. Materials Science and Technology, 2010, 18(S1): 158-161. [本文引用:1]
[9]	张晓丽, 李晓星, 周贤宾, 等. 复杂截面铝合金型材拉弯成形有限元模拟[J]. 塑性工程学报, 2004, 11(4): 44-47. Zhang Xiao-li, Li Xiao-xing, Zhou Xian-bin, et al. Finite element simulation for stretch-wrap bending of aluminium profile with complex cross section[J]. Journal of Plasticity Engineering, 2004, 11(4): 44-47. [本文引用:1]
[10]	金朝海, 周贤宾. 基于PS2F的铝型材拉弯回弹研究[J]. 塑性工程学报, 2007, 14(3): 1-4. Jin Chao-hai, Zhou Xian-bin. PS2F-based study on springback in stretch-wrap bending of aluminum profiles[J]. Journal of Plasticity Engineering, 2007, 14(3): 1-4. [本文引用:1]
[11]	金朝海, 周贤宾, 谷诤巍, 等. 基于位移控制的型材2D张臂式拉弯加载轨迹设计及数控代码生成[J]. 塑性工程学报, 2009, 16(2): 66-71. Jin Chao-hai, Zhou Xian-bin, Gu Zheng-wei, et al. Jaw trajectory design for displacement-controlled profile 2D stretch-wrap bending and part program generation[J]. Journal of Plasticity Engineering, 2009, 16(2): 66-71. [本文引用:1]

2013

0.0

. 2013, 43(6):1546-1550 DOI:doi:10.7964/jdxbgxb201306019

Stretch bend forming defects of stainless steel profiles of metro vehicles

用于地铁车辆的不锈钢型材拉弯成形缺陷

Wang Sheng-man.

王胜满

摘　要：对某型地铁车辆用不锈钢车顶弯梁的拉弯成形工艺进行了模拟研究，研究了此类构件起皱、截面畸变及轮廓精度差等成形缺陷的成因及控制方法。结果表明：预拉量、补拉量等工艺参数对起皱缺陷影响较小，增加弯曲拉量能够有效控制构件起皱；对拉弯件的截面收缩量补偿后，可以消除截面小边外翻的畸变缺陷；采用合理的拉弯工艺参数及精确补偿的拉弯胎具，可以显著减小弯曲回弹，提高轮廓精度，获得高质量的拉弯件。

... 0 引言轨道交通运输具有高效、节能和环保的特点,一直是大规模交通运输的主要方式^[1] ...

2010

0.0

. 2010, 40(增刊1):247-251

Forming defects of outside profile pillar parts of CRH train

高速动车组端角柱构件的弯曲成形缺陷

Wang Sheng-man.

王胜满

Bending process of outside profile pillar assembled in highspeed railway vehicle was simulated and analyzed using finite element software PamStamp 2G for researching bending process of large scale profile with complicated nonsymmetrical hollow section. Methods for controlling bending defects such as cross section distortion, line segment curve and low longitudinal profile precision were proposed. The results show that line segment curve can be improved effectively by adjusting forming direction and using back load is. The larger the back loadis, the smaller the curve value of line segment becomes. A new mandrel was used for controlling cross section distortion and improving longitudinal profile precision, and the smaller gaps between mandrel and inside wall of profile yields smaller section distortion value and higher longitudinal profile precision. The rationality of optimized process was tested and verified by experiments.

通过PamStamp 2G有限元软件对高速轨道车辆端角柱的弯曲成形过程进行模拟分析，研究了大型复杂非对称封闭截面型材的弯曲成形工艺，提出了端角柱零件截面畸变、直线段弯曲以及纵向轮廓精度差等缺陷的控制方法。结果表明：调整成形方向并对直线段施加背压力能够有效减小工件直线段的弯曲缺陷，背压力越大，直线段弯曲越小；型材内部添加新型支撑芯轴能够有效控制工件截面畸变，提高纵向轮廓精度，且支撑芯轴与型材表面间隙越小，成形后零件的截面畸变量越小，纵向轮廓精度越高。通过试验对比，验证了优化工艺的合理性。

... 近年来随着高铁技术的发展及推广,轨道交通运输越来越受到人们的关注^[2] ...

2005

0.0

. 2005, 31(2):134-137 DOI:doi:10.3969/j.issn.1001-5965.2005.02.006

Stretch bending of aluminum extrusion

矩形截面型材拉弯成形

Diao Ke-shan , Zhou Xian-bin , Li Xiao-xing

刁可山, 周贤宾, 李晓星

An experimental study on stretch bending of aluminum extrusion was conducted under different pre- and post-stretching elongation. Cross section distortion caused by radial stress during bending process is one of main parameters concerning forming precision. As shown in the test, cross section distorted as the extrusion was bent into contact with the die. Main distortion of cross section is sagging of upper flange. Sagging distribution along the extrusion was given and sagging of middle cross section is not the maximum. It can be seen that the larger is pre- or post-stretching elongation, the larger is cross section distortion. Springback is a common phenomenon during the unloading process, which is influenced by many parameters and difficulty to be eliminated. Pre-and post-stretching elongation can both reduce springback. When pre-stretching elongation exceeds a certain value, its effect on reducing springback is not obvious, which is similar with post-stretching elongation.

针对铝合金矩形中空截面挤压型材进行了不同预拉和补拉的拉弯成形试验研究,获取了预拉和补拉对成形精度的影响规律.截面畸变是影响成形精度最主要的因素,由弯曲过程中的径向压力引起.试验表明,型材靠模弯曲即发生截面畸变,主要表现为上腹板的塌陷,沿型材长度方向截面畸变量不同,最大畸变量并不位于型材中间对称截面处;增大预拉和补拉,截面畸变增大.弯曲卸载回弹是影响零件贴模度的主要因素,其大小受多种因素影响,规律复杂.增大预拉和补拉,回弹减小;当预拉和补拉增大到一定值时,增大拉伸量减小回弹的效果不再明显.

... 刁可山和周贤宾等^[3,4]对闭截面型材的拉弯成形的工艺参数影响规律及零件成形性能进行了研究 ...

2006

0.0

. 2006, 32(10):1168-1173 DOI:doi:10.3969/j.issn.1001-5965.2006.10.009

Stretch bending formability of profile

闭截面型材的拉弯成形性

Zhou Xian-bin , Diao Ke-shan , Li Xiao-xing

周贤宾, 刁可山, 李晓星

Stretch-wrap bending is the essential forming processing for profile. Cross section distortion is the common defect during the stretch-wrap bending of profile, and it brings cross-effect with thinning of thickness and springback. The stretch-wrap bending formability for profile is much more difficult to analyze and to evaluate than that for sheet forming. The concept of stretch-wrap bending formability for profile was presented and an analytic model for profile with rectangular section was established. The effect of the geometric parameters such as section configuration, relative height and wall-thickness distribution of profile on stretch-wrap bending formability was studied based on finit element method(FEM) numerical simulation. The principle for optimization design of cross section was proposed in order to improve the stretch-wrap bending formability of profile.

拉弯是型材的基本成形方法.截面畸变是型材拉弯成形中的常见缺陷,并对型材的回弹和变薄有交叉影响,型材拉弯成形性的分析评估远比板材成形复杂.提出了型材拉弯成形性的概念,建立了矩形截面型材拉弯成形性分析模型,基于有限元数值模拟研究了截面结构、相对高度和壁厚分布等几何参数对拉弯成形性的影响规律,从提高拉弯成形性出发提出了型材截面优化设计的原则.

... 刁可山和周贤宾等^[3,4]对闭截面型材的拉弯成形的工艺参数影响规律及零件成形性能进行了研究 ...

2004

0.0

. 2004, 12(6):572-575 DOI:doi:10.3969/j.issn.1005-0299.2004.06.004

Numerical simulation of a stretch bending process for extruded aluminum rectangular tubes

铝合金矩形管拉弯成形过程的数值模拟

Jin Chao-hai , Zhou Xian-bin , Diao Ke-shan

金朝海, 周贤宾, 刁可山

采用动力显式有限元程序Pam-Stamp2000对铝合金矩形管的一种拉弯成形过程进行了模拟,分析了模具最大作用力、管材截面畸变、成形件回弹的变化规律.模拟结果和文献给出的实验结果相当吻合,即模具最大作用力、管材截面畸变均随预拉力的增加而增加,而成形零件的回弹随预拉的增加而减小;相同预拉状况下,增加壁厚有利于减小截面畸变.此外,数值模拟给出了模具对管材作用力及管材夹持端轴向拉伸作用力随模具行程的变化规律,揭示了本文的拉弯实质上是一种非恒定轴向作用力(呈渐增趋势)的拉弯成形方式,这与本文的解析结果高度一致.

... 金朝海等^[5,6]对铝合金矩形管拉弯成形的成形缺陷进行了数值模拟研究 ...

2004

0.0

. 2004, 12(4):394-397 DOI:doi:10.3969/j.issn.1005-0299.2004.04.016

Springback analysis for stretch bending of aluminum profile

铝合金型材拉弯成形回弹的有限元模拟

Jin Chao-hai , Zhou Xian-bin , Diao Ke-shan

金朝海, 周贤宾, 刁可山

对回弹进行有效预测与控制是提高型材弯曲件精度的关键.为了分析轴向作用力对拉弯制件回弹的影响,采用动力显式有限元仿真软件Pam-Stamp2000对中空矩形截面铝型材AA6082(T5)转臂式拉弯成形过程进行了数值模拟,并与实验结果进行了对比.结果表明:增加预拉可以减小制件的回弹,但预拉达到一定水平后,继续加大预拉力对减小回弹将基本不起作用;当预拉不充分时,增加补拉同样有利于减小制件的回弹,但过大的补拉力对于减小回弹几乎没有任何帮助.可见,型材拉弯成形制件的回弹不仅与加载顺序及加载程度密切相关,同时也受到材料应变硬化特性的制约.

... 金朝海等^[5,6]对铝合金矩形管拉弯成形的成形缺陷进行了数值模拟研究 ...

2008

0.0

. 2008, 33(5):160-164 DOI:doi:10.3969/j.issn.1000-3940.2008.05.042

FEM simulation technology on stretch bending of long profile with complex section

大型异型材拉弯成形有限元模拟技术研究

Wan Min , Hong Zhen-jun , Li Wei-dong

万敏, 洪振军, 李卫东

异型材几何截面非对称特征与拉弯围转成形特点构成了型材拉弯有限元模拟过程中的许多特殊的问题,如易发生较大的扭转变形,出现贴模错误,初始接触错误,加载轨迹长,动态效应明显,刚体发生变形,计算量过大等.本文针对某飞机上大型复杂异型截面型材零件拉弯过程有限元模拟技术进行了研究,通过对加引导面模具设计、网格划分、加载轨迹设计、夹钳及毛料圆角处理等关键技术的研究,解决了型材拉弯成形模拟中的上述问题,应用有限元分析软件ABAQUS,实现了大型异型材的拉弯成形数值模拟.

... 万敏等^[7]给出了避免大型异型材拉弯成形模拟过程中的动态效应的夹钳轨迹设计方法 ...

2010

0.0

. 2010, 18(S1):158-161

Development of trajectory design of jaws in profile stretch-bending based on CATIA

基于CATIA的型材拉弯夹钳加载轨迹设计系统

Liu Zhen-yu , Jin Chao-hai , Li Xiao-qiang

刘振宇, 金朝海, 李小强

针对型材拉弯成形过程中的夹钳加载轨迹，基于CATIA V5平台，利用其二次开发工具CAA,开发了相关系统，工艺设计人员可以直接在CATIA环境里对型材拉弯过程中的相关参数进行控制，并计算出夹钳加载轨迹,利用所开发的系统，对某一典型型材零件拉弯成形夹钳轨迹进行了设计，并进行了有限元模拟分析，为该零件的实际拉弯成形提供了指导。

... 刘振宇等^[8]基于CATIAV5平台,利用其二次开发工具CAA开发了相关系统,对某一典型型材零件拉弯成形夹钳轨迹进行了设计 ...

2004

0.0

. 2004, 11(4):44-47 DOI:doi:10.3969/j.issn.1007-2012.2004.04.010

Finite element simulation for stretch-wrap bending of aluminium profile with complex cross section

复杂截面铝合金型材拉弯成形有限元模拟

Zhang Xiao-li , Li Xiao-xing , Zhou Xian-bin

张晓丽, 李晓星, 周贤宾

本文对矩形管截面铝合金型材拉弯成形工艺进行了研究,建立了位移控制拉弯工艺的有限元模型,采用ABAQUS软件对几种不同截面的铝合金型材拉弯成形过程进行了数值模拟,分析了不同补拉量对型材的截面畸变和回弹的影响以及不同截面形状抵抗拉弯成形时截面畸变的能力.其结果和方法对铝合金型材的拉弯成形工艺具有参考价值.

... 张晓丽等^[9]利用数学解析法给出了一种夹钳轨迹计算方法 ...

2007

0.0

. 2007, 14(3):1-4 DOI:doi:10.3969/j.issn.1007-2012.2007.03.001

PS2F-based study on springback in stretch-wrap bending of aluminum profiles

基于PS2F的铝型材拉弯回弹研究

Jin Chao-hai , Zhou Xian-bin.

金朝海, 周贤宾

采用型材2D拉弯仿真软件PS2F对矩形截面铝型材张臂式拉弯进行了分析,探讨了弯曲半径、弯曲角度及铝合金材料性能对型材单曲率拉弯回弹的影响.研究结果表明,在缺省的拉伸力控制参数设置及夹钳加载轨迹由软件自动优化的情况下,对于给定的弯曲半径,型材零件端部的回弹量随弯曲角度的增加呈指数上升趋势;对于一定的弯曲角度,零件端部回弹量随弯曲半径的增加而线性增加;在相同弯曲半径和弯曲角度的情况下,材料性能对拉弯回弹量有重要的影响.

... 金朝海和谷诤巍等^[10,11]利用数控拉弯机配套软件PS2F(Profile stretch 2D forming)提供了一种由数控代码反求出夹钳运动轨迹的方法 ...

2009

0.0

. 2009, 16(2):66-71

Jaw trajectory design for displacement-controlled profile 2D stretch-wrap bending and part program generation

基于位移控制的型材2D张臂式拉弯加载轨迹设计及数控代码生成

Jin Chao-hai , Zhou Xian-bin , Gu Zheng-wei

金朝海, 周贤宾, 谷诤巍

针对Cyril Bath公司数控型材2D张臂式拉弯设备,提出了型材拉弯过程中轴向拉伸变形量的控制方法,解决了位移控制模式下型材拉弯夹钳加载轨迹较难设计的问题,为通过有限元模拟进行夹钳运动轨迹的优化奠定了基础.同时研究了拉弯设备的数控代码格式,给出了由夹钳运动轨迹自动生成数控代码的方法.通过实例验证了所提出算法的有效性和可靠性.

... 金朝海和谷诤巍等^[10,11]利用数控拉弯机配套软件PS2F(Profile stretch 2D forming)提供了一种由数控代码反求出夹钳运动轨迹的方法 ...