复杂工况下基于最佳滑移率的汽车牵引力控制算法

引用本文

刘刚, 靳立强, 陈鹏飞. 复杂工况下基于最佳滑移率的汽车牵引力控制算法. 2016, 46(5): 1391-1398
LIU Gang, JIN Li-qiang, CHEN Peng-fei. Vehicle traction control algorithm based on optimal slip ratio under complicated road conditions. Journal of Jilin University Engineering and Technology Edition, 2016, 46(5): 1391-1398 复制到剪切板

Permissions

复杂工况下基于最佳滑移率的汽车牵引力控制算法

刘刚^1,², 靳立强¹, 陈鹏飞¹

1.吉林大学汽车仿真与控制国家重点实验室,长春 130022

2.河南工学院,河南新乡 453002

通信作者:靳立强(1976-),男,教授,博士生导师.研究方向:汽车底盘电子控制技术,电动汽车四轮独立驱动技术.E-mail:jinlq@jlu.edu.cn

作者简介:刘刚(1981-),男,博士研究生.研究方向:汽车底盘电子控制技术.E-mail:gliu14@mails.jlu.edu.cn

基金:国家自然科学基金项目(50907030); 中国博士后科学基金项目(2013M54024B)

摘要

为了提高车辆在复杂路面下的起步加速驱动能力和稳定性,提出了基于最佳滑移率的牵引力控制策略。根据当前路况下的滑转率和附着系数采用可变遗忘因子最小二乘法求出最佳滑转率。系统通过发动机转矩调节和主动制动调节两种方式协调控制,将车轮的滑转率保持在最佳滑转率附近,从而提高车辆加速性能和稳定性。在Matlab/Simulink下的仿真结果及实车冬季场地试验表明了该系统的有效性和工程应用价值。

关键词: 车辆工程; 牵引力控制系统; 驱动防滑; 主动制动; 转矩调节; 协调控制

中图分类号:U461 文献标志码:A 文章编号:1671-5497(2016)05-1391-08

Vehicle traction control algorithm based on optimal slip ratio under complicated road conditions

LIU Gang^1,², JIN Li-qiang¹, CHEN Peng-fei¹

1.State Key Laboratory of Automotive Simulation and Control, Jilin University,Changchun 130022,China

2.Henan Institute of Technology, Xinxiang 453002, China

Abstract

In order to improve vehicle starting acceleration performance and stability under complicated road conditions, a traction control algorithm based on extremum-seeking with forgetting factors Recursive Least Square (RLS) algorithm was proposed. The tire slip ratio close to the optimal slip ratio can be controlled by the coordinate strategy between the engine torque control and the active brake control. Simulation and winter road test results show that the proposed control strategy can improve the vehicle dynamics performance.

Keyword: vehicle engineering; traction control system; driving slip; active braking; torque adjustment; coordinated control

Show Figures

0 引言

牵引力控制系统(Traction control system, TCS)是电子稳定程序(Electronic stability program, ESP)的一个重要组成部分^{[1, 2, 3, 4, 5]}。TCS可以有效地抑制车辆在低附着路面、分离路面等复杂工况下起步或者加速时出现的驱动轮打滑现象, 使车辆获得较好的地面摩擦力, 提高车辆的加速性能和稳定性。TCS是通过将驱动轮控制在最佳滑转率附近从而获得良好的驱动力, 实现方法有多种, 如调整发动机的输出扭矩、驱动轮的主动制动、差速器锁止控制以及变速箱的控制等^{[6, 7, 8, 9, 10, 11]}。国内外学者在TCS控制算法和策略方面做了大量研究。文献[12]针对于不平路面的行驶工况, 采用逻辑门限值算法对车辆的驱动轮进行控制; 文献[13]提出了基于可变参数自适应PID控制的TCS系统, 该算法根据滑移率与目标滑移率的差值调整PID参数, 以使车辆适应各种复杂路况; 文献[14]采用滑模极值搜索算法计算出当前路况下的轮胎力-滑转率曲线的极值点作为目标滑转率进行牵引力控制; 文献[15]采用基于最优滑转率的模型预测控制算法, 并通过硬件在环仿真验证了TCS系统的可靠性和鲁棒性。

本文针对乘用车TCS系统进行研究, 提出了牵引力控制策略。首先对地面附着系数进行估计, 再利用可变遗忘因子最小二乘法估算当前行驶工况的最佳滑转率, 然后采用模糊PID算法和模糊算法分别对车辆的发动机转矩和主动制动转矩进行调整, 使得车辆在复杂工况下仍能保持良好驱动性能。仿真和冬季场地试验表明该方法控制效果良好。

1 路面附着系数估计

路面附着系数的准确估计一直是牵引力控制中的难点, 国内外学者在此方向做了大量的研究。文献[16]采用模糊逻辑算法对路面附着系数进行了估计。文献[17]针对Dugoff轮胎模型采用扩展卡尔曼滤波的方式进行路面附着系数估计。文献[18]采用基于多传感器信息融合的方式估计附着系数。由于牵引力控制算法运行周期约为1 ms, 因此路面附着系数估计实时性很重要, 本文利用动力学模型进行路面附着系数的估计。

本文设计的牵引力控制算法只涉及直线加速行驶的低附着路况, 因此忽略车辆坡道阻力, 根据纵向驱动力及行驶阻力模型可得:

$\begin{matrix} M a_{x} = \frac{T_{d}}{r} - F_{w} - F_{f} (1) \end{matrix}$

式中:F_w为风阻; T_d为车辆的驱动力矩; M为车辆质量; r为车轮半径; a_x为车辆纵向加速度; F_f为车辆所受滚动阻力。

考虑到风阻F_w正比于车辆车速v的平方, 因此式(1)可整理为:

$\begin{matrix} T_{d} = M a_{x} r + F_{f} r + k_{w} v^{2} r (2) \end{matrix}$

式中:k_w为风阻系数。

根据车辆单轮模型可得车轮滚动方程:

$\begin{matrix} I_{w} \overset{\cdot}{ω} = T_{d} - F_{x} r (3) \end{matrix}$

式中:I_w为转动惯量; $\begin{matrix} \overset{\cdot}{ω} \end{matrix}$ 为车轮转速微分, 即角加速度。

根据式(2)和(3)可得车辆的车轮与地面的纵向作用力F_x:

$\begin{matrix} F_{x} = \frac{M a_{x} + F_{f} + k_{w} v^{2}}{2} - \frac{I_{w} \overset{\cdot}{ω}}{r^{2}} (4) \end{matrix}$

车辆在直线加速行驶的情况下, 侧向加速度较小, 因此可以忽略侧向的载荷转移的情况, 车辆所受垂向力为:

$\begin{matrix} F_{z} = \frac{M (L_{2} g - h_{g} a_{x})}{2 (L_{1} + L_{2})} (5) \end{matrix}$

式中:L₁和L₂分别为车辆质心与前、后轴的距离; h_g为车辆的质心高度; g为重力加速度。

附着系数的计算公式为:

$\begin{matrix} μ = F_{x} / F_{z} (6) \end{matrix}$

在附着系数估计的过程中, 车辆的车速v是根据轮速估计而得, 纵向加速度a_x由偏航率传感器测量而得。

2 最优滑转率估计

车辆在行驶过程中, 滑转率和附着系数之间的关系可用Kiencke等^[19]提出的模型表示:

$\begin{matrix} μ (λ) = \frac{ξλ}{1 + p_{1} λ + p_{2} λ^{2}} (7) \end{matrix}$

式中:p₁和p₂在不同路况下有不同的典型值; μ (λ )为路面附着系数; λ 为车辆滑转率; ξ 为调试系数。

对式(7)求极值可得车辆在当前路况下的最大附着系数和最优滑转率:

$\begin{matrix} \{\begin{matrix} λ_{p} = {p_{2}}^{- 1 / 2} \\ μ_{p} (λ_{p}) = \frac{ξ}{p_{1} + 2 {p_{2}}^{\frac{1}{2}}} \end{matrix} (8) \end{matrix}$

根据式(8)可知, 当前最大附着系数和最优滑转率是一个关于参数p₁和p₂的函数。实时地估算出参数p₁和p₂是求当前路况最优滑转率的关键。

将式(7)做等效变换可得:

$\begin{matrix} \begin{matrix} 30 λ - μ (λ) = μ (λ) λ p_{1} + μ (λ) p_{2} λ^{2} = \\ [μ (λ) λ μ (λ) λ^{2}] [p_{1} p_{2}]^{T} (9) \end{matrix} \end{matrix}$

式(9)经过数学处理后得到最小二乘法形式的模型。当前路况下的附着系数μ (λ )和滑转率λ 可以通过实时计算得到。对式(9)做离散化处理得:

$\begin{matrix} \begin{matrix} y (k) = Φ^{T} (k) θ (k) (10) \\ 式中 : \\ \{\begin{matrix} θ (k) = [p_{1} (k) p_{2} {(k)]}^{T} \\ y (k) = 30 λ (k) - μ (k) \\ Φ^{T} (k) = [μ (k) λ (k) μ (k) λ^{2} (k)] \end{matrix} \end{matrix} \end{matrix}$

对式(10)采用可变遗忘因子递推最小二乘法, 算法如下:

$\begin{matrix} \{\begin{matrix} θ (k) = θ (k - 1) + G (k) [y (k) - Φ^{T} (k) θ (k - 1)] \\ G (k) = \frac{P (k - 1) Φ (k)}{Λ + Φ^{T} P (k - 1) Φ (k)} \\ P (k) = \frac{1}{Λ} [I - G (k) Φ^{T} (k)] P (k - 1) \end{matrix} (11) \end{matrix}$

式中:G(k)为增益向量; P(k)为协方差矩阵; Λ 为遗忘因子, 作用在于决定新老数据在参数递推中的权重。Λ 的取值范围为(0, 1), 若遗忘因子较大, 则递推所得参数p₁和p₂的值对噪声不敏感, 且收敛误差较小; 若遗忘因子小, 则系统跟踪系统强, 在路况发生变化时递推所得参数值能够及时更新, 但是对噪声较为敏感。因此, 车辆行驶路况发生变化时遗忘因子Λ 可以减小, 以减小历史数据影响, 增强新数据在递推算法中的作用。Λ 的计算式如下:

$\begin{matrix} Λ = \{\begin{matrix} Λ_{0}, 单一路面下行驶 \\ Λ_{1} + (Λ_{0} - Λ_{1}) [1 - \exp (- τk)], \\ 路况发生变化 \end{matrix} (12) \end{matrix}$

式中:τ 用来调整遗忘因子的变化速率。

3 控制器设计

3.1 控制策略

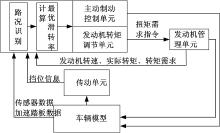
TCS控制是整个ESC系统的一个重要部分。TCS控制算法由发动机扭矩调节部分和驱动轮主动制动部分构成。在发动机扭矩调节控制中, 控制器通过CAN总线将需求的扭矩值发送给发动机管理单元(EMS)。EMS根据控制器的扭矩调节需求值对发动机进行调节。现在大部分车辆的EMS能够进行快速扭矩调节和慢速扭矩调节。其中, 慢速调节多是对节气门开度进行控制, 该方式响应时间较慢, 特别是在车辆转弯TCS介入时无法满足调节需求。快速扭矩调节多采用点火提前角调节或燃油供给调节方式, 该方式响应速度快, 但是车辆舒适性较差且易引起发动机爆震的现象。发动机扭矩调节部分将慢速扭矩调节和快速扭矩调节相结合, 这样既可满足系统控制实时性的需求, 又可提高车辆的舒适性。车辆在低附着路面起步时, TCS系统介入控制主要采用的是发动机扭矩调节。发动机转矩调节算法部分需要设置滑转率门限λ _L和λ _F, 且λ _L< λ _F。车辆在直线低附着工况下启动时, 当驱动轮的滑转率大于λ _F时采用快速扭矩调节, 当前驱动轮车轮滑转率在(λ _L, λ _F)时采用慢速减钮调节。一般来说, 车辆在刚启动时驱动轮的滑转率较大, 此时采用快速扭矩调节以使滑转率稳定在最优滑转率附近, 待滑转率稳定在两个门限值之间的时间大于2 s后, 发动机转矩调节部分开始采用慢速扭矩调节以保证车辆的稳定性和舒适性。

车辆在分离路面行驶, 接触低附着路面的驱动轮出现较大滑转时, 发动机转矩调节输出转矩迅速降低, 主动制动控制部分对低附着一侧车轮施加制动力, 保证车辆的驱动力。

控制策略如图1所示, TCS控制模块根据车辆的油门踏板行程信号、发动机转速信号、挡位信号判断驾驶员的驾驶意图; 根据车辆模型部分的车速和轮速信号判断车辆是否出现滑转现象; TCS根据输入的滑转率和附着系数计算出最优滑转率, 根据当前路况确定采用单纯的发动机转矩调节还是两种执行器协调作用。

	Figure Option View Download New Window
	图1 牵引力控制系统控制结构图Fig.1 Logical structure of TCS

3.2 发动机转矩调节

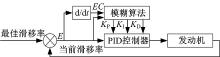
发动机转矩调节采用自整定模糊PID算法, 控制器结构如图2所示, 输入量E=λ _p-λ , 输入量EC=E(k)-E(k-1)。输出量为PID的三个参数K_P、K_I、K_D。自整定模糊PID算法的控制逻辑如下:系统不断地将E和EC输入模糊控制器, 模糊控制器根据模糊规则对PID的三个参数进行在线修改, 使车辆根据实时路况对发动机进行转矩调整, 滑转率始终工作在最优滑转率附近。

	Figure Option View Download New Window
	图2 模糊PID控制器结构图Fig.2 Structure of fuzzy PID controller

PID三个参数K_P、K_I、K_D的变化规律如下:

(1)当|E|大时, 增加K_P、减小K_D并限制K_I, 这样可以使得发动机输出转矩迅速, 当前滑转率快速接近当前最优滑转率, 同时避免出现超调。

(2)当|E|为中度时, 减小K_I、保持K_P, 适当减小K_D, 以使控制器保持响应速度, 持续调整当前滑转率的值。

(3)当|E|小时, 增大K_P和K_I, K_D取值适中, 同时要避免系统在目标值附近出现震荡。

将模糊控制器的变量设置模糊论域、制定模糊规则、解模糊等步骤, 发动机转矩调整部分中的节气门开度模糊PID控制器输出表达式为:

u_n=K_PE_n+K_I∑ E_nΔ t+K_DΔ E_nΔ t (13)

式中:E_n为车辆当前滑转率与最优滑转率的差值。

同理可求得燃油供给的模糊PID的输出值, 发动机转矩调节部分总的扭矩输出值可以表示为:

$\begin{matrix} T_{tar} = T_{thr} + T_{ign} (14) \end{matrix}$

式中:T_tar为发动机目标扭矩; T_thr为节气门部分模糊PID控制器的扭矩输出值; T_ign为燃油供给调节部分扭矩输出值。

3.3 主动制动控制

在分离路面工况下, 接触低附着路面的驱动轮会出现滑转现象, 且由于差速器作用使得高低附着两侧的驱动轮驱动力矩相等, 车辆驱动力不足。针对于此种情况, 采用基于模糊算法的主动制动控制调整两驱动轮的轮速差, 然后再采用发动机扭矩调节提高驱动力, 从而提高车辆的加速度性能。

模糊控制器具有两个输入变量E和EC, E为两驱动轮之间的轮速差, 即E=ω _L-ω _R, EC为E的变化率。输出变量为目标压力的变化量Δ p。E的语言变量量化为[负大(NB)、负中(NM)、零(Z)、正小(PS)、正中(PM)、正大(PB)]; EC的语言变量量化为[负大(NB)、负中(NM)、负小(NS)、零(Z)、正小(PS)、正中(PM)、正大(PB)]; 压力变化量量化为[NB、Z、PS、PB]。隶属度函数采用具有较强灵敏度和鲁棒性的三角形隶属度函数。模糊规则的制定依靠经验关系及后期车辆匹配调试, 规则如表1所示。最后采用重心法对推理结果进行解模糊处理。

表1 TCS模糊控制器规则表 Table 1 Table of fuzzy control rules

4 仿真与试验

4.1 Simulink仿真

为了验证车辆模型、最优滑转率及控制算法, 在Matlab/Simulink中建立仿真模型进行算法验证。车辆模型参数采用国产某车型, 参数如下:车辆质量为1560 kg; 质心高度为0.53 m; 前轴、后轴到质心距离分别为1.275 m和1.437 m; 绕X轴、Y轴、Z轴转动惯量分别为350、1674和1800 kg· m²; 车轮转动惯量为5.2 kg· m²; 轮胎阻尼常数为50 N· s/m。仿真车型加速踏板的位移和车辆速度成正比。车辆速度最大值为110 km/h, 此时踏板行程为满行程的90%。

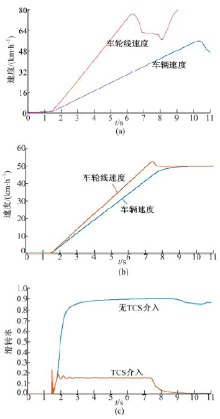
图3为在低附着路面(附着系数0.2的压实雪路面)仿真车辆加速踏板位移从0加到满行程的50%时的仿真结果对比图。图3(a)为无TCS介入时车辆速度和车轮线速度对比图, 可以看到车轮线速度急剧增加, 远超过当前车辆速度。图3(b)为TCS介入, 车轮线速度得到有效控制。图3(c)为无TCS和有TCS介入时车辆滑移率的对比图, 无TCS介入时, 驱动轮滑移率在0.85左右, 驱动轮出现过度滑转; 在有TCS介入时滑移率则保持在最佳滑转率0.16附近, 此时车辆驱动轮获得了较大的纵向驱动力。

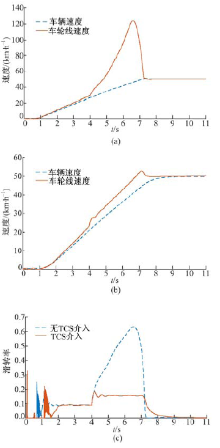
	Figure Option View Download New Window
	图3 低附着路面起步加速仿真结果对比图Fig.3 Simulation result in low mue surface

对接路面工况在验证算法实时性方面具有代表意义, 所以设置了车辆行驶从湿土路面(峰值附着系数为0.5)到压实雪路面的对接路面仿真试验, 路况转换发生在第4 s, 仿真结果如图4所示。图4(a)为无TCS介入时, 车辆在中附着路面行驶没有出现驱动轮打滑现象, 车辆在过渡到低附着路面后, 车轮开始急剧打滑; 图4(b)为车辆有TCS介入的仿真结果, 车辆在路况变化时有效控制车轮线速度, 充分利用了路面附着力; 图4(c)为无TCS和有TCS介入对接路况下滑转率的对比图, 由图可见, 在路况发生变化时, 有TCS系统的仿真车辆能够实时计算出当前路况下最优滑转率, 及时调整输入转矩, 使得当前滑转率稳定在最优滑转率附近, 得到较大附着力。

	Figure Option View Download New Window
	图4 对接路面起步加速仿真结果对比图Fig.4 Simulation result in mue-jump surface

4.2 冬季场地试验

试验车型为某乘用车前置前驱自动挡轿车, 轮胎采用雪地轮胎, 所有测试项目均是在油门全开和轻载的条件下进行。由于本文所设计的TCS控制系统为乘用车电子稳定系统(ESP)项目中重要的组成部分, 所以保留原车ESP控制器中的液压单元和电磁阀部分, 仅将ECU单元更换为本项目组开发的ECU控制单元。车辆的轮速传感器、双轴加速度传感器、横摆角速度传感器等均保持不变。ECU控制单元安装和试验场地如图5所示, 试验时间为2015年2月, 试验场地为黑河红河谷冬季试验场。试验车辆所有试验数据均通过Vector公司的CANalyzer分析仪采集, 数据通过CAN总线发送, 周期为10 ms。

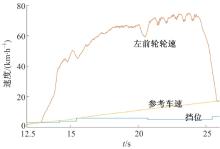
	Figure Option View Download New Window
	图5 控制器及试验场地Fig.5 Photo of ECU and test site

图6为车辆在关闭TCS功能后在冰直路面的试验数据。在开始阶段, 加速踏板开度达100%, 图中车轮速度为车轮角速度乘以车轮半径, 由图可见, 车辆前驱动轮远大于车身速度, 表明前驱动轮出现严重打滑, 且自动变速器频繁跳档, 车辆稳定性较差。试验车辆在25 s的时间仅加速到17 km/h。

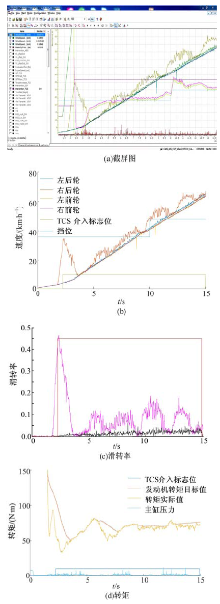
	Figure Option View Download New Window
	图6 无TCS介入冰路面直线起步加速Fig.6 Driven wheels/vehicle velocity curves on ice road without TCS

图7为冰直路面直线起步加速试验结果。图7(a)是CANalyzer采集得到的数据, 将该数据导入Matlab软件中进行整理后得到图7(b)(c)(d)。由图7(b)可见, 起步阶段加速踏板开度迅速增大到100%, 此时前左车轮和前右车轮有轻微打滑。2 s时, 驱动轮滑移率达到门限值, TCS介入控制, TCS系统根据当前路况附着系数和车轮滑转率计算出最优滑转率, 然后对发动机输出转矩进行调整, 使得车辆滑转率位置在最优滑转率附近, 从而获得良好的附着力。与图7(a)相比, 装配TCS功能的试验车辆在25 s的时间加速到40 km/h, 车辆加速度大于未装配TCS功能车辆的加速度。图7(c)为车辆当前滑转率, 输出值大部分维持在0.05~0.2。图7(d)为车辆的发动机目标转矩和实际转矩对比图, 可以看出对节气门和燃油供给的协调控制有效地控制了驱动轮的滑转, 发动机实际输出转矩紧密跟踪目标值。

	Figure Option View Download New Window
	图7 低附着路面试验结果Fig.7 Test result with TCS under low-mue surface

图8(a)为试验车辆在对开路面的试验结果截屏图。试验车辆左轮在低附着路面(冰路面, 附着系数为0.1, 最优滑转率为0.07左右), 右轮在高附着路面(水泥路面, 附着系数为0.85左右)。由图8(b)可以看到, 车辆在起步阶段, 加速踏板开度达到100%, 车辆左前驱动轮出现打滑, TCS迅速介入控制, 此后车辆左前驱动轮没再出现车轮打滑的现象。图8(c)为试验车辆左前驱动轮和右前驱动轮的滑转率, 左前车轮滑转率维持在0.05~0.15范围内, 保证了车辆获得足够的附着力。由图8(d)可知, 车辆在对开路面加速过程中, 低附着路面在出现滑转后, TCS控制系统迅速降低发动机转矩, 主动制动单元制动干预, 从而保证了左前驱动轮滑转率维持在最优滑转率附近, 保证了车辆纵向稳定性。

	Figure Option View Download New Window
	图8 对开路面试验结果Fig.8 Test result with TCS under split-mue surface

5 结论

(1)采用基于最佳滑转率的牵引力控制策略, 实现了实时计算当前路况的最佳滑转率并作为控制目标, 控制方法采用调整发动机转矩和主动制动调节相结合的方式。通过两种方式的协调控制, 为今后实现车辆的ESP控制打下基础。

(2)搭建了基于Matlab/Simulink的TCS控制仿真平台, 通过对仿真结果分析可知, 该控制策略较好地维持了车辆在复杂工况下的稳定性。

(3)在冬季场地试验中, 装配TCS控制器的车辆在低附着冰路面路况试验中, 起步加速过程加速度比未装配TCS的车辆提高了54%, 且车辆在行驶过程驱动轮不打滑、噪音低, 舒适性优于未装配TCS的车辆。

The authors have declared that no competing interests exist.

参考文献

View Option

[1]	van Zanten A T. Control aspect of Bosch-VDC[C]∥The 3rd International Symposium on Advanced Vehicle Control, Aachen, Germany, 1996: 573-607. [本文引用:1]
[2]	郭孔辉, 王德平. 汽车驱动防滑控制理论的初步研究[J]. 吉林工业大学学报, 1997, 27(3): 1-5. Guo Kong-hui, Wang De-ping. A preliminary theoretical study on anti-slip regulation[J]. Journal of Jilin University of Technology, 1997, 27(3): 1-5. [本文引用:1]
[3]	史俊武, 鲁统利, 李小伟, 等. 自动变速车辆低附着路面牵引力控制研究[J]. 汽车工程, 2011, 33(2): 127-133. Shi Jun-wu, Lu Tong-li, Li Xiao-wei, et al. A study on traction control for automatic transmission vehicle on low-adhesion road[J]. Automotive Engineering, 2011, 33(2): 127-133. [本文引用:1]
[4]	胡建军, 王银, 秦大同, 等. 基于轴间转矩分配的四轮驱动汽车牵引力控制[J]. 华南理工大学学报: 自然科学版, 2010, 38(1): 108-114. Hu Jian-jun, Wang Yin, Qin Da-tong, et al. Traction control of four-wheel drive vehicles based on inter-axle torque distribution[J]. Journal of South China University of Technology(Natural Science Edition), 2010, 38(1): 108-114. [本文引用:1]
[5]	Ise K, Fujita K, Inoue Y, et al. The “Lexus” Natural Science Edition traction control (TRAC) system[C]∥SAE Paper, 900212, 1990. [本文引用:1]
[6]	Li H Z, Li L, He L, et al. PID plus fuzzy logic method for torque control in traction control system[J]. International Journal of Automotive Technology, 2012, 13(3): 441-450. [本文引用:1]
[7]	Park J H, Kim C Y. Wheel slip control in traction control system for vehicle stability[J]. Vehicle System Dynamics: International Journal of Vehicle Mechanics and Mobility, 1999, 31(4): 263-278. [本文引用:1]
[8]	赵峰, 罗禹贡, 褚文博, 等. 深度混合动力电动汽车牵引力控制方法[J]. 吉林大学学报: 工学版, 2011, 41(增刊2): 47-53. Zhao Feng, Luo Yu-gong, Chu Wen-bo, et al. Traction control method for full hybrid electric vehicle[J]. Journal of Jilin University (Engineering and Technology Edition), 2011, 41(Sup. 2) : 47-53. [本文引用:1]
[9]	Deur J, Pavković D, Burgio G, et al. A model-based traction control strategy non-reliant on wheel slip information[J]. Vehicle System Dynamics: International Journal of Vehicle Mechanics and Mobility, 2011, 49(8): 1245-1265. [本文引用:1]
[10]	Pasillas-Lepine W, Loria A, Gerard M. Design and experimental validation of a nonlinear wheel slip control algorithm[J]. Automatica, 2012, 48(8): 1852-1859. [本文引用:1]
[11]	Tanelli M, Vecchio C, Corno M, et al. Traction control for ride-by-wire sport motorcycles: a second-order sliding mode approach[J]. IEEE Transactions on Industrial Electronics, 2009, 56(9): 3347-3356. [本文引用:1]
[12]	苑绍志, 李静, 李幼德. 考虑路面不平的牵引力控制系统[J]. 吉林大学学报: 工学版, 2007, 37(5): 990-994. Yuan Shao-zhi, Li Jing, Li You-de. Traction control system with consideration of road surface roughness[J]. Journal of Jilin University (Engineering and Technology Edition), 2007, 37(5): 990-994. [本文引用:1]
[13]	李亮, 康铭鑫, 宋健, 等. 汽车牵引力控制系统的变参数自适应PID控制[J]. 机械工程学报, 2011, 47(12): 92-98. Li Liang, Kang Ming-xin, Song Jian, et al. Adaptive PID controller with variable parameters for vehicle traction control system[J]. Journal of Mechanical Engineering, 2011, 47(12): 92-98. [本文引用:1]
[14]	周兵, 徐蒙, 袁希文, 等. 基于滑模极值搜索算法的车辆驱动防滑控制策略[J]. 农业机械学报, 2015, 46(2): 307-313. Zhou Bing, Xu Meng, Yuan Xi-wen, et al. Acceleration slip regulation based on extremum seeking control with slide mode[J]. Transactions of the Chinese Society for Agricultural Machinery, 2015, 46(2): 307-313. [本文引用:1]
[15]	Borrelli F, Bemporad A, Fodor M, et al. An MPC/hybrid system approach to traction control[J]. IEEE Transactions on Control Systems Technology, 2006, 14(3): 541-553. [本文引用:1]
[16]	李亮, 冉旭, 李红志, 等. 用于汽车牵引力控制的复杂路面轮胎-道路附着状态判断[J]. 机械工程学报, 2012, 48(10): 109-114. Li Liang, Ran Xu, Li Hong-zhi, et al. Identification of tire-road adhension state on complicated road surface for traction control system[J]. Journal of Mechanical Engineering, 2012, 48(10): 109-114. [本文引用:1]
[17]	武钟财. 基于扩展卡尔曼滤波的路面附着系数估计算法研究[D]. 长春: 吉林大学汽车工程学院, 2008. Wu Zhong-cai. Research on the algorithm of the road friction coefficient estimation based on the extended Kalman filter[D]. Changchun: College of Automotive Engineering, Jilin University, 2008. [本文引用:1]
[18]	宋健, 杨财, 李红志, 等. AYC系统基于多传感器数据融合的路面附着系数估计算法[J]. 清华大学学报: 自然科学版, 2009, 49(5): 101-104. Song Jian, Yang Cai, Li Hong-zhi, et al. Road friction coefficient estimation algorithm based on multi-sensor data fusion for AYC system[J]. Journal of Tsinghua University(Science and Technology), 2009, 49(5): 101-104. [本文引用:1]
[19]	Kiencke U. Realtime estimation of adhesion characteristic between tires and road[C]∥Proceeding of IFAC World Congr, Sydney, 1993: 15-18. [本文引用:1]

1996

0.0

... 0 引言牵引力控制系统(Traction control system,TCS)是电子稳定程序(Electronic stability program,ESP)的一个重要组成部分^[1,2,3,4,5] ...

1997

0.0

. 1997, 27(3):1-5

A preliminary theoretical study on anti-slip regulation

汽车驱动防滑控制理论的初步研究

Guo Kong-hui , Wang De-ping

郭孔辉, 王德平

采用滑模变结构控制方法，探讨了通过调节发动机节气门开度来进行汽车驱动防滑控制的理论，并进行了仿真计算，从而定量地说明了汽车驱动防滑控制能改善车辆驱动性及操纵稳定性。

... 0 引言牵引力控制系统(Traction control system,TCS)是电子稳定程序(Electronic stability program,ESP)的一个重要组成部分^[1,2,3,4,5] ...

2011

0.0

. 2011, 33(2):127-133

A study on traction control for automatic transmission vehicle on low-adhesion road

自动变速车辆低附着路面牵引力控制研究

Shi Jun-wu , Lu Tong-li , Li Xiao-wei

史俊武, 鲁统利, 李小伟

提出了一种基于发动机节气门开度与变速器挡位协调控制的自动变速车辆牵引力控制系统。针对滑移率控制系统的非线性与参数不确定性，根据微分几何理论对其进行了反馈线性化并施加滑模控制。同时利用动态规划方法求得能产生所需驱动转矩的节气门开度与变速器挡位。仿真结果表明，此种牵引力控制系统具有设计简单和控制效果良好等特点。

... 0 引言牵引力控制系统(Traction control system,TCS)是电子稳定程序(Electronic stability program,ESP)的一个重要组成部分^[1,2,3,4,5] ...

2010

0.0

... 0 引言牵引力控制系统(Traction control system,TCS)是电子稳定程序(Electronic stability program,ESP)的一个重要组成部分^[1,2,3,4,5] ...

0.0

... 0 引言牵引力控制系统(Traction control system,TCS)是电子稳定程序(Electronic stability program,ESP)的一个重要组成部分^[1,2,3,4,5] ...

2012

0.0

... TCS是通过将驱动轮控制在最佳滑转率附近从而获得良好的驱动力,实现方法有多种,如调整发动机的输出扭矩、驱动轮的主动制动、差速器锁止控制以及变速箱的控制等^{[6,7,8,9,10,11]} ...

1999

0.0

2011

0.0

. 2011, 41(增刊2):47-53

Traction control method for full hybrid electric vehicle

深度混合动力电动汽车牵引力控制方法

Zhao Feng , Luo Yu-gong , Chu Wen-bo

赵峰, 罗禹贡, 褚文博

针对单发动机动力源设计的传统内燃机汽车牵引力控制系统的控制方法无法应用于由发动机和电机共同组成的混合动力驱动系统。针对此问题,提出了基于深度混合动力电动汽车的牵引力分层控制方法。上层控制中提出基于动态滑模的驱动轮目标驱动力矩制定策略,求解保证驱动轮不打滑时的目标驱动力矩;下层控制中提出电机转矩单独控制策略、基于转矩动态协调的发动机电机协调控制策略以及工况识别逻辑,解决了不同工况下的发动机电机转矩协调控制问题。最后开发了仿真实验平台和硬件在环实验平台,结果表明,基于深度混合动力电动汽车的牵引力分层控制方法能够快速、准确、平稳地实现对打滑车轮的控制,改善了深度混合动力电动汽车的起步性能、加速性能以及稳定性能,增加了行驶安全性。

2011

0.0

2012

0.0

2009

0.0

2007

0.0

. 2007, 37(5):990-994 DOI:doi:10.3969/j.issn.1671-5497.2007.05.002

Traction control system with consideration of road surface roughness

考虑路面不平的牵引力控制系统

Yuan Shao-zhi , Li Jing , Li You-de

苑绍志, 李静, 李幼德

摘　要：分析了路面不平对牵引力控制系统的影响,提出了基于车轮加速度的路面识别方法,在此基础上提出了考虑路面不平度的牵引力控制算法.应用MATLAB建立了仿真模型,通过对不平路面的牵引力控制算法进行的仿真结果表明,考虑路面不平的牵引力控制系统能够识别路面不平,并能有效控制驱动轮的过度滑转.

... 文献[12]针对于不平路面的行驶工况,采用逻辑门限值算法对车辆的驱动轮进行控制 ...

2011

0.0

. 2011, 47(12):92-98 DOI:doi:10.3901/JME.2011.12.092

Adaptive PID controller with variable parameters for vehicle traction control system

汽车牵引力控制系统的变参数自适应PID控制

Li Liang , Kang Ming-xin , Song Jian

李亮, 康铭鑫, 宋健

合理的驱动轮滑转率控制是保证汽车具有良好急加速驱动性能和稳定性的前提.复杂路面条件下汽车牵引力控制系统对驱动轮滑转率的控制需要基于驾驶员加速驾驶意图判断结果,通过合理协调发动机转矩干预和主动制动来实现.由于驾驶意图和路面附着条件的改变引起汽车动力学参量以及实际控制系统边界条件的改变,使得传统的PID控制的应用受到限制,因而提出一种可变参数的自适应PID控制器,根据驱动轮实际滑转率与目标滑转率的偏差自适应的调整PID控制器中的整定参数值,从而改善PID控制的控制品质,使汽车在复杂路况和工况条件下均能实现良好的驱动轮滑转率控制.根据不同控制参数组合方式,系统可以在发动机转矩控制、主动制动控制以及两种执行器耦合作用等三种控制模式中切换,实现驱动轮滑转率控制的目标.仿真与实车道路试验验证了这一方法的有效性.

... 文献[13]提出了基于可变参数自适应PID控制的TCS系统,该算法根据滑移率与目标滑移率的差值调整PID参数,以使车辆适应各种复杂路况 ...

2015

0.0

. 2015, 46(2):307-313 DOI:doi:10.6041/j.issn.1000-1298.2015.02.045

Acceleration slip regulation based on extremum seeking control with slide mode

基于滑模极值搜索算法的车辆驱动防滑控制策略

Zhou Bing , Xu Meng , Yuan Xi-wen

周兵, 徐蒙, 袁希文

In order to improve the vehicle anti-slip performance, an acceleration slip regulation strategy based on extremum seeking control with sliding mode was proposed. Extremum seeking control with sliding mode was used as a self-optimizing way to find the extreme point of tire force-slip rate curve. In this condition, the tire slip ratio near the optimal slip ratio can be controlled without having to estimate the road surface friction coefficient or establishing the ideal reference model to improve the vehicle dynamic performance and directional stability. Moreover, a validated full vehicle simulation model was built in Matlab/Simulink. And the controller based on extremum seeking control with sliding mode was carefully designed. Finally, simulation results showed that during acceleration the vehicle can quickly reach the optimal slip ratio which corresponded to the real-time road conditions with the proposed control strategy. It implied that the proposed control strategy can improve vehicle dynamic performance.

为了提高车辆的驱动防滑能力，提出了一种基于滑模极值搜索算法的驱动防滑控制策略。采用滑模极值搜索算法作为一种自寻优方法找到轮胎力—滑转率曲线的极值点，无需估计路面附着系数和建立理想参考模型就可以将轮胎的滑转率控制在最优滑转率附近，提高车辆的动力性和方向稳定性。在Matlab/Simulink中建立车辆系统仿真模型。仿真结果表明，此控制策略能使车辆在驱动过程中快速达到实时路面条件下的最优滑转率，增强了车辆的动力性能。

... 文献[14]采用滑模极值搜索算法计算出当前路况下的轮胎力-滑转率曲线的极值点作为目标滑转率进行牵引力控制 ...

2006

0.0

... 文献[15]采用基于最优滑转率的模型预测控制算法,并通过硬件在环仿真验证了TCS系统的可靠性和鲁棒性 ...

2012

0.0

. 2012, 48(10):109-114 DOI:doi:10.3901/JME.2012.10.109

Identification of tire-road adhension state on complicated road surface for traction control system

用于汽车牵引力控制的复杂路面轮胎-道路附着状态判断

Li Liang , Ran Xu , Li Hong-zhi

李亮, 冉旭, 李红志

对开附着路面条件下,汽车附着状态识别误差极易引起牵引力控制系统对高附—侧施加主动压力控制,使制动力与驱动力对耗,造成汽车抖振.因此牵引力控制中对复杂路面附着条件识别的准确性和快速性,成为评价控制器鲁棒性的关键指标,也是提高牵引力控制效果的必备因素.提出一种综合的路面附着条件识别方法,该基于模糊逻辑的路面附着识别算法,采用驱动轮左右两侧利用附着系数绝对差和滑转速度绝对差作为输入量,并引入置信度的概念,根据置信度所处区间来判断路面附着状态.通过仿真和实车试验,验证路面附着状态识别方法的有效性和及时性.

... 文献[16]采用模糊逻辑算法对路面附着系数进行了估计 ...

2008

0.0

. 2008, :-

Research on the algorithm of the road friction coefficient estimation based on the extended Kalman filter

基于扩展卡尔曼滤波的路面附着系数估计算法研究

Wu Zhong-cai

武钟财

随着汽车电子和控制技术的发展,汽车稳定性控制在最近几年得到了很快的发展。目前我国还没有建立起完善的控制算法和试验手段,处于理论研究阶段。在汽车稳定性控制系统产品开发过程中,准确的估计出路面状态是必须攻克的难关。本文在研究了卡尔曼滤波理论和扩展卡尔曼滤波理论的基础上,以估计汽车行驶过程中的运动状态变量为基础,重点研究了轮胎与地面之间的路面附着系数估计算法,包括基于扩展卡尔曼滤波的纵向车速、侧向车速、横摆角速度等汽车运动状态变量的估计算法,以及在此基础上的基于扩展卡尔曼滤波的路面附着系数估计算法。最后,利用成熟商用软件CarSim对所研究的状态估计算法和路面附着系数估计算法进行了仿真验证。结果表明,该算法可以较好的估计出汽车的行驶状态和路面附着系数。

... 文献[17]针对Dugoff轮胎模型采用扩展卡尔曼滤波的方式进行路面附着系数估计 ...

2009

0.0

. 2009, 49(5):101-104

Road friction coefficient estimation algorithm based on multi-sensor data fusion for AYC system

AYC系统基于多传感器数据融合的路面附着系数估计算法

Song Jian , Yang Cai , Li Hong-zhi

宋健, 杨财, 李红志

为提高车辆行驶安全性,研究适用于车辆稳定性控制系统的实时路面附着系数估计算法。利用多传感器数据融合综合车辆稳定性控制系统的各传感器数据,从中提取轮胎-路面附着系数得到充分利用的特征信息。根据路面附着系数充分利用时的侧向加速度估算路面附着系数。通过15自由度硬件在环仿真平台以及实车试验两种方式对算法进行验证。一定条件下的仿真结果表明算法的最大估算误差不超过0.04,车辆双移线实车试验的通过率从25%提高到100%。

... 文献[18]采用基于多传感器信息融合的方式估计附着系数 ...

1993

0.0

... 2 最优滑转率估计车辆在行驶过程中,滑转率和附着系数之间的关系可用Kiencke等^[19]提出的模型表示: ...