双电机四驱电动汽车自适应复合防抱死控制

引用本文

孙大许, 兰凤崇, 何幸福, 陈吉清. 双电机四驱电动汽车自适应复合防抱死控制. 2016, 46(5): 1405-1413
SUN Da-xu, LAN Feng-chong, HE Xing-fu, CHEN Ji-qing. Self-adaptive composite ABS of dual-motor four-wheel drive electric vehicle. Journal of Jilin University Engineering and Technology Edition, 2016, 46(5): 1405-1413 复制到剪切板

Permissions

双电机四驱电动汽车自适应复合防抱死控制

孙大许^1,², 兰凤崇^1,³, 何幸福^1,³, 陈吉清^1,³

1.华南理工大学机械与汽车工程学院,广州 510640

2.广东机电职业技术学院,广州 510515

3.华南理工大学广东省汽车工程重点实验室,广州 510640

通信作者:陈吉清(1966-),女,教授,博士生导师.研究方向:汽车结构与安全.E-mail:chjq@scut.edu.cn

作者简介:孙大许(1973-),男,讲师,博士研究生.研究方向:新能源汽车.E-mail:sundx55@126.com

基金:广东省科技计划项目(2014B010106002,2014B010125001)

摘要

为了进一步提高双电机四驱电动汽车防抱死控制的响应速度和精度,在电液复合变参数PID防抱死系统的基础上,采用径向基函数神经网络系统对电动汽车电液复合制动系统进行在线辨识,利用车轮滑移率对于电机制动转矩变化的灵敏度信息对PID的控制参数进行滚动优化调整,实现自适应复合防抱死控制。运用离线仿真和快速控制原型在环实时实验对控制算法和在线实时控制效果进行了验证,结果表明:改进的控制算法提高了系统的控制精度和响应速度,而且满足控制系统的实时性要求。

关键词: 车辆工程; 径向基函数; 神经网络; 防抱死系统; 电动汽车

中图分类号:U461.3 文献标志码:A 文章编号:1671-5497(2016)05-1405-09

Self-adaptive composite ABS of dual-motor four-wheel drive electric vehicle

SUN Da-xu^1,², LAN Feng-chong^1,³, HE Xing-fu^1,³, CHEN Ji-qing^1,³

1.School of Mechanical and Automotive Engineering, South China University of Technology, Guangzhou 510640,China

2.Guangdong Mechanical & Electrical Polytechnic, Guangzhou 510515,China

3.Guangdong Key Laboratory of Vehicle Engineering, South China University of Technology, Guangzhou 510640, China

Abstract

On the basis of electro-hydraulic varying parameters PID control, to further improve the response rate and accuracy of anti-lock breaking system of a dual-motor four-wheel drive electric vehicle, the neural network system based on radial basis function is introduced to realize online identification of electro-hydraulic braking system. The sensitivity of the wheel slip ratio to motor braking torque is used to achieve scroll optimal adjustment of parameters of PID control, and to increase the response rate and accuracy. The off-line simulation and hardware in loop real time simulation are carried out to test the control algorithm. Results show that the improve control algorithm can increase the accuracy and regulating rate of the system, and meet the real time requirements of the control system.

Keyword: vehicle engineering; radial basis function; neural network; anti-lock braking system(ABS); electric vehicle

Show Figures

0 引言

液压防抱死制动系统(Anti-lock braking system, ABS)技术成熟, 可靠性高, 并符合安全规定, 已经在车辆制动系统中得到广泛应用, 但液压系统有延迟性, 无法实现对车轮滑移率的精确实时控制。另外, 电动汽车中的驱动电机具有驱动和制动的双重作用, 并且具有控制容易、快速、准确的优点, 但制动转矩受到电机功率、电流以及电池SOC的限制, 不能满足所有的制动需求, 技术上也没有液压系统成熟可靠。电液复合ABS结合了液压控制的可靠性及电机控制的快速和准确的优势, 在电动汽车制动系统研究领域受到了国内外学者的广泛关注^{[1, 2, 3, 4, 5]}。Khatun等^[6]采用模糊逻辑控制算法对电动车ABS进行了研究, 开发的模糊鲁棒性控制器改善了电动汽车的制动性能。Dash等^[7]以一款混合动力汽车为研究对象, 将模糊控制算法与滑模控制算法相结合, 开发了模糊适应性滑移率控制器, 通过仿真验证了控制算法可有效地消除滑膜控制的颤振, 达到良好的控制效果。Tur等^[8]建立了1/4轮毂电机电动汽车模型, 对电机ABS和液压ABS进行了仿真对比分析, 结果表明电机ABS比液压ABS具有更好的效果。王吉^[5]以四轮独立驱动的轮毂电机电动汽车为研究对像, 建立了不同路面的PID参数库, 采用变参数PID控制及等时轮加速度控制算法, 开发了基于电机制动力与液压制动力协调工作的ABS控制器, 并通过仿真的方法验证了电液复合控制具有良好的控制效果。Yin等^[9]研究了混合动力汽车的再生制动与ABS的联合控制问题, 采用滑模控制方法把车轮滑移率控制在最优的范围之内。

在对各种控制算法研究分析的基础上, 发现基于参数库的变参数PID控制方法不需要知道控制对象的数学模型, 具有控制简单, 更易于工程应用的优点, 但对于复杂的非线性时变系统, PID控制方法对控制初始状况具有很强的依赖性, 对路况的变化适应性不强, 鲁棒性不好的缺点。为了提高基于参数库的变参数ABS控制的精度及鲁棒性, 进一步改善ABS控制器的适应性, 本文以一款双电机四驱电动汽车为研究对象, 在基于参数库的PID控制方法的基础上, 采用基于径向基函数(Radial basis function, RBF)神经网络系统辨识的方法^[10], 获取制动时车轮滑移率对于电机制动转矩变化的灵敏度信息对PID的控制参数进行在线滚动优化调整, 提高PID控制算法的鲁棒性、快速性和准确性, 并通过离线仿真和快速控制原型在环仿真的方法对开发的控制算法的控制效果及实时性进行验证。

1 整车参数及复合控制逻辑

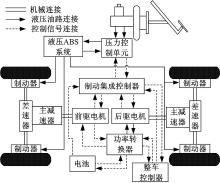
研究目标车型为双电机四驱电动汽车, 其拓扑结构如图1所示。整车及主要部件的主要参数如下:整车整备质量为1250 kg; 轴距为2400 mm; 质心到前轴和后轴的距离均为1200 mm; 质心高度为540 mm; 车轮转动惯量为0.6 kg· m²; 减速器传动比为5.46; 迎风面积为2.2 m²; 空气阻力系数为0.33; 前后驱动电机额定功率为10 kW, 最大功率为20 kW; 前、后电机额定转速为2000 r/min, 最高转速为3750 r/min。两个驱动电机分别驱动前、后轴, 前、后驱动系统完全相同, 结构上前后对称, 前、后轴上的制动力可以根据电机的输出能力进行调节, 前、后轴上的制动能量均可进行回收。液压制动部分采用三通道四传感器液压ABS, 前、后轴间的液压制动力按照固定值 $\begin{matrix} β \end{matrix}$ 进行分配, 在制动主油路与ABS模块之间增加了压力控制单元, 用以根据制动集成控制器的控制指令对ABS主油路的压力进行调节。

	Figure Option View Download New Window
	图1 目标车型的拓扑布局Fig.1 Topology of target model

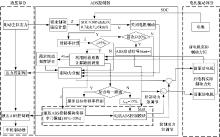
双电机四驱电动汽车电液复合ABS控制框图如图2所示。总体设计思路是在液压ABS系统的基础上增加电机ABS控制, 按照制动主缸的压力估算需求的计算强度, 根据制动强度对制动的模式(是否为紧急制动)进行判别, 判断是否启动电机制动; 再根据车轮的滑移率进行路面最大附着系数的识别, 得出路面的最佳目标滑移率, 同时利用计算的路面最大附着系数对需求的总制动强度进行矫正; 根据矫正的制动强度以及电机的最大制动力矩, 合理分配电机制动力和液压制动力; 液压ABS系统与电机ABS控制模块同时进行ABS控制, 液压ABS采用滑移率固定门限值(10%~20%)控制, 保证系统的可靠性和鲁棒性, 电机ABS采用基于径向基函数神经网络辨识的自适应控制, 保证系统控制的精确性和快速性。

	Figure Option View Download New Window
	图2 复合ABS控制逻辑图Fig.2 Composite ABS control logic diagram

2 路面识别方法

2.1 利用附着系数的估算

采用车轮动力学模型估算的方法进行利用附着系数的计算。以前轮为例, 左、右两轮的动力学模型分别为:

$\begin{matrix} \begin{matrix} J_{FL} {\overset{\cdot}{ω}}_{FL} = T_{d_FL} + T_{hy_FL} - F_{f_FL} R (1) \\ J_{FR} {\overset{\cdot}{ω}}_{FR} = T_{d_FR} + T_{hy_FR} - F_{f_FR} R (2) \end{matrix} \end{matrix}$

式中: $\begin{matrix} J_{FL} 、 J_{FR} \end{matrix}$ 分别为前方左、右两侧车轮的转动惯量; $\begin{matrix} T_{d_FL} 、 T_{d_FR} \end{matrix}$ 分别为前方左、右两侧作用在车轮上的驱动力矩; $T_{hy_FL} 、 T_{hy_FR}$ 分别为前方左、右制动器上的液压制动转矩; $\begin{matrix} F_{f_FL} 、 F_{f_FR} \end{matrix}$ 分别为左、右两侧驱动轮与地面间的纵向地面驱动力; $\begin{matrix} R \end{matrix}$ 为车轮的有效滚动半径。

由式(1)加式(2)得:

$\begin{matrix} \begin{matrix} J_{FL} {\overset{\cdot}{ω}}_{FL} + J_{FR} {\overset{\cdot}{ω}}_{FR} = (T_{d_FL} + T_{d_FR}) + \\ (T_{hy_FL} + T_{hy_FR}) - (F_{f_FL} R + F_{f_FR} R) (3) \end{matrix} \end{matrix}$

假设汽车左、右两侧的车轮转动惯量、滚动半径完全相同, 则式(3)又可写为:

$\begin{matrix} \begin{matrix} J ({\overset{\cdot}{ω}}_{FL} + {\overset{\cdot}{ω}}_{FR}) = (T_{d_FL} + T_{d_FR}) + \\ (T_{hy_FL} + T_{hy_FR}) - (F_{f_FL} + F_{f_FR}) R (4) \end{matrix} \end{matrix}$

从驱动电机到驱动轮的动力学模型为:

$\begin{matrix} T_{EM} i_{0} i_{1} η = (T_{d_FL} + T_{d_FR}) + J_{0} {\overset{\cdot}{ω}}_{0} (5) \end{matrix}$

式中: $T_{EM}$ 为驱动电机的输出转矩; $i_{0} 、 i_{1}$ 分别为减速器和主减速器的传动比; η 为传动系的传动效率; $J_{0}$ 为传动系旋转部件的等效转动惯量; ${\overset{\cdot}{ω}}_{0}$ 为传动系等效角加速度。

利用附着系数 $\begin{matrix} μ \end{matrix}$ 为:

$\begin{matrix} μ = F_{d} / N (6) \end{matrix}$

式中: $F_{d}$ 为地面驱动力; $\begin{matrix} N \end{matrix}$ 为轮胎的垂直载荷。

制动过程中, 用前轮来估算利用附着系数, $\begin{matrix} F_{d} 和 N \end{matrix}$ 的计算式为:

$\begin{matrix} \begin{matrix} F_{d} = F_{f_FL} + F_{f_FR} (7) \\ N = mg \frac{b}{L} - m {\overset{\cdot}{v}}_{x} \frac{h_{g}}{L} (8) \end{matrix} \end{matrix}$

2.2 路面最佳滑移率识别

路面识别是主动安全控制中实现精确控制的前提, 基于精确控制的ABS必须与准确的路面识别算法相结合。在车辆制动过程中, 轮胎与地面之间的利用附着系数 $μ$ 与滑移率 $\begin{matrix} λ \end{matrix}$ 有密切的关系, 在不同的路面有不同的 $\begin{matrix} μ - λ \end{matrix}$ 关系, 由汽车理论中 $μ - λ$ 曲线可以看出, $\begin{matrix} μ \end{matrix}$ 有极大值。在ABS控制中, 需要很短的时间内对路面的附着系数进行识别, 因此要求识别算法简单, 实时性好。在文献[5, 11]中, 采用的利用附着系数极大值的方法具有算法简单、实时性好的优点, 本文中也采用此方法对路面状况进行识别。具体识别算法如下:

$\begin{matrix} \begin{matrix} dμ (λ (k)) = μ (λ (k)) - μ (λ (k - 1)) (9) \\ dμ (λ (k - 1)) = μ (λ (k - 1)) - μ (λ (k - 2)) (10) \end{matrix} \end{matrix}$

式中: $\begin{matrix} λ (k) \end{matrix}$ 为 $k$ 时刻车轮的滑移率; $μ (λ (k))$ 为 $\begin{matrix} k \end{matrix}$ 时刻车轮对应的利用附着系数。

当 $dμ (λ (k))$ 且 $dμ (λ (k - 1)) > 0$ 时, $\begin{matrix} μ \end{matrix}$ 出现极大值, 极大值可近似为:

$\begin{matrix} μ_{\max} \approx μ (λ (k - 1)) (11) \end{matrix}$

在实际车辆制动过程中, 即使在均一路面上, 系统识别出 $μ_{\max}$ 也会在一定的范围内进行波动, 需要对已识别出来的 $μ_{\max}$ 进行整理, 如 $\begin{matrix} 0.05 \leq μ_{\max} \leq 0.15 \end{matrix}$ 为冰路面, $0.15 < μ_{\max} \leq 0.25$ 为压实雪路面, $\begin{matrix} 0.4 < μ_{\max} \leq 0.5 \end{matrix}$ 为湿沥青路面等。根据文献[5]及汽车理论, 冰路面对应的最佳滑移率为0.10, 压实雪路面对应的最佳滑移率为0.15, 湿沥青路面对应的最佳滑移率为0.20。建立路面与最佳滑移率的映射库, 在路面识别的基础上, 进一步对最佳滑移率进行识别。为避免在非均一复杂路面上路面识别系统辨识的目标滑移率频繁波动, 同时也为了保证系统控制的可靠性, 在非均一路面上时, 采用固定滑移率目标值0.15对车轮的滑移率进行控制。

3 径向基函数系统辨识控制算法

基于径向基函数系统辨识的自适应控制算法, 是在基于最优参数库的PID控制算法基础上, 对PID的控制参数进一步进行自适应调整。最优参数库的PID控制算法是指分别在不同的路面上进行PID控制算法的控制参数优化, 获得不同路面上的PID控制最优参数, 从而建立不同路面的PID控制最优参数的参数库, 当车辆在不同的路面制动时, 系统调用最优的PID控制参数进行控制。与固定参数值的PID控制算法相比, 最优参数库的PID控制算法提高了PID算法的适应性及快速性。基于径向基函数系统识别的自适应控制算法是通过神经网络辨识的方法获取车轮滑移率对电机制动转矩变化的灵敏度信息(雅可比信息), 利用该信息对PID的控制参数进行滚动优化调整, 进一步提高控制系统的精度和调整速度。

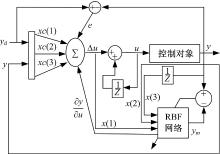
基于径向基函数系统辨识的自适应控制框图如图3所示。该控制算法是对PID控制算法的自适应性改进算法, 增量型PID控制算法如下:

$\begin{matrix} \begin{matrix} μ (k) = μ (k - 1) + k_{P} (e (k) - \\ e (k - 1)) + k k_{I} e (k) + \\ k_{D} (e (k) - 2 e (k - 1) + e (k - 2)) (12) \\ 令 : \\ \{\begin{matrix} xc (1) = e (k) - e (k - 1) \\ xc (2) = e (k) \\ xc (3) = e (k) - 2 e (k - 1) + e (k - 2) \end{matrix} \\ (13) \end{matrix} \end{matrix}$

$\begin{matrix} k_{P}, k_{I}, k_{D} \end{matrix}$ 采用梯度下降法进行自调整, 其调整算法为:

$\begin{matrix} \{\begin{matrix} Δ k_{P} (k) = η_{P} e (k) \frac{\partial y}{\partial Δu} xc (1) \\ Δ k_{I} (k) = η_{I} e (k) \frac{\partial y}{\partial Δu} xc (2) \\ Δ k_{D} (k) = η_{D} e (k) \frac{\partial y}{\partial Δu} xc (3) \\ k_{P} (k) = k_{P} (k - 1) + Δ k_{P} (k) \\ k_{I} (k) = k_{I} (k - 1) + Δ k_{I} (k) \\ k_{D} (k) = k_{D} (k - 1) + Δ k_{D} (k) \end{matrix} (14) \end{matrix}$

式中: $\begin{matrix} η_{P} 、 η_{I} 、 η_{D} \end{matrix}$ 分别为比例、积分和微分项的学习速率; $\begin{matrix} \frac{\partial y}{\partial Δu} \end{matrix}$ 为对象的输出对控制输入变化的灵敏度, 由RBF网络对系统辨识得到。

	Figure Option View Download New Window
	图3 径向基函数系统辨识的自适应控制框图Fig.3 RBF self-adaptive control structure

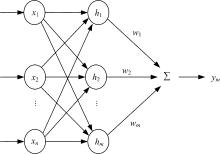
RBF网络神经结构如图4所示, 径向基函数是具有单隐层的三层前馈网络, 模拟了人脑中局部调整、相互覆盖接收域的神经网络结构, 是一种局部逼近网络, 理论上可以以任意精度逼近任意连续函数。网络结构中, 网络输入量 $x = [x_{1}, x_{2}, \dots, x_{n}]^{T}$ , 径向基向量 $h = [h_{1}, h_{2}, \dots, h_{n}]^{T}$ , 其中 $\begin{matrix} h_{j} \end{matrix}$ 一般采用高斯基函数表示:

$\begin{matrix} h_{j} = \exp (- \frac{‖ x - c_{j} ‖^{2}}{2 b_{j}^{2}}), j = 1, 2, \dots, n (15) \end{matrix}$

式中: $c_{j}$ 为第 $j$ 个节点的中心矢量, $\begin{matrix} c_{j} = [c_{j 1}, c_{j 2}, \dots, c_{ji}, \dots, c_{jn}]^{T}, i = 1, 2, \dots, n 。 \end{matrix}$

	Figure Option View Download New Window
	图4 RBF网络结构Fig.4 RBF network

网络的基宽向量为 $B = [b_{1}, b_{2}, \dots, b_{n}]^{T}$ , $b_{j}$ 为节点 $j$ 的基宽参数, 且大于零。网络的权向量为 $\begin{matrix} w = [w_{1}, w_{2}, \dots, w_{n}]^{T} 。 \end{matrix}$ 辨识网络的输出为:

$\begin{matrix} y_{m} (k) = \overset{m}{\sum_{i = 1}} w_{i} h_{i} (16) \end{matrix}$

辨识器的性能指标为:

$\begin{matrix} J = \frac{1}{2} (y (k) - y_{m} {(k))}^{2} (17) \end{matrix}$

根据梯度下降法, 输出权、节点中心及节点宽度参数的迭代算法如下:

$\begin{matrix} \{\begin{matrix} Δ w_{j} (k) = η (y (k) - y_{m} (k)) h_{j} \\ w_{j} (k) = w_{j} (k - 1) + Δ w_{j} (k) + \\ α (w_{j} (k - 1) - w_{j} (k - 2)) \\ Δ b_{j} (k) = η (y (k) - y_{m} (k)) w_{j} h_{j} \frac{‖ x - c_{j} ‖^{2}}{b_{j}^{3}} \\ b_{j} (k) = b_{j} (k - 1) + Δ b_{j} (k) + \\ α (b_{j} (k - 1) - b_{j} (k - 2)) \\ Δ c_{j} (k) = η (y (k) - y_{m} (k)) w_{j} \frac{x_{j} - c_{ji}}{b_{j}^{2}} \\ c_{ji} (k) = c_{ji} (k - 1) + Δ c_{ji} (k) + \\ α (c_{ji} (k - 1) - c_{ji} (k - 2)) \end{matrix} (18) \end{matrix}$

式中: $η$ 为学习速率; $\begin{matrix} α \end{matrix}$ 为动量因子。

Jacobian阵的算法为:

$\begin{matrix} \frac{\partial y (k)}{\partial Δu (k)} \approx \frac{\partial y_{m} (k)}{\partial Δu (k)} = \overset{m}{\sum_{j = 1}} w_{j} h_{j} \frac{c_{ji} - x_{1}}{b_{j}^{2}} (19) \end{matrix}$

式中: $\begin{matrix} x_{1} = Δu (k) 。 \end{matrix}$

神经网络自适应整定的性能指标为:

$\begin{matrix} E (k) = \frac{1}{2} e {(k)}^{2} = \frac{1}{2} (y_{d} (k) - y {(k))}^{2} (20) \end{matrix}$

神经网络的三项输入为:

$\begin{matrix} \{\begin{matrix} x_{1} = Δu (k) \\ x_{2} = y (k) \\ x_{3} = y (k - 1) \end{matrix} (21) \end{matrix}$

4 离线仿真分析

根据双电机四驱电动汽车拓扑结构及数据, 在AVL CRUISE环境中建立整车仿真模型, 复合ABS控制器结合dSPACE接口在Matlab/Simulink环境中开发。当电动汽车在路面上进行制动时, 由复合ABS控制逻辑图可知, 当车轮的滑移率大于20%, 系统启动电液复合ABS控制, 式(14)中的 $\begin{matrix} k_{P} (k) 、 k_{I} (k) 、 k_{D} (k) \end{matrix}$ 的初值由不同路面的最优参考参数库提供。考虑到前、后轴驱动系统的独立性, 而又在制动过程中相互约束, 在不同路面上制动时, 前、后电机自适应ABS控制参数η _{P_F}、η _{I_F}、η _{D_F}、η _{P_R}、η _{I_R}、η _{D_R}、η _F、η _F、α 采用多目标遗传算法优化获得。在冰路面, 压实雪路面以及湿沥青路面上, 多目标优化的结果如表1所示。

表1 RBF系统辨识自适应控制参数优化结果 Table 1 RBF self-adaptive control parameters

路面	η _{P_F}	η _{I_F}	η _{D_F}	η _{P_R}	η _{I_R}	η _{D_R}	η _F	η _R	$\begin{matrix} α \end{matrix}$
冰	0.36	0.62	0.41	0.40	0.69	0.55	0.73	0.78	0.38
压实雪	0.43	0.65	0.53	0.55	0.69	0.47	0.65	0.79	0.42
湿沥青	0.45	0.11	0.39	0.66	0.43	0.35	0.57	0.87	0.60

表1 RBF系统辨识自适应控制参数优化结果 Table 1 RBF self-adaptive control parameters

分别在均一路面上(冰路面, 压实雪路面, 湿沥青路面), 对接路面(冰变压实雪路面, 冰变湿沥青路面, 压实雪变冰路面, 湿沥青变冰路面)以及对开路面(冰路面与压实雪路面、冰路面与湿沥青路面)进行制动测试, 对基于RBF系统辨识的复合ABS自适应控制器进行验证。制动最终压力为9 MPa(对应制动强度为0.68), 从0到9 MPa的压力建立时间为1 s。

4.1 均一路面测试

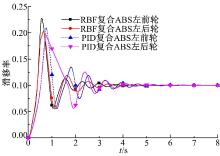
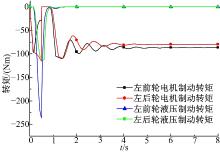
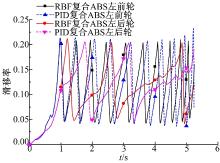
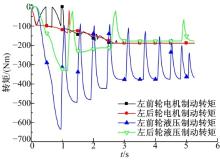
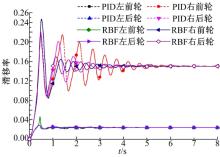
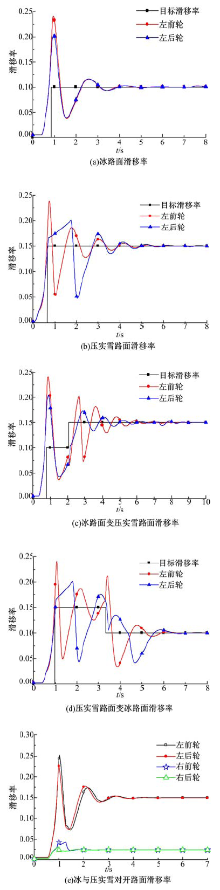
在冰路面上进行制动测试时, 前、后车轮的滑移率曲线以及作用在前、后车轮上的液压制动力矩与电机制动力矩曲线如图5和图6所示。从图5可以看出:在冰路面上时, 路面识别系统识别出路面的最佳滑移率为0.1, 采用RBF复合ABS时, 车轮的滑移率与PID控制算法相比提高了控制精度和速度。从图6可以看出:冰路面上制动时, 完全由电机提供制动力矩。

	Figure Option View Download New Window
	图5 冰路面前后轮滑移率Fig.5 Slip ratio on ice road

	Figure Option View Download New Window
	图6 冰路面前后电机及液压力矩Fig.6 Braking torque of motor and hydraulic on ice road

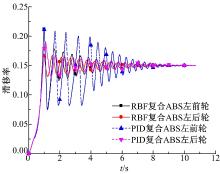
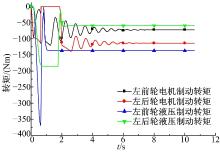
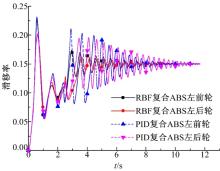
压实雪路面上进行制动测试时, 前、后轮的滑移率曲线及前、后车轮上的电机制动力矩和液压制动力矩如图7和图8所示。由图7可以看出:滑移率的调整精度和速度也明显改善。从图8可以看出:制动转矩由电机制动转矩和液压制动转矩共同提供, 当车轮的滑移率在0.1~0.2时, 液压制动转矩处于保压阶段, ABS主要靠电机制动来调整和保持。

	Figure Option View Download New Window
	图7 压实雪路面前后轮滑移率Fig.7 Slip ratio on compacted snow road

	Figure Option View Download New Window
	图8 压实雪路面前后电机及液压转矩Fig.8 Torque of motor and hydraulic on compacted snow road

湿沥青路面上进行制动时, 复合ABS系统的工作情况如图9和图10所示。从图9可以看出:在湿沥青路面上进行制动时, 路面识别系统识别出路面的最佳滑移率为0.2, 电机ABS以0.2为目标滑移率进行控制, 而液压ABS系统的滑移率控制范围为0.1~0.2, 二者存在一定的冲突, 又因为此时需求制动力较大, 液压制动力开始起主导作用, 电机制动力失去调节能力, 因而两种控制算法下的车轮滑移率几乎没有区别。在后面的测试中, 不再对湿沥青以及附着系数更大的路面测试。

	Figure Option View Download New Window
	图9 湿沥青路面前后轮滑移率Fig.9 Slip ratio on wet asphalt road

	Figure Option View Download New Window
	图10 湿沥青路面前后电机及液压转矩Fig.10 Torque of motor and hydraulic on wet asphalt road

4.2 对接路面测试

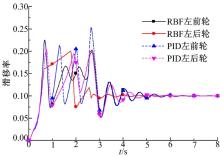
在冰变压实雪路面或压实雪变冰路面的对接路面上进行制动时, 前、后车轮的滑移率变化情况如图11和图12所示。从图11看出:在路面切换的过程中, RBF控制算法比PID控制算法具有更好的调节速度和适应能力。

	Figure Option View Download New Window
	图11 冰路面变压实雪路面前后轮滑移率Fig.11 Slip ratio from ice to compacted snow road

	Figure Option View Download New Window
	图12 压实雪路面变冰路面前后轮滑移率Fig.12 Slip ratio from compacted snow to ice road

4.3 对开路面测试

在冰与压实雪的对开路面上进行制动时复合ABS的工作情况如图13所示。可以看出, 系统识别出车辆行驶在非均一路面上, 冰路面上的车轮滑移率较大, 被控制在经验目标值0.15左右, 与PID控制算法相比, RBF控制算法仍然具有较好的调节能力。

	Figure Option View Download New Window
	图13 冰与压实雪路面滑移率Fig.13 Slip ratio on ice and compacted snow road

5 快速控制原型在环实时实验

采用dSPACE硬件在环实时集成环境对开发的控制器进行测试。整车模型在AVL CRUISE中建立, 通过编译后加载到dSPACE Ds1006板卡中, 作为整车仿真器使用。自适应复合ABS控制器模型通过RTICAN接口编译后加载到MicroAutobox Ds1401中, 从而建立起自适应复合ABS的快速控制原型。快速控制原型硬件在环实时实验的实物连接如图14所示。

	Figure Option View Download New Window
	图14 快速控制原型在环连接图Fig.14 Rapid control prototyping in loop

分别在均一路面、对接路面、对开路面上进行制动实验, 初速度为80 km/h, 制动压力为9 MPa对应制动强度为0.68, 驾驶员踩下制动踏板, 从0~9 MPa的反应时间为1 s, 计算步长为5 ms, CAN通讯协议采用ISO11898, 通讯波特率为500 kbit/s。

快速控制原型实时实验的结果如图15所示。从实时仿真结果来看, 实时实验测试结果与离线仿真结果一致, 说明基于RBF算法的复合ABS系统能够实现在中低附着路面上对车轮滑移率的精确控制, 并能够在实车控制中应用。

	Figure Option View Download New Window
	图15 路面滑移率Fig.15 Slip ratio

6 结论

(1)采用基于径向基函数神经网络辨识的复合ABS能够达到ABS控制的要求, 成功地实现了液压ABS可靠性及鲁棒性控制与电机ABS精确性控制的结合, 在中低附着路面上能够充分发挥电机控制的优势, 实现对车轮滑移率的精确控制。

(2)基于径向基函数神经网络辨识的自适应复合ABS比最优参数库的PID复合ABS具有更好的控制精度和速度。

(3)通过开发的复合ABS快速控制原型测试, 基于径向函数系统辨识的自适应复合ABS满足控制的实时性要求, 控制结果符合实际情况, 与离线仿真结果一致。

The authors have declared that no competing interests exist.

参考文献

View Option

[1]	Oleksowicz S A, Burnham K J, Barber P, et al. Investigation of regenerative and anti-lock braking interaction[J]. International Journal of Automotive Technology, 2013, 14(4): 641-650. [本文引用:1]
[2]	Sakai S, Sado H, Hori Y. Motion control in an electric vehicle with four independently driven in-wheel motors[J]. IEEE/ASME Transactions on Mechatronics, 1999, 4(1): 9-16. [本文引用:1]
[3]	Sakai S, Hori Y. Advantage of electric motor for anti-skid control of electric vehicle[J]. EPE Journal, 2001, 11(4): 26-32. [本文引用:1]
[4]	Mi C, Lin H, Zhang Y. Iterative learning control of antilock braking of electric and hybrid vehicles[J]. IEEE Transactions on Vehicular Technology, 2005, 54(2): 486-494. [本文引用:1]
[5]	王吉. 电动轮汽车制动集成控制策略与复合ABS控制研究[D]. 长春: 吉林大学汽车工程学院, 2011. Wang Ji. Study on brake integrated control strategy and composite ABS control for electric-wheel vehicle[D]. Changchun: College of Automotive Engineering, Jilin University, 2011. [本文引用:4]
[6]	Khatun P, Bingham C M, Schofield N, et al. Application of fuzzy control algorithms for electric vehicle antilock braking/traction control systems[J]. IEEE Transactions On Vehicular Technology, 2003, 52(5): 1356-1364. [本文引用:1]
[7]	Dash B K, Subudhi B. A fuzzy adaptive sliding mode slip ratio controller of a HEV[C]∥IEEE International Conference on Fuzzy Systems, Hyderabad, 2013: 1-8. [本文引用:1]
[8]	Tur O, Tur O, Ustun O, et al. An introduction to regenerative braking of electric vehicles as anti-lock braking system[C]∥IEEE Intelligent Vehicles Symposium, Istanbul, 2007: 944-948. [本文引用:1]
[9]	Yin G, Jin X. Cooperative control of regenerative braking and antilock braking for a hybrid electric vehicle[J]. Mathematical Problems in Engineering, 2013(4): 1-9. [本文引用:1]
[10]	刘寅虎, 李绍铭. 基于动态RBF神经网络在线辨识的单神经元PID控制[J]. 系统仿真学报, 2006, 18(增刊2): 804-807. Liu Yin-hu, Li Shao-ming. Single neuron PID control based on dynamic RBF neural network on-line identification[J]. Journal of System Simulation, 2006, 18(Sup. 2): 804-807. [本文引用:1]
[11]	余卓平, 左建令, 陈慧. 基于四轮轮边驱动电动车的路面附着系数估算方法[J]. 汽车工程, 2007, 29(2): 141-145. Yu Zhuo-ping, Zuo Jian-ling, Chen Hui. Tire-road friction coefficient estimation with four wheel in-wheel-motor drive vehicle[J]. Automotive Engineering, 2007, 29(2): 141-145. [本文引用:1]

2013

0.0

... 电液复合ABS结合了液压控制的可靠性及电机控制的快速和准确的优势,在电动汽车制动系统研究领域受到了国内外学者的广泛关注^[1,2,3,4,5] ...

1999

0.0

... 电液复合ABS结合了液压控制的可靠性及电机控制的快速和准确的优势,在电动汽车制动系统研究领域受到了国内外学者的广泛关注^[1,2,3,4,5] ...

2001

0.0

... 电液复合ABS结合了液压控制的可靠性及电机控制的快速和准确的优势,在电动汽车制动系统研究领域受到了国内外学者的广泛关注^[1,2,3,4,5] ...

2005

0.0

... 电液复合ABS结合了液压控制的可靠性及电机控制的快速和准确的优势,在电动汽车制动系统研究领域受到了国内外学者的广泛关注^[1,2,3,4,5] ...

2011

0.0

. 2011, :-

Study on brake integrated control strategy and composite ABS control for electric-wheel vehicle

电动轮汽车制动集成控制策略与复合ABS控制研究

Wang Ji

王吉

由于在环保、节能等方面的巨大优势,电动汽车的研发与应用成为了汽车研究领域发展的重要方向,而其主动安全性与能量回收领域的研究水平也日益提高。普通的电动汽车往往传承了传统内燃机汽车的液压制动系统,这种制动模式忽略了驱动电机再生制动能够有效回收制动能量这一因素,因此当今许多车辆采用了电机再生制动与传统液压制动相结合的复合制动系统。而电动汽车复合制动系

... 电液复合ABS结合了液压控制的可靠性及电机控制的快速和准确的优势,在电动汽车制动系统研究领域受到了国内外学者的广泛关注^[1,2,3,4,5] ...

... 王吉^[5]以四轮独立驱动的轮毂电机电动汽车为研究对像,建立了不同路面的PID参数库,采用变参数PID控制及等时轮加速度控制算法,开发了基于电机制动力与液压制动力协调工作的ABS控制器,并通过仿真的方法验证了电液复合控制具有良好的控制效果 ...

... 在文献[5,11]中,采用的利用附着系数极大值的方法具有算法简单、实时性好的优点,本文中也采用此方法对路面状况进行识别 ...

... 根据文献[5]及汽车理论,冰路面对应的最佳滑移率为0 ...

2003

0.0

... Khatun等^[6]采用模糊逻辑控制算法对电动车ABS进行了研究,开发的模糊鲁棒性控制器改善了电动汽车的制动性能 ...

2013

0.0

... Dash等^[7]以一款混合动力汽车为研究对象,将模糊控制算法与滑模控制算法相结合,开发了模糊适应性滑移率控制器,通过仿真验证了控制算法可有效地消除滑膜控制的颤振,达到良好的控制效果 ...

2007

0.0

... Tur等^[8]建立了1/4轮毂电机电动汽车模型,对电机ABS和液压ABS进行了仿真对比分析,结果表明电机ABS比液压ABS具有更好的效果 ...

0.0

... Yin等^[9]研究了混合动力汽车的再生制动与ABS的联合控制问题,采用滑模控制方法把车轮滑移率控制在最优的范围之内 ...

2006

0.0

. 2006, 18(增刊2):804-807 DOI:doi:10.3969/j.issn.1004-731X.2006.z2.227

Single neuron PID control based on dynamic RBF neural network on-line identification

基于动态RBF神经网络在线辨识的单神经元PID控制

Liu Yin-hu , Li Shao-ming

刘寅虎, 李绍铭

针对工业控制领域中复杂非线性时变系统,提出了基于动态RBF神经网络辨识的单神经元PID控制方法.采用动态RBF神经网络辨识器在线辨识系统模型,获得PID参数在线调整信息,并由单神经元PID控制器完成控制器参数的在线自整定,实现系统的智能控制.仿真结果表明,与常规RBF神经网络辨识的PID控制方法相比,该方法具有控制精度高、响应速度快的优点,并且具备较强的自适应性和鲁棒性.

... 为了提高基于参数库的变参数ABS控制的精度及鲁棒性,进一步改善ABS控制器的适应性,本文以一款双电机四驱电动汽车为研究对象,在基于参数库的PID控制方法的基础上,采用基于径向基函数(Radial basis function,RBF)神经网络系统辨识的方法^[10],获取制动时车轮滑移率对于电机制动转矩变化的灵敏度信息对PID的控制参数进行在线滚动优化调整,提高PID控制算法的鲁棒性、快速性和准确性,并通过离线仿真和快速控制原型在环仿真的方法对开发的控制算法的控制效果及实时性进行验证 ...

2007

0.0

. 2007, 29(2):141-145 DOI:doi:10.3321/j.issn:1000-680X.2007.02.013

Tire-road friction coefficient estimation with four wheel in-wheel-motor drive vehicle

基于四轮轮边驱动电动车的路面附着系数估算方法

Yu Zhuo-ping , Zuo Jian-ling , Chen Hui

余卓平, 左建令, 陈慧

路面附着系数是影响车辆行驶安全性的重要因素,利用轮边驱动电动汽车驱动力矩可以对路面利用附着系数进行观测.当观测到μ-λ曲线接近于峰值点时,将该时刻的轮胎利用附着系数作为路面峰值附着系数,并根据识别的路面峰值附着系数进行驱动防滑控制.该方法能够有效防止轮胎滑转,提高车辆行驶稳定性.

... 在文献[5,11]中,采用的利用附着系数极大值的方法具有算法简单、实时性好的优点,本文中也采用此方法对路面状况进行识别 ...