前向补偿结合滑模控制的液压泵/马达斜盘角度控制器

引用本文

沈伟, 张迪嘉, 孙毅, 姜继海. 前向补偿结合滑模控制的液压泵/马达斜盘角度控制器. 2016, 46(5): 1513-1519
SHEN Wei, ZHANG Di-jia, SUN Yi, JIANG Ji-hai. Control design of the swash plate angle for hydraulic pump/motor based on FSMI method. Journal of Jilin University Engineering and Technology Edition, 2016, 46(5): 1513-1519 复制到剪切板

Permissions

前向补偿结合滑模控制的液压泵/马达斜盘角度控制器

沈伟¹, 张迪嘉², 孙毅³, 姜继海²

1.上海理工大学机械工程学院,上海 200093

2.哈尔滨工业大学机电工程学院,哈尔滨 150080

3.北京精密机电控制设备研究所, 北京 100076

作者简介:沈伟(1984-),男,讲师,博士.研究方向:液压混合动力技术.E-mail:shenwei@usst.edu.cn

基金:国家自然科学基金项目(51505289,51275123).

摘要

为了降低液压混合动力挖掘机控制油路的溢流损失,同时提高液压泵/马达斜盘角度控制系统的鲁棒性,本文应用基于改进积分型的前向补偿结合滑模控制的方法(FSMI)设计了控制器。首先,介绍了可切换控制的基于压力共轨系统(CPR)的液压混合动力挖掘机的工作原理以及降低控制油路压力的必要性。然后,通过分析斜盘所受的轴向压紧力和传统数学模型的结构对系统模型进行了改进,同时利用数学分析的方法将FSMI方法应用于该模型。最后,结合仿真分析的工况搭建了试验台并进行了试验。仿真和试验的结果表明,所提出的控制方法可以有效地提高斜盘角度控制的鲁棒性。

关键词: 流体传动与控制; 斜盘角度控制; 前向补偿; 滑模控制

中图分类号:TH137 文献标志码:A 文章编号:1671-5497(2016)05-1513-07

Control design of the swash plate angle for hydraulic pump/motor based on FSMI method

SHEN Wei¹, ZHANG Di-jia², SUN Yi³, JIANG Ji-hai²

1.School of Mechanical Engineering, University of Shanghai for Science and Technology, Shanghai 200093,China

2.School of Mechatronics Engineering, Harbin Institute of Technology, Harbin 150080,China

3.Beijing Institute of Mechanical and Electrical Control Equipment, Beijing 100076,China

Abstract

In order to reduce the throttling loss of the control circuit of the hydraulic hybrid excavator, the control pressure of the loop should be reduced. However, it would tend to deteriorate the control performance of the swash plate angle. Hence, the fee forward compensation combining with the sliding mode control based on the improved integral method (FSMI) is used to enhance the robust performance. First, the basic principle of the hydraulic hybrid excavator based on common pressure rail combined with switched function (HHES) is introduced and the necessity of reducing the control pressure is explained. Then, the improved mathematical model of the system is presented by analyzing the force applied on the swash plate; meanwhile, the FSMI is stated in details. Finally, the test rig is constructed corresponding to the simulation. Both of the simulation and experimental results show that the proposed method is effective and can enhance the robust performance of the system.

Keyword: turn and control of fluid; control of the swash plate angle; feed forward compensation; sliding mode control

Show Figures

0 引言

近年来, 随着燃油价格的不断增加以及对环保要求的日趋严格, 挖掘机的节能研究成为广大科研工作者的热点课题^{[1, 2, 3, 4]}。基于压力共轨系统(CPR)的液压混合动力挖掘机由于其不仅在理论上消除了传统阀控系统存在的节流损失, 更可以回收制动能和重力势能, 所以具备广阔的应用前景^{[5, 6, 7]}。文献[8]详细介绍了该系统的工作原理, 另外, 关于回转系统以及动臂系统等子系统都有文献对其进行了控制特性和节能特性分析^{[9, 10, 11, 12]}。但是, 这些文献大都将系统中的控制量(液压泵/马达的斜盘摆角和液压变压器的配流盘旋转角度)作为理想量进行研究, 并没有考虑这些变量的控制特性, 更需要指出的是, 由于成本原因, 控制回路采用的仍然是定量泵加溢流阀的供油方式, 如果减小控制油路的压力可以有效地减少控制回路的节流损失。但如何在降低控制油路压力条件下保持或者提高斜盘角度控制的鲁棒性和准确性是节能的前提条件。本文以液压泵/马达的控制油路(即伺服阀控制变量缸)为研究对象, 利用基于改进积分型的前向补偿结合滑模控制的方法(FSMI)对该系统进行了仿真和试验研究, 同时, 该控制算法可扩展到液压变压器以及主泵的控制机构。

1 系统建模

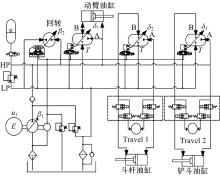
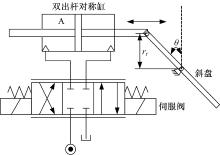
图1为新型液压混合动力挖掘机液压系统简图, 由于挖掘机在实际工作时, 驱动系统和斗杆以及铲斗系统很少同时工作, 所以本方案采用切换控制方案, 即利用控制斗杆和铲斗的两个液压变压器通过开关阀组的切换完成对斗杆、铲斗以及驱动系统的控制。该新型系统除了保留了文献[8]中的优点外, 相对于已经公开的发明专利(公开号为CN101718107A)里面所需的两个变量行走液压泵/马达价格高、产量少, 现在这个方案只需用定量马达, 而增加的阀组成本很低, 所以改造成本降低了。另外, 由于现有的挖掘机制造体系用的都是定量马达, 所以通过该方案基于现有挖掘机制造体系改造难度小。具体工作原理为, 通过调整液压泵/马达的排量或者液压变压器配流盘的角度来完成对负载变化的适应。因此, 控制油路均为液压位置控制系统。液压泵/马达变量机构的原理简图如图2所示。

	Figure Option View Download New Window
	图1 可切换控制的液压混合动力挖掘机液压系统Fig.1 Hydraulic system of switch control hybrid excavator

	Figure Option View Download New Window
	图2 变量机构原理简图Fig.2 Principle diagram of variable mechanism

斜盘由一个双出杆对称缸驱动, 斜盘所受外力矩包括弹簧力、滑靴施加于斜盘的阻力矩以及黏性摩擦力矩。具体表达式为:

$\begin{matrix} \begin{matrix} J_{p} \frac{d^{2} θ}{d t^{2}} = [A (p_{A} - p_{B}) - 2 k_{t} r_{r} sinθ - \\ 2 f_{v} r_{r} \frac{dθ}{dt} cosθ] r_{r} cosθ - T_{x} (1) \end{matrix} \end{matrix}$

式中: $J_{p}$ 为斜盘组件的等效惯量; $k_{t}$ 为弹簧刚度; $θ$ 为斜盘摆角; $A$ 为对称缸面积; $p_{A}$ 和 $p_{B}$ 分别为对称缸两腔的压力; $f_{v}$ 为黏性摩擦因数; $r_{r}$ 为斜盘半径; $T_{x}$ 为滑靴施加在斜盘上的转矩在 $\begin{matrix} x \end{matrix}$ 轴方向的分转矩。

在传统的控制方式中, 都是将柱塞施加于斜盘的压紧力以及油源的压力变化忽略, 这个假设在油源压力较大且稳定的情况下适用, 但是以节能为目的需要将控制油源减小的条件下, 这个力对于控制系统的影响会增加。另外, 在工程机械中, 控制油路的泵通常与主泵一起通轴连接到发动机上, 所以油源压力会经常波动, 这样会同时增加控制的难度。

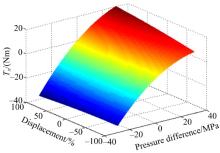
为了克服上面所述的难点, 首先分析轴向压紧力的特点和估计值, 轴向的压紧力实际上是多个柱塞作用于斜盘上的合力在轴向方向的分力, 这个力随着泵压差、转速以及泵排量的变化而变化, 由于运动过程比较复杂, 所以通过理论建模方式很难得到准确的值, 本文利用文献[13]所提出的数值分析方法以及数据, 得到 $\begin{matrix} T_{x} \end{matrix}$ 与泵转速, 排量以及压差的变化趋势如图3所示。

	Figure Option View Download New Window
	图3 在转速为1440 r/min条件下的T_x值Fig.3 T_x values under the condition of speed 1440 r/min

利用传统的数学建模方法对该位置控制系统进行建模, 首先, 伺服阀的传递函数可简化为:

$\begin{matrix} \frac{Y (s)}{U (s)} = \frac{K_{v}}{\frac{s^{2}}{ω_{sv}^{2}} + \frac{2 ξ_{sv}}{ω_{sv}} s + 1} (2) \end{matrix}$

式中: $Y (s)$ 为伺服阀阀芯位移; $U (s)$ 为控制电压; $ω_{sv}$ 为伺服阀固有频率; $\begin{matrix} ξ_{sv} \end{matrix}$ 为伺服阀阻尼系数。

$\begin{matrix} \begin{matrix} Q_{1} = y_{v} d_{v} \sqrt{p_{s} - p_{A}} (3) \\ Q_{2} = y_{v} d_{v} \sqrt{p_{B}} (4) \end{matrix} \end{matrix}$

式中: $p_{s}$ 为油源压力; $Q_{1}$ 和 $Q_{2}$ 分别为对称缸两腔的流量; $\begin{matrix} d_{v} \end{matrix}$ 为常数项。

$\begin{matrix} \begin{matrix} {\overset{\cdot}{p}}_{A} = \frac{β_{e}}{V_{A}} (Q_{1} - A {\overset{\cdot}{x}}_{p} - k p_{A}) (5) \\ {\overset{\cdot}{p}}_{B} = \frac{β_{e}}{V_{B}} (Q_{2} - A {\overset{\cdot}{x}}_{p} - k p_{B}) (6) \end{matrix} \end{matrix}$

式中: $β_{e}$ 为体积弹性模量; $k$ 为常数项; $\begin{matrix} x_{p} \end{matrix}$ 为变量油缸的位移。

假设 $\begin{matrix} V_{A} = V_{B} = V_{p}, Q_{1} = - Q_{2}, Δp = p_{A} - p_{B}, \end{matrix}$ 由于该斜盘的摆动角度最大± 18° , 所以 $\begin{matrix} sinθ \approx θ, cosθ \approx 1, \end{matrix}$ 则该位置控制系统的状态方程为:

$\begin{matrix} \{\begin{matrix} {\overset{\cdot}{x}}_{1} = Δ \overset{\cdot}{p} = \frac{β_{e}}{V_{p}} (2 d_{v} y_{v} \sqrt{\frac{1}{2} | p_{s} - Δp |} - \\ 2 A r_{r} θ - k_{t} Δp) \\ {\overset{\cdot}{x}}_{2} = \overset{\cdot \cdot}{θ} = \frac{1}{J_{p}} [(AΔp - 2 k_{t} r_{r} θ - \\ 2 f_{v} r_{r} \overset{\cdot}{θ}) r_{r} + T_{x}] \\ {\overset{\cdot}{x}}_{3} = \overset{\cdot}{θ} = x_{2} \end{matrix} (7) \end{matrix}$

需要指出的是, 伺服阀的阀芯位置的频响很高, 所以式(7)中阀芯位置量 $\begin{matrix} y_{v} 可用控制电压 u \end{matrix}$ 代替。A4V变量泵变量组件的固有频率远大于所用伺服阀的固有频率, 所以控制目标(即斜盘摆角)主要由伺服阀的输出流量来决定, 即:

$\begin{matrix} \overset{\cdot}{θ} = norm (\frac{Q_{p}}{A}) (8) \end{matrix}$

式中:norm为归一化函数。

另外, 式(8)表明, 控制量 $\begin{matrix} u \end{matrix}$ 与目标量间是多阶函数, 过高阶次的微分会导致噪声急剧增加从而导致实际应用受阻。同时, 控制量与干扰量之间没有直接联系, 所以无法对干扰量进行直接的抑制。综上, 需要对该模型进行分析, 由于斜盘组件的等效惯量小, 所以假设 $\begin{matrix} J_{p} = 0, \end{matrix}$ 则

$\begin{matrix} \begin{matrix} [A (p_{A} - p_{B}) - 2 k_{t} r_{r} sinθ - \\ 2 f_{v} r_{r} \frac{dθ}{dt} cosθ] r_{r} cosθ - T_{x} = 0 (9) \\ p_{s} = (p_{s} - p_{A}) + (p_{A} - p_{B}) + p_{B} = \\ 2 [{(\frac{Q_{p}}{y_{v} d_{v}})}^{2} + \frac{k_{t} {r_{r}}^{2} θ - T_{x}}{A r_{r}}] (10) \\ Q_{p} = y_{v} d_{v} \sqrt{0.5 (p_{s} - \frac{2 k_{t} {r_{r}}^{2} θ - M_{x}}{A r_{r}})} (11) \end{matrix} \end{matrix}$

角位置的导数为:

$\begin{matrix} \overset{\cdot}{θ} = \frac{uB}{A} \sqrt{\frac{1}{2} \{p_{s} - \frac{1}{A} [2 k_{t} r_{r} θ - \frac{{\hat{T}}_{x}}{r_{r}} sgn (u)]\} + Δ} (12) \end{matrix}$

式中: $B$ 为常数项, 关于流量系数的变化以及未建模型都统一为参数变化量 $\begin{matrix} Δ 。 \end{matrix}$

2 控制策略分析

重新强调本文的目的是通过设计合理的控制器使得斜盘能够在油源变化和模型不确定性的前提下抵抗干扰转矩的影响, 从而获得较好的位置控制效果。通过上述的分析, 本文采用基于改进积分型的前向补偿结合滑模控制的方法(简称FSMI方法), 具体来说是将控制量分为三个部分:第一部分为通过前馈补偿的方式来抵抗轴向压紧力变化的影响, $\begin{matrix} T_{x} \end{matrix}$ 可以通过上述的数值分析方法进行估计, 第二部分通过滑模控制器来适应由于参数不确定性带来的干扰, 最后一部分用于提高静态跟踪精度。

$u = u_{f} + u_{b} + u_{I} (13)$

其中:

$\begin{matrix} \begin{matrix} u_{f} = \frac{{\overset{\cdot}{θ}}_{d} A}{B \sqrt{\frac{1}{2} \{p_{s} - \frac{1}{A} [2 {\hat{k}}_{t} r_{r} θ - \frac{{\hat{T}}_{x}}{r_{r}} sgn (u)]\}}} \\ u_{b} = - K_{b} sgn (\overset{\cdot}{θ} - {\overset{\cdot}{θ}}_{d}) = - K_{b} sgn (e) \\ u_{I} = k_{I} \int_{t_{1}}^{t_{2}} e dt \end{matrix} \end{matrix}$

式中:上标^表示参数的估计值; $K_{b}$ 为变结构控制的增益值; $θ_{d}$ 为目标转角; $K_{I}$ 为积分补偿项的增益值。为了得到 $K_{b}$ 的取值, $u_{b}$ 需要满足 $\overset{\cdot}{e} < 0$ 以及 $\begin{matrix} \lim_{t \to \infty} e = 0 。 \end{matrix}$

$\begin{matrix} \begin{matrix} \overset{\cdot}{e} = \overset{\cdot}{θ} - {\overset{\cdot}{θ}}_{d} = (u_{f} + u_{b}) \frac{B}{A} \times \\ \sqrt{\frac{1}{2} \{p_{s} - \frac{1}{A} [2 k_{t} r_{r} θ - \frac{T_{x}}{r_{r}} sgn (u)]\} + Δ} - {\overset{\cdot}{θ}}_{d} = \\ {\overset{\cdot}{θ}}_{d} \{\frac{\sqrt{\frac{1}{2} \{p_{s} - \frac{1}{A} [2 k_{t} r_{r} θ - \frac{T_{x}}{r_{r}} sgn (u)]\} + Δ}}{\sqrt{\frac{1}{2} \{p_{s} - \frac{1}{A} [2 k_{t} r_{r} θ - \frac{{\hat{T}}_{x}}{r_{r}} sgn (u)]\}}} - 1\} - \\ K_{b} sgn (e) \frac{B}{A} \sqrt{\frac{1}{2} \{p_{s} - \frac{1}{A} [2 k_{t} r_{r} θ - \frac{T_{x}}{r_{r}} sgn (u)]\} + Δ} (14) \\ 可求出 : \\ K_{b} > \frac{‖ {\overset{\cdot}{θ}}_{d} ‖_{\infty}}{B} \times \\ \{\frac{1}{\sqrt{\frac{1}{2} \{p_{s} - \frac{1}{A} [2 k_{t} r_{r} θ - \frac{{\hat{T}}_{x}}{r_{r}} sgn (u)]\}}} - \\ \frac{1}{\sqrt{\frac{1}{2} \{p_{s} - \frac{1}{A} [2 k_{t} r_{r} θ - \frac{T_{x}}{r_{r}} sgn (u)]\} + Δ}}} (15) \end{matrix} \end{matrix}$

另外, 由于伺服阀的频宽限制, $\begin{matrix} u \end{matrix}$ 是一个有限制的控制输入, 为了避免变结构控制产生波动, 饱和函数sat(· )被引入, 输出为-1到1, 则

$\begin{matrix} \begin{matrix} u = \frac{{\overset{\cdot}{θ}}_{d}}{{\hat{D}}_{t}} {\{\frac{1}{2} [p_{s} - \frac{1}{A} (2 k_{t} r_{r} θ - \frac{T_{x}}{r_{r}} sgn (u))]\}}^{- 1 / 2} - \\ Ksat (\frac{e}{φ}) + k_{I} \int_{t_{1}}^{t_{2}} e dt (16) \end{matrix} \end{matrix}$

3 仿真分析

为了验证所采用的基于改进积分型的前向补偿结合滑模控制器的有效性和适用性, 仿真分析部分的建模仍然采用传统的非线性建模法, 即包括了阀动态以及斜盘组件动态和压力变化部分, 同时还加入了轴向压紧力的干扰和随机有界扰动, 利用Simulink搭建系统模块。

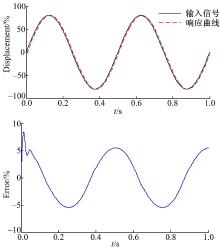
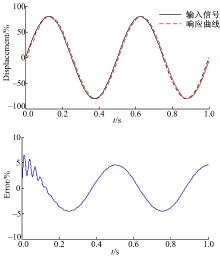
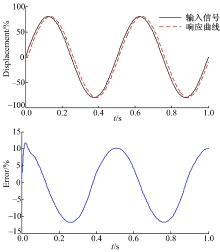
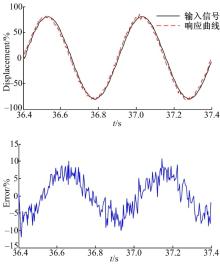
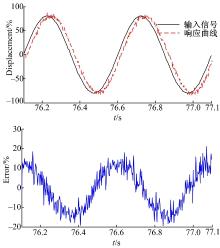
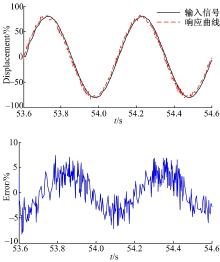
由 $\begin{matrix} T_{x} \end{matrix}$ 随转速、压差以及排量的变化图(图3)可以看出, 当转速一定时, 液压泵/马达A和B口压差最大时的干扰力矩最大, 所以仿真工况选择两种, 一种为轻载工况(即控制油路供油压力为3 MPa且A口和B口压差为0); 另一种为极限工况(即控制油路供油压力为2 MPa且A口和B口压差为25 MPa)。另外, 为了对比所提出控制策略的性能, 同时采用传统的PI控制作为对比。两种方法的动态响应都能满足要求, 实际工作中主要要求的是其伺服特性, 所以以跟踪正弦信号的响应作为研究方法。

从图4~图7的仿真结果可以看出(图中实线为输入信号, 虚线表示响应曲线), 在轻载工况时, 两种控制方法都能较好地跟踪目标信号, FSMI控制器并没有显现出明显优势。但是在极限工况下, 由于轴向干扰力矩变大而且供油压力减小, 采用PI控制已经出现较大的滞后, 跟踪误差最大达到12.5%, 而FSMI控制器由于其前向补偿以及滑模控制可以较快地到滑模面, 跟踪误差最大达到6%左右, 所以显示出了较强的鲁棒性和自适应性。

	Figure Option View Download New Window
	图4 轻载工况下的PI控制仿真曲线Fig.4 Simulation result of light load condition with PI control

	Figure Option View Download New Window
	图5 轻载工况下的FSMI控制仿真曲线Fig.5 Simulation result of light load condition with FSMI control

	Figure Option View Download New Window
	图6 极限工况下的PI控制仿真曲线Fig.6 Simulation result of limited condition with PI control

	Figure Option View Download New Window
	图7 极限工况下的FSMI控制仿真曲线Fig.7 Simulation result of limited condition with FSMI control

4 试验

试验装置如图8所示, 液压泵/马达由电动机驱动, 负载由溢流阀调定。对应仿真部分的工况, 试验分别在溢流阀调定压力为25 MPa以及0 MPa两种情况下进行, 其中电机转速设定为1440 r/min。微电方面, 将前文中利用Simulink搭建的模型去除模型部分, 增加数据采集口, 然后将该控制器下载到NI公司的板卡中。

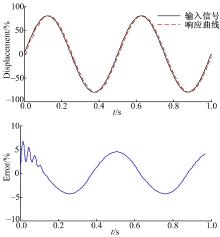
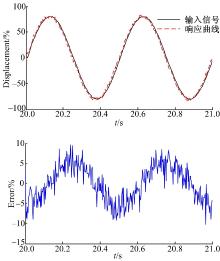
	Figure Option View Download New Window
	图8 试验平台Fig.8 Test rig

试验结果如图9~图12所示。试验结果表明, 在轻载工况下, 两种控制算法均能较好地跟踪目标信号, 其中PI控制在跟踪误差方面甚至略优于FSMI控制器。但是在重载工况下, PI控制已经显现出较大的滞后, 在忽略传感器噪声的前提下, 最大跟踪误差达到18.75%, 而FSMI控制仍能将误差控制在7%的范围内, 体现出较好的鲁棒性, 同时大体趋势与仿真趋势相符, 在具体数值上略高于仿真结果。这里需要指出的是, 本文所采用的PI控制采用的是固定的值, 即通过设定不同组PI参数来查看试验结果, 在选出一组适用于多种工况的参数下保持这种参数值不变, 然后与FSMI控制相比较, 这与实际应用的方法是相符的。

	Figure Option View Download New Window
	图9 轻载工况下的PI控制试验曲线Fig.9 Experiment result of light load condition with PI control

	Figure Option View Download New Window
	图10 轻载工况下的FSMI控制试验曲线Fig.10 Experiment result of light load condition with FSMI control

	Figure Option View Download New Window
	图11 极限工况下的PI控制试验曲线Fig.11 Experiment result of limited condition with PI control

	Figure Option View Download New Window
	图12 极限工况下的FSMI控制试验曲线Fig.12 Experiment result of limited condition with FSMI control

5 结束语

提出用降低控制油路油源压力的方法来减少节流损失, 同时针对这种方法导致的斜盘角度控制性能降低的问题, 通过分析斜盘所受外力指出 $\begin{matrix} T_{x} \end{matrix}$ 是在油源压力降低条件下对控制性能影响较大的干扰转矩, 应用基于改进积分型的前向补偿结合滑模控制的方法来提高控制性能。仿真和试验结果表明, 在轻载工况下, 传统的PI控制和FSMI控制都能较好地跟踪正弦目标信号, PI控制还略优于FSMI控制。但是, 在极限工况下, 由于 $\begin{matrix} T_{x} \end{matrix}$ 的增大以及控制油压力的降低, PI控制出现较大的滞后, 而FSMI仍然显现出较好的适应性能, 说明本文所应用的控制方法可以有效地保证斜盘角度控制系统的性能。

The authors have declared that no competing interests exist.

参考文献

View Option

[1]	Xiao Q, Wang Q, Zhang Y. Control strategies of power system in hybrid hydraulic excavator[J]. Automation in Construction, 2008, 17(4): 361-367. [本文引用:1]
[2]	Griffin P W, Hammond G P, Ng K R, et al. Impact review of past UK public industrial energy efficiency[J]. Energy Conversion and Management, 2012, 60(8): 243-250. [本文引用:1]
[3]	Kim H, Choi J, Yi K. Development of supervisory control strategy for optimized fuel consumption of the compound hybrid excavator[J]. Journal of Automobile Engineering, 2012, 226(12): 1652-1666. [本文引用:1]
[4]	Cetinkunt S, Pinsopon U, Chen C, et al. Positive flow control of closed-center electrohydraulic implement-by-wire systems for mobile equipment applications[J]. Mechatronics, 2004, 114(4): 403-420. [本文引用:1]
[5]	Achten P A J, Vael G, Zhao F. The Innas hydraulic transformer-the key to the hydrostatic common pressure rail[C]∥SAE Paper, 2000-01-2561. [本文引用:1]
[6]	Shen W, Jiang J. Analysis and development of the hydraulic secondary regulation system based on the CPR[C]∥International Conference on Fluid Power and Mechatronics, Beijing, 2011: 117-222. [本文引用:1]
[7]	Ahn K K, Ho T H, Dinh Q T. A study on energy saving potential of hydraulic on energy saving potential of hydraulic control system using switching type closed loop constant pressure system[C]∥Proceedings of the 7th JFPS International Symposium on Fluid Power, Toyama, Japan, 2008: 317-322. [本文引用:1]
[8]	姜继海, 于安才, 沈伟. 基于CPR网络的全液压混合动力挖掘机[J]. 液压与气动, 2010(9): 44-47. Jiang Ji-hai, Yu An-cai, Shen Wei. The review of full hydraulic hybrid excavator based on common pressure rail network[J]. Chinese Hydraulics & Pneumatics, 2010(9): 44-47. [本文引用:2]
[9]	闫丽娟, 孙辉, 刘伟, 等. 行走工程机械液压混合动力技术[J]. 吉林大学学报: 工学版, 2014, 44(2): 364-368. Yan Li-juan, Sun Hui, Liu Wei, et al. Hydraulic hybrid technology of moving construction machinery[J]. Journal of Jilin University (Engineering and Technology Edition), 2014, 44(2): 364-368. [本文引用:1]
[10]	沈伟, 姜继海, 王克龙. 液压变压器控制挖掘机动臂油缸动态分析[J]. 农业机械学报, 2013, 44(4): 27-32. Shen Wei, Jiang Ji-hai, Wang Ke-long. Dynamic response analysis of the boom cylinder controlled by the hydraulic transformer[J]. Transactions of the Chinese Society of Agricultural Machinery, 2013, 44(4): 27-32. [本文引用:1]
[11]	Achten P, Zhao F, Vael G E M. Transforming future hydraulics: a new design of a hydraulic transformer[C]∥The Fifth Scand inavian International Conference on Fluid Power, Linköping, Sweden, 1997: 1-24. [本文引用:1]
[12]	Sgro S, Inderelst M, Murrenhoff H. Energy efficiency of mobile working machines[C]∥7th International Fluid Power Conference, Aachen, Germany, 2010: 1-12. [本文引用:1]
[13]	Ivantysy J, Ivantysynova M. Hydrostatic Pumps and Mortors[M]. New Delhi, India: Akademia Books International, 2001. [本文引用:1]

2008

0.0

... 0 引言近年来,随着燃油价格的不断增加以及对环保要求的日趋严格,挖掘机的节能研究成为广大科研工作者的热点课题^[1,2,3,4] ...

2012

0.0

... 0 引言近年来,随着燃油价格的不断增加以及对环保要求的日趋严格,挖掘机的节能研究成为广大科研工作者的热点课题^[1,2,3,4] ...

2012

0.0

... 0 引言近年来,随着燃油价格的不断增加以及对环保要求的日趋严格,挖掘机的节能研究成为广大科研工作者的热点课题^[1,2,3,4] ...

2004

0.0

... 0 引言近年来,随着燃油价格的不断增加以及对环保要求的日趋严格,挖掘机的节能研究成为广大科研工作者的热点课题^[1,2,3,4] ...

2000

0.0

... 基于压力共轨系统(CPR)的液压混合动力挖掘机由于其不仅在理论上消除了传统阀控系统存在的节流损失,更可以回收制动能和重力势能,所以具备广阔的应用前景^[5,6,7] ...

2011

0.0

2008

0.0

2010

0.0

. 2010, (9):44-47 DOI:doi:10.3969/j.issn.1000-4858.2010.09.016

The review of full hydraulic hybrid excavator based on common pressure rail network

基于CPR网络的全液压混合动力挖掘机

Jiang Ji-hai , Yu An-cai , Shen Wei

姜继海, 于安才, 沈伟

针对挖掘机运行过程中所产生的能量损失,分析了现有全液压挖掘机系统的优缺点,综述了挖掘机节能技术的发展状况.依据液压泵/马达(二次元件)四象限工作特性和液压变压器的特点,建立了基于CPR网络的全液压混合动力挖掘机系统,采用液压泵/马达回收挖掘机旋转运动制动动能,采用液压变压器回收挖掘机直线运动势能,解决了现有挖掘机的传动效率和能量利用率低的问题.

... 文献[8]详细介绍了该系统的工作原理,另外,关于回转系统以及动臂系统等子系统都有文献对其进行了控制特性和节能特性分析^[9,10,11,12] ...

... 该新型系统除了保留了文献[8]中的优点外,相对于已经公开的发明专利(公开号为CN101718107A)里面所需的两个变量行走液压泵/马达价格高、产量少,现在这个方案只需用定量马达,而增加的阀组成本很低,所以改造成本降低了 ...

2014

0.0

. 2014, 44(2):364-368 DOI:doi:10.13229/j.cnki.jdxbgxb201402014

Hydraulic hybrid technology of moving construction machinery

行走工程机械液压混合动力技术

Yan Li-juan , Sun Hui , Liu Wei

闫丽娟, 孙辉, 刘伟

The operating characteristic of moving construction machinery is analyzed and the energy saving potential is evaluated. In view of the characteristics that moving construction machinery frequently start and stop, different energy saving schemes are proposed. Regenerative braking strategy and energy reuse strategy are designed based on the advantage of high power density of hydraulic accumulator. Prototypes of hydraulic hybrid loader and hydraulic hybrid concrete mixer truck are developed. Experiment results show that the hydraulic hybrid system can effectively recover and reuse the braking energy. The control strategies reasonably switch among various operation modes, reduce fuel consumption and improve the dynamic performance of the machine.

对比了行走工程机械与公路车辆的作业特点，分析了行走工程机械的节能潜力。针对其频繁起停、往复运动的作业特点，提出液压混合动力系统的节能方案，设计了再生制动策略和能量利用策略，开发了混合动力装载机和混凝土搅拌车样车。试验结果表明，行走机械液压混合动力系统能够实现各种工作模式的合理切换，有效地回收和再利用整机的制动动能，降低燃油消耗，提高整机的动力性能。

... 文献[8]详细介绍了该系统的工作原理,另外,关于回转系统以及动臂系统等子系统都有文献对其进行了控制特性和节能特性分析^[9,10,11,12] ...

2013

0.0

. 2013, 44(4):27-32 DOI:doi:10.6041/j.issn.1000-1298.2013.04.005

Dynamic response analysis of the boom cylinder controlled by the hydraulic transformer

液压变压器控制挖掘机动臂油缸动态分析

Shen Wei , Jiang Ji-hai , Wang Ke-long

沈伟, 姜继海, 王克龙

To enhance the hydraulic system efficiency of excavator, one system which adopted the novel hydraulic transformer (NHT) was proposed to control boom cylinder due to the great recoverable energy of boom. Firstly, according to the tough working period, especially for the load fluctuates frequently and violently, the rod side of the boom cylinder was connected to the high pressure line of common pressure rail (CPR). Moreover, the proposed system was analyzed by using of mathematical method and the model was constructed. Measurement data about the boom load change of one excavator was input into the simulation model. Finally, the valid angle range of NHT was studied and the pressure feedback loop was applied. Results showed that the proposed system possessed good servo performance under great fluctuating load. 

采用液压摆动马达直接控制配流盘旋转的斜盘柱塞式新型液压变压器构造了挖掘机动臂液压系统。针对挖掘机的液压油缸在实际工况中要承受2个方向的负载且负载变化频繁剧烈的问题，将动臂油缸无杆腔与压力共轨高压端相连通，建立了所提出系统的数学模型，并将试验中采集到的挖掘机实际工作过程中动臂油缸的负载数据作为模型的输入；在分析了液压变压器控制角的合理工作范围并提出增加压力反馈回路的控制策略后，对系统的速度响应进行了分析。结果表明提出的动臂系统可以较好地跟踪速度目标信号，在变负载情况下鲁棒性强，从而可以满足工程实际需要。

... 文献[8]详细介绍了该系统的工作原理,另外,关于回转系统以及动臂系统等子系统都有文献对其进行了控制特性和节能特性分析^[9,10,11,12] ...

1997

0.0

... 文献[8]详细介绍了该系统的工作原理,另外,关于回转系统以及动臂系统等子系统都有文献对其进行了控制特性和节能特性分析^[9,10,11,12] ...

2010

0.0

... 文献[8]详细介绍了该系统的工作原理,另外,关于回转系统以及动臂系统等子系统都有文献对其进行了控制特性和节能特性分析^[9,10,11,12] ...

2001

0.0

... 为了克服上面所述的难点,首先分析轴向压紧力的特点和估计值,轴向的压紧力实际上是多个柱塞作用于斜盘上的合力在轴向方向的分力,这个力随着泵压差、转速以及泵排量的变化而变化,由于运动过程比较复杂,所以通过理论建模方式很难得到准确的值,本文利用文献[13]所提出的数值分析方法以及数据,得到 Tx与泵转速,排量以及压差的变化趋势如图3所示 ...