电动汽车侧向换道行驶主动避撞控制算法

引用本文

田彦涛, 王晓玉, 胡蕾蕾, 廉宇峰, 赵云, 尹诚. 电动汽车侧向换道行驶主动避撞控制算法. 2016, 46(5): 1587-1594
TIAN Yan-tao, WANG Xiao-yu, HU Lei-lei, LIAN Yu-feng, ZHAO Yun, YIN Cheng. Active collision avoidance algorithm in electric vehicle lateral lane change. Journal of Jilin University Engineering and Technology Edition, 2016, 46(5): 1587-1594 复制到剪切板

Permissions

电动汽车侧向换道行驶主动避撞控制算法

田彦涛^1,², 王晓玉¹, 胡蕾蕾¹, 廉宇峰¹, 赵云¹, 尹诚³

1.吉林大学通信工程学院, 长春 130022

2.吉林大学工程仿生教育部重点实验室,长春 130022

3.长春丽明科技开发股份有限公司,长春 130117

作者简介:田彦涛(1958-),男,教授,博士生导师.研究方向:复杂系统建模、优化与控制.E-mail:tianyt@jlu.edu.cn

基金:中国电动汽车国家重点科技计划项目(JS-102); 吉林大学“985工程”项目.

摘要

为实现四轮独立驱动电动车的侧向主动安全避撞控制,建立了车辆侧向换道的安全距离模型,在此模型基础上依据避撞要求设计了相应侧向控制器。利用线性二次型调节器(LQR)方法求解出侧向换道最优反馈矩阵,并采用基于输入补偿的前馈补偿策略对系统进行偏转角控制跟踪,保证系统能精确跟随给定期望横摆角。最后,通过实验验证了电动车主动安全距离模型和车辆避撞控制器的有效性,实现了车辆安全稳定避撞功能要求。

关键词: 自动控制技术; 主动避撞系统; 安全距离模型; 侧向换道; 最优控制

中图分类号:TP273 文献标志码:A 文章编号:1671-5497(2016)05-1587-08

Active collision avoidance algorithm in electric vehicle lateral lane change

TIAN Yan-tao^1,², WANG Xiao-yu¹, HU Lei-lei¹, LIAN Yu-feng¹, ZHAO Yun¹, YIN Cheng³

1.College of Communication Engineering, Jilin University, Changchun 130022, China

2.Key Laboratory of Bionic Engineering of Ministry of Education, Jilin University, Changchun 130022, China

3.Changchun Liming Technology Development Incorporated Company, Changchun 130117, China

Abstract

In order to achieve lateral active safety collision avoidance control of four-wheel independent drive electric vehicle, the safety distance model in vehicle lateral lane-change is proposed. On the basis of the proposed safety distance model, an appropriate lateral controller is designed, which meets the collision avoidance requirements. The Linear Quadratic Regulator (LQR) method is used to solve the optimal feedback matrix of the lateral lane-change. Then, the feed-forward compensation strategy based on input offset is taken to track the slip angle, so that the system could accurately follow the given expected yawing angle. The electric vehicle active safety distance model and the effectiveness of the vehicle collision avoidance controller are verified by experiments. The strategy realizes the safety and stability function requirements of the vehicle collision avoidance system.

Keyword: automatic control technology; active collision avoidance system; safety distance model; lateral lane-changing; optimal controller

Show Figures

0 引言

近年来, 车辆主动安全控制的研究和开发日益引起汽车研发人员的重视^[1]。侧向换道是一种有效地针对前车阻碍导致碰撞危险的主动避撞方法。安全车距模型是进行安全状态判断的前提, 为提高避撞系统的安全性能, 本田公司在传统安全距离模型基础上, 分别建立了报警临界距离和制动临界距离^[2]。马自达公司考虑了系统和驾驶员的延迟时间, 深入研究了预警安全距离和制动临界距离的计算, 并提出更为精确的计算方法^[3]。考虑到换道过程中行车平顺性和安全性, Ruder等^[4]开发了一套辅助换道系统HLCAM(Highway lane change assistant monitor)。系统实时对车辆行车环境做出探测, 判断是否存在危及本车安全的可能危险, 一旦存在, 自动警告驾驶员注意。对于侧向安全控制器的设计, Lin等^[5]在传统车辆二自由度动力学模型基础上采用最优理论设计换道控制器, 并对不同车速下的换道过程进行了仿真分析。Hessburg等^[6]在考虑分析驾驶员经验数据基础上建立了模糊规则库, 并设计了车辆换道模糊控制器。国内学者付锐等^[7]以道路实验数据为基础, 确定驾驶人换道时的安全间距, 建立了对本车与周围车辆的换道预警规则; 王荣本等^[8]对车辆碰撞条件、换道最小安全距离进行了研究; 李寿涛等^[9]采用模糊逻辑控制方法对汽车转向稳定性进行了研究。

制动安全距离模型的研究通常是针对纵向, 忽略了侧向换道避撞的策略, 同时, 常规避撞控制器大多存在鲁棒性差、驾驶员特性考虑不足等缺陷。本文提出了一种基于侧向换道的四轮独立驱动电动汽车主动避撞策略, 建立了综合考虑驾驶员特性和路面摩擦力影响因素的安全车距模型, 并设计具有鲁棒性的主动避撞控制器。

1 电动车动力学建模

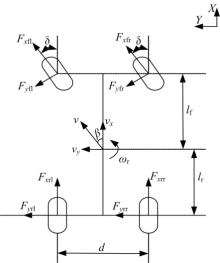
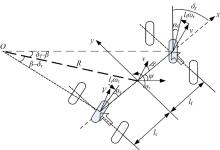
为了实现车辆安全稳定控制, 建立合适的车辆动力学模型是进行电动车主动避撞研究的基础。本文采用7个状态量对电动汽车行驶状态进行完整表征, 如图1所示^[10]。电动汽车动力学模型的建立基于以下假设:①两个前轮、后轮的轮距一致, 悬架特性忽略不计; ②车辆纵向与侧向的俯仰角和侧倾角忽略不计。

	Figure Option View Download New Window
	图1 纯电动汽车7自由度模型Fig.1 Pure electric vehicle model of 7 degrees-of-freedom

基于上述分析, 电动车的动力学方程和力矩平衡方程如下:

沿 $\begin{matrix} X \end{matrix}$ 轴的纵向动力学方程:

$\begin{matrix} \begin{matrix} M a_{x} = M ({\overset{\cdot}{v}}_{x} - v_{y} w_{r}) = \\ (F_{xfl} + F_{xfr}) cosδ + (F_{xrl} + F_{xrr}) - \\ (F_{yrl} + F_{yfr}) sinδ - F_{w} (1) \end{matrix} \end{matrix}$

沿 $\begin{matrix} Y \end{matrix}$ 轴的侧向动力学方程:

$\begin{matrix} \begin{matrix} M a_{y} = M ({\overset{\cdot}{v}}_{y} + v_{x} w_{r}) = \\ (F_{xfl} + F_{xfr}) sinδ + (F_{yfl} + F_{yfr}) cosδ + \\ (F_{yrl} + F_{yrr}) (2) \end{matrix} \end{matrix}$

横摆力矩平衡方程:

$\begin{matrix} \begin{matrix} I_{z} {\overset{\cdot}{w}}_{r} = (F_{xfl} + F_{xfr}) sinδ l_{f} + (F_{yfl} + F_{yfr}) cosδ l_{f} - \\ (F_{xfl} - F_{xfr}) cosδ \frac{d}{2} + (F_{yfl} - F_{yfr}) sinδ \frac{d}{2} - \\ (F_{xrl} - F_{xrr}) \frac{d}{2} - (F_{yrl} - F_{yrr}) l_{r} (3) \end{matrix} \end{matrix}$

式中: $M$ 为汽车质量; $\begin{matrix} a_{x} \end{matrix}$ 为车身坐标系下的纵向加速度; $\begin{matrix} v \end{matrix}$ 为车身在大地坐标系下的速度; $\begin{matrix} β \end{matrix}$ 为车辆质心侧偏角( $\begin{matrix} β = \arctan (v_{y} / v_{x})); w_{r} \end{matrix}$ 为车身横摆角速度; $\begin{matrix} δ \end{matrix}$ 为车轮转向角; $\begin{matrix} F_{w} \end{matrix}$ 为空气阻力; $\begin{matrix} I_{z} \end{matrix}$ 为整车在质心处的转动惯量; $\begin{matrix} I_{w} \end{matrix}$ 为车轮转动惯量; $\begin{matrix} F_{xfl} 、 F_{xfr} 、 F_{xrl} 、 F_{xrr} \end{matrix}$ 分别为左前轮、右前轮、左后轮、右后轮纵向力; $F_{yfl} 、 F_{yfr} 、 F_{yrl} 、 F_{yrr}$ 分别为左前轮、右前轮、左后轮、右后轮侧向力; $\begin{matrix} l_{f} 、 l_{r} \end{matrix}$ 分别为质心到前轴和后轴的距离。

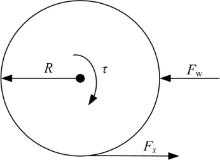
基于式(1)(2)(3), 车辆行驶过程中的侧向驱动力可依据安全距离模型的纵向期望加速度 $\begin{matrix} a_{x} \end{matrix}$ 与传感器反馈车轮转角 $\begin{matrix} δ \end{matrix}$ 获得, 为后期研究四轮独立驱动电动汽车避撞系统的制动力矩分配策略奠定基础。

如图2所示, 为了保证车轮的稳定性, 车轮在行驶过程中需要保持力矩平衡状态。以任意一个车轮为例, 单个车轮力矩平衡方程为:

$\begin{matrix} \{\begin{matrix} J \overset{\cdot}{w} = T_{d} - T_{b} - F_{w} R \\ T_{b} = F_{x} R \end{matrix} (4) \end{matrix}$

式中: $\begin{matrix} F_{w} \end{matrix}$ 为空气阻力; $\begin{matrix} F_{x} \end{matrix}$ 为地面摩擦力; $\begin{matrix} R \end{matrix}$ 为轮胎滚动半径; $\begin{matrix} T_{d} 、 T_{b} \end{matrix}$ 分别为电机驱动力矩、制动力矩; $\begin{matrix} T_{d} / I_{w} \end{matrix}$ 为电机提供的驱动力; $\begin{matrix} w \end{matrix}$ 为车轮角速度; J为车轮转动惯量。

	Figure Option View Download New Window
	图2 单个车轮在行驶中的受力情况Fig.2 Single wheel force in driving

轮胎侧偏角为:

$\begin{matrix} \begin{matrix} α_{f} = δ_{f} - β - l_{f} w_{r} / v_{x} (5) \\ α_{r} = - β + l_{r} w_{r} / v_{x} (6) \end{matrix} \end{matrix}$

轮胎受到的侧向力和回正力矩可由轮胎模型的魔术公式获得。当侧向加速度≤ 0.4g(g=9.8 m/s²), 侧偏角≤ 5° 时, 魔术公式对常规轮胎具有很高的拟合精度^[11]。

2 电动汽车避撞安全距离模型

2.1 安全距离模型建模分析

安全距离模型需综合考虑诸多因素的影响, 满足如下特点^[12]:①具有一定适用性, 能适用大多数路况; ②模型参数容易获取; ③计算简便、能快速运算; ④符合驾驶员一般操作特性, 并尽可能实现驾驶舒适性。

2.2 侧向换道主动避撞安全控制

侧向换道行为是车辆在高速交通系统中常采用的策略, 但不当的换道行为会引发车辆碰撞事故或交通拥挤等。

(1)侧向换道安全距离模型建立

本文以被控车(F车)与目标车道前车(B车)为例分析换道模型建立条件。由于换道情况复杂, 为了简化模型, 首先作如下假设:①忽略车辆在减速/加速过程中加速度变化过程; ②所有车规格相同, 即长度、宽度都相同; ③换道过程中, F车纵向分运动与侧向分运动相对独立。

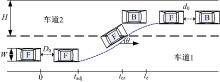
车辆侧向安全换道示意图如图3所示。侧向安全距离模型建立中涉及的相关参数如下:t_adj为车进行侧向换道行为起始时刻; t_cr为到达最大临撞点时刻; t_e为安全完成换道时刻( $\begin{matrix} v_{y} 、 a_{y} \end{matrix}$ 都为0); $\begin{matrix} φ \end{matrix}$ 为轮胎与路面的附着系数; $θ$ 为换道过程中车辆轨迹与纵向( $x$ 轴)夹角; $D_{0} 、 d_{0}$ 分别为两车初始纵向间距和两车间需保持的最小纵向间距; $H 、 W 、 L$ 分别为车道宽度、车体的宽度和长度; $v_{x} 、 v_{y}$ 分别为车速在纵向( $x$ 轴)和侧向( $y$ 轴)上的分量; v_F0、v_B0分别为F车、B车纵向初始车速。

	Figure Option View Download New Window
	图3 F车侧向安全换道示意图Fig.3 Schematic diagram of F car lateral safety lane-changing

基于换道过程中侧向速度的变化趋势, F车的侧向加速度采用正弦函数车道变换模型^{[13, 14]}, 相关横向加速度、横向速度、换道轨迹模型分别为:

$\begin{matrix} \begin{matrix} a_{yF} = \{\begin{matrix} (\frac{2 πH}{t_{e}^{2}}) \sin [\frac{2 π (t - t_{adj})}{t_{e}}], t \in [t_{cr}, t_{e}] \\ 0, 其他 \end{matrix} (7) \\ v_{yF} = \{\begin{matrix} \frac{H}{t_{e}} [1 - \cos (\frac{2 π (t - t_{adj})}{t_{e}})], t \in [t_{adj}, t_{e}] \\ 0, 其他 \end{matrix} (8) \\ y_{yF} = \\ \{\begin{matrix} \frac{H}{t_{e}} (t - t_{adj}) - \frac{H}{2 π} \sin (\frac{2 π}{t_{e}} (t - t_{adj})), t \in [t_{adj}, t_{e}] \\ H, t \in (t_{e}, \infty) \end{matrix} (9) \end{matrix} \end{matrix}$

(0, t_adj)阶段:驾驶员以一定减速度a_adj减缓车速, 为换道做准备工作。在t=t_adj时刻, F车的速度、位移与两车当前间距表达式为:

$\begin{matrix} \{\begin{matrix} v_{F} (t_{adj}) = v_{F 0} - a_{adj} t_{adj} \\ X_{F 1} = v_{F 0} t_{adj} + 0.5 a_{adj} t_{adj}^{2} \\ D_{1} = D_{0} + X_{B} - X_{F 1} \end{matrix} (10) \end{matrix}$

(t_adj, t_cr)阶段:F车开始进行侧向换道, 纵向速度不变, 车辆的运动轨迹为纵向和侧向的合成运动。F车速度和距离表达式如下:

$\begin{matrix} \{\begin{matrix} v_{Fx} = v_{F} (t_{adj}) \\ v_{Fy} = \frac{H}{t_{e}} \{1 - \cos (\frac{2 π}{t_{e}} (t - t_{adj}))\} \\ D_{2} = D_{1} (t_{adj}) + (v_{B} - v_{Fx}) (t - t_{adj}) \end{matrix} (11) \end{matrix}$

(t_cr, t_e)阶段:F车已经进入相邻车道, 基本完成换道避撞行为, 适应相邻车道上车辆的整体行驶状态。

综合上述分析, 在整个安全换道过程中, F车侧向换道的安全距离为:

$\begin{matrix} \begin{matrix} D_{br} = D_{1} + D_{2} + D_{3} + d_{0} (12) \\ D_{w} = D_{br} + v_{1} (T_{r} + T_{s}) + v'_{1} T_{s} (13) \end{matrix} \end{matrix}$

式中: $D_{br}$ 为极限安全距离; $D_{w}$ 为报警安全距离; $T_{r}$ 为驾驶员反应时间; $\begin{matrix} T_{s} \end{matrix}$ 为制动系统延迟时间。

(2)换道中安全性条件分析

为了提高系统安全性, 需要明确车辆行驶转角 $\begin{matrix} θ \end{matrix}$ 的变化情况, 了解实现安全换道的必要条件。如图4所示, 为了保证F车能顺利从原车道换行到相邻车道, 需保证F车侧向实际位移小于理论计算值 $\begin{matrix} (y_{Fy} \leq y_{B} - W) 。 \end{matrix}$

	Figure Option View Download New Window
	图4 F车与B车换道过程Fig.4 F car and B car lane-changing process

以 $\begin{matrix} t = 0 \end{matrix}$ 时刻F车车头左上角所在位置为坐标原点, 则F车与B车纵向间距表达式为:

$\begin{matrix} \{\begin{matrix} D (0) = D_{0} \\ D (t) = X_{B} (t) - X_{F} (t) + D (0) \end{matrix} (14) \end{matrix}$

考虑到一般性, 式(14)可改写为:

$\begin{matrix} \begin{matrix} D (t) = D (0) + \int_{0}^{t} \int_{0}^{λ} a_{B} (τ) - a_{F} (τ)] dτdλ + \\ [v_{B} (0) - v_{F} (0)] t (15) \end{matrix} \end{matrix}$

可见, $\begin{matrix} D (0) \end{matrix}$ 的正确选取是保证F-B车、F-D车无碰撞的前提条件。F-D、F-B无碰撞条件如下:

$\begin{matrix} \{\begin{matrix} D_{F - D} (t_{cr}) > d_{0}, t \in (t_{adj}, t_{cr}) \\ D_{F - B} (t_{e}) > d_{0}, t \in (t_{cr}, t_{e}) \end{matrix} (16) \end{matrix}$

2.3 侧向安全距离模型验证

(1)F车匀速换道情况, 车道上所有车辆都匀速行驶

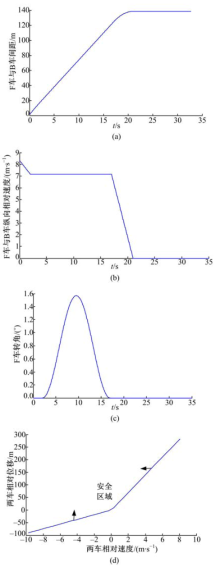
初始参数为:D₀=1 m, v_B=v_D=40 km/h, v_F=70 km/h, T=35 s, y_B=0.9H, t_adj=2 s, a_adj=-0.588 m/s²。F车在安全换道策略下的各个参量变化如图5所示。

	Figure Option View Download New Window
	图5 一般情况下F车匀速换道仿真图Fig.5 In general, F car lane-changing simulation figure with a constant speed

图5(a)(b)(c)表明, t=0 s时, F车与D车间距1 m, 初始相对速度为30 km/h, 选择换道避撞方式。经2 s的车速车姿调整阶段后, 车辆开始转向; 在t=9.86 s时, F车转角达到最大值; 在t=17.61 s时, F车转角 $\begin{matrix} θ = 0, \end{matrix}$ 表示F车已经成功避开D车换到相邻车道, F车进入相邻车道后开始进行减速调整。在t=21.88 s时, F车与B车相对速度为0, 两车保持合适间距匀速行驶, 整个换道过程结束。从图5(d)可以看出:F车速度比B车速度越大, 两车碰撞的可能性越大, 两车相对速度越小, 越容易实现安全避撞。

(2)F车在换道过程中进行纵向变速运动, 其他车进行纵向匀速运动

初始参数为:D₀=1 m, v_B=v_D=40 km/h, v_F=70 km/h, T=35 s, y_B=0.9H, t_adj=0 s, a_adj=-0.588 m/s²。F车在上述安全换道策略下的各运动状态量的变化如图6所示。

	Figure Option View Download New Window
	图6 t_adj=0时F车匀减速换道仿真图Fig.6 when t_adj=0, F car deceleration lane-changing simulation figure

图6(a)(b)(c)表明, t=0 s时, F与D车间距1 m, 初始相对速度为30 km/h, 由于纵向间距不足以实现纵向制动过程, 因此选择换道避撞方式。当F车不经历车速车姿调整阶段, 在t=0 s时刻直接开始做边减速边转向运动, 则车辆转角逐渐增大; 在t=6.88 s时, F车转角达到最大值, F车纵向车速为3.62 m/s; 在t=12 s时, F车转角又归于0, 表示F车已经换道到相邻车道, 成功避开D车; F车进入相邻车道后仍然需要继续减速, 直至在t=12.45 s时F车与B车相对速度为0, 两车保持合适间距匀速行驶, 整个换道过程结束。

对比图5和图6可以看出, 换道中减速行驶比起匀速行驶安全区域会减小。但减速换道比匀速换道需要的时间更少, 能更快速地实现换道过程。

3 电动汽车避撞控制器设计

从安全性、快速性、稳定性以及行车舒适性角度看, 控制系统应具有如下特点:①能快速、准确地响应驾驶员针对当前路况做出的决策指令; ②具有较好鲁棒性, 受行驶环境变化与车辆状态的影响较小; ③易于操作, 符合驾驶员操作特性。

3.1 侧向换道控制

(1)侧向车辆动力学模型线性化

假设当车辆以较小角度转向换道时, 车辆两前轮与两后轮的转向动作分别保持一致。此时电动汽车模型等效为自行车模型进行研究, 如图7所示。

	Figure Option View Download New Window
	图7 二自由度车辆线性动力学模型Fig.7 Two degrees of freedom vehicle linear dynamic model

侧向加速度 $\begin{matrix} a_{y} 主要是由沿 y \end{matrix}$ 轴加速度和向心力 $\begin{matrix} v_{x} w_{r} \end{matrix}$ 构成的, 从而得到二自由度等效自行车模型动力学方程:

$\begin{matrix} \{\begin{matrix} M (\overset{\cdot \cdot}{y} + w_{r} v_{x}) = 2 F_{yf} + 2 F_{yr} \\ I_{z} \overset{\cdot \cdot}{ψ} = I_{z} {\overset{\cdot}{w}}_{r} = 2 F_{yl} l_{f} - 2 F_{yr} l_{r} \end{matrix} (17) \end{matrix}$

由图7可知, 当轮胎侧偏角较小时, 轮胎侧向力与轮胎侧偏角近似呈线性关系。得到前轮、后轮侧偏力分别为:

$\begin{matrix} \{\begin{matrix} F_{yf} = K_{f} (δ_{f} - β - l_{f} w_{r} / v_{x}) \\ F_{yr} = K_{r} (- β + l_{r} w_{r} / v_{x}) \end{matrix} (18) \end{matrix}$

式中: $\begin{matrix} K_{f} 、 K_{r} \end{matrix}$ 分别为前轮和后轮的侧偏刚度。

综合以上分析, 得到简化自行车模型的车辆动力学状态方程为:

$\begin{matrix} \begin{matrix} \frac{dβ}{dt} = - \frac{2 K_{f} + 2 K_{r}}{M v_{x}} β - (\frac{2 K_{f} l_{f} - 2 K_{r} l_{r}}{M v_{x}^{2}} - 1) w_{r} + \frac{2 K_{f}}{M v_{x}} δ \\ \frac{d w_{r}}{dt} = - \frac{2 K_{f} l_{f} - 2 K_{r} l_{r}}{I_{z}} β - \frac{2 K_{f} l_{f}^{2} + 2 K_{r} l_{r}^{2}}{I_{z} v_{x}} w_{r} + \frac{2 K_{f} l_{f}}{I_{z}} δ (19) \end{matrix} \end{matrix}$

通过对自行车模型分析可知, 车辆的侧向控制主要是由车轮侧偏角 $\begin{matrix} ψ \end{matrix}$ 来实现。

为了能对车轮实际换道轨迹进行跟踪, 车辆模型需要建立关于误差状态量的状态方程, 车辆期望行驶方向为ψ _des, 得到:

$\begin{matrix} \{\begin{matrix} {\overset{\cdot}{e}}_{1} = \overset{\cdot}{y} + v_{x} (ψ - ψ_{des}) \\ e_{2} = (ψ - ψ_{des}) \end{matrix} (20) \end{matrix}$

式中: $\begin{matrix} e_{1} \end{matrix}$ 为车辆质心与道路中心线的距离; $\begin{matrix} e_{2} \end{matrix}$ 为行进方向与期望行驶方向的差值。

定义侧向系统的状态 $\begin{matrix} x = {[\begin{matrix} e_{1} & {\overset{\cdot}{e}}_{1} & e_{2} & {\overset{\cdot}{e}}_{2} \end{matrix}]}^{T}, \end{matrix}$ 则侧向动力学模型为:

$\begin{matrix} \overset{\cdot}{x} = Ax + B_{1} δ + B_{2} {\overset{\cdot}{ψ}}_{des} (21) \end{matrix}$

(2)基于前馈补偿的LQR侧向控制

车辆侧向运动控制主要是通过对侧偏角 $\begin{matrix} ψ \end{matrix}$ 的跟踪来实现期望轨迹。通过分析侧向动力学误差模型, 系统 $\begin{matrix} (A, B_{1}) \end{matrix}$ 是可控的。对于控制输入 $\begin{matrix} δ, \end{matrix}$ 基于状态反馈采用

$\begin{matrix} \begin{matrix} δ = Kx = k_{1} e_{1} + k_{2} {\overset{\cdot}{e}}_{1} + k_{3} e_{2} + k_{4} {\overset{\cdot}{e}}_{2} \\ 则 \overset{\cdot}{x} = (A - B_{1} K) x + B_{2} {\overset{\cdot}{ψ}}_{des} (22) \end{matrix} \end{matrix}$

车辆转向过程中, 侧向控制器应对车辆期望横摆角度ψ _des迅速精确跟踪, 可用线性二次型调节器LQR进行优化, 减少系统控制误差并提高控制性能^[15]。

基于车辆侧向动力学模型(21), LQR的性能指标为:

$\begin{matrix} J_{LQR} = \int_{0}^{\infty} x^{T} Qx + u^{T} Ru) dt (23) \end{matrix}$

根据LQR理论, 性能指标 $J_{LQR}$ 要求在控制输入 $\begin{matrix} u (u \end{matrix}$ 为前轮转角 $\begin{matrix} δ \end{matrix}$ )尽量小的前提下使车辆系统的跟踪误差最小。其中, $\begin{matrix} Q = I_{4 \times 4}, R \end{matrix}$ 为常数, 可用于调节系统响应的快速性。

通过求解黎卡提方程, 基于LQR的状态反馈控制器为:

$\begin{matrix} K = R^{- 1} {B^{T}}_{1} P (24) \end{matrix}$

通过对引入LQR反馈控制后的模型(22)进行分析, 系统在达到稳态时将存在稳态误差, 状态误差 $\begin{matrix} e_{2} \end{matrix}$ 满足下式:

$\begin{matrix} \begin{matrix} {\overset{\cdot \cdot}{e}}_{2} = (A_{42} - b_{14} k_{2}) {\overset{\cdot}{e}}_{1} + (A_{43} - b_{14} k_{3}) e_{2} + \\ (A_{44} - b_{14} k_{4}) {\overset{\cdot}{e}}_{2} + b_{24} {\overset{\cdot}{ψ}}_{des} (25) \\ 解得 : \\ e_{2} = \frac{- b_{24}}{(A_{43} - b_{14} k_{3})} {\overset{\cdot}{ψ}}_{des} (26) \end{matrix} \end{matrix}$

可见, 系统稳态时的误差 $\begin{matrix} e_{2} \end{matrix}$ 只与 $\begin{matrix} {\overset{\cdot}{ψ}}_{des} \end{matrix}$ 有关。采用基于输入补偿的前馈补偿策略对系统进行控制, 令 $\begin{matrix} ψ'_{des} = K_{2} ψ_{des}, \end{matrix}$ 则输入系统的偏转角速率为 $\begin{matrix} ψ ″_{des} = K_{2} {\overset{\cdot}{ψ}}_{des}, \end{matrix}$ 则

$\begin{matrix} K_{2} = {\overset{\cdot}{ψ}}_{des} / [{\overset{\cdot}{ψ}}_{des} - (b_{24} {\overset{\cdot}{ψ}}_{des} \frac{)}{(} A_{43} - b_{14} k_{3})] (27) \end{matrix}$

在系统能够快速达到稳态的条件下, 基于输入补偿的前馈补偿控制器 $K_{2}$ 可以使系统精确跟随期望的横摆角度 $ψ_{des}$ 。考虑到控制器 $K_{2}$ 的分母特殊性, 实际的 $\begin{matrix} K_{2} \end{matrix}$ 采用

$\begin{matrix} K_{2} = \{\begin{matrix} 0, ψ_{des} = 0 且 {\overset{\cdot}{ψ}}_{des} = 0 \\ k_{const}, | K_{2} |< λ \\ ψ_{des} / K_{i}, others \end{matrix} (28) \end{matrix}$

式中: $K_{i} = ψ_{des} - \frac{b_{24} {\overset{\cdot}{ψ}}_{des}}{A_{43} - b_{14} k_{3}}; k_{const}$ 和 $λ$ 为常数, 并且 $\begin{matrix} λ < 1 。 \end{matrix}$

为了实现上层侧向换道控制器的规划轨迹, 由速度转换公式可得系统的期望横摆角度为:

$\begin{matrix} ψ_{des} = \arcsin (\frac{v_{X}}{\sqrt{v_{x}^{2} + v_{y}^{2}}}) - \arcsin (\frac{v_{x}}{\sqrt{v_{x}^{2} + v_{y}^{2}}}) (29) \end{matrix}$

式中: $\begin{matrix} v_{X} \end{matrix}$ 为大地坐标系下的车辆速度。

3.2 实验仿真与分析

车辆侧向换道控制策略采用二自由度的侧向自行车模型进行仿真实验, 结构参数如下:汽车质量M=1573 kg; 整车转动惯量为I_z=2873 kg· m²; 质心距前轴距离l_f= 1.1 m; 质心距后轴距离l_r=1.58 m; 汽车行驶速度v_x=10 m/s; 前轮、后轮刚度系数K_f=K_r=80 000 N/rad。

(1)基于前馈补偿的LQR侧向控制

当系统给定的期望横摆角度为ψ _des=t时, 分别采用LQR策略和带有前馈补偿的LQR策略进行控制器设计。LQR性能指标所采用的加权矩阵为 $\begin{matrix} Q = I_{4 \times 4}, R = 19.5 。 \end{matrix}$ 由此产生的LQR控制器参数 $\begin{matrix} K = [0.2265 0.1058 1.4318 0.1520] 。 \end{matrix}$ 实验结果如图8所示。

	Figure Option View Download New Window
	图8 LQR控制与基于前馈补偿LQR控制的侧向运动效果Fig.8 Lateral movement with the LQR control and LQR control based on feed-forward compensation effect

从图8(c)可以看出, 经过调整后, LQR控制和基于前馈补偿LQR控制都能良好跟随期望横摆角度ψ _des。根据两个控制效果的侧偏角误差曲线, 控制器在经过大约0.5 s调整时间后趋于稳定。由于横摆角速率 $\begin{matrix} {\overset{\cdot}{ψ}}_{des} \end{matrix}$ 的存在, 系统稳态会存在稳态误差。基于状态反馈的LQR控制器只能获得最小的误差性能指标, 并不能消除稳态误差; 而基于前馈补偿的LQR控制器则根据系统的稳态误差对系统给定输入进行补偿, 增加(或减小)系统的前轮控制转角δ , 使稳态误差减小, 大大提高了系统的精确程度。

系统在全局坐标系下的运动速度可通过式(29)进行坐标变换求解。由于 $\begin{matrix} ψ_{des} = t, \end{matrix}$ 车辆动力学系统在基于前馈补偿LQR控制策略进行圆周运动, 实际运动效果如图8(d)所示。

(2)外界干扰变化对车辆控制效果影响分析

在车辆实际行驶过程中, 外界环境会干扰车辆状态。为了验证基于前馈补偿控制算法的抗扰性能, 车辆在模型参数改变情况下的控制效果如图9和图10所示。

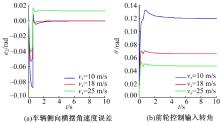	Figure Option View Download New Window
	图9 基于前馈补偿的LQR控制器在v_x变化下的控制效果Fig.9 Control effect with the LQR controller of feed- forward compensation under the v_x changes

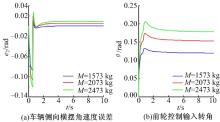	Figure Option View Download New Window
	图10 基于前馈补偿的LQR控制器在M变化下的控制效果Fig.10 Control effect with the LQR controller of feed- forward compensation under the M changes

当车速 $\begin{matrix} v_{x} \end{matrix}$ 增大, 车辆在基于前馈补偿LQR控制作用下减小前轮控制输入转角δ , 使系统快速趋于稳定状态, 稳态误差仍然控制在很小的范围内, 保证了控制系统的跟随精确度和鲁棒抗扰性。当车辆的质量M增加时, 车辆在基于前馈补偿LQR控制作用下增大前轮控制输入转角δ , 使汽车轮胎的侧向力增大, 保证对系统期望侧向横摆角度的跟随。可见, 基于前馈补偿LQR的侧向偏转控制策略对车辆侧向动力学模型摄动具有一定的鲁棒抗扰性能。

4 结束语

提出了基于侧向换道安全距离模型的四轮独立驱动电动汽车的主动避撞的方法, 并对侧向换道避撞的可行性与安全性进行了研究。运用基于前馈补偿的线性二次型方法设计了侧向换道控制器, 并对控制器性能进行了分析和验证。基于输入补偿的前馈补偿策略能对系统的偏转角控制跟踪, 保证系统能够精确跟随给定期望横摆角, 通过实验验证了控制策略的有效性。本文研究对于后期电动车主动安全课题的深入研究具有重要意义。

The authors have declared that no competing interests exist.

参考文献

View Option

[1]	陈虹, 宫洵, 胡云峰, 等. 汽车控制的研究现状与展望[J]. 自动化学报, 2013, 39(4): 322-346. Chen Hong, Gong Xun, Hu Yun-feng, et al. Automotive control: the state of the art and perspective[J]. Journal of Automation, 2013, 39(4): 322-346. [本文引用:1]
[2]	侯德藻, 刘刚, 高锋, 等. 新型汽车主动避撞安全距离模型[J]. 汽车工程, 2005, 27(2): 186-190. Hou De-zao, Liu Gang, Gao Feng, et al. A new safety distance model for vehicle collision avoidance[J]. Automotive Engineering, 2005, 27(2): 186-190. [本文引用:1]
[3]	李晓霞, 李百川, 侯德藻, 等. 汽车追尾碰撞预警系统开发研究[J]. 中国公路学报, 2001, 14(3): 93-95. Li Xiao-xia, Li Bai-chuan, Hou De-zao, et al. Basic study of rear-end collision warning system[J]. China Journal of Highway and Transport, 2001, 14(3): 93-95. [本文引用:1]
[4]	Ruder M, Enkelmann W, Garnitz R. Highway lane change assistant[J]. Intelligent Vehicle Symposium, 2002(1): 240-244. [本文引用:1]
[5]	Lin Y S, Cook G. Automobile steering autopilot with lane change capability[C]∥23rd International Conference on Industrial Electronics, Control and Instrumentation. New Orleans: IEEE, 1997: 143-148. [本文引用:1]
[6]	Hessburg T, Tomizuka M. Fuzzy logic control for lane change maneuvers in lateral vehicle guidance[C]∥California Partners for Advanced Transit and Highways, University of California, USA, 1995: 2-10. [本文引用:1]
[7]	付锐, 马勇, 郭应时, 等. 基于实车实验数据的换道预警规则[J]. 吉林大学学报: 工学版, 2015, 45(2): 379-388. Fu Rui, Ma Yong, Guo Ying-shi, et al. Lane change warning rules based on real vehicle test data[J]. Journal of Jilin University(Engineering and Technology Edition), 2015, 45(2): 379-388. [本文引用:1]
[8]	王荣本, 游峰, 崔高建, 等. 车辆安全换道分析[J]. 吉林大学学报: 工学版, 2005, 35(2): 179-182. Wang Rong-ben, You Feng, Cui Gao-jian, et al. Analysis on lane-changing safety of vehicle[J]. Journal of Jilin University(Engineering and Technology Edition), 2005, 35(2): 179-182. [本文引用:1]
[9]	李寿涛, 马用学, 郭鹏程, 等. 基于电控液压制动系统的车辆稳定性控制策略[J]. 吉林大学学报: 工学版, 2015, 45(2): 526-532. Li Shou-tao, Ma Yong-xue, Guo Peng-cheng, et al. Strategy of vehicle stability control based on EHB system[J]. Journal of Jilin University(Engineering and Technology Edition), 2015, 45(2): 526-532. [本文引用:1]
[10]	张钦爽. 四轮驱动电动汽车转向稳定性控制研究[D]. 沈阳: 沈阳工业大学电气工程学院, 2012. Zhang Qin-shuang. Four wheel drive electric vehicle steering stability control research[D]. Shenyang: School of Electrical Engineering, Shenyang University of Technology, 2012. [本文引用:1]
[11]	Pacejka H B, Bakker E. The magic formula tyre model[J]. Vehicle System Dynamics, 1992, 21(Sup. 1): 1-18. [本文引用:1]
[12]	侯德藻. 汽车纵向主动避撞系统的研究[D]. 北京: 清华大学机械工程学院, 2004. Hou De-zao. Study on vehicle forward collision avoidance system[D]. Beijing: School of Mechanical Engineering, Tsinghua University, 2004. [本文引用:1]
[13]	边明远. 基于紧急变道策略的汽车主动避障安全车距模型[J]. 重庆理工大学学报: 自然科学, 2012, 26(4): 1-4. Bian Ming-yuan. A vehicle safety distance model for collision avoidance system based on emergency lane change motion[J]. Journal of Chongqing University of Science and Technology (Natural Science), 2012, 26(4): 1-4. [本文引用:1]
[14]	Jula H, Kosmatopoulos E B, Ioannou P A. Collision avoidance analysis for lane change and merging[J]. IEEE Transactions on Vehicular Technology, 2000, 49(6): 2295-2308. [本文引用:1]
[15]	Zhang Rong-hui, Jia Hong-guang, Chen Tao. Dynamics simulation on control technology for 4WS vehicle steering performance[C]∥2008 ISECS International Colloquium on Computing, Communication, Control, and Management. Guangzhou: IEEE, 2008: 206-209. [本文引用:1]

2013

0.0

. 2013, 39(4):322-346 DOI:10.3724/SP.J.1004.2013.00322

Automotive control: the state of the art and perspective

汽车控制的研究现状与展望

Chen Hong , Gong Xun , Hu Yun-feng

陈虹, 宫洵, 胡云峰

1. State Key Laboratory of Automotive Simulation and Control, Changchun 130025; 2. Department of Control Science and Engineering, Jilin University, Changchun 130025

Automotive control technology plays a significant role for the sustainable development of the auto-industry. Under gradually fierce circumstance of competition around the world, how to strengthen our capacity of independent research and development of auto-control technology through the innovation of theory and method presents a grand challenge of our time. This paper introduces the state of the art of automotive control focusing on the power-train control, active safety control and new energy vehicles control, then summaries their common problems and finally puts forward a series of perspective for the future researches.

汽车控制技术是推动汽车工业可持续发展的重要保障. 在全球汽车行业竞争日益激烈的背景下, 如何通过理论与方法的创新, 提高我国汽车控制系统的自主研发能力, 完成从消费大国向制造强国的过渡是我们目前面临的重大挑战. 本文主要围绕汽车动力总成系统、主动安全系统及新能源汽车中的关键控制问题展开论述, 总结国内外的研究状况, 提炼共性问题, 对汽车控制的发展趋势给出了一些观点.

... 0 引言近年来,车辆主动安全控制的研究和开发日益引起汽车研发人员的重视^[1] ...

2005

0.0

. 2005, 27(2):186-190 DOI:doi:10.3321/j.issn:1000-680X.2005.02.015

A new safety distance model for vehicle collision avoidance

新型汽车主动避撞安全距离模型

Hou De-zao , Liu Gang , Gao Feng

侯德藻, 刘刚, 高锋

针对现有模型的不足,以驾驶员车间距保持目的假设为基础建立了一种新型汽车主动避撞安全距离模型,通过驾驶员试验获得了反映驾驶员驾驶特点的模型参数.经仿真及试验对比,该模型计算结果体现了驾驶员的驾驶特点,能够适用于多种交通状况,满足了汽车主动避撞系统的要求.

... 安全车距模型是进行安全状态判断的前提,为提高避撞系统的安全性能,本田公司在传统安全距离模型基础上,分别建立了报警临界距离和制动临界距离^[2] ...

2001

0.0

. 2001, 14(3):93-95 DOI:doi:10.3321/j.issn:1001-7372.2001.03.021

Basic study of rear-end collision warning system

汽车追尾碰撞预警系统开发研究

Li Xiao-xia , Li Bai-chuan , Hou De-zao

李晓霞, 李百川, 侯德藻

在理论建模的基础上，设计开发了汽车追尾碰撞预警测控系统；经阶段性装车试验，结果表明所开发的预警系统是有效和可行的；最后分析指出了本系统尚需改进的方向。

... 马自达公司考虑了系统和驾驶员的延迟时间,深入研究了预警安全距离和制动临界距离的计算,并提出更为精确的计算方法^[3] ...

0.0

... 考虑到换道过程中行车平顺性和安全性,Ruder等^[4]开发了一套辅助换道系统HLCAM(Highway lane change assistant monitor) ...

1997

0.0

... 对于侧向安全控制器的设计,Lin等^[5]在传统车辆二自由度动力学模型基础上采用最优理论设计换道控制器,并对不同车速下的换道过程进行了仿真分析 ...

1995

0.0

... Hessburg等^[6]在考虑分析驾驶员经验数据基础上建立了模糊规则库,并设计了车辆换道模糊控制器 ...

2015

0.0

. 2015, 45(2):379-388 DOI:doi:10.13229/j.cnki.jdxbgxb201502007

Lane change warning rules based on real vehicle test data

基于实车实验数据的换道预警规则

Fu Rui , Ma Yong , Guo Ying-shi

付锐, 马勇, 郭应时

In order to set the lane change warning parameters being more suitable to the characteristics of domestic drivers, the influences of relative speed and distance between the subject vehicle and its neighboring vehicles on the lane change behavior are investigated using road experiment data. Then the safety distance that allows the driver to perform the lane change operation under different speed levels is determined. Besides, to identify the driver's subjective basis for risk assessment, different characteristics of the driver in cancelling and performing lane change are analyzed. Finally, the warning rules for the neighboring vehicles in different speed levels are proposed. The results show that the warning proportion in the road experiments is basically consistent with the actual situation, which demonstrate the feasibility of the proposed warning rules.

为了使换道预警值的设定更符合我国驾驶人的驾驶习惯，以道路试验数据为基础，分析了换道时本车与周围车辆的相对速度和距离对换道行为的影响，确定了不同速度级别下允许驾驶人执行换道操作的安全间距。研究了驾驶人取消换道和执行换道操作行为的不同特征，探讨了驾驶人对于危险判断的主观依据。最后，提出不同速度级别下针对本车周围车辆条件的预警规则，并进行了验证。结果表明:道路试验中针对周围车辆的预警比例与实际情况基本相符，提出的预警规则可行。

... 国内学者付锐等^[7]以道路实验数据为基础,确定驾驶人换道时的安全间距,建立了对本车与周围车辆的换道预警规则 ...

2005

0.0

. 2005, 35(2):179-182 DOI:国家自然科学基金资助项目

Analysis on lane-changing safety of vehicle

车辆安全换道分析

Wang Rong-ben , You Feng , Cui Gao-jian

王荣本, 游峰, 崔高建

通过分析换道时车辆的运动关系，使用最小安全距离作为安全换道的指标，并将安全车距的计算与车辆的当前速度，到达临界碰撞点的时间，两车的相对速度、加速度关联起来，研究了车辆碰撞的条件，给出了换道最小安全距离的计算方法，并进行了仿真与分析。本文的研究结果为下一步的自动换道辅助系统和自动超车辅助系统的研究奠定了理论基础。

... 王荣本等^[8]对车辆碰撞条件、换道最小安全距离进行了研究 ...

2015

0.0

. 2015, 45(2):526-532 DOI:doi:10.13229/j.cnki.jdxbgxb201502028

Strategy of vehicle stability control based on EHB system

基于电控液压制动系统的车辆稳定性控制策略

Li Shou-tao , Ma Yong-xue , Guo Peng-cheng

李寿涛, 马用学, 郭鹏程

摘　要：针对带有电控液压制动（EHB）系统的乘用车进行研究,提出了一种新的稳定性控制策略。首先利用模糊推理的方法分别对横摆角速度偏差和质心侧偏角速率的门限值进行确定,然后利用逻辑门限PI控制方法计算出附加横摆力矩,最后在EHB系统上对附加横摆力矩加以实现。另外,还采用模糊PI自整定算法对EHB系统轮缸的目标压力进行优化控制。仿真及实验结果表明：模糊PI自整定算法在EHB的整个工作区段都具有良好的控制效果;当车辆在转向过程中失去稳定时,本文所提出的控制策略能够及时地对车辆进行稳定性控制,提高了车辆在行驶过程中的安全性。

... 李寿涛等^[9]采用模糊逻辑控制方法对汽车转向稳定性进行了研究 ...

2012

0.0

. 2012, :-

Four wheel drive electric vehicle steering stability control research

四轮驱动电动汽车转向稳定性控制研究

Zhang Qin-shuang

张钦爽

多轮独立驱动是电动汽车采用电机牵引带来的独特优势。特别是电动轮技术,使汽车摆脱了复杂的机械机构,这种创新性的车辆结构及牵引方式,为电动汽车在性能上全面超越传统汽车提供了空间,同时也使传统的底盘控制方法难以适应。多轮驱动电动汽车在简单的机械结构下,需要更多地依赖先进的控制策略实现车辆操控。本文以四轮驱动电动汽车为对象,研究汽车的动态控制方案。一方面通过多电机牵引控制和差速控制,使车辆行驶路径跟踪驾驶指令;另一方面针对汽车在不同操纵工况下,行驶过程受车辆非线性影响难以动态保持最佳行驶姿态的问题,采用模型跟踪自适应控制结构与鲁棒控制策略相结合的方法,动态纠正驾驶路径和车辆姿态,改善车辆行驶的稳定性和操控性,进而提升汽车的安全性。从车辆动力学的本质及电动汽车的系统结构出发,建立了三自由度的整车动力学模型,采用Pacejka模型作为车辆的轮胎模型,并在Matlab/Simulink和Carsim两个不同仿真环境下,通过对同一操纵工况下的仿真结果进行对比分析,证明了整车动力学模型的正确性及可行性。采用直接转矩控制为永磁同步牵引电机的控制策略,Ackermann-Jeantand模型作为电动汽车转向差速模型,实现四轮独立驱动控制,并在Matlab/Simulink仿真平台下,对车辆直行与转向过程的差速及牵引性能进行了验证。针对汽车在极限操纵工况行驶过程中难以保持稳定的问题,以车辆的姿态为控制目标,横摆角速度和车身侧偏角为姿态参数,模型跟踪控制为控制结构,构建车辆稳定性控制系统。理想模型采用线性状态下具有轻微不足转向的车辆模型输出,控制器则以线性矩阵不等式的鲁棒性问题为理论基础,设计控制器。通过鱼钩测试(fish-hook)及J-turn两种不同的工况下车辆的闭环仿真,证明本文的鲁棒模型跟踪控制策略可以显著提高车辆在非线性工况下的稳定性及安全性,系统对车辆的参数的非线性具有很好的鲁棒性。最后,采用双轮驱动模型车进行了差速实验,该模型车以单片机控制,通过独立控制的两个直流电机驱动后轮,并采用独立控制的舵机实现转向,实验获得了很好的差速性能。

... 本文采用7个状态量对电动汽车行驶状态进行完整表征,如图1所示^[10] ...

1992

0.0

... 时,魔术公式对常规轮胎具有很高的拟合精度^[11] ...

2004

0.0

. 2004, :-

Study on vehicle forward collision avoidance system[D]. Beijing: School of Mechanical Engineering,

汽车纵向主动避撞系统的研究

Hou De-zao

侯德藻

道路交通事故是现代社会的一大公害,与之相关的先进安全技术研究日益受到重视。基于智能交通系统的汽车主动避撞系统是先进安全技术的一项重要内容,国内外相继开展了相关的研究,但迄今为止在该技术领域还存在许多尚未解决的问题。对汽车主动避撞系统所涉及的相关理论及技术问题进行研究,对于提高道路交通的安全水平,降低交通事故发生率,促进智能交通系统在我国的发展及实现具有重要意义。本文以汽车纵向主动避撞系统为研究对象,以车辆动力学及控制理论为基础,对汽车纵向主动避撞系统功能实现所涉及的车辆动力学建模与控制、行车安全距离模型、实际交通环境中目标车辆识别及运动信息获取、实车实验平台的开发等进行了研究,实现了纵向主动避撞的系统功能。本文首先进行了汽车纵向主动避撞系统的总体设计,在定义系统功能的基础上,完成了系统总体方案规划,并确定了实现系统功能所需的关键技术及其相互关系。作为汽车纵向主动避撞系统功能实现及评价的基础,本文进行了主动避撞汽车动力学系统建模的研究。以实验车辆动力学系统特点和执行器结构特点为基础,建立了能够反映系统动态特性的主动避撞汽车动力学系统模型,该模型能够模拟车辆运行复杂过程,并兼顾了模型的精确性和简洁性。为解决实时行车安全距离的获得问题,本文提出了一种新的安全距离模型。该模型以驾驶员距离保持目的假设为基础,通过驾驶员实验获得模型参数,计算结果体现了实际驾驶员的驾驶特点,能够适用于多种交通状况。以主动避撞汽车动力学系统模型和车间距保持安全距离模型为基础,本文对汽车主动避撞控制系统进行了研究,设计了能够自动进行功能切换的控制功能定义层和体现驾驶员操作特点的汽车主动避撞鲁棒控制器。控制功能定义层按照汽车纵向主动避撞系统的总体功能定义和驾驶员优先原则设计,在多种工况下都能对避撞系统应当实现的控制功能做出合理定义;体现驾驶员操作特点的汽车主动避撞鲁棒控制器包括基于H∞控制理论和模型匹配控制器结构设计的 WP=5 模型匹配鲁棒下位控制器和以最优跟踪理论和实际驾驶员操作特点为基础设计的上位控制器,实现了多种复杂工况下体现实际驾驶员操作特点的主动避撞车辆动力学控制。为解决实际交通环境中行车信息的获得问题,本文对交通环境中目标车辆识别及运动信息获取方法进行了研究。以我国道路技术规范为基础建立了多目标交通环境中的有效目标车辆识别方法,实现了复杂交通环境中的目标车辆识别;以四阶卡尔曼滤波器为基础建立了目标车辆运动信息提取方法,实现了目标车辆运动信息的准确、实时提取;以假设检验为基础建立了目标车辆跟踪方法,实现了对同一目标车辆的连续跟踪测量。为验证汽车纵向主动避撞系统总体功能及关键技术的研究结果,同时为关于汽车主动避撞的研究提供一个实车平台,本文以常规车辆结构为基础建立了实用化的汽车主动避撞系统实车实验平台。最后,利用仿真及实车试验对避撞系统总体功能及相关研究内容的正确性进行了验证,并对系统在提高车辆主动安全性方面的效果进行了初步评价。结果表明,通过本文的研究实现了汽车纵向主动避撞系统的各项基本功能;所开发的汽车主动避撞系统,对于提高车辆的主动安全性,降低交通事故发生率,减小交通事故带来的损害,保障安全行车具有重要意义。

... 1 安全距离模型建模分析安全距离模型需综合考虑诸多因素的影响,满足如下特点^[12]:①具有一定适用性,能适用大多数路况 ...

2012

0.0

. 2012, 26(4):1-4 DOI:doi:10.3969/j.issn.1674-8425-B.2012.04.001

A vehicle safety distance model for collision avoidance system based on emergency lane change motion

基于紧急变道策略的汽车主动避障安全车距模型

Bian Ming-yuan

边明远

作为汽车主动避撞系统中判定车辆是否处于安全行驶状态的依据，及进行汽车主动避险控制的基础，汽车安全车距确定是主动避撞系统中的一个重要环节。本文基于最佳路径规划策略，提出了一种结合车辆纵向速度调节控制和车道变换操作的车辆紧急避障方法，提出了紧急车道变换工况下的安全车距模型，并分析了不同的制动作用调整车速时间对车辆变道行驶轨迹和安全车距确定的影响。通过在同车道前方静态障碍物工况的仿真，验证了本文提出的安全车距模型的有效性。

... 基于换道过程中侧向速度的变化趋势,F车的侧向加速度采用正弦函数车道变换模型^[13,14],相关横向加速度、横向速度、换道轨迹模型分别为: ...

2000

0.0

... 基于换道过程中侧向速度的变化趋势,F车的侧向加速度采用正弦函数车道变换模型^[13,14],相关横向加速度、横向速度、换道轨迹模型分别为: ...

2008

0.0

... _des迅速精确跟踪,可用线性二次型调节器LQR进行优化,减少系统控制误差并提高控制性能^[15] ...