作者简介:曹福成(1976-),男,副教授,在站博士后.研究方向:人机交互与机器人控制.E-mail:arthurcao@hotmail.com
针对下肢康复机器人训练任务规划和主动康复控制问题,提出了一种能够根据受损患肢病况进行步态轨迹规划的策略,并设计了可实现主动康复训练的控制算法。步态轨迹规划能够根据不同患肢按需自适应调整训练任务轨迹与正常步态轨迹的偏离程度,阻抗控制可以提高训练中受损患肢的主动参与力,自适应滑膜控制可以消除机器人结构模型的参数不确定性和训练过程中因肌肉痉挛等造成的外力干扰,并且对系统的非线性有一定的鲁棒作用。实验结果表明,该方法能够有效地解决不同受损患肢步态康复训练的自适应任务规划和主动康复训练过程中的柔顺运动控制,任务轨迹跟踪精度较高。
Considering the training task planning and active rehabilitation control design for lower limb rehabilitation, a gait trajectory planning strategy was proposed according to the damaged limb and the control algorithm to complete the active rehabilitation training. The gait trajectory planning method can adjust adaptively the deviation between the training trajectory and normal gait trajectory on the demand of different limbs. Impedance control can enhance the active forces of the damaged limb in training. Adaptive sliding mode control can eliminate the influence of model structure uncertainty and parameter uncertainty, which are caused by external forces due to muscle spasm in training, and is robust to nonlinearity of the system. Simulation results show that the proposed method is effective to the adaptive gait trajectory planning and active compliant control for different damaged limbs in gait rehabilitation training, and the tracking accuracy is higher.
国际机器人研究已把重建肢体运动功能的康复机器人作为一个热点研究领域, 特别是在控制策略和方法上, 研究者更加关注患者患肢在训练过程中的主动参与程度及训练本身的安全性和舒适性[1, 2]。下肢康复训练机器人作为康复机器人中重要的一类, 它可以承担人体的一部分重量, 帮助早期中风或脊髓伤害患者模拟正常人的步态运动规律, 锻炼下肢肌肉, 进而重塑神经系统对行走功能的运动机能和正常的行走步态, 达到恢复下肢运动功能的目的[3]。
下肢康复医学上通常采用让患肢重复特定训练任务的运动方法, 这种方法在临床上已表现出了很好的治疗效果。随着机器人技术和康复医学的发展以及人们对行走步态的更加深入认识, 越来越多的科研机构和国际大公司开发研制了一些更符合人体运动机理的下肢康复训练机器人。如2001年, 瑞士HOCOMA医疗器械公司与瑞士苏黎士BALGRIST医学院康复中心合作研究的LOKOMAT, 其作为减重步行训练康复机器人的典型代表, 已成功推向市场, 可实现患者训练状态的实时监测、评价和引导, 并且能够根据患者个体差异提供特定可选的步态训练方案, 但LOKOMAT的动力学模型较为复杂, 控制难度较大。美国加利福尼亚大学伯克利分校研制的BLEEX外骨骼由40多个传感器以及液压关节组成, 可以根据使用者的运动状态计算出所需的力量分配, 然后控制它的仿生机械腿, 尽量减少穿戴者的负荷。这种机器人不但能帮助正常人增加承载能力, 也可以用于下肢运动障碍患者的行走恢复。但该设备只适用于较轻病情的患者, 设计复杂, 对传感器的要求高。这些造成设备的制造成本非常昂贵。目前的研究显示, 下肢康复机器人疗法已经由最初的集中在肌肉的运动知觉反馈上, 扩展到以功能电刺激与虚拟现实为基础的治疗中。但是这些治疗方法由于涉及的技术更加宽泛和复杂, 还不够成熟, 能用于临床的更少。
康复机器人, 尤其是肢体康复机器人, 研究中一定要解决两个重要问题:一是如何根据患肢的情况自适应的调整训练任务; 二是如何根据患肢主动作用力的大小, 采取合理的优化控制策略。在实现患肢关节和肌肉的训练任务时, 不但要保持机器人和患肢紧密接触, 而且也要保证患肢按特定轨迹运动的同时, 关节运动的速度和加速度稳定可控。另外, 出于对患肢安全性的考虑, 必须能够约束机器人提供辅助力矩的大小, 算法上采用一定的柔顺性控制策略, 才能提高患者的训练质量和舒适度[4, 5]。文献[6]和文献[7]针对机器人辅助患肢交互运动安全性的问题, 提出了安全监督策略下的阻抗控制。为了实现这样的机器人运动控制效果, 有必要把训练任务的规划和控制策略作为整体来来统一考虑[8]。虽然机器人的路径规划和控制方法有很多种, 如文献[9]实现了复杂情况下的某种最优, 文献[10]应用脉冲控制的方法实现了两足行走机器人行走步态的稳定控制, 但是考虑到康复机器人要完成的特殊任务, 这些传统工业机器人的路径规划方法和控制策略都不能够直接采用。康复机器人的任务规划和控制方法必须要考虑上面提到的两个重要问题。本文在综合分析研究当前康复机器人领域国内外文献的基础上, 将任务规划和控制算法作为一个整体来统一考虑, 提出了适用下肢康复机器人的步态自适应阻抗控制策略, 实现不同患者在不同康复阶段任务的自适应调整和康复运动训练任务中受损患肢主动运动功能的最大化。
下肢康复机器人的关节空间动力学模型可用如下的公式表示:
式中:
假设1 患者主动作用力测量噪声有界, 其上界为
性质1 惯性矩阵
性质2 如果矩阵
性质3
阻抗控制早期被用于处理机器人与环境的交互问题, 通过调整机器人的机械阻抗以实现末端执行器的位置偏差与环境接触力之间的理想动态关系。阻抗控制被用于中风患者下肢康复的治疗中, 不需要训练过程严格按照预先规划的步态轨迹运动, 而是允许有一个可变的偏差存在, 偏离程度的大小决定了患肢主动作用力的大小, 并且可以根据患肢的不同病况进行调整[11, 12]。基于康复患者主动训练的舒适性考虑, 本文引进如下阻抗控制模型:
式中:
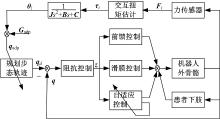
在患者的主动康复训练中, 也需要处理类似的人机交互问题, 此时训练者被视为外界系统, 当人机发生耦合作用时, 如:患者肌肉痉挛产生的异常运动等, 为保证机器人系统和外界的物理相容性, 步行康复训练机器人应具有阻抗特性, 以达到对人体作用力的感知、适应和跟随, 实现人机系统力和位置动态关系的柔顺性控制。根据这种需要, 本文提出了一张轨迹自适应滑模阻抗控制策略, 其算法框图见图1。
下面设计如何实现病人根据自己意愿进行康复训练, 即如何通过控制策略驱动机器人执行机构提供一定的辅助力, 在保证与患肢主动作用力交互的基础上使患肢关节运动轨迹偏离预先设定的步态轨迹运动, 偏差的大小取决于患肢主动力作用力的大小和阻抗参数, 当然, 这些参数与患肢具体的病况相关。首先, 定义误差信号如下:
式中:
定义增强型阻抗误差如下:
式中:
构造两个正定矩阵
则上式可表示成
其中
为了简化问题的说明, 定义一辅助变量
于是, 可以得到下式
由式(10)和(5)可以看出,
关节空间内, 下肢康复机器人的控制目标就是在控制律作用下, 确保各个关节的输出
其中,
另外, 假设在期望的规划轨迹下,
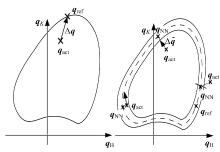
下肢康复机器人以实际测量的步态轨迹为基础, 采用关节空间法进行轨迹规划。通常的做法是根据大量的实验数据, 测得健康人的步态轨迹并将它作为参考轨迹[13]。在康复训练中, 控制的目标就是让患肢沿着固定的参考轨迹进行重复运动[14]。对于不同的康复患者而言, 因个体患肢的病况严重程度不同, 在相同的参考轨迹下, 训练可能对患者来说, 十分不舒适, 甚至是很难达到预期的训练目标。所以不同患者训练过程中步态轨迹的规划应充分考虑各自患肢特定病况下的生理局限, 要保证激发患肢最大主动运动力的情况下, 完成特定康复运动目标的训练任务, 避免对患者造成二次伤害。本文提出的基于人机交互力的自适应轨迹规划方法, 主要根据患肢主动作用力的大小来调节患肢实际训练轨迹和理想参考轨迹的偏差, 偏差大小由康复治疗师来根据患者患肢的病况进行调节。
自适应轨迹规划框图如图2所示, 需要调整的轨迹角度
式中:
滑模控制也叫变结构控制, 本质上是一类特殊的非线性控制, 且非线性表现为控制的不连续性。滑模控制近年来受到越来越多的重视, 它能够克服系统的不确定性, 对干扰和未建模动态具有很强的鲁棒性, 尤其对非线性系统具有良好的控制效果。但是在实际应用过程中, 由于控制律的切换时间存在有限时延, 控制律的切换频率不能够无限大, 所以理想的滑模是不可能达到的。因为滑模控制律的非连续性, 控制器的输出会在滑模面附近产生高频的抖震, 这可能导致系统的性能退化, 系统不稳定和机械零件的高磨损。本文提出了一种自适应滑模阻抗控制器, 在抑制传统滑模控制抖震的情况下完成下肢康复机器人主动康复训练。自适应滑模控制律可设计成:
式中:

其中, 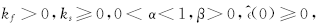
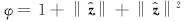
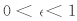
由式(8), 可以得到
式中:
为了后面在性能分析中更加清楚地论述问题, 定义另外一个变量:
构造李雅普诺夫函数如下:
式(24)表示的函数对时间求导可得:
根据前面的定义, 有
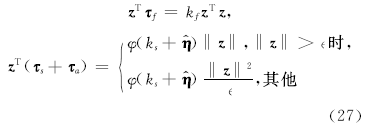
由第2节模型描述可知,
为了更具有广义性, 选择可导的
于是, 当
由于 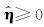
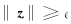


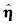
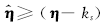
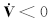
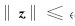
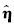
因为 
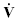
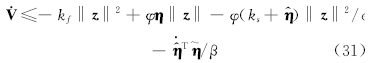
由式(31)可以看出, 当且仅当 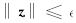

即
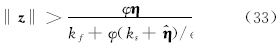
满足
另外由
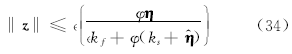
由式(32)可知 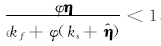
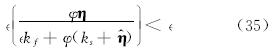
综上所述, 可以确定
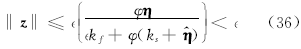
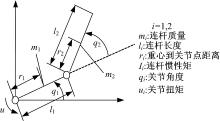
为了验证算法的有效性, 本文以平面两自由度机械臂结构为研究对象, 参数变量具体意义及结构如图3所示, 其中参数的取值如下:
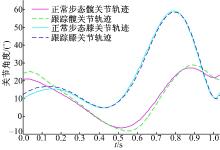
多项式中具体参数见表1, 轨迹如图4所示, 一个完整步态的训练周期为1 s。假定在一个步态训练周期内, 受损患肢的主动运动作用力是随不同步态和时间变化的, 力矩大小满足下面的关系:
| 表1 步态轨迹参数 Table 1 Parameters of gait |
控制器采用文中提出的自适应滑膜阻抗控制算法, 具体参数如下:
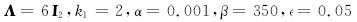
决定人机交互作用力大小的阻抗控制参数, 期望惯性矩阵
式中:
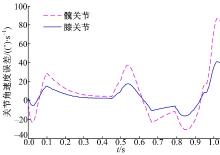
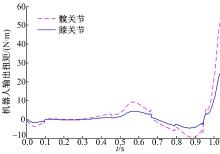
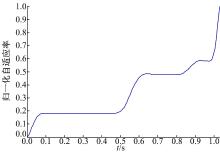
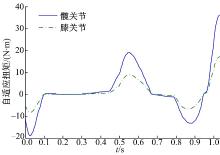
仿真实验结果如图5~图8所示。可以看出本文提出的控制方法, 可以保证受损患肢在一定阻抗参数的设定前提下, 根据患肢的运动状况, 自适应的规划训练任务的具体轨迹, 保证在一定的轨迹跟踪误差范围内和机器人尽量少的辅助力帮助下, 完成按需的主动康复训练。
下肢康复机器人是与人体功能受损患肢交互运动的设备, 应充分考虑不同患肢的状况, 保证机器人和患肢之间的交互运动处于一种舒适、自然、柔顺的环境中。而且, 为了增强康复的效果, 也要尽量提高患肢主动运动作用力的最大化。为了实现这种康复训练控制目标, 本文提出了一种轨迹自适应阻抗控制方法, 该方法能够特别适用于受损患肢主动运动功能的恢复阶段训练, 其训练任务可以根据患者的不同年龄、患肢的不同受损情况自适应规划, 同时, 阻抗控制作为一种有效的主动康复训练策略, 可以大大地提高受损患肢运动功能恢复的康复治疗进程。
The authors have declared that no competing interests exist.
| [1] |
|
| [2] |
|
| [3] |
|
| [4] |
|
| [5] |
|
| [6] |
|
| [7] |
|
| [8] |
|
| [9] |
|
| [10] |
|
| [11] |
|
| [12] |
|
| [13] |
|
| [14] |
|