探测器软着陆小行星的自适应超螺旋控制

引用本文

张鹏, 刘小松, 董博, 刘克平, 李元春. 探测器软着陆小行星的自适应超螺旋控制. 2016, 46(5): 1609-1615
ZHANG Peng, LIU Xiao-song, DONG Bo, LIU Ke-ping, LI Yuan-chun. Adaptive supper-twisting control for spacecraft soft landing on asteroids. Journal of Jilin University Engineering and Technology Edition, 2016, 46(5): 1609-1615 复制到剪切板

Permissions

探测器软着陆小行星的自适应超螺旋控制

张鹏^1,², 刘小松¹, 董博³, 刘克平³, 李元春^1,³

1.吉林大学通信工程学院, 长春 130012

2.中国电子科技集团第二十七研究所,郑州 450047

3.长春工业大学电气与电子工程学院,长春 130012

通信作者:李元春(1962-),男,教授,博士生导师.研究方向:复杂系统建模,智能机械与机器人控制.E-mail:liyc@ccut.edu.cn

作者简介:张鹏(1989-),男,博士研究生.研究方向:航天器制导与控制.E-mail:zhangpenginjlu@163.com

基金:“973”国家重点基础研究发展计划项目(2012CB720000); “863”国家高技术研究发展计划项目(2015AA7034053A-2)

摘要

针对探测器软着陆小行星的轨道控制问题,本文提出了一种基于自适应超螺旋算法的控制方法,避免了传统滑模控制的高频抖振,并且结构简单、无需已知外界扰动时间导数的上界。首先,将软着陆的轨道控制问题描述为一类非线性系统的镇定问题。其次,基于球谐系数法表示的小行星引力场模型设计前馈控制律,将系统解耦为三个滑模函数的一阶子系统。然后,针对每个子系统设计自适应超螺旋控制器,并证明闭环系统的稳定性。最后,将本文提出的控制方法与传统的自适应滑模控制进行了对比仿真,结果表明,所提出的算法能使系统更快地收敛到滑模面上,同时有效抑制抖振效应。

关键词: 自动控制技术; 软着陆小行星; 自适应超螺旋控制; 抖振抑制; 高阶滑模控制

中图分类号:TP273 文献标志码:A 文章编号:1671-5497(2016)05-1609-07

Adaptive supper-twisting control for spacecraft soft landing on asteroids

ZHANG Peng^1,², LIU Xiao-song¹, DONG Bo³, LIU Ke-ping³, LI Yuan-chun^1,³

1.College of Communication Engineering, Jilin University, Changchun 130012, China

2.The 27st Research Institute of CETC,Zhengzhou 450047, China

3.College of Electrical and Electronic Engineering, Changchun University of Technology, Changchun 130012, China

Abstract

In order to alleviate the chartering problem of the traditional sliding model control, an adaptive supper-twisting controller was designed for the spacecraft soft landing on asteroids. The controller has a simple algorithm structure and does not need to know the upper bound of the external disturbance's derivative. First, the control problem of soft landing was formulated as the stabilization of a nonlinear system. Second, a feedback control based on the spheric harmonic expansion model of the asteroid gravity was applied to decouple the system. Then, three adaptive supper-twisting controllers were designed to stabilize the subsystems. Simulations of soft landing on the Eros433 were performed to verify the effectiveness of the proposed controller. The simulation results were compared with the traditional adaptive sliding mode control to show the advantages of the proposed controller.

Keyword: automatic control technology; soft landing on asteroids; adaptive super-twisting control; chattering attenuation; high-order sliding mode control

Show Figures

0 引言

探测器软着陆小行星是深空探测中的重要内容之一。小行星距离地球遥远, 在其附近探测器与地面控制中心的通信有很长时延。同时, 小行星的引力场具有强不规则性, 探测器在其周围的轨道运动机理十分复杂。因此, 传统的地面控制难以保证软着陆的安全性, 探测器的自主控制成为了研究的热点^[1]。探测器软着陆小行星的轨道控制问题主要有如下特点:要求以“ 零速度-零误差” 着陆, 即系统稳态误差能收敛到零点; 要求控制算法结构简单, 计算量小; 要求控制算法的鲁棒性较强。由于满足上述要求, 滑模算法被广泛应用在软着陆自主轨道控制中^{[2, 3, 4, 5, 6, 7]}。然而, 传统一阶滑模算法存在抖振问题^{[8, 9]}, 不仅难以工程实现, 而且可能威胁软着陆的安全性。Furfaro等^[10]提出一种基于齐次高阶滑模算法的软着陆制导律, 但该制导律用轨道误差作为滑模函数, 算法的滑动阶数与滑模的相对阶数相同, 难以确保对抖振的有效抑制。

超螺旋(Super-twisting)算法^[11]是一类结构简单的高阶滑模算法, 能有效抑制抖振问题, 且仅需要系统的一阶滑模信息。然而, 设计超螺旋算法的参数需要已知外界扰动时间导数的上界^[12], 限制了其在实际系统中的应用。Shtessel等^[13]提出了一种自适应超螺旋算法, 但需要外界扰动满足特定的假设条件。李鹏^[14]提出了一种仅需要扰动时间导数有界的自适应超螺旋算法。Utkin等^[15]基于一阶滤波器实现了对超螺旋算法参数的自适应估计。然而, 这些算法都是针对一阶SISO系统设计的, 而且自适应律也相对复杂。

针对探测器软着陆小行星的轨道控制问题, 本文设计了一类基于自适应超螺旋算法的控制器。该控制器在保持传统滑模控制精度高、鲁棒性强等优点的同时结构简单、限制条件少、能有效抑制控制抖振。首先, 建立了探测器的轨道动力学方程, 基于多项式制导法设计了标称轨道, 将软着陆轨道控制问题转化为一类非线性MIMO系统的镇定问题。然后, 基于球谐系数法表示的小行星引力势函数设计了前馈控制, 将原系统解耦为3个一阶子系统, 并设计了自适应超螺旋控制器来确保子系统的状态收敛到滑模面上。最后, 采用小行星Eros433的物理参数进行了数值仿真, 并将所设计的控制算法与传统滑模算法进行了对比。

1 问题描述

探测器在小行星固连坐标系中的轨道运动可以描述为:

$\begin{matrix} \overset{\cdot \cdot}{r} + \overset{\cdot}{Ω} \times r + 2 Ω \times \overset{\cdot}{r} + Ω \times (Ω \times r) = V_{r} + a + d (1) \end{matrix}$

式中: $\begin{matrix} r = {[\begin{matrix} r_{x} & r_{y} & r_{z} \end{matrix}]}^{T} \end{matrix}$ 为探测器在小行星固连坐标系中的位置矢量; $\begin{matrix} Ω \end{matrix}$ 为小行星自旋的角速度矢量; $\begin{matrix} a \end{matrix}$ 为控制加速度; $\begin{matrix} d \end{matrix}$ 为探测器受到的太阳光压和其他天体引力; $\begin{matrix} V_{r} = \partial V (r) / \partial r \end{matrix}$ 为探测器受到的引力加速度, $\begin{matrix} V (r) \end{matrix}$ 为小行星的引力势函数。

小行星的引力势函数通常难以精确获得, 因此将其表示为:

$\begin{matrix} V (r) = V_{n} (r) + Δ (r) (2) \end{matrix}$

式中: $\begin{matrix} Δ (r) \end{matrix}$ 为模型不确定性; $\begin{matrix} V_{n} (r) \end{matrix}$ 为小行星引力势函数的名义模型, 用 $\begin{matrix} n \end{matrix}$ 阶球谐系数法^[16]表示为:

$\begin{matrix} \begin{matrix} V_{n} (r) & = \frac{μ}{R} [1+ \overset{n}{\sum_{i = 1}} \overset{i}{\sum_{j = 0}} {(\frac{R_{0}}{R})}^{i} P_{i}^{j} (sinθ) Φ] (3) \\ Φ & = C_{ij} \cos (jγ) + S_{ij} \sin (jγ) (4) \end{matrix} \end{matrix}$

式中: $\begin{matrix} μ \end{matrix}$ 为小行星的引力常数; $\begin{matrix} R_{0} \end{matrix}$ 为小行星的名义半径; $\begin{matrix} P_{i}^{j} (sinθ) \end{matrix}$ 为 $\begin{matrix} sinθ \end{matrix}$ 的缔合勒让德多项式; $\begin{matrix} C_{ij} 、 S_{ij} \end{matrix}$ 为小行星的球谐系数; $\begin{matrix} R \end{matrix}$ 为探测器到小行星质心的距离; $\begin{matrix} θ \end{matrix}$ 为探测器的纬度; $\begin{matrix} γ \end{matrix}$ 为探测器的经度。

通过设计标称轨道, 可以将探测器软着陆小行星的轨道控制问题视为非线性系统(1)的状态轨迹追踪问题。

根据已知的探测器初始位置 $\begin{matrix} r_{0} 、 \end{matrix}$ 初始速度 $\begin{matrix} {\overset{\cdot}{r}}_{0} 、 \end{matrix}$ 着陆点位置 $\begin{matrix} r_{f} \end{matrix}$ 和着陆时间 $\begin{matrix} t_{f}, \end{matrix}$ 基于多项式制导法^[4]设计软着陆标称轨道为:

$\begin{matrix} \begin{matrix} \tilde{r} (t) = r_{0} + {\overset{\cdot}{r}}_{0} t + (3 r_{f} - 3 r_{0} - 2 {\overset{\cdot}{r}}_{0} t_{f}) {(t / t_{f})}^{2} + \\ (2 r_{0} + {\overset{\cdot}{r}}_{0} t_{f} - 2 r_{f}) {(t / t_{f})}^{3} (5) \end{matrix} \end{matrix}$

定义误差向量为:

$\begin{matrix} e = r - \tilde{r} (6) \end{matrix}$

假设小行星绕其主自转轴稳定自旋, 则 $\begin{matrix} \overset{\cdot}{Ω} = 0, Ω = {[0, 0, ω]}^{T} 。 \end{matrix}$ 将式(6)与式(1)联立, 可以得到轨迹追踪的误差方程为:

$\begin{matrix} \overset{\cdot \cdot}{e} = - 2 Ω \times \overset{\cdot}{e} - Ω \times (Ω \times e) + V_{r} + a + d - φ (7) \end{matrix}$

式中: $\begin{matrix} φ = 2 Ω \times \overset{\cdot}{\tilde{r}} + Ω \times (Ω \times \tilde{r}) - \overset{\cdot \cdot}{\tilde{r}} 。 \end{matrix}$

定义滑模面为:

$\begin{matrix} s = Ke + \overset{\cdot}{e} (8) \end{matrix}$

式中: $\begin{matrix} K = diag (k_{i}), k_{i} > 0, i = x, y, z 。 \end{matrix}$

将式(7)与式(8)联立, 则得到滑模状态方程为:

$\begin{matrix} \begin{matrix} \overset{\cdot}{s} = K \overset{\cdot}{e} - 2 Ω \times \overset{\cdot}{e} - Ω \times (Ω \times e) + V_{r} + \\ a + d - φ (9) \end{matrix} \end{matrix}$

若控制器 $\begin{matrix} a \end{matrix}$ 能使系统(9)的状态收敛到原点, 即滑模流形 $\begin{matrix} s = \overset{\cdot}{s} = 0 \end{matrix}$ 上, 则误差状态方程(7)能够渐进稳定。这样, 探测器软着陆小行星的轨道追踪控制问题就可以视为非线性系统(9)的镇定控制问题。

2 控制器设计

由于非线性系统式(9)为MIMO系统, 难以直接对其设计自适应超螺旋控制器。考虑到系统中耦合项的结构已知, 采用前馈控制对其解耦。

定义控制器为:

$\begin{matrix} a = v + u (10) \end{matrix}$

式中: $\begin{matrix} v \end{matrix}$ 为前馈控制。

$\begin{matrix} \begin{matrix} v = - K \overset{\cdot}{e} + 2 Ω \times \overset{\cdot}{e} + Ω \times (Ω \times e) - \\ \partial V_{n} / \partial r + φ (11) \end{matrix} \end{matrix}$

将式(11)、式(10)代入式(9), 得:

$\begin{matrix} \overset{\cdot}{s} = u + f (12) \end{matrix}$

式中: $\begin{matrix} f = [f_{x}, f_{y}, f_{z}]^{T} = \partial Δ / \partial r + d \end{matrix}$ 为系统的外界扰动, 物理含义为探测器受到的太阳光压、其他天体引力和小行星引力的模型不确定性。

假设1 $\begin{matrix} \overset{\cdot}{f} \end{matrix}$ 有界且 $\begin{matrix} |{\overset{\cdot}{f}}_{i}| \leq δ_{i}, δ_{i} \end{matrix}$ 为未知正常数, $\begin{matrix} i = x, y, z 。 \end{matrix}$

针对非线性系统(12), 设计自适应超螺旋控制器为:

$\begin{matrix} \begin{matrix} \{\begin{matrix} u_{i} = - χ_{i} {|s_{i}|}^{\frac{1}{2}} sign (s_{i}) + {\tilde{u}}_{i} \\ {\overset{\cdot}{\tilde{u}}}_{i} = - α_{i} sign (s_{i}), {\tilde{u}}_{i} (0) = 0 \end{matrix} (13) \\ i = x, y, z \end{matrix} \end{matrix}$

式中: $\begin{matrix} χ_{i} \end{matrix}$ 为非零常数; $\begin{matrix} α_{i} \end{matrix}$ 为自适应参数且 $\begin{matrix} α_{i} (0) = 0, \end{matrix}$ 自适应律为:

$\begin{matrix} {\overset{\cdot}{α}}_{i} = {|s_{i}|}^{\frac{1}{2}}, i = x, y, z (14) \end{matrix}$

定理对于符合动力学模型(7)和假设1的探测器软着陆小行星的轨道控制问题, 采用如式(10)~(14)所示的自适应增益超螺旋控制。若控制器参数满足 $\begin{matrix} χ_{i} > 2, \end{matrix}$ 则系统能收敛到滑模流形 $\begin{matrix} s = \overset{\cdot}{s} = 0 \end{matrix}$ 上。

证明定义状态变换为:

$\begin{matrix} ε_{i} = f_{i} - \int_{0}^{t} α_{i} sign (s_{i}) dτ, i = x, y, z (15) \end{matrix}$

将式(15)代入式(12)可以得到:

$\begin{matrix} \begin{matrix} \{\begin{matrix} {\overset{\cdot}{s}}_{i} = - χ_{i} {|s_{i}|}^{\frac{1}{2}} sign (s_{i}) + ε_{i} \\ {\overset{\cdot}{ε}}_{i} = - α_{i} sign (s_{i}) + {\overset{\cdot}{f}}_{i} \end{matrix} (16) \\ i = x, y, z \end{matrix} \end{matrix}$

定义状态向量:

$\begin{matrix} η_{i} = {[\begin{matrix} {|s_{i}|}^{\frac{1}{2}} sign (s_{i}) & ε_{i} \end{matrix}]}^{T}, i = x, y, z (17) \end{matrix}$

则:

$\begin{matrix} \begin{matrix} \{\begin{matrix} {\overset{\cdot}{η}}_{i 1} = \frac{1}{2 {|s_{i}|}^{\frac{1}{2}}} (- χ_{i} {|s_{i}|}^{\frac{1}{2}} sign (s_{i}) + ε_{i}) \\ {\overset{\cdot}{η}}_{i 2} = - α_{i} sign (s_{i}) + {\overset{\cdot}{f}}_{i} \end{matrix} (18) \\ i = x, y, z \end{matrix} \end{matrix}$

定义:

$\begin{matrix} A_{i} = [\begin{matrix} - \frac{χ_{i}}{2} & \frac{1}{2} \\ - α_{i} & 0 \end{matrix}], B = {[\begin{matrix} 0 & 1 \end{matrix}]}^{T}, C = [\begin{matrix} 1 & 0 \end{matrix}] (19) \end{matrix}$

令 $\begin{matrix} \overset{\cdot}{Δ}'_{i} = {|s_{i}|}^{\frac{1}{2}} {\overset{\cdot}{f}}_{i}, \end{matrix}$ 则有:

$\begin{matrix} {\overset{\cdot}{η}}_{i} = \frac{1}{{|s_{i}|}^{\frac{1}{2}}} (A_{i} η_{i} + B \overset{\cdot}{Δ}'_{i}) (20) \end{matrix}$

定义李亚普诺夫函数为:

$\begin{matrix} \begin{matrix} V (η, α) = η^{T} Pη + \sum_{i = x, y, z} \frac{1}{3} {({\tilde{α}}_{i} - α_{i})}^{3} = \\ \sum_{i = x, y, z} ({η^{T}}_{i} P_{i} η_{i} + \frac{1}{3} {({\tilde{α}}_{i} - α_{i})}^{3}) = \\ \sum_{i = x, y, z} V_{i} (η_{i}, α_{i}) (21) \end{matrix} \end{matrix}$

式中: $\begin{matrix} η = {[\begin{matrix} η_{x} & η_{y} & η_{z} \end{matrix}]}^{T}; P = diag (P_{i}) \end{matrix}$ 为正定对称矩阵, 且:

$\begin{matrix} P_{i} = \frac{1}{2} [\begin{matrix} 4 {\tilde{α}}_{i} + χ_{i}^{2} & - χ_{i} \\ - χ_{i} & 2 \end{matrix}] (22) \end{matrix}$

$\begin{matrix} {\tilde{α}}_{i} \end{matrix}$ 为正常数, 满足:

$\begin{matrix} {\tilde{α}}_{i} > \frac{δ_{i}^{2}}{χ_{i}} - \frac{χ_{i}}{4} [6 - {(χ_{i} - 2)}^{2}], 且 {\tilde{α}}_{i} \geq α_{i}^{\max} (23) \end{matrix}$

$\begin{matrix} α_{i}^{\max} \end{matrix}$ 为自适应参数 $\begin{matrix} α_{i} \end{matrix}$ 的上界。由自适应律式(14)可知, 当系统处于滑动状态时, $\begin{matrix} {\overset{\cdot}{α}}_{i} = 0 \end{matrix}$ , 因此 $\begin{matrix} α_{i}^{\max} \end{matrix}$ 存在。

对李亚普诺夫函数求导, 得:

$\begin{matrix} \overset{\cdot}{V} (η, α) = \sum_{i = x, y, z} {\overset{\cdot}{V}}_{i} (η_{i}, α_{i}) (24) \end{matrix}$

将式(19)代入 $\begin{matrix} {\overset{\cdot}{V}}_{i} (η_{i}, α_{i}), \end{matrix}$ 可得:

$\begin{matrix} \begin{matrix} {\overset{\cdot}{V}}_{i} (η_{i}, α_{i}) = {\overset{\cdot}{η}}^{T}_{i} P_{i} η_{i} - {\overset{\cdot}{α}}_{i} {(\tilde{α} - α_{i})}^{2} = \\ \frac{1}{{|s_{i}|}^{\frac{1}{2}}} (2 {η^{T}}_{i} {A^{T}}_{i} + 2 \overset{\cdot}{Δ}'_{i} B^{T}) P_{i} η_{i} - \\ {\overset{\cdot}{α}}_{i} {(\tilde{α} - α_{i})}^{2} \leq \frac{1}{{|s_{i}|}^{\frac{1}{2}}} [2 {η^{T}}_{i} {A^{T}}_{i} P_{i} η_{i} + \\ 2 \overset{\cdot}{Δ}'_{i} B^{T} P_{i} η_{i} + δ_{i}^{2} |s_{i}| - \overset{\cdot}{Δ}'_{i}^{2}] - {\overset{\cdot}{α}}_{i} {(\tilde{α} - α_{i})}^{2} = \\ \frac{1}{{|s_{i}|}^{\frac{1}{2}}} [2 {η^{T}}_{i} {A^{T}}_{i} P_{i} η_{i} + 2 \overset{\cdot}{Δ}'_{i} B^{T} P_{i} η_{i} + \\ δ_{i}^{2} {η^{T}}_{i} C^{T} C η_{i} - \overset{\cdot}{Δ}'_{i}^{2}] - {\overset{\cdot}{α}}_{i} {(\tilde{α} - α_{i})}^{2} \leq \\ \frac{1}{{|s_{i}|}^{\frac{1}{2}}} [2 {η^{T}}_{i} {A^{T}}_{i} P_{i} η_{i} + δ_{i}^{2} {η^{T}}_{i} C^{T} C η_{i} + \\ {η^{T}}_{i} P_{i} B B^{T} P_{i} η_{i}] - {\overset{\cdot}{α}}_{i} {(\tilde{α} - α_{i})}^{2} = \\ \frac{1}{{|s_{i}|}^{\frac{1}{2}}} [2 {η^{T}}_{i} {A^{T}}_{i} P_{i} η_{i} + δ_{i}^{2} {η^{T}}_{i} C^{T} C η_{i} + \\ {η^{T}}_{i} P_{i} B B^{T} P_{i} η_{i}] - {|s_{i}|}^{\frac{1}{2}} {(\tilde{α} - α_{i})}^{2} = \\ \frac{1}{{|s_{i}|}^{\frac{1}{2}}} \times {η^{T}}_{i} {{A^{T}}_{i} P_{i} + {P^{T}}_{i} A_{i} + \\ [δ_{i}^{2} - {(\tilde{α} - α_{i})}^{2}] C^{T} C + P_{i} B B^{T} P_{i}} η_{i} (25) \end{matrix} \end{matrix}$

定义矩阵:

$\begin{matrix} \begin{matrix} Q_{i} = - {{A_{i}}^{T} P_{i} + {P^{T}}_{i} A_{i} + [δ_{i}^{2} - \\ (\tilde{α} - α_{i} {)]}^{2} C^{T} C + P_{i} B B^{T} P_{i}} (26) \end{matrix} \end{matrix}$

将式(20)(22)代入式(26)可得:

$\begin{matrix} \begin{matrix} Q_{i} = [\begin{matrix} q_{i 1} & q_{i 2} \\ q_{i 2} & q_{i 3} \end{matrix}] (27) \\ q_{i 1} = χ_{i} (2 {\tilde{α}}_{i} - α_{i}) + \frac{χ_{i}^{3}}{2} - \frac{χ_{i}^{2}}{4} - \\ [δ_{i}^{2} - {({\tilde{α}}_{i} - α_{i})}^{2}] (28) \\ \begin{matrix} q_{i 2} = α_{i} - {\tilde{α}}_{i} - \frac{χ_{i}^{2}}{2} + \frac{χ_{i}}{2} (29) \\ q_{i 3} = \frac{χ_{i}}{2} - 1 (30) \end{matrix} \end{matrix} \end{matrix}$

根据Shur补^[17]的性质可知, $\begin{matrix} Q_{i} \end{matrix}$ 正定的条件为:

① $\begin{matrix} q_{i 3} > 0 \end{matrix}$ , 即:

$\begin{matrix} \frac{χ_{i}}{2} - 1 > 0 \Rightarrow χ_{i} > 2 (31) \end{matrix}$

② $\begin{matrix} q_{i 1} - q_{i 2}^{2} / q_{i 3} > 0, \end{matrix}$ 即:

$\begin{matrix} \begin{matrix} χ_{i} (2 {\tilde{α}}_{i} - α_{i}) - {(α_{i} - {\tilde{α}}_{i} - \frac{χ_{i}^{2}}{2} + \frac{χ_{i}}{2})}^{2} - \\ (δ_{i}^{2} - {({\tilde{α}}_{i} - α_{i})}^{2}) + \frac{χ_{i}^{3}}{2} - \frac{χ_{i}^{2}}{4} = \\ χ_{i} (2 {\tilde{α}}_{i} - α_{i}) + (α_{i} - {\tilde{α}}_{i}) (χ_{i}^{2} - χ_{i}) + \\ \frac{χ_{i}^{3}}{2} - \frac{χ_{i}^{2}}{4} - δ_{i}^{2} - \frac{1}{4} {(χ_{i}^{2} - χ_{i})}^{2} = \\ (3 - χ_{i}) χ_{i} {\tilde{α}}_{i} + \frac{χ_{i}^{2}}{4} [6- {(χ_{i} - 2)}^{2}] + \\ (χ_{i} - 2) χ_{i} α_{i} - δ_{i}^{2} \geq \\ χ_{i} \tilde{α} + (2 - χ_{i}) χ_{i} α_{i} + \frac{χ_{i}^{2}}{4} [6- {(χ_{i} - 2)}^{2}] + \\ (χ_{i} - 2) χ_{i} α_{i} - δ_{i}^{2} = χ_{i} {\tilde{α}}_{i} + \\ \frac{χ_{i}^{2}}{4} [6- {(χ_{i} - 2)}^{2}] - δ_{i}^{2} (32) \end{matrix} \end{matrix}$

根据式(23)可知, 当 $\begin{matrix} χ_{i} > 2 \end{matrix}$ 时 $\begin{matrix} {\tilde{α}}_{i} \end{matrix}$ 存在且使 $\begin{matrix} q_{i 1} - q_{i 2}^{2} / q_{i 3} > 0 。 \end{matrix}$ 此时, $\begin{matrix} Q_{i} \end{matrix}$ 正定, 其特征值的最小值 $\begin{matrix} λ_{\min} (Q) > 0 。 \end{matrix}$ 根据式(25)和式(17)有:

$\begin{matrix} {\overset{\cdot}{V}}_{i} (η_{i}, α_{i}) \leq - \frac{λ_{\min} (Q)}{|η_{i 1}|} {η^{T}}_{i} η_{i} \leq - λ_{\min} (Q) ‖ η_{i} ‖ (33) \end{matrix}$

根据式(24), $\begin{matrix} \overset{\cdot}{V} (η, α) \leq 0 \end{matrix}$ 且仅在 $\begin{matrix} η = 0 \end{matrix}$ 时为零。由李雅普诺夫稳定性定理可知, 系统状态可以收敛滑模流形 $\begin{matrix} s = \overset{\cdot}{s} = 0 \end{matrix}$ 上, 定理得证。

3 数值仿真

采用小行星Eros433作为软着陆目标进行数值仿真。以NASA公布的1708个面的形状数据为基础(如图1所示), 假设其密度为2.670 g/cm³, 用多面体法^[18]建立Eros433的引力场模型作为其真实引力场 $\begin{matrix} V (r); \end{matrix}$ 用二阶球谐系数法建立的引力场模型作为其名义引力场 $\begin{matrix} V_{2} (r), \end{matrix}$ 物理参数如下:球谐系数 $\begin{matrix} C_{20} \end{matrix}$ =0.052 47; 球谐系数 $\begin{matrix} C_{22} \end{matrix}$ =0.082 53; 引力参数 $\begin{matrix} μ \end{matrix}$ =8.86× 10⁵ N· m²/kg; 名义半径 $\begin{matrix} R_{0} \end{matrix}$ =16 km; 自旋角速度 $\begin{matrix} ω \end{matrix}$ =3.314× 10^-4 rad/s。

	Figure Option View Download New Window
	图1 小行星Eros433的多面体模型Fig.1 Polyhedron model of the Eros433

由于着陆过程的时间较短, 过程中小行星与太阳的相对位置变化不大, 因此假设探测器在小行星周围受到的太阳光压和其他天体引力在小行星轨道坐标系下为常向量, 定义仿真中小行星固连坐标系下探测器受到的外界扰动为:

$\begin{matrix} d = [\begin{matrix} \cos (ωt) & \sin (ωt) & 0 \\ - \sin (ωt) & \cos (ωt) & 0 \\ 0 & 0 & 1 \end{matrix}] [\begin{matrix} 3 \\ 4 \\ 5 \end{matrix}] \times 10^{- 7} m / s^{2} (34) \end{matrix}$

仿真中探测器软着陆标称轨道的初始位置为[26, 20, 22] km, 初始速度为[0.5, -0.9, 1.3] m/s, 着陆点位置为[0, 4, 2] km, 着陆时间为8000 s。控制器参数为 $\begin{matrix} χ_{i} = 3, k_{i} = 0.03, i = x, y, z 。 \end{matrix}$ 假设探测器的初始位置和初始速度有一定误差, 实际为[25.9, 20.1, 21.9] km和[0, 0, 1] m/s。

设计自适应滑模控制(ASMC)^[19]如式(35)所示, 将其与本文设计的自适应超螺旋算法(AGSTC)分别仿真进行对比分析。为了更好地对比算法自身的性能, ASMC采用了与AGSTC同样的滑模函数。

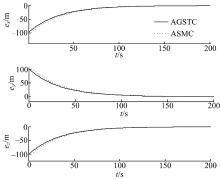
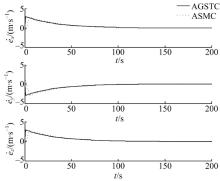
$\begin{matrix} \begin{matrix} \{\begin{matrix} \tilde{a} = - K \overset{\cdot}{e} + 2 Ω \times \overset{\cdot}{e} + Ω \times (Ω \times e) - \\ \partial V_{n} / \partial r - φ - \{c_{i} sign (s_{i})\} \\ {\overset{\cdot}{c}}_{i} = \frac{1}{10} |s_{i}|, c_{i} (0) = 0 \end{matrix} (35) \\ i = x, y, z \end{matrix} \end{matrix}$

仿真中, 两种控制下探测器的动态性能如图2、图3和图4所示。从图2和图3可以看出, 两种控制下探测器轨道的位置误差和速度误差都能收敛到0, AGSTC的收敛速度略快于ASMC, 这是由于AGSTC算法能使系统状态更快地收敛到滑模面上, 如图4所示。上述仿真结果表明, 本文设计的控制器能有效地实现探测器对着陆轨道的追踪, 并且追踪误差的收敛速度快于传统滑模算法。

	Figure Option View Download New Window
	图2 探测器轨道的三轴位置误差Fig.2 Tracking error of the spacecraft's position

	Figure Option View Download New Window
	图3 探测器轨道的三轴速度误差Fig.3 Tracking error of the spacecraft's velocity

	Figure Option View Download New Window
	图4 探测器的滑模函数变化曲线Fig.4 Curve of the spacecraft's sliding mode function

从图5可以看出, 由于ASMC控制器 $\begin{matrix} u \end{matrix}$ 中含有用来抑制不确定性的非线性控制项 $\begin{matrix} c_{i} sign (s_{i}), \end{matrix}$ 因此系统在滑动状态时存在控制器抖振。而AGSTC控制将非线性项放入控制器的高阶项 $\begin{matrix} \overset{\cdot}{u} \end{matrix}$ 中, 有效地抑制了控制器抖振。

	Figure Option View Download New Window
	图5 三轴上的控制加速度曲线(AGSTC& ASMC)Fig.5 Control accelerations in the three axes (AGSTC& ASMC)

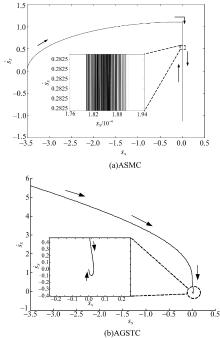
图6为两种控制下探测器在固连坐标系 $\begin{matrix} x \end{matrix}$ 轴上轨道的滑模函数 $\begin{matrix} s - \overset{\cdot}{s} \end{matrix}$ 的相轨迹。从图6(a)可以看出, ASMC算法只能使系统收敛到滑模面 $\begin{matrix} s = 0 \end{matrix}$ 上, 但二阶滑模函数 $\begin{matrix} \overset{\cdot}{s} \end{matrix}$ 则存在抖振。从图6(b)可以看出, AGSTC算法可以使系统经过有限次螺旋, 收敛到滑模流形 $\begin{matrix} s = \overset{\cdot}{s} = 0 \end{matrix}$ 上, 使系统的稳定性和动态性能更好。

	Figure Option View Download New Window
	图6 x轴上的s- $\begin{matrix} \overset{\cdot}{s} \end{matrix}$ 相轨迹Fig.6 Phase trajectory of s- $\begin{matrix} \overset{\cdot}{s} \end{matrix}$ in the x-axis

用边界层法改进式(35)中的ASMC算法, 将符号函数 $\begin{matrix} c_{i} sign (s_{i}) \end{matrix}$ 替换为 $\begin{matrix} c_{i} sat (s_{i}), \end{matrix}$ 然后将其与本文设计的AGSTC进行仿真对比, 结果如图7、图8所示。从图7可以看出, 经过边界层法的改进后, ASMC2的控制输出抖振得到了有效抑制。然而, 应用饱和函数替换后, ASMC2不再渐进稳定, 无法使系统收敛到原点, 存在一定的稳态误差。而本文设计的AGSTC在抑制抖振的同时仍能使系统收敛到原点, 控制精度更高, 如图8所示。

	Figure Option View Download New Window
	图7 三轴上的控制加速度曲线(AGSTC& ASMC2)Fig.7 Control acceleration in the three axes (AGSTC& ASMC2)

	Figure Option View Download New Window
	图8 探测器的稳态滑模函数变化Fig.8 Curve of the spacecraft's sliding mode function

综上所述, 本文设计的自适应超螺旋算法能够使系统到达并保持在滑模流形 $\begin{matrix} s = \overset{\cdot}{s} = 0 \end{matrix}$ 上, 从而实现探测器对标称轨道的追踪。与传统滑模算法相比, 具有结构简单、控制精度高、限制条件少、收敛速度快等优点, 并且能有效抑制控制输出抖振。

4 结束语

以探测器软着陆小行星的轨道控制任务为背景, 针对传统滑模控制中存在的控制抖振问题, 将自适应算法与超螺旋算法相结合设计了一类控制器。该控制器继承了传统滑模鲁棒性强的优点, 对引力场建模不确定性、太阳光压、其他天体引力等外界扰动不敏感。除此之外, 该控制器还有如下优势:①结构简单, 计算量小; ②系统滑动在滑模流形 $\begin{matrix} s = \overset{\cdot}{s} = 0 \end{matrix}$ 上, 收敛速度快; ③不需要外界扰动时间导数的上界, 限制条件少; ④能有效抑制控制器抖振。通过对小行星Eros433的数值仿真验证了所提出算法的有效性和优越性。

The authors have declared that no competing interests exist.

参考文献

View Option

[1]	Scheeres, D J. Close proximity dynamics and control about asteroids[C]∥American Control Conference(ACC), Portland , Oregon, USA, 2014: 1584-1598. [本文引用:1]
[2]	Liaw D C, Cheng C C, Liang Y W. Three-dimensional guidance law for land ing on a celestial object[J]. Journal of Guidance, Control, and Dynamics, 2000, 23(5): 890-892. [本文引用:1]
[3]	李爽, 崔平远. 着陆小行星的滑模变结构控制[J]. 宇航学报, 2005, 26(6): 808-812. Li Shuang, Cui Ping-yuan. Variable structure with sliding-mode control for land ing on asteroids[J]. Journal of Astronautics, 2005, 26(6): 808-812. [本文引用:1]
[4]	Zhang Z, Wang W, Li L, et al. Robust sliding mode guidance and control for soft land ing on small bodies[J]. Journal of the Franklin Institute, 2012, 349(2): 493-509. [本文引用:2]
[5]	Lan Q, Li S, Yang J, et al. Finite-time soft land ing on asteroids using nonsingular terminal sliding mode control[J]. Transactions of the Institute of Measurement and Control, 2013, 36(2): 216-223. [本文引用:1]
[6]	Liu K, Liu F, Wang S, et al. Finite-time spacecraft's soft land ing on asteroids using PD and nonsingular terminal sliding mode control[J]. Mathematical Problems in Engineering, 2015, 510618. [本文引用:1]
[7]	Lee D, Vukovich G. Adaptive sliding mode control for spacecraft body-fixed hovering in the proximity of an asteroid[J]. Aerospace Science and Technology, 2015, 46: 471-483. [本文引用:1]
[8]	Utkin V, Lee H. Chattering problem in sliding mode control systems[C]∥2006 International Workshop on Variable Structure Systems, Alghero, 2006: 346-350. [本文引用:1]
[9]	吕建婷, 马广富, 李传江. 卫星姿态跟踪的模糊滑模控制器设计[J]. 吉林大学学报: 工学版, 2007, 37(4): 955-958. Lyu Jian-ting, Ma Guang-fu, Li Chuan-jiang. Fuzzy sliding mode controller design for satellite attitude tracking[J]. Journal of Jilin University (Engineering and Technology Edition), 2007, 37(4): 955-958. [本文引用:1]
[10]	Furfaro R. Hovering in asteroid dynamical environments using higher-order sliding control[J]. Journal of Guidance, Control, and Dynamics, 2015, 38(2): 263-279. [本文引用:1]
[11]	Levant A. Higher-order sliding modes, differentiation and output-feedback control[J]. International Journal of Control, 2003, 76(9-10): 924-941. [本文引用:1]
[12]	Davila J, Fridman L, Levant A. Second-order sliding-mode observer for mechanical systems[J]. IEEE Transactions on Automatic Control, 2005, 50(11): 1785-1789. [本文引用:1]
[13]	Shtessel Y B, Moreno J A, Plestan F, et al. Super-twisting adaptive sliding mode control: a lyapunov design[C]∥49th IEEE Conference on Decision and Control, Atlanta, 2010: 5109-5113. [本文引用:1]
[14]	李鹏. 传统和高阶滑模控制研究及其应用[D]. 长沙: 国防科学技术大学机电工程与自动化学院, 2011. Li Peng. Research and application of traditional and higher-order sliding mode control[D]. Changsha: College of Mechatronic Engineering and Automation, National University of Defense Technology, 2011. [本文引用:1]
[15]	Utkin V I, Poznyak A S. Adaptive sliding mode control with application to super-twist algorithm: equivalent control method[J]. Automatica, 2013, 49(1): 39-47. [本文引用:1]
[16]	Scheeres D J, Williams B G, Miller J K. Evaluation of the dynamic environment of an asteroid: applications to 433 Eros[J]. Journal of Guidance Control and Dynamics, 2000, 23(3): 466-475. [本文引用:1]
[17]	吴敏, 何勇, 佘锦华. 鲁棒控制理论[M]. 北京: 高等教育出版社, 2010. [本文引用:1]
[18]	Werner R, Scheeres D. Exterior gravitation of a polyhedron derived and compared with harmonic and mascon gravitation representations of asteroid 4769 Castalia[J]. Celestial Mechanics and Dynamical Astronomy, 1997, 65(3): 313-344. [本文引用:1]
[19]	刘金琨. 滑模变结构控制 MATLAB 仿真[M]. 北京: 清华大学出版社, 2005. [本文引用:1]

2014

0.0

... 因此,传统的地面控制难以保证软着陆的安全性,探测器的自主控制成为了研究的热点^[1] ...

2000

0.0

... 由于满足上述要求,滑模算法被广泛应用在软着陆自主轨道控制中^{[2,3,4,5,6,7]} ...

2005

0.0

. 2005, 26(6):808-812 DOI:doi:10.3321/j.issn:1000-1328.2005.06.027

Variable structure with sliding-mode control for landing on asteroids

着陆小行星的滑模变结构控制

Li Shuang , Cui Ping-yuan

李爽, 崔平远

针对由于目标小行星的各种物理参数和运动信息不能精确获取而导致着陆小行星的动力学方程中存在不确定项这一问题,设计了一种基于滑模变结构的软着陆小行星的制导控制方案.在考虑安全软着陆约束条件下规划了标称着陆轨迹;通过滑模变结构控制方法设计制导控制律,实现对理想标称轨迹的鲁棒跟踪,从而保证成功着陆小行星;最后通过计算机仿真验证了方案的可行性.

... 由于满足上述要求,滑模算法被广泛应用在软着陆自主轨道控制中^{[2,3,4,5,6,7]} ...

2012

0.0

... 由于满足上述要求,滑模算法被广泛应用在软着陆自主轨道控制中^{[2,3,4,5,6,7]} ...

... 根据已知的探测器初始位置 r0、初始速度 r·0、着陆点位置 rf和着陆时间 tf,基于多项式制导法^[4]设计软着陆标称轨道为: ...

2013

0.0

... 由于满足上述要求,滑模算法被广泛应用在软着陆自主轨道控制中^{[2,3,4,5,6,7]} ...

2015

0.0

... 由于满足上述要求,滑模算法被广泛应用在软着陆自主轨道控制中^{[2,3,4,5,6,7]} ...

2015

0.0

... 由于满足上述要求,滑模算法被广泛应用在软着陆自主轨道控制中^{[2,3,4,5,6,7]} ...

2006

0.0

... 然而,传统一阶滑模算法存在抖振问题^[8,9],不仅难以工程实现,而且可能威胁软着陆的安全性 ...

2007

0.0

. 2007, 37(4):955-958 DOI:doi:10.3969/j.issn.1671-5497.2007.04.046

Fuzzy sliding mode controller design for satellite attitude tracking

卫星姿态跟踪的模糊滑模控制器设计

Lyu Jian-ting , Ma Guang-fu , Li Chuan-jiang

吕建婷, 马广富, 李传江

针对刚体卫星的姿态跟踪问题,提出了一种模糊滑模变结构控制器设计方法.首先根据由误差四元数和误差角速度描述的跟踪误差动力学和运动学方程,设计了基于李亚普诺夫方法的滑模变结构控制律.为克服滑模控制中存在的固有的抖振问题,采用模糊控制方法设计了切换控制项.最后对卫星姿态跟踪控制系统进行了仿真研究.结果表明,在参数不确定性及外干扰存在时,所设计的控制方案在实现姿态跟踪控制的同时,对于卫星转动惯量的摄动及外部扰动力矩是鲁棒的.

... 然而,传统一阶滑模算法存在抖振问题^[8,9],不仅难以工程实现,而且可能威胁软着陆的安全性 ...

2015

0.0

... Furfaro等^[10]提出一种基于齐次高阶滑模算法的软着陆制导律,但该制导律用轨道误差作为滑模函数,算法的滑动阶数与滑模的相对阶数相同,难以确保对抖振的有效抑制 ...

2003

0.0

... 超螺旋(Super-twisting)算法^[11]是一类结构简单的高阶滑模算法,能有效抑制抖振问题,且仅需要系统的一阶滑模信息 ...

2005

0.0

... 然而,设计超螺旋算法的参数需要已知外界扰动时间导数的上界^[12],限制了其在实际系统中的应用 ...

2010

0.0

... Shtessel等^[13]提出了一种自适应超螺旋算法,但需要外界扰动满足特定的假设条件 ...

2011

0.0

. 2011, :- DOI:doi:10.7666/d.d160024

Research and application of traditional and higher-order sliding mode control

传统和高阶滑模控制研究及其应用

Li Peng

李鹏

不确定性条件下的控制问题是现代控制中的一个重要课题,因为在任何控制问题中,实际的控制对象和用于控制器设计的数学模型总是存在差异,这种差异主要来自于外界干扰、未知的对象参数和未建模动态。作为现代控制理论的一个重要分支,滑模控制以实现简单以及系统处于滑动模态时对满足匹配条件的外界干扰、模型的不确定性和未建模动态具有不变性而著称,且已成功应用于机器人、航空航天等领域。论文研究了传统滑模和高阶滑模控制问题,并将部分研究成果应用于机器人和飞行器的控制中。主要研究内容和创新点如下: (1)研究了传统滑模控制中采用Slotine形式的滑模面和积分滑模面,利用边界层和幂次趋近律来抑制抖振时,系统的稳态跟踪误差界问题。利用有界输入有界输出(BIBO)稳定的方法,推导出了比现有文献的结果更为精确的稳态跟踪误差界。进一步,通过给定的稳态跟踪误差要求,可以设计合适的边界层厚度或幂次趋近律参数,不用通过仿真实验来试凑。最后,所得到的结果应用到n关节机械臂的跟踪控制中。 (2)为了减小稳态跟踪误差,不少学者将积分项引入到滑模面的设计中。然而,在大的初始误差条件下,积分会出现累积效应(Windup),引起大的超调和执行器饱和,甚至导致系统不稳定。因此,提出了一类具有“小误差放大,大误差饱和”功能的光滑非线性饱和函数以改进传统积分滑模控制,在保持传统积分滑模控制跟踪精度的同时获得更好的暂态性能。应用Lyapunov稳定性理论和LaSalle不变性原理证明了对常值或最终常值干扰可以完全抑制。并在此基础上提出了全程非线性积分滑模控制方法,消除了滑模的到达阶段,具有全程鲁棒性。 (3)基于非光滑的类二次型Lyapunov函数,对二阶滑模Super-Twisting算法的有限时间收敛性进行了分析。系统受常值干扰时,通过Lyapunov方程证明了该算法有限时间收敛,并给出了收敛时间的最优估计;系统受时变干扰时,通过求解代数Riccati方程得出了一组保证该算法有限时间收敛的参数取值范围,并给出了收敛时间的估计值。同时,在此基础上提出自适应Super-Twisting算法,该算法不需要知道不确定性变化率的界。 (4)证明了幂次趋近律本质上是二阶滑模,且趋近过程品质较好,但鲁棒性差。因此,设计了非齐次干扰观测器和快速幂次趋近律相结合的二阶滑模算法,这种二阶滑模算法适用于相对阶为1的系统。经与Shtessel在Automatica上提出的光滑二阶滑模算法进行比较,本算法具有更好的暂态性能。将该算法应用于一类无尾飞行器的姿态控制中,仿真结果表明了该算法的有效性。 (5)利用有限时间控制技术中的齐次理论,并结合自适应控制思想,提出了一种鲁棒自适应二阶滑模控制方法,不需要知道系统不确定性的界。并设计了一类新的非线性函数替代齐次系统中的幂函数,克服了齐次系统在状态远离平衡点时收敛速度慢的缺陷,系统的状态能快速有限时间收敛。该算法形式简单,控制律的设计只需要系统的相对阶信息,并将其应用于Nubot全向移动机器人的轨迹跟踪控制中。 (6)基于齐次理论和有限时间快速收敛Lyapunov函数,提出了鲁棒自适应任意阶滑模控制方法。将SISO系统的r阶滑模控制问题转化为受扰动的r重积分链的有限时间镇定问题,依据第七章的思路,将控制律的设计分成两个部分:名义控制部分和补偿控制部分。名义控制部分分别采用齐次理论和快速有限时间Lyapunov稳定性理论进行设计,补偿控制部分采用自适应一阶滑模方法,综合得到了鲁棒自适应任意阶滑模控制律,并应用于轮式移动机器人的控制中。

... 李鹏^[14]提出了一种仅需要扰动时间导数有界的自适应超螺旋算法 ...

2013

0.0

... Utkin等^[15]基于一阶滤波器实现了对超螺旋算法参数的自适应估计 ...

2000

0.0

... Vn(r)为小行星引力势函数的名义模型,用 n阶球谐系数法^[16]表示为: ...

2010

0.0

... 根据Shur补^[17]的性质可知, Qi正定的条件为: ...

1997

0.0

... 670 g/cm³,用多面体法^[18]建立Eros433的引力场模型作为其真实引力场 V(r) ...

2005

0.0

... 设计自适应滑模控制(ASMC)^[19]如式(35)所示,将其与本文设计的自适应超螺旋算法(AGSTC)分别仿真进行对比分析 ...