大部件喷涂中的移动机械臂站位规划

引用本文

任书楠, 杨向东, 王国磊, 刘志, 陈恳. 大部件喷涂中的移动机械臂站位规划. 吉林大学学报:工学版, 2016, 46(6): 1995-2002
REN Shu-nan, YANG Xiang-dong, WANG Guo-lei, LIU Zhi, CHEN Ken. Base position planning of mobile manipulator for large parts painting. Journal of Jilin University Engineering and Technology Edition, 2016, 46(6): 1995-2002 复制到剪切板

Doi:10.13229/j.cnki.jdxbgxb201606032
Permissions

大部件喷涂中的移动机械臂站位规划

任书楠^1,^2,³, 杨向东^1,^2,³, 王国磊^1,^2,³, 刘志^1,^2,³, 陈恳^1,^2,³

1.清华大学机械工程系,北京 100084

2.清华大学精密超精密制造装备及控制北京市重点实验室, 北京 100084

3.清华大学摩擦学国家重点实验室, 北京 100084

作者简介:任书楠(1988-),男,博士研究生.研究方向:喷涂机器人运动规划.E-mail:renshunan@gmail.com

基金项目:国家自然科学基金项目(61403226); 摩擦学国家重点实验室项目(SKLT09A03)

摘要

由于机械臂的后三个关节具有极大的灵活度,且其运动对腕心的位置没有影响,因此以腕心为假想基座,采用D-H方法对机械臂进行重新建模,于是机械臂基座成为姿态固定的名义末端执行器。由名义末端执行器的可达位置的集合构成机械臂实际基座可行位置空间。在喷涂作业过程中,基座可行位置空间随腕心位置移动。通过对基座可行位置空间的交集进行分析,即可确定机械臂在实施区域喷涂作业时的可行站位区域。仿真试验结果表明:与固定规则站位生成方法相比,通过引入基座可行位置空间的概念能够快速确定机械臂站位的可选区域,扩大单次停站作业范围。

关键词: 机械制造自动化; 站位规划; 基座可行位置空间; 可移动机械臂; 喷涂机器人; 移动平台

中图分类号:TP24 文献标志码:A 文章编号:1671-5497(2016)06-1995-08

Base position planning of mobile manipulator for large parts painting

REN Shu-nan^1,^2,³, YANG Xiang-dong^1,^2,³, WANG Guo-lei^1,^2,³, LIU Zhi^1,^2,³, CHEN Ken^1,^2,³

1.Department of Mechanical Engineering, Tsinghua University, Beijing 100084, China

2.Beijing Key Laboratory of Precision/Ultra-precision Manufacturing Equipments and Control, Tsinghua University, Beijing 100084, China

3.State Key Laboratory of Tribology,Tsinghua University,Beijing 100084, China

Abstract

Considering that the last three wrist joints of a manipulator are highly dexterous and hove no influence on the position of the writ center point when moving, a mathematical model of the manipulator is reconstructed with origin at the wrist center point. Thus, the base of the manipulator becomes the nominal end effector with fixed orientation. All possible locations of the new end effector can be viewed as the Base's Workable Location Space (BWLS). The BWLS moves along with the wrist center point during the painting task. Through analysis of the intersection set of the BWLSs, the feasible base position area of the manipulator is established. Motion simulations on painting plane and curved surfaces referred to the concept of BWLS are performed. The results show the optional base position area of the manipulator can be quickly obtained and the once stop painting area is extended compared to the fixed rules.

Key words: mechanical manufacturing and automation; base position planning; base's workable location space; mobile manipulator; painting robot; mobile platform

Show Figures

0 引言

在进行大部件外表面的喷涂作业时, 为了最大限度地保证动态精度, 降低规划难度, 其工作模式是通过移动平台搭载工业机械臂到达指定站位, 移动平台锁止后由工业机械臂单独完成局部区域的作业任务, 单次停站作业区域由规划人员按照工艺需求提前划分完成。间歇式工作模式对工业机械臂的站位规划提出了较高的要求, 需要针对每一块作业区域选择合适的站位, 使得机械臂各关节在喷涂过程中不超限。

在实际操作中发现, 仅凭操作工人的个人经验, 或是与喷涂曲面外形无关的固定规则, 比如目前所采用的将喷涂区域中心点沿法向移动若干距离作为站位, 单次停站作业区域较小, 且随着曲面复杂程度增加, 规划难度也相应增加, 规划效率大大降低。

在早期的研究中, 研究者大多关注于单一工业机械臂应用于喷涂作业的研究, 并分别在喷枪模型^[1]、工艺参数^{[2, 3]}、涂层分布模型^[4]、喷涂轨迹规划^{[5, 6]}、喷涂表面几何特性^[7]以及工业机械臂动态性能^[8]等方面取得较为详尽的研究成果, 对于可移动机械臂的研究较少。相关的研究也由于其搬运和装配的应用背景, 大多关注于移动平台与工业机械臂的联动控制^{[9, 10]}, 着重研究点到点的位置精度控制, 忽视了对于多站位喷涂质量和效率等至关重要的机械臂停站的控制。

为了解决工程应用中站位规划困难以及规划区域较小的问题, 本文根据机械臂运动学的相关理论, 针对一套由三自由度数控移动平台搭载ABB IRB5500型工业机械臂构成的大型部件喷涂系统, 提出了一种新的建模思路, 解析化地描述腕心处于某一位置时基座的可行位置空间, 并以此为基础来确定执行某一区域加工作业时机械臂基座的可行停站位置。

1 基座端可行位置空间的建立

目前, 工业机械臂的运动学建模方法大多以1955年Denavit和Hartenberg提出的D-H方法^[11]为基础, 但对于可移动机械臂, 这种方法却不十分适用。根据作业要求, 机械臂末端在经过目标点时同时保持指定的姿态, 这样6个自由度的位姿状态很难在三维工作空间得到表达, 也就难以对机械臂基座停站位置进行准确估计。

由于机械臂手臂关节决定腕心的位置, 而腕关节具有相当大的灵活度, 认为其可以实现末端执行器的方向变换。在喷涂过程中, 腕心位置可以由轨迹点坐标及其法向以及固定的喷枪工具几何参数计算获得。这样, 在求取腕心位置以后, 即可根据机械臂几何构型获得机械臂基座可能的空间位置而不必考虑此时喷枪的朝向, 实现对站位规划问题的降维。

1.1 机械臂腕心的定义

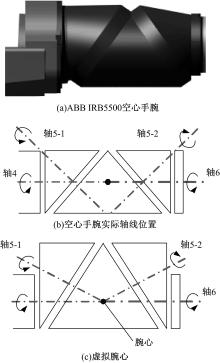
根据机器人学理论, 对于具有球型手腕的机械臂, 后三个关节轴线相交于一点, 此点被定义为机械臂的腕心。对于具有空心非球型手腕的机械臂, 如ABB IRB5500型机械臂, 其后三个关节轴线并非时刻相交于一点。为解决这个问题, 本课题组在之前的研究中提出了虚拟腕心的概念^[12], 即仍假设腕关节轴线交于一点, 并以此点作为机械臂的腕心, 如图1所示。相对于机械臂的工作空间, 腕心位置偏差足够小以至于可以忽略。

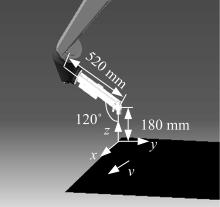
	Figure Option View Download New Window
	图1 腕心定义Fig.1 Definition of wrist center point

根据腕心的定义, 可以根据如图2所示的工艺距离参数和机械臂末端喷枪结构参数, 由喷涂轨迹上的一点及其法向计算得出机械臂腕心的位置。

	Figure Option View Download New Window
	图2 腕心位置的计算方法Fig.2 Position of wrist center point

1.2 基座端运动方程的建立

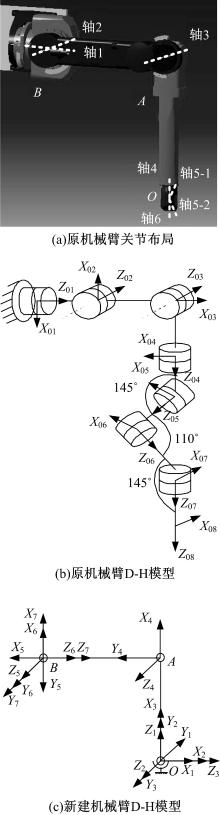
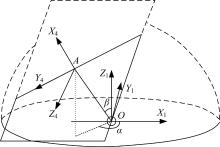
图3(a)(b)为ABB IRB5500型喷涂机械臂关节布局及D-H模型。根据如表1所示的ABB IRB5500型工业机械臂的D-H参数, 本文提出将基础坐标系设定在工业机械臂的腕心O点处, 将机械臂的基座看作末端执行器, 通过在腕心处虚拟三自由度球关节来表示原机械臂中运动范围很大的三个腕关节, 按照如下所述的D-H模型建立方法为各连杆建立坐标系:

(1)对连杆进行编号, 从基础连杆起依次记为连杆0, 1, …, n;

(2)连杆i-1和连杆i的连接运动副记为第i个关节;

(3)记第i个关节的轴线为Z_i;

(4)将Z_i-₁和Z_i的公垂线记作X_i;

(5)Y_i根据右手定则由X_i和Z_i得出。

	Figure Option View Download New Window
	图3 原机械臂和新建机械臂D-H模型Fig.3 D-H models of original and new manipulators

图3(c)为按照上述方法建立的各连杆坐标系示意图, 记各个坐标系分别为F₁、F₂、F₃、F₄、F₅、F₆, 其中点O为基础坐标系原点, 对应于原机械臂的腕心, OA连杆对应于原机械臂的小臂, AB连杆对应于原机械臂的的大臂, 所提取出的D-H参数如表2所示。

表1 ABB IRB5500型工业机械臂的D-H参数 Table 1 D-H parameters of ABB IRB5500

表2 新建关节构型的D-H参数 Table 2 D-H parameters of new configuration

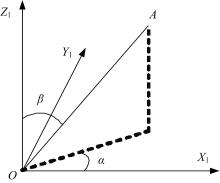
	Figure Option View Download New Window
	图4 连杆OA的位姿描述Fig.4 Descriptions of position and orientation of link OA

为了描述和计算方便, 本文中采用球坐标描述连杆OA的位姿, 如图4所示。图4中, α 为连杆OA在X₁OY₁平面的投影与X₁轴的夹角; β 为连杆OA与Z₁轴的夹角。则OA杆末端A的位置可以表示为:

$\begin{matrix} P_{A} = [\begin{matrix} _{}^{1} x_{A} \\ _{}^{1} y_{A} \\ _{}^{1} z_{A} \end{matrix}] = [\begin{matrix} a_{3} cosαsinβ \\ a_{3} sinαsinβ \\ cosβ \end{matrix}] \end{matrix}$ (1)

同时, 在F₄标架下, 连杆AB末端点B(即原机械臂的基座)可以表示为:

$\begin{matrix} _{}^{4} P_{B} = [\begin{matrix} _{}^{4} x_{B} \\ _{}^{4} y_{B} \\ _{}^{4} z_{B} \end{matrix}] = [\begin{matrix} a_{4} \cos θ_{4} \\ a_{4} \sin θ_{4} \\ 0 \end{matrix}] \end{matrix}$ (2)

现在考虑将 $\begin{matrix} _{}^{4} \end{matrix}$ P_B变换到F₁标架下。在原机械臂实际运动过程中, 基座的位置会随着移动平台做三自由度直线运动, 故姿态一直保持不变。这样, 当连杆OA绕O点在空间内旋转时, 为保证新建机械臂末端能够保持原有的姿态, 就要求Z₄轴线始终与Y₁OZ₁面保持平行, 如图5所示。此时X₄和Z₄在F₁标架下的方向表达分别为:

$\begin{matrix} \begin{matrix} X_{4} = [\begin{matrix} cosαsinβ \\ sinαsinβ \\ cosβ \end{matrix}] (3) \\ Z_{4} = [\begin{matrix} 0 \\ - \frac{cosβ}{\sqrt[]{co s^{2} β + si n^{2} βsi n^{2} α}} \\ \frac{sinαsinβ}{\sqrt[]{co s^{2} β + si n^{2} βsi n^{2} α}} \end{matrix}] (4) \end{matrix} \end{matrix}$

于是, 标架F₄到标架F₁的旋转矩阵可以写为:

$\begin{matrix} R = [\begin{matrix} cosαsinβ & - \sqrt[]{1 - co s^{2} αsi n^{2} β} & 0 \\ sinαsinβ & - \frac{sinαcosαsi n^{2} β}{F} & - \frac{cosβ}{F} \\ cosβ & \frac{cosαsinβcosβ}{F} & \frac{sinαsinβ}{F} \end{matrix}] \end{matrix}$ (5)

式中:F= $\begin{matrix} \sqrt[]{co s^{2} β + si n^{2} αsi n^{2} β} \end{matrix}$ 。

由于关节5和6的旋转不影响B点在F₄标架下的位置, 所以B点在标架F₁下的位置可以用前4个关节变量表达为:

$\begin{matrix} Φ_{1} (q) = [\begin{matrix} _{}^{1} x_{B} \\ _{}^{1} y_{B} \\ _{}^{1} z_{B} \end{matrix}] = R [\begin{matrix} a_{4} \cos θ_{4} \\ a_{4} \sin θ_{4} \\ 0 \end{matrix}] + [\begin{matrix} _{}^{1} x_{A} \\ _{}^{1} y_{A} \\ _{}^{1} z_{A} \end{matrix}] \end{matrix}$ (6)

式中:Φ ₁(q)中的自变量α 、β 、θ ₄分别表示为q₁、q₂和q₃, 并且为满足θ ₆∈ [-1.65, 1.65], 令β ∈ [0, $\begin{matrix} \frac{π}{2} \end{matrix}$ ], 其他变量α ∈ (0, 2π ), θ ₄∈ [ $\begin{matrix} \frac{π}{2} \end{matrix}$ - $\begin{matrix} \frac{70 π}{180} \end{matrix}$ , $\begin{matrix} \frac{π}{2} \end{matrix}$ + $\begin{matrix} \frac{70 π}{180} \end{matrix}$ ]。

特别地, 当α =0或α =π , 且β =π /2时, 轴4的轴线方向Z₄可以指向Y₁OZ₁平面内的任意方向, 则B点的位置表达需要修正为式(7)或式(8)的形式:

$\begin{matrix} \begin{matrix} Φ_{2} (q) = {[\begin{matrix} _{}^{1} x_{B} & _{}^{1} y_{B} & _{}^{1} z_{B} \end{matrix}]}^{T} = \\ [\begin{matrix} 1 & 0 & 0 \\ 0 & - sinφ & - cosφ \\ 0 & cosφ & - sinφ \end{matrix}] [\begin{matrix} a_{4} \cos θ_{4} \\ a_{4} \sin θ_{4} \\ 0 \end{matrix}] + [\begin{matrix} _{}^{1} x_{A} \\ _{}^{1} y_{A} \\ _{}^{1} z_{A} \end{matrix}] (7) \\ Φ_{3} (q) = {[\begin{matrix} _{}^{1} x_{B} & _{}^{1} y_{B} & _{}^{1} z_{B} \end{matrix}]}^{T} = \\ [\begin{matrix} - 1 & 0 & 0 \\ 0 & sinφ & - cosφ \\ 0 & - cosφ & - sinφ \end{matrix}] [\begin{matrix} a_{4} \cos θ_{4} \\ a_{4} \sin θ_{4} \\ 0 \end{matrix}] + [\begin{matrix} _{}^{1} x_{A} \\ _{}^{1} y_{A} \\ _{}^{1} z_{A} \end{matrix}] (8) \end{matrix} \end{matrix}$

式中:φ 为轴4的轴线方向Z₄在Y₁OZ₁平面内的旋转角度, 且φ ∈ [-π /2, π /2]。

	Figure Option View Download New Window
	图5 连杆OA姿态的约束条件Fig.5 Orientation constraint of link OA

1.3 基座端可行位置空间的建立

通过式(6)(7)(8)可以获得B点(原机械臂基座)在标架F₁处的位置表达。下面确定B点可行位置空间的边界面。

首先求取Φ ₁(q)的雅克比矩阵:

$\begin{matrix} Φ_{q} = [\frac{\partial Φ_{i}}{\partial q_{j}}] \end{matrix}$ (9)

同时, 为了使关节角的不等式约束成为等式约束, 令:

$\begin{matrix} \begin{matrix} q = Ψ (λ) = [\begin{matrix} π + πsin λ_{1} \\ \frac{π}{4} + \frac{π}{4} \sin λ_{2} \\ \frac{π}{2} + 1.22 \sin λ_{3} \end{matrix}] (10) \\ 则有 : \\ Ψ_{λ} = [\begin{matrix} πcos λ_{1} & 0 & 0 \\ 0 & \frac{π}{4} \cos λ_{2} & 0 \\ 0 & 0 & 1.22 \cos λ_{3} \end{matrix}] (11) \end{matrix} \end{matrix}$

构建矩阵G^*, 并令:

$\begin{matrix} G^{*} = [\begin{matrix} - Φ_{q} & 0 \\ I & Ψ_{λ} \end{matrix}] \end{matrix}$ (12)

则当G^*为行秩亏矩阵时, 机械臂构型为奇异状态^[13]。解得当β =0时, $\begin{matrix} |Φ_{q}| \end{matrix}$ =0, 另当各关节变量取到极限时, $\begin{matrix} |G^{*}| \end{matrix}$ =0, 即获取对应的6个奇异解集为:

s¹={Φ ₁|α =0},

s²={Φ ₁|α =π },

s³={Φ ₁|β =0},

s⁴={Φ ₁|β = $\begin{matrix} \frac{π}{2} \end{matrix}$ },

s⁵={Φ ₁|θ ₄= $\begin{matrix} \frac{π}{2} \end{matrix}$ - $\begin{matrix} \frac{70 π}{180} \end{matrix}$ },

s⁶={Φ ₁|θ ₄= $\begin{matrix} \frac{π}{2} \end{matrix}$ + $\begin{matrix} \frac{70 π}{180} \end{matrix}$ }。

同时, 当α =0且β =π /2, 以及α =π 且β =π /2时, 可以分别获取另外两个边界表达形式:

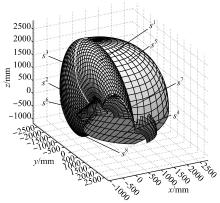
$\begin{matrix} \begin{matrix} s^{7} = {Φ_{2} | φ \in [- \frac{π}{2}, \frac{π}{2}], θ_{4} \in [\frac{π}{2} - \\ \frac{70 π}{180}, \frac{π}{2} + \frac{70 π}{180}]} \\ s^{8} = {Φ_{3} | φ \in [- \frac{π}{2}, \frac{π}{2}], θ_{4} \in [\frac{π}{2} - \\ \frac{70 π}{180}, \frac{π}{2} + \frac{70 π}{180}]} \end{matrix} \end{matrix}$

s¹~s⁶所对应的边界曲面剖视图如图6所示。

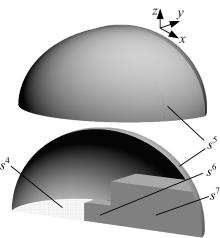
	Figure Option View Download New Window
	图6 基座可行位置空间的边界面Fig.6 Boundary surface of BWLS

下面对基座可行位置空间的边界曲面进行简化处理。因为在基座的可行位置空间内, α 在0、π 、2π 处, 以及β 在0点处是连续变化的, 故仅考虑s⁴、s⁵、s⁶、s⁷、s⁸, 又考虑实际喷涂过程中, 基座一般位于腕心所在的水平面之上, 故又忽略掉s⁸。则最终的可行位置空间边界由s⁴、s⁵、s⁶、s⁷组成。

s⁴曲面为平面:

$\begin{matrix} z = 0 (13) \end{matrix}$

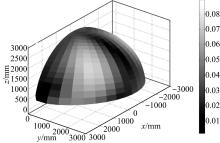
通过观察s⁵曲面的特点, 考虑采用两个关于xoz平面对称的椭球面拟合, 由于原始边界曲面存在绕z轴的旋转, 故在拟合方程中添加了绕z轴的旋转项。得到如式(14)所示的拟合结果。拟合误差分布如图7所示, 其中各点的颜色表示该位置处误差与拟合椭球半径的比值, 该比值均小于0.1。

$\begin{matrix} \{\begin{matrix} {(xcos 0.6363 - ysin 0.6363 + 48.7)}^{2} / 3123^{2} + \\ {(ycos 0.6363 + xsin 0.6363 - 74.2)}^{2} / \\ 2371 . 6^{2} + z^{2} / 2817 . 2^{2} = 1, y > 0 \\ {(xcos 0.6363 + ysin 0.6363 + 48.7)}^{2} / 3123^{2} + \\ {(ycos 0.6363 - xsin 0.6363 + 74.2)}^{2} / \\ 2371 . 6^{2} + z^{2} / 2817 . 2^{2} = 1, y < 0 \end{matrix} \end{matrix}$ (14)

	Figure Option View Download New Window
	图7 基座可行空间外边界曲面的拟合误差分布Fig.7 Fitting error distribution of outer boundary of BWLS

由于s⁶形状不规则, 采用包围盒代替, 表达形式为:

$\begin{matrix} \begin{matrix} {s | x \in [- 570, 320], y \in [- 560, 560], \\ z \in [0, 570]) \end{matrix} \end{matrix}$ (15)

s⁷曲面是一标准球面, 其表达方程为:

$\begin{matrix} {(x - 1578)}^{2} + y^{2} + z^{2} = 1300^{2} \end{matrix}$ (16)

为了在进行后面计算时比较方便, 采用包围盒来代替s⁷曲面, 表达形式为:

$\begin{matrix} \begin{matrix} {s | x \in [278, 2878], y \in [- 1300, 1300], \\ z \in [0, 1300]} (17) \end{matrix} \end{matrix}$

对s⁴、s⁵、s⁶、s⁷的最终简化结果如图8所示。

	Figure Option View Download New Window
	图8 边界曲面的简化结果Fig.8 Simplified boundaries of BWLS

2 单次停站作业区域站位选取方法

对于大部件外表面的喷涂作业, 由于不能实现一次性全覆盖, 需由规划人员提前根据工艺要求将待喷涂表面划分成若干小区域, 再由可移动喷涂机械臂逐次完成各局部区域的喷涂作业。在这个过程中, 移动机械臂的站位选择尤为重要。现有系统中采用的站位生成依赖于固定规则, 具体为:①求取局部曲面中心; ②获取中心点的位置和法向; ③以中心点为起点, 沿法向平移2000 mm作为停站位置。

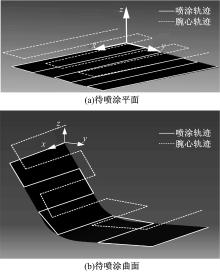
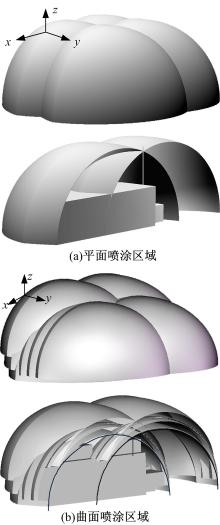
在应用中, 这种固定规则的站位计算方法存在诸多不足, 如喷涂区域较小、失败率高、规划人员需要手动多次调整站位等, 亟待改进。在获得基座可行位置空间的简化结果以后, 本节通过仿真试验来验证采用求取基座可行位置空间交集的方法选取站位时的效果, 并与现有固定规则站位生成方法进行比较。图9为待喷涂的平面和曲面。图10为可行位置空间交集求取结果。

平面x向和y向的长度分别为1980 mm和1750 mm, 曲面x向的长度为2370 mm, 另一边界路径长度为3300 mm。依据喷涂工艺的要求, 设计喷涂轨迹如图中白色实线所示。根据1.1节中的介绍, 可以求出喷涂轨迹所对应的腕心轨迹, 如图中白色虚线所示。将图9中的基座可行位置空间原点分别平移至腕心轨迹点处, 那么这些基座可行空间的交集即可认为是机械臂站位的可选区域。同时为降低操作复杂度, 可根据待喷涂曲面的特点选择特定的腕心位置进行求交运算。例如对于平面喷涂, 可仅选定外围的4个角点进行计算, 而对于曲面喷涂, 可选定腕心轨迹中的拐点进行计算。

	Figure Option View Download New Window
	图9 待喷涂平面和曲面Fig.9 Plane and curved surface to be painted

	Figure Option View Download New Window
	图10 可行位置空间的交集Fig.10 Intersection set of BWLSes

在三维建模软件中查看求交运算结果, 如图10所示。

为了使规划站位远离基座可行位置空间的边界, 即机械臂奇异位置, 选取交集的中线, 如图10中标识线段所示, 可以得到其位置和长度分别为:

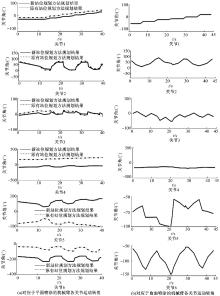
$\begin{matrix} \begin{matrix} \{\begin{matrix} x = 775 \\ y = 1342, z \in [1740, 2934] \end{matrix} (18) \\ \{\begin{matrix} x = 776 \\ y = 2128, z \in [433, 1275] \end{matrix} (19) \end{matrix} \end{matrix}$

再选取两线段的中点p₁=[775, 1342, 2337]^T和p₂=[776, 2128, 854]^T作为机械臂基座在喷涂平面和曲面的规划停站位置, 代入末端喷涂轨迹点位姿, 并利用之前提出的机械臂逆运动学求解方法^[12]对喷涂过程中机械臂各关节进行运动仿真分析, 结果如图11所示。

从图11可以看出:对于平面喷涂, 两种计算方法得出的站位位置均可以满足机械臂喷涂要求, 其在执行喷涂任务时的各关节转角如图11(a)所示。

	Figure Option View Download New Window
	图11 仿真结果Fig.11 Simulation results

可以看出, 机械臂位于两个站位下的关节轨迹相似, 关节1和关节3的旋转幅度在采用本文方法时略小。对于曲面喷涂, 系统固定规则得出的站位位置不能满足机械臂喷涂要求, 在喷涂过程中关节角度超出限制, 在机械臂位于采用基座可行位置空间得出的站位时, 其各关节转角如图11(b)所示。其中, 机械臂关节3接近于下限位, 说明本文方法较大限度地利用了机械臂的操作空间, 扩大了单次停站的喷涂范围。

3 结束语

针对可移动工业机械臂在执行大尺寸零部件加工中不易确定基座位置的问题, 提出了一种从分析工业机械臂基座可行位置空间出发的站位规划方法。在根据喷涂轨迹点位姿信息求出机械臂腕心位置后, 得出机械臂基座可行位置空间的解析表达式, 并通过获取基座可行位置空间的交集, 确定了机械臂的停站位置。在仿真试验中, 选取实际喷涂中应用较多的平面和曲面区域作为试验对象。试验结果表明, 本文提出的站位规划方法相较于固定规则站位生成方法, 可以优化喷涂过程中机械臂关节性能, 同时扩展单次停站可喷涂区域的范围, 验证了该方法的可行性和有效性。由于该方法的实现与喷涂区域的形状无关, 故在实际应用中具有较强的通用性和可靠性。

The authors have declared that no competing interests exist.

参考文献

View Option

[1]	潘玉龙, 王国磊, 朱丽, 等. 管道喷涂机器人喷枪运动速度优化[J]. 清华大学学报: 自然科学版, 2014, 54(2): 212-216. Pan Yu-long, Wang Guo-lei, Zhu Li, et al. Optimization of spray gun speed for pipe painting robots[J]. Journal of Tsinghua University(Science and Technology), 2014, 54(2): 212-216. [本文引用:1]
[2]	Arikan M A S, Balkan T. Modeling of paint flow rate flux for circular paint sprays by using experimental paint thickness distribution[J]. Mechanics Research Communications, 1999, 26(5): 609-617. [本文引用:1]
[3]	From P J, Gunnar J, Gravdahl J T. Optimal paint gun orientation in spray paint applications-experimental results[J]. IEEE Transactions on Automation Science and Engineering, 2011, 8(2): 438-442. [本文引用:1]
[4]	王国磊, 陈恳, 陈雁, 等. 变参数下的空气喷枪涂层厚度分布建模[J]. 吉林大学学报: 工学版, 2012, 42(1): 188-192. Wang Guo-lei, Chen Ken, Chen Yan, et al. Filmthickness distribution model with variable parameters for air spray gun[J]. Journal of Jilin University(Engineering and Technology Edition), 2012, 42(1): 188-192. [本文引用:1]
[5]	Chen He-ping, Xi Ning. Automated robot tool trajectory connection for spray forming process[J]. Journal of Manufacturing Science and Engineering, 2012, 134(2): 021017. [本文引用:1]
[6]	Sheng Wei-hua, Chen He-ping, Xi Ning, et al. Optimal tool path planning for compound surfaces in spray forming processes[C]∥2004 IEEE International Conference on Robotics and Automation, New Orleans, LA, USA, 2004: 45-50. [本文引用:1]
[7]	Atkar P N, Greenfield A, Conner D C, et al. Uniform coverage of automotive surface patches[J]. The International Journal of Robotics Research, 2005, 24(11): 883-898. [本文引用:1]
[8]	张永贵. 喷漆机器人若干关键技术研究[D]. 西安: 西安理工大学机械与精密仪器工程学院, 2008. Zhang Yong-gui. Study on some key techniques for spraying painting robot[D]. Xi'an: School of Mechanical and Precision Instrument Engineering, Xi'an University of Technology, 2008. [本文引用:1]
[9]	Zhang Yu-nong, Li Wei-bing, Liao Bo-lin, et al. Analysis and verification of repetitive motion planning and feedback control for omnidirectional mobile manipulator robotic systems[J]. Journal of Intelligent & Robotic Systems, 2014, 75(3/4): 393-411. [本文引用:1]
[10]	Huang Q, Tanie K, Sugano S. Coordinated motion planning for a mobile manipulator considering stability and manipulation[J]. International Journal of Robotics Research, 2000, 19(8): 732-742. [本文引用:1]
[11]	Denavit J, Hartenberg R S. A kinematic notation for lower-pair mechanisms based on matrices[J]. Transaction of the ASME. Journal of Applied Mechanics, 1955, 22(2): 215-221. [本文引用:1]
[12]	Wu Liao, Yang Xiang-dong, Miao Dong-jing, et al. Inverse kinematics of a class of 7R 6-DOF robots with non-spherical wrist[C]∥2013 IEEE International Conference on Mechatronics and Automation, Takamatsu, Kagawa, Japan, 2013: 69-74. [本文引用:2]
[13]	Yeh H J. Singularity and workspace analyses of serial robot manipulators[D]. Iowa City: College of Engineering, University of Iowa, 1996. [本文引用:1]

2014

0.0

. 2014, 54(2):212-216

Optimization of spray gun speed for pipe painting robots

管道喷涂机器人喷枪运动速度优化

Pan Yu-long , Wang Guo-lei , Zhu Li

潘玉龙, 王国磊, 朱丽

为提高机器人喷涂时涂层厚度均匀性,首先根据机器人喷涂时涂层形状呈椭圆形的实际情况,选择双β分布喷枪模型对涂层厚度分布进行描述,在此基础上分析喷枪运动过程中涂层厚度累积机理。通过喷枪匀速运动条件下的圆形管道喷涂实验,研究管道内壁涂层厚度与涂料涂着效率变化规律之间的关系,提出机器人喷涂作业时喷枪运动速度优化方法,即保持喷枪运动速度与涂料涂着效率之间比值恒定。实验结果表明,该速度优化方法可有效提高涂层厚度均匀性。

... 在早期的研究中,研究者大多关注于单一工业机械臂应用于喷涂作业的研究,并分别在喷枪模型^[1]、工艺参数^[2,3]、涂层分布模型^[4]、喷涂轨迹规划^[5,6]、喷涂表面几何特性^[7]以及工业机械臂动态性能^[8]等方面取得较为详尽的研究成果,对于可移动机械臂的研究较少 ...

1999

0.0

2011

0.0

2012

0.0

. 2012, 42(1):188-192

Filmthickness distribution model with variable parameters for air spray gun

变参数下的空气喷枪涂层厚度分布建模

Wang Guo-lei , Chen Ken , Chen Yan

王国磊, 陈恳, 陈雁

摘　要：首先分析了影响空气喷枪涂层厚度及喷涂机器人作业过程中的可调和常变因素,然后利用BP神经网络方法对平板直行喷涂实验获得的实验数据加以拟合,建立以喷涂距离、喷枪移动速度、喷枪流量和测量点与喷枪轴线距离作为输入的喷枪喷涂模型。与传统模型相比,该模型用相对少量的实验数据就可以预测不同喷涂距离、喷枪移动速度和喷枪流量下的涂层厚度分布。实验数据表明,该模型准确、有效。

2012

0.0

2004

0.0

2005

0.0

2008

0.0

2014

0.0

... 相关的研究也由于其搬运和装配的应用背景,大多关注于移动平台与工业机械臂的联动控制^[9,10],着重研究点到点的位置精度控制,忽视了对于多站位喷涂质量和效率等至关重要的机械臂停站的控制 ...

2000

0.0

1955

0.0

... 1 基座端可行位置空间的建立目前,工业机械臂的运动学建模方法大多以1955年Denavit和Hartenberg提出的D-H方法^[11]为基础,但对于可移动机械臂,这种方法却不十分适用 ...

2013

0.0

... 为解决这个问题,本课题组在之前的研究中提出了虚拟腕心的概念^[12],即仍假设腕关节轴线交于一点,并以此点作为机械臂的腕心,如图1所示 ...

... 再选取两线段的中点p₁=[775,1342,2337]^T和p₂=[776,2128,854]^T作为机械臂基座在喷涂平面和曲面的规划停站位置,代入末端喷涂轨迹点位姿,并利用之前提出的机械臂逆运动学求解方法^[12]对喷涂过程中机械臂各关节进行运动仿真分析,结果如图11所示 ...

1996

0.0

... 为行秩亏矩阵时,机械臂构型为奇异状态^[13] ...