基于悬架虚拟主销运动计算的主动回正控制

引用本文

丁金全, 许男, 郭孔辉. 基于悬架虚拟主销运动计算的主动回正控制. 2017, 47(1): 21-27
DING Jin-quan, XU Nan, GUO Kong-hui. Active return control based on imaginary king-pin kinematics calculation. Journal of Jilin University Engineering and Technology Edition, 2017, 47(1): 21-27 复制到剪切板

Permissions

基于悬架虚拟主销运动计算的主动回正控制

丁金全, 许男, 郭孔辉

吉林大学汽车仿真与控制国家重点实验室,长春 130022

通讯作者:许男(1988-),男,讲师,博士.研究方向:汽车系统动力学与控制.E-mail:xu.nan0612@gmail.com

作者简介:丁金全(1985-),男,博士研究生.研究方向:汽车系统动力学与控制.E-mail:dingjqxs@163.com

基金:国家自然科学基金项目(51405185); 中国博士后科学基金项目(2015M581399).

摘要

根据多连杆悬架的运动学特点,对车轮转向过程中虚拟主销的运动学特性进行了分析。应用瞬时轴线理论,对虚拟主销的运动量进行解算,计算出主销后倾拖距的变化。提出了一种主动回正控制策略,对车辆回正过程由于虚拟主销移动及载荷转移造成的回正力矩减小量进行补偿。仿真结果表明,应用基于虚拟主销运动计算的主动回正控制可以改善车辆的回正性能。

关键词: 车辆工程; 多连杆悬架; 虚拟主销; 运动学计算; 主动回正控制

中图分类号:U461.6 文献标志码:A 文章编号:1671-5497(2017)01-0021-07

Active return control based on imaginary king-pin kinematics calculation

DING Jin-quan, XU Nan, GUO Kong-hui

State Key Laboratory of Automotive Simulation and Control, Jilin University, Changchun 130022,China

Abstract

According to the structure characteristics of multi-link suspension mechanism, the kinematics characteristics of the imaginary kingpin in steering process was analyzed. The theorem of instantaneous screw axis was employed to calculate the movement and the caster offset of the imaginary kingpin. An active return control strategy was proposed and used to compensate the reduced aligning torque caused by the movement of the imaginary kingpin and load transfer. The results show that, using the active return control strategy based on imaginary kingpin kinematics calculation, the return-to-center performance of the vehicle was improved.

Keyword: vehicle engineering; multi-link suspension; imaginary kingpin; kinematics calculation; active return control

Show Figures

0 引言

悬架主销后倾拖距与车轮转动惯量的比值对车辆力输入运动的稳定性, 起着至关重要的作用^[1]。在转向过程中, 多连杆悬架上、下控制臂确定的虚拟主销会产生运动, 造成主销后倾角/主销后倾拖距, 主销内倾角/主销内倾偏移距等悬架主销定位参数的变化, 由于内、外轮载荷转移的附加作用, 对车辆的回正性能产生重要影响^{[2, 3]}。

对独立悬架而言, 悬架的主销轴是影响车辆操纵和平顺性的重要因素^{[4, 5, 6]}。麦弗逊和双横臂悬架的主销轴基本固定不动, 而多连杆悬架的虚拟主销在转向过程中时刻发生改变, 在空间运动解算过程中, 传统的几何解算方法不再适用^[7]。

在传统的电动助力转向系统基础上, 可以实现主动回正控制, 主动回正力矩主要是根据方向盘的回正角度进行计算, 但没有考虑悬架的转向运动学特性及引起的主销移动, 载荷转移对车辆回正性能产生的影响^{[8, 9, 10]}。

本文在实际开发电动车悬架-转向系统的过程中, 根据多体动力学理论, 对在转向过程中, 多连杆悬架虚拟主销的运动学特性及悬架主销定位参数的变化进行了分析。应用瞬时轴线理论对转向过程中虚拟主销的运动量进行了计算。提出一种基于虚拟主销运动计算的主动回正控制方法, 对车辆回正过程中由于虚拟主销移动及载荷转移造成的回正力矩减小量进行补偿, 从而改善车辆的回正性能。

1 多连杆悬架运动学分析

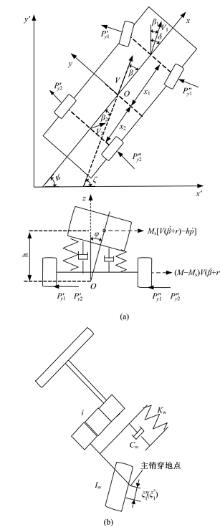
设计的多连杆独立悬架-转向系统, 如图1所示。其中:与转向器输出轴连接的左摇臂, 前端通过横拉杆与右摇臂连接; 左转向侧拉杆一端通过球铰与左摇臂相连接, 另一端通过球铰与转向节臂连接; 右转向侧拉杆一端通过球铰与右摇臂相连接, 另一端通过球铰与转向节臂连接。

	Figure Option View Download New Window
	图1 多连杆悬架-转向系统Fig.1 Steering system of multi-link suspension

在转向过程中, 车轮绕主销轴线转动, 多连杆悬架的前下控制臂、前上控制臂、后下控制臂和后上控制臂的外球头位置会发生变化, 由上、下控制臂决定的虚拟交点随之变化, 悬架-转向系统的运动学模型如图2所示。

	Figure Option View Download New Window
	图2 悬架-转向系统的运动学模型Fig.2 Kinematic model of suspension

点 $\begin{matrix} F \end{matrix}$ 表示悬架两个上控制臂向量 $\begin{matrix} u_{1} \end{matrix}$ 与 $\begin{matrix} u_{2} \end{matrix}$ 的虚拟交点; 点 $\begin{matrix} G \end{matrix}$ 表示悬架两个下控制臂向量 $\begin{matrix} u_{3} \end{matrix}$ 与 $\begin{matrix} u_{4} \end{matrix}$ 的虚拟交点; $\begin{matrix} u_{7} \end{matrix}$ 为虚拟主销向量; 点 $\begin{matrix} H \end{matrix}$ 表示转向侧拉杆向量 $\begin{matrix} u_{5} \end{matrix}$ 与转向节臂的交点。在转向过程中, 点 $\begin{matrix} F \end{matrix}$ 和 $\begin{matrix} G \end{matrix}$ 会产生移动, 造成主销后倾角/主销后倾拖距, 主销内倾角/主销内倾偏移距等悬架主销定位参数的变化。

2 虚拟主销运动计算

基于瞬时轴线理论^[11], 车轮转动过程中, 绕着虚拟主销 $\begin{matrix} u_{7} \end{matrix}$ 的运动可以分解为车轮绕虚拟主销转过角度 $\begin{matrix} φ \end{matrix}$ 和沿着虚拟主销轴线移动 $\begin{matrix} t, \end{matrix}$ 如图3所示。

	Figure Option View Download New Window
	图3 虚拟主销运动解算Fig.3 Kinematics calculation of imaginary kingpin

定义 $\begin{matrix} n \end{matrix}$ 为虚拟主销 $\begin{matrix} u_{7} \end{matrix}$ 上的单位向量, $\begin{matrix} r_{0} \end{matrix}$ 为位于虚拟主销轴线上一点的半径向量:

$n \cdot n = 1$ (1)

$n \cdot r_{0} = 0$ (2)

式中:向量 $\begin{matrix} n = n_{x} i + n_{y} j + n_{z} k, \end{matrix}$ 其中 $\begin{matrix} i 、 j \end{matrix}$ 和 $\begin{matrix} k \end{matrix}$ 为坐标系 $\begin{matrix} x - y - z \end{matrix}$ 的单位向量。

定义 $\begin{matrix} ru \end{matrix}$ 为点 $\begin{matrix} Q \end{matrix}$ 和 $\begin{matrix} P'_{i} \end{matrix}$ 之间的向量( $\begin{matrix} u \end{matrix}$ 为单位向量), 向量 $\begin{matrix} v \end{matrix}$ 垂直于向量 $\begin{matrix} n \end{matrix}$ 和 $\begin{matrix} u \end{matrix}$ :

$\begin{matrix} v = n \times u \end{matrix}$ (3)

从图3(b)可以得出:

$\begin{matrix} P' = Q + (rcosφ) u + (rsinφ) v \end{matrix}$ (4)

由于 $\begin{matrix} ru = P - Q, \end{matrix}$ 方程(3)为:

$\begin{matrix} v = n \times \frac{P - Q}{r} \end{matrix}$ (5)

由于 $\begin{matrix} n \times Q = 0 \end{matrix}$ 和 $\begin{matrix} Q = n (n \cdot P), \end{matrix}$ 方程(4)可以转化为:

$\begin{matrix} P' = n (n \cdot P) (1 - cosφ) + Pcosφ + (n \times P) sinφ \end{matrix}$ (6)

方程(6)代入向量的坐标阵和坐标方阵运算:

$\begin{matrix} \{P'\} = [cosφI + (1 - cosφ) \{n\} {\{n\}}^{T} + sinφ < n >] \{P\} \end{matrix}$ (7)

式中: $\begin{matrix} \{P'\} \end{matrix}$ 为向量 $\begin{matrix} P' \end{matrix}$ 的坐标阵; $\begin{matrix} \{P\} \end{matrix}$ 为向量 $\begin{matrix} P \end{matrix}$ 的坐标阵; $\begin{matrix} \{n\} \end{matrix}$ 为向量 $\begin{matrix} n \end{matrix}$ 的坐标阵, $\begin{matrix} \{n\} = {[\begin{matrix} n_{x} & n_{y} & n_{z} \end{matrix}]}^{T}; < n > \end{matrix}$ 为向量 $\begin{matrix} n \end{matrix}$ 的坐标方阵, $\begin{matrix} < n > = [\begin{matrix} 0 & - n_{z} & n_{y} \\ n_{z} & 0 & - n_{x} \\ - n_{y} & n_{x} & 0 \end{matrix}]; \{n \times P\} = < n > \{P\}; \{n (n \cdot P)\} = \{n\} {\{n\}}^{T} \{P\} 。 \end{matrix}$

瞬时旋转矩阵 $\begin{matrix} R \end{matrix}$ 为:

$\begin{matrix} R = cosφI + (1 - cosφ) \{n\} {\{n\}}^{T} + sinφ < n > \end{matrix}$ (8)

式中: $\begin{matrix} I \end{matrix}$ 为单位矩阵。

轮胎由点 $\begin{matrix} P_{i} 运动到 P_{i + 1}, \end{matrix}$ 相应向量的运动方程为:

$\begin{matrix} {P_{i + 1} - r_{0}} = R {P_{i} - r_{0}} + t {n} \end{matrix}$ (9)

式中:P_i+1 和P_i 分别为点P_i 和P_i+1对应的向量, {P_i+1-r₀}为向量P_i+1-r₀ 的坐标阵; {P_i-r₀}为向量P_i-r₀的坐标阵。

对方程(8)左、右两边分别进行矩阵对角求和运算, 可得:

$tr (R) = cosφtr (I) + (1 - cosφ) tr ({n} {n}^{T}) + sinφtr (< n >) = 1 + 2 cosφ$ (10)

$φ = co s^{- 1} ((tr (R) - 1) / 2)$ (11)

式中: $\begin{matrix} tr (< n > = 0), tr ({n} {n}^{T}) = 1 。 \end{matrix}$

对方程(8)左、右两边进行矩阵转置运算, 可得:

$\begin{matrix} R^{T} = cosφI + (1 - cosφ) ({n} {n}^{T})^{T} + sinφ < n >^{T} \end{matrix}$ (11)

由于 $\begin{matrix} ({n} {n}^{T})^{T} = {n} {n}^{T} 和 < n >^{T} = - < n >, \end{matrix}$ 方程(8)和(12)左右两边相减可得:

$\begin{matrix} (R - R^{T}) = 2 sinφ < n > \end{matrix}$ (12)

根据式(13)可以得出:

$\begin{matrix} < n > = (R - R^{T}) / (2 sinφ) \end{matrix}$ (13)

在 $\begin{matrix} t_{i} 与 t_{i + 1} \end{matrix}$ 时刻, 车轮相对于固定参考系的前束角、车轮滚动角和外倾角可由悬架K& C试验台测出, 并分别记为: $\begin{matrix} δ_{i} 、 κ_{i} 、 β_{i} 与 δ_{i + 1} 、 κ_{i + 1} 、 β_{i + 1} 。 \end{matrix}$ 则在这两个时刻, 轮胎坐标系相对于固定坐标系的姿态矩阵分别为:

$R_{i} = [\begin{matrix} \cos δ_{i} & - \sin δ_{i} & 0 \\ \sin δ_{i} & \cos δ_{i} & 0 \\ 0 & 0 & 1 \end{matrix}] [\begin{matrix} \cos κ_{i} & 0 & \sin κ_{i} \\ 0 & 1 & 0 \\ - \sin κ_{i} & 0 & \cos κ_{i} \end{matrix}] \times [\begin{matrix} 1 & 0 & 0 \\ 0 & \cos β_{i} & - \sin β_{i} \\ 0 & \sin β_{i} & \cos β_{i} \end{matrix}]$ (15)

$R_{i + 1} = [\begin{matrix} \cos δ_{i + 1} & - \sin δ_{i + 1} & 0 \\ \sin δ_{i + 1} & \cos δ_{i + 1} & 0 \\ 0 & 0 & 1 \end{matrix}] \times [\begin{matrix} \cos κ_{i + 1} & 0 & \sin κ_{i + 1} \\ 0 & 1 & 0 \\ - \sin κ_{i + 1} & 0 & \cos κ_{i + 1} \end{matrix}] \times [\begin{matrix} 1 & 0 & 0 \\ 0 & \cos β_{i + 1} & - \sin β_{i + 1} \\ 0 & \sin β_{i + 1} & \cos β_{i + 1} \end{matrix}]$ (16)

又有变换矩阵 $\begin{matrix} R 与姿态矩阵 R_{i} 和 R_{i + 1} \end{matrix}$ 的关系为:

$\begin{matrix} R = R_{i + 1} R_{i}^{- 1} \end{matrix}$ (17)

根据方程(11)(14)(17)可以解算出虚拟主销的单位向量n, 主销后倾角γ 与内倾角λ 如下:

$γ = \frac{π}{2} - co s^{- 1} [{[\begin{matrix} n_{x} \\ 0 \\ n_{z} \end{matrix}]}^{T} \cdot [\begin{matrix} 1 \\ 0 \\ 0 \end{matrix}] / \sqrt[]{n_{x}^{2} + n_{z}^{2}}]$ (18)

$λ = \frac{π}{2} - co s^{- 1} [{[\begin{matrix} 0 \\ n_{y} \\ n_{z} \end{matrix}]}^{T} \cdot [\begin{matrix} 0 \\ 1 \\ 0 \end{matrix}] / \sqrt[]{n_{y}^{2} + n_{z}^{2}}]$ (19)

主销后倾拖距为:

$\begin{matrix} ξ = a + γR \end{matrix}$ (20)

式中: $\begin{matrix} a \end{matrix}$ 为前移量; $\begin{matrix} R \end{matrix}$ 为轮胎半径。

在转向过程中主销后倾拖距随车轮转角的变化曲线如图4所示。

	Figure Option View Download New Window
	图4 主销后倾拖距的变化曲线Fig.4 Kingpin caster trail

3 方向盘力输入车辆模型

3.1 轮胎模型及辨识

轮胎模型是轮胎力学特性的数学描述, UniTire轮胎模型^{[12, 13]}定义无量纲的相对纵向、侧向和综合滑移率 $\begin{matrix} ϕ_{x} 、 ϕ_{y} \end{matrix}$ 和 $\begin{matrix} ϕ \end{matrix}$ 分别为:

$ϕ_{x} = \frac{K_{x} S_{x}}{μ_{x} F_{z}}, ϕ_{y} = \frac{K_{y} S_{y}}{μ_{y} F_{z}}, ϕ = \sqrt[]{ϕ_{x}^{2} + ϕ_{y}^{2}}$ (21)

式中: $\begin{matrix} K_{x} \end{matrix}$ 与 $\begin{matrix} K_{y} \end{matrix}$ 分别为轮胎的纵滑刚度和侧偏刚度; $\begin{matrix} S_{x} \end{matrix}$ 和 $\begin{matrix} S_{y} \end{matrix}$ 分别为轮胎的纵向滑移率和侧向滑移率; $\begin{matrix} μ_{x} \end{matrix}$ 和 $\begin{matrix} μ_{y} \end{matrix}$ 分别为接触印迹内纵向及侧向的摩擦系数; $\begin{matrix} F_{z} \end{matrix}$ 为垂直载荷。

无量纲总切力为:

$\begin{matrix} \bar{P} = 1 - \exp [- ϕ - E \cdot ϕ^{2} - (E^{2} + 1 / 12) \cdot ϕ^{3}] \end{matrix}$ (22)

定义无量纲纵向力 $\begin{matrix} {\bar{P}}_{x} \end{matrix}$ 及无量纲侧向力 $\begin{matrix} {\bar{P}}_{y}, \end{matrix}$ 按照无量纲滑移率的比例进行分配:

${\bar{P}}_{x} = \bar{P} \frac{ϕ_{x}}{ϕ}, {\bar{P}}_{y} = \bar{P} \frac{ϕ_{y}}{ϕ}$ (23)

$\bar{P} = \sqrt[]{{\bar{P}}_{x}^{2} + {\bar{P}}_{y}^{2}}$ (24)

轮胎所受的纵向力及侧向力分别为:

$\begin{matrix} P_{x} = {\bar{P}}_{x} μ_{x} F_{z}, P_{y} = {\bar{P}}_{y} μ_{y} F_{z} \end{matrix}$ (25)

侧向力引起的回正力矩为:

$\begin{matrix} M_{z} = P_{y} D_{x} \end{matrix}$ (26)

式中: $\begin{matrix} D_{x} = (D_{x 0} - D_{e}) \cdot \exp \exp (- D_{1} \cdot ϕ - D_{2} \cdot ϕ^{2}) + D_{e}; D_{x 0} = \\ m_{1} + m_{2} \cdot F_{zn} + m_{3} \cdot F_{zn}^{2}; D_{e} = m_{4} + m_{5} \cdot F_{zn} + m_{6} \cdot F_{zn}^{2}; D_{1} = \\ m_{7}^{2} \cdot \exp (- F_{zn} / m_{8}); D_{2} = m_{9}^{2} \cdot \exp (- F_{zn} / m_{10}) 。 \end{matrix}$

在轮胎试验机上进行轮胎力学特性试验, 轮胎模型的辨识结果如图5和6所示。

	Figure Option View Download New Window
	图5 轮胎侧向力的变化曲线Fig.5 Tire lateral force

	Figure Option View Download New Window
	图6 轮胎回正力矩的变化曲线Fig.6 Tire aligning torque

3.2 车辆模型

如图7所示, 根据达朗贝尔原理, 建立车辆方向盘力输入四自由度操纵模型, 非簧载质量和簧载质量的侧向加速度分别为:

$\overset{\cdot \cdot}{Y} = \overset{\cdot}{ζ} V = V (\frac{dψ}{dt} + \frac{dβ}{dt}) = V (r + \overset{\cdot}{β})$ (27)

${\overset{\cdot \cdot}{Y}}_{s} = V \overset{\cdot}{β} + Vr - h \overset{\cdot}{p}$ (28)

沿 $\begin{matrix} y \end{matrix}$ 轴力平衡式为:

$(M - M_{s}) (r + \overset{\cdot}{β}) V + M_{s} [(r + \overset{\cdot}{β}) V - h \overset{\cdot}{p}] = P'_{y 1} + P ″_{y 1} + P'_{y 2} + P ″_{y 2}$ (29)

绕 $\begin{matrix} z \end{matrix}$ 轴力矩平衡式为:

$\begin{matrix} I_{z} \overset{\cdot}{r} - I_{xz} \overset{\cdot}{p} = x_{1} (P'_{y 1} + P ″_{y 1}) + x_{2} (P'_{y 2} + P ″_{y 2}) \end{matrix}$ (30)

式中: $\begin{matrix} I_{z} \end{matrix}$ 为绕 $\begin{matrix} z \end{matrix}$ 轴的转动惯量; $\begin{matrix} I_{xz} \end{matrix}$ 为惯性积。

绕 $\begin{matrix} x \end{matrix}$ 轴力矩平衡式为:

$I_{φ} \overset{\cdot}{p} - I_{xz} \overset{\cdot}{r} - M_{s} hV (\overset{\cdot}{β} + r) = (- K_{φ} + M_{s} gh) φ - C_{φ} p$ (31)

	Figure Option View Download New Window
	图7 方向盘力输入车辆模型Fig.7 Vehicle model of force input

式中: $\begin{matrix} I_{φ} 为绕 x \end{matrix}$ 轴的转动惯量。

绕主销的力矩平衡式为:

$\begin{matrix} T + P'_{y 1} ζ'_{1} + P ″_{y 1} ζ ″_{1} = I_{w} \overset{\cdot \cdot}{δ} \end{matrix}$ (32)

式中: $\begin{matrix} P'_{y 1} 、 P ″_{y 1} 、 P'_{y 2} 、 P ″_{y 2} \end{matrix}$ 为根据式(25)计算的侧向力。

图7中, O为车辆质心; β 为质心侧偏角; $\begin{matrix} β_{1} 、 β_{2} \end{matrix}$ 分别为前、后轴轮胎侧偏角; $\begin{matrix} V \end{matrix}$ 为车辆质心速度; $\begin{matrix} δ \end{matrix}$ 为前轮转角; $\begin{matrix} r \end{matrix}$ 为横摆角速度; $\begin{matrix} x_{1} 、 x_{2} \end{matrix}$ 分别为质心到前、后轴的距离; $\begin{matrix} ψ \end{matrix}$ 为方向角; $\begin{matrix} ζ \end{matrix}$ 为速度 $\begin{matrix} V \end{matrix}$ 与 $\begin{matrix} x \end{matrix}$ 轴的夹角; $\begin{matrix} M \end{matrix}$ 为车辆质量; $\begin{matrix} M_{s} \end{matrix}$ 为簧载质量; $\begin{matrix} φ \end{matrix}$ 为车身侧倾角; $\begin{matrix} p \end{matrix}$ 为车身侧倾角速度; $\begin{matrix} h \end{matrix}$ 为非簧载质量的质心到侧倾中心的垂直距离; $\begin{matrix} K_{φ} \end{matrix}$ 为车身侧倾角刚度; $\begin{matrix} C_{φ} \end{matrix}$ 为车身侧倾角阻尼; $\begin{matrix} I_{w} \end{matrix}$ 为绕主销的转向系统等效转动惯量; $\begin{matrix} i \end{matrix}$ 为转向角传动比; $\begin{matrix} ζ'_{1} 、 ζ ″_{1} \end{matrix}$ 分别为内、外轮的主销后倾拖距; $\begin{matrix} K_{w} \end{matrix}$ 为转向系统角刚度; $\begin{matrix} C_{w} \end{matrix}$ 为转向系统角阻尼; $\begin{matrix} T \end{matrix}$ 为驾驶员输入方向盘的力矩。

4 主动回正控制

4.1 主动回正控制算法

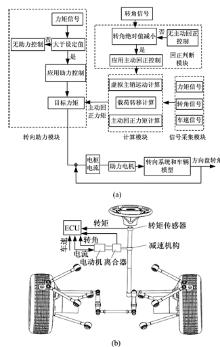
应用主动回正控制的方法, 改善由于虚拟主销移动和载荷的转移对车辆回正性能的影响。在电动助力转向系统的基础上, 可以实现主动回正控制功能, 控制原理如图8所示。

	Figure Option View Download New Window
	图8 主动回正控制原理Fig.8 Control principle of active return

具体控制过程如下:

(1)首先, 对车辆的回正过程进行判别:根据采集模块的信息, 方向盘转角绝对值处于减小的过程, 则为回正过程, 应用主动回正控制^[14]; 若车辆不处于回正过程, 主动回正控制不起作用。

(2)其次, 主动回正力矩的计算方法为:根据图4可以计算出初始状态主销不移动时的后倾拖距 $\begin{matrix} ξ_{0} \end{matrix}$ 及由于虚拟主销运动造成的内、外轮主销后倾拖距 $\begin{matrix} ξ'_{1} 、 ξ ″_{1} \end{matrix}$ 变化。

由于侧向加速度的作用, 造成内轮的垂直载荷减小, 外轮的垂直载荷增大, 垂直载荷转移量 $\begin{matrix} Δ F_{z} \end{matrix}$ 为:

$\begin{matrix} Δ F_{z} = (F_{sy} h_{s} + K_{φ} φ + F_{uy} h_{u}) / B \end{matrix}$ (33)

式中: $\begin{matrix} B \end{matrix}$ 为轮距; $\begin{matrix} F_{sy} \end{matrix}$ 为簧载质量的离心力; $\begin{matrix} F_{uy} \end{matrix}$ 为非簧载质量的离心力; $\begin{matrix} h_{s} \end{matrix}$ 为簧载质量的质心高度; $\begin{matrix} h_{u} \end{matrix}$ 为非簧载质量的质心高度。

由内、外轮侧向力 $\begin{matrix} P'_{y 1} 、 P ″_{y 2} \end{matrix}$ 产生的回正力矩分别为:

$M'_{y 1} = P'_{y 1} ξ'_{1}$ (34)

$M ″_{y 1} = P ″_{y 1} ξ ″_{1}$ (35)

内、外轮之间的载荷转移和虚拟主销移动造成的回正力矩减小量 $\begin{matrix} ΔM \end{matrix}$ 为:

$\begin{matrix} ΔM = (P'_{y 1} + P ″_{y 1}) ξ_{0} - (P'_{y 1} ξ'_{1} + P ″_{y 1} ξ ″_{1}) \end{matrix}$ (36)

(3)最后, 进行主动回正力矩的加载。

如图9所示, 助力电机为永磁直流电机, 电压 $\begin{matrix} U \end{matrix}$ 与电感 $\begin{matrix} L 、 \end{matrix}$ 电枢电阻 $\begin{matrix} R 、 \end{matrix}$ 反电动势常数 $\begin{matrix} K_{b} 、 \end{matrix}$ 电枢电流 $\begin{matrix} I \end{matrix}$ 之间的关系为:

$\begin{matrix} U = L \frac{dI}{dt} + RI + K_{b} {\overset{\cdot}{θ}}_{m} \end{matrix}$ (37)

式中: $\begin{matrix} {\overset{\cdot}{θ}}_{m} \end{matrix}$ 为电动机转动角速度。

	Figure Option View Download New Window
	图9 电机模型Fig.9 Electromotor model

根据直流电动机的工作原理可知, 电动机电磁转矩 $\begin{matrix} T_{m} \end{matrix}$ 与电枢电流 $\begin{matrix} I \end{matrix}$ 成比例, 即:

$\begin{matrix} T_{m} = K_{m} I \end{matrix}$ (38)

式中: $\begin{matrix} K_{m} \end{matrix}$ 为电动机的力矩常数。

因此, 主动回正力矩的大小可以通过控制电动机电枢电流来达到, 控制规律为:

$\begin{matrix} I = K_{ai} (\frac{ΔM}{g_{m} i}) + K_{ci} {\overset{\cdot}{θ}}_{m} \end{matrix}$ (39)

式中: $\begin{matrix} i \end{matrix}$ 为转向系统角传动比; $\begin{matrix} g_{m} \end{matrix}$ 为电动机到转向柱的减速比; $\begin{matrix} ΔM \end{matrix}$ 为方程(36)计算的回正力矩减小量; $\begin{matrix} K_{ai} \end{matrix}$ 为比例控制系数; $\begin{matrix} K_{ci} \end{matrix}$ 为微分控制系数。

将式(39)代入式(38), 可求出电动机电磁转矩:

$\begin{matrix} T_{m} = K_{m} (K_{ai} (\frac{ΔM}{g_{m} i}) + K_{ci} {\overset{\cdot}{θ}}_{m}) \end{matrix}$ (40)

电动机产生的主动回正力矩作用于车轮的回正过程, 运动微分方程为:

$\begin{matrix} T_{m} g_{m} i + P'_{y 1} ζ'_{1} + P ″_{y 1} ζ ″_{1} = I_{w} \overset{\cdot \cdot}{δ} \end{matrix}$ (41)

4.2 回正过程仿真结果

车辆仿真参数如下:车辆质心到前轴距离x₁=1241 mm; 车辆轴距为2997 mm; 整车质量M=1589.9 kg; 簧载质量M_s=1094 kg; 转向系统角传动比 $\begin{matrix} i \end{matrix}$ =22; 电机力矩常数K_m=0.0718 (N· m· A^-1); 转向系统转动惯量I_w=3.92 (kg· m²); 电机到转向柱的减速比g_m=19.5。低速回正性能仿真为:以车速30 km/h, 使侧向加速度达到(3± 0.2) m/s², 松开方向盘, 方向盘转角的响应曲线如图10所示。高速回正性能仿真为:以车速70 km/h, 使侧向加速度达到(2± 0.2) m/s², 松开方向盘, 方向盘转角的响应曲线如图11所示。从图10和图11可以得出, 采用基于虚拟主销运动计算的主动回正控制策略, 方向盘转角响应收敛速度明显加快, 改善了车辆的低速和高速回正性能。

	Figure Option View Download New Window
	图10 低速回正时方向盘转角响应Fig.10 Steering angle response of low-speed return

	Figure Option View Download New Window
	图11 高速回正时方向盘转角响应Fig.11 Steering angle response of high-speed return

5 结论

(1)对转向过程中多连杆悬架虚拟主销的运动学特性进行了分析, 虚拟主销的移动会造成主销后倾拖距与内倾偏移距等悬架主销定位参数的变化, 对车辆回正性能产生影响。

(2)根据悬架的运动学特性, 应用瞬时轴线理论对转向过程中虚拟主销的运动量及主销后倾拖距的变化进行了计算。

(3)提出一种主动回正控制策略, 对车辆回正过程中由虚拟主销移动及载荷转移造成的回正力矩减小量进行补偿。结果表明, 应用基于虚拟主销运动计算的主动回正控制方法改善车辆的回正性能。

The authors have declared that no competing interests exist.

参考文献

View Option

[1]	郭孔辉. 汽车操纵动力学原理[M]. 南京: 江苏科学技术出版社, 2012. [本文引用:1]
[2]	Attia H A. Kinematic analysis of the multi-link five-point suspension system in point coordinates[J]. KSME International Journal, 2003, 17(8): 1133-1139. [本文引用:1]
[3]	Lu M W, Zhao W Q. Kinematics analysis and numerical method for multi-link suspension[J]. Advanced Materials Research, 2011, 314: 810-814. [本文引用:1]
[4]	Mántaras D A, Luque P. Virtual test rig to improve the design and optimization process of the vehicle steering and suspension systems[J]. Vehicle System Dynamics, 2012, 50(10): 1563-1584. [本文引用:1]
[5]	French T, Roland A, Sluiter M. Multilink suspension & steering system for cal poly formula electric[D]. Sacrameto: Mechanical Engineering Department, Canifornia Polytechnic State University, 2013. [本文引用:1]
[6]	Kim S S, Kim S H. Steering axis analysis of multi-link suspensions with bushing compliance[J]. Transactions of the Korean Society of Automotive Engineers, 2014, 22(3): 194-202. [本文引用:1]
[7]	Da Lio M. Robust design of linkages-synthesis by solving non-linear optimization problems[J]. Mechanism and Machine Theory, 1997, 32(8): 921-932. [本文引用:1]
[8]	Chabaan R C, Wang L Y. Control of electrical power assist systems: H_∞ design, torque estimation and structural stability[J]. JSAE Review, 2001, 22(4): 435-444. [本文引用:1]
[9]	Yang S, Guo X, Yang B, et al. Return-to-center control of electric power steering[C]//The 9th International Conference on Electronic Measurement & Instruments, Beijing, China, 2009: 3435-3439. [本文引用:1]
[10]	Lee A N, Jung J H, Koo B G, et al. Steering assist torque control enhancing vehicle stabiliity[C]//Proceedings of the 17th World Congress IFAC, Seoul, Korea, 2008. [本文引用:1]
[11]	Spoor C W, Veldpaus F E. Rigid body motion calculated from spatial co-ordinates of markers[J]. Journal of Biomechanics, 1980, 13(4): 391-393. [本文引用:1]
[12]	郭孔辉, 王裕民, 刘蕴博, 等. 轮胎侧偏特性的半经验模型[J]. 汽车工程, 1986, 8(2): 44-52. Guo Kong-hui, Wang Yu-min, Liu Yun-bo, et al. The semi-empirical model for tire lateral properties[J]. Automotive Engineering, 1986, 8(2): 44-52. [本文引用:1]
[13]	郭孔辉. 用于汽车制动、驱动与转向运动模拟的轮胎力学统一模型[J]. 汽车技术, 1992(1): 11-18. Guo Kong-hui. UniTire model for the simulation of vehicle braking, driving and steering[J]. Automotive Technology, 1992 (1): 11-18. [本文引用:1]
[14]	郭孔辉, 丁金全, 张雷, 等. 一种电动轮悬架主动回正控制系统[P]. 中国: 201520617280, 2015-08-17. [本文引用:1]

2012

0.0

... 0 引言悬架主销后倾拖距与车轮转动惯量的比值对车辆力输入运动的稳定性,起着至关重要的作用^[1] ...

2003

0.0

... 在转向过程中,多连杆悬架上、下控制臂确定的虚拟主销会产生运动,造成主销后倾角/主销后倾拖距,主销内倾角/主销内倾偏移距等悬架主销定位参数的变化,由于内、外轮载荷转移的附加作用,对车辆的回正性能产生重要影响^[2,3] ...

2011

0.0

2012

0.0

... 对独立悬架而言,悬架的主销轴是影响车辆操纵和平顺性的重要因素^[4,5,6] ...

2013

0.0

... 对独立悬架而言,悬架的主销轴是影响车辆操纵和平顺性的重要因素^[4,5,6] ...

2014

0.0

... 对独立悬架而言,悬架的主销轴是影响车辆操纵和平顺性的重要因素^[4,5,6] ...

1997

0.0

... 麦弗逊和双横臂悬架的主销轴基本固定不动,而多连杆悬架的虚拟主销在转向过程中时刻发生改变,在空间运动解算过程中,传统的几何解算方法不再适用^[7] ...

2001

0.0

... 在传统的电动助力转向系统基础上,可以实现主动回正控制,主动回正力矩主要是根据方向盘的回正角度进行计算,但没有考虑悬架的转向运动学特性及引起的主销移动,载荷转移对车辆回正性能产生的影响^[8,9,10] ...

2009

0.0

2008

0.0

1980

0.0

... 2 虚拟主销运动计算基于瞬时轴线理论^[11],车轮转动过程中,绕着虚拟主销 u7的运动可以分解为车轮绕虚拟主销转过角度 φ和沿着虚拟主销轴线移动 t,如图3所示 ...

1986

0.0

. 1986, 8(2):44-52

The semi-empirical model for tire lateral properties

轮胎侧偏特性的半经验模型

Guo Kong-hui , Wang Yu-min , Liu Yun-bo

郭孔辉, 王裕民, 刘蕴博

本文首先叙述了以前的理论模型(Fiala公式)和半经验模型(如桥石公式)的不足处。它们不能适用于接近极限工况而且试验结果与桥石公式差别不小。作者以Fiala公式为基础提出一个新公式,其中一些系数通过与试验数据拟合求得。作者还用同样方法提出了回正力矩的新半经验模型。

... 1 轮胎模型及辨识轮胎模型是轮胎力学特性的数学描述,UniTire轮胎模型^[12,13]定义无量纲的相对纵向、侧向和综合滑移率 ϕx、ϕy和 ϕ分别为: ...

1992

0.0

... 1 轮胎模型及辨识轮胎模型是轮胎力学特性的数学描述,UniTire轮胎模型^[12,13]定义无量纲的相对纵向、侧向和综合滑移率 ϕx、ϕy和 ϕ分别为: ...

2015

0.0

... (1)首先,对车辆的回正过程进行判别:根据采集模块的信息,方向盘转角绝对值处于减小的过程,则为回正过程,应用主动回正控制^[14] ...