水下地磁导航技术中的地磁场空间差分测量方法

引用本文

赵塔, 朱小宁, 程德福, 周志坚. 水下地磁导航技术中的地磁场空间差分测量方法. 2017, 47(1): 316-322
ZHAO Ta, ZHU Xiao-ning, CHENG De-fu, ZHOU Zhi-jian. Geomagnetic field spatial difference measuring method for underwater geomagnetic navigation technology. Journal of Jilin University Engineering and Technology Edition, 2017, 47(1): 316-322 复制到剪切板

Permissions

水下地磁导航技术中的地磁场空间差分测量方法

赵塔^1,², 朱小宁^1,², 程德福^1,², 周志坚^1,²

1.吉林大学国家地球物理探测仪器工程技术研究中心,长春 130026

2.吉林大学仪器科学与电气工程学院,长春 130026

通讯作者:周志坚(1980-),男,讲师,博士.研究方向:弱信号检测,智能仪器.E-mail:zhouzhijian@jlu.edu.cn

作者简介:赵塔(1987-),男,博士研究生.研究方向:弱磁信号检测,地磁导航.E-mail:zhao_ta_ok@126.com

基金:国家重大科研装备研制项目(ZDYZ2012-1-02); 国家自然科学青年基金项目(41304140).

摘要

为了实现水下载体对地磁场的精确测量,提高地磁辅助导航的精度,提出了一种基于多传感器的空间差分地磁场三分量测量方法。首先,分析了水下载体周围磁场的种类及空间分布特性,并建立了磁矢量传感器新的测量模型。然后,利用干扰磁场自身特性以及和地磁场之间的耦合关系构建方程组,推导出空间差分模型表达式。最后,通过仿真分析和地面实验分别将本文方法与传统测量方法进行了对比。结果表明:当外界干扰磁场为1000 nT时,差分测量结果能使测量误差控制在150 nT以内,很好地抑制了干扰源对地磁场测量造成的影响,提高了水下载体地磁场三分量测量的抗干扰能力。

关键词: 信息处理技术; 水下载体; 地磁导航; 空间差分模型; 干扰磁场

中图分类号:TH762 文献标志码:A 文章编号:1671-5497(2017)01-0316-07

Geomagnetic field spatial difference measuring method for underwater geomagnetic navigation technology

ZHAO Ta^1,², ZHU Xiao-ning^1,², CHENG De-fu^1,², ZHOU Zhi-jian^1,²

1.National Geophysical Exploration Equipment Engineering Research Center, Jilin University, Changchun 130026,China

2.College of Instrumentation and Electrical Engineering, Jilin University, Changchun 130026,China

Abstract

In order to accurately measure the geomagnetic field around an underwater vehicle and improve the precision of geomagnetic aided navigation, a spatial difference measuring method is proposed based on multi-sensor. First, a new measurement model of magnetic vector sensors is established by analyzing the magnetic field types and the spatial distribution characteristics around the vehicle. Then, the spatial difference model expression is deduced according to the characteristics of interference magnetic field and its coupling relationship with the magnetic field. The proposed method was compared with traditional method by simulation and ground experiment. Results show that the proposed method can obviously restrain the impact of the interference magnetic field. When the intensity of the outside interference magnetic field is 1000 nT, the measurement error can be controlled under 150 nT by the spatial difference measuring method, which is able to improve the ability of anti-jamming in geomagnetic field measurement.

Keyword: information processing; underwater vehicle; geomagnetic navigation; spatial difference model; interference magnetic field

Show Figures

0 引言

进入21世纪以来, 世界上已有10多个国家的1000余艘各种用途的水下载体投入到军用或民用的领域, 其导航方式也根据应用场合的不同逐渐从单一向组合导航系统发展^[1]。地磁/惯性组合导航系统能够有效解决惯性导航系统误差随时间累积问题, 既不要求水下载体上浮, 又不向外辐射能量, 具有极好的隐蔽性, 大大提高了载体在水下的生存和应用能力^{[2, 3]}。然而构建足够精确的水下地磁数据库或地磁图是实现地磁/惯性组合导航技术的关键问题。因此, 为了详细了解水下环境磁场特性, 获得更加准确的地磁数据, 有必要进行水下地磁场的实地测量。

由于单一总场存在地磁等值线的问题, 而地磁场的三分量包含更多的地球物理信息。因此, 地磁场的矢量测量必然成为导航技术发展的趋势。日本最早提出一种地磁场三分量的船载式测量方法(STCM), 主要通过传统测量模型对载体自身干扰磁场进行补偿, 地磁场三分量测量精度为(50± 25) nT^[4]。国内的闫辉、肖昌汉等^{[5, 6]}也针对海洋环境地磁场三分量的测量进行了研究, 并采用“ 两步法” 验证了测量方法的正确性和可行性。但是上述方法主要采取单传感器测量, 抗干扰能力差, 而且没有考虑外界磁源产生的干扰磁场对测量系统造成的影响, 这也是地磁场实际测量造成误差的原因之一。

本文在STCM的基础之上, 充分考虑了干扰磁场的空间分布特性和来源情况, 通过多传感器测量组建的方程组推导出空间差分模型, 最后通过仿真和地面实验验证了本文方法的正确性和可行性。

1 载体磁场分析与测量模型建立

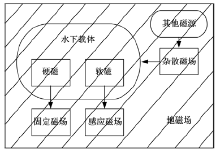
目前, 水下大部分载体由铁磁性材料建造而成, 可以将其分为硬磁材料和软磁材料, 它们在地磁场的作用下会被磁化而向外辐射磁场。

	Figure Option View Download New Window
	图1 水下载体主要干扰磁场组成Fig.1 Main components of interference magnetic field around underwater vehicle

同时, 水下环境复杂多变, 载体周围会随时出现一些其他磁源, 这些未知的磁源将产生一些杂散磁场, 从而对测量造成影响。因此, 如图1所示, 上述多种混合磁场的矢量叠加构成了载体周围干扰磁场的主要成分。

硬磁材料具有较高的矫顽力和剩余磁场值, 由于载体在建造过程中或长期停靠时期受到相同方向地磁场的磁化, 产生的这部分剩磁可以保留较长时间且不随载体的航向和位置发生变化^{[7, 8]}, 因此也称之为固定磁场, 其矢量在载体坐标系中表示为 $\begin{matrix} H_{S} = {[H_{SX}, H_{SY}, H_{SZ}]}^{T} 。 \end{matrix}$

软磁材料的矫顽力较低, 且具有较窄的磁滞回线, 能够在较弱的磁场中被磁化而产生感应磁场, 它会随着外磁场的改变而改变, 也会随着载体形状、姿态、位置的不同而发生变化。根据泊松方程, 感应磁场矢量和地磁场矢量之间满足如下关系:

$\begin{matrix} \{\begin{matrix} H_{RX} = K_{XX} \cdot H_{GX} + K_{XY} \cdot H_{GY} + K_{XZ} \cdot H_{GZ} \\ H_{RY} = K_{YX} \cdot H_{GX} + K_{YY} \cdot H_{GY} + K_{YZ} \cdot H_{GZ} \\ H_{RZ} = K_{ZX} \cdot H_{GX} + K_{ZY} \cdot H_{GY} + K_{ZZ} \cdot H_{GZ} \end{matrix} \end{matrix}$ (1)

式中: $\begin{matrix} H_{R} = {[H_{RX}, H_{RY}, H_{RZ}]}^{T} \end{matrix}$ 为载体坐标系中的感应磁场矢量; $\begin{matrix} H_{G} = {[H_{GX}, H_{GY}, H_{GZ}]}^{T} \end{matrix}$ 为载体坐标系中的地磁场矢量; $\begin{matrix} K_{ij} \end{matrix}$ 为地磁场矢量与感应磁场矢量之间的磁化系数; $\begin{matrix} j \end{matrix}$ 表示地磁场的矢量方向; i表示j方向地磁场矢量对感应磁场的磁化方向, 例如:K_ij表示地磁场Y分量对感应磁场X方向的磁化系数。将式(1)写成矩阵的形式为:

$\begin{matrix} [\begin{matrix} H_{RX} \\ H_{RY} \\ H_{RZ} \end{matrix}] = [\begin{matrix} K_{XX} & K_{XY} & K_{XZ} \\ K_{YX} & K_{YY} & K_{YZ} \\ K_{ZX} & K_{ZY} & K_{ZZ} \end{matrix}] \cdot [\begin{matrix} H_{GX} \\ H_{GY} \\ H_{GZ} \end{matrix}] \end{matrix}$ (2)

式中:由 $\begin{matrix} K_{ij} \end{matrix}$ 组成的3× 3方阵被称为感应系数矩阵, 用 $\begin{matrix} K \end{matrix}$ 表示, 内部元素值都小于1, 大小与载体材料特性、形状、传感器的安装位置有关。研究表明^[6], 固定磁场和感应磁场是构成载体干扰磁场的主要成分, 而发动机、电气设备等产生的磁场可以通过合理的滤波器和合理的布线方案等方式进行去除。因此, 在载体坐标系下STCM方法中提出的传统测量模型表达式为:

$\begin{matrix} H_{G} = {(E + K)}^{- 1} \cdot (H_{M} - H_{S}) \end{matrix}$ (3)

式中:H_M 为载体坐标系下传感器的矢量测量值; E为单位矩阵。

在水下环境中, 载体周围还可能存在着很多未知的其他磁源, 如水面上的船只, 海底雷区或沉船、水下的其他运行载体等, 这些铁磁性的物体也会被磁化而向外辐射磁场, 产生的杂散磁场用∑ H_N表示。∑ H_N是多种磁场的矢量叠加, 具有很强的突发性和不确定性, 既无法测量其大小也无法判断其方向, 但它确实是测量中不可避免而又容易忽视的一种干扰磁场成分。由于在传统模型方法中采用单传感器测量, 模型中无法去除∑ H_N而忽略了这部分磁场, 但这部分磁场一旦出现会直接叠加到传感器的测量值中, 对地磁场矢量的最终计算造成较大误差。如何合理地去除∑ H_N, 提高地磁场矢量测量精度成为了研究的重点问题。因此, 载体坐标系下传感器更加完整的新测量模型为:

$\begin{matrix} H_{G} = {(E + K)}^{- 1} \cdot (H_{M} - H_{S} - \sum H_{N}) \end{matrix}$ (4)

2 测量原理及测量模型

2.1 空间差分测量原理

根据磁场强度在水中衰减的经验公式^[9]:

$\begin{matrix} H = 1.5 M / R^{3} \end{matrix}$ (5)

式中: $\begin{matrix} H \end{matrix}$ 为磁化体向外辐射的磁场强度; $\begin{matrix} M \end{matrix}$ 为被磁化体的等效磁矩; $\begin{matrix} R \end{matrix}$ 为离开磁化体的距离。

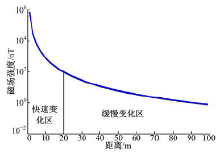
磁场强度随距离衰减曲线如图2所示, 在前20 m的距离磁场梯度较大, 磁场强度衰减了约10⁴倍, 称该区域为快速变化区。而随着距离的增加磁场曲线的斜率也趋于平缓, 即磁场梯度越来越小, 称该区域为缓慢变化区。

	Figure Option View Download New Window
	图2 磁场强度随距离衰减曲线Fig.2 Decay curve of magnetic field intensity with distance

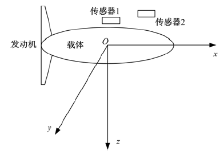
通过上面的分析, 将干扰磁场分为自身干扰磁场和外界干扰磁场。自身干扰磁场包括 $\begin{matrix} H_{R} \end{matrix}$ 和 $\begin{matrix} H_{S}, \end{matrix}$ 这部分磁场是由载体材料磁化产生, 距离传感器较近, 一般小于5 m的距离, 因此属于快速变化区磁场。外界干扰磁场是由其他载体或磁化体产生, 由于水下载体运行过程中与周围其他物体保持一定的安全距离, 因此, 这部分磁场与载体上传感器的距离一般都较远, 属于缓慢变化区磁场。

图3为水下载体坐标系及传感器安装图, x轴在载体左右对称的纵剖面上, 指向载体前进方向为正; y轴在载体中心平面上, 指向右侧为正; z轴垂直xy平面, 向下为正。在载体上中轴线两侧非对称位置捷联安装两个三分量传感器, 根据载体尺寸和传感器测量精度合理选择安装距离, 一般控制在2~5 m以内。由于载体自身产生的干扰磁场在两传感器处产生的磁场梯度较大, 属于图2中快速变化区磁场, 在差分计算时具有明显的差异性, 而∑ H_N是由较远距离的单个或多个磁化体产生, 一般距离大于20 m, 属于图2中缓慢变化区磁场, 在载体处产生的磁场梯度很小, 在两个传感器处的响应值大致相同, 因此在相同坐标系下可以通过差分处理将其去掉。

	Figure Option View Download New Window
	图3 水下载体坐标系及传感器安装图Fig.3 Coordinate system and sensor installation drawing of underwater vehicle

2.2 差分测量模型

地磁场是一种天然的物理场, 当不存在磁异常点时它的各个分量自身梯度很小, 中国从南到北地磁场水平分量强度主要随纬度变化^[10], 水平分量强度每纬度最大变化了10 nT, 垂直分量强度每纬度最大变化了7 nT。而根据两个传感器的实际安装距离, 在载体坐标系下传感器测量的地磁场三分量值与载体位置的地磁场三分量值基本相同, 满足下面关系:

$\begin{matrix} H_{1 G} \approx H_{2 G} \approx H_{G} \end{matrix}$ (6)

根据式(4)对两个传感器新的测量模型构建如下方程组:

$\begin{matrix} \{\begin{matrix} H_{1 M} = (E + K_{1}) \cdot H_{1 G} + H_{1 S} + \sum H_{1 N} \\ H_{2 M} = (E + K_{2}) \cdot H_{2 G} + H_{2 S} + \sum H_{2 N} \end{matrix} \end{matrix}$ (7)

通过上面的分析可知, 外界杂散干扰磁场在两个传感器处满足:

$\begin{matrix} \sum H_{1 N} \approx \sum H_{2 N} \end{matrix}$ (8)

对式(7)中的两个方程做差, 得到:

$\begin{matrix} \begin{matrix} H_{G} = (K_{1} - K_{2})^{- 1} \cdot [(H_{1 M} - \\ H_{2 M}) - (H_{1 S} - H_{2 S})] \end{matrix} \end{matrix}$ (9)

式(9)为地磁场三分量的差分测量模型, 感应系数矩阵 $\begin{matrix} K_{1} \end{matrix}$ 和 $\begin{matrix} K_{2} \end{matrix}$ 以及固定磁场 $\begin{matrix} H_{1 S} \end{matrix}$ 和 $\begin{matrix} H_{2 S} \end{matrix}$ 具有快速变化区磁场特性, 在距离载体的不同位置和高度处存在明显差异, 确保了差分后不会出现奇异矩阵, 可以通过“ 360° ” 旋转法或“ 8字” 旋转法估计得到^[11]。 $\begin{matrix} H_{1 M} \end{matrix}$ 和 $\begin{matrix} H_{2 M} \end{matrix}$ 可以通过磁矢量传感器直接测量得到。通过上述方法得到的地磁场三分量值为载体坐标系下的测量值, 在地磁辅助导航技术中常常应用的是地理坐标系下的地磁场信息, 因此, 需要对载体坐标系下的地磁场测量值进行坐标变换, 得到地理坐标系下的地磁场三分量值 $\begin{matrix} H'_{G} : \end{matrix}$

$\begin{matrix} H'_{G} = D \cdot H_{G} \end{matrix}$ (10)

式中: $\begin{matrix} D \end{matrix}$ 为坐标旋转矩阵, 它是由载体姿态传感器提供的姿态角度换算得到, 包括横摇角 $\begin{matrix} α 、 \end{matrix}$ 纵倾角 $\begin{matrix} θ \end{matrix}$ 和航向角 $\begin{matrix} φ, \end{matrix}$ 构成的坐标变换矩阵可以表示为:

$\begin{matrix} \begin{matrix} D = [\begin{matrix} 1 & 0 & 0 \\ 0 & cosα & sinα \\ 0 & - sinα & cosα \end{matrix}] \cdot [\begin{matrix} cosθ & 0 & sinθ \\ 0 & 1 & 0 \\ - sinθ & 0 & cosθ \end{matrix}] \cdot \\ [\begin{matrix} cosφ & sinφ & 0 \\ - sinφ & cosφ & 0 \\ 0 & 0 & 1 \end{matrix}] \end{matrix} \end{matrix}$ (11)

3 仿真验证及分析

为了验证本文提出的空间差分测量方法的可行性, 利用国际标准地磁场IGRF-11/2010模型中提供的地磁场数据, 按照所述的原理应用大型有限元仿真软件Comsol Multiphysics针对本文方法进行仿真验证。

3.1 仿真条件

载体模型建立条件如下:采用单椭球模型来构建载体, 模型为长度50 m, 宽度和高度均为10 m的椭球形空腔, 腔体厚度为0.05 m, 后端带有尾翼, 材料的相对磁导率为100。在上表面中轴线两侧捷联式安装两个传感器, 左侧传感器离载体表面高度为0.2 m, 右侧传感器离载体表面高度为1.2 m, 两个传感器的直线距离为2.0 m。在长、宽、高均为100 m的正方体求解域中加入 $\begin{matrix} x 、 y 、 z \end{matrix}$ 三个方向的矢量数据来提供均匀背景地磁场。仿真模型如图4所示。

	Figure Option View Download New Window
	图4 载体仿真模型Fig.4 Vehicle simulation model

在理想环境(∑ H_N=0, H_G变化平缓且已知)中进行感应系数矩阵和固定磁场的仿真求解。首先设置两个传感器处的固定磁场三分量分别为675.0、-575.0、342.0 nT和485.0、-185.0、852.0 nT。然后根据IGRF-11/2010模型选取中国南海北纬5° 东经110° 坐标点的地磁三分量数据40858.8、161.8、-3908.8 nT作为背景地磁场, 使模型进行水平360° 旋转, 并伴有横摇和纵倾动作, 且横摇和纵倾角不超过5° , 角度产生的最大测量误差为0.001° 。

然后在北纬5° 东经110° 到北纬6° 东经111° 海域均匀选取20个地磁场三分量数据作为背景地磁场, 假设仿真过程中载体坐标系与地理坐标系相同。为了更接近真实水下载体周围磁场环境(∑ H_N≠ 0, H_G未知), 进一步验证地磁场三分量差分测量方法的有效性, 在传感器1的仿真测量数据中加入最大幅值为± 25 nT随机误差来模拟实际环境中的外界杂散磁场, 设 $\begin{matrix} x 、 y 、 z \end{matrix}$ 方向的梯度为1.0 nT/m, 由于两传感器的直线距离为2.0 m, 因此传感器2处的干扰磁场在传感器1的基础之上变化2.0 nT。不考虑测量中引入的其他误差。

3.2 仿真结果及分析

采用最小二乘法拟合出每个传感器处感应系数矩阵和固定磁场的结果, 如表1所示。

表1 系数矩阵和固定磁场拟合结果 Table 1 Fitting results of coefficient matrix and permanent magnetic field

序号	$\begin{matrix} \hat{K} \end{matrix}$	$\begin{matrix} {\hat{H}}_{SX} \end{matrix}$ /nT	$\begin{matrix} {\hat{H}}_{SY} \end{matrix}$ /nT	$\begin{matrix} {\hat{H}}_{SZ} \end{matrix}$ /nT
1	$\begin{matrix} [\begin{matrix} - 0.0241 & - 0.0053 & 0.0144 \\ - 0.0233 & - 0.0613 & - 0.1340 \\ 0.0333 & - 0.1453 & 0.0522 \end{matrix}] \end{matrix}$	676.3	-572.7	343.4
2	$\begin{matrix} [\begin{matrix} 0.0020 & 0.0228 & 0.0234 \\ 0.0236 & - 0.0751 & 0.0923 \\ 0.0214 & 0.0862 & 0.0354 \end{matrix}] \end{matrix}$	483.6	-184.6	854.5

表1 系数矩阵和固定磁场拟合结果 Table 1 Fitting results of coefficient matrix and permanent magnetic field

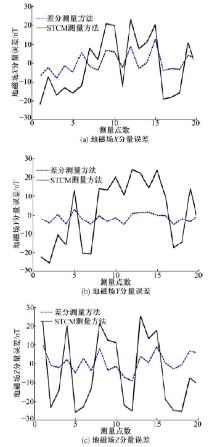
表1中 $\begin{matrix} \hat{K} 、 {\hat{H}}_{SX} 、 {\hat{H}}_{SY} 和 {\hat{H}}_{SZ} \end{matrix}$ 表示各个参数的拟合值, 固定磁场最大相对误差为0.4%。通过对两个传感器采取的空间非对称安装布局方式, 使感应系数矩阵内部元素差值的有效位数最小为10^-2数量级, 不会因为差分计算而出现奇异矩阵, 确保了该差分测量模型数学表达式的可解性。将表1中求解出的数值作为已知参数分别应用于差分测量方法和STCM测量方法中, 得到如图5所示的地磁场三分量测量结果与真实值之间的误差曲线。

通过图5可以看出, 本文提出的空间差分测量方法对地磁场三分量的测量误差明显低于传统STCM测量方法的误差。由于仿真中设置 $\begin{matrix} X \end{matrix}$ 分量的地磁场绝对值比较大, 因此空间差分方法在 $\begin{matrix} X \end{matrix}$ 分量上产生的误差也最大, 最大误差为15 nT, 而在地磁场绝对值比较小的 $\begin{matrix} Y \end{matrix}$ 分量上产生的最大误差仅为5 nT。

	Figure Option View Download New Window
	图5 地磁场三分量测量误差曲线Fig.5 Error curves of three-component geomagnetics field measurement

而传统STCM方法受到外界杂散磁场的干扰比较大, 在每一个分量上产生的误差基本相同, 最大绝对值都在25 nT左右。说明空间差分方法能够更好地适应水下复杂磁场环境下地磁场分量的测量, 具有更好的抗干扰能力, 可为地磁辅助导航提供更加准确的地磁场信息。

4 地面实验验证

为了方便实验, 载体模型采用长度80 cm、直径20 cm、管壁厚度1 cm的钢管制作(比仿真所用模型缩小了约50倍), 表面涂有灰色油漆, 重45 kg。两侧梯形尾翼对称焊接, 上底边长为10 cm, 下底边长为20 cm, 高度为20 cm, 厚度为1 cm。实验平台用木板制作, 长度为100 cm, 宽度为80 cm, 厚度为3 cm, 平台上固定有载体安装槽、4个Mag-03三分量传感器安装桩和数显倾角仪安装孔等, 此实验中使用的是对角的两个传感器安装桩, 高度差约为5 cm, 全部仪器采用无磁塑料螺丝安装和固定, 具体如图6所示。

	Figure Option View Download New Window
	图6 载体实验平台Fig.6 Experiment platform of vehicle

主要进行了3个实验的测量:①载体实验平台差分参数估计实验; ②载体实验平台差分方法的测线验证实验; ③载体实验平台差分方法与STCM方法对比实验。

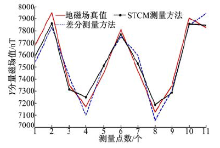
首先无载体时测量点 $\begin{matrix} P \end{matrix}$ 位置0° 航向的三分量数据, 然后放上载体通过改变航向使实验平台以点 $\begin{matrix} P \end{matrix}$ 为圆心做360° 旋转, 每隔45° 进行一次测量, 并伴有俯仰和翻滚动作各一次。通过无磁经纬仪在 $\begin{matrix} P \end{matrix}$ 点事先测量标定好8个方位作为航向角的基准, 经纬仪的水平测量偏差为2″, 通过与实验平台捷联的数显倾角仪显示载体当前俯仰和翻滚姿态角度, 倾角仪的静态测量精度为4', 共记录24组数据。

然后让载体实验平台沿着一条200 m测线进行直线运动, 共记录下11组三分量测量数据, 地磁场 $\begin{matrix} Y \end{matrix}$ 分量的测量结果如图7所示。

	Figure Option View Download New Window
	图7 测线上地磁场Y分量测量结果Fig.7 Y component results of geomagnetic field on measuring-line

最后保持载体实验平台不动, 让一辆金杯面包车模拟周围突然出现的外界杂散干扰磁场源, 从实验平台左侧3 m处驶过, 地磁场3个分量的测量结果如图8所示。

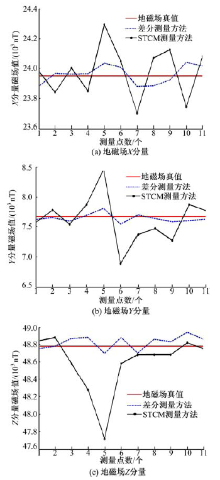	Figure Option View Download New Window
	图8 外界存在杂散干扰磁源时地磁场三分量测量结果Fig.8 Three-component results of geomagnetic field when outside interference magnetic field is appearing

图8中地磁场分量真值通过无载体时传感器测量得到。通过图7可以看出当背景环境中磁场分布比较均匀, 无杂散干扰源时, 由于航向角的测量会引入误差使STCM传统测量方法和差分测量方法的地磁场测量结果均产生了一定的误差, 但该误差均小于100 nT。当外界出现未知杂散干扰磁源时, 如图8中(a)(b)(c)所示, STCM传统测量方法受到很强烈的干扰, 导致地磁场三分量测量误差随干扰磁源的出现明显增大, 最大值约为1000 nT, 而差分测量方法的测量误差仍然很平稳, 保持在150 nT以内。

5 结束语

水下地磁场的实地测量是实现高精度地磁辅助导航的关键技术。本文针对STCM传统测量方法使用单磁传感器在地磁场测量方面存在的抗干扰能力差、测量精度低的问题, 提出了基于多传感器的空间差分测量方法。能够有效去除载体自身干扰磁场以及外界磁异常体对地磁场测量造成的影响, 增强了测量过程中抵抗外界干扰磁场的能力。仿真结果表明:当外界干扰磁源在载体处产生的最大干扰磁场为25 nT, 且梯度为1 nT/m时, 空间差分测量方法的测量误差为(10± 5) nT, 比传统STCM测量方法的误差明显降低了1/2左右。地面实验结果表明:STCM传统方法产生的误差会随外界未知干扰磁场变化而变化, 而空间差分方法几乎不受外界干扰磁源的影响, 测量误差控制在自身稳定的范围内。因此, 通过上面的研究验证了空间差分方法的合理性和可行性, 为水下地磁辅助导航技术在实际中的应用奠定了基础。

The authors have declared that no competing interests exist.

参考文献

View Option

[1]	Cui Rong-xin, Sam Ge Shuzhi, Ee H B V, et al. Leader-follower formation control of under actuated autonomous underwater vehicles[J]. Ocean Engineering, 2010, 37(17-18): 1491-1502. [本文引用:1]
[2]	Lesur V, Clark T, Turbitt C, et al. A technique for estimating the absolute vector geomagnetic field from a marine vessel[J]. Journal of Geophysics and Engineering, 2004, 1(2): 109-115. [本文引用:1]
[3]	金春水, 杨功流, 李士心, 等. 地磁辅助惯性导航系统的数据融合算法[J]. 中国惯性技术学报, 2007, 15(1): 47-50. Jin Chun-shui, Yang Gong-liu, Li Shi-xin, et al. Data fusing algorithm in geomagnetic aided INS[J]. Journal of Chinese Inertial Technology, 2007, 15(1): 47-50. [本文引用:1]
[4]	Isesaki N. A new shipboard three-component magnetometer[J]. Geophysics, 1986, 51(10): 1992-1998. [本文引用:1]
[5]	闫辉, 肖昌汉. 一种海洋环境地磁场三分量的测量方法[J]. 海军工程大学学报, 2005, 17(6) : 80-83. Yan Hui, Xiao Chang-han. A method of measuring three-component geomagnetic field on ocean[J]. Journal of Naval University of Engineering, 2005, 17(6): 80-83. [本文引用:1]
[6]	闫辉, 肖昌汉, 沈明, 等. 船载三分量测量算法的实验验证[J]. 海洋测绘, 2010, 30(3): 27-29. Yan Hui, Xiao Chang-han, Shen Ming, et al. The experimental verification of ship three-component geomagnetic field measurement method[J]. Hydrographic Surveying and Charting, 2010, 30(3): 27-29. [本文引用:2]
[7]	Zhu Xing-le, Xiao Chang-han, Yao Zhen-ning. Calculation error's correction of three-component geomagnetic field's marine survey[J]. Advanced Materials Research, 2013, 756-759: 323-326. [本文引用:1]
[8]	Wynn R B, Huvenne V A I, Le Bas T P, et al. Autonomous underwater vehicles (AUVs): their past, present and future contributions to the advancement of marine geoscience[J]. Marine Geology, 2014, 352: 451-468. [本文引用:1]
[9]	张晓明, 赵剡. 基于椭圆约束的新型载体磁场标定及补偿技术[J]. 仪器仪表学报, 2009, 30(11): 2438-2443. Zhang Xiao-ming, Zhao Yan. New auto calibration and compensation method for vehicle magnetic field based on ellipse restriction[J]. Chinese Journal of Scientific Instrument, 2009, 30(11): 2438-2443. [本文引用:1]
[10]	扬世周. 航空磁力反潜浅谈[J]. 舰船科学技术, 1979 (12): 66-76. Yang Shi-zhou. Discussion of aeromagnetic antisubmarine[J]. Ship Science and Technology, 1979(12): 66-76. [本文引用:1]
[11]	王琦, 林君, 于生宝, 等. 航空瞬变电磁反演中灵敏度的快速高精度计算[J]. 吉林大学学报: 工学版, 2015, 45(6): 2020-2025. Wang Qi, Lin Jun, Yu Sheng-bao, et al. Calculation of sensitivities for airborne electromagnetic inversion progress[J]. Journal of Jilin University (Engineering and Technology Edition), 2015, 45(6): 2020-2025. [本文引用:1]

2010

0.0

... 0 引言进入21世纪以来,世界上已有10多个国家的1000余艘各种用途的水下载体投入到军用或民用的领域,其导航方式也根据应用场合的不同逐渐从单一向组合导航系统发展^[1] ...

2004

0.0

... 地磁/惯性组合导航系统能够有效解决惯性导航系统误差随时间累积问题,既不要求水下载体上浮,又不向外辐射能量,具有极好的隐蔽性,大大提高了载体在水下的生存和应用能力^[2,3] ...

2007

0.0

. 2007, 15(1):47-50 DOI:doi:10.3969/j.issn.1005-6734.2007.01.013

Data fusing algorithm in geomagnetic aided INS

地磁辅助惯性导航系统的数据融合算法

Jin Chun-shui , Yang Gong-liu , Li Shi-xin

金春水, 杨功流, 李士心

对地磁辅助导航技术的基本原理进行分析,详细介绍了采样卡尔曼滤波算法并将其用于惯性/地磁导航系统的数据融合,即通过设计少量的sigma点,并计算这些sigma点通过非线性函数的变换,从而获得滤波值基于非线性状态方程的更新.仿真表明,特别是当系统非线性较大时,采样卡尔曼器性能明显优于扩展卡尔曼滤波器.因此,从某种程度上说,采样卡尔曼滤波可以替代扩展卡尔曼滤波在地磁辅助导航系统中使用.

1986

0.0

... 25) nT^[4] ...

2005

0.0

. 2005, 17(6):80-83 DOI:doi:10.3969/j.issn.1009-3486.2005.06.016

A method of measuring three-component geomagnetic field on ocean

一种海洋环境地磁场三分量的测量方法

Yan Hui , Xiao Chang-han.

闫辉, 肖昌汉

提出了一种利用安装在舰船上的三分量磁传感器进行地磁场测量的方法.从理论上解决了在任意舰船姿态下,消除测量中舰船磁场干扰的问题.为测量船在海上测量地磁场的三分量奠定了理论基础.根据我国舰船普遍安装的导航设备的精度,进行了计算机仿真.从仿真结果看,其误差不超过50 nT,能够满足舰载消磁系统对三分量磁场的精度要求.

... 国内的闫辉、肖昌汉等^[5,6]也针对海洋环境地磁场三分量的测量进行了研究,并采用#cod#x0201c ...

2010

0.0

. 2010, 30(3):27-29 DOI:doi:10.3969/j.issn.1671-3044.2010.03.008

The experimental verification of ship three-component geomagnetic field measurement method

船载三分量测量算法的实验验证

Yan Hui , Xiao Chang-han , Shen Ming

闫辉, 肖昌汉, 沈明

安装在铁磁性的测量载体上的地磁场三分量测量系统,由于受到载体磁化磁场的干扰,给地磁场的解算带来了极大的困难。针对船载地磁场三分量动态测量系统,阐明了地磁场的解算原理,指出了其中的难点问题。对地磁场三分量的动态解算方法进行了实验室模拟,结果表明地磁场三分量航海测量具有实施的可行性。

... 国内的闫辉、肖昌汉等^[5,6]也针对海洋环境地磁场三分量的测量进行了研究,并采用#cod#x0201c ...

... 研究表明^[6],固定磁场和感应磁场是构成载体干扰磁场的主要成分,而发动机、电气设备等产生的磁场可以通过合理的滤波器和合理的布线方案等方式进行去除 ...

2013

0.0

... 硬磁材料具有较高的矫顽力和剩余磁场值,由于载体在建造过程中或长期停靠时期受到相同方向地磁场的磁化,产生的这部分剩磁可以保留较长时间且不随载体的航向和位置发生变化^[7,8],因此也称之为固定磁场,其矢量在载体坐标系中表示为 HS=HSX,HSY,HSZT ...

2014

0.0

2009

0.0

. 2009, 30(11):2438-2443 DOI:doi:10.3321/j.issn:0254-3087.2009.11.035

New auto calibration and compensation method for vehicle magnetic field based on ellipse restriction

基于椭圆约束的新型载体磁场标定及补偿技术

Zhang Xiao-ming , Zhao Yan.

张晓明, 赵剡

在地磁导航中进行地磁测量时会受到载体磁场的影响,因此必须对测量数据中的载体磁场进行精确补偿,以提高磁场测量精度.本文根据硬磁材料磁场和软磁材料磁场的数学模型,提出了一种基于椭圆约束的载体磁场标定及补偿方法.该方法首先采用带椭圆约束的最小二乘拟合方法对捷联式磁传感器测量数据进行椭圆拟合,保证了拟合曲线必为椭圆,从而实现载体磁场的准确标定,然后利用标定参数实现对载体磁场的精确补偿.最后进行了一系列的仿真试验.试验结果表明了该方法具有简单快速,易于实现的特点,可以达到与磁传感器等精度的补偿效果,且在低信噪比情况下具有较强的鲁棒性 Abstract： It is unavoidable that the geomagnetic field measurement is disturbed by the magnetic field of vehicle in geomagnetic navigation. In order to improve the measurement accuracy, the magnetic field of vehicle must be correctly compensated. According to the magnetic field model of ferromagnetic material in vehicle, a new magnetic calibration and compensation method is proposed. Firstly, the proposed method adopts the least square algorithm under ellipse restriction, rather than common iterative algorithms, for fitting the scattered or noisy measurement data to an ellipse, and the magnetic field parameters of vehicle are calibrated rapidly. Then the error caused by the magnetic field of vehicle is compensated correctly. Finally, several experiments have been carried out to assess the validity of the method. Experiment results show that the proposed method is simple, stable, and robust for magnetic field compensation.

... 1 空间差分测量原理根据磁场强度在水中衰减的经验公式^[9]: ...

1979

0.0

... 2 差分测量模型地磁场是一种天然的物理场,当不存在磁异常点时它的各个分量自身梯度很小,中国从南到北地磁场水平分量强度主要随纬度变化^[10],水平分量强度每纬度最大变化了10 nT,垂直分量强度每纬度最大变化了7 nT ...

2015

0.0

. 2015, 45(6):2020-2025 DOI:doi:10.13229/j.cnki.jdxbgxb201506041

Calculation of sensitivities for airborne electromagnetic inversion progress

航空瞬变电磁反演中灵敏度的快速高精度计算

Wang Qi , Lin Jun , Yu Sheng-bao

王琦, 林君, 于生宝

摘　要：为了满足在航空电磁反演迭代过程中灵敏度的计算要求,提出了多步长差分累加算法,以差分代替微分计算,用差分步长系数控制累加次数,通过多个步长中心差分结果的累加平均,实现了灵敏度的快速高精度计算。计算了多组大地模型灵敏度,结果表明：差分步长系数选取10,灵敏度矩阵元素的误差均可控制在0.1%以内。与传统中心差分方式和解析法进行对比分析,得到多步长差分累加算法在计算精度上优于中心差分方法;在计算速度上优于解析法,对于15层大地模型,计算速度提高5倍。最后,通过航空瞬变电磁反演仿真实例,证明了该算法能够满足航空电磁海量数据对反演精度和反演速度的要求。

... 旋转法估计得到^[11] ...