基于交通状态估计的快速路交通联合控制

引用本文

贾洪飞, 李永行, 杨丽丽. 基于交通状态估计的快速路交通联合控制. 2017, 47(1): 76-81
JIA Hong-fei, LI Yong-xing, YANG Li-li. Expressway traffic joint control based on traffic state estimation. Journal of Jilin University Engineering and Technology Edition, 2017, 47(1): 76-81 复制到剪切板

Permissions

基于交通状态估计的快速路交通联合控制

贾洪飞, 李永行, 杨丽丽

吉林大学交通学院,长春 130022

作者简介:贾洪飞(1969-),男,教授,博士生导师.研究方向:交通网络分析技术.E-mail:jiahf@jlu.edu.cn

基金:国家自然科学基金项目(51278221,51378076).

摘要

采用模糊 C均值聚类方法将快速路交通状态划分为畅通、轻度拥挤和拥挤状态。将快速路二阶宏观交通流模型与粒子滤波算法相结合,实现对快速路交通状态参数的估计,并将交通状态参数估计结果划分到对应状态中,得到交通状态估计结果。在交通状态估计的基础上,考虑3种交通状态下的交通运行特性,结合可变限速控制和入口匝道控制建立快速路联合控制模型。采集吉林省长春市东部快速路交通数据进行实例验证,结果表明:联合控制模型的应用减少了快速路交通流总时间费用消耗的4.55%,降低了交通流密度,在一定程度上缓解了交通拥挤。

关键词: 交通运输系统工程; 快速路; 交通状态估计; 可变限速控制; 入口匝道控制

中图分类号:U491 文献标志码:A 文章编号:1671-5497(2017)01-0076-06

Expressway traffic joint control based on traffic state estimation

JIA Hong-fei, LI Yong-xing, YANG Li-li

College of Transportation,Jilin University,Changchun 130022,China

Abstract

Expressway traffic state is divided into unimpeded, slight smooth and congested sub-states by fuzzy C-means clustering method. Combining expressway second-order macroscopic traffic flow model with particle filter algorithm, the traffic state parameters are estimated. By clustering the estimation values of the parameters to one of the three kinds of traffic sub-states, the corresponding traffic state estimation is obtained. Based on the traffic state estimation and the characteristics of each traffic sub-state, an expressway joint control model is established, which combines variable speed-limit control and on-ramp control. The traffic data of Changchun East-expressway is used to validate the model. Results show that the total time spend of the expressway is reduced by 4.55% and the traffic flow density is also reduced. The traffic congestion is eased to certain extent.

Keyword: engineering of communications and transportation system; expressway; traffic state estimation; variable speed-limit control; on-ramp control

Show Figures

0 引言

快速路是城市的快速交通走廊, 能够以较大的服务容量和较高的服务水平为城市交通做出积极贡献, 修建城市快速路也通常被认为是缓解城市交通拥挤的一种重要手段。然而, 由于日益增长的城市交通需求, 城市快速路出现了严重的交通拥挤现象, 由此带来了一系列交通问题, 实行交通控制是解决城市快速路交通问题的有效手段, 经过多年的研究, 许多关于快速路可变限速控制^[1]、入口匝道控制^[2]、出口匝道控制^[3]、多匝道协调控制^[4]的模型被提出来, 并应用在快速路交通控制中, 但是, 现有研究都是在一天的交通中采用一种控制方案或几种控制方案, 也就是说不管主线交通状态如何变化都采用一种控制方案或几种方案之间的转换, 这就使得快速路交通控制的针对性不强, 出现控制效果不佳的现象^{[4, 5]}。另外, 现有快速路交通控制的研究中, 都是在实时检测数据的基础上进行的, 会出现控制延迟的现象。

本文在快速路交通状态估计的基础上, 考虑不同交通状态下的交通运行特性, 将可变限速控制和入口匝道控制联合起来, 建立快速路联合控制模型, 实现对快速路交通的实时有效控制。

1 快速路交通控制思路

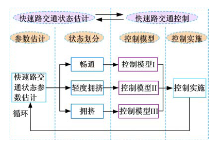
快速路交通控制实质上是一个参数估计→ 状态划分→ 控制模型→ 控制实施→ 参数估计的循环控制过程。图1为快速路交通控制框架。

	Figure Option View Download New Window
	图1 快速路交通控制框架Fig.1 Framework of expressway traffic control

考虑不同交通状态下的交通运行特性, 构建相应的可变限速与入口匝道联合控制模型, 实现对快速路交通的实时有效控制, 并将控制结果反馈给快速路交通状态参数估计模型, 实现对快速路交通的循环控制。

2 快速路交通状态估计

2.1 快速路交通状态划分

由于快速路交通状态之间的界限不是很清晰, 存在一定的模糊性, 适合采用模糊聚类的方法对其进行划分。采用模糊C均值聚类方法对交通状态进行划分, 一般选取包含占有率、速度、流量3个参数的样本点, 本文为了与状态参数估计结果对应, 选取具有速度和密度参数的样本点。根据相关研究^{[6, 7]}, 采用模糊C均值聚类方法对交通状态进行划分时, 划分为3类(畅通、轻度拥挤和拥挤状态)的聚类效果最佳, 所以分类数取3。

2.2 快速路交通状态参数估计

近年来, 粒子滤波算法因其具有非线性和非高斯特性, 逐渐被应用到交通状态的估计中, Bi等^{[8, 9]}基于粒子滤波算法建立了交通状态参数估计模型, 并对其进行了优化处理, 估计效果较好。

本文采用二阶宏观交通流模型与粒子滤波相结合的方式实现对快速路交通状态参数的估计。首先, 采集快速路交通数据, 构建快速路二阶宏观交通流模型; 然后, 将快速路二阶宏观交通流模型与粒子滤波算法相结合, 构建快速路交通状态参数估计模型; 最后, 采用Matlab软件编程, 实现快速路交通状态参数估计模型对交通状态参数的估计, 具体流程如图2所示。

	Figure Option View Download New Window
	图2 快速路交通状态参数估计流程Fig.2 Process of expressway traffic state estimation

3 快速路可变限速与入口匝道联合控制

3.1 快速路可变限速与入口匝道控制模型

(1)可变限速控制模型

根据快速路二阶宏观交通流模型, 快速路交通流速度与密度的关系公式为:

$\begin{matrix} V (ρ_{i} (k)) = v_{f} \cdot \exp [- \frac{1}{α} {(\frac{ρ_{i} (k)}{ρ_{cr}})}^{α}] \end{matrix}$ (1)

式中: $\begin{matrix} V (ρ_{i} (k)) \end{matrix}$ 为路段 $\begin{matrix} i \end{matrix}$ 的车流平均速度; $\begin{matrix} v_{f} \end{matrix}$ 为自由行驶状态下的速度; $\begin{matrix} ρ_{i} (k) \end{matrix}$ 为路段 $\begin{matrix} i \end{matrix}$ 的车流密度; $\begin{matrix} ρ_{cr} \end{matrix}$ 为交通量达到道路通行能力时的密度; $\begin{matrix} α \end{matrix}$ 为待定参数。

在式(1)中引入控制变量 $\begin{matrix} u_{i}, \end{matrix}$ 得到可变限速控制模型^[10]:

$\begin{matrix} v_{ctrl, i} = u_{i} \cdot v_{f} \cdot \exp [- \frac{1}{α} {(\frac{ρ_{i} (k)}{ρ_{cr}})}^{α}] \end{matrix}$ (2)

式中: $\begin{matrix} v_{ctrl, i} \end{matrix}$ 为路段 $\begin{matrix} i \end{matrix}$ 的控制限速值。

(2)入口匝道控制模型

快速路主线比较拥挤、入口匝道交通需求较大的情况下, 由于主线车辆具有优先通行权, 入口匝道上的车辆无法快速进入主线, 在匝道上形成排队现象。根据物质守恒定律, 流入量-流出量=匝道车辆的变化, 得到快速路入口匝道排队模型:

$\begin{matrix} w_{j} (k + 1) = w_{j} (k) + T [d_{j} (k) - q_{j} (k)] \end{matrix}$ (3)

式中:T为时间间隔; w_j(k)为入口匝道排队长度; d_j (k)为入口匝道的平均到达车流量; q_j(k)为从入口匝道汇入快速路的平均流量。

从入口匝道汇入快速路主线的平均流量 $\begin{matrix} q_{j} (k) \end{matrix}$ 由以下公式求得:

$\begin{matrix} \{\begin{matrix} q_{j} (k) = r_{j} (k) {\hat{q}}_{j} (k) \\ {\hat{q}}_{j} (k) = \min {{\hat{q}}_{j, 1} (k), {\hat{q}}_{j, 2} (k)} \\ {\hat{q}}_{j, 1} (k) = d_{j} (k) + w_{j} (k) / T \\ {\hat{q}}_{j, 2} (k) = Q_{j} \min \{1, \frac{ρ_{jam} - ρ_{j} (k)}{ρ_{jam} - ρ_{c}}\} \end{matrix} \end{matrix}$ (4)

式中:r_j (k)为匝道调节率; ${\hat{q}}_{j} (k)$ 为入口匝道流量; ${\hat{q}}_{j, 1} (k)$ 为入口匝道需求流量; ${\hat{q}}_{j, 2} (k)$ 为快速路最大可用容量; ρ _jam 为快速路交通流阻塞密度; Q_j为入口匝道全开情况下所能通过的最大交通量。

(3)可变限速与入口匝道联合控制

可变限速控制与入口匝道控制都是解决快速路交通拥挤问题的有效手段, 单独实施可变限速控制或入口匝道控制, 都能在一定程度上保证快速路交通的快速有效运行。然而, 两者的独立控制效果又都是有限的, 可变限速控制只能对快速路主线车流进行控制, 起到均匀交通流、有效利用道路空间等作用, 对于进入快速路主线车流过多而导致的交通拥挤问题, 则很难有较好的控制效果, 不能从源头上对快速路的交通进行控制; 入口匝道控制只能对将要经过入口匝道进入快速路主线的车流进行调节, 将部分想要进入快速路主线的交通量转移到相邻道路上, 从而起到减小快速路交通压力的作用, 不能对已经进入快速路主线的车辆进行干预。

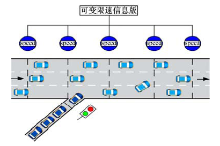
将可变限速与入口匝道控制联合起来(后面简称“ 联合控制” ), 可充分发挥两种控制的优势, 同时控制主线车流的速度及入口匝道的进入量, 实现对已经进入和将要进入快速路的车辆的联合控制。图3为可变限速与入口匝道联合控制示意图。

	Figure Option View Download New Window
	图3 可变限速与入口匝道联合控制示意图Fig.3 Schematic diagram of combining variable speed-limit with on-ramp control

3.2 快速路交通控制最优问题

(1)畅通状态下的控制最优问题

快速路主线交通畅通状态下, 由于车辆之间的约束很小, 驾驶员往往会比较放松, 对交通安全的警惕性下降, 易导致事故发生, 这就需要采取可变限速的控制策略, 稳定交通流, 提高安全性。而此时交通流量不大, 不需要对匝道的进入量进行控制。在快速路交通控制中, 一般将车流的总时间费用消耗TTS(Total time spend)作为控制的目标^[11], 为了防止控制速度变化过大, 引入速度的控制项 $\begin{matrix} \sum_{i} \end{matrix} \begin{matrix} {[\frac{v_{ctrl, i} (k) - v_{ctrl, i} (k - 1)}{v_{f}}]}^{2} \end{matrix}$ , 得到快速路畅通状态下控制最优问题的目标函数 $\begin{matrix} F_{1} (k) 。 \end{matrix}$

$\begin{matrix} \begin{matrix} F_{1} (k) = T \sum_{k} \{\frac{}{} [\sum_{i} ρ_{i} (k) L_{i} λ_{i} + α_{queue} \sum_{j} w_{j} (k)] + \\ α_{speed} \sum_{i} {[\frac{v_{ctrl, i} (k) - v_{ctrl, i} (k - 1)}{v_{f}}]}^{2}\} \end{matrix} \end{matrix}$ (5)

式中:T $\begin{matrix} \sum_{k} \end{matrix} \begin{matrix} [\sum_{i} ρ_{i} (k) L_{i} λ_{i} + α_{queue} \sum_{j} w_{j} (k)] \end{matrix}$ 为快速路车流的总时间费用消耗; L_i为路段i的长度; λ _i 为路段i的车道数; α _speed 为速度控制调节系数; α _queue 为匝道排队长度控制系数; v_{ctrl, i}(k)为路段i的限速值。

(2)轻度拥挤状态下的控制最优问题

快速路主线交通轻度拥挤状态下, 需要采取主线交通可变限速和入口匝道控制相结合的控制方式, 平稳主线交通流的同时, 控制进入主线的车流量。在总时间费用消耗TTS的基础上, 加入速度控制项 $\begin{matrix} \sum_{i} \end{matrix} \begin{matrix} {[\frac{v_{ctrl, i} (k) - v_{ctrl, i} (k - 1)}{v_{f}}]}^{2} \end{matrix}$ 和匝道调节率控制项 $\begin{matrix} \sum_{j} \end{matrix} \begin{matrix} {[\frac{r_{j} (k) - r_{j} (k - 1)}{r_{\max}}]}^{2} \end{matrix}$ , 得到快速路交通轻度拥挤状态下控制最优问题的目标函数 $\begin{matrix} F_{2} (k) 。 \end{matrix}$

$\begin{matrix} \begin{matrix} F_{2} (k) = T \sum_{k} \{\frac{}{} [\sum_{i} ρ_{i} (k) L_{i} λ_{i} + α_{queue} \sum_{j} w_{j} (k)] + \\ α_{ramp} \sum_{j} {[\frac{r_{j} (k) - r_{j} (k - 1)}{r_{\max}}]}^{2} + \\ α_{speed} \sum_{i} {[\frac{v_{ctrl, i} (k) - v_{ctrl, i} (k - 1)}{v_{f}}]}^{2}\} \end{matrix} \end{matrix}$ (6)

式中:r_j(k)为匝道调节率; r_max为匝道调节率的最大值, 取值为1; α _ramp为匝道调节系数。

(3)拥挤状态下的控制最优问题

快速路主线交通拥挤状态下, 更直接的控制目的应该是在保证交通顺畅的情况下, 尽量降低主线交通流的密度, 与此同时, 为不影响辅道交通的正常通行, 尽量减小匝道车辆排队长度。所以, 在总时间费用消耗TTS的基础上, 加入速度控制项 $\begin{matrix} \sum_{i} \end{matrix} \begin{matrix} {[\frac{v_{ctrl, i} (k) - v_{ctrl, i} (k - 1)}{v_{f}}]}^{2} \end{matrix}$ 、匝道调节率控制项 $\begin{matrix} \sum_{j} \end{matrix} \begin{matrix} {[\frac{r_{j} (k) - r_{j} (k - 1)}{r_{\max}}]}^{2} \end{matrix}$ 和主线密度控制项 $\begin{matrix} \sum_{i} \end{matrix}$ [ρ _i(k)-ρ _cr]², 得到快速路拥挤状态下控制最优问题的目标函数 $\begin{matrix} F_{3} (k) 。 \end{matrix}$

$\begin{matrix} \begin{matrix} F_{3} (k) = T \sum_{k} \{[\sum_{i} ρ_{i} (k) L_{i} λ_{i} + α_{queue} \sum_{j} w_{j} (k)] + \\ α_{ramp} \sum_{j} {[\frac{r_{j} (k) - r_{j} (k - 1)}{r_{\max}}]}^{2} + \\ α_{speed} \sum_{i} {[\frac{v_{ctrl, i} (k) - v_{ctrl, i} (k - 1)}{v_{f}}]}^{2} + \\ α_{density} \sum_{i} {[ρ_{i} (k) - ρ_{cr}]}^{2}\} \end{matrix} \end{matrix}$ (7)

式中: $\begin{matrix} α_{density} \end{matrix}$ 为密度控制调节系数。

3.3 快速路联合控制约束条件

快速路联合控制的约束条件有:快速路主线约束和入口匝道约束。主线交通畅通状态下, 不需要对匝道进行控制, 因此不需要考虑匝道约束。主线交通轻度拥挤和拥挤状态下, 实行可变限速与入口匝道联合控制, 则需要考虑快速路主线约束和入口匝道约束。

3.3.1 快速路主线约束

快速路主线约束主要指路段通行能力约束和可变限速值约束。

(1)路段通行能力约束

路段的交通流量不超过其通行能力:

$\begin{matrix} q_{i} (k) \leq C_{i} \end{matrix}$ (8)

式中:q_i(k)为路段交通流量; C_i为路段通行能力。

(2)可变限速值约束

快速路可变限速值只能在最小限速值和最大限速值之间变化:

$\begin{matrix} v_{ctrl, \min} \leq v_{ctrl, i} \leq v_{ctrl, \max} \end{matrix}$ (9)

式中:v_{ctrl, i} 为可变限速值; v_{ctrl, max}为最大限速值, 可变限速值不超过畅通状态下的自由速度值, 这里取v_{ctrl, max}=v_f; v_{ctrl, min}为最小限速值, 可变限速值不小于拥挤状态聚类中心的速度值v_jl, 这里取v_{ctrl, min}=v_jl 。

3.3.2 快速路入口匝道约束

入口匝道约束主要指入口匝道通行能力约束和入口匝道排队长度约束。

(1)入口匝道通行能力约束

从入口匝道汇入快速路主线的车流量, 不超过匝道全开情况下所能通过的最大交通量:

$\begin{matrix} s_{j} (k) \leq Q_{j} \end{matrix}$ (10)

式中: $\begin{matrix} s_{j} (k) \end{matrix}$ 为从入口匝道汇入快速路主线的流量。

(2)入口匝道排队长度约束

为避免对辅道车流产生较大影响, 在对快速路入口匝道进行控制的过程中, 要保证车辆排队长度不超过匝道所能承受的最大排队长度:

$\begin{matrix} L_{j} (k) \leq L_{jmax} \end{matrix}$ (11)

式中:L_j(k)为入口匝道排队长度; L_jmax为最大排队长度。

4 实例

4.1 交通数据的采集

选取吉林省长春市东部快速路中的自由大路至南湖大路路段(由南向北的车流)为研究对象, 采用人工录制视频的方式进行快速路交通数据的采集。考虑出入口匝道的位置, 设置A、B、C、D和E五个观测点同时进行视频数据的采集,路段AB、BC、CD和DE的长度均为315 m。

4.2 长春市东部快速路交通状态估计

选取高峰和平峰时段的613组交通数据(交通流速度和密度)对交通状态进行模糊聚类分析。迭代到30次时, 目标函数收敛, 得到聚类中心P₁=[19.19, 55.73; 35.24, 37.85; 62.41, 21.73], 畅通状态的聚类中心(19.19, 55.73), 轻度拥挤状态的聚类中心(35.24, 37.85), 拥挤状态的聚类中心(62.41, 21.73)。

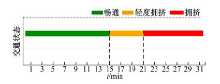
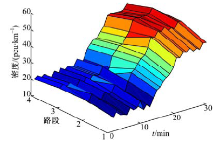
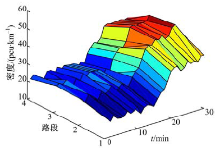
选择快速路各路段的速度和密度作为估计变量, 通过Matlab软件编程, 实现交通状态参数估计模型对快速路交通流密度和速度的估计, 得到快速路各路段交通流密度和速度的估计结果。计算各交通状态参数估计结果与各聚类中心之间的欧式距离, 将由状态参数估计结果组成的样本归到与其距离最近的类中心所代表的状态中, 得到交通状态的估计结果。路段BC和路段CD的交通状态估计结果分别如图4和5所示。

	Figure Option View Download New Window
	图4 路段BC的交通状态估计结果Fig.4 Traffic state estimation result of segment BC

	Figure Option View Download New Window
	图5 路段CD的交通状态估计结果Fig.5 Traffic state estimation result of segment CD

4.3 长春市东部快速路联合控制

(1)联合控制模型的建立及求解

根据长春市东部快速路交通状态估计结果, 构建联合控制模型, 并在交通状态参数估计结果的基础上对快速路交通进行控制, 相关参数设置如下:α _speed=1.0; α _ramp=1.0; v_{ctrl, max}=80 km/h; α _queue=1.0; α _density=1.0; v_{ctrl, min}=21.73 km/h。

采用遗传算法对快速路联合控制模型进行求解。根据相关研究^[12], 设置遗传算法相关参数如下:种群大小为100; 变量个数为4; 选择概率为0.8; 交叉概率为0.8; 变异概率为0.2; 最大迭代次数为100。

(2)联合控制结果分析

不实行交通控制时, 快速路交通流的总时间费用为2662 pcuh; 实行快速路可变限速与入口匝道联合控制时, 快速路交通流的总时间费用为2541 pcuh, 减少了4.55%。

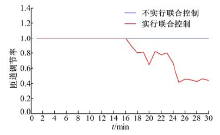
不实行联合控制和实行联合控制的匝道调节率变化情况如图6所示。在不实行联合控制的情况下, 入口匝道调节率始终为1, 即车辆可经匝道随意进入快速路主线。在实行联合控制的情况下, 入口匝道的调节率在0~1之间变化, 畅通状态下, 入口匝道调节率为1, 不对匝道进行控制; 轻度拥挤状态下, 入口匝道调节率开始降低; 拥挤状态下, 入口匝道调节率变的很小, 随着拥挤程度的增加, 入口匝道调节率变的更小。

	Figure Option View Download New Window
	图6 匝道调节率变化情况对比Fig.6 Comparison of ramp metering rates with and without joint control

图7和图8分别为不实行联合控制和实行联合控制的密度变化情况。实行联合控制以后, 在畅通状态下密度没有明显变化, 在交通拥挤状态下密度有所下降, 也就是说, 实行快速路交通控制可以有效降低拥挤程度, 从而达到缓解快速路

	Figure Option View Download New Window
	图7 不实行联合控制的密度变化Fig.7 Varying of density without joint control

	Figure Option View Download New Window
	图8 实行联合控制的密度变化Fig.8 Varying of density with joint control

交通拥挤的目的。

5 结论

(1)快速路交通控制实质上是一个参数估计→ 状态划分→ 控制模型→ 控制实施→ 参数估计的循环控制过程。

(2)基于交通状态估计的快速路交通控制可首先采用模糊C均值聚类方法将快速路交通状态划分为畅通、轻度拥挤和拥挤状态3种; 其次, 将快速路二阶宏观交通流模型与粒子滤波算法结合, 实现对交通状态参数的估计, 并将交通状态参数估计结果划分到对应状态中, 得到交通状态估计结果; 最后, 针对城市快速路交通流3种交通状态下的交通运行特性, 构建相应的可变限速与入口匝道联合控制模型。

(3)通过实例分析, 快速路可变限速和入口匝道联合控制减少了快速路交通流总时间费用消耗的4.55%, 降低了交通流密度, 在一定程度上缓解了交通拥挤。

The authors have declared that no competing interests exist.

参考文献

View Option

[1]	Chen D, Ahn S. Variable speed limit control for severe non-recurrent freeway bottlenecks[J]. Transportation Research Part C, 2015, 51: 210-230. [本文引用:1]
[2]	陈学文, 王殿海, 金盛, 等. 城市快速路入口匝道控制方法[J]. 吉林大学学报: 工学版, 2008, 38(增刊): 43-48. Chen Xue-wen, Wang Dian-hai, Jin Sheng, et al. On-ramp metering control strategy of urban expressway[J]. Journal of Jilin University(Engineering and Technology Edition), 2008, 38(Sup. ): 43-48. [本文引用:1]
[3]	Lim K, Kim J H, Shin E, et al. A signal control model integrating arterial intersections and freeway off-ramps[J]. KSCE Journal of Civil Engineering, 2011, 15(2): 385-394. [本文引用:1]
[4]	Geroliminis N, Srivastava A, Michalopoulos P. A dynamic-zone-based coordinated ramp-metering algorithm with queue constraints for Minnesota's freeways[J]. IEEE Transactions on Intelligent Transportation Systems, 2011, 12(4): 1576-1586. [本文引用:2]
[5]	Carlson R C, Papamichail I, Papageorgion M, et al. Optimal motorway traffic flow control involving variable speed limits and ramp metering[J]. Transportation Science, 2010, 44(2): 238-253. [本文引用:1]
[6]	姜桂艳, 郭海锋, 吴超腾. 基于感应线圈数据的城市道路交通状态判别方法[J]. 吉林大学学报: 工学版, 2008, 38(增刊): 37-42. Jiang Gui-yan, Guo Hai-feng, Wu Chao-teng. Identification method of urban road traffic conditions based on inductive coil data[J]. Journal of Jilin University(Engineering and Technology Edition), 2008, 38(Sup. ): 37-42. [本文引用:1]
[7]	岳立. 基于FCM的城市快速路交通状态动态识别研究[D]. 成都: 西南交通大学数学学院, 2013. Yue Li. Dynamic discrimination of urban freeway traffic state based on fuzzy C-means[D]. Chengdu: School of Mathematics, Southwest Jiaotong University, 2013. [本文引用:1]
[8]	Bi Jun, Guan Wei, Qi Long-tao. A genetic resampling particle filter for freeway traffic state estimation[J]. Chinese Physics B, 2012, 21(6): 068901. [本文引用:1]
[9]	Bi Jun, Chang Can, Fan Yang. Particle filter for estimating freeway traffic state in Beijing[J]. Mathematical Problems in Engineering, 2013, 2013: 382042. [本文引用:1]
[10]	孙静怡, 沈俊江, 刘拥华, 等. 城市快速路可变限速策略[J]. 公路交通科技, 2012, 29(11): 98-103. Sun Jing-yi, Shen Jun-jiang, Liu Yong-hua, et al. Variable speed limits strategy of urban expressway[J]. Journal of Highway and Transportation Research and Development, 2012, 29(11): 98-103. [本文引用:1]
[11]	柴干, 谢永利. 高速公路匝道多性能指标优化控制方法[J]. 中国公路学报, 2012, 25(6): 115-122. Chai Gan, Xie Yong-li. Control method of multi-performance indexes optimizing on expressway ramp metering[J]. China Journal of Highway and Transport, 2012, 25(6): 115-122. [本文引用:1]
[12]	高祥云, 柴干. 高速公路入口匝道的协调优化控制[J]. 交通运输工程与信息学报, 2013, 11(3): 106-112. Gao Xiang-yun, Chai Gan. Optimal coordination control of entry ramp of freeway[J]. Journal of Transportation Engineering and Information, 2013, 11(3): 106-112. [本文引用:1]

2015

0.0

... 然而,由于日益增长的城市交通需求,城市快速路出现了严重的交通拥挤现象,由此带来了一系列交通问题,实行交通控制是解决城市快速路交通问题的有效手段,经过多年的研究,许多关于快速路可变限速控制^[1]、入口匝道控制^[2]、出口匝道控制^[3]、多匝道协调控制^[4]的模型被提出来,并应用在快速路交通控制中,但是,现有研究都是在一天的交通中采用一种控制方案或几种控制方案,也就是说不管主线交通状态如何变化都采用一种控制方案或几种方案之间的转换,这就使得快速路交通控制的针对性不强,出现控制效果不佳的现象^[4,5] ...

2008

0.0

. 2008, 38(增刊):43-48

On-ramp metering control strategy of urban expressway

城市快速路入口匝道控制方法

Chen Xue-wen , Wang Dian-hai , Jin Sheng

陈学文, 王殿海, 金盛

Taking Beijing urban expressway system as a research object, its traffic flow characteristics were analyzed based on the survey data collected from its representative sections, and a optimization control strategy for the onramp metering was suggested. A feedback control to the onramp was realized by the ime occupancy and the vehile speed as the control variables, and using the comprehensive control effect of both parameters to determine the onramp metering rate. The critical threshold in the model was calibrated using the linear discriminant function in the pattern recognition. The suggested strategy was verified by simulation with software VISSIM. The results show that compared with those of without signal control mode, the suggested strategy increases the average speed on the mainline upstream at onramp by about 8%, and decreases the travel time on the mainline section by 7.2%.

2011

0.0

2011

0.0

2010

0.0

2008

0.0

. 2008, 38(增刊):37-42

Identification method of urban road traffic conditions based on inductive coil data

基于感应线圈数据的城市道路交通状态判别方法

Jiang Gui-yan , Guo Hai-feng , Wu Chao-teng.

姜桂艳, 郭海锋, 吴超腾

以SCOOT系统感应线圈检测器采集到的交通数据为基础，设计了一种基于模糊聚类的城市道路交通状态实时判别算法及其评价方法，并提出了交通状态判别时间间隔的确定方法。以VISSIM为工具，对上述方法进行了模拟。对比分析结果表明，所提出的算法能够提高城市道路交通状态实时判别的效果。

... 根据相关研究^[6,7],采用模糊C均值聚类方法对交通状态进行划分时,划分为3类(畅通、轻度拥挤和拥挤状态)的聚类效果最佳,所以分类数取3 ...

2013

0.0

. 2013, :- DOI:doi:10.7666/d.Y2320256

Dynamic discrimination of urban freeway traffic state based on fuzzy C-means

基于FCM的城市快速路交通状态动态识别研究[D]

Yue Li.

岳立

由于人类社会的不断发展，城市不断扩张，社会经济飞速发展，城市交通问题成为全球性问题。恰当分析道路交通，掌握实时的交通信息，不仅是交通管理者及时了解路网运行情况、及时消散突发性堵塞的基本途径，也使对交通参与者进行诱导逐渐成为可能和必要，使其避开交通拥堵、减少不必要的路上时间消耗，从而改善路网运行状况、提高道路有效使用率。现在我国很多大中城市已经具备一定规模的交通信息采集系统，采集了大量的交通数据。因此，如何从大量的交通数据中提取有用的交通信息，对交通状态进行实时的识别具有一定的研究价值。　　目前，城市交通绝大部分...

... 根据相关研究^[6,7],采用模糊C均值聚类方法对交通状态进行划分时,划分为3类(畅通、轻度拥挤和拥挤状态)的聚类效果最佳,所以分类数取3 ...

2012

0.0

... 2 快速路交通状态参数估计近年来,粒子滤波算法因其具有非线性和非高斯特性,逐渐被应用到交通状态的估计中,Bi等^[8,9]基于粒子滤波算法建立了交通状态参数估计模型,并对其进行了优化处理,估计效果较好 ...

2013

0.0

2012

0.0

. 2012, 29(11):98-103 DOI:doi:10.3969/j.issn.1002-0268.2012.11.018

Variable speed limits strategy of urban expressway

城市快速路可变限速策略

Sun Jing-yi , Shen Jun-jiang , Liu Yong-hua

孙静怡, 沈俊江, 刘拥华

The theory of variable speed limit control strategy for urban expressway was researched. Based on analysing different characteristics of speeds at mainline, entrance and exit ramps, diverge and merge of urban expressway, the model of dynamic relation between traffic speed and density of expressway mainline was set up, and the safety based constraint condition of mainline speed considering exit ramp, bad weather and road alignment was put forward. The entrance ramp control model was established by using integral regulator. Four variable speed limit target functions based on road service traffic volume, travel time, average waiting time at entrance ramp, and travel time delay were put forward. By using the linear combination of the four objective functions, three kinds of system optimal objective were established. The first is the largest capacity and the shortest travel time in low density state, the second is the largest capacity and the shortest average wait time at entrance ramp in medium density state, and the third is the shortest average wait time at entrance ramp and the shortest travel time on the main line in high density state. Finally, with VISSIM simulation software, the established model was analysed, and the results of traffic flow with/without controlled variable speed limits strategy were obtained and compared, which shows that the variable speed limit control strategy is effective.

对城市快速路可变限速控制策略的理论基础进行了研究。在对快速路上的主线车速、进出口匝道车速、分流点合流点车速的特性及速度分布特性进行深入分析的基础上，建立了快速路主线车速-密度动态关系模型，提出考虑出口匝道、不良天气以及道路线形因素下基于安全性的3种主线车速的约束条件。利用积分调节器建立了入口匝道控制模型；提出了基于道路服务流量、行程时间、入口匝道平均等待时间以及行程时间延误4种可变限速的目标函数，利用4种目标函数的线性组合建立了3种系统最优问题,即:低密度状态下路段通行能力最大，行程时间最短；中密度状态下路段通行能力最大，入口匝道平均等待时间最短；以及高密度状态下入口匝道平均等待时间最短，主线车流行程时间延误最短。利用VISSIM仿真模拟手段对可变限速控制模型进行分析，得到可变限速控制策略下与未采取控制策略下的交通流参数结果，验证了可变限速控制策略的有效性。

... 在式(1)中引入控制变量 ui,得到可变限速控制模型^[10]: ...

2012

0.0

. 2012, 25(6):115-122

Control method of multi-performance indexes optimizing on expressway ramp metering

高速公路匝道多性能指标优化控制方法

Chai Gan , Xie Yong-li.

柴干, 谢永利

Aimed at the problem of unilateral evaluation of single-performance index on expressway ramp metering, a control method of multi-performance indexes optimizing was proposed. Based on the modeling of traffic flow characteristics and control system by using METANET model, main-stream traffic efficiency, queue length and queue fairness index were designed to describe the efficiency and fairness of expressway network. According to Pareto principle, non-dominated sorting genetic algorithm Ⅱ (NSGA-Ⅱ) was introduced to optimize several performance indexes at the same time, so that the optimal solution could be found from Pareto solutions. Taking Lishui-Jiangning section of Ninghang expressway as an example, optimal solution from Pareto solutions, variation of queue length and control effect were analyzed. The results indicate that this method can consider several performance indexes comprehensively, reduce the dependence on working experience and improve the metering efficiency and fairness.

针对高速公路匝道控制中单一性能指标评价具有片面性的问题,提出了一个基于多性能指标优化的高速公路匝道控制方法。在应用METANET模型进行交通流特性与控制建模的基础上,设计了主线运营效益、排队长度和排队公平指数3个性能指标,用于描述高速公路路网的运营效率和公平性。根据Pareto原理,利用非支配性快速遗传算法对多个性能指标进行综合优化,依据所求得的较优解集筛选最优解。以宁杭高速溧水—江宁段的匝道控制为例,从Pareto最优解筛选、排队长度的变化状况、控制效果比选等方面进行了比较。分析结果表明:该方法可综合考虑多个指标,减少对工作经验的依赖,使匝道控制效果在效率和公平的博弈中达到最好。

... 在快速路交通控制中,一般将车流的总时间费用消耗TTS(Total time spend)作为控制的目标^[11],为了防止控制速度变化过大,引入速度的控制项 ∑ivctrl,i(k)-vctrl,i(k-1)vf2,得到快速路畅通状态下控制最优问题的目标函数 F1(k) ...

2013

0.0

. 2013, 11(3):106-112 DOI:doi:10.3969/j.issn.1672-4747.2013.03.018

Optimal coordination control of entry ramp of freeway

高速公路入口匝道的协调优化控制

Gao Xiang-yun , Chai Gan.

高祥云, 柴干

摘　要：为了实施高速公路路网交通流的优化控制，采用MATANET模型进行路网交通流建模，应用非线性最优控制方法，构造了路网入口匝道的协调控制模型。该模型应用全局实时交通数据，以总费用时间与密度控制的组合构建性能指标，能够提高交通运行效率，并有效处理交通拥挤。针对模型的非线性，应用遗传算法对性能指标进行优化，探究TTS-密度控制指标的优化对路网交通拥挤状况的控制效果。以南京市周边高速公路路网作为应用实例，验证了所研究模型与优化方法的可行性。

... 根据相关研究^[12],设置遗传算法相关参数如下:种群大小为100 ...