全地形铰接式履带车辆俯仰运动性能

引用本文

董超, 成凯, 胡康乐, 胡文强. 全地形铰接式履带车辆俯仰运动性能. 吉林大学学报(工学版), 2017, 47(3): 827-1705160840-2-836
DONG Chao, CHENG Kai, HU Kang-le, HU Wen-qiang. Pitching movement performance of all terrain articulated tracked vehicles. Journal of Jilin University Engineering and Technology Edition, 2017, 47(3): 827-1705160840-2-836 复制到剪切板

Doi:10.13229/j.cnki.jdxbgxb201703019
Permissions

全地形铰接式履带车辆俯仰运动性能

董超, 成凯, 胡康乐, 胡文强

吉林大学机械科学与工程学院,长春 130022

成凯(1962-),男,教授,博士生导师.研究方向:工程车辆运动学与动力学.E-mail:kaicheng62@163.com

作者简介:董超(1988-),男,博士研究生.研究方向:工程车辆运动学与动力学.E-mail:miqidongchao@163.com

基金项目:国家自然科学基金项目(51375202); 国家科技计划和重大专项基金项目(2009DFR80010)

摘要

为了准确求解全地形铰接式履带车辆俯仰运动过程中的运动学和力学相关参数,在深入研究全地形铰接式履带车辆俯仰运动机理的基础上,采用数学建模的方法建立了全地形铰接式履带车辆俯仰运动过程中的运动学和力学模型,理论上推导出用于求解前后车体最大俯仰角度、俯仰高度、重心运动轨迹半径以及车辆顺利完成俯仰运动时铰接机构所需要提供的最小拉力等的理论计算公式,并以某一具体铰接式履带车辆为例进行了数值求解。最后,采用虚拟样机技术对所建立的理论模型进行了验证,结果表明:理论计算值与虚拟样机仿真得到的结果较为接近,其相对误差均没有超过15%,满足工程实践的要求,进而验证了理论模型的正确性。该研究成果可为全地形铰接式履带车辆的结构设计和优化以及俯仰液压缸的选型等问题提供理论依据。

关键词: 机械工程; 全地形铰接式履带车辆; 俯仰运动; 运动学模型; 力学模型; 虚拟样机技术

中图分类号:TH113 文献标志码:A 文章编号:1671-5497(2017)03-0827-10

Pitching movement performance of all terrain articulated tracked vehicles

DONG Chao, CHENG Kai, HU Kang-le, HU Wen-qiang

College of Mechanical Science and Engineering, Jilin University, Changchun 130022, China

Abstract

To accurately solve the kinematic and mechanical parameters of the all terrain articulated tracked vehicle in the process of pitching movement, mathematical modeling method is adopted to establish the kinematic and mechanical models of the vehicle in pitching movement. The theoretical formulas of the maximum pitching angles, the maximum pitching heights, the motion trail radii of the centers of gravity of the front and rear vehicles, and the maximum pulling force of the articulated units are derived. Then, taking a specific articulated tracked vehicle as an example, the formulas are numerically solved. Finally, a virtual prototype of the articulated tracked vehicle is adopted to verify the theoretical models. It is shown that the theoretical and simulation results are in good agreement, the relative errors between the theoretical and simulation results do not exceed 15%. This error range meets the requirements of engineering practice. The results of this research work can provide a theoretical basis for designing and optimizing the structure of all terrain articulated tracked vehicles, and selecting the type of the pitching hydraulic cylinders.

Key words: machanical engineering; all terrain articulated tracked vehicles; pitching movement; kinematic model; mechanical model; virtual prototype technology

Show Figures

0 引言

全地形铰接式履带车辆是一类通过铰接机构将多节车厢串联在一起组成多履带行走系统的特种运输车辆, 如:瑞典生产的Bv206, 芬兰生产的NA-140, 俄罗斯生产的Vityaz-30等^{[1, 2]}。该型履带车辆不仅具有较大的载重量和更强的机动性, 还能出色地完成其他传统单履带车辆难以顺利完成的高难度动作, 如:俯仰运动、前后车体相对扭动、沼泽地形中的“ 蛇形” 移动等, 因此它被广泛地运用于农业运输、林业运输、军事以及工程建筑运输等领域, 在国防安全建设及国民经济建设等方面发挥着不可替代的作用。

目前, 国内、外学者针对全地形铰接式履带车辆开展了一系列研究工作, 如:Watanabe等^[3]研究了离心力对铰接式履带车辆转向性能的影响; Edlund等^[4]设计了一种采用新型转向架的铰接式履带车并对其转向性能进行了分析; Fijalkowski等^[5]详细介绍了全电动智能铰接式履带车, 并建立了用于研究铰接式履带车转向性能的理论模型; Yao等^[6]对六履带车辆的转向性能进行了研究; 吉林大学成凯等^{[7, 8]}利用有限元软件对铰接式履带车辆的关键零部件在特定工况下的刚度、强度进行了分析; 中南大学陈波^[9]和张敏^[10]对铰接式履带采矿车辆的运动轨迹的规划和控制等问题进行了研究。虽然上述研究取得了一定的阶段性成果, 但是现阶段的研究工作较少涉及对铰接式履带车辆俯仰运动性能的研究。铰接式履带车属于非公路运输车辆, 其行驶路况大多数是以一些地形地貌较为恶劣的山地、丛林地带为主, 因此在某些特定的极限路况下(如:壕沟、山冈等), 铰接式履带车辆只能采用俯仰运动才能顺利通过。所以, 从工程实际的角度出发研究铰接式履带车辆俯仰运动性能对车辆总体结构的设计和优化以及车辆通过性能的评价等具有重要的现实意义, 同时也对促进铰接式履带车辆行驶力学的发展具有重要理论意义。

为了建立一套确实可行的用于求解铰接式履带车辆俯仰运动过程中的运动学和力学相关参数的理论方法, 本文在深入研究铰接式履带车辆俯仰运动机理的基础上, 采用数学建模的思想建立了铰接式履带车辆俯仰运动过程中的运动学和力学模型, 从理论上推导出用于求解前后车体最大俯仰角度、俯仰高度、重心运动轨迹半径以及车辆完成俯仰运动时铰接机构所需提供的最小拉力等的理论公式, 并以某一具体车型为例进行了数值求解。最后, 采用多体动力学软件Recurdyn建立铰接式履带车虚拟样机模型对理论模型进行了验证。本文研究成果可为铰接式履带车辆的结构设计和优化以及液压缸的选型等问题提供理论依据。

1 铰接式履带车辆满载状态下前、后车体重心位置的确定

铰接式履带车辆通常采用串联形式进行布置, 它由前车体、铰接机构以及后车体3部分构成(见图1)。

在分析铰接式履带车辆俯仰运动性能之前需要准确地计算出车辆满载工作状态下前、后车体的重心位置。为了便于研究, 分别以前车驱动轮的轮毂中心O₁₁和后车驱动轮的轮毂中心O₂₂为坐标原点建立局部坐标系O₁₁-x₁O₁₁y₁、O₂₂-x₂O₂₂y₂, 如图1所示。图1中, G₁和G₂分别为车辆满载状态下前、后车体的重心; G₃和G₄分别为车辆空载状态下前、后车体的重心; G₅和G₆分别为前、后货厢的重心。

根据多质点系统重心求解公式, 可以求得铰接式履带车辆满载工作状态下前车重心位置G₁的坐标(x₁₁, y₁₁)和后车重心位置G₂的坐标(x₂₂, y₂₂)分别为^{[11, 12]}:

$\{\begin{array}{l} x_{11} = \overset{2}{\sum_{i = 1}} m_{ii} x_{i} / \overset{2}{\sum_{i = 1}} m_{ii} \\ y_{11} = \overset{2}{\sum_{i = 1}} m_{ii} y_{i} / \overset{2}{\sum_{i = 1}} m_{ii} \end{array}$ (1)

$\{\begin{array}{l} x_{22} = \overset{4}{\sum_{j = 3}} m_{jj} x_{j} / \overset{4}{\sum_{j = 3}} m_{jj} \\ y_{22} = \overset{4}{\sum_{j = 3}} m_{jj} y_{j} / \overset{4}{\sum_{j = 3}} m_{jj} \end{array}$ (2)

式中:m₁₁、m₄₄分别为前、后车体空载时的质量; m₂₂、m₃₃分别为前、后车体载货时的质量; x₁和y₁分别为G₃的横、纵坐标值; x₂和y₂分别为G₄的横、纵坐标值; x₃和y₃分别为G₅的横、纵坐标值; x₄和y₄分别为G₆的横、纵坐标值。

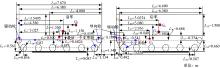	Figure Option View Download New Window
	图1 铰接式履带车结构示意图以及主要尺寸参数Fig.1 Structure diagram and major dimension parameters of articulated tracked vehicle

表1给出了铰接式履带车各部分的质量以及各部分重心位置的坐标值。

表1 铰接式履带车各部分的质量和重心位置的坐标值 Table 1 Parameters of gravity centers and quality of vehicle

将表1中的相关参数代入式(1)(2)中便可以求得G₁和G₂的坐标(m)分别为:

$\{\begin{array}{l} x_{11} = 3.5495 \\ y_{11} = 0.6824 \end{array}$ (3)

$\{\begin{array}{l} x_{22} = 3.0254 \\ y_{22} = 0.6880 \end{array}$ (4)

此时, 铰接式履带车辆满载工作状态下前、后车体的质量(kg)分别为:

$\{\begin{array}{l} m_{G_{1}} = m_{11} + m_{22} = 19000 + 12000 = 31000 \\ m_{G_{2}} = m_{33} + m_{44} = 18000 + 11000 = 29000 \end{array}$ (5)

2 铰接式履带车辆俯仰运动时的运动学模型

为了便于研究, 作如下假设:

(1)铰接式履带车辆在水平面上始终保持稳态俯仰运动。

(2)铰接式履带车辆作稳态俯仰运动过程中各条履带不发生弹性变形。

(3)不考虑土壤沉陷变形对车辆俯仰运动的影响。

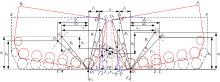
铰接式履带车辆作俯仰运动时, 前、后车体的驱动轮均处于自锁状态, 此时前车体绕着前车体最后一个支重轮的接地点O₁俯仰θ ₁角, 后车体绕着后车体第一个支重轮的接地点O₂俯仰θ ₂角; 前、后车体由位置Ⅰ 同时运动到位置Ⅱ 处, 前车体的重心G₁沿着半径为R₁的圆弧1绕过θ ₁角运动到G'₁处, 后车体的重心G₂沿着半径为R₃的圆弧4绕过θ ₂角运动到G'₂处; 前、后车体的履带接地段O₁A和O₂S分别绕O₁、O₂点转过θ ₁、θ ₂角到达A₁、S₁位置处(如图2所示)。图2中R₁、R₃分别为前、后车体重心G₁和G₂的运动轨迹半径; R₂、R₄分别为前、后车厢端点C和D的运动轨迹半径; θ ₁、θ ₂分别为前、后车体的俯仰角度; h₃、h₄分别为前、后车体的俯仰高度; Δ x₁、Δ y₁分别为前车体重心G₁的横向和纵向运动距离; Δ x₂、Δ y₂分别为后车体重心G₂的横向和纵向运动距离。

从图2中的运动学关系可以看出:车辆俯仰运动过程中, 当前车厢末端点C与后车厢前端点D相互发生干涉时(即C点和D点同时运动到圆弧2与圆弧3相交点O)或者前后车体的导向轮和后车体的驱动轮都和地面相互接触时前后车体的俯仰角度达到最大值。此时存在如下关系:

$\{\begin{array}{l} 0 \leq n_{1} + n_{2} \leq u \\ 0 \leq m_{1} \leq h_{1} \\ 0 \leq m_{2} \leq h_{2} \end{array}$ (6)

式中:n₁、n₂分别为车辆俯仰运动时C、D点的横向移动距离; m₁、m₂分别为车辆俯仰运动时C、D点的纵向移动距离; u分别为C、D点的初始距离; h₁、h₂分别为前车体的导向轮和后车体的驱动轮距离水平面的高度。

根据图2中的几何关系, 可以求得n₁、n₂、m₁、m₂分别为:

	Figure Option View Download New Window
	图2 铰接式履带车辆俯仰运动时的运动学模型Fig.2 Kinematic model of articulated tracked vehicle in process of pitch movement

$\{\begin{array}{l} n_{1} = l_{C_{1} M} = l_{EF} = l_{O_{1} F} - l_{O_{1} E} \\ n_{2} = l_{D_{1} N} = l_{HK} = l_{O_{2} K} - l_{O_{2} H} \\ m_{1} = l_{CM} = l_{CE} - l_{C_{1} F} \\ m_{2} = l_{DN} = l_{DH} - l_{D_{1} K} \end{array}$ (7)

式中: $l_{O_{1} F}$ , $l_{O_{2} K}$ , $l_{C_{1} F}$ 和 $l_{D_{1} K}$ 可以根据直角三角形的边角关系求得, 分别对Rt△ CO₁E、Rt△ C₁O₁F、Rt△ DO₂H和Rt△ D₁O₂K求解可以得到如下关系:

$\{\begin{array}{l} R_{2} = \sqrt[]{l_{CE}^{2} + l_{O_{1} E}^{2}} \\ R_{4} = \sqrt[]{l_{DH}^{2} + l_{O_{2} H}^{2}} \\ tan∠ C O_{1} E = l_{CE} / l_{O_{1} E} \\ tan∠ D O_{2} H = l_{DH} / l_{O_{2} H} \\ ∠ C_{1} O_{1} F = ∠ C O_{1} E - θ_{1} \\ ∠ D_{1} O_{2} K = ∠ D O_{2} K - θ_{2} \\ l_{C_{1} F} = R_{2} sin∠ C_{1} O_{1} F \\ l_{D_{1} K} = R_{4} sin∠ D_{1} O_{2} K \\ l_{O_{1} F} = R_{2} cos∠ C_{1} O_{1} F \\ l_{O_{2} K} = R_{4} cos∠ D_{1} O_{2} K \end{array}$ (8)

式中:R₂为前车厢末端点C的运动轨迹半径; R₄为后车厢末端点D的运动轨迹半径。

将式(7)(8)代入式(6)中, 可以求出前、后车体俯仰角度的变化范围为:

$\{\begin{array}{l} l_{O_{1} E} + l_{O_{2} H} \leq R_{2} \cos [\arctan (l_{CE} / l_{O_{1} E}) - θ_{1}] + \\ R_{4} \cos [\arctan (l_{DH} / l_{O_{2} H}) - \\ θ_{2}] \leq u + l_{O_{1} E} + l_{O_{2} H} \\ 0 \leq l_{CE} - R_{2} \sin [\arctan (l_{CE} / l_{O_{1} E}) - θ_{1}] \leq h_{1} \\ 0 \leq l_{DH} - R_{4} \sin [\arctan (l_{DH} / l_{O_{2} H}) - θ_{2}] \leq h_{2} \end{array}$ (9)

当前、后车体分别俯仰θ ₁角和θ ₂角时, 前、后车体重心G₁、G₂的位置变化关系可以分别表示为:

$\{\begin{array}{l} Δ x_{1} = l_{O_{1} T} - l_{O_{1} W} \\ Δ y_{1} = l_{G'_{1} W} - l_{G_{1} T} \end{array}$ (10)

$\{\begin{array}{l} Δ x_{2} = l_{O_{2} T_{1}} - l_{O_{2} Z} \\ Δ y_{2} = l_{G'_{2} Z} - l_{G_{2} T_{1}} \end{array}$ (11)

式中:Δ x₁、Δ x₂分别为车辆俯仰运动时前车重心G₁和后车重心G₂的横向移动距离; Δ y₁、Δ y₂分别为车辆俯仰运动时前车重心G₁和后车重心G₂的纵向移动距离。

式(10)(11)中的 $l_{O_{1} W}$ , $l_{O_{2} Z}$ , $l_{G'_{1} W}$ 和 $l_{G'_{2} Z}$ 可以根据Rt△ G'₁O₁W、Rt△ G'₂O₂Z、Rt△ G₁O₁T和Rt△ G₂O₂T₁的边角关系求得:

$\{\begin{array}{l} R_{1} = \sqrt[]{l_{G_{1} T}^{2} + l_{O_{1} T}^{2}} \\ R_{3} = \sqrt[]{l_{G_{2} T_{1}}^{2} + l_{O_{2} T_{1}}^{2}} \\ tan∠ G_{1} O_{1} T = l_{G_{1} T} / l_{O_{1} T} \\ tan∠ G_{2} O_{2} T_{1} = l_{G_{2} T_{1}} / l_{O_{2} T_{1}} \\ ∠ G'_{1} O_{1} W = ∠ G_{1} O_{1} T + θ_{1} \\ ∠ G'_{2} O_{2} Z = ∠ G_{2} O_{2} T_{1} + θ_{2} \\ l_{G'_{1} W} = R_{1} \sin [\arctan (l_{G_{1} T} / l_{O_{1} T}) + θ_{1}] \\ l_{G'_{2} Z} = R_{3} \sin [\arctan (l_{G_{2} T_{1}} / l_{O_{2} T_{1}}) + θ_{2}] \\ l_{O_{1} W} = R_{1} \cos [\arctan (l_{G_{1} T} / l_{O_{1} T}) + θ_{1}] \\ l_{O_{2} Z} = R_{3} \cos [\arctan (l_{G_{2} T_{1}} / l_{O_{2} T_{1}}) + θ_{2}] \end{array}$ (12)

将式(12)代入式(10)(11)可以求得前、后车体重心G₁和G₂的位置变化分别为:

$\{\begin{array}{l} Δ x_{1} = l_{O_{1} T} - R_{1} \cos [\arctan (l_{G_{1} T} / l_{O_{1} T}) + θ_{1}] \\ Δ y_{1} = R_{1} \sin [\arctan (l_{G_{1} T} / l_{O_{1} T}) + θ_{1}] - l_{G_{1} T} \end{array}$ (13)

$\{\begin{array}{l} Δ x_{2} = l_{O_{2} T_{1}} - R_{3} \cos [\arctan (l_{G_{2} T_{1}} / l_{O_{2} T_{1}}) + θ_{2}] \\ Δ y_{2} = R_{3} \sin [\arctan (l_{G_{2} T_{1}} / l_{O_{2} T_{1}}) + θ_{2}] - l_{G_{2} T_{1}} \end{array}$ (14)

此时, 前、后车体俯仰高度可以分别表示为:

$\{\begin{array}{l} h_{3} = l_{O_{1} A_{1}} \times \sin θ_{1} \\ h_{4} = l_{O_{2} S_{1}} \times \sin θ_{2} \end{array}$ (15)

表2给出了求解铰接式履带车辆俯仰运动时的运动学模型涉及到的参数。

表2 求解运动学模型时涉及到的参数 Table 2 Involved parameters of solving kinematic model m

参数	计算过程及数值
$l_{O_{1} E}$	f₁=L₁₄=1.134
$l_{O_{2} H}$	L₂₂+L₂₃-L₂₄=0.856+6.6-6.38=1.076
u	L₁₈+L₁₉+L₂₄-L₂₃= 1.348+0.482-6.6+6.38=1.61
l_CE	L₇+L₈+L₁₇+L₁₃= 1.3+0.5+0.561+0.087=2.448
l_DH	L₃₅+L₃₁+L₃₄+L₃₂= 1.5+0.334+0.66+0.087=2.581
h₁	L₁₇+L₁₃=0.561+0.087=0.648
h₂	L₃₄+L₃₂=0.66+0.087=0.747
$l_{O_{1} T}$	L₂-L₄-L₁₄=6.38-3.5495-1.134=1.6965
$l_{O_{2} T_{1}}$	L₂₅-L₂₂=3.0254-0.856=2.1694
$l_{G_{1} T}$	L₁₀+L₁₇+L₁₃=0.6824+0.561+0.087=1.3304
$l_{G_{2} T_{1}}$	L₃₀+L₃₄+L₃₃=0.688+0.66+0.087=1.435
$l_{O_{1} A_{1}}$	L₂-L₁₄-L₁₅+0.5× L₁₆= 6.38-1.134-0.846+0.5× 0.83=4.815
$l_{O_{2} S_{1}}$	L₃₃-L₂₂+0.5× L₁₆= 5.372-0.846+0.5× 0.83=4.931

表2 求解运动学模型时涉及到的参数 Table 2 Involved parameters of solving kinematic model m

将表2中的数据代入式(6)~(15)中可以计算出铰接式履带车辆俯仰运动过程中的各个运动学参数为:

R₁= $\sqrt[]{1 . 3304^{2} + 1 . 6965^{2}}$ =2.1559 m

R₂= $\sqrt[]{2 . 448^{2} + 1 . 134^{2}}$ =2.6979 m

R₃= $\sqrt[]{1 . 435^{2} + 2 . 1694^{2}}$ =2.6011 m

R₄= $\sqrt[]{2 . 581^{2} + 1 . 076^{2}}$ =2.7963 m

0° ≤ θ ₁≤ 23.2945°

0° ≤ θ ₂≤ 26.3837°

Δ x_1max=1.6965-2.1559cos[arctan(1.3304/1.6965)+23.2945° ]=0.6645 m

Δ y_1max=2.1559sin[arctan(1.3304/1.6965)+23.2945° ]-1.3304=0.5624 m

Δ x_2max=2.1694-2.6011cos[arctan(1.435/2.1694)+26.3837° ]=0.8636 m

Δ y_2max=2.6011sin[arctan(1.435/2.1694)+ 26.3837° ]-1.435=0.9192 m

h_3max=4.815× sin23.2945° =1.904 m

h_4max=4.931× sin26.3837° =2.1912 m

3 铰接履带车作俯仰运动时的力学模型

铰接式履带车辆作稳态俯仰运动过程中前、后车体受到的外力主要包括:前、后车车体自身的重力(F₁和F₂)、俯仰液压缸对前、后车体产生的拉力(F₅和F₆)、支重轮受到来自地面的摩擦力(F_u₁和F_u₂)以及地面对支重轮产生的支撑力(F₃和F₄), 具体如图3所示。图3中存在如下关系:∠UO₁J=∠θ ₁, ∠UO₁J+∠O₁JU=90° , ∠EGU+∠O₁JU=90° , ∠UO₁J=∠EGU=∠θ ₁, ∠VO₂R+∠VRO₂=90° , ∠VZ₁H+∠VRO₂=90° , ∠VZ₁H=∠VO₂R=∠θ ₂。

当铰接履带车辆作稳态俯仰运动时前、后车体在任意时刻车体质心处受力是平衡的, 因此存在如下力学关系:

$\{\begin{array}{l} F_{1} + F_{5 y} - F_{3} = 0 \\ F_{5 x} + F_{u 1} = 0 \\ F_{3} l_{O_{1} W} + F_{u 1} l_{G'_{1} W} - F_{5 y} l_{UW} + k_{1} F_{5 x} = 0 \end{array}$ (16)

$\{\begin{array}{l} F_{2} - F_{6 y} - F_{4} = 0 \\ F_{6 x} + F_{u 2} = 0 \\ F_{4} l_{O_{2} Z} + F_{u 2} l_{G'_{2} Z} + F_{6 y} e_{2} + k_{2} F_{6 x} = 0 \end{array}$ (17)

式中:F₁、F₂分别为前、后车体的重力, F₁= $m_{G_{1}}$ g, F₂=m_G₄g, g=9.8 m/s²; F_u₁、F₃分别为前车体最后一个支重轮受到来自地面的摩擦力和支撑力; F_u₂、F₄分别为后车体第一个支重轮受到来自地面的摩擦力和支撑力; F₅_x、F₅_y、F₆_x、F₆_y分别为俯仰液压缸对前、后车体产生的拉力在水平面内和垂直面内上的分量, 可以用以下公式进行求解:

$\{\begin{array}{l} F_{5 x} = \cos β \times F_{5} \\ F_{5 y} = \sin β \times F_{5} \end{array}$ (18)

$\{\begin{array}{l} F_{6 x} = \cos β \times F_{6} \\ F_{6 y} = \sin β \times F_{6} \end{array}$ (19)

式(16)(17)中k₁、l_UW、e₂和k₂可以根据图3中的几何关系求得, 即:

	Figure Option View Download New Window
	图3 铰接式履带车辆俯仰运动时的力学模型Fig.3 Mechanical model of articulated tracked vehicle in process of pitch movement

$\{\begin{array}{l} k_{1} = l_{G'_{1} W} - l_{GU} \\ k_{2} = l_{G'_{2} Z} - l_{Z_{1} V} \\ l_{UW} = l_{O_{1} W} + l_{O_{1} E} + l_{EU} \\ e_{2} = l_{O_{2} Z} + l_{O_{2} H} + l_{HV} \end{array}$ (20)

将式(19)(20)代入式(16)(17)可以求得铰接式履带车辆俯仰运动时前、后车体所需要提供的最小拉力分别为:

$\{\begin{array}{l} F_{5} = F_{1} l_{O_{1} W} / [l_{G'_{1} W} \cos β + (l_{O_{1} W} + l_{O_{1} E} + \\ l_{EU}) \sin β - (l_{G'_{1} W} - l_{GU}) \cos β - l_{O_{1} W} \sin β] \\ F_{6} = F_{2} l_{O_{2} Z} / [l_{O_{2} Z} \sin β + l_{G'_{2} Z} \cos β - (l_{O_{2} Z} + \\ l_{O_{2} H} + l_{HV}) \sin β - (l_{G'_{2} Z} - l_{Z_{1} V}) \cos β] \end{array}$ (21)

式中:l_EU、l_HV、l_GU和 $l_{Z_{1} V}$ 可以根据Rt△ O₁JU、Rt△ GIJ、Rt△ Z₁RQ、Rt△ O₂VR、Rt△ LEU和Rt△ Z₁VH的边角关系求得:

$\{\begin{array}{l} l_{O_{1} U} = l_{UJ} \cot θ_{1} \\ l_{EU} = l_{O_{1} U} - l_{O_{1} E} = l_{UJ} \cot θ_{1} - l_{O_{1} E} \\ l_{GU} = \cot θ_{1} l_{EU} = \cot θ_{1} (l_{UJ} \cot θ_{1} - l_{O_{1} E}) \\ l_{O_{2} V} = l_{VR} \cot θ_{2} \\ l_{HV} = l_{O_{2} V} - l_{O_{2} H} = l_{VR} \cot θ_{2} - l_{O_{2} H} \\ l_{Z_{1} V} = \cot θ_{2} l_{HV} = \cot θ_{2} (l_{VR} \cot θ_{2} - l_{O_{2} H}) \end{array}$ (22)

由于前、后车俯仰角度θ ₁和θ ₂角度较小, 因此铰接式车辆在俯仰过程中可以近似认为l_JU=l_CM, l_DN=l_VR。

式(21)中β 可以根据图3中的几何关系求得, 通过求解Rt△ GLZ₁可以求得β 为:

$β = \arctan (l_{GL} / l_{L Z_{1}})$ (23)

式中:l_GL和 $l_{L Z_{1}}$ 可以表示为:

$\{\begin{array}{l} l_{GL} = l_{GU} - l_{LU} \\ l_{L Z_{1}} = l_{UV} = l_{O_{2} H} + l_{EH} + l_{O_{1} E} - l_{O_{1} U} - l_{O_{2} V} \end{array}$ (24)

将式(7)(22)(24)代入式(23)中, β 可以表示为:

$β = \arctan (A / B)$ (25)

式中:

A=l_CEcot²θ ₁-R₂sin[arctan(l_CE/ $l_{O_{1} E}$ )-θ ₁]cot²θ ₁- $l_{O_{1} E}$ cotθ ₁-l_DHcot²θ ₂+

R₄sin[arctan(l_DH/ $l_{O_{2} H}$ )-θ ₂]cot²θ ₂+ $l_{O_{2} H}$ cotθ ₂;

B= $l_{O_{1} E}$ + $l_{O_{2} H}$ +u-l_CEcotθ ₁+R₂sin[arctan(l_CE/ $l_{O_{1} E}$ )-θ ₁]cotθ ₁-l_DHcotθ ₂+R₄sin[arctan(l_DH/ $l_{O_{2} H}$ )-θ ₂]cotθ ₂

表3给出了求解铰接式履带车辆俯仰运动时的力学模型涉及到的参数。

表3 求解力学模型时涉及到的参数 Table 3 Involved parameters of solving mechanical model m

参数	计算过程及数值
$l_{O_{1} W}$	L₂-L₄-L₁₄-Dx₁= 6.38-3.5495-1.134-0.6645=1.032
$l_{G'_{1} W}$	L₁₀+L₁₇+L₁₃+Dy₁= 0.6824+0.561+0.087+0.5624=1.8928
$l_{O_{2} Z}$	L₂₅-L₂₂-Dx₂= 3.0254-0.856-0.8636=1.3058
$l_{G'_{2} Z}$	L₃₀+L₃₄+L₃₃+Dy₂= 0.688+0.66+0.087+0.9192=2.3542

表3 求解力学模型时涉及到的参数 Table 3 Involved parameters of solving mechanical model m

将表3中的数据代入式(16)~式(25)中, 且前、后车体的俯仰角度分别取最大值(θ ₁=23.2945° , θ ₂=26.3837° )时, 可以计算出铰接式履带车辆俯仰运动时前后车体所需要的最小拉力(kN)分别为:

$\{\begin{array}{l} F_{5} = 361.38 \\ F_{6} = 431.14 \end{array}$ (26)

由于铰接式履带车辆俯仰运动过程中前、后车体所需要的拉力是由两个液压缸共同提供。因此车辆顺利完成俯仰运动时单个俯仰液压缸所需要提供的最小压力为:

$P_{1} (s_{1} - s_{2}) = P_{1} (π D_{1}^{2} / 4 - π d_{1}^{2} / 4) = \max {F_{5}, F_{6}} / 2$ （27）

式中:P₁为俯仰液压缸内压力; D₁为俯仰液压缸的缸筒直径; d₁为俯仰液压缸的活塞杆的直径。

若选定俯仰液压缸的缸筒直径D₁=180 mm, 俯仰液压缸的活塞杆的直径d₁=65 mm, 将其代入式(27)中, 可以求得车辆顺利完成俯仰运动时俯仰液压缸需要的最小压力(MPa)为:

$\begin{array}{l} P_{1} (π D_{1}^{2} / 4 - π d_{1}^{2} / 4) = \max {F_{5}, F_{6}} / 2 \Rightarrow \\ P_{1} = \frac{\max {F_{5}, F_{6}} / 2}{(π D_{1}^{2} / 4 - π d_{1}^{2} / 4)} \Rightarrow \\ P_{1} = \frac{431.14 \times 10^{3} / 2}{3.14 \times (0 . 18^{2} - 0 . 065^{2}) / 4} = 9.75 \end{array}$ （28）

综上所述, 铰接式履带车辆的俯仰液压缸的基本参数为:D₁=180 mm; d₁=65 mm; P₁=15 MPa; 俯仰液压缸内液压油的流量Q=236 L/min。

4 铰接式履带车俯仰运动仿真分析

虚拟样机仿真技术不仅可以直观地反映出车辆的运动状态, 更重要的是它不需要昂贵的试验费用就能获得较高精度的结果^{[13, 14]}。因此, 本文采用Recurdyn软件建立铰接式履带车辆的虚拟样机仿真模型来验证理论模型的有效性。

铰接式履带车辆的虚拟样机仿真模型由前车体、后车体、铰接机构、4条履带系统以及行驶路面5部分组成。其参数设定如下:地面设定为硬质路面; 前、后车体的质量分别设定为31000和29000 kg; 前车体重心位置相对于前车驱动轮的坐标值设定为(3.5495, 0.6824, -1.6), 后车体重心位置相对于后车驱动轮的坐标值设定为(3.0254, 0.6880, -1.6); 俯仰液压缸的基本参数设定参见第3节。铰接机构与车体连接点处的运动副设定为转动副, 转向液压缸与俯仰液压缸处添加平动副, 具体如图4所示。仿真过程中, 设定仿真时间T为8 s。

	Figure Option View Download New Window
	图4 铰接机构处运动副添加情况Fig.4 Deputy campaigns of articulated unit

图5给出了俯仰液压缸的控制原理图, 其控制原理如下:当弹簧A伸长, 弹簧B缩短时, 压力油从第2个换向阀的A₃₃通道流入, 此时压力油同时进入第1和第2个俯仰液压缸的活塞杆端孔口中, 这样两个俯仰液压缸同时收缩, 车辆实现俯仰运动。当弹簧A缩短, 弹簧B伸长时, 压力油从第2个换向阀的B₃₃通道流入, 此时压力油同时进入第1和第2个俯仰液压缸的活塞孔口中, 这样两个俯仰液压缸同时伸长, 车辆逐渐恢复到水平状态。

	Figure Option View Download New Window
	图5 俯仰液压缸的控制原理示意图Fig.5 Control schematic of pitching hydraulic cylinders

图6给出了虚拟样机仿真模型得到的铰接式履带车辆俯仰运动位姿变化情况。图6(a)为铰接式履带车辆初始位置, 此时车辆尚未开始俯仰运动。图6(b)为车辆俯仰运动过程中前、后车体位姿变化情况。从图6中可以看出:铰接式履带车辆在俯仰液压缸驱动下, 前车体以最后一个支重轮的接地点为旋转中心向上作俯仰运动, 后车体则以第一个支重轮的接地点为旋转中心向上作俯仰运动。

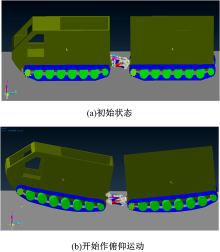	Figure Option View Download New Window
	图6 虚拟样机仿真模型得到的铰接式履带车辆俯仰运动过程中前、后车体的位姿变化情况Fig.6 Position changes of front and rear vehicles in process of pitching movement by using virtual prototype simulation model

图7给出了铰接式履带车辆俯仰运动过程中前、后车体的重心位置变化轨迹。从图7中可以看出:前、后车体的重心轨迹运动半径的仿真结果与理论计算值较为接近, 两者的误差未超过10%; 前、后车体的最大俯仰角度的仿真结果与理论计算值也较为接近, 两者的误差均未超过8%, 进而说明了上述理论计算结果的有效性。

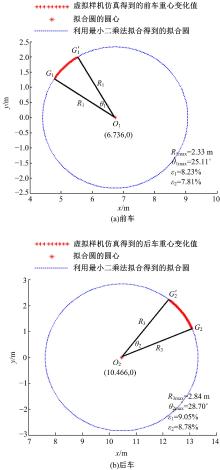	Figure Option View Download New Window
	图7 虚拟样机仿真模型得到的铰接式履带车辆俯仰运动过程中前、后车重心运动轨迹Fig.7 Moving trajectory of gravity centers of front and rear vehicles in process of pitching movement by using virtual prototype simulation model

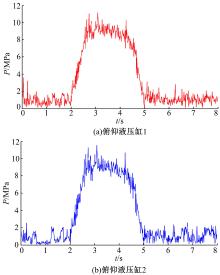	Figure Option View Download New Window
	图8 虚拟样机仿真得到的车辆俯仰运动过程中俯仰液压缸内压力值的变化曲线Fig.8 Pressure change curves of hydraulic cylinders in process of pitching movement by using virtual prototype simulation model

图8为铰接履带车辆俯仰运动过程中俯仰液压缸内压力值的变化曲线。从图8中可以看出:车辆俯仰运动过程中俯仰液压缸内压力值的变化历经了4个阶段:①T为0~2 s阶段, 俯仰液压缸1和俯仰液压缸2内的压力值为0 MPa, 此阶段为车辆处于俯仰运动的准备阶段, 车辆尚未进行俯仰运动。②T为2~3 s阶段, 俯仰液压缸1和俯仰液压缸2内的压力值急剧增大, 此阶段铰接履带车辆正在进行俯仰运动。③T为3~5 s阶段, 俯仰液压缸1和俯仰液压缸2内的压力值趋于平稳状态且压力值达到最大值, 此阶段铰接履带车辆俯仰运动达到了最大位置, 此时俯仰液压缸1和俯仰液压缸2内的压力值主要集中于10 Mpa范围内变化, 其仿真结果与理论计算值(9.75 MPa)较为接近, 相对误差范围为2.56%, 在工程实践中该误差范围可以接受, 从而证明了上述理论计算方法的有效性。④T为5~8 s阶段, 俯仰液压缸1和俯仰液压缸2内的压力值逐渐减小, 最后为0 MPa, 此时铰接履带车逐渐返回初始位置, 完成俯仰运动。

表4给出了铰接式履带车辆俯仰运动时运动学和力学相关参数的理论计算值与仿真值之间的对比结果。从表4中数据可以看出:理论计算值与仿真结果较为接近, 其相对误差都没有超过15%, 误差在可以接受的范围之内, 从而验证了理论模型的正确性。

表4 理论计算值与仿真结果对比 Table 4 Theoretical calculated value compared with simulation results

5 结论

(1)在深入研究全地形铰接式履带车辆俯仰运动特性的基础之上, 采用数学建模的思想建立了铰接式履带车辆俯仰运动过程中的运动学模型, 从理论上推导出用于求解前后车体最大俯仰角度、俯仰高度、重心运动轨迹半径等参数的数学公式, 可以为求解分析铰接式履带车辆俯仰运动过程中的运动学相关参数、俯仰液压缸的有效行程以及设计俯仰液压缸几何尺寸等问题提供理论依据。

(2)在深入分析铰接式履带车辆俯仰运动过程中车体受力情况的基础上, 建立了铰接式履带车辆俯仰运动过程中的力学模型, 从理论上推导出用于求解分析车辆俯仰运动时所需要的最小拉力、单个液压缸所需提供的最小压力等的计算公式, 可以为铰接机构的设计和优化、俯仰液压缸最小压力的选择以及俯仰液压缸的选型问题等提供理论依据。

(3)采用虚拟样机技术验证了所建理论模型的有效性, 说明该方法适用于分析铰接式履带车辆俯仰运动过程中的运动学和力学相关问题, 从对比虚拟样机仿真结果与理论计算值吻合度可知:在工程实践误差允许的范围之内, 采用虚拟样机对铰接式履带车辆行驶力学分析也是一种高效、快捷的方法。

The authors have declared that no competing interests exist.

参考文献

View Option

[1]	Janarthanan B, Padmanabhan C, Sujatha C. Longitudinal dynamics of a tracked vehicle: simulation and experiment[J]. Journal of Terramechanics, 2012, 49(2): 63-72. [本文引用:1]
[2]	郑鑫, 姚寿文. 全地形履带车橡胶扭力轴套扭转刚度特性研究[J]. 汽车工程学报, 2013, 3(2): 125-132. Zheng Xin, Yao Shou-wen. Research on torsional stiffness of rubber torsion bushing for all-terrain tracked vechicle[J]. Chinese Journal of Automotive Engineering, 2013, 3(2): 125-132. [本文引用:1]
[3]	Watanabe K, Kitano M. Study on steerability of articulated tracked vehicles, part1: theoretical and experimental analysis[J]. Journal of Terramechanics, 1986, 23(2): 69-83. [本文引用:1]
[4]	Edlund J, Keramati E, Servin M. A long-tracked bogie design for forestry machines on soft and rough terrain[J]. Journal of Terramechanics, 2013, 50(2): 73-83. [本文引用:1]
[5]	Fijalkowski B T. Novel mobility and steerability enhancing concept of all-electric intelligent articulated tracked vehicles[C]//2003 IEEE Intelligent Vehicles Symposium, Columbus, USA, 2003: 225-230. [本文引用:1]
[6]	Yao Zong-wei, Wang Guo-qiang, Guo Rui, et al. Theory and experimental research on six-track steering vehicles[J]. Vehicle System Dynamics: International Journal of Vehicle Mechanics and Mobility, 2013, 51(2): 218-235. [本文引用:1]
[7]	魏小强, 成凯, 林源. 某型履带式运输车扭杆悬挂装置力学性能分析与优化[J]. 汽车工程, 2012, 34(1): 67-71. Wei Xiao-qiang, Cheng Kai, Lin Yuan. Mechanical performance analysis and optimization of the torsion bar suspension system in an articulated tracked carrier[J]. Automotive Engineering, 2012, 34(1): 67-71. [本文引用:1]
[8]	成凯, 魏小强, 李贵助. 铰接履带式运输车转向俯仰装置强度刚度分析[J]. 长安大学学报: 自然科学版, 2013, 33(2): 95-100. Cheng Kai, Wei Xiao-qiang, Li Gui-zhu. Strength and stiffness analysis of articulated steeringand pitching device on the all-terrain articulated tracked carrier[J]. Journal of Chang'an University(Natural Science Edition), 2013, 33(2): 95-100. [本文引用:1]
[9]	陈波. 钴结壳采矿车行走路径控制研究[D]. 长沙: 中南大学机电工程学院, 2012. Chen Bo. Research on tracking predetermined path for the cobalt crust mining vehicle[D]. Changsha: College of Mechanical and Electrical Engineering, Central South University, 2012. [本文引用:1]
[10]	张敏. 基于模糊神经网络的海底采矿车路径跟踪行走控制研究[D]. 长沙: 中南大学机电工程学院, 2010. Zhang Min. The walking path following control of the seabed mining vehicle research based on the fuzzy neural network[D]. Changsha: College of Mechanical and Electrical Engineering, Central South University, 2010. [本文引用:1]
[11]	杨一岱, 荆武兴, 刘玥. 挠性航天器浮动质心动力学建模[J]. 哈尔滨工业大学学报, 2015, 47(5): 7-12. Yang Yi-dai, Jing Wu-xing, Liu Yue. Dynamic modeling of flexible spacecraft based on floating centroid system[J]. Journal of Harbin Institute of Technology, 2015, 47(5): 7-12. [本文引用:1]
[12]	王志强, 姜洪源, Roman Kamnik. 康复机器人辅助站立人体质心动量测试及模拟[J]. 吉林大学学报: 工学版, 2015, 45(3): 844-850. Wang Zhi-qiang, Jiang Hong-yuan, Roman Kamnik. Experiment and simulation on body center-of-mass momentum during sit-to-stand assistedby rehabilitation robot[J]. Journal of Jilin University (Engineering and Technology Edition), 2015, 45(3): 844-850. [本文引用:1]
[13]	Omar M A. Chain drive simulation using spatial multibody dynamics[J]. Advances in Mechanical Engineering, 2014, 6: 378030. [本文引用:1]
[14]	Cheng Y B, Yin S B, Wang X P, et al. Design and analysis of double-side meshing and dual-phase driving timing silent chain system[J]. Journal of Mechanical Engineering, 2016, 62(2): 127-136. [本文引用:1]

2012

0.0

... 0 引言全地形铰接式履带车辆是一类通过铰接机构将多节车厢串联在一起组成多履带行走系统的特种运输车辆,如:瑞典生产的Bv206,芬兰生产的NA-140,俄罗斯生产的Vityaz-30等^[1,2] ...

2013

0.0

. 2013, 3(2):125-132 DOI:doi:10.3969/j.issn.2095-1469.2013.02.08

Research on torsional stiffness of rubber torsion bushing for all-terrain tracked vechicle

全地形履带车橡胶扭力轴套扭转刚度特性研究

Zheng Xin , Yao Shou-wen.

郑鑫, 姚寿文

在全地形履带车辆中,体积小、重量轻的橡胶扭力轴套悬架逐渐取代了扭杆等传统悬架形式,其中扭转刚度特性是车辆减振性能的关键。针对橡胶扭力轴套中扭转刚度特性设计缺乏的问题,从线性和非线性两种情况,分别依据扭杆悬架、单双气室油气悬架的刚度特性,推导了等效扭转刚度特性下的扭力轴套扭转刚度模型。基于全地形车动力学模型进行了仿真,通过平顺性指标对不同的扭转刚度特性进行了评价。仿真结果表明,依据单气室油气悬架刚度特性设计的扭转刚度模型具有较好的平顺性表现。扭力轴套扭转刚度的研究为全地形车橡胶扭力轴套刚度特性的设计提供了理论依据。

1986

0.0

... 目前,国内、外学者针对全地形铰接式履带车辆开展了一系列研究工作,如:Watanabe等^[3]研究了离心力对铰接式履带车辆转向性能的影响 ...

2013

0.0

... Edlund等^[4]设计了一种采用新型转向架的铰接式履带车并对其转向性能进行了分析 ...

2003

0.0

... Fijalkowski等^[5]详细介绍了全电动智能铰接式履带车,并建立了用于研究铰接式履带车转向性能的理论模型 ...

2013

0.0

... Yao等^[6]对六履带车辆的转向性能进行了研究 ...

2012

0.0

. 2012, 34(1):67-71 DOI:doi:10.3969/j.issn.1000-680X.2012.01.015

Mechanical performance analysis and optimization of the torsion bar suspension system in an articulated tracked carrier

某型履带式运输车扭杆悬挂装置力学性能分析与优化

Wei Xiao-qiang , Cheng Kai , Lin Yuan.

魏小强, 成凯, 林源

摘　要：采用有限元法对某铰接履带式运输车扭杆悬挂装置的力学性能进行了分析,计算该悬挂装置的强度和刚度。最后对平衡肘进行了拓扑优化,根据优化结果和设计经验提出了结构改进措施,重新分析的结果表明,缩减平衡肘35%材料是可行的。

... 吉林大学成凯等^[7,8]利用有限元软件对铰接式履带车辆的关键零部件在特定工况下的刚度、强度进行了分析 ...

2013

0.0

. 2013, 33(2):95-100

Strength and stiffness analysis of articulated steeringand pitching device on the all-terrain articulated tracked carrier

铰接履带式运输车转向俯仰装置强度刚度分析

Cheng Kai , Wei Xiao-qiang , Li Gui-zhu.

成凯, 魏小强, 李贵助

摘　要：由于转向俯仰装置是某铰接履带式运输车前车和后车的中间连接部分,对实现车架水平、垂直及扭转平面内的运动有重要作用,且该装置结构复杂,利用理论公式计算法不能满足对其整体结构进行分析的要求,故基于有限元理论,利用ANSYS软件对它的强度刚度进行有限元计算,分析该装置各部分在载重工作时抵抗断裂破坏和变形的能力,从而对该装置的设计合理性进行验证。选取该车载重工作时比较典型和危险的15种工况,对每种工况选择不同的约束加载,同时模型的建模也采取一些特殊的处理方法,以模拟真实的受力状态。分析结果表明：转向俯仰装置的设计基本合理,但也存在不合理区域,针对不合理区域提出了改善方案;改善后制造的样车经过试验场运行试验后表明该装置的分析方法是正确的,提出的改善方案是合理的。

... 吉林大学成凯等^[7,8]利用有限元软件对铰接式履带车辆的关键零部件在特定工况下的刚度、强度进行了分析 ...

2012

0.0

. 2012, :- DOI:doi:10.7666/d.y2195717

Research on tracking predetermined path for the cobalt crust mining vehicle[D]. Changsha: College of Mechanical and Electrical Engineering,

钴结壳采矿车行走路径控制研究[D]

Chen Bo.

陈波

富钴结壳是一种极具经济价值和战略意义的海洋矿产资源。由于富钴结壳富存于海山表面，所处地形地貌极其复杂，开采极为困难。本论文针对钴结壳采矿系统关键技术之一的采矿车行走路径控制问题进行了研究。本文主要研究工作如下:　　 1.采用了车体转向式铰接履带车为钴结壳采矿车行走方案，构建了采矿车动力学模型，提出了采矿车直线行走控制方案。　　 2.分析了障碍物和采矿车特性对路径规划的影响，采用了障碍物膨化处理和镜像路径曲线的方法，设计了采矿车路径规划总体方案，确定了遗传算法的路径编码方式、路径基因初始种群设定、路径适应度函数和...

... 中南大学陈波^[9]和张敏^[10]对铰接式履带采矿车辆的运动轨迹的规划和控制等问题进行了研究 ...

2010

0.0

. 2010, :- DOI:doi:10.7666/d.y1718946

The walking path following control of the seabed mining vehicle research based on the fuzzy neural network[D]. Changsha: College of Mechanical and Electrical Engineering,

基于模糊神经网络的海底采矿车路径跟踪行走控制研究[D]

Zhang Min.

张敏

富钴结壳是一种赋存于800-2500m海山侧表面上的海底矿产资源。钴结壳海底采矿车采用具有良好越障性能和爬坡能力及机动性能的铰接式履带车作为其行走机构。海底采矿车按预定路径行走控制为采矿作业关键技术之一。本文以海底采矿车多刚体动力学模型为基础,提出了一种基于ANFIS的模糊神经网络行走控制方法,并建立了基于Simulink、ADAMS和LabVIEW的海底采矿车协同仿真模型,从而为海底采矿车自动行走控制研究提供了新的方法和思路。首先,设计了以Compact RIO控制器为核心的海底采矿车控制系统方案,提出了在LabVIEW测控平台上采用内环速度控制和外环路径控制的智能自动行走控制方案。在此基础上,开展了海底采矿车运动学分析和建模,构建了基于ANFIS的模糊神经网络外环路径控制和PID内环速度控制的按预定路径行走控制模型；同时,基于ANFIS神经模糊推理系统,根据训练数据,完成了模糊神经网络路径控制器设计；设计了PID控制器,并对参数进行了整定；建立了速度分配模块、滑转率控制模块、滑转率实时计算模块和延时模块等模型。其次,建立了海底采矿车动力学机械模型与按预定路径行走控制模型的协同仿真模型,开展了海底采矿车越单边障碍、偏离路径跟踪、爬坡滑转率控制的直线路径跟踪控制的仿真研究,仿真结果表明,海底采矿车行走路径跟踪控制和滑转率控制效果良好,表明所设计的基于ANFIS的模糊神经网络的行走控制算法是有效的。然后,利用SIT Sever,建立了基于Simulink、ADAMS和LabVIEW的海底采矿车协同仿真模型,实现了Simulink、ADAMS和LabVIEW三个软件的协同仿真,为海底采矿车自动行走控制提供了技术支持。最后,开展了海底采矿车模型机行走实验,实现了海底采矿车行走控制算法与LabVIEW测控系统的联接,验证了所设计的基于ANFIS的模糊神经网络外环控制和PID内环速度控制的算法是有效的。

... 中南大学陈波^[9]和张敏^[10]对铰接式履带采矿车辆的运动轨迹的规划和控制等问题进行了研究 ...

2015

0.0

. 2015, 47(5):7-12 DOI:doi:10.11918/j.issn.0367-6234.2015.05.002

Dynamic modeling of flexible spacecraft based on floating centroid system

挠性航天器浮动质心动力学建模

Yang Yi-dai , Jing Wu-xing , Liu Yue.

杨一岱, 荆武兴, 刘玥

In order to improve the accuracy of the attitude-orbit coupling control problem of spacecraft with flexible attachments, a study on dynamic modeling of flexible spacecraft is conducted. As a result, a high-precision dynamic model based on the floating centroid frame system(FCFS) which can describe the attitude movement of spacecraft as well as the coupling relationship between the attitude maneuvering and the orbit movement better than the old ones is proposed by using the method of Finite-element along with Newton mechanics.The simulation result demonstrates that the FCFS model fits the practical restraint well and thus is applicable. The dynamic influence on the spacecraft caused by the vibration of the flexible attachments during the attitude maneuvering procedure can be calculated accurately by using the FCFS model and so is the changing of dynamic factors, such as the the velocity and the displacement of the centroid.The research results can provide theoretical basis for attitude-orbit coupling control problem of flexible spacecraft and thus achieve the purpose of improving control accuracy.

为提高挠性卫星的姿轨耦合控制精度,针对挠性卫星的姿态动力学建模问题展开研究．采用有限元与牛顿力学相结合的方法,提出一套体现卫星真实质心的浮动运动的浮动质心模型及建立在卫星浮动质心上的高精度动力学模型．利用此模型描述挠性卫星的姿态运动状态,能够准确反映出卫星的姿态运动与轨道运动之间的耦合关系以及卫星附件的挠性振动对卫星质心位置、速度的影响,进而准确估计出在挠性卫星有姿态机动的情况下各动力学要素与动态性能指标受挠性振动的影响,为提高卫星控制精度提供依据．通过仿真计算可知,应用该模型对卫星姿态机动过程进行动力学仿真所得到的结果符合实际工程约束,具有良好的可行性．

... 根据多质点系统重心求解公式,可以求得铰接式履带车辆满载工作状态下前车重心位置G₁的坐标(x₁₁,y₁₁)和后车重心位置G₂的坐标(x₂₂,y₂₂)分别为^[11,12]: ...

2015

0.0

. 2015, 45(3):844-850 DOI:doi:10.13229/j.cnki.jdxbgxb201503023

Experiment and simulation on body center-of-mass momentum during sit-to-stand assistedby rehabilitation robot

康复机器人辅助站立人体质心动量测试及模拟

Wang Zhi-qiang , Jiang Hong-yuan , Roman Kamnik.

王志强, 姜洪源

摘　要：为了分析康复机器人辅助站立过程中人体质心动量的变化规律，使用所建模型对机器人辅助站立过程中人体质心轨迹、线性动量和角动量进行了测试。依据拉格朗日方程推导人体质心动量数学模型，并利用辅助平行四边形法确定质心位置。分别对慢速、常速和快速辅助站立时，人体质心轨迹、线性动量及角动量进行了测试，利用所推导数学模型，在Matlab／Sim—ulink中建模并对人体质心动量和轨迹进行了模拟。结果表明：当采用不同辅助站立速度时，康复机器人仍能保持人体平稳地完成站立。通过分析质心水平和垂直动量得出：水平动量是站立稳定性的决定因素，而垂直动量是完成竖直站立的决定因素。模拟值与测试值重合度较好，表明所建模型可实现对质心位置和动量的有效预测，为分析辅助站立的稳定性和康复训练奠定了基础。

2014

0.0

... 4 铰接式履带车俯仰运动仿真分析虚拟样机仿真技术不仅可以直观地反映出车辆的运动状态,更重要的是它不需要昂贵的试验费用就能获得较高精度的结果^[13,14] ...

2016

0.0