作者简介:刘晓为(1955-),男,教授,博士生导师.研究方向:MEMS,传感器,集成电路.E-mail:lxw@hit.edu.cn
提出应用静电力矩反馈的方法解决一种新型转子式陀螺的欠阻尼问题。设计了静电力矩反馈的机械结构,并对其进行了建模分析以及有限元仿真验证。通过对比不同反馈条件下陀螺的动态响应发现,该方法可以显著改善陀螺的动态特性。随着反馈电压的增加,陀螺系统从欠阻尼状态无限趋近临界阻尼状态。考虑到介质击穿的限制以及反馈强度对幅频特性的影响,最终确定反馈电压应设置在100 V附近。此时,系统单位阶跃响应的过冲由开环时的87%以上降低到约5%,稳定时间由1.3 s缩短为0.1 s左右。
An electrostatic torque feedback approach is used to solve the underdamping problem of a novel rotational gyro. The electrostatic torque feedback structure is designed, modeled and validated by finite element analysis. By comparing the dynamic responses of the gyro to different feedback conditions, the approach is demonstrated to be able to significantly improve the dynamic characteristics of the gyro. As feedback voltage increases, the system can infinitely approach the critically damped state from the underdamped state. Due to the restriction of dielectric breakdown and the side effect of the feedback strength on the magnitude-frequency response, the feedback voltage should be about 100 V, where, the overshooting of the unit step is reduced from 87% to about 5% and the settling time is reduced from 1.3 s to about 0.1 s compared with the open-loop system.
作为惯性导航系统中的重要传感器, 陀螺仪被广泛应用于航空、航海等领域[1]。研究人员一直在努力改善陀螺仪性能, 减小成本、体积及功耗[2]。本文提及的陀螺是一种新型的转子式陀螺, 它比常规转子式陀螺具有更简单的结构和更小的体积, 比常规微机械加工(MEMS)振动式陀螺能够实现更高的性能[3]。该陀螺系统目前处于开环工作状态, 测量表明陀螺的满刻度量程显著小于理论值。这是由于该开环系统处于显著的欠阻尼状态, 其动态特性欠佳[4]。工程上有许多方法可以改善系统的阻尼状态, 为了不引入其他干扰力矩, 应该首选非接触式的阻尼方法。在陀螺仪领域中, 常见的非接触式反馈方法包括磁反馈和静电反馈方法。其中, 磁反馈不适合该陀螺仪, 因为其转子由电磁转矩驱动, 使用磁反馈会导致驱动磁场与反馈磁场间相互干扰; 静电反馈方法由于其功耗低、响应速度快等特点, 目前被广泛应用于MEMS陀螺领域[5]。
本文根据该陀螺特点, 提出了一种基于静电力矩的反馈方法以改善该陀螺仪的动态特性。提出了陀螺的静电反馈结构的设计/反馈策略, 建立了陀螺开环系统和带静电力矩反馈系统的系统级模型。通过对系统的单位阶跃响应参数进行比较分析, 评价了反馈力矩对陀螺动态特性的影响。结果表明, 该静电力矩反馈方法可以显著改善陀螺的动态特性。
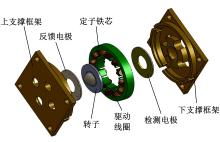
本文所述陀螺结构如图1所示。其核心部件主要由上、下支撑框架、转子、定子铁芯、驱动线圈、检测和反馈电极构成。转子为球-碟结构, 球由不锈钢材料制成, 碟由2J85半硬磁材料制成并且被径向充磁。转子的球结构与上、下支撑框架形成球连接, 使得转子在小范围内具有3个旋转自由度。通过在驱动线圈上施加交变电流, 在转子所在空间处产生旋转磁场, 该磁场带动转子绕其旋转轴高速旋转。在转子的一侧, 在下支撑框架上装配4片旋转对称的检测电极片, 与转子构成两对检测电容器。根据角动量守恒定律, 当陀螺输入垂直于转子转轴的角速度时, 转子将偏离其平衡位置。这将导致检测电容改变, 在相同坐标轴上的一对电容构成差分电容, 并由相应的差分电容检测电路转换为电压信号, 从而实现角速度信号的检测。目前, 陀螺为一个开环系统, 转子的倾斜运动仅受定子产生的电磁力矩以及支撑连接的阻尼转矩的影响。
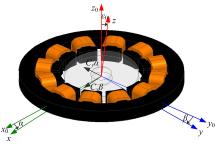
图2为陀螺动力学模型的坐标系及符号定义。该坐标系与定子固定, 以定子几何中心为原点, 以转子稳态旋转时的转动轴为z轴, 并任取与其垂直的过原点的两个径向矢量方向分别为x轴和y轴, 构成右手坐标系。根据双自由度转子式陀螺的基本原理, 在小角度倾斜运动的情况下, 转子的径向角运动可以表示为[6]:
式中:Ix、Iy分别为转子绕x轴、y轴的转动惯量; H为转子绕z轴的角动量; α 、β 分别为转子绕y轴和x轴负方向的倾斜角度; Dx、Dy分别为转子绕x轴、y轴的阻尼系数[7]; Cx、Cy分别为转子绕x轴、y轴的弹性系数; ω x、ω y分别为转子绕x轴、y轴的输入角速度;
对于开环陀螺系统而言, 由于没有外加的反馈力矩, 式(1)中的外力矩
静电反馈系统如图4(a)所示。当转子发生偏转时, 该偏转角度将改变检测电容数值, 并通过检测电路被转变为电压信号。该信号经过数字信号处理器(DSP)的解算获取相应输入角速度信息, 并据此控制电压发生器产生或关闭所述反馈电极上的电压来实现阻尼控制。
与检测电容相同, 转子与4片反馈电极分别构成四个等效反馈电容, 如图4(b)所示。在充电的平行板电容器中, 正负电荷之间的相互吸引导致电极之间存在一个静电力试图将两个电极彼此拉近[8, 9]。该吸引力可由下式计算:
式中:C为平行平板电容值; U为两极板之间的电压; h为两极板之间的距离。
相应的静电力矩可被计算为静电力与等效力臂的向量的叉乘。如图4(c)所示, 当转子接近平衡位置时, 相对于转子几何中心的静电力矩可以根据理想的平行板电容器来计算, 如式(3)所示:
式中:T为静电力矩; a为等效力臂。
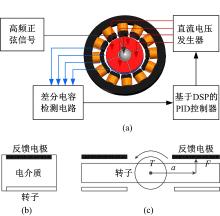 | 图4 陀螺反馈系统框图及静电力矩反馈结构示意图Fig.4 Schematic of feedback system of gyro and electrostatic torque feedback structure |
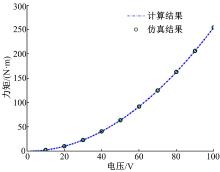
通过对这种反馈结构的静电建模和有限元分析, 可以获取静电反馈力矩与反馈电压之间的关系, 如图5所示。可见, 静电反馈力矩与电压的平方成正比, 该结果与式(3)计算的结果吻合。
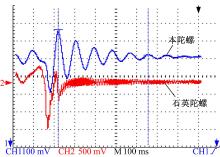
将开环陀螺与一款石英陀螺同时进行窄脉冲角速度冲激试验, 测待如图6所示的两个陀螺的窄脉冲角速度冲激响应曲线。由图6可见, 该陀螺输出呈现阻尼振荡的形式, 表明该转子的倾斜角经历了振荡衰减的过程。通过对比两条曲线可以发现, 开环状态下该陀螺的动态响应明显差于石英陀螺, 系统处于显著欠阻尼状态。
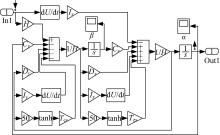
将静电力矩反馈结构加入该系统以改善其阻尼特性, 这实质上是引入了新的力矩组件, 即式(1)中的
为了保持系统函数的连续性, 本文应用在零位置处变化较大的双曲正切函数(tanh)代替了开关逻辑, 来实现在低偏转角速度(上述角速度阈值)情况下的近似无反馈力矩的效果。静电反馈力矩的数学模型如式(4)所示:
式中:k为角速度放大倍数, 本文以k=50为例; Tes为指定电压下反馈电容产生的静电力矩数值。
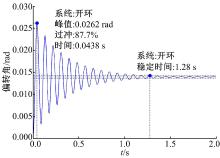
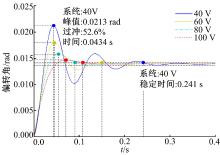
图8为不同反馈电压下陀螺系统的单位阶跃响应。由图可见, 随着反馈电压的增大, 系统的过冲和稳定时间都显著减少, 这表明该静电力矩反馈方法有效地改善了陀螺仪的动态特性[10]。
图9为不同反馈电压下陀螺系统的频率响应。与开环系统相比, 静电反馈结构系统的幅频特性曲线的过冲大大降低, 其相-频特性也有所改善, 这些都有利于提高陀螺系统的稳定性。然而, 随着电压继续增大, 幅频特性曲线的平带区域带宽将快速减小, 对于系统而言显然是不利的, 因此反馈电压不能过高。
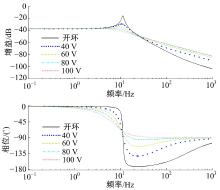 | 图9 不同反馈电压下陀螺系统的波特图 与开环系统对比Fig.9 Bode plots of gyro with different feedback voltages compared with open-loop system |
随着反馈电压的增大, 反馈电极与转子之间的空气介质也将承受更大强度的电场, 直至介质击穿, 此时静电力矩反馈将失效。根据当前陀螺结构计算, 反馈电容能承受的最大电压为300 V, 为了保证其在转子发生径向偏转时仍能正常工作, 并且考虑到反馈电压对于系统幅频特性的不利影响, 本文将反馈电压限制在100 V以内。在此电压范围内陀螺系统的动态参数随电压变化的关系如图10所示。
 | 图10 系统单位阶跃响应的过冲和稳定时间随反馈电压的变化关系Fig.10 Overshoot and settling time of unit step response of system as functions of voltage |
由图10可以看出, 陀螺系统的单位阶跃响应过冲随着反馈电压的增大而迅速减小; 稳定时间则先随电压的增大而迅速减小, 到80 V附近出现极小值, 随后缓慢增加。整体上, 陀螺的动态响应随着反馈电压的增大而变好。在100 V附近, 过冲约为5%、稳定时间为0.1 s。进一步的分析结果表明, 随着反馈电压的增大, 系统将无限趋近于临界阻尼状态, 然而当电压达到120 V后(过冲为2%, 稳定时间0.11 s), 再增加反馈电压, 系统响应速度的提升和过冲的降低变得异常缓慢, 并且更高的反馈电压增加了系统的硬件设计难度和局部介质击穿的风险。因此, 将反馈电压设置在100 V附近更为合理。
对一种新型转子式陀螺进行了动力学建模。模型分析和测试结果表明:开环状态下陀螺的动态特性较差, 直接影响陀螺系统的稳定性和响应速度。为此本文提出了利用静电力矩反馈改善陀螺动态特性的方法。设计了反馈结构并确定了依据转子偏转角速度信息控制反馈力矩的策略。对陀螺系统的动力学模型分析表明, 该方法能够有效改善陀螺的动态特性, 当反馈电压为100 V时, 系统单位阶跃响应的过冲由原来的87%降低到5%, 建立时间从原来的1.3 s减少到0.1 s。该方法计算简单, 对电压精度和电极加工精度要求很低, 易于软、硬件实现。
The authors have declared that no competing interests exist.
| [1] |
|
| [2] |
|
| [3] |
|
| [4] |
|
| [5] |
|
| [6] |
|
| [7] |
|
| [8] |
|
| [9] |
|
| [10] |
|