有刷直流电机非线性控制系统设计

引用本文

顾万里, 张森, 胡云峰, 陈虹. 有刷直流电机非线性控制系统设计. 吉林大学学报(工学版), 2017, 47(3): 900-907
GU Wan-li, ZHANG Sen, HU Yun-feng, CHEN Hong. Nonlinear controller design of brushed DC motor. Journal of Jilin University Engineering and Technology Edition, 2017, 47(3): 900-907 复制到剪切板

Doi:10.13229/j.cnki.jdxbgxb201703029
Permissions

有刷直流电机非线性控制系统设计

顾万里^1,², 张森², 胡云峰^1,^2,³, 陈虹^1,²

1.吉林大学汽车仿真与控制国家重点实验室,长春 130022

2.吉林大学通信工程学院,长春 130022

3.吉林大学工程仿生教育部重点实验室,长春 130022

胡云峰(1983-),男,讲师,博士.研究方向:非线性控制应用及汽车电子控制.E-mail:huyf@jlu.edu.cn

作者简介:顾万里(1988-),男,博士研究生.研究方向:非线性控制系统设计.E-mail:guwl13@mails.jlu.edu.cn

基金项目:国家自然科学基金重点项目(61520106008,61374046,61573165)

摘要

为了提高有刷直流电机调速的平稳性和快速性,在经典双闭环电机控制系统设计方案的基础上,针对转速环模型中存在非线性及负载扭矩不可测的特点,提出了基于扩张状态观测器的三步法非线性转速控制策略。首先,设计了三步法(TS)非线性速度控制器,该控制器由类稳态控制、参考动态前馈控制及积分误差反馈控制组成,具有工程意义明确、实现方便的优点。然后,设计了扩张状态观测器(ESO)对系统中负载扭矩等干扰进行在线估计并实时补偿,证明了观测器误差系统的有限时间收敛性及有界性;同时将观测器误差考虑成有界的扰动输入,在输入到状态稳定性理论框架下,证明了闭环误差系统的鲁棒性。针对电流响应较快、极易达到稳态的特点,设计了工程中常用的前馈加PI反馈结构的二自由度控制器,同时采用模拟电路实现该控制器,减小了电流环控制周期,从而抑制了电流波动。为了验证整个控制系统的有效性和工程可实现性,通过有刷直流电机阶跃及正弦转速跟踪实验,证明了本文所设计控制系统能够显著提高电机的瞬态性能和稳态性能。

关键词: 自动控制技术; 车辆工程; 有刷直流电机; 非线性控制方法; 扩张状态观测器; 鲁棒性

中图分类号:TM331 文献标志码:A 文章编号:1671-5497(2017)03-0900-08

Nonlinear controller design of brushed DC motor

GU Wan-li^1,², ZHANG Sen², HU Yun-feng^1,^2,³, CHEN Hong^1,²

1.State Key Laboratory of Automotive Simulation and Control, Jilin University, Changchun 130022,China

2.College of Communication Engineering,Jilin University, Changchun 130022,China

3.Key Laboratory of Bionic Engineering, Ministry of Education, Changchun 130022,China

Abstract

In order to improve the transient and steady-state performance of brushed DC motor, a novel control system is developed on the basis of dual closed-loop control system. For the speed loop, considering the nonlinear characteristics of the friction torque and the un-measurable load torque, an Extended State Observer (ESO) based Triple-Step (TS) nonlinear control method is developed. First, the speed controller is designed using the TS method, which consists of the steady-state control, the feed-forward control related to the reference variation and the error feedback control. The structure of the designed nonlinear controller is concise. Then, an ESO based on model compensation is applied to estimate and compensate disturbances. The estimated errors are bounded and can converge to a prescribed range in a finite time. The estimated error is considered as disturbance input with the bounded amplitude. The method to analyze the robustness of this system is discussed in the framework of input state stability theory. For the current loop, current dynamics is neglected due to the fast electric response, the commonly used feedforward controller and PI feedback controller are designed to reduce torque ripple. The designed control system is evaluated by experiments. Results show that the proposed controller can improve the transient and steady-state performance of brushed DC motor significantly. The effectiveness and engineering implementation of this controller is also verified.

Key words: automatic control teehnology; vehicle engineering; brush DC motor; nonlinear control method; extended state observer; robustness

Show Figures

0 引言

有刷直流电机(Brush DC motor)具有力矩系数大、过载能力强、可靠性高等优点, 广泛应用于移动机器人以及航天器地面移动基座运动跟踪控制中, 其驱动电机速度跟踪效果的优劣将直接影响移动机器人运动跟踪的效果。移动基座在空间合作目标地面运动再现中的应用, 对移动基座运行速度提出了宽调速、高精度的需求。因此, 需要驱动电机能够快速、准确地跟踪期望速度。但是, 有刷直流电机同样存在现有电机控制系统在低速运行时普遍遇到的问题, 即系统容易出现不稳定的现象, 且主要受非线性摩擦力以及电机力矩波动的影响^[1]。这对有刷直流电机的精确控制提出了挑战。

目前, 基于经典的双闭环电机控制框架, 已经提出了许多具有各自特点的有刷直流电机速度控制方法。早期主要采用PID算法^[2]进行调速, 这种算法性能可靠、结构简单。但是采用该方法的系统响应速度不够快, 且在低速运行时无法克服非线性摩擦力以及电机力矩波动对转速控制产生的影响。针对PID控制无法适用于强非线性系统的缺点, 一些学者提出摩擦力矩前馈补偿方法^[3], 通过建立精确的摩擦模型, 采用前馈校正的形式, 将摩擦力矩转化为相反的控制信号加到控制器中。但在实际工况中, 模型参数受到温度、湿度、润滑情况、负载、接触面压力、相对速度及位置等多方面因素的影响, 对摩擦力矩进行补偿是个非常复杂的课题。针对摩擦力模型中的参数不确定性, 文献[4, 5]采用自适应控制进行参数辨识, 根据系统的输入、输出状态以及某种性能指标来修正非线性摩擦力以及电机力矩波动模型中的不确定项, 但该方法无法补偿未建模的干扰部分。针对电机摩擦力模型中的参数不确定性以及不可测干扰的特点, 文献[6, 7]提出了基于干扰观测器的电机控制系统设计方法, 将外部干扰和模型不确定项合成为误差项, 对其进行估计和动态补偿, 但由于摩擦力在转速过零点处存在不连续跳变, 使观测器产生观测误差, 降低了观测器的估计和补偿效果。

本文针对电机模型中存在较强的非线性及负载扭矩等不可测干扰的特点, 提出了基于扩张状态观测器(ESO)的有刷直流电机控制系统。针对模型中存在的非线性, 基于三步非线性系统设计方法^{[8, 9]}设计了非线性速度控制器。该控制器由类稳态控制、参考动态前馈控制和误差反馈控制3部分组成。该方法不仅可以保证系统的性能, 同时具有设计思路清晰、物理意义明确、工程结构简单等优点。在此基础上, 引入基于模型的扩张状态观测器, 对参数不确定性以及负载转矩等干扰进行估计和实时补偿。该方法既提高了系统的响应速度, 又抑制了摩擦力跳变对观测器的影响, 而且降低了观测器的计算负担, 进而提高了观测器的估计和补偿效果。

1 模型及控制系统设计

本文研究的有刷直流电机, 其简化数学模型如下:

$\begin{matrix} \{\begin{matrix} \overset{\cdot}{i} = - \frac{R}{L} i - \frac{K_{e}}{L} ω + \frac{u}{L} \\ \overset{\cdot}{ω} = \frac{K_{m}}{J} i - \frac{1}{J} T_{f} - \frac{1}{J} T_{d} \end{matrix} \end{matrix}$ （1）

式中:i为电枢电流; L为电枢电感; R电枢电阻; K_e为电动势常数; ω 为角速度; u为电机电枢电压; K_m为转矩常数; J为转动惯量; T_d为扰动力矩; T_f为摩擦力矩。

由Stribeck稳态模型确定, 即:

$\begin{matrix} T_{f} (ω) = [T_{c} + (T_{s} - T_{c}) e^{- (ω / ω_{s})^{2}} + K_{v} \cdot |ω|] sgn (ω) \end{matrix}$ (2)

式中:T_c为库仑摩擦力; T_s为最大静摩擦力; ω _s为Stribeck速率; K_v为黏滞摩擦因数。Stribeck模型中的4个未知参数可通过实验方法^[10]测得。

在数值上, 电磁时间常数远小于机电时间常数, 因此可以认为电流环和转速环解耦, 简化为串级系统分别进行控制, 工业上采用基于电流环和转速环的双闭环控制策略对直流电机进行速度控制。

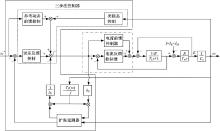
本文在经典的双闭环控制的基础上, 提出了基于扩张状态观测器^[11]的有刷直流电机控制系统。系统整体控制框图如图1所示, 图1中, T_L为负载力矩; b₀=K_m/J; I为振动电流; I_d1为等效的负载电流; I_df为等效的摩擦力电流。转速环控制器如图中实线框所示, 该控制器由三步法非线性控制器和扩张状态观测器两部分组成。三步法控制器用于补偿非线性摩擦力的影响以及抑制系统偏差, 由类稳态控制、参考动态前馈控制和误差反馈控制3部分组成。类稳态控制保证系统在达到稳态过程中, 处于小偏差调节状态, 以提高系统的稳态性能。参考动态前馈控制具有预测功能, 可以及时地根据参考信号的变化给出控制量, 从而提高控制系统的快速性。误差反馈控制用于抑制系统偏差, 提高系统鲁棒性。扩张状态观测器用于估计和实时补偿参数不确定性以及负载转矩等干扰。电流环控制器如图中点划线框所示, 由于电流具有快速响应特性, 忽略其动力学, 本文设计了前馈加PI反馈控制器。

	Figure Option View Download New Window
	图1 系统整体控制框图Fig.1 System control diagram

2 转速环控制器设计

设计转速环控制器的目的是使转速跟踪上给定的转速参考值。

2.1 三步法控制器设计

第1步类稳态控制。

转速环状态方程为:

$\begin{matrix} \overset{\cdot}{ω} = \frac{K_{m}}{J} i - \frac{1}{J} T_{f} - \frac{1}{J} T_{d} \end{matrix}$ (3)

假设转速已经达到稳态, 采用的稳态控制输入为i=i_s。根据稳态条件, 令 $\begin{matrix} \overset{\cdot}{ω} \end{matrix}$ =0, 代入式(3)得:

$K_{m} i_{s} - T_{f} - T_{L} - T_{d} = 0$ (4)

则：

$\begin{matrix} i_{s} = \frac{T_{f} + T_{L} + T_{d}}{K_{m}} \end{matrix}$ （5）

第2步参考动态前馈控制。

为了反映当转速参考值动态变化时, 系统有相应的调节作用, 在稳态控制的基础上, 假设控制率为i=i_s+i_f, 代入式(3)得:

$J \overset{\cdot}{ω} = K_{m} (i_{s} + i_{f}) - T_{f} - T_{L} - T_{d}$ （6）

化简得到：

$J \overset{\cdot}{ω} = K_{m} i_{f}$ （7）

令 $\begin{matrix} \overset{\cdot}{ω} \end{matrix}$ = $\begin{matrix} {\overset{\cdot}{ω}}^{*} \end{matrix}$ , 将其代入式(7)得到:

$i_{f} = \frac{J {\overset{\cdot}{ω}}^{*}}{K_{m}}$ （8）

第3步误差反馈控制。

为了提高控制系统的控制性能, 以及对扰动和不确定性的鲁棒性, 在以上设计的基础上引入反馈控制u_e, 以实现最小偏差系统的调节, 假设控制率为i=i_s+i_f+i_e, 且定义跟踪误差为ω _e=ω ^*-ω , 则有:

$J \overset{\cdot}{ω} = K_{m} (i_{s} + i_{f} + i_{e}) - T_{f} - T_{L} - T_{d}$ （9）

化简得到：

$\begin{matrix} J {\overset{\cdot}{ω}}_{e} = K_{m} i_{e} \end{matrix}$ （10）

为了分析系统的稳定性, 取李雅普诺夫函数:

$\begin{matrix} V = \frac{1}{2} J ω_{e}^{2} + \frac{1}{2} k_{ω 0} χ_{ω}^{2} \end{matrix}$ （11）

式中:χ _ω=∫ ω _e, 则有:

$\begin{matrix} \overset{\cdot}{V} = J ω_{e} {\overset{\cdot}{ω}}_{e} + K_{ω 0} ω_{e} \int ω_{e} \end{matrix}$ （12）

取K_mi_e=-k_ω₁ω _e-k_ω₀∫ ω _e, 其中k_ω₁> 0, k_ω₀> 0, 代入式(12)得到:

$\begin{matrix} \overset{\cdot}{V} = - k_{ω 1} ω_{e}^{2} \end{matrix}$ （13）

即系统是渐近稳定的。则总的控制律为:

i=i_s+i_f+i_e= $\begin{matrix} \frac{J {\overset{\cdot}{ω}}^{*}}{K_{m}} \end{matrix}$ + $\begin{matrix} \frac{T_{f} + T_{L} + T_{d}}{K_{m}} \end{matrix}$ - $\begin{matrix} \frac{k_{ω 1} ω_{e}}{K_{e}} \end{matrix}$ - $\begin{matrix} \frac{k_{ω 0}}{K_{e}} \end{matrix}$ ∫ ω _e(14)

从以上步骤可以看出, 三步法具有以下特点:

(1)当系统近似达到稳态时, 稳态控制起主导作用。

(2)针对系统的动态需求, 参考动态前馈控制能够提供相应的动作。

(3)在稳态控制和参考动态前馈控制的基础上, 误差反馈控制器能够对系统的误差进行抑制。

2.2 扰动补偿策略

对于控制器(14)中的负载转矩T_L和干扰项T_d不可测, 如果直接忽略, 会对转速平稳性带来很大影响。本文通过扩张状态观测器对负载转矩T_L和干扰项T_d进行估计和补偿。由式(2)可以看出, 摩擦力在ω =0点存在跳变, 如果直接对式(3)中的摩擦力矩、负载转矩和干扰进行估计, 会使估计误差变大。为了改善系统的动态响应和鲁棒性, 本文采用基于摩擦力模型补偿的扩张状态观测器对电机负载转矩等干扰进行估计和补偿。将摩擦力模型补偿给扩张状态观测器的输入项, 克服了由于摩擦力矩不连续给扩张状态观测器带来的估计误差。其具体设计过程如下:

根据有刷直流电机的状态方程, 可以定义如下状态变量:

$\begin{matrix} \{\begin{matrix} x_{1} = ω \\ x_{2} = (T_{d} + T_{L}) / J \\ u = i \\ b_{0} = K_{m} / J \end{matrix} \end{matrix}$ （15）

令 $\begin{matrix} {\overset{\cdot}{x}}_{2} \end{matrix}$ =h(t), 将状态变量代入式(3)可得:

$\begin{matrix} \{\begin{matrix} {\overset{\cdot}{x}}_{1} = b_{0} u - T_{f} / J + x_{2} \\ {\overset{\cdot}{x}}_{2} = h (t) \end{matrix} \end{matrix}$ （16）

基于模型补偿的扩张状态观测器设计为:

$\begin{matrix} \{\begin{matrix} {\overset{\cdot}{\hat{x}}}_{1} = - T_{f} / J + {\hat{x}}_{2} + b_{0} u - 2 λ_{0} ({\hat{x}}_{1} - x_{1}) \\ {\overset{\cdot}{\hat{x}}}_{2} = - λ_{0}^{2} ({\hat{x}}_{1} - x_{1}) \end{matrix} \end{matrix}$ （17）

式中: $\begin{matrix} \hat{x} \end{matrix}$ =[ $\begin{matrix} {\hat{x}}_{1} \end{matrix}$ , $\begin{matrix} {\hat{x}}_{2} \end{matrix}$ ]为估计的状态且λ ₀> 0, 该估计器的特性可以由其特征多项式进行分析:

$\begin{matrix} N (s) = (s + λ_{0})^{2} \end{matrix}$ （18）

令 $\begin{matrix} {\tilde{x}}_{1} \end{matrix}$ =x₁- $\begin{matrix} {\hat{x}}_{1} \end{matrix}$ , $\begin{matrix} {\tilde{x}}_{2} \end{matrix}$ =x₂- $\begin{matrix} {\hat{x}}_{2} \end{matrix}$ , 则估计误差为:

$\begin{matrix} \{\begin{matrix} {\overset{\cdot}{\tilde{x}}}_{1} = {\tilde{x}}_{2} - 2 ω_{0} {\tilde{x}}_{1} \\ {\overset{\cdot}{\tilde{x}}}_{2} = h (t) - ω_{0}^{2} {\tilde{x}}_{1} \end{matrix} \end{matrix}$ （19）

定义 $\begin{matrix} \overset{\cdot}{ξ} \end{matrix}$ = $\begin{matrix} {\tilde{x}}_{1} \end{matrix}$ , ξ ₂= $\begin{matrix} {\tilde{x}}_{2} \end{matrix}$ /ω ₀, 则:

$\begin{matrix} \overset{\cdot}{ξ} = ω_{0} Aξ + B h (t) / λ_{0} \end{matrix}$ （20）

式中:A为赫尔维兹矩阵, A= $\begin{matrix} [\begin{matrix} - 2 & 1 \\ - 1 & 0 \end{matrix}] \end{matrix}$ ; B= $\begin{matrix} [0 \begin{matrix} 1 \end{matrix}] \end{matrix}$ 。

引理1^[12] 如果h(t)有界, 则估计状态也有界, 且存在常数σ _i> 0和有限时间T₁使得:

$\begin{matrix} \{\begin{matrix} |{\tilde{x}}_{i}| \leq σ_{i} \\ σ_{i} = ο (1 / λ_{0}^{k}) \\ \forall T_{1} \end{matrix} \end{matrix}$ （21）

式中:k为正整数; i=1, 2; o(· )为无穷小量。

引理1表明, 通过调整带宽λ ₀, 估计误差可以收敛到任意小的界。但λ ₀过大会放大系统噪声, 所以, 需要在估计误差和高增益带来的影响之间做权衡。

结合控制器(14)和该观测器估计输出量, 控制器(14)可以重写为:

$\begin{matrix} i = i_{s} + i_{f} + i_{e} = \frac{J {\overset{\cdot}{ω}}^{*}}{K_{m}} + \frac{T_{f}}{K_{m}} - \frac{k_{ω 1} ω_{e}}{K_{e}} - \frac{k_{ω 0}}{K_{e}} \int ω_{e} + \frac{J {\hat{x}}_{2}}{K_{m}} \end{matrix}$ (22)

2.3 鲁棒性分析

由于观测器存在有界的观测误差, 仅分析系统的稳定性是不够的, 需进行鲁棒性分析。本文将观测误差考虑成有界的扰动输入, 在输入到状态稳定性理论框架下, 证明闭环误差系统的鲁棒性。

将控制器(22)代入系统方程(3), 得误差方程为:

$\begin{matrix} J {\overset{\cdot}{ω}}_{e} = - k_{ω 0} ω_{e} - k_{ω 1} \int ω_{e} + {\tilde{x}}_{2} \end{matrix}$ (23)

再次对李雅普诺夫函数(11)求导数, 得:

$\begin{matrix} \overset{\cdot}{V} = - k_{ω 1} ω_{e}^{2} + ω_{e} {\tilde{x}}_{2} \end{matrix}$ (24)

利用杨氏不等式, 可以进一步得到:

$\begin{matrix} \overset{\cdot}{V} \leq - k_{ω 1} ω_{e}^{2} + \frac{1}{2} ω_{e}^{2} + \frac{1}{2} {\tilde{x}}_{2}^{2} \end{matrix}$ （25）

定义W(e)=-k_ω₁ $\begin{matrix} ω_{e}^{2} \end{matrix}$ + $\begin{matrix} \frac{1}{2} \end{matrix} \begin{matrix} ω_{e}^{2} \end{matrix}$ , 对于状态e= $\begin{matrix} [χ_{ω}, ω_{e}]^{T} \end{matrix}$ , 如果选择k_ω₁> 1/2, 则能保证W(e)是连续负定函数。因此, 根据输入到状态稳定性定理^[13], 误差系统状态ω _e对于扰动输入 $\begin{matrix} {\tilde{x}}_{2} \end{matrix}$ 是输入-状态稳定的, 即对扰动具有鲁棒性。

3 电流环控制器设计

电流环控制器的作用为控制电流跟踪转速环给出的期望电流值。由于电磁时间常数远小于机电时间常数, 电流响应较快, 极易达到稳态, 其响应时间相对于转速环控制周期可以忽略不计, 本文设计了基于稳态的前馈控制器加PI反馈控制器, 用于跟踪期望电流值。

电流状态方程为:

$\begin{matrix} \overset{\cdot}{i} = - \frac{R}{L} i - \frac{K_{e}}{L} ω + \frac{u}{L} \end{matrix}$ （26）

令 $\begin{matrix} \overset{\cdot}{i} \end{matrix}$ =0, 即:

$\begin{matrix} u = i_{d} R + K_{e} ω \end{matrix}$ （27）

第1步前馈控制。

假设电流已达到期望稳态即i=i^*, 采用的前馈控制输入为u=u_f, 代入式(27)得:

$\begin{matrix} u_{f} = i^{*} R + K_{e} ω \end{matrix}$ （28）

第2步误差反馈控制。

为了提高控制系统的控制性能, 以及对扰动和不确定性的鲁棒性, 在此设计的基础上引入比例积分反馈控制律u_e, 实现最小偏差系统的调节, 即:

$\begin{matrix} u_{e} = - k_{i 1} i_{e} - k_{i 0} \int i_{e} \end{matrix}$ （29）

式中:k_i₁> 0, k_i₀> 0, 则总的控制律为:

$\begin{matrix} u = u_{f} + u_{e} = i^{*} R + k_{e} ω - k_{i 1} i_{e} - k_{i 0} \int i_{e} \end{matrix}$ （30）

电流环扰动主要由电流换向引起。由于电流环响应速度较快, 本文将PI控制器采用模拟电路实现, 通过减小控制周期来抑制电流换向给电流的影响。模拟PI电路实物图如图2所示。

	Figure Option View Download New Window
	图2 模拟PI电路实物图Fig.2 Realized PI controller in analog hardware

4 对比实验及分析

为了验证本文所设计的有刷直流电机速度控制算法的有效性, 搭建了MicroAutoBox快速原型实验平台, 并与传统双闭环PI控制进行对比。本文以北京勇光高特微电机有限公司的J60LYX系列稀土永磁直流力矩电机作为执行机构, 并以高精度光电编码器作为转速反馈, LEM闭环霍尔电流传感器作为电流反馈。电流环PI控制器由采用TI高精度轨至轨运算放大器THS4222D搭建的模拟电路实现。所采用的电机参数如表1所示。

表1 电机参数表 Table 1 Parameters of motor

首先, 在高幅值阶跃输入和正弦输入参考速度下验证了本文算法对系统快速性的提升效果。由于有刷直流电机仅在低速区表现较强的非线性摩擦力矩以及扰动力矩, 且摩擦力在ω =0点存在跳变, 通过在低速区跟踪常值和正弦输入参考速度, 验证了本文设计的基于模型补偿的扩张状态观测器在模型存在跳变过程中对干扰的估计和实时补偿效果。对于每一种工况分别取不同的参数进行了大量对比实验, 分别取两种算法最好的控制效果进行对比。

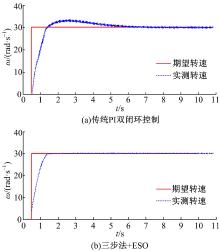
(1)跟踪期望速度为30 rad/s阶跃输入信号, 观察闭环系统的动态响应。图3为永磁直流力矩电机动态输出对比图。从图3可以看出, 本文方法能够更快地跟踪给定速度。

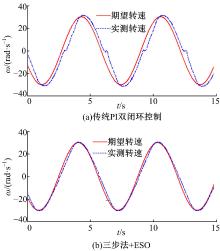
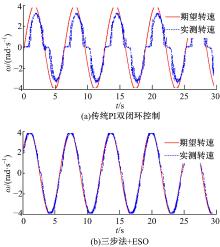
	Figure Option View Download New Window
	图3 幅值30 rad/s阶跃响应跟踪效果对比曲线Fig.3 Tracking effect contrast curves of 30 rad/s step signal

(2)跟踪期望速度为幅值30 rad/s, 周期2π 的正弦信号, 观察实际输出速度曲线对参考信号的延迟。图4为永磁直流力矩电机动态输出对比图。从图4可以看出, 该控制方法具有较小的延迟, 且电机转速穿过零点时(即电机转向变换时), 能够平滑过渡。

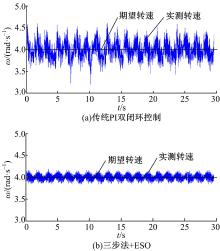
	Figure Option View Download New Window
	图4 幅值30 rad/s正弦信号跟踪效果对比曲线Fig.4 Tracking effect contrast curves of 30 rad/s sinusoidal signal

(3)跟踪期望速度为4 rad/s恒定信号, 以验证本文方法在低速区对干扰的估计和实时补偿效果。从图5可以看出, 传统PI双闭环控制在跟踪恒定的低速期望信号有较大的误差, 峰值误差在12.5%左右, 而采用本文方法跟踪时误差较小, 峰值误差在3.8%左右, 可以看出本文方法对未知扰动有很好的估计和实时补偿能力。

	Figure Option View Download New Window
	图5 幅值4 rad/s恒定信号对比曲线Fig.5 Tracking effect contrast curves of 4 rad/s constant signal

(4)跟踪期望速度为幅值4 rad/s, 周期2π 的正弦信号, 以验证当系统非线性摩擦力在ω =0点存在跳变时, 本文所设计观测器对干扰的估计和实时补偿效果。图6为永磁直流力矩电机动态输出对比图。由于系统摩擦力在ω =0点存在跳变以及干扰力矩的存在, 从图6可以看出, 双闭环PI控制器控制效果很差。但本文方法能够较好地抑制非线性摩擦力的影响, 且本文设计的基于模型补偿的扩张状态观测器能够克服摩擦力在ω =0点存在跳变对观测器带来的观测误差的影响, 即能够对干扰进行较好的估计和实时补偿。

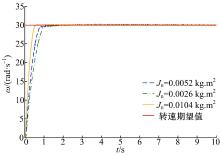
	Figure Option View Download New Window
	图6 幅值4 rad/s正弦信号跟踪效果对比曲线Fig.6 Tracking effect contrast curves of 4 rad/s sinusoidal signal

(5)验证当参数变化时, 本文所设计的控制器的控制效果。对于模型(1), 当负载变化时, 容易引起转动惯量变化。图7为本文设计控制器在转动惯量取不同值下跟踪幅值为30 rad/s的阶跃信号的实验曲线, 转动惯量取值分别为J_n、0.5J_n和2J_n, 其中J_n为转动惯量标称值。可以看出, 当系统的转动惯量发生变化时, 仅对系统的瞬态响应有部分影响。

	Figure Option View Download New Window
	图7 在不同转动惯量下系统的阶跃响应曲线Fig.7 Step response curves of different inertia

综合以上实验数据, 可以得出如下结论:

(1)根据图3和图4可以看出, 由于三步法引入了参考动态前馈控制, 大大改善了系统的瞬态响应。

(2)引入基于模型的扩张状态观测器, 对引起转速波动的干扰进行估计和补偿。该观测器能够大大改善由于非线性摩擦力在ω =0点存在跳变而给观测器带来的估计误差。

5 结束语

在经典的双闭环电机控制系统设计方案的基础上, 提出了基于扩张状态观测器的有刷直流电机控制系统。针对转速环模型中存在非线性及负载扭矩等干扰不可测的特点, 提出了基于扩张状态观测器的三步法非线性转速控制策略。该方法大大提升了系统的瞬态响应性能, 且所设计观测器能够克服摩擦力不连续给观测器带来的估计误差, 对干扰具有较好的估计和实时补偿效果, 显著提升系统稳态性能。针对电流响应速度较快的特点, 忽略其动力学, 设计了工程中常用的前馈加PI反馈结构的二自由度控制器。为了减小电流环控制周期, 设计了模拟电路实现该控制器。对比实验结果表明:该控制系统与传统的双闭环控制器相比能够显著提高电机的瞬态性能和稳态性能, 同时也验证了整个控制系统的有效性和工程可实现性。

The authors have declared that no competing interests exist.

参考文献

View Option

[1]	Wu Wei. Disturbance compensation using feedforward and feedback for scanner direct current motor mechanism low speed regulation[J]. Journal of Dynamic Systems, Measurement, &Control, 2015, 137(4): 044502. [本文引用:1]
[2]	陈伯时. 电力拖动自动控制系统[M]. 北京: 机械工业出版社, 1997. [本文引用:1]
[3]	李拥军, 杨文淑, 范永坤, 等. 高精度转台摩擦力矩补偿控制器设计与仿真[J]. 光电工程, 2008, 35(12): 126-130. Li Yong-jun, Yang Wen-shu, Fan Yong-kun, et al. Controller design and simulation for friction moment compensation on high-precision turntable[J]. Opto-Electronic Engineering, 2008, 35(12): 126-130. [本文引用:1]
[4]	Wang Xing-jian, Wang Shao-ping. High performanceadaptive control of mechanical servo system with LuGre friction model: identification and compensation[J]. Journal of Dynamic Systems Measurement and Control, 2012, 134(1): 011021. [本文引用:1]
[5]	Bao Wen-liang, Huang Xian-lin, Yin Hang. Adaptive dynamic friction compensation for an electro-optical platform inertial stabilization system[J]. ElectronicsOptics & Control, 2012, 19(4): 50-54. [本文引用:1]
[6]	Hoshino D, Kamamichi N, Ishikawa J. Friction compensation using time variant disturbance observer based on the LuGre model[C]//12th IEEE International Workshop on Advanced Motion Control, Sarajevo, 2012: 1-6. [本文引用:1]
[7]	Ruderman M. Tracking control of motor drives using feedforward friction observer[J]. IEEE Transactions onIndustrial Electronics, 2014, 61(7): 3727-3735. [本文引用:1]
[8]	Chen Hong, Gong Xun, Liu Qi-fang. Triple-step method to design non-linear controller for rail pressure of gasoline direct injection engines[J]. IET Control Theory & Applications, 2014, 8(11): 948-959. [本文引用:1]
[9]	Gao Bing-zhao, Chen Hong, Liu Qi-fang, et al. Position control of electric clutch actuator using a triple-step nonlinear method[J]. IEEE Transactions on Industrial Electronics, 2014, 61(12): 6995-7003. [本文引用:1]
[10]	黄科. 力矩电机动力学性能测试研究[D]. 长沙: 国防科学技术大学机电工程与自动化学院, 2007. Huang Ke. Test and study on dynamical performance of torque motor[D]. Changsha: College of Mechatronic Engineering and Automation, National University of Defense Technology, 2007. [本文引用:1]
[11]	韩京清. 一类不确定对象的扩张状态观测器[J]. 控制与决策, 1995, 10(1): 85-88. Han Jing-qing. The extended state observer of a class of uncertain systems[J]. Control and Decision, 1995, 10(1): 85-88. [本文引用:1]
[12]	Guo Bao-zhu, Zhao Zhi-liang. On the convergence of an extended state observer for nonlinear systems with uncertainty[J]. Systems & Control Letters, 2011, 60(6): 420-430. [本文引用:1]
[13]	Sontag E D. Input to state stability: basic concepts and results[DB/OL]. [2016-01-08]. http://www.mit.edu/~esontag/FTP_DIR/04cetraro.pdf. [本文引用:1]

2015

0.0

... 但是,有刷直流电机同样存在现有电机控制系统在低速运行时普遍遇到的问题,即系统容易出现不稳定的现象,且主要受非线性摩擦力以及电机力矩波动的影响^[1] ...

1997

0.0

... 早期主要采用PID算法^[2]进行调速,这种算法性能可靠、结构简单 ...

2008

0.0

. 2008, 35(12):126-130

Controller design and simulation for friction moment compensation on high-precision turntable

高精度转台摩擦力矩补偿控制器设计与仿真

Li Yong-jun , Yang Wen-shu , Fan Yong-kun

李拥军, 杨文淑, 范永坤

... 针对PID控制无法适用于强非线性系统的缺点,一些学者提出摩擦力矩前馈补偿方法^[3],通过建立精确的摩擦模型,采用前馈校正的形式,将摩擦力矩转化为相反的控制信号加到控制器中 ...

2012

0.0

2012

0.0

2012

0.0

2014

0.0

2014

0.0

... 针对模型中存在的非线性,基于三步非线性系统设计方法^[8,9]设计了非线性速度控制器 ...

2014

0.0

... 针对模型中存在的非线性,基于三步非线性系统设计方法^[8,9]设计了非线性速度控制器 ...

2007

0.0

. 2007, :- DOI:doi:10.7666/d.y1298059

Test and study on dynamical performance of torque motor[D]. Changsha:College of Mechatronic Engineering and Automation,

力矩电机动力学性能测试研究[D]

Huang Ke.

黄科

随着信息化技术的飞速发展，光电稳定跟踪系统在侦察、导航、定位等场合的作用日益重要。力矩电机可以低转速、大转矩输出，能和负载直接相连，具有反应速度快、线性度好等优点，已成为该类机电伺服系统的关键部件。因此，准确测试力矩电机的各项性能指标，掌握伺服机构的动力学性能，对光电稳定跟踪系统的设计具有重要意义。本文围绕力矩电机的动力学性能，对其工作原理、运行特性和性能测试方法等进行了深入的分析和研究，目的是为高精度伺服系统中的电机选择和性能控制提供依据。论文首先设计完成了基于工控机和数据采集卡的电机自动测试系统。工控机主要...

... Stribeck模型中的4个未知参数可通过实验方法^[10]测得 ...

1995

0.0

. 1995, 10(1):85-88

The extended state observer of a class of uncertain systems

一类不确定对象的扩张状态观测器

Han Jing-qing.

韩京清

摘　要：利用观测器形式的跟踪一微分器，对形如ｘ＾（ｎ）＝ｆ（ｘ，ｘ，．．．Ｘ＾（ｎ－１），ｔ）＋Ｗ（ｔ）的不确定系统给出了“扩张状态观测器”。只要适当选取观测器中的非线性函数和相应参数，它能很好地跟踪一批不确定对象的扩张状态。

... 本文在经典的双闭环控制的基础上,提出了基于扩张状态观测器^[11]的有刷直流电机控制系统 ...

2011

0.0

... 引理1^[12] 如果h(t)有界,则估计状态也有界,且存在常数#cod#x003c3 ...

0.0

... 因此,根据输入到状态稳定性定理^[13],误差系统状态#cod#x003c9 ...