基于齿条近似法的谐波传动空间齿廓设计方法

引用本文

王家序, 袁攀, 谭春林, 何永强, 李俊阳, 肖科. 基于齿条近似法的谐波传动空间齿廓设计方法. 2017, 47(4): 1121-1129
WANG Jia-xu, YUAN Pan, TAN Chun-lin, HE Yong-qiang, LI Jun-yang, XIAO Ke. Spatial tooth profile design of harmonic drive by rack approximation method. Journal of Jilin University Engineering and Technology Edition, 2017, 47(4): 1121-1129 复制到剪切板

Permissions

基于齿条近似法的谐波传动空间齿廓设计方法

王家序¹, 袁攀¹, 谭春林², 何永强², 李俊阳¹, 肖科¹

1.重庆大学机械传动国家重点实验室, 重庆 400044

2.北京空间飞行器总体设计部,北京 100094

作者简介:王家序(1954-),男,教授,博士生导师.研究方向:机器人驱动机构.E-mail:jxwang@cqu.edu.cn

基金:“973”国家重点基础研究发展计划项目(2013CB733000); “863”国家高技术研究发展计划项目(2015AA043001).

摘要

针对渐开线谐波传动齿廓设计中啮合侧隙过大造成传动精度降低以及柔轮轴向偏斜产生齿廓干涉等问题,提出一种基于齿条近似法的谐波传动齿廓设计方法。该方法考虑了实际啮合情况,利用齿条近似法对柔轮齿相对于刚轮齿的实际运动轨迹进行近似齿廓设计与修形。并考虑了柔轮在装配变形下的偏斜,对柔轮齿在主截面以外的其他截面进行空间齿廓设计。结果表明:基于齿条近似法设计的谐波传动齿廓啮合侧隙很小并且啮合范围很广,按照线性关系改变柔轮齿根处壁厚可以实现柔轮齿在空载状态下任意截面的无干涉啮合。

关键词: 机械设计; 谐波传动; 齿条近似法; 啮合理论; 空间齿廓

中图分类号:TH132.43 文献标志码:A 文章编号:1671-5497(2017)04-1121-09

Spatial tooth profile design of harmonic drive by rack approximation method

WANG Jia-xu¹, YUAN Pan¹, TAN Chun-lin², HE Yong-qiang², LI Jun-yang¹, XIAO Ke¹

1.State Key Laboratory of Mechanical Transmissions, Chongqing University, Chongqing 400044, China

2.China Academy of Space Technology, Beijing 100094, China

Abstract

To solve the problems of transmission precision reduction caused by large meshing backslash and tooth profile interference caused by axial coning in the design of involute tooth profile of harmonic drive, a tooth profile new design method of harmonic drive based on rack approximation method was presented. The method considers the actual meshing situation and takes advantage of rack approximation design to design and correct the approximate tooth profile based on the actual movement route of flexspline relative to circular spline. The flexspline coning caused by assembly deformation is also considered to design the spatial tooth profile of flexspline at sections other than the main section. Results show that the tooth profile of harmonic drive designed by the proposed method has very small backslash and very wide-range meshing. Non-interfering engagement at arbitrary section can be achieved under no-load condition by changing the thickness of the tooth bottom rim of flexspline based on linear relationship.

Keyword: mechanical design; harmonic drive; rack approximation method; engagement theory; spatial tooth profile

Show Figures

0 引言

在啮合理论方面, 主要有图解分析法、等速曲线法、幂级数法、包络法和改进运动学法^[1], 但是前3种方法在理论及实际中都存在一定的缺陷^[2], 因而应用得很少。包络法和改进运动学法^[3]是当前研究谐波传动齿廓广泛采用的方法, 但是利用这两种方法只能获得共轭齿廓的数值解^[4], 不能获得共轭齿廓的精确解析表达式。在谐波传动齿廓研究方面^{[5, 6]}, 主要出现过如下几种齿廓:直线齿廓、渐开线齿廓、圆弧齿廓以及S型齿廓。直线齿廓是谐波传动发明人Musser提出的, 但是该齿形没有考虑柔轮弹性变形引起的周向位移和法线转角^[1]。渐开线齿廓由于在加工工艺上易于实现而得到最广泛的应用, 其齿廓参数研究已比较成熟, 但是渐开线齿廓的共轭区间分布在长轴附近较小的区间内, 而且在受载变形后产生了尖点啮合, 造成受力不均匀^[2]。圆弧齿廓中的公切线双圆弧齿廓是目前国内研究最热门的齿廓齿形^{[6, 7, 8, 9]}, 主要原因是其相对于渐开线齿廓和单圆弧齿廓具有参与啮合的齿数多的优点, 不但可以改善齿根的应力状况和传动的啮合质量, 提高承载能力和扭转刚度, 而且能够缩短柔轮的轴向尺寸, 减小产品的体积和质量。虽然有上述优点, 但是双圆弧齿廓啮合侧隙不均匀, 特别是在脱离啮合前的一段啮合区内, 啮合侧隙比较大^{[9, 10]}。S型齿廓由日本学者Ishikawa等^[11]在1989年基于齿条近似法提出, 其根据曲线映射关系设计的S型齿廓可实现与同类齿廓的连续接触。基于齿条近似法, 该学者提出过很多种类型的齿廓^{[12, 13]}, 但是这些齿廓都是在假设柔轮和刚轮为无穷多齿数的情况下进行近似设计。在随后的研究中, 该学者考虑了实际运动轨迹与近似运动轨迹的不同以及柔轮齿中心线的偏转角对S型齿廓进行了齿廓修形^{[14, 15]}。在空间啮合方面, Ishikawa等^{[15, 16]}基于齿条近似法设计了不同类型的三维齿廓; 王家序等^[17]提出了双圆弧谐波传动的三维齿廓设计方法; 刘邓辉等^[18]对渐开线谐波传动的空间齿廓进行了设计。

基于此, 本文综合考虑谐波传动的弹性变形、柔轮齿偏转、轴向偏斜等因素, 根据谐波传动的运动几何关系建立了柔轮齿相对于刚轮齿的实际运动轨迹, 通过曲线映射关系求出其近似凸齿廓。考虑柔轮齿偏转角对近似凸齿廓进行齿廓修形, 并对柔轮和刚轮的凹齿廓进行了齿廓设计。最后考虑柔轮装配变形产生的轴向偏斜, 对柔轮齿进行了空间齿廓设计。

1 主截面齿廓设计与分析

1.1 柔轮与刚轮转角的关系

以波发生器回转中心 $\begin{matrix} o \end{matrix}$ 为原点、长轴为 $\begin{matrix} y \end{matrix}$ 轴, 则波发生器、柔轮、刚轮的运动几何关系如图1所示。其中各参数意义如下: $\begin{matrix} θ \end{matrix}$ 为 $\begin{matrix} o_{f} \end{matrix}$ 点矢径与长轴的夹角; $\begin{matrix} μ \end{matrix}$ 为法线转角; $\begin{matrix} r_{m} \end{matrix}$ 为未变形柔轮中性层半径; $\begin{matrix} c \end{matrix}$ 为刚轮齿槽中心线; $\begin{matrix} e \end{matrix}$ 为柔轮齿中心线; $\begin{matrix} ρ \end{matrix}$ 为 $\begin{matrix} o_{f} \end{matrix}$ 点矢径; $\begin{matrix} ξ \end{matrix}$ 为轴 $\begin{matrix} c \end{matrix}$ 与轴 $\begin{matrix} e \end{matrix}$ 的夹角; $\begin{matrix} ε \end{matrix}$ 为轴 $\begin{matrix} c \end{matrix}$ 与矢径 $\begin{matrix} ρ \end{matrix}$ 的夹角; $\begin{matrix} e \end{matrix}$ 为柔轮齿中心线; $\begin{matrix} φ \end{matrix}$ 为柔轮未变形端转角; $\begin{matrix} ϕ \end{matrix}$ 为刚轮转角; 1为柔轮齿廓; 2为刚轮齿廓。

	Figure Option View Download New Window
	图1 谐波传动模型Fig.1 Model of harmonic drive

柔轮中性层曲线采用余弦凸轮曲线时, 其极坐标系下的方程为:

$\begin{matrix} ρ = r_{m} + kmcos (2 θ) (1) \end{matrix}$

式中: $\begin{matrix} k \end{matrix}$ 为柔轮径向变形量系数; $\begin{matrix} m \end{matrix}$ 为模数。

柔轮装配变形后, 其柔轮齿法线转角为:

$\begin{matrix} μ = - \arctan (ρ' / ρ) (2) \end{matrix}$

由柔轮变形后中性层曲线不伸长的假设可得:

$\begin{matrix} r_{m} φ = \int_{0}^{θ} \sqrt[]{ρ^{2} + ρ'^{2}} dθ (3) \end{matrix}$

在整理时忽略高阶项, 取一阶近似可得:

$\begin{matrix} φ \approx θ + 0.5 kmsin (2 θ) / r_{m} (4) \end{matrix}$

根据谐波传动关系有:

$\begin{matrix} ϕ = \frac{z_{1}}{z_{2}} \times (θ + 0.5 kmsin (2 θ) / r_{m}) (5) \end{matrix}$

式中: $\begin{matrix} z_{1} \end{matrix}$ 为柔轮齿数; $\begin{matrix} z_{2} \end{matrix}$ 为刚轮齿数。

根据图1中几何关系可得:

$ε = θ - ϕ (6)$

$\begin{matrix} \begin{matrix} ξ = ε + μ (7) \end{matrix} \end{matrix}$

1.2 谐波传动齿廓设计

1.2.1 齿条近似法原理

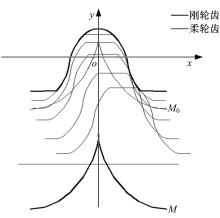
齿条近似法^[12]是在假设谐波传动齿数为无穷多情况下的近似齿廓设计方法, 此时柔轮齿相对于刚轮齿沿着运动轨迹作平移运动。图2为齿条近似法原理图, 图中曲线 $\begin{matrix} AB \end{matrix}$ 为柔轮齿顶相对于刚轮的齿条近似运动轨迹。将 $\begin{matrix} B \end{matrix}$ 点(刚轮齿顶点)作为曲线映射的基点, 以0.5倍的比例关系进行相似坐标变换, 得到新的曲线BC, 曲线BC为刚轮凸齿廓。以 $\begin{matrix} C \end{matrix}$ 为基点将曲线 $\begin{matrix} BC \end{matrix}$ 旋转180° 得到曲线AC, 曲线AC为柔轮凸齿廓。当柔轮齿相对于刚轮齿沿着运动轨迹移动时, 由于曲线的相似映射关系, 曲线AC将和曲线BC保持连续接触, 也就是柔轮凸齿廓相对于刚轮凸齿廓始终保持连续接触, 从而实现了柔轮齿和刚轮齿的连续啮合。

	Figure Option View Download New Window
	图2 近似法原理图Fig.2 Schematic diagram of approximation method

1.2.2 近似齿廓

以刚轮的齿槽中心线为 $\begin{matrix} y \end{matrix}$ 轴, 以刚轮的分度圆切线为 $\begin{matrix} x \end{matrix}$ 轴建立坐标系o-xy。如果以图1中柔轮中性层曲线上的点 $\begin{matrix} o_{f} \end{matrix}$ 为研究对象, 则该点在坐标系 $\begin{matrix} o - xy \end{matrix}$ 中的表达式为:

$\begin{matrix} \{\begin{matrix} x = ρsinε \\ y = ρcosε - 0.5 m z_{2} \end{matrix} (8) \end{matrix}$

以极角 $\begin{matrix} θ \end{matrix}$ 为自变量, 将式(1)(6)带入式(8)即可得柔轮中性层上的点 $\begin{matrix} o_{f} \end{matrix}$ 相对于刚轮分度圆的运动轨迹。图3为齿条近似情况下的运动轨迹图, 图中轨迹 $\begin{matrix} M \end{matrix}$ 为由式(8)得到的实际运动轨迹, 曲线 $\begin{matrix} M_{0} \end{matrix}$ 为齿条近似情况下, 柔轮齿顶中点相对于刚轮分度圆的运动轨迹。由齿条近似法原理可知, 此时柔轮齿相对于刚轮齿沿着运动轨迹作平移运动, 所以运动轨迹 $\begin{matrix} M_{0} \end{matrix}$ 和运动轨迹 $\begin{matrix} M \end{matrix}$ 形状相同但轴向位置不同。

	Figure Option View Download New Window
	图3 运动轨迹Fig.3 Movement locus

因为运动轨迹M和运动轨迹M₀只是 $\begin{matrix} y \end{matrix}$ 轴的轴向位置不同, 所以运动轨迹 $\begin{matrix} M_{0} \end{matrix}$ 可以表达为:

$\begin{matrix} \{\begin{matrix} x_{0} = ρsinε \\ y_{0} = ρcosε - 0.5 m z_{2} + h \end{matrix} (9) \end{matrix}$

式中: $\begin{matrix} h = (h_{a}^{*} + h_{f}^{*}) m + t / 2 \end{matrix}$ , 其中 $h_{a}^{*}$ 为柔轮齿顶高系数; $\begin{matrix} h_{f}^{*} \end{matrix}$ 为齿根高系数; $\begin{matrix} t \end{matrix}$ 为柔轮齿根处壁厚。

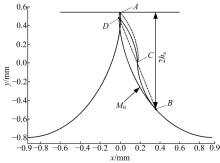
图4为基于齿条近似法得到的运动轨迹 $\begin{matrix} M_{0} \end{matrix}$ 与近似齿廓的关系图, 由图可知, 当径向变形量系数 $\begin{matrix} k = 1 \end{matrix}$ 时, 运动轨迹 $\begin{matrix} M_{0} \end{matrix}$ 实际上为正偏离轨迹, 所以近似齿廓的运动轨迹不能包括轨迹 $\begin{matrix} AD \end{matrix}$ 段, 否则考虑柔轮齿倾斜角后, 柔轮和刚轮的凸齿廓在AD段运动时会产生干涉。图4中A点、B点和D点均为运动轨迹M₀上的点, 其中A点为运动轨迹的顶点, 设其坐标为(x_A, y_A), B点到A点的垂直距离为两倍齿顶高, 设其坐标为(x_B, y_B), D点为轨迹 $\begin{matrix} M_{0} \end{matrix}$ 在斜率倒数为零时的点。根据齿条近似法原理, 可以求得 $\begin{matrix} θ_{D} \leq θ \leq θ_{B} \end{matrix}$ 下时刚轮近似凸齿廓为:

$\begin{matrix} \{\begin{matrix} x_{c} = x_{B} - 0.5 (x_{B} - x_{0}) + χ + τ \\ y_{c} = y_{b} - 0.5 (y_{B} - y_{0}) \end{matrix} (10) \end{matrix}$

	Figure Option View Download New Window
	图4 运动轨迹与近似齿廓的关系图Fig.4 Approximate tooth profile context diagram

$\begin{matrix} θ_{D} \leq θ \leq θ_{B} \end{matrix}$ 下柔轮的近似凸齿廓为:

$\begin{matrix} \{\begin{matrix} x_{f} = x_{A} + 0.5 (x_{B} - x_{0}) - χ + τ \\ y_{f} = y_{A} + 0.5 (y_{B} - y_{0}) \end{matrix} (11) \end{matrix}$

式中:τ =0.5π m/(1+k)-x_B/2, 其中k为齿厚比; $\begin{matrix} χ \end{matrix}$ 为侧隙控制量; θ _D为D点所对应的角度θ ; θ _B为B点所对应的角度 $\begin{matrix} θ 。 \end{matrix}$

1.2.3 近似齿廓修形

因为在用齿条近似法求近似齿廓时, 假设柔轮和刚轮为无穷多齿, 而实际谐波减速器的齿数是有限的, 因而柔轮齿相对于刚轮齿不仅沿着运动轨迹作平移运动, 而且还有旋转运动。在考虑柔轮齿的转动后, 近似齿廓的接触点在水平和竖直方向上都产生了偏移, 要实现近似齿廓的等齿侧间隙修形十分困难, 因此采用如下的近似齿廓修形过程。

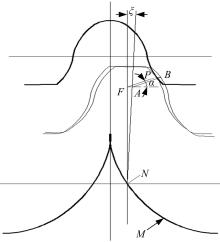
	Figure Option View Download New Window
	图5 齿廓修形原理图Fig.5 Schematic diagram of tooth profile modification

图5为考虑实际啮合情况后的齿廓修形原理图^{[14, 15]}, 由图可知, 在考虑柔轮齿的倾斜角 $\begin{matrix} ξ \end{matrix}$ 后, 柔轮和刚轮在齿厚方向产生了干涉。齿厚干涉量可以通过柔轮齿和刚轮齿的接触点 $\begin{matrix} P \end{matrix}$ 的位移来计算。图5中 $\begin{matrix} F \end{matrix}$ 点为接触点 $\begin{matrix} P \end{matrix}$ 在近似齿廓处的法线与柔轮齿中心线的交点。假设 $\begin{matrix} P \end{matrix}$ 点在倾斜角 $\begin{matrix} ξ \end{matrix}$ 的作用下产生的位移很小, 而这个位移可以分为点 $\begin{matrix} F \end{matrix}$ 在倾斜角 $\begin{matrix} ξ \end{matrix}$ 的作用下产生的在垂直于柔轮齿中心线的方向上的位移和点 $\begin{matrix} P \end{matrix}$ 在倾斜角 $\begin{matrix} ξ \end{matrix}$ 的作用下产生的在齿廓方向上的位移, 但是点 $\begin{matrix} P \end{matrix}$ 在倾斜角 $\begin{matrix} ξ \end{matrix}$ 的作用下产生的位移并不引起齿廓干涉, 因此只需考虑点 $\begin{matrix} F \end{matrix}$ 产生的位移 $\begin{matrix} FA 。 \end{matrix}$ 也就是说, 接触点 $\begin{matrix} P \end{matrix}$ 处的齿厚干涉量 $\begin{matrix} PB \end{matrix}$ 近似等于 $\begin{matrix} F \end{matrix}$ 点在倾斜角 $\begin{matrix} ξ \end{matrix}$ 作用下的位移 $\begin{matrix} FA 。 \end{matrix}$

$\begin{matrix} F \end{matrix}$ 点在倾斜角 $\begin{matrix} ξ \end{matrix}$ 作用下的位移 $\begin{matrix} d x_{1} \end{matrix}$ 取近似值, 其表达式为:

$\begin{matrix} d x_{1} \approx l_{NF} ξ (12) \end{matrix}$

式中:l_NF为直线NF的长度:

$\begin{matrix} l_{N F} = h_{f}^{*} m + t / 2 + y_{f} - x_{f} tanα (13) \end{matrix}$

式中:α =tan^-1(dx_f/dy_f), 其中α 为柔轮凸齿廓接触点P的切线与y轴的夹角。

$\begin{matrix} F \end{matrix}$ 点在倾斜角 $\begin{matrix} ξ \end{matrix}$ 作用下的位移 $\begin{matrix} d x_{1} \end{matrix}$ 也是接触点 $\begin{matrix} P \end{matrix}$ 的齿廓修形量, 但是该齿廓修形量为柔轮齿和刚轮齿在齿厚方向上总的修形量, 因此对于单个齿, 其实际修形量为 $\begin{matrix} 0.5 d x_{1} 。 \end{matrix}$ 在考虑齿廓修形量后, 即可得到无干涉的谐波传动齿廓。所以实际的齿廓表达式如下:

$\begin{matrix} θ_{D} \leq θ \leq θ_{B} \end{matrix}$ 时柔轮凸齿廓表达式:

$\begin{matrix} \{\begin{matrix} x_{fA} = x_{A} + 0.5 (x_{B} - x_{0}) - χ + τ - 0.5 d x_{1} \\ y_{fA} = y_{a} + 0.5 (y_{B} - y_{0}) \end{matrix} (14) \end{matrix}$

$\begin{matrix} θ_{D} \leq θ \leq θ_{B} \end{matrix}$ 时刚轮凸齿廓表达式:

$\begin{matrix} \{\begin{matrix} x_{cA} = x_{B} - 0.5 (x_{B} - x_{0}) + χ + τ + 0.5 d x_{1} \\ y_{cA} = y_{B} - 0.5 (y_{B} - y_{0}) \end{matrix} (15) \end{matrix}$

由齿条近似法^[12]原理可知, 柔轮凹齿廓和刚轮凹齿廓可以设计为刚轮凸齿廓和柔轮凸齿廓的相似齿廓, 但必须保证齿廓之间不干涉。本文将柔轮凹齿廓设计为刚轮凸齿廓减去间隙量 $\begin{matrix} d_{f}, \end{matrix}$ 刚轮凹齿廓设计为柔轮凸齿廓加上间隙量 $\begin{matrix} d_{c} 。 \end{matrix}$

$\begin{matrix} θ_{D} \leq θ \leq θ_{B} \end{matrix}$ 时柔轮凹齿廓表达式为:

$\begin{matrix} \{\begin{matrix} x_{fB} = x_{B} - 0.5 (x_{B} - x_{0}) + χ + \\ τ + 0.5 d x_{1} - d_{f} \\ y_{fB} = y_{B} - 0.5 (y_{B} - y_{0}) \end{matrix} (16) \end{matrix}$

$\begin{matrix} θ_{D} \leq θ \leq θ_{B} \end{matrix}$ 时刚轮凹齿廓表达式为:

$\begin{matrix} \{\begin{matrix} x_{cB} = x_{A} + 0.5 (x_{B} - x_{0}) - χ + \\ τ - 0.5 d x_{1} + d_{c} \\ y_{cB} = y_{A} + 0.5 (y_{B} - y_{0}) \end{matrix} (17) \end{matrix}$

凸齿廓和凹齿廓之间并不相接, 因此该齿廓的凸齿廓与凹齿廓之间还需要一小段过渡直线, 由柔轮齿的凸齿廓和凹齿廓端点可求得柔轮齿的过渡直线, 由刚轮齿的凸齿廓和凹齿廓端点可求得刚轮齿的过渡直线。

1.3 运动仿真分析

为了验证基于齿条近似法的谐波传动齿廓设计的合理性, 对上述方法设计的柔轮和刚轮齿廓进行Matlab运动仿真分析, 得到在90° 范围内柔轮齿相对于刚轮齿槽的运动仿真图, 如图6所示。

	Figure Option View Download New Window
	图6 运动仿真Fig.6 Motion simulation of gear tooth

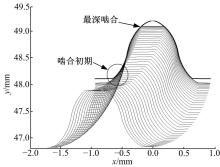
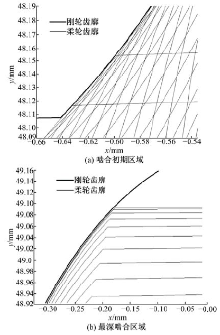
该齿廓的基本参数为:模数为0.6, 柔轮齿数为160, 刚轮齿数为162, 径向变形量系数为1, 齿顶高系数为0.82, 齿根高系数为1, 齿厚比为1.3, 侧隙控制量都为0.2 μ m, 间隙量 $\begin{matrix} d_{f} \end{matrix}$ 为3 μ m, 间隙量 $\begin{matrix} d_{c} \end{matrix}$ 为3 μ m。由图6可知, 基于齿条近似法设计的谐波传动齿廓啮合状况十分好, 齿廓之间不存在任何的干涉, 并且啮合侧隙很小。柔轮齿和刚轮齿的主要啮合区发生在柔轮凸齿廓和刚轮凸齿廓之间, 即谐波传动的主要工作齿廓为基于齿条近似法设计的柔轮凸齿廓和刚轮凸齿廓。

图7为谐波传动啮合初期区域和最深啮合区域的局部放大图。

由图7(a)可知, 在啮合初期, 刚轮凸齿廓和柔轮凸齿廓之间无齿廓干涉并且啮合侧隙十分小。结合图4可知, 当运动轨迹确定后, 柔轮和刚轮的啮合齿数实际上由齿顶高决定, 齿顶高越大, 参与啮合的齿数越多。由图7(b)可知, 在最深啮合区域, 柔轮凸齿廓与刚轮凹齿廓之间无齿廓干涉, 但此时的啮合侧隙比啮合初期的要大些。

	Figure Option View Download New Window
	图7 局部放大图Fig.7 Drawing of partial enlargement

1.4 啮合侧隙分析

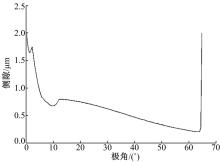
谐波传动空载啮合侧隙的大小以及分布是影响啮合力的一个重要因素, 对谐波传动的性能影响很大。啮合侧隙是评价谐波传动实际啮合性能和获得可靠啮合力的关键。图8为基于齿条近似法设计的谐波传动齿廓的啮合侧隙分布图, 图中横坐标为极角 $\begin{matrix} θ \end{matrix}$ , 以波发生器的长轴右侧为正数; 纵坐标为侧隙 $\begin{matrix} δ, \end{matrix}$ 单位为μ m。从图8可以看出, 该齿廓的最大啮合侧隙为2.1 μ m, 在波发生器长轴处; 最小啮合侧隙为0.2 μ m, 在脱离啮合处。由式(14)(15)可求得谐波传动的凸齿廓共轭区为6° ~65° 。结合图8可知, 在凸齿廓共轭区, 其啮合侧隙均匀分布在1 μ m以内。综上可知, 基于齿条近似法设计的谐波传动齿廓啮合侧隙十分小, 轮齿间侧隙分布均匀, 有利于合理分配齿间啮合力, 提高谐波传动的承载能力和传动性能。

	Figure Option View Download New Window
	图8 齿间侧隙分布Fig.8 Backlash distribution among gear tooth

2 空间齿廓设计

2.1 柔轮装配变形分析

图9为柔轮装配变形状态图, 图中截面1为后端截面, 截面2为中间截面, 截面3为前端截面。图9(a)为柔轮未变形状态图, 图9(b)为波发生器装入柔轮后在长轴截面上的变形图, 图9(c)波发生器装入柔轮后在短轴截面上的变形图。

	Figure Option View Download New Window
	图9 柔轮装配变形状态图Fig.9 Assembly deflection state diagram of flexspline

由图9可知, 柔轮在波发生器作用下, 在轴向产生了偏斜。由于该偏斜的存在, 使得柔轮在不同轴向截面有着不同的径向变形量。由图9可知, 如果设计主截面在中间截面2, 那么柔轮轮齿前端截面3的径向变形量将大于主截面2, 轮齿后端截面1的径向变形量将小于主截面2。因为前端和后端截面的径向变形量都不同, 所以柔轮齿相对于刚轮齿的运动轨迹也会发生变化。

	Figure Option View Download New Window
	图10 前端截面和后端截面运动仿真Fig.10 Motion simulation of opening cross section and end cross section

图10为考虑柔轮轴向偏斜后轮齿前端截面和后端截面的运动仿真图, 由图可知, 在主截面前端, 柔轮齿顶在长轴附近超出刚轮齿槽, 在主截面后端, 柔轮齿顶在啮合初期与刚轮齿顶产生了干涉。如果不考虑柔轮在轴向的偏斜, 那么柔轮齿和刚轮齿必定会产生干涉, 因此必须对其他截面的柔轮齿廓进行调整。

2.2 柔轮空间齿廓设计

2.2.1 轮齿径向变形量系数

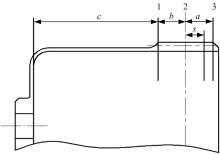
图11为柔轮轮齿的轴向位置图^[16]。图11中 $\begin{matrix} a \end{matrix}$ 表示主截面到前端截面的距离, $\begin{matrix} b \end{matrix}$ 表示主截面到后端截面的距离, $\begin{matrix} c \end{matrix}$ 表示后端截面到柔轮内壁杯底的距离, $\begin{matrix} s \end{matrix}$ 为柔轮齿在轴向的各截面到主截面的距离。

	Figure Option View Download New Window
	图11 柔轮齿轴向位置图Fig.11 Axial direction of flexspline tooth

在波发生器装入柔轮后, 柔轮在垂直于轴向的截面上发生了椭圆变形, 又因为柔轮母线在轴向只有一个固定点和一个接触点, 所以柔轮的径向变形量在轴向呈线性变化。如果主截面的径向变形量系数为1, 那么主截面到前端截面范围内的径向变形量系数可以表示为:

$\begin{matrix} k = (s + b + c \frac{)}{(} b + c) (18) \end{matrix}$

主截面到后端截面范围内的径向变形量系数可以表示为:

$\begin{matrix} k = (- s + b + c \frac{)}{(} b + c) (19) \end{matrix}$

因为 $\begin{matrix} s \end{matrix}$ 为正数, 所以前端截面范围内的系数 $\begin{matrix} k > 1, \end{matrix}$ 后端截面范围内的系数 $\begin{matrix} k < 1 。 \end{matrix}$

2.2.2 轮齿前半部分空间齿廓设计

对柔轮齿进行空间齿廓设计时, 必须保证轮齿在各个截面的齿廓形状和主截面一致, 否则柔轮齿的加工将会变得十分复杂。参考文献^[14]可知, 为了确保各截面齿廓形状和主截面形状一致而又不产生干涉, 可通过改变柔轮齿根处壁厚的方式进行空间齿廓设计。

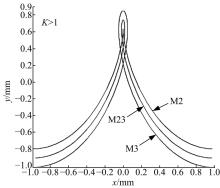
图12为轮齿前半部分3个截面的运动轨迹图。其中M2为主截面2的运动轨迹, M3为前端截面3的运动轨迹, M23为截面在 $\begin{matrix} s = 0.5 a \end{matrix}$ 时的运动轨迹。由图12可知, 长轴附近的前端截面运动轨迹均在其余截面运动轨迹外侧, 远离长轴的其余部分运动轨迹都在主截面的运动轨迹下方。

	Figure Option View Download New Window
	图12 柔轮齿前半部分运动轨迹图Fig.12 Movement route of flexspline tooth front half section

因为柔轮凸齿廓的表示式十分复杂, 所以要通过该表达式求解其包络线基本不可能。本文将柔轮凸齿廓进行单侧逼近圆弧拟合得到凸齿廓的近似圆弧齿廓, 利用包络理论求解近似圆弧齿廓的包络线, 得到如图13所示的柔轮齿根处壁厚改变前、后的近似凸齿廓包络线和刚轮凹齿廓的关系。

由图13可知, 通过改变柔轮齿根处壁厚的方式得到的前端截面柔轮近似圆弧凸齿廓包络线在刚轮齿廓内侧, 并且按照线性关系改变轮齿前半部分中间截面壁厚后得到的包络线也在刚轮齿廓内侧。因此, 先通过包络法确定前端截面壁厚调整量, 然后再根据线性关系确定前端截面和主截面之间的各截面壁厚调整量即可得到柔轮齿前半部分的空间齿廓。

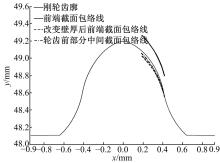	Figure Option View Download New Window
	图13 柔轮凸齿包络线和刚轮凹齿廓的关系Fig.13 Relation between envelope of flexspline convex tooth profile and circular spline concave tooth profile

假设由包络法确定的前端截面壁厚调整量为 $\begin{matrix} Δ t_{3}, \end{matrix}$ 其径向变形量系数 $\begin{matrix} k_{3}, \end{matrix}$ 则柔轮齿前半部分各截面的壁厚调整量为:

$\begin{matrix} Δ t_{23} = [(k - 1) / (k_{3} - 1)] Δ t_{3} (20) \end{matrix}$

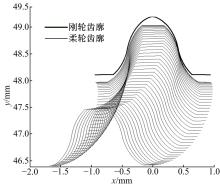图14为按照上述方法进行空间齿廓设计后得到的径向变形量系数 $\begin{matrix} k = 1.3 \end{matrix}$ 的前端截面齿廓运动仿真图。由图14可知, 改变壁厚后柔轮齿廓和刚轮齿廓不再存在干涉。

	Figure Option View Download New Window
	图14 改变壁厚后前端截面运动仿真图Fig.14 Motion simulation of flexspline tooth opening cross section after shift thickness of tooth bottom rim

2.2.3 轮齿后半部分空间齿廓设计

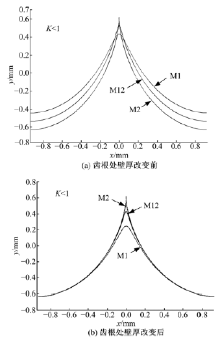
图15为柔轮齿后半部分在改变齿根处壁厚前后的运动轨迹图。其中M1为后端截面1的运动轨迹, M12为截面在 $\begin{matrix} s = - 0.5 a \end{matrix}$ 时的运动轨迹。

	Figure Option View Download New Window
	图15 轮齿后半部分运动轨迹图Fig.15 Movement route of flexspline tooth end half section

由图15可知, 按照一定关系改变齿根处壁厚后, 柔轮齿后半部各截面的运动轨迹都在主截面运动轨迹内侧, 并且这些运动轨迹在最低处相切。由1.2.3节可知柔轮齿沿着运动轨迹平动和转动, 而柔轮齿后半部分各截面的运动轨迹在改变壁厚后都在主截面的运动轨迹以下, 所以在改变壁厚后, 柔轮齿和刚轮齿将不再产生干涉。

轮齿后半部分的齿廓设计方法为使柔轮齿根处壁厚调整量等于径向变形量变化量, 即:

$\begin{matrix} Δ t_{12} = (1 - k) m (21) \end{matrix}$

图16为按照上述方法进行空间齿廓设计后得到的径向变形量系数 $\begin{matrix} k = 0.7 \end{matrix}$ 的后端截面齿廓运动仿真图。由图16可知, 按照上述方式改变齿根处壁厚后, 柔轮齿廓和刚轮齿廓不再产生干涉。

	Figure Option View Download New Window
	图16 改变壁厚后后端截面运动仿真图Fig.16 Motion simulation of flexspline tooth end cross section after shift thickness of tooth bottom rim

图17为按照上述方式设计的空间齿廓。其中虚线为壁厚改变前的齿廓线, 实线为壁厚改变后的齿廓线。

	Figure Option View Download New Window
	图17 空间齿廓Fig.17 Spatial tooth profile

3 结论

(1)本文提出的基于齿条近似法的谐波传动齿廓设计与传统的包络啮合理论齿廓设计有很大的区别。与包络理论通过已知柔轮齿廓求共轭齿廓的数值解不同, 本文方法可以根据运动轨迹确定柔轮和刚轮的齿廓表达式。

(2)谐波传动的主要工作齿廓实际上为柔轮凸齿廓和刚轮凸齿廓。基于齿条近似法设计的谐波传动齿廓啮合侧隙很小, 在凸齿廓共轭区, 其啮合侧隙均匀分布在1 μ m以内。齿顶高是影响谐波传动齿廓啮合范围的重要因素, 柔轮齿顶高越大, 同时参与啮合的齿数越多。

(3)因为柔轮在轴向存在偏斜, 其在主截面以外的其他截面径向变形量不同, 所以在其他截面存在干涉。考虑柔轮轴向偏斜产生的干涉, 对柔轮齿进行空间齿廓设计。保证其他截面的齿廓形状和主截面齿廓形状一致, 按照线性关系改变柔轮齿根处壁厚, 那么在空载状态下主截面以外的其他截面的齿廓也可以实现无干涉啮合。

The authors have declared that no competing interests exist.

参考文献

View Option

[1]	Musser C W. Strain wave gearing[P]. United State Patent: 2906143, 1959-09-29. [本文引用:2]
[2]	沈允文, 叶庆泰. 谐波齿轮传动的理论和设计[M]. 北京: 机械工业出版社, 1985. [本文引用:2]
[3]	辛洪兵. 研究谐波齿轮传动啮合原理的一种新方法[J]. 中国机械工程, 2002, 13(3): 181-183. Xin Hong-bing. A new method for research on engagement principle of harmonic drive[J]. China Mechanical Engineering, 2002, 13(3): 181-183. [本文引用:1]
[4]	范元勋, 王华坤, 宋德锋. 谐波齿轮传动共轭齿廓的计算机数值模拟研究[J]. 南京理工大学学报: 自然科学版, 2002, 26(4): 389-392. Fan Yuan-xun, Wang Hua-kun, Song De-feng. Research on computer simulation for conjugate tooth profiles of the harmonic drive[J]. Journal of Nanjing University of Science and Technology(Nature Science), 2002, 26(4): 389-392. [本文引用:1]
[5]	沈允文. 论谐波齿轮传动的齿形[J]. 齿轮, 1986, 10(4): 51-56. Shen yun-wen. Research on tooth profile of harmonic gear drive[J]. Journal of Gear, 1986, 10(4): 51-56. [本文引用:1]
[6]	辛洪兵. 双圆弧谐波齿轮传动基本齿廓设计[J]. 中国机械工程, 2011, 22(6): 656-662. Xin hong-bing. Design for basic rack of harmonic drive with double-circular-arc tooth profile[J]. China Mechanical Engineering. 2011, 22(6): 656-662. [本文引用:2]
[7]	王家序, 周祥祥, 李俊阳, 等. 不同共轭原理的双圆弧齿廓谐波齿轮传动分析[J]. 四川大学学报: 工程科学版, 2015, 47(5): 160-166. Wang Jia-xu, Zhou Xiang-xiang, Li Jun-yang, et al. The double-cir-cular-arc tooth profile of harmonic drive analysis based on different conjugate principle[J]. Journal of Sichuan University(Engineering Science Edition), 2015, 47(5): 160-166. [本文引用:1]
[8]	吴伟国, 于鹏飞, 侯月阳, 等. 短筒柔轮谐波齿轮传动新设计新工艺与实验[J]. 哈尔滨工业大学学报, 2014, 46(1): 40-46. Wu Wei-guo, Yu Peng-fei, Hou Yue-yang, et al. New design, new process of harmonic drive with short flexspline and its experiment[J]. Journal of Harbin Institute of Technology, 2014, 46(1): 40-46. [本文引用:1]
[9]	Chen X X, Liu Y S, Xing J Z, et al. The parametric design of double-circular-arc tooth profile and its influence on the functional backlash of harmonic drive[J]. Mechanism and Machine Theory, 2014, 73: 1-24. [本文引用:2]
[10]	陈晓霞, 林树忠, 邢静忠, 等. 圆弧齿廓谐波齿轮侧隙及干涉检查仿真[J]. 计算机集成制造系统, 2011, 17(3): 643-648. Chen Xiao-xia, Lin shu-zhong, Xing Jing-zhong, et al. Simulation on gear backlash and interference check of harmonic drive with circular-arc teeth profile[J]. Computer Integrated Manufacturing Systems, 2011, 17(3): 643-648. [本文引用:1]
[11]	Ishikawa Shoichi, Kanagawa Yokohama. Tooth profile of spline of strain wave[P]. United State Patent: 4823638, 1989-04-25. [本文引用:1]
[12]	Ishikawa Shoichi, Kanagawa Yokohama, Kiyosawa Yoshihide, et al. Flexible meshing gearing having three-dimensional, non-interactive wide-area intermeshing tooth profile[P]. United State Patent: 5458023, 1995-10-17. [本文引用:3]
[13]	Ishikawa Shoichi, Kanagawa Yokohama, Takizawa Noboru, et al. Wave gear drive with continuous meshing, high ratcheting torque tooth profile[P]. United State Patent: 7694607 B2, 2010-04-13. [本文引用:1]
[14]	Ishikawa Shoichi, Kanagawa Yokohama. Strain wave gearing having a non-interfering wide mesh range tooth profile[P]. United State Patent: 5918508, 1999-07-06. [本文引用:3]
[15]	Ishikawa Shoichi, Kanagawa Yokohama. Flexible meshing type gearing having three-dimensional, non-interactive wide-area intermeshing tooth profile[P]. United State Patent: 6167783 B1, 2001-01-02. [本文引用:3]
[16]	Ishikawa Shoichi, Kanagawa Yokohama. Wave gear device having three-dimensionally contactable shifted tooth profile[P]. United State Patent: 8776638 B2, 2014-07-15. [本文引用:2]
[17]	王家序, 周祥祥, 李俊阳, 等. 杯形柔轮谐波传动三维双圆弧齿廓设计[J]. 浙江大学学报: 工学版, 2016, 50(4): 616-624. Wang Jia-xu, Zhou Xiang-xiang, Li Jun-yang, et al. Three dimensional profile design of cup harmonic drive with double-circular-arc common-tangent tooth profile[J]. Journal of Zhejiang University (Engineering Science), 2016, 50(4): 616-624. [本文引用:1]
[18]	刘邓辉, 邢静忠, 陈晓霞. 渐开线谐波齿轮空间齿廓设计及仿真分析[J]. 计算机集成制造系统, 2015(3): 709-715. Liu Deng-hui, Xing Jing-zhong, Chen Xiao-xia. Spatial tooth profile design and simulation analysis of harmonic drive with involute tooth profile[J]. Computer Integrated Manufacturing Systems, 2015(3): 709-715. [本文引用:1]

1959

0.0

... 0 引言在啮合理论方面,主要有图解分析法、等速曲线法、幂级数法、包络法和改进运动学法^[1],但是前3种方法在理论及实际中都存在一定的缺陷^[2],因而应用得很少 ...

... 直线齿廓是谐波传动发明人Musser提出的,但是该齿形没有考虑柔轮弹性变形引起的周向位移和法线转角^[1] ...

1985

0.0

... 渐开线齿廓由于在加工工艺上易于实现而得到最广泛的应用,其齿廓参数研究已比较成熟,但是渐开线齿廓的共轭区间分布在长轴附近较小的区间内,而且在受载变形后产生了尖点啮合,造成受力不均匀^[2] ...

2002

0.0

... 包络法和改进运动学法^[3]是当前研究谐波传动齿廓广泛采用的方法,但是利用这两种方法只能获得共轭齿廓的数值解^[4],不能获得共轭齿廓的精确解析表达式 ...

2002

0.0

1986

0.0

... 在谐波传动齿廓研究方面^[5,6],主要出现过如下几种齿廓:直线齿廓、渐开线齿廓、圆弧齿廓以及S型齿廓 ...

2011

0.0

. 2011, 22(6):656-662

Design for basic rack of harmonic drive with double-circular-arc tooth profile

双圆弧谐波齿轮传动基本齿廓设计

Xin hong-bing

辛洪兵

North China Electric Power University,Baoding,Hebei,071003

According to the fluctuating factors of the target components’ structural parameters and the interval characterization of the material properties, this paper adopted reliability analysis and structural optimization method, and analyzed the control parameters, material strength and load distribution considering uncertainty of structural parameters of the target components.The reliability index with structural failure probability was constructed by using non-probabilistic interval reliability analysis. And combined with N-dimensional complex optimal algorithm with interval constraints, the optimal results were obtained. To billet slings clamp plate, for example, this method was proved to be practical and effective. And it is a new way of the reliability-based design.

根据影响目标零件结构参数变化因素以及材料性能参数的区间特性，采用可靠性分析技术与结构优化方法，对目标零件结构的控制参数、材料强度及载荷分布等参量的不确定性进行分析，通过对非概率区间可靠性进行分析，构造出结构失效概率度量的可靠性指标，结合区间约束的n维复形调优算法，获得了结构参数的最优结果。以钢坯吊具钳板为例，验证了该方法的实用性和有效性。该方法为基于可靠性的产品设计提供了新的途径。

... 在谐波传动齿廓研究方面^[5,6],主要出现过如下几种齿廓:直线齿廓、渐开线齿廓、圆弧齿廓以及S型齿廓 ...

... 圆弧齿廓中的公切线双圆弧齿廓是目前国内研究最热门的齿廓齿形^[6,7,8,9],主要原因是其相对于渐开线齿廓和单圆弧齿廓具有参与啮合的齿数多的优点,不但可以改善齿根的应力状况和传动的啮合质量,提高承载能力和扭转刚度,而且能够缩短柔轮的轴向尺寸,减小产品的体积和质量 ...

2015

0.0

2014

0.0

2014

0.0

... 虽然有上述优点,但是双圆弧齿廓啮合侧隙不均匀,特别是在脱离啮合前的一段啮合区内,啮合侧隙比较大^[9,10] ...

2011

0.0

... 虽然有上述优点,但是双圆弧齿廓啮合侧隙不均匀,特别是在脱离啮合前的一段啮合区内,啮合侧隙比较大^[9,10] ...

1989

0.0

... S型齿廓由日本学者Ishikawa等^[11]在1989年基于齿条近似法提出,其根据曲线映射关系设计的S型齿廓可实现与同类齿廓的连续接触 ...

1995

0.0

... 基于齿条近似法,该学者提出过很多种类型的齿廓^[12,13],但是这些齿廓都是在假设柔轮和刚轮为无穷多齿数的情况下进行近似设计 ...

... 齿条近似法^[12]是在假设谐波传动齿数为无穷多情况下的近似齿廓设计方法,此时柔轮齿相对于刚轮齿沿着运动轨迹作平移运动 ...

... 由齿条近似法^[12]原理可知,柔轮凹齿廓和刚轮凹齿廓可以设计为刚轮凸齿廓和柔轮凸齿廓的相似齿廓,但必须保证齿廓之间不干涉 ...

2010

0.0

... 基于齿条近似法,该学者提出过很多种类型的齿廓^[12,13],但是这些齿廓都是在假设柔轮和刚轮为无穷多齿数的情况下进行近似设计 ...

1999

0.0

... 在随后的研究中,该学者考虑了实际运动轨迹与近似运动轨迹的不同以及柔轮齿中心线的偏转角对S型齿廓进行了齿廓修形^[14,15] ...

... 图5为考虑实际啮合情况后的齿廓修形原理图^[14,15],由图可知,在考虑柔轮齿的倾斜角 ξ后,柔轮和刚轮在齿厚方向产生了干涉 ...

... 参考文献^[14]可知,为了确保各截面齿廓形状和主截面形状一致而又不产生干涉,可通过改变柔轮齿根处壁厚的方式进行空间齿廓设计 ...

2001

0.0

... 在随后的研究中,该学者考虑了实际运动轨迹与近似运动轨迹的不同以及柔轮齿中心线的偏转角对S型齿廓进行了齿廓修形^[14,15] ...

... 在空间啮合方面,Ishikawa等^[15,16]基于齿条近似法设计了不同类型的三维齿廓 ...

... 图5为考虑实际啮合情况后的齿廓修形原理图^[14,15],由图可知,在考虑柔轮齿的倾斜角 ξ后,柔轮和刚轮在齿厚方向产生了干涉 ...

2014

0.0

... 在空间啮合方面,Ishikawa等^[15,16]基于齿条近似法设计了不同类型的三维齿廓 ...

... 图11为柔轮轮齿的轴向位置图^[16] ...

2016

0.0

... 王家序等^[17]提出了双圆弧谐波传动的三维齿廓设计方法 ...

2015

0.0

... 刘邓辉等^[18]对渐开线谐波传动的空间齿廓进行了设计 ...