针对大滞后系统的滞后时间削弱自抗扰控制方法

引用本文

王春阳, 辛瑞昊, 史红伟. 针对大滞后系统的滞后时间削弱自抗扰控制方法. 2017, 47(4): 1231-1237
WANG Chun-yang, XIN Rui-hao, SHI Hong-wei. Decreasing time delay auto-disturbance rejection control method for large time delay systems. Journal of Jilin University Engineering and Technology Edition, 2017, 47(4): 1231-1237 复制到剪切板

Permissions

针对大滞后系统的滞后时间削弱自抗扰控制方法

王春阳, 辛瑞昊, 史红伟

长春理工大学电子信息工程学院,长春 130022

作者简介:王春阳(1964-),女,教授,博士生导师.研究方向:复杂运动系统高精稳定控制.E-mail:wangchunyang19@cust.edu.cn

基金:吉林省发展和改革委员会项目(201410157).

摘要

针对工业中较难控制的大滞后系统,提出了一种滞后时间削弱的自抗扰控制方法,该方法首先将大滞后对象转化为小滞后对象,然后结合自抗扰控制思想对简化后的小滞后对象进行控制。本文方法解决了传统Smith预估控制等方法在被控对象模型预估不准确的情况下很难取得较好的控制效果的问题,并改善了自抗扰控制器在滞后时间较大的情况下稳定时间较长的缺点。最后将该方法与传统的PID结合Smith预估控制及自抗扰控制的控制效果进行对比。仿真结果表明,本文控制方法可以有效地改善大滞后对象的控制效果,提高了系统的动态性能和鲁棒性。

关键词: 自动控制技术; 大滞后系统; 控制理论; 自抗扰控制; 滞后时间削弱

中图分类号:TP13 文献标志码:A 文章编号:1671-5497(2017)04-1231-07

Decreasing time delay auto-disturbance rejection control method for large time delay systems

WANG Chun-yang, XIN Rui-hao, SHI Hong-wei

School of Electronic and Information Engineering, Changchun University of Science and Technology, Changchun 130022,China

Abstract

In this paper, a new method is proposed to control large time delay systems. First, the large lag time is transformed into small lag time through the decreasing time delay theory. Then, auto-disturbance rejection control theory is used in the transformed object to improve the performance of the system. The method can be used to solve the problem that traditional PID with Smith control method can not achieve better control effect on the inaccurate object model. The method also overcomes the shortcoming that the single auto-disturbance rejection controller has a long setting time. The control effect of this method is compared with the traditional PID with Smith control method and the single active disturbance rejection control method. Simulation results show that this method can achieve a better control effect for large time delay systems. It can effectively improve the dynamic performance and robustness of the system.

Keyword: automatic control technology; large time delay systems; control theory; auto-disturbance rejection control; decreasing time delay

Show Figures

0 引言

大滞后对象广泛存在于化工、石油、冶金、制药和造纸等工业生产过程中。由于时滞的存在, 当前施加到系统的控制量要经过一段时间的延时才能反映到系统输出端; 而且当系统受到干扰而引起被调量改变时, 控制器产生的控制作用不能立即对干扰产生有效的抑制作用, 因此控制系统容易产生较大的超调量和较长的调节时间^{[1, 2, 3]}。一般用滞后系统的滞后时间常数 $\begin{matrix} τ \end{matrix}$ 和积分时间常数 $\begin{matrix} T \end{matrix}$ 之比 $\begin{matrix} τ / T \end{matrix}$ 来衡量滞后对系统的影响。当 $\begin{matrix} τ / T < 0.5 \end{matrix}$ 时, 通常称该系统为一般滞后系统, 可用常规的PID等控制方法对系统进行控制; 而当 $\begin{matrix} τ / T \geq 0.5 \end{matrix}$ 时, 则称该系统为大滞后系统。随着滞后时间常数 $\begin{matrix} τ \end{matrix}$ 所占比倒的增大, 其控制难度会逐渐增大。因此, 大滞后系统被认为是一类较难控制的系统。

针对大滞后系统的研究一直是国内外众多学者关注的热点。传统的控制方法如Smith预估控制^[4]、Dahlin算法等^{[5, 6]}, 从理论上解决了大滞后系统的控制问题, 但在实际应用中仍存在较大的局限。传统的控制方法严重依赖于被控对象的模型, 当建模存在微小误差或者由于干扰而产生变化时, 就会对系统产生较大影响, 甚至造成系统不稳定。因此, 在实际工程中, 需要的是不依赖于模型的控制方法。近年来, 随着模糊控制、神经网络控制、分数阶控制等研究的深入, 有些学者将这些方法与Smith预估控制等方法相结合, 提出了一些针对大滞后系统的改进控制方法^{[7, 8, 9, 10]}。虽然有些控制方法效果不错, 但是系统的复杂程度和调试难度也会随之增大, 在实际应用中难以推广。

相比之下, 自抗扰控制技术(Auto-disturbance rejection control, ADRC)是一种不依赖于系统模型的新型控制技术, 它继承了PID控制技术“ 基于误差来消除误差” 的思想, 具有精度高、扰动抑制能力强及算法简单等优点^{[11, 12, 13, 14]}。文献[15, 16]阐述了自抗扰控制技术的基本思想, 并证明了自抗扰控制器具有良好的适应性和鲁棒性。文献[17]中首次将自抗扰控制器用于大滞后系统, 为大滞后系统的研究提供了一个新的途径。但是, 由于自抗扰控制器本身的特点, 该控制系统的稳定时间大概为滞后时间的3~4倍^[18], 严重影响了系统的动态性能。

针对这一问题, 本文提出了一种滞后时间削弱的自抗扰控制方法。首先采用滞后时间削弱方法, 将大滞后时间转化为小滞后时间。然后结合自抗扰控制方法对转化后的小滞后对象进行控制。仿真结果表明, 该方法克服了Smith预估控制等传统方法对被控对象精确模型的依赖问题, 同时解决了自抗扰控制器稳定时间长的缺点。当模型存在误差和干扰时, 本文方法可有效地对误差进行补偿, 提高系统的动态性能、鲁棒性和抗干扰能力, 较好地改善了大滞后系统的控制效果。

1 控制系统设计

1.1 系统结构

本文选择带有纯滞后的一阶惯性环节作为系统的被控对象, 该对象通常被认为是研究滞后问题的典型对象, 设被控对象的传递函数为:

$\begin{matrix} G (s) = \frac{1}{Ts + 1} e^{- τs} (1) \end{matrix}$

令1⁄( Ts+1)=G₀(s), 本文选取被控对象的积分时间常数为T=0.1, 滞后时间常数为τ =30。由于滞后时间常数与积分时间常数之比为τ /T=300, 因此, 该对象是典型的大滞后被控对象。

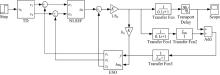
构建大滞后控制系统结构如图1所示。该控制系统包含有两部分:一部分为自抗扰控制器, 其中包括跟踪微分器(Tracking differentiator, TD)、扩张状态观测器(Extended state observer, ESO)以及非线性状态误差反馈(Nonlinear state error feedback, NLSEF); 另一部分为滞后时间削弱系统 $\begin{matrix} G_{eq} (s) 。 \end{matrix}$ 其中, $\begin{matrix} G_{0} (s) e^{- τs} \end{matrix}$ 为系统被控对象, $\begin{matrix} v (t) \end{matrix}$ 为输入量, $\begin{matrix} y (t) \end{matrix}$ 为输出量。

	Figure Option View Download New Window
	图1 系统结构框图Fig.1 System structure diagram

1.2 滞后时间削弱原理

滞后时间削弱的目的是将大时间延迟转化为小时间延迟, 以减小纯滞后时间对系统性能的影响。如图1所示, 被控对象 $\begin{matrix} G_{0} (s) e^{- τs} \end{matrix}$ 可以分为两部分:一部分为不含滞后的环节 $\begin{matrix} G_{0} (s), \end{matrix}$ 另一部分为纯滞后环节e^{-τ s} 。假设将G_p(s)串联一个常数 $\begin{matrix} L_{m}, \end{matrix}$ 然后将它们与被控对象并联, 最后在反馈中串联一个常数1⁄( L_m+1)。若G_p(s)=G₀(s), 得

$\begin{matrix} G_{eq} (s) = \frac{G_{p} (s) e^{τs} + G_{0} (s) L_{m}}{L_{m} + 1} (2) \end{matrix}$

对时滞环节 $\begin{matrix} e^{- τs} \end{matrix}$ 进行线性化处理, 采用一阶Taylor级数展开^[19], 即 $\begin{matrix} e^{- τs} \approx 1 - τs, \end{matrix}$ 可得:

$\begin{matrix} G_{eq} (s) = G_{0} (s) (1 - \frac{τs}{L_{m} + 1}) (3) \end{matrix}$

再次利用 $\begin{matrix} e^{- τs} \approx 1 - τs \end{matrix}$ 对式(3)化简, 式(3)就可以近似为:

$\begin{matrix} G_{eq} (s) = G_{0} (s) e^{- \frac{τs}{L_{m} + 1}} (4) \end{matrix}$

比较式(1)和式(4)可以看出, 等效的被控对象环节G_eq(s)的纯滞后时间是被控对象纯滞后时间的1/(L_m+1)倍^{[10, 20]}。因此大滞后被控对象被化简为了小滞后被控对象。

在对被控对象化简的理论分析中, 采用了两次Taylor近似, 相当于在被控对象模型中引入了不确定因素。由于在工业生产中, 实际被控对象与模型不一致是普遍存在的, 而且要远大于Taylor近似引入的误差, 所以这种近似具有可行性。将近似引入的误差视为系统不确定性的一部分, 其影响可以由自抗扰控制策略加以估计和补偿。

由图1可以看出, 系统的实际输出为y(t), 系统的反馈为 $y_{f} (t) = \frac{L_{m} y_{m} (t) + y (t)}{1 + L_{m}}$ 。当L_m→ 0时, y_f(t)=y(t), 为系统未加入削弱环节的输出。当L_m→ ∞ 时, y_f(t)=y_m(t), 为一阶惯性环节的输出。所以滞后时间削弱环节并非真正减小滞后时间, 而是通过减小反馈中滞后因素的加权比例来改善系统的控制性能。通过调节加权系数L_m, 修改y(t)与y_m(t)的权值, 就可以实现系统的优化。

1.3 自抗扰控制原理

由于在工程上时滞环节可以等效近似为一阶惯性环节, 因此本文采用二阶自抗扰控制器(ADRC)来控制大滞后系统, 即相当于用二阶ADRC来控制一个二阶对象。如图1所示, 图中虚框中ADRC主要由TD、ESO、NLSEF三部分组成。

TD目的是对初始信号进行预处理, 要求合理地跟踪原信号并提取其微分信号, 为系统提供一个过渡过程, 避免由信号跳变引起的激烈震荡, 可以较好地解决系统“ 快速性” 和“ 超调” 之间的矛盾, 提高了系统的鲁棒性。

TD控制率如下:

$\begin{matrix} \{\begin{matrix} k = v_{1} - v \\ f h = f h an (k, v_{2}, r_{0}, h) \\ v_{1} = v_{1} + h v_{2} \\ v_{2} = v_{2} + h f h \end{matrix} (5) \end{matrix}$

式中: $\begin{matrix} v \end{matrix}$ 为TD的输入信号; $\begin{matrix} v_{1} \end{matrix}$ 和 $\begin{matrix} v_{2} \end{matrix}$ 为输出信号, 其中, $\begin{matrix} v_{1} \end{matrix}$ 跟踪信号 $\begin{matrix} v, v_{2} \end{matrix}$ 是 $\begin{matrix} v_{1} \end{matrix}$ 的微分; TD中有两个可调参数r和h, h为采样周期, r会影响输出信号的跟踪精度和过渡过程时间, r越大过渡时间越短; 非线性函数 $\begin{matrix} f h an (v_{1}, v_{2}, r, h) \end{matrix}$ 为快速最优控制函数, 其算法如下:

$\begin{matrix} \begin{matrix} \{\begin{matrix} d = r h^{2} \\ a_{0} = h x_{2} \\ y = x_{1} + a_{0} \\ a_{1} = \sqrt[]{d (d + 8 |y|)} \\ a_{2} = a_{0} + sign (y) (a_{1} - d) / 2 \\ a = (a_{0} + y) fsg (y, d) + \\ a_{2} (1 - fsg (y, d)) \\ f h an = - r (\frac{a}{d}) fsg (a, d) - \\ rsign (a) (1 - fsg (a, d)) \end{matrix} (6) \end{matrix} \end{matrix}$

式中：

$fsg (x, d) = [sign (x + d) - sign (x - d)] / 2$

ESO是自抗扰控制技术的核心, 它将系统内部和外部的各种扰动都归结为系统的总扰动, 并将这些影响系统输出的总扰动因素扩张成新的状态变量, 并用特殊的反馈机制来消除这些扰动因素; 然后对系统状态和总扰动进行实时估计; 最终实现对扰动的补偿。

ESO控制率如下:

$\begin{matrix} \{\begin{matrix} e = z_{1} - y \\ z_{1} = z_{1} + h (z_{2} - β_{01} e) \\ z_{2} = z_{2} + h (z_{3} - β_{02} fal (e, a_{01}, δ) + b_{0} u) \\ z_{3} = z_{3} + h (- β_{03} fal (e, a_{02}, δ)) \end{matrix} (7) \end{matrix}$

式中: $\begin{matrix} fal (e, a, δ) = \{\begin{matrix} {|e|}^{a} sgne, |e| > δ \\ e / δ^{1 - a}, |e| \leq δ \end{matrix}; z_{1} 、 z_{2} \end{matrix}$ 和 $\begin{matrix} z_{3} \end{matrix}$ 为系统的输出信号, 其中 $\begin{matrix} z_{1} \end{matrix}$ 跟踪输入 $\begin{matrix} y, z_{2} \end{matrix}$ 为输出的微分, $\begin{matrix} z_{3} \end{matrix}$ 为总扰动的观测值。

三阶ESO共有7个参数, 分别为 $\begin{matrix} a_{01} 、 a_{02} 、 δ 、 b_{0} 、 β_{01} 、 β_{02} 、 β_{03} 。 \end{matrix}$ 其中参数 $\begin{matrix} a_{01} 、 a_{02} 、 δ \end{matrix}$ 是非线性函数 $\begin{matrix} fal () \end{matrix}$ 的参数; $\begin{matrix} β_{01} 、 β_{02} 、 β_{03} \end{matrix}$ 为观测器的3个状态的修正系数; $\begin{matrix} b_{0} \end{matrix}$ 为补偿因子。

NLSEF通过非线性函数把由TD产生的跟踪信号和微分信号与被控对象的状态估计量的误差进行非线性组合, 得到被控对象初步的控制量; 然后结合扩张状态观测器对系统总扰动的估计量对误差进行补偿, 得到最终的控制量, 并输入给被控对象。NLSEF控制率如下:

$\begin{matrix} u_{0} = β_{1} fal (e_{1}, α_{1}, δ_{0}) + β_{2} fal (e_{2}, α_{2}, δ_{0}) (8) \end{matrix}$

式中: $\begin{matrix} 0 < α_{1} < 1 < α_{2} 。 a_{1} 、 a_{2} 、 δ_{0} 、 β_{1} 、 β_{2} \end{matrix}$ 均为可调参数, 其中 $\begin{matrix} a_{1} 、 a_{2} 、 δ_{0} \end{matrix}$ 是非线性函数 $\begin{matrix} f a l () \end{matrix}$ 的参数; $\begin{matrix} β_{1} 、 β_{2} \end{matrix}$ 为误差状态偏差的反馈系数。

2 仿真验证

本文选取的被控对象传递函数为:

$\begin{matrix} G (s) = \frac{1}{0.1 s + 1} e^{- 30 s} \end{matrix}$

该对象为典型的一阶大滞后研究对象, 可以表示工业中大多数大滞后系统的特性。为验证本文控制方法的控制效果, 选择传统PID结合Smith预估控制和单一的自抗扰控制两种控制方法作为对比, 对3种方法的控制效果进行对比分析。

根据所提出的控制方案, 在Matlab/Simulink中搭建了图2所示的控制系统仿真模型。

	Figure Option View Download New Window
	图2 Matlab/Simulink仿真模型Fig.2 Simulation model in Matlab/Simulink

2.1 系统的单位阶跃响应

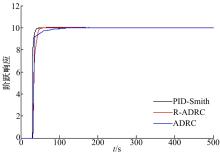
选择输入信号为阶跃信号, 信号幅值为10个单位。系统的阶跃响应如图3所示。为增加自抗扰控制器与滞后时间削弱控制器的可比性, 设定两个控制器参数基本一致。3种控制器的参数选择如下:

PID结合Smith预估控制参数为: $\begin{matrix} K_{P} = 2.5, K_{I} = 1 。 \end{matrix}$

单一的自抗扰控制器参数为:r=1.1, h=0.01, a₀₁=0.5, a₀₂=0.25, δ =0.05, b₀=88, β ₀₁=40, β ₀₂=200, β ₀₃=400, a₁=0.5, a₂=1.25, δ ₀=0.3, β ₁=25.5, β ₂=33。

滞后时间削弱自抗扰控制器参数为:r=1.02, h=0.01, a₀₁=0.5, a₀₂=0.25, δ =0.03, b₀=88, β ₀₁=40, β ₀₂=200, β ₀₃=400, a₁=0.5, a₂=1.25, δ ₀=0.3, β ₁=25.1, β ₂=32.8, L_m=3。

	Figure Option View Download New Window
	图3 系统阶跃响应Fig.3 Step response of system

由图3可知, 在被控对象模型精确的情况下, PID结合Smith预估控制效果最好, 稳定时间大约为45 s; 其次为滞后时间削弱的自抗扰控制器, 稳定时间大约为50 s; 而单一的自抗扰控制器稳定时间为110 s, 稳定时间约为滞后时间的3~4倍, 与文献[18]在被控对象一致情况下, 所得到的仿真结论一致。比较单一自抗扰控制器参数与滞后时间削弱的自抗扰控制器参数可以看出, 两种方法所采用的控制参数并没有太大的变化, 但是滞后时间削弱的自抗扰控制器取得了更好的控制效果, 稳定时间缩小了1倍以上。

2.2 被控对象发生变化时系统的阶跃响应

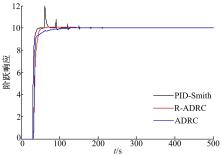
研究当被控对象模型不准确时3种控制方法的控制效果。保持3种控制器参数不变, 将被控对象积分时间常数T增大10倍, 系统阶跃响应控制效果如图4所示。

	Figure Option View Download New Window
	图4 积分时间常数T增大10倍系统的阶跃响应Fig.4 Integral time constant T increased by 10 times

与图3相比, PID结合Smith预估控制产生了严重的超调, 稳定时间也相应增大, 控制效果明显变差。而单一的自抗扰控制器与滞后时间削弱的自抗扰控制器的控制效果并未发生明显变化。

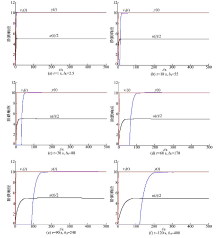
同样保持3种控制器参数不变, 在被控对象积分时间常数T增大10倍的基础上, 将滞后时间常数 $\begin{matrix} τ \end{matrix}$ 增加20%。系统的阶跃响应如图5所示。

	Figure Option View Download New Window
	图5 滞后时间常数τ 增加20%系统阶跃响应Fig.5 Delay time constant increased by 20%

从图5可以看出, PID结合Smith预估控制已经产生了明显的发散震荡, 而采用自抗扰控制理论的两种控制方法, 其控制效果仍然没有发生太大的变化, 表明采用自抗扰控制理论的两种系统具有非常高的鲁棒性, 即在模型不准确的情况下, 一旦调好了参数, 被控对象的积分时间常数与滞后时间常数在小范围变化不会太影响被控量的控制效果。

2.3 被控对象发生变化时系统的阶跃响应

针对单一的自抗扰控制器与滞后时间削弱的自抗扰控制器, 在控制器参数不变的情况下, 在250 s时再接入一个幅值为0.2的阶跃扰动。控制效果如图6所示。可见, 在系统无外扰时输出可以很快地跟踪设定值, 扰动到来时两种方法的输出偏离设定值, 然后又很快恢复。时滞越大, 偏离设定值时间越长, 但之后都能逐渐恢复过来, 且滞后时间削弱的自抗扰控制器要比单一的自抗扰控制器恢复时间短。

	Figure Option View Download New Window
	图6 扰动下系统的阶跃响应Fig.6 Unit step response with external disturbance

2.4 多种时滞下系统的控制性能

研究滞后时间削弱的自抗扰控制方法在多种时滞下系统的控制性能。保持被控对象积分时间常数 $\begin{matrix} T = 0.1 \end{matrix}$ 不变, 分别研究滞后时间常数τ =1、10、30、60、90、120 s时系统的控制效果。如图7所示, 在控制器参数保持不变的情况下, 即时滞系统参数调节好之后, 随着时滞的变大或减小, 只需要相应地增大或减小补偿因子 $\begin{matrix} b_{0} \end{matrix}$ 就可以获得良好的控制效果, 说明该控制方法对不同滞后时间的控制具有普遍性, 解决了滞后时间常数对系统性能的影响。

	Figure Option View Download New Window
	图7 多种时滞下系统的响应Fig.7 System responses with different delay time constant

3 结束语

本文针对工业中常见的大滞后系统, 提出了一种滞后时间削弱的自抗扰控制方法。该方法首先通过滞后时间削弱理论将大滞后时间转化为小滞后时间, 然后采用自抗扰控制理论对转化后的小滞后对象进行控制。仿真结果表明, 该方法有效地消除了系统大滞后环节和参数不确定等因素对系统的影响, 克服了Smith预估算法等传统控制方法严重依赖于被控对象精确模型的缺点, 并改善了单一自抗扰控制器稳定时间长的问题, 使控制系统具有更好的动态性能、鲁棒性和抗干扰性。

The authors have declared that no competing interests exist.

参考文献

View Option

[1]	马增辉, 刘长良, 开平安. 基于扰动补偿的大滞后系统的控制[J]. 信息与控制, 2013, 42(5): 570-576. Ma Zeng-hui, Liu Chang-liang, Kai Ping-an, et al. Control of dead-time systems based on disturbance compensation[J]. Information and Control, 2013, 42(5): 570-576. [本文引用:1]
[2]	Ajmeri M, Ali A. Simple tuning rules for integrating processes with large time delay[J]. Asian Journal of Control, 2015, 17(5): 2033-2040. [本文引用:1]
[3]	Narasimhulu T, Krishna B. Design of compensator of approximation of large time delay systems via reduced order model[J]. International Journal of Engineering Sciences & Research Technology, 2013, 2(8): 1934-1941. [本文引用:1]
[4]	张颖超, 叶小岭, 郭姝梅. 串级控制与Smith预估器结构融合[J]. 吉林大学学报: 工学版, 2004, 34(增刊1): 270-273. Zhang Ying-chao, Ye Xiao-ling, Guo Shu-mei. A research of serial control and Smith's predictor[J]. Journal of Jilin University(Engineering and Technology Edition), 2004, 34(Sup. 1): 270-273. [本文引用:1]
[5]	Teng F C, Ledwich G F, Tsoi A C. Extension of the Dahlin-Higham controller to multivariable systems with time delays[J]. Internation Journal of Systems Science, 1994, 25(2): 337-350. [本文引用:1]
[6]	Raja G L, Ali A. Smith predictor based parallel cascade control strategy for unstable and integrating processes with large time delay[J]. Journal of Process Control, 2017, 52: 57-65. [本文引用:1]
[7]	Lai C L, Hsu P L. Design the remote control system with the time-delay estimator and the adaptive Smith predictor[J]. IEEE Transactions on Industrial Informatics, 2010, 6(1): 73-80. [本文引用:1]
[8]	Lee K N, Yeo Y K. A new predictive PID controller for the processes with time delay[J]. Korean Journal of Chemical Engineering, 2009, 26(5): 1194-1200. [本文引用:1]
[9]	Vu T N L, Lee M. Smith predictor based fractional-order PI control for time-delay processes[J]. Korean Journal of Chemical Engineering, 2014, 31(8): 1-9. [本文引用:1]
[10]	Xin R H, Wang C Y, Liu X L, et al. Robust fractional order proportional integral control for large time-delay system[J]. Applied Mechanics & Materials, 2014, 716-717: 1614-1619. [本文引用:2]
[11]	崔宁, 陈兴林, 曹开锐, 等. 空间光通信精跟踪系统的模糊自抗扰控制[J]. 光学精密工程, 2015, 23(5): 1394-1400. Cui Ning, Chen Xing-lin, Cao Kai-rui, et al. Fuzzy active disturbance rejection control of fine tracking system for free space optical communication[J]. Optics and Precision Engineering, 2015, 23(5): 1394-1400. [本文引用:1]
[12]	魏伟, 戴明, 李嘉全, 等. 航空光电稳定平台的自抗扰控制系统[J]. 光学精密工程, 2015, 23(8): 2296-2305. Wei Wei, Dai Ming, Li Jia-quan, et al. ADRC control system for airborne opto-electronic platform[J]. Optics and Precision Engineering, 2015, 23(8): 2296-2305. [本文引用:1]
[13]	周涛. 永磁同步电机调速系统的自抗扰控制[J]. 光学精密工程, 2016, 24(3): 582-589. Zhou Tao. Active disturbance rejection control of speed governing system for PMSM[J]. Optics and Precision Engineering, 2016, 24(3): 582-589. [本文引用:1]
[14]	张明月, 杨洪波, 章家保, 等. 改进自抗扰控制谐波式电动舵机伺服系统[J]. 光学精密工程, 2014, 22(1): 99-108. Zhang Ming-yue, Yang Hong-bo, Zhang Jia-bao, et al. Servo system of harmonic drive electromechanical actuator using improved ADRC[J]. Optics and Precision Engineering, 2014, 22(1): 99-108. [本文引用:1]
[15]	韩京清. 自抗扰控制器及其应用[J]. 控制与决策, 1998, 13(1): 19-23. Han Jing-qing. Auto-disturbance-rejection controller and it's applications[J]. Control and Decision, 1998, 13(1): 19-23. [本文引用:1]
[16]	韩京清. 从PID技术到“自抗扰控制”技术[J]. 控制工程, 2002, 9(3): 13-18. Han Jing-qing. From PID technique to active disturbances rejection control technique[J]. Control Engineering of China, 2002, 9(3): 13-18. [本文引用:1]
[17]	韩京清, 张文革. 大时滞系统的自抗扰控制[J]. 控制与决策, 1999, 14(4): 354-358. Han Jing-qing, Zhang wen-ge. ADRC control for large time-delay systems[J]. Control and Decision, 1999, 14(4): 354-358. [本文引用:1]
[18]	韩京清. 时滞对象的自抗扰控制[J]. 控制工程, 2008, 15(增刊2): 7-10. Han Jing-qing. Auto-disturbances rejection control for time-delay systems[J]. Control Engineering of China, 2008, 15(Sup. 2): 7-10. [本文引用:1]
[19]	刘开培, 吕鹏刚, 黄天戍, 等. 时滞系统几种控制算法的相互关系及其近似实现[J]. 武汉大学学报: 工学版, 2002, 35(2): 83-87. Liu Kai-pei, Lv Peng-gang, Huang tian-shu, et al. Relationship between control algorithms for systems with time delay and approximated implementation[J]. Engineering Journal of Wuhan University, 2002, 35(2): 83-87. [本文引用:1]
[20]	李钟慎. 一种高鲁棒性的大滞后系统控制方法[J]. 智能控制技术, 2009, 31(2): 35-37. Li Zhong-shen. A high robustness control method for large time delay system[J]. Intelligent Control Technics, 2009, 31(2): 35-37. [本文引用:1]

2013

0.0

. 2013, 42(5):570-576 DOI:doi:10.3724/SP.J.1219.2013.00570

Control of dead-time systems based on disturbance compensation

基于扰动补偿的大滞后系统的控制

Ma Zeng-hui , Liu Chang-liang , Kai Ping-an

马增辉, 刘长良, 开平安

For the dead-time and parameter uncertainties, a new improvement program of Smith prediction control system is presented based on the deduced parameter changes disturbance compensation formula of second-order system. Deadtime system control problem is effectively solved by this proposed method even in case that the mathematical model is unknown. The method includes simple structure and less tuning parameters, and it allows adjustment and realization easily.The simulation results show that this method has better adaptive capacity and robustness.

针对系统的大滞后和参数不确定性，依据推导出的二阶系统参数变化扰动补偿公式，提出了一种新的Smith预估控制系统的改进方案．即使在未知被控对象数学模型的情况下，该方案也可以很好地解决大滞后系统的控制问题．本文提出的方法结构简单，可调参数少，易于调整和实现．仿真实验证明，该方法具有更好的自适应能力和鲁棒性能．

... 而且当系统受到干扰而引起被调量改变时,控制器产生的控制作用不能立即对干扰产生有效的抑制作用,因此控制系统容易产生较大的超调量和较长的调节时间^[1,2,3] ...

2015

0.0

2013

0.0

2004

0.0

. 2004, 34(增刊1):270-273

A research of serial control and Smith's predictor

串级控制与Smith预估器结构融合

Zhang Ying-chao , Ye Xiao-ling , Guo Shu-mei.

张颖超, 叶小岭, 郭姝梅

对串级控制系统来说,一个快速内回路是至关重要的.当副回路存在较大纯滞后时,系统控制品质会很差.Smith预估器是用于解决大纯滞后对象的有效方法.本文提出了串级控制与Smith预估补偿相结合的控制策略.针对纯滞后问题,讨论了串级控制与Smith补偿的互补性.从理论和仿真两个方面讨论了这种系统相结合的可行性和应用价值.仿真结果的表明,这种控制系统抗二次干扰的能力大大提高,其鲁棒稳定性和动态品质均优于单纯的Smith预估补偿控制和单纯的串级控制.

... 传统的控制方法如Smith预估控制^[4]、Dahlin算法等^[5,6],从理论上解决了大滞后系统的控制问题,但在实际应用中仍存在较大的局限 ...

1994

0.0

... 传统的控制方法如Smith预估控制^[4]、Dahlin算法等^[5,6],从理论上解决了大滞后系统的控制问题,但在实际应用中仍存在较大的局限 ...

2017

0.0

... 传统的控制方法如Smith预估控制^[4]、Dahlin算法等^[5,6],从理论上解决了大滞后系统的控制问题,但在实际应用中仍存在较大的局限 ...

2010

0.0

... 近年来,随着模糊控制、神经网络控制、分数阶控制等研究的深入,有些学者将这些方法与Smith预估控制等方法相结合,提出了一些针对大滞后系统的改进控制方法^[7,8,9,10] ...

2009

0.0

2014

0.0

2014

0.0

... 比较式(1)和式(4)可以看出,等效的被控对象环节G_eq(s)的纯滞后时间是被控对象纯滞后时间的1/(L_m+1)倍^[10,20] ...

2015

0.0

. 2015, 23(5):1394-1400 DOI:doi:10.3788/OPE.20152305.1394

Fuzzy active disturbance rejection control of fine tracking system for free space optical communication

空间光通信精跟踪系统的模糊自抗扰控制

Cui Ning , Chen Xing-lin , Cao Kai-rui

崔宁, 陈兴林, 曹开锐

摘　要：针对输入光束抖动及卫星本体微振动对空间光通信系统跟踪精度的影响,设计了模糊自抗扰控制器,提出了对精跟踪系统进行控制的方法。首先,建立了精跟踪系统模型,对系统内外扰动进行分析,并模拟了卫星振动信号。针对系统自身所受的扰动及输入光信号的不确定性,设计了模糊自抗扰控制器。提出的控制方法通过扩张状态观测器观测卫星本体振动及系统未建模动态,应用微分跟踪器提高系统动态响应性能,并用模糊控制原理改进了非线性状态误差反馈控制律,使其可以自适应调整比例和微分增益。最后进行了实验分析,结果表明：与PID控制方法相比,模糊自抗扰控制方法在不同频率及幅值的输入信号下均能提高系统跟踪精度,跟踪精度可以达到±8μrad,跟踪误差减小了50%左右。该方法基本满足空间光通信精跟踪系统对跟踪速度、跟踪精度及抗干扰能力的要求。

... 的思想,具有精度高、扰动抑制能力强及算法简单等优点^{[11,12,13,14]} ...

2015

0.0

. 2015, 23(8):2296-2305

ADRC control system for airborne opto-electronic platform

航空光电稳定平台的自抗扰控制系统

Wei Wei , Dai Ming , Li Jia-quan

魏伟, 戴明, 李嘉全

... 的思想,具有精度高、扰动抑制能力强及算法简单等优点^{[11,12,13,14]} ...

2016

0.0

... 的思想,具有精度高、扰动抑制能力强及算法简单等优点^{[11,12,13,14]} ...

2014

0.0

... 的思想,具有精度高、扰动抑制能力强及算法简单等优点^{[11,12,13,14]} ...

1998

0.0

. 1998, 13(1):19-23

Auto-disturbance-rejection controller and it's applications

自抗扰控制器及其应用

Han Jing-qing.

韩京清

摘　要：自抗扰控制器是自动检测系统的模型和外扰实时作用并予以补偿的新型控制器。介绍了自抗扰控制器对时变系统，多变量系统，最小相位系统等不同对象的使用方法。

2002

0.0

1999

0.0

. 1999, 14(4):354-358

Zhang wen-ge. ADRC control for large time-delay systems

大时滞系统的自抗扰控制

Han Jing-qing

韩京清, 张文革

2008

0.0

. 2008, 15(增刊2):7-10

Auto-disturbances rejection control for time-delay systems

时滞对象的自抗扰控制

Han Jing-qing.

韩京清

... 但是,由于自抗扰控制器本身的特点,该控制系统的稳定时间大概为滞后时间的3~4倍^[18],严重影响了系统的动态性能 ...

2002

0.0

. 2002, 35(2):83-87 DOI:doi:10.3969/j.issn.1671-8844.2002.02.020

Relationship between control algorithms for systems with time delay and approximated implementation

时滞系统几种控制算法的相互关系及其近似实现

Liu Kai-pei , Lv Peng-gang , Huang tian-shu

刘开培, 吕鹏刚, 黄天戍

讨论了时滞系统的常规PID控制、Dahlin控制、Smith控制和内模控制(IMC)之间的相互关系.证明Dahlin控制是Smith控制的一个特例,Smith控制器的参数经过适当整定可以得到与Dahlin控制完全相同的结果;证明Smith预估控制具有内模控制结构,在一定条件下可以实现内模控制算法.最后证明了Dahlin控制就是内模控制.采用Taylor逼近和Pade逼近方法对纯滞后环节进行近似处理,给出了各种算法的简化形式,这些算法都可以用工业上常用的PID控制器来近似实现.

... 对时滞环节 e-τs进行线性化处理,采用一阶Taylor级数展开^[19],即 e-τs≈1-τs,可得: ...

2009

0.0

. 2009, 31(2):35-37 DOI:doi:10.3969/j.issn.1000-3886.2009.02.013

A high robustness control method for large time delay system

一种高鲁棒性的大滞后系统控制方法

Li Zhong-shen.

李钟慎

提出一种大滞后系统的控制方法.首先引入滞后时间削弱器,将大滞后的对象演变成小滞后的对象,然后采用神经网络不完全微分PID控制器对演变后的小滞后对象进行控制.仿真结果表明,该控制方法使大滞后系统取得更好的控制效果,系统的鲁棒性高,自适应能力强,具有抗外来扰动的能力.

... 比较式(1)和式(4)可以看出,等效的被控对象环节G_eq(s)的纯滞后时间是被控对象纯滞后时间的1/(L_m+1)倍^[10,20] ...